2012年山东专升本高等数学真题答案
专升本 高等数学 2012年专升本高等数学(二)参考答案

第一部分 极限和连续同步练习题1.1参考答案一、选择题1.C2.A3. A 二、填空题4. [4,2][2,4]-- 。
5. π。
6.3cos x 。
三、解答题7.2,1,tan ,12y u u v v w z z x ==+==-。
8.222112111()1()2()1()()21xf x f x x x x x x =++=++→=++。
同步练习题1.2参考答案一、选择题1.D2.C3.D4. C5.B6.C7.C 二、填空题8.2,3 9. 1 10. 0 11. 2-三、解答题12 (1)2121230113lim lim 230332433nn n n n n n n ++→∞→∞⎛⎫+ ⎪++⎝⎭===++⎛⎫+ ⎪⎝⎭。
(2) 221...111lim lim 1...111n n n n n n a a a a b b b b b a b a →∞→∞++++---=⨯=++++---。
(3)111lim ...1335(21)(21)111111111lim 1...lim 12335(21)(21)2(21)2n n n n n n n n →∞→∞→∞⎡⎤++⎢⎥⨯⨯-+⎣⎦⎡⎤⎡⎤=-+-+-=-=⎢⎥⎢⎥-++⎣⎦⎣⎦(4)1lim[ln(1)ln]lim ln(1)ln1xx xx x x ex→+∞→+∞+-=+==。
(5)1114x xx→→→===(6)16x x→→==。
(7)22lim2x xx x→→==--(8)0001(1)11lim lim lim()112x x x x x xx x xe e e e e ex x x x---→→→------==+=+=-。
13.100lim(1)lim[(1)]nmn mnx mxx xmx mx e→→+=+=。
14. ()lim(1)lim[(1)]txt x xt tf x et tπππππ→∞→∞=+=+=,(ln3)3fπ=。
2012年普通高等学校招生全国统一考试(山东卷)数学试题 (文科) 解析版

2012年普通高等学校招生全国统一考试(山东卷)文科数学第Ⅰ卷(共60分)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.(1)若复数z 满足(2)117i(i z i -=+为虚数单位),则z 为(A)3+5i (B)3-5i (C)-3+5i (D)-3-5i 【解析】i i i i i i i i z 5352515)2)(2()2)(711(2711+=+=+-++=-+=.故选A.【答案】A (2)已知全集{0,1,2,3,4}U =,集合{1,2,3}A =,{2,4}B =,则B AC U )(为(A){1,2,4}(B){2,3,4}(C){0,2,4}(D){0,2,3,4}【解析】}4,0{=A C U ,所以}42,0{,)(=B A C U ,选C.【答案】C(3)函数1()ln(1)f x x =++(A)[2,0)(0,2]- (B)(1,0)(0,2]- (C)[2,2]-(D)(1,2]-【解析】要使函数有意义则有⎪⎩⎪⎨⎧≥-≠+>+040)1ln(012x x x ,即⎪⎩⎪⎨⎧≤≤-≠->2201x x x ,即01<<-x 或20≤<x ,选B.【答案】B(4)在某次测量中得到的A 样本数据如下:82,84,84,86,86,86,88,88,88,88.若B 样本数据恰好是A 样本数据都加2后所得数据,则A ,B 两样本的下列数字特征对应相同的是(A)众数(B)平均数(C)中位数(D)标准差【解析】设A 样本的数据为变量为X ,B 样本的数据为变量为Y ,则满足2+=X Y ,根据方差公式可得DX X D DY =+=)2(,所以方差相同,标准差也相同,选D.【答案】D(5)设命题p :函数sin 2y x =的最小正周期为2π;命题q :函数cos y x =的图象关于直线2x π=对称.则下列判断正确的是(A)p 为真(B)q ⌝为假(C)p q ∧为假(D)p q ∨为真【解析】函数x y 2sin =的周期为ππ=22,所以命题p 为假;函数x y cos =的对称轴为Z k k x ∈=,π,所以命题q 为假,所以q p ∧为假,选C.【答案】C(6)设变量,x y 满足约束条件22,24,41,x y x y x y +≥⎧⎪+≤⎨⎪-≥-⎩则目标函数3z x y =-的取值范围是(A)3[,6]2-(B)3[,1]2--(C)[1,6]-(D)3[6,]2-【解析】做出不等式所表示的区域如图,由y x z -=3得z x y -=3,平移直线x y 3=,由图象可知当直线经过点)0,2(E 时,直线z x y -=3的截距最小,此时z 最大为63=-=y x z ,当直线经过C 点时,直线截距最大,此时z 最小,由⎩⎨⎧=+-=-4214y x y x ,解得⎪⎩⎪⎨⎧==321y x ,此时233233-=-=-=y x z ,所以y x z -=3的取值范围是]6,23[-,选A.【答案】A(7)执行右面的程序框图,如果输入a =4,那么输出的n 的值为(A)2(B)3(C)4(D)5【解析】当4=a 时,第一次1,3,140====n Q P ,第二次2,7,441====n Q P ,第三次3,15,1642====n Q P ,此时Q P <不满足,输出3=n ,选B.【答案】B(8)函数2sin (09)63x y x ππ⎛⎫=-≤≤ ⎪⎝⎭的最大值与最小值之和为(A)2-(B)0(C)-1(D)1--【解析】因为90≤≤x ,所以6960ππ≤≤x ,369363πππππ-≤-≤-x ,即67363ππππ≤-≤-x ,所以当336πππ-=-x 时,最小值为3)3sin(2-=-π,当236πππ=-x 时,最大值为22sin 2=π,所以最大值与最小值之和为32-,选A.【答案】A(9)圆22(2)4x y ++=与圆22(2)(1)9x y -+-=的位置关系为(A)内切(B)相交(C)外切(D)相离【解析】两圆的圆心分别为)0,2(-,)1,2(,半径分别为2=r ,3=R 两圆的圆心距离为17)10()22(22=-+--,则r R r R +<<-17,所以两圆相交,选B.【答案】B(10)函数cos622x xx y -=-的图象大致为【解析】函数为奇函数,所以图象关于原点对称,排除A,令0=y 得06cos =x ,所以ππk x +=26,ππ612k x +=,函数零点有无穷多个,排除C,且y 轴右侧第一个零点为)0,12(π,又函数x x y --=22为增函数,当120π<<x 时,022>-=-x x y ,06cos >x ,所以函数0226cos >-=-x x x y ,排除B ,选D.【答案】D(11)已知双曲线1C :22221(0,0)x y a b a b-=>>的离心率为2.若抛物线22:2(0)C x py p =>的焦点到双曲线1C 的渐近线的距离为2,则抛物线2C 的方程为(A)23x y =(B)23x y =(C)28x y =(D)216x y=【解析】抛物线的焦点)2,0(p ,双曲线的渐近线为x a b y ±=,不妨取x a b y =,即0=-ay bx ,焦点到渐近线的距离为2222=+⨯b a p a ,即c b a ap 4422=+=,所以4p a c =双曲线的离心率为2=a c ,所以24==p a c ,所以8=p ,所以抛物线方程为y x 162=,选D.【答案】D(12)设函数1()f x x=,2()g x x bx =-+.若()y f x =的图象与()y g x =的图象有且仅有两个不同的公共点1122(,),(,)A x y B x y ,则下列判断正确的是(A)12120,0x x y y +>+>(B)12120,0x x y y +>+<(C)12120,0x x y y +<+>(D)12120,0x x y y +<+<【解析】方法一:在同一坐标系中分别画出两个函数的图象,要想满足条件,则有如图,做出点A 关于原点的对称点C,则C 点坐标为),(11y x --,由图象知,,2121y y x x >-<-即0,02121<+>+y y x x ,故答案选B.方法二:设32()1F x x bx =-+,则方程()0F x =与()()f x g x =同解,故其有且仅有两个不同零点12,x x .由()0F x '=得0x =或23x b =.这样,必须且只须(0)0F =或2()03F b =,因为(0)1F =,故必有2()03F b =由此得b =.不妨设12x x <,则223x b ==.所以21()()(F x x x x =--,比较系数得1x -=,故1x =.120x x +=>,由此知12121212110x x y y x x x x ++=+=<,故答案为B.【答案】B第Ⅱ卷(共90分)二、填空题:本大题共4小题,每小题4分,共16分.(13)如图,正方体1111ABCD A B C D -的棱长为1,E 为线段1B C 上的一点,则三棱锥1A DED -的体积为_____.【解析】以△1ADD 为底面,则易知三棱锥的高为1,故111111326V =⋅⋅⋅⋅=.【答案】61(14)右图是根据部分城市某年6月份的平均气温(单位:℃)数据得到的样本频率分布直方图,其中平均气温的范围是[20.5,26.5],样本数据的分组为[20.5,21.5),[21.5,22.5),[22.5,23.5),[23.5,24.5),[24.5,25.5),[25.5,26.5].已知样本中平均气温低于22.5℃的城市个数为11,则样本中平均气温不低于25.5℃的城市个数为____.【解析】最左边两个矩形面积之和为0.10×1+0.12×1=0.22,总城市数为11÷0.22=50,最右面矩形面积为0.18×1=0.18,50×0.18=9.【答案】9(15)若函数()(0,1)x f x a a a =>≠在[-1,2]上的最大值为4,最小值为m ,且函数()(14g x m =-在[0,)+∞上是增函数,则a =____.【解析】当1a >时,有214,a a m -==,此时12,2a m ==,此时()g x =.若01a <<,则124,a a m -==,故11,416a m ==,检验知符合题意.【答案】14(16)如图,在平面直角坐标系xOy 中,一单位圆的圆心的初始位置在(0,1),此时圆上一点P 的位置在(0,0),圆在x 轴上沿正向滚动.当圆滚动到圆心位于(2,1)时,OP 的坐标为____.【解析】因为圆心移动的距离为2,所以劣弧2=PA ,即圆心角2=∠PCA,,则22π-=∠PCA ,所以2cos )22sin(-=-=πPB ,2sin 22cos(=-=πCB ,所以2sin 22-=-=CB x p ,2cos 11-=+=PB y p ,所以)2cos 1,2sin 2(--=OP .另解:根据题意可知滚动制圆心为(2,1)时的圆的参数方程为⎩⎨⎧+=+=θθsin 1cos 2y x ,且223,2-==∠πθPCD ,则点P 的坐标为⎪⎩⎪⎨⎧-=-+=-=-+=2cos 1)223sin(12sin 2)223cos(2ππy x ,即)2cos 1,2sin 2(--=OP .【答案】)2cos 1,2sin 2(--三、解答题:本大题共6小题,共74分.(17)(本小题满分12分)在△ABC 中,内角,,A B C 所对的边分别为,,a b c ,已知sin (tan tan )tan tan B A C A C +=.(Ⅰ)求证:,,a b c 成等比数列;(Ⅱ)若1,2a c ==,求△ABC 的面积S .【答案】(17)(I)由已知得:sin (sin cos cos sin )sin sin B A C A C A C +=,sin sin()sin sin B A C A C +=,2sin sin sin B A C =,再由正弦定理可得:2b ac =,所以,,a b c 成等比数列.(II)若1,2a c ==,则22b ac ==,∴2223cos 24a cb B ac +-==,sin C =∴△ABC 的面积11sin 1222S ac B ==⨯⨯⨯.(18)(本小题满分12分)袋中有五张卡片,其中红色卡片三张,标号分别为1,2,3;蓝色卡片两张,标号分别为1,2.(Ⅰ)从以上五张卡片中任取两张,求这两张卡片颜色不同且标号之和小于4的概率;(Ⅱ)现袋中再放入一张标号为0的绿色卡片,从这六张卡片中任取两张,求这两张卡片颜色不同且标号之和小于4的概率.【答案】(18)(I)从五张卡片中任取两张的所有可能情况有如下10种:红1红2,红1红3,红1蓝1,红1蓝2,红2红3,红2蓝1,红2蓝2,红3蓝1,红3蓝2,蓝1蓝2.其中两张卡片的颜色不同且标号之和小于4的有3种情况,故所求的概率为310P =.(II)加入一张标号为0的绿色卡片后,从六张卡片中任取两张,除上面的10种情况外,多出5种情况:红1绿0,红2绿0,红3绿0,蓝1绿0,蓝2绿0,即共有15种情况,其中颜色不同且标号之和小于4的有8种情况,所以概率为815P =.(19)(本小题满分12分)如图,几何体E ABCD -是四棱锥,△ABD 为正三角形,,CB CD EC BD =⊥.(Ⅰ)求证:BE DE =;(Ⅱ)若∠120BCD =︒,M 为线段AE 的中点,求证:DM ∥平面BEC .【答案】(19)(I)设BD 中点为O ,连接OC ,OE ,则由BC CD =知,CO BD ⊥,又已知CE BD ⊥,所以BD ⊥平面OCE .所以BD OE ⊥,即OE 是BD 的垂直平分线,所以BE DE =.(II)取AB 中点N ,连接,MN DN ,∵M 是AE 的中点,∴MN ∥BE ,∵△ABD 是等边三角形,∴DN AB ⊥.由∠BCD =120°知,∠CBD =30°,所以∠ABC =60°+30°=90°,即BC AB ⊥,所以ND ∥BC ,所以平面MND ∥平面BEC ,故DM ∥平面BEC .(20)(本小题满分12分)已知等差数列{}n a 的前5项和为105,且2052a a =.(Ⅰ)求数列{}n a 的通项公式;(Ⅱ)对任意*m ∈N ,将数列{}n a 中不大于27m 的项的个数记为m b .求数列{}m b 的前m 项和m S .【答案】(I)由已知得:111510105,92(4),a d a d a d +=⎧⎨+=+⎩解得17,7a d ==,所以通项公式为7(1)77n a n n =+-⋅=.(II)由277m n a n =≤,得217m n -≤,即217m m b -=.∵211217497m k m k b b ++-==,∴{}m b 是公比为49的等比数列,∴7(149)7(491)14948m m m S -==--.(21)(本小题满分13分)如图,椭圆2222:1(0)x y M a b a b+=>>,直线x a =±和y b =±所围成的矩形ABCD 的面积为8.(Ⅰ)求椭圆M 的标准方程;(Ⅱ)设直线:()l y x m m =+∈R 与椭圆M 有两个不同的交点,,P Q l 与矩形ABCD 有两个不同的交点,S T .求||||PQ ST 的最大值及取得最大值时m 的值.【答案】(21)(I)22234c a b e a a -===……①矩形ABCD 面积为8,即228a b ⋅=……②由①②解得:2,1a b ==,∴椭圆M 的标准方程是2214x y +=.(II)222244,58440,x y x mx m y x m ⎧+=⇒++-=⎨=+⎩,设1122(,),(,)P x y Q x y ,则21212844,55m xx m x x -+=-=,由226420(44)0m m ∆=-->得m <<.||PQ=.当l 过A 点时,1m =,当l 过C 点时,1m =-.①当1m <<-时,有(1,1),(2,2),||)S m T m ST m ---+=+,||||PQ ST ==其中3t m =+,由此知当134t =,即45,(1)33t m ==-∈-时,||||PQ ST.②由对称性,可知若1m <<53m =时,||||PQ ST.③当11m -≤≤时,||ST =||||PQ ST =,由此知,当0m =时,||||PQ ST.综上可知,当53m =±和0时,||||PQ ST.(22)(本小题满分13分)已知函数ln ()(e xx k f x k +=为常数,e=2.71828…是自然对数的底数),曲线()y f x =在点(1,(1))f 处的切线与x 轴平行.(Ⅰ)求k 的值;(Ⅱ)求()f x 的单调区间;(Ⅲ)设()()g x xf x '=,其中()f x '为()f x 的导函数.证明:对任意20,()1e x g x -><+.【答案】(I)1ln ()e xx k x f x --'=,由已知,1(1)0e k f -'==,∴1k =.(II)由(I)知,1ln 1()e xx x f x --'=.设1()ln 1k x x x=--,则,即()k x 在(0,)+∞上是减函数,由(1)0k =知,当01x <<时()0k x >,从而()0f x '>,当1x >时()0k x <,从而()0f x '<.综上可知,()f x 的单调递增区间是(0,1),单调递减区间是(1,)+∞.(III)由(II)可知,当1x ≥时,()()g x xf x '=≤0<1+2e -,故只需证明2()1e g x -<+在01x <<时成立.当01x <<时,e x >1,且()0g x >,∴1ln ()1ln e xx x x g x x x x --=<--.设()1ln F x x x x =--,(0,1)x ∈,则()(ln 2)F x x '=-+,当2(0,e )x -∈时,()0F x '>,当2(e ,1)x -∈时,()0F x '<,所以当2e x -=时,()F x 取得最大值22()1e F e --=+.所以2()()1e g x F x -<≤+.综上,对任意0x >,2()1e g x -<+.。
2012年山东省普通高等教育专升本
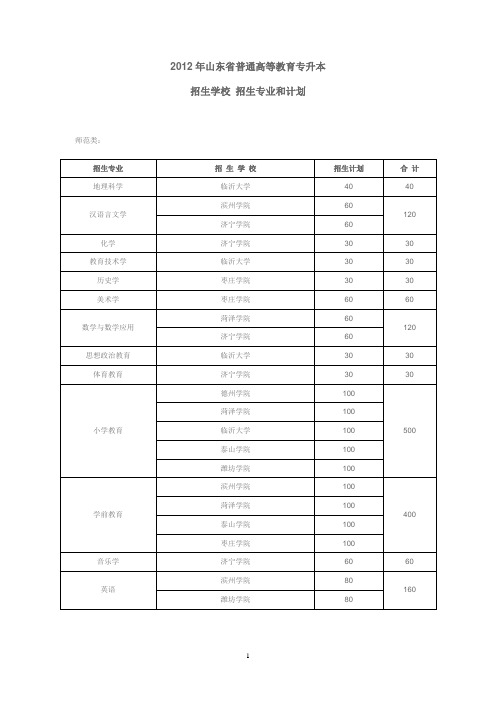
2012年山东省普通高等教育专升本招生学校招生专业和计划师范类:高职高专类:泰山学院50潍坊学院60 药学滨州医学院100 100 医学检验泰山医学院50 50 医学影像学泰山医学院50 50艺术设计滨州学院50300 菏泽学院50济宁学院50泰山学院50潍坊学院50枣庄学院50英语滨州学院80300 菏泽学院50济宁学院70山东师范大学历山学院50枣庄学院50园艺青岛农业大学海都学院40 40 针灸推拿学山东中医药大学50 50 中药学山东中医药大学50 50中医学山东中医药大学100 100 2012年山东省普通高等教育专升本各招生专业考试科目2012年山东省普通高等教育专升本各招生专业考试科目师范类:招生专业考试科目及范围高职高专类:麻醉学1. 计算机;2. 英语;3.综合一(生理学、人体解剖学、麻醉解剖学);4.综合二(外科学、临床麻醉学、重症监测)药学1. 计算机;2. 英语;3.综合一(药物化学、微生物学);4.综合二(有机化学、药物分析)医学检验1. 计算机;2. 英语;3.综合一(临床检验基础、生物化学检验);4.综合二(微生物学检验、免疫学检验)医学影像学1. 计算机;2. 英语;3.综合一(生理学、影像电子学基础);4.综合二(医学影像诊断学、医学影像设备学)针灸推拿学1. 计算机;2. 英语;3.综合一(中医基础理论、中药学);4.综合二(诊断学基础、针灸临床学)中药学1. 计算机;2. 英语;3.综合一(中医基础理论、中药鉴定学、药理学);4.综合二(中药炮制学、中药药剂学)中医学1. 计算机;2. 英语;3.综合一(中医基础理论、方剂学、中药学、);4.综合二(诊断学基础、中医内科学)动物医学1. 计算机;2. 英语;3.综合一(动物生理学、遗传学);4.综合二(内科学、外科学、传染病)2012年山东专升本考试主考学校和专业2012年山东省普通高等教育专升本考试主考学校和专业师范类主考学校主考专业山东师范大学学前教育、英语(师范类)、小学教育、音乐学、美术学、地理科学山东理工大学体育教育、汉语言文学、化学、历史学、教育技术学、思想政治教育、数学与应用数学高职高专类主考学校主考专业山东中医药大学中药学、中医学、针灸推拿学曲阜师范大学公共事业管理、市场营销山东交通学院(长清校区)交通运输、机械设计制造及其自动化山东财经大学(筹)(舜耕校金融学、工商管理区)聊城大学土木工程、旅游管理、工程管理青岛科技大学化学工程与工艺、电气工程及其自动化青岛农业大学园艺、生物科学、动物医学、朝鲜语、电子信息工程济南大学英语(高职高专类)、国际经济与贸易、服装设计与工程、电子商务德州学院会计学潍坊医学院口腔医学、护理学、药学潍坊学院日语、法学、计算机科学与技术、艺术设计泰山医学院临床医学、医学检验、医学影像学、麻醉学2012年山东省专升本计算机(公共课)考试要求2012年山东省普通高等教育专升本计算机(公共课)考试要求一、指导思想本考试大纲依据山东省教育厅《关于加强普通高校计算机基础教学的意见》(鲁教高字〔1995〕9号)中所要求的计算机教学的基本目标,根据当前山东省高校计算机文化基础课程教学的实际情况而制订。
2012年成人高考专升本高等数学一考试真题及参考答案

2012年成人高考专升本高等数学一考试真题及参考答案第一篇:2012年成人高考专升本高等数学一考试真题及参考答案2012年成人高考专升本高等数学一考试真题及参考答案一、选择题:每小题4分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求。
参考答案:A参考答案:C参考答案:D参考答案:A参考答案:B参考答案:D参考答案:C参考答案:B参考答案:A参考答案:B二、填空题:本大题共10小题。
每小题4分,共40分,将答案填在题中横线上。
第11题参考答案:0 第12题设y=sin(x+2),则Y'=_________ 参考答案:cos(x+2)第13题设y=ex-3,则dy=_________.第14题参考答案:5sinx+C 第15题第16题曲线Y=x2-x在点(1,0)处的切线斜率为_________.参考答案:1 第17题设y=x3+2,则y''=__________.参考答案:6x 第18题设z=x2-y,则dz=_________.参考答案:2xdx-dy 第19题过点M(1,2,3)且与平面2x—Y+z=0平行的平面方程为_________.参考答案:2x—y+z=3 第20题参考答案:3π三、解答题:本大翘共8个小题,共70分。
解答应写出推理,演算步骤。
第21题参考答案:第22题参考答案:第23题设函数f(x)=x-1nx,求f(x)的单调增区间.参考答案:第24题参考答案:第25题参考答案:第26题参考答案:第27题设L是曲线y=x2+3在点(1,4)处的切线。
求由该曲线,切线L及y轴围成的平面图形的面积S.参考答案:第28题参考答案:第二篇:2013年成人高考专升本高等数学一考试真题及参考答案2013年成人高考专升本高等数学一考试真题及参考答案一、选择题:每小题4分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求。
参考答案:C参考答案:A参考答案:B参考答案:D参考答案:B参考答案:A参考答案:D参考答案:B参考答案:C参考答案:A二、填空题:本大题共10小题。
12年专升本高数真题答案

2023年河南省普通高等学校选拔优秀专科毕业生进入本科阶段学习考试高等数学 解析及解析一、选择题(每小题2分,共60分)1.解析:C.【解析】:40400x x x x +≥⎧⇒≥-≠⎨≠⎩且.选C.2.解析:B.【解析】:A 、D 为非奇非偶函数,B 为偶函数,C 为奇函数。
选B.3.解析:D.【解析】:0x →时,ln(12)~2x x +.选D.4.解析:D.【解析】:0x =处没有定义,显然是间断点;又0x →时21sin x地极限不存在,故是第二类间断点。
选D.5.解析:C.【解析】:函数地定义域为(),-∞+∞,0lim lim (0)0x x f +-→→===,显然是连续地;又0(0)lim lim (0)x x f f +++-→→''===+∞=,因此在该点处不可导。
选C.6.解析:A.【解析】:易知(0)=0f ,且00()0(0)lim lim ()(0)x x x x f x xϕϕϕ+++→→-'===,00()0(0)lim lim ()(0)(0)x x x x f x f xϕϕϕ-+-+→→--''==-=-≠.故(0)f '不存在。
选A.7.解析:B.【解析】:根据复合函数求导法则可知:d ()()xxy f u du f e de ''==.选B.8.解析:B.【解析】:根据水平渐近线地求法可知:当lim ()x f x →∞=∞时,1lim0()x f x →∞=,即0y =时1()y f x =地一条水平渐近线,选B.9.解析:D.【解析】:对x x y sin 21-=两边同时求微分有:1cos 2dy dx xdx =-,所以d d x y =xcos 22-.选D.10.解析:B【解析】:易知(0)=1f ,011(0)lim 1x x f x++→+-'==,0sin 11sin (0)lim lim 1x x x xf x x---→→+-'===,故(0)1f '=.选B.11.解析:D.【解析】:令3()3f x x x c =++,则有2()330f x x '=+>,即函数在定义域内是单调递增地,故最多只有一个实根。
2012年高数专升本真题及其参考答案.

Passage four Animals seem to have the sense to eat when they are hungry and they do not eat more than their bodies need. It has been demonstrated that rats will, when given a choice over a period of time, prefer water with vitamins to water without vitamins even though there is no difference in taste or smell between the two water bottles. When a fragrant flavor was added to the vitamin-enriched fluid, the rats did seem to develop a taste for it and kept drinking it ,even after the vitamins were switched to the clear water. In time, however ,they broke the habit and went back to where the necessary vitamins were.In a classic experiment, babies of 6 to 12 months old were placed in a cafeteria feeding arrangement, with a wide selection of baby food before them. They were given whatever food they pointed to or appeared interested in. We are told that at first they showed some unusual eating patterns, but that over a period of time they managed to select well-balanced diet.So, in selecting food, rats and babies do seem to know and act on what's best for them. Apparently, there is a kind of "body wisdom,"which humans soon lose. Most of us do not eat as wisely as we could. Many of our food preferences are culturally determined and influenced by long-established habits. Some people eat fox, dog and blackbirds ,while we eat cows and pigs. So what people eat and how much they eat seems to be greatly influenced by what is going on around them.76. In the experiment on rats, a fragrant flavor was added to the rat's drinking water to___.A. encourage rats to drink vitamin-enriched water B. find out rats preference in flavor C. test whether rats know which drink is good for them D. demonstrate that vitamins are tasteless 77. The expression "the habit" (para.1, sentence 4 refers to drinking water which_________. A. has no smell B. is tasteless C. has vitamins D. is flavored 78. According to the passage ,adults eating habits differ from those of babies because_____.A. adults know better than babies what kind of food are good for their healthB. adults usually cannot resist the temptation of various delicious foodsC. adults' eating habits areclosely related to the social and cultural customs D. adults have more choices of food than babies in eating patterns 79. The author implied in the passage that most ofus_________. A. eat a balanced dietB. choose the food that is of nutritionC. have the habits influenced by the surroundingsD. like to eat the food with a fragrant flavor80. As far as their eating habits are concerned, babies and rats are similar inthat______. A. both have the wisdom to choose a balanced diet B. both prefer flavored food and drinkC. both have the same eating patternsD. both develop a taste for the same kinds of flavors Part IV. Translation . ( 30pointSection A: Directions: There are 10 sentences in this section. Please translate sentences 81-85 from Chinese into English, and translate sentences 86-90 from English into Chinese. Write your answer on the Answer Sheet.81 我们向李先生学习,因为他有丰富的工作经验。
2012年普通高等学校招生全国统一考试(山东卷)文科数学及答案
2012年普通高等学校招生全国统一考试(山东卷)数 学(供文科考生使用)锥体的体积公式:13V Sh =,其中S 是锥体的底面积,h 是锥体的高.如果事件,A B 互斥,那么()()()P A B P A P B +=+.一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.若复数z 满足()2117z i i -=+(i 为虚数单位),则z 为( )A.35i +B.35i -C.35i -+D.35i -- 2.已知全集{}0,1,2,3,4U =,集合{}{}1,2,3,2,4A B ==,则(C U A )B 为( )A.{}1,2,4B.{}2,3,4C.{}0,2,4D.{}0,2,3,43.函数()()1ln 1f x x =++( ) A.[)(]2,00,2- B.()(]1,00,2- C.[]2,2-D.(]1,2-4.在某次测量中得到的A 样本数据如下:82,84,84,86,86,86,88,88,88,88.若B 样本数据恰好是A 样本数据每个都加2后所得数据.则,A B 两样本的下列数字特征对应相同的是( )A.众数B.平均数C.中位数D.标准差5.设命题:p 函数sin 2y x =的最小正周期为π2;命题:q 函数cos y x =的图象关于直线π2x =对称.则下列判断正确的是( )A.p 为真B.q ⌝为假C.p q ∧为假D.p q ∨为真 6.设变量,x y 满足约束条件2224,41x y x y x y +≥⎧⎪+≤⎨⎪-≥-⎩则目标函数3z x y =-的取值范围是( )A.3[,6]2-B.3[,1]2--C.[1,6]-D.3[6,]2-7.执行如图的程序框图,如果输入4a =,那么输出的n 的值为( )A.2B.3C.4D.58.函数ππ2sin()(09)63x y x =-≤≤的最大值与最小值之和为( )A.2B.0C.1-D.1-- 9.圆22(2)4x y ++=与圆22(2)(1)9x y -+-=的位置关系为( )A.内切B.相交C.外切D.相离10.函数cos622x xxy -=-的图象大致为( )11.已知双曲线()22122:10,0x y C a b a b-=>>的离心率为2,若抛物线22:2(0)C x py p =>的焦点到双曲线1C 的渐近线的距离为2,则抛物线2C 的方程为( )A.2x y =B.2x y =C.28x y =D.216x y =12.设函数()()21,f x g x x bx x==-+,若()y f x =的图象与()y g x =的图象有且仅有两个不同的公共点()()1122,,,A x y B x y ,则下列判断正确的是( )A.12120,0x x y y +>+>B.12120,0x x y y +>+<C.12120,0x x y y +<+>D.12120,0x x y y +<+< 二、填空题(本大题共4小题,每小题4分,共16分) 13.如图,正方体1111ABCD A B C D -的棱长为1,E 为线段1B C 上一点,则三棱锥1A DED -的体积为________14.如图是根据部分城市某年6月份的平均气温(单位:℃)数据得到的样本频率分布直方图,其中平均气温的范围是[]20.5,26.5.样本数据的分组为[)[)[)[)[)20.5,21.5,21.5,22.5,22.5,23.5,23.5,24.5,24.5,25.5,[]25.5,26.5.已知样本中平均气温低于22.5℃的城市个数为11,则样本中平均气温不低于25.5℃的城市个数为________15.若函数()()0,1x f x a a a =>≠在[]1,2-上的最大值为4,最小值为m ,且函数()(14g x m =-[)0,+∞上是增函数,则a =________16.如图,在平面直角坐标系xOy 中,一单位圆的圆心的初始位置在()0,1,此时圆上一点P 的位置在()0,0,圆在x 轴上沿正向滚动,当圆滚动到圆心位于()2,1时,OP的坐标为________三、解答题(本大题共6小题,共74分.解答题应写出文字说明,证明过程或演算步骤.)17.(本小题12分)在ABC ∆中,内角,,A B C 所对的边分别为,,a b c ,已知()s i n t a n t a n t a n t a n B A CA C +=. (1)求证:,,a b c 成等比数列;(2)若1,2a c ==,求ABC ∆的面积S .18.(本小题12分)袋中有五张卡片,其中红色卡片三张,标号分别为1,2,3;蓝色卡片两张,标号分别为1,2.(1)从以上五张卡片中任取两张,求这两张卡片颜色不同且标号之和小于4的概率;(2)向袋中再放入一张标号为0的绿色卡片,从这六张卡片中任取两张,求这两张卡片颜色不同且标号之和小于4的概率.DCB A平均气温/︒CC 1D 1B 1A 1E D CBA19.(本小题12分)如图,几何体E ABCD -是四棱锥,ABD ∆为正三角形,,CB CD EC BD =⊥(1)求证:BE DE =;(2)若120,BCD M ∠=︒为线段AE 的中点,求证:DM 平面BEC .20.(本小题12分)已知等差数列{}n a 的前5项和为105,且1052a a =,(1)求数列{}n a 的通项公式;(2)对任意m N *∈,将数列{}n a 中不大于27m 的项的个数记为m b ,求数列{}n b 的前m 项和m S .21.(本小题13分)如图,椭圆()2222:10x y M a b a b+=>>直线x a =±和y b =±所围成的矩形ABCD 的面积为8.(1)求椭圆M 的标准方程;(2)设直线():l y x m m R =+∈与椭圆M 有两个不同的交点,,P Q l 与矩形ABCD 有两个不同的交点,S T .求||||PQ ST 的最大值及取得最大值时m 的值.22.(本小题13分)已知函数()ln xx kf x e +=(k 为常数, 2.71828e =⋅⋅⋅是自然对数的底数),曲线()yf x =在点()()1,1f 处的切线与x 轴平行.(1)求k 的值;(2)求()f x 的单调区间;(3)设()()'g x xf x =,其中()'f x 为()f x 的导函数.证明:对任意()20,1x g x e -><+.E D C B A一、 选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的。
山东省普通高等教育专升本统一考试 近三年《高等数学》真题(部分)(1)
山东省普通高等教育专升本统一考试近三年《高等数学》真题(部分)一、 选择题1、函数22712arcsin x x x y -+-=的定义域为( )【2011年真题】A 、]4,3[-B 、 )4,3(-C 、 ]2,0[D 、 )2,0(【答案】选C.2、如果级数)0(1≠∑∞=n n n u u 收敛,则必有( )【2011年真题】A 、级数∑∞=11n n u 发散 B 、级数)1(1n u n n +∑∞=收敛C 、级数∑∞=1n n u 收敛D 、级数n n n u ∑∞=-1)1(收敛【答案】选A.二、填空题:1、由方程0422=--xy y x 确定的隐函数的导数dx dy = 【2011年真题】【答案】填 x y yx 22+-.2、向量)4,1,1(=与向量)2,2,1(-=b 的夹角余弦值是 . 【2011年真题】 【答案】填1827.3、级数∑∞=n nn x !的收敛区间为_______.【2010年真题】【答案】),(+∞-∞. 【解析】收敛半径:∞=+=+==∞→∞→+∞→)1(lim !)!1(lim ||lim 1n n n a a R n n n nn ,所以,收敛区间为:),(+∞-∞.4、当26ππ≤<x 时,x xx f sin )(=是_______函数(填“单调递增”、“单调递减”)【2009年真题】【答案】单调递减 【解析】,sin cos )(2x x x x x f -='令,sin cos )(x x x x g -= ,sin cos sin cos )(x x x x x x x g -=--='当26ππ≤<x 时,0)(<'x g ,从而,,0)(<'x f 故函数)(x f 单调递减.二、计算下列各题:1、求函数)0(1>⎪⎭⎫ ⎝⎛+=x x x y x 的导数. 【2011年真题】 【解析】两边取对数,)]1ln([ln ln x x x y +-=两边对x 求导数,x x x x x x x x y y ++⎪⎭⎫ ⎝⎛+=⎥⎦⎤⎢⎣⎡+-+⎪⎭⎫ ⎝⎛+='111ln 1111ln 1 所以,⎥⎦⎤⎢⎣⎡++⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+=x x x x x dx dy x 111ln 1. 2、级数∑∞=n nn x !的收敛区间为___________.【2010年真题】 【解析】收敛半径:∞=+=+==∞→∞→+∞→)1(lim !)!1(lim ||lim 1n n n a a R n n n n n , 所以,收敛区间为:),(+∞-∞.3、求幂级数 +-+-+--nx x x x n n 132)1(32的收敛半径和收敛域. 【2009年真题】 【解析】 收敛半径: 11lim lim1=+==∞→+∞→n n a a R n n n n , 当1-=x 时,级数∑∑∞=∞=--=--1111)1()1(n n n n n n 发散; 当1=x 时,级数∑∞=--111)1(n n n收敛. 所以,级数的收敛域为:]1,1(-.三、证明题:1、某车间靠墙壁要盖一间长方形小屋,现有存砖只能够砌成20m 长的墙壁..0663********sin 6cos 6)6()(<-⋅=-⋅=-⋅=<ππππππg x g问:应围成怎样的长方形才能使这间小屋面积最大. 【2011年真题】【解析】设小屋宽为x 米,则长为(20-2x )米,小屋面积为:)220(x x y -=,0420=-='x y 得,5=x由实际问题的实际意义知,当围成宽5米,长10米的长方形时小屋面积最大.2、求抛物线221x y =将圆822=+y x 分割后形成的两部分的面积. 【2011年真题】 【解析】联立⎪⎩⎪⎨⎧=+=821222y x x y ,得2±=x 面积2032402022131)cos 22(22182x dt t dx x x A -=⎪⎭⎫ ⎝⎛--=⎰⎰π 342382sin 21838)2cos 1(84040+=-⎥⎦⎤⎢⎣⎡+=-+=⎰πππt t dt t . 另一部分面积346812-=-=ππA A .3、设函数)(x f 在[0,1]上连续,且1)(0≤≤x f ,证明:存在ξξξ=∈)(],1,0[f 使.【2010年真题】【解析】本题考查闭区间上连续函数的性质——零点定理.证明. 令x x f x g -=)()(,则)(x g 在[0,1]上连续,且,0)0(0)0()0(≥=-=f f g ,01)1()1(≤-=f g若等号成立,即1)1(,0)0(==f f 或,则端点0或1即可作为要找的ξ;若等号不成立,即,0)1()0(<⋅g g 由零点定理知,存在0)(),1,0(=∈ξξg 使,即ξξ=)(f . 综上可证,存在ξξξ=∈)(],1,0[f 使.4、某工厂需要围建一个面积为2512m 的矩形堆料场,一边可以利用原有的墙壁,其他三边需要砌新的墙壁.问堆料场的长和宽各为多少时,才能使砌墙所用的材料最省?【2009年真题】【解析】求最值问题.首先根据题意建立数学函数,然后求导数,并求出使一阶导数等于零的点,若只求得一个驻点,则可直接断定结论.解 设宽为x 米,则长为x512米. 新砌墙的总长度为: x x y 5122+=由051222=-='x y ,得16=x (16-=x 舍去), 32512=x 所以,当堆料场的长为32米,宽为16米时砌墙所用的材料最省.。
2012年山东卷(理科数学)
2012年普通高等学校招生全国统一考试理科数学(山东卷)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一个是符合题目要求的.1.若复数z 满足(2)117z i i -=+(i 为虚数单位),则z 为A.35i +B.35i -C.35i -+D.35i -- 2.已知全集{0,1,2,3,4}U =,集合{1,2,3}A =,{2,4}B =,则()U C A B =U A.{1,2,4} B.{2,3,4} C.{0,2,4} D.{0,2,3,4} 3.设0a >,1a ≠,则“函数()x f x a =在R 上是减函数”,是“函数3()(2)g x a x =-在R 上是增函数”的A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件4.采用系统抽样方法从960人中抽取32人做问卷调查,为此将他们随机编号为1,2,…,960,分组后在第一组采用简单随机抽样的方法抽到的号码为9.抽到的32人中,编号落入区间[1,450]的人做问卷A ,编号落入区间[451,750]的人做问卷B ,其余的人做问卷C .则抽到的人中,做问卷B 的人数为 A .7 B .9 C .10 D .155.设变量x ,y 满足约束条件222441x y x y x y +≥⎧⎪+≤⎨⎪-≥-⎩,则目标函数3z x y =-的取值范围是A.3[,6]2-B.3[,1]2--C.[16]-,D.3[6]2-,6.执行下面的程序图,如果输入4a =,那么输出的n 的值为A .2B .3C .4D .57.若[,]42ππθ∈,sin 2θ=sin θ=A.35B.45C.4D.348.定义在R 上的函数()f x 满足(6)()f x f x +=,当31x -≤<-时,2()(2)f x x =-+ ,当13x -≤<时,()f x x =,则(1)(2)(3)(2012)f f f f ++++=L A.335 B.338 C.1678 D.20129.函数cos622x x xy -=-的图像大致为10.已知椭圆C:22221x y a b+=(0a b >>)双曲线221x y -=的渐近线与圆有四个交点,以这四个交点为顶点的四边形的面积为16,则椭圆C 的方程为A.22182x y += B.221126x y += C.221164x y += D.221205x y += 11.现有16张不同的卡片,其中红色、黄色、蓝色、绿色卡片各4张,从中任取3张,要求这卡片不能是同一种颜色,且红色卡片至多1张,不同取法的种数为 A .232 B .252 C .472 D .48412.设函数1()f x x=,2()g x ax bx =+(a ,b R ∈,0a ≠),若()y f x =的图像与()y g x =图像有且仅有两个不同的公共点11(,)A x y ,22(,)A x y ,则下列判断正确的是A.当0a <时,120x x +<,120y y +>B.当0a <时,120x x +>,120y y +>C.当0a >时,120x x +<,120y y +<D.当0a >时,120x x +>,120y y +> 二、填空题:本大题共4小题,每小题4分,共16分.13.若不等式42kx -≤的解集为{}13x x ≤≤,则实数k = .14.如图,正方体1111ABCD A B C D -的棱长为1,E ,F 分别为线段1AA ,1B C 上的点,则三棱锥1D EDF -的体积 _.15.设0a >.若曲线y =x a =,0y =所围成封闭图形的面积为a ,则a = 16.如图,在平面直角坐标系xoy 中,一单位圆的圆心的初始位置在(0,1),此时圆上一点P 的位置在(0,0),圆在x 轴上沿正向滚动。
山东省2012年普通高等学校招生全国统一考试理科数学真题
以 k 16,17,..., 25 共 10 个数,即应该有 10 人做试卷 B. 方法二, (整除法)由题意可知,系统抽样中每一组的样本数为 做问卷 A 的人编号在区间 [1, 450] 内,而 15 组,每组抽取一个,共抽取 15 人. 而编号在区间 [1, 750] 内的人需要做 A 卷或 B 卷,而 的人应分为 25 组,每组抽取一个,共抽取 25 人. 所以作 B 问卷的人有 25 15 10 人. 5.答案:A 如图画出不等式组所表示的平面区域,
1 , g ( x ) ax 2 bx ,若 y f ( x ) 的图象与 y g ( x ) 的图象有且仅有 x
)
两个不同的公共点 A( x1 , y1 ) , B ( x2 , y2 ) ,则下列判断正确的是( A. 当 a 0 时, x1 x2 0 , y1 y2 0 B. 当 a 0 时, x1 x2 0 , y1 y2 0 C. 当 a 0 时, x1 x2 0 , y1 y2 0 D. 当 a 0 时, x1 x2 0 , y1 y2 0 第Ⅱ卷(共 90 分)
2012 年普通高等学校招生全国统一考试(山东卷)
理科数学
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。全卷满分 150 分,考试 时间 120 分钟。 第 I 卷(共 60 分) 一、选择题:本大题共 12 小题,每小题 5 分,共 60 分,在每小题给出的四个选项中, 只有一项是符合题目要求的. (1)若复数 z 满足 z (2 i ) 11 7i ( i 为虚数单位) ,则 z 为( A. 3 5i B. 3 5i C. 3 5i D. 3 5i ) )
1 x 3 时, f ( x) x .则 f (1) f (2) f (3) ... f (2012) (
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
n•
= lim =
n →∞
1+ n 2 2 n
1 2
1 x −1 1 x −1
4 解: lim e +
x →1 x →1
= +∞(e
1 x −1
x → 1+ e +∞ → +∞)
lim e = 0(e −
1 x −1
x → 1− e −∞ → 0)
1 1 1 + + 2 2011n 2 求 lim 2011 2011 x →∞ 1 1 1 + + 2 2012 2012 2012n
3 设 f ( x) = e , 求 lim
x
1
1 ln [ f (1) f (2) f (n) ] x →∞ n 2
4. lim e x −1
x →1
x+a 5.若 lim = e ,试求常数 a x →∞ x − a
x x2 + 1
x
,则 f [ f ( x) ] =
3. lim(1 + ) =
x →0
1 x
4.曲线 = y x ln(2 + ) 的渐近线为 5.函数 y =
1 x
1 e
x x−2
的间断点为
−1
2
三、计算题(共 50 分,每小题 5 分) 1.设函数 f ( x) = sin x, f [ ( x) ] = 1 − x ,求 ( x)
n
收敛
B.
∑ (−1) a
n =1
∞
n 收敛
C.
∑a a
n =1
∞
n n +1
D.
∑
an + an +1 2 n =1
∞
二、填空题(共 15 分,每小题 3 分)
−1, x < 0 = y sgn = x = 0, x 0 的值域为 1.函数 1, x > 0
第 1 页 共 8 页
2.设 f ( x) =
x →1 x →1 1 1 − −∞ x −1 x −1 lim 0( 1 e e x e → 0) = → − 1
左右极限不相等则 lim e x −1 不存在
x →1
x+a x 5 解: lim( ) x →∞ x − a x − a + 2a x = lim( ) x →∞ x−a 2a x = lim(1 + ) x →∞ x−a
lim x
x→∞ x − a 2a x−a 1 2a = lim(1 + ) x →∞ x−a 2a
=e
2a
6 解: y =
/
a 1 + ax a / y// = ( ) 1 + ax
= −
a2 (1 + ax) 2
1 dy (arctan t )′ 1 + t 2 1 + t 7.解 : = = = 1 1+ t2 dx (ln(1 + t ))′ 1+ t
2 4. y ln x + =
{
}
x x2 + 2
1 2
5.x=0,
x=2
三、计算题
第 3 页 共 8 页
1,解;因为 f ( x) = sin x 则 f (( x)) = sin(( x)) 又 f (( x)) = 1 − x 2 所以 sin (( x)) = 1 − x 2 )
所以 = ( x) arcsin(1 − x 2 )
山东省 2012 年普通高等教育专升本统一考试 高数试卷
一、 单选题(共 15 分,每小题 3 分)
1,. 函数 y =
x +1 +1 的定义域为 x + x −1
B, −1,
A, [ −1, +∞ )
1 , +∞ 2
1 2 1 1 ∪ , +∞ 2 2
1
左右极限不相等则 lim e x −1 不存在
x →1
5 解: lim(
x →∞
x+a x ) x−a x − a + 2a x = lim( ) x →∞ x−a 2a x = lim(1 + ) x →∞ x−a x 1 x2−aa ) • = lim (1 + x →∞ x−a x−a 2a 2a
1 . 12
3.求
dy y + x 2 − y 2 的通解. = dx x
4.证明:双曲线 xy = 1 上任一点处的切线与两坐标轴所围三角形的面积均相等.
山东省 2012 年普通高等教育专升本统一考试 高数答案
一、选择题: D A C B D 二、填空题 1. y y = −1, y = 0, y = 1 2. 3. e
0 x + 3y + 2z +1 = 与平面 4 x − 2 y + z − 2 = 0 的关系为 0 2 x − y − 10 z + 3 =
B.直线与平面垂直 C. 直线与平面平行 D.直线与平面斜交
∞
A.直线在平面上 5.若级数
∑a
n =1
∞
n
收敛,下列结论正确的是
n
A. n =
∑a
n =1
1 1 (1 − ) n 2011 2011 2.解;= lim n →∞ 1 1 2012(1 − ) 2011n 2012 = . 2011
提示:等比数列求和公式: sn = 3.解; lim
an (1 − q n ) 1− q
1 ln [ f (1)............. f (n) ] n →∞ n 2 ln f (1) + ln f (2) + ........ln f (n) = lim n →∞ n2 1 + 2 + 3......... + n = lim n →∞ n2 1+ n n• 2 = lim n →∞ n2 1 = 2 1 1 + +∞ x −1 x −1 4 解: lim ( 1 e e x e → +∞) = +∞ → +
2
x y
∂ 2u . ∂x∂y
x 3 ∫∫ e dxdy ,其中,D 为 y = x 与 y = x 所围区域. D
四.应用和证明题(每小题 5 分,共 20 分) 1.求 lim( 1 + 2 + + n − 1 + 2 + + ( n − 2)) .
n →∞
2.在曲线 = y x 2 , ( x > 0) 上求一点,使得曲线在该店处的切线与曲线一起 x 轴所围图面积为
即 y′ = 令
y = u ,即 y =ux ⇒ y′ =u + xu ′ x
代入上式得
u + xu ′ = u + 1− u2
⇒x du =1 − u 2 dx
⇒
1 = dx x 1− u
2
du
∫
1 = ∫ dx x 1− u2
du
⇒ arcsin u = ln x + c
即 arcsin = ln + c
6 解: y =
/
a 1 + ax a / y// = ( ) 1 + ax
= −
a2 (1 + ax) 2
1 dy (arctan t )′ 1 + t 2 1 + t 7.解 : = = = 1 1+ t2 dx (ln(1 + t ))′ 1+ t 1+ t ′ 1 + t ′ 1 + t 2 − (1 + t ) ⋅ 2t 1 1 − 2t − t 2 1 (1 − 2t − t 2 )(1 + t ) d2y )x ( = )t = ( = = ⋅ ⋅ = 1 (1 + t 2 ) 2 (1 + t 2 ) 2 d 2x 1+ t2 1+ t2 (1 + t 2 ) 2 xt′ 1+ t
6.设 ,求 y '' = y ln (1 + ax ) . ( a > 0 ) ) 7.设
x
= x 6n(1 + t ) d2y ,求 2 . dx y = arctan t
8.设 f ′(ln x) = 1 + x ,求 f ( x) .
第 2 页 共 8 页
9.若 u = e ,求 10.求
所以 = ( x) arcsin(1 − x 2 )
1 1 (1 − ) n 2011 2011 2.解;= lim n →∞ 1 1 2012(1 − ) 2011n 2012 = . 2011
提示:等比数列求和公式: sn = 3.解; lim
an (1 − q n ) 1− q
1 ln [ f (1)............. f (n) ] n →∞ n 2 ln f (1) + ln f (2) + ........ln f (n) = lim n →∞ n2 1 + 2 + 3......... + n = lim n →∞ n2
∂u x 1 e ( x + y) 1 1 1 1 = e (− 2 ) ⋅ + e ⋅ (− 2 ) = − (e ⋅ ) y′ = (e ) y′ ⋅ + e ⋅ ( ) y′ = ∂x∂y y y y y y y y3
2
第 5 页 共 8 页
