大学物理2-1质点系的内力和外力质心质心运动定理

合集下载

物理-质心与质心运动定理

x
——动量中心系
在质质心心参位考矢系中r：C x 质心速度 υC
0drC
dt
0
质点系m的i总i 动m量C 0
质心系是零动量系
质心的运动轨迹？
——抛物线.
0 O x1
m xC x2 C
mx
二、质心运动定理
锥体为什么会上滚？
锥体上滚是由其质（重）心下降所引起的。
令人称奇的“水往高处流”。
上坡省力，下坡费劲的“怪坡 ”
三、质心参考系
【质心参考系】：以质心为坐标原点的参考系。
y
r2
O
y
mi
m2 ri
ri
C
rC m1 r1
m1
l
C
m2
x
O
xC
m2 m1 m2
l
m1
l
C
m2
m1l1 m2l2
l1
l2
（与坐标系无关）
质心坐标与所选坐标系有关，
但质心相对物体各部分位置是确定的.
一、质心
例2 求半径为R的匀质半圆环的质心.
y
Rdθ
dθ
R
θ
O R cos θ
y R sin θ
x
一、质心
例2 求半径为R的匀质半圆环的质心.
C 恒矢量
当质点系所受合外力为零时，其质心保持原来的静止或匀速直线运动状态不变。 ——质心的“惯性运动”
质心的“惯性运动”与质点系动量守恒等价！
随堂练习
例：设有一枚炮弹发射的初速率为 0，发射角为，它飞行在最高点处爆炸成质量相等的两个碎片，其中一个竖直下落，另一个水平抛出，求这两部分的着地点（忽略空气阻力）。
(1) 直角坐标系中的质心坐标

大学物理质心、动量

F
dP
dt
p mvc
F mac
2.内容
质点系质心的运动决定于质点系合外力
若 F合外力 0 ，
则 vc (Pc ) 不变
即系统内力不会影响质心的运动
如抛掷的物体、跳水的运动员、爆炸的焰火等
例：水平桌面上拉动纸，纸张上有一均匀球，球的质量M，纸被拉动时与球的摩擦力为 F，求：t 秒后球相对桌面移动多少距离？
N
rc
mi ri
i 1 N
mi
N
mi ri
i 1
m
i 1
N
mi xi
y
xc
i 1
m
2.质量连续分布的物质
N
rc
mi ri
i 1 N
mi
rdm m
i 1
z
r
xO
dm
×C
rC m
y
xdm
ydm
zdm
xc m
yc m
zc m
3. 质心的计算 1) 均匀的杆、圆盘、圆环和球的质心 —— 几何中心 2) 小线度物体质心和重心是重合的
3) 对于确定的质点系,质心位置是唯一确定的
例：任意三角形的每个顶点有一质量m，求质心。
y
（x1，y1）
o
x2 x
N
mi xi
xc
i 1
m
1.质心公式 2.求质心
xc
mx1 mx2 3m
x1 x2 3
yc
my1 3m
y1 3
[例] 如图示，从半径为R的均质圆盘上挖掉一块
半径为r的小圆盘，两圆盘中心O和O′相距为d，
第二章运动的守恒量和守恒定律
2 - 1 质心质心运动定理

动量定理质心运动定理_guys

§2 质心与质心运动定理
一．质点系内力与外力二．质心 1、质心的概念 2、质心位置 3、质心计算三．质心运动定理四．质心运动定理的应用五．质心系
§3 质心与质心运动定理一、质点系内力与外力
1、质点系一定量的质点(或物体)组成的系统任何物体都可看成由许多质点组成的质点系 2、外力与内力 F2
T
a
aC a
T
解：研究对象：三个小球及轻绳组成的质点系所受外力： O点对绳子的拉力T 采用质心运动定理求解
解：
m
m
m
T
a
aC a
T
在系统决定的直线上，与O点相距为 (1)质心位置：
Lc (am 2am 3am) 3m 2a
(2) 由质心运动定理：F 得：
ac R 2 Lc 2 该质心C绕O点以角速度匀速转动
三、质心运动定理
drc dvc dp mac m Fe m dt dt dt
其中：
drc vc m dt 2 dvc d rc 2 ac dt dt p mi vi mvc ——系统总动量
mi v i
c
y
yC o
(2)竖直方向作用于链条的合外力为
(3) 由质心运动定律:
d yC F y g l 2 dt
而
2
y
F
c
d yc d y ( ) 2 dt dt 2 l
2
2
2
y
yC
dy d y dv o 考虑到 v 2 , 0 dt dt dt 2 2 d yC v 得到 F y g l l 2 dt l
外力(External Force)

大学物理第2章-质点动力学基本定律

②保守力作功。
势能的绝对值没有意义，只关心势能的相对值。势能是属于具有保守力相互作用的系统计算势能时必须规定零势能参考点。但是势能差是一定的，与零点的选择无关。如果把石头放在楼顶，并摇摇欲坠，你就不会不关心它。一块石头放在地面你对它并不关心。
重力势能：以地面为势能零点
01
万有引力势能：以无限远处为势能零点
m
o
θ
设：t 时刻质点的位矢
质点的动量
运动质点相对于参考原点O的角动量定义为：
大小：
方向：右手螺旋定则判定
若质点作圆周运动，则对圆心的角动量：
质点对轴的角动量:
质点系的角动量:
设各质点对O点的位矢分别为
动量分别为
二.角动量定理
对质点:
---外力对参考点O 的力矩
力矩的大小：
力矩的方向:由右手螺旋关系确定
为质点系的动能，
令
---质点系的动能定理
讨论
内力和为零,内力功的和是否为零？
不一定为零
A
B
A
B
S
L
例:炸弹爆炸，过程内力和为零，但内力所做的功转化为弹片的动能。
内力做功可以改变系统的总动能
例用铁锤将一只铁钉击入木板内,设木板对铁钉的阻力与铁钉进入木板之深度成正比,如果在击第一次时,能将钉击入木板内 1 cm, 再击第二次时（锤仍以第一次同样的速度击钉）,能击入多深？第一次的功第二次的功解：
（1）重力的功
重力做功仅取决于质点的始、末位置za和zb，与质点经过的具体路径无关。
（2）万有引力的功
*
设质量M的质点固定，另一质量m的质点在M 的引力场中从a运动到b。
M
a
b

大学物理-质心质心运动定律

角动量守恒条件
当刚体绕定轴转动时，如果作用于刚体上的外力矩为零，则刚体的角动量守恒。
角动量守恒应用
利用角动量守恒原理可以解决一些实际问题，如陀螺仪的工作原理、天体运动中行星轨道的确定等。
角动量不守恒情况
当作用于刚体上的外力矩不为零时，刚体的角动量将发生变化。此时需要根据外力矩的作用时间和大小来计算角动量的变化量。
适用范围和条件
01
适用范围：质心运动定律适用于任何由多个质点组成的系统，无论这些质点之间是否存在相互作用力。
02
适用条件：质心运动定律的应用需要满足以下两个条件
03
质点系所受的外力可以视为作用于质心上的合力。
04
质点系内部的相互作用力对质心的运动没有影响，或者其影响可以忽略不计。
质点系相对于质心参
角动量
描述刚体绕定轴转动时动量的大小和方向，等于转动惯量与角速度的乘积。
刚体绕定轴转动时质心位置变化规律
质心位置不变
刚体绕定轴转动时，其质心位置保持不变，始终位于转轴上。
质心速度为零
由于质心位于转轴上，因此质心的速度为零。
质心加速度为零
由于质心速度为零，因此质心的加速度也为零。
刚体绕定轴转动时角动量守恒原理
02
考系运动
质点系内各点相对于质心参考系位移
01
02
03
定义
质点系内各点相对于质心的位置矢量称为相对位移。
性质
相对位移是描述质点系内各点相对于质心位置变化的物理量，具有矢量性。
计算方法
通过几何方法或解析方法求出各点相对于质心的位置矢量。
质点系内各点相对于质心参考系速度
定义
质点系内各点相对于质心的速度称为相对速度。

大学物理力学：1.5 从质点到质点系统、质心、质心运动定理

dP
F外 dt
m1
F2
F1
F 外dt＝d P 微分形式 F3
m2
t2 t1
F外dt＝
P2 P1
d
P
P
积分形式
m3
17
二、质点系的动量守恒定律
当F外
0时，d P dt
0 ，P
常矢量
pi mi vi 常矢量
i
i
一个质点系所受的合外力为零时，
说明这一质点系的总动量就保持不变。
t2
Fdt
t1
单位：Ns 量纲：MLT－1
三、动量定理将力的作用过程与效果〔动量变化〕联系在一起
10
I
t2
Fdt
t1
F
dP
dt
dP Fdt
P2
dP
t2
Fdt
P1
t1
P2
P1
I＝
t2
t1
Fdt
I Fdt＝P 在坐标下可有分量表达式
质点所受合外力的冲量，等于该质点动量的增量。这个结论称为动量定理。
dt
x
柔绳对桌面的冲力F＝－F’ 即：
F ρ v2 M v2 而v2 2gx F 2Mgx / L
L
而已落到桌面上的柔绳的重量为mg = Mgx/L
所以F总=F+mg=2Mgx/L+Mgx/L=3mg
16
2.2 动量守恒定律
一、质点系的动量定理质点系（内力、外力）
以F外和P表示系统的合外力和总动量，则：
此半圆形铁丝的质心。
y
解：选如图坐标系，取长为dl 的铁丝，质量为dm，以λ表示
质量线密度，dm= dl。分析得
质心应在y轴上。

2-1 质心质心运动定理

Ch2 运动的守恒量和守恒定律§2-1质点系的内力外力质心质心运动定理§2-1 质心质心运动定理动量守恒定律1、质点系的内力和外力质心质心的位置例：任意三角形的每个顶点有一质量m 的小球，求/r m r M =∑G Gz yOΔm ir微元分割！例3-7 求腰长为a等腰直角三角形均匀薄板的质心位置。

3、质心运动定理质心运动定理G G G G G d v1 G m 1 a1 = m 1 = F1 外 + f 12 + f 13 + " + f 1 n , dt G G G G G d v2 G m 2a2 = m 2 = F2 外 + f 21 + f 23 + " + f 2 n , dt G G G G G d vn G = Fn外 + f n 1 + f n 2 + " + f n ( n − 1) , m nan = m n dt G G G G 由于内力 f12 + f 21 = 0," , f in + f ni = 0, ...由牛顿第二定律:""∴G ∑ m i ai =G ∑ F i外11/18中国矿业大学（北京）质心运动定理G ∑ m i ai =G ac =G ∑ F i外 G ∑ m i aiG ac =G ∑ Fi外∑m∑m=G ∑ Fi外 Mi∑G G Fi外 = M a ci质心运动定理不管物体质量如何分布，也不管外力作用在物体什么位置上，质心的运动就象是物体的质量全都集中于此，而且所有外力也都集中作用其上的一个质点的运动一样。

12/18 中国矿业大学（北京）补充例题1例1 质量为m1 和m2的两个小孩，在光滑水平冰面上用绳彼此拉对方。

开始时静止，相距为l。

问他们将在何处相遇？m2m1Ox20x10x13/18中国矿业大学（北京）补充例题1解：可直接由质心运动定律求出。

初始静止时，小孩系统的质心位置： m 1 x 10 + m 2 x 20 1 xc = m1 + m 2m2C xcx10m1∑G G G Fi外 = M a c ⇒ a c = 0O x20x质心位置，在过程中应该始终保持静止。

§2-1 质点系的内力和外力质心质心运动定理

4.将坐标原点取在质心上，坐标轴与某惯性系平行的平动参照系称作质心坐标系或质心系．对于外力的矢量和为零或不受外力作用的体系的质心参照系为惯性系，否则为非惯性系．
§2-1 质点系的内力和外力质心质心运动定理
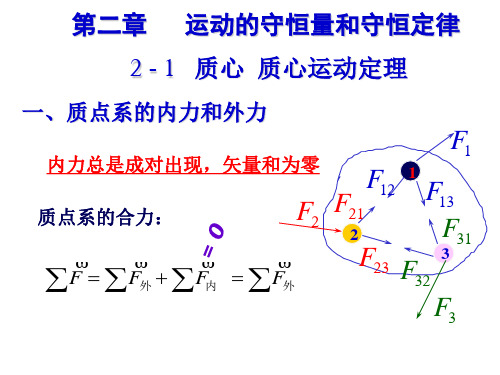
一、质点系的内力与外力内力: 质点系内各个质点间的相互作用。外力: 质点系外物体对系统内质点所施加的力。
系统内，内力是成对出现的。
返回退出
ቤተ መጻሕፍቲ ባይዱ
§2-1 质点系的内力和外力质心质心运动定理
二、质心
质心是与质量分布有关的一个代表点，它的位置在平均意义上代表着质量分布的中心。
rC
r dm/m
(m dm)
分量式： xC x d m / m yC y d m / m
zC z d m / m
线分布 d m dl
面分布 d m d S 体分布 d m dV
质心与重心是两个不同的概念，重心是地球对物体各部分引力的合力(即重力)的作用点，质心与重心的位置不一定重合。
返回退出
对于N个质点组成的质点系：
m 1
r1,
,r2m,2,, ri,,mi，,rN，mN
质心的位矢：
rC miri / m
(m mi )
直角坐标系中的分量式：
xC mi xi / m yC mi yi / m zC mi zi / m
返回退出
对于质量连续分布的物体
质心的位矢：
第二章运动的守恒量和守恒定律
§2-1 质点系的内力和外力质心质心运动定理 §2-2 动量定理动量守恒定律 §2-3 功能量动能定理 §2-4 保守力成对力的功势能 §2-5 质点系的功能原理机械能守恒定律 §2-6 碰撞 §2-7 质点的角动量和角动量守恒定律 §2-8 对称性和守恒定律

2-1-1质点系的内力和外力质心

rc r d m / M
xc x d m / M
分量形式 yc y d m / M zc z d m / M
线分布 d m dl 面分布 d m d S 体分布 d m dV
质心
注意：
质心的位矢与参考系的选取有关。
刚体的质心相对自身位置确定不变。
质量均匀的规则物体的质心在几何中心。
2. 质心运动定理
设有一个质点系，由 n 个质点组成，它的质心
的位矢是：
rc
mi ri
mi
m1r1
m2 r2
mn rn
m1 m2 mn
质心的速度为
vc
d rc dt
mi
d ri dt
mi
mi vi mi
质心运动定理
质心的加速度为
ac
d vc dt
mi
d vi dt
4、如果合外力在某一方向上的分量为零，则该分量的动量也守恒。即使这时其它的动量分量和系统总动量不守恒。
5、动量守恒式中的速度必须是针对惯性系的速度。通常地球可看作近似的惯性系。
注意：动量守恒定律中系统内各
质点动量都是针对同一参考系，而且这个参考系必须是惯性系。对于非惯性系，动量守恒定律不成立
质心运动定理还表明：质心的运动状态完全决定于质点系所受的外力，内力不能改变质心的运动
如：炮弹在其飞行轨道上爆炸，它的碎片散向四面八方。如果把炮弹看作一个质心系统，由于爆炸力为内力，内力不能改变质心的运动，那么炮弹碎片的质心仍将按原来的弹道曲线运动。
例如：人在水平地面上行走，靠地面给予鞋底的摩擦力，使人的质心获得水平方向的加速度，摩擦力对人来讲是外力。
Mvc
=常矢量
i

程守洙《普通物理学》(第6版)(上册)(课后习题详解运动的守恒量和守恒定律)

2.2　课后习题详解一、复习思考题§2-1 质点系的内力和外力质心质心运动定理2-1-1 一物体能否有质心而无重心？试说明之．答：一物体可能有质心而无重心．（1）质心是表征物体系统质量分布的一个几何点，任何物体都有其质量分布，因此物体都有质心．（2）重心是地球对物体重力的作用点．在失重环境中，物体不受重力作用，重心就没有意义．2-1-2 人体的质心是否固定在体内？能否从体内移到体外？答：（1）质心是从平均意义上来表示物体的质量分布中心．它的位置由物体的质量分布来决定．所以，当物体质量改变时，质心的位置可以不固定．（2）质心可以由体内移到体外．人体在直立时，质心在体内，如果人体弯曲，就可把质心从体内移到体外．2-1-3 有人说：“质心是质量集中之处，因此在质心处必定要有质量”．这话对吗？答：（1）说法不对．（2）质心是描述物体系统质量分布的一个几何点，并非质量集中之处，质心所在处不一定有质量分布．如：质量均匀分布的空心球，其质心在球心，但质量却均匀分布于球面上．§2-2 动量定理动量守恒定律2-2-1 能否利用装在小船上的风扇扇动空气使小船前进？答：这是可以的．（1）假定风扇固定在小船上．当风扇不断地向船尾扇动空气时，风扇同时也受到了空气的反作用力．（2）该反作用力是向着船头的、并通过风扇作用于船身．根据动量定理，该力持续作用时会使船向前运动的动量获得增量．（3）当该作用力大于船向前运动时所受的阻力时，小船就可向前运动了．2-2-2 在地面的上空停着一气球，气球下面吊着软梯，梯上站着一个人．当这人沿软梯往上爬时，气球是否运动？答：选择人、气球和软梯组成的系统为研究对象．（1）当人相对软梯静止时，系统所受合力等于零．系统的动量在垂直方向上等于零并守恒，系统的质心将保持原有的静止状态不变．（2）当人沿软梯往上爬时，人与软梯间的相互作用力是内力，系统所受合外力仍为零，总动量恒定不变．系统的质心位置仍保持不变．根据动量守恒定律可知，当人沿软梯往上爬时，气球和软梯将向下运动．2-2-3 对于变质量系统，能否应用？为什么？答：（1）变质量系统的问题属于质点系的动力学问题，牛顿第二定律依然适用，但式中mν应理解为质点系的总动量．（2）这类问题的代表是发射中的火箭、下落中的雨滴等问题，其研究对象一般是主体的运动规律，对于运动过程中所吸附或排出的那一部分质量，在变化前后与运动主体有不同的运动速度，所以用来处理主体的运动是不正确的．（3）一般从质点系的动量定理的角度入手，由系统的动量定理可得式中m 为运动主体的质量，为附加物在吸附或排出后相对于运动主体的速度．上式变形得：该式是指主体的动量变化率等于主体所受的外力与单位时间内附加物变化的动量的矢量和．2-2-4 物体m 被放在斜面m'上，如把m 与m'看成一个系统，问在下列何种情形下，系统的水平方向分动量是守恒的？（1）m 与m'间无摩擦，而m'与地面间有摩擦；（2）m 与m'间有摩擦，而m'与地面间无摩擦；（3）两处都没有摩擦；（4）两处都有摩擦．图2-1-1答：如图2-1-1所示，物体与斜面视为一个系统，对系统进行受力分析：物体与斜面受到重力作用，地面对斜面有支持力，地面与斜面之间存在摩擦力．其中物体与斜面间的摩擦力和支持力均是系统的内力．当系统在水平方向的合外力为零时，系统的水平方向分动量守恒．讨论如下：（1）m'与地面间有摩擦时，系统在水平方向的合外力不为零，故水平方向的分动量不守恒．（2）m'与地面间无摩擦时，系统的水平方向的分动量守恒．（3）与（2）结论一致，系统的水平方向的分动量守恒．（4）与（1）结论一致，系统的水平方向的分动量不守恒．2-2-5 用锤压钉，很难把钉压入木块，如用锤击钉，钉就很容易进入木块，这是为什么？答：钉子打入木块，主要是钉子与木块之间的摩擦力小于钉子所受的作用力．（1）锤压钉子的压力一般不大，当钉子所受的摩擦力大于锤对钉子的压力时，钉子就无法进入木块，，因此难以把钉压入木块．（2）锤击钉子时，具有一定的动量，打击到钉子后，动量变成零．根据动量定理和牛顿第三定律，由于打击时间很短，钉子受到平均冲力很大，因此很容易克服木块的阻力而进入木块．2-2-6 如图2-1-2所示，用细线把球挂起来，球下系一同样的细线．拉球下细线，逐渐加大力量，哪段细线先断？为什么？如用较大力量突然拉球下细线，哪段细线先断？为什么？图2-1-2答：任何细线只能承受一定张力，当给予细线的拉力超过它所能承受的极限张力，线就会断掉．如图示的情况：（1）当逐渐加大力量拉球下线时：在任一时刻，线中的张力与拉力达到平衡，而球上面线中的张力等于拉力和球的重力．因此，在渐渐增大拉力的过程中，球上面的线中的张力首先超过其极限张力会先断．（2）当用较大的力量突然拉球下线时：由动量定理可知，作用在线上的拉力就是冲力，由于力的作用时间较短，冲力还未传到球上面的线前，球下面的线就已经断了．2-2-7 有两只船与堤岸的距离相同，为什么从小船跳上岸比较难，而从大船跳上岸却比较容易？答：（1）选择人和船作为一个系统，并将人和船视为质点，忽略水的阻力．人以水平速度跳出时，系统在水平方向的动量分量守恒，即（2）由上式可知，大船没有小船后退厉害，人与小船的作用时间比较短了，在作用力相等时，所得的冲量就比较小了．因此人用同样大的力自小船上前跳的速度比自大船上前跳时的小，所以从小船跳上岸比从大船要困难．§2-3 功动能动能定理2-3-1 物体可否只具有机械能而无动量？一物体可否只有动量而无机械能？试举例说明．答：一个物体的动能和动量与相对于某参考系的速度有关；而物体的势能则与势能零点的选取有关．机械能是动能和势能的代数和．（1）一物体可能只具有机械能而无动量．如：①静止在离地面h 处的物体，它的动能和动量均为零．不将势能零点选在离地面高h 处时，物体就具有势能．因此，物体具有机械能而无动量．②弹簧振子在水平面内振动，在位移最大处，速度等于零，动能和动量也等于零．如将弹簧的原长处作为弹性势能的零点，那么此时弹簧振子具有弹性势能，其机械能不为零而动量为零．（2）一物体也可能只有动量而无机械能．如：物体离地面h 处自由下落至地面时，物体速度不为零，那么物体具有动量和动能．如将重力势能的零点选定在物体下落处，则到达地面时具有重力势能-mgh ．由于开。

质点系质心运动定律

3
O
x
x
2
dx
这个结果和熟知的三角形重心位置一致。
上页下页返回退出
例一段均匀铁丝弯成半圆形，其半径为R,求此半圆形铁丝的质心。
解：建立如图坐标系任取一小段铁丝，其长度为 dl ，质量为 dm ，以 λ 表示铁丝的线密度
dm dl
xc 0 , yc 2R /
上页下页返回退出
上页下页返回退出
选择进入下一节 §2-0 教学基本要求 §2-1 质点系的内力质心质心运动定理 §2-2 动量定理动量守恒定律 §2-3 功动能动能定理 §2-4 保守力成对力的功势能 §2-5 质点系的功能原理机械能守恒定律 §2-6 碰撞 §2-7 质点的角动量和角动量守恒定律 §2-8 对称性和守恒定律
dt
mi
d ri dt
mi
mi vi mi
上页下页返回退出
质心的加速度为
ac
d vc
dt
mi
d vi dt
mi
mi ai mi
由牛顿第二定律得
m1a1
m2a2
m1 m2
d v1 d t d v2 dt
F1 f12 f13 f1n
F2 f22 f23 f2
R 0
R2 y2 d y2 4R3 / 3
3R 8
质心在距球心 3R/8处。
上页下页返回退出
三、质心运动定理
设有一个质点系，由 n 个质点组成，它的质
心的位矢是：
rc
mi ri mi
m1r1 m2r2 mnrn m1 m2 mn
质心的速度为
vc
d rc

大学物理1教学大纲

《大学物理Ⅰ》教学大纲课程名称：大学物理Ⅰ课程编号：课程类别：专业基础课/必修课学时/学分：60学时/3学分开设学期：第二学期开设单位：物理与机电工程学院适用专业：电气工程及其自动化说明一、课程性质与说明1．课程性质专业基础课/必修课2．课程说明物理学的研究对象具有极大的普遍性，它的基本理论渗透在自然科学的一切领域，广泛地应用于生产技术的各个部门，它是自然科学和工程技术的基础，也是许多高新技术发展的源泉和先导。

因此，《大学物理》课程是理工科各专业学生的一门重要必修基础课。

以物理学为基础的大学物理课程主要包括：力学、振动和波动、热学、电磁学、光学、狭义相对论基础、量子物理基础等基础知识，以及它们在现代科学技术中的应用等。

通过大学物理课程的教学，应为学生进一步学习打下坚实的物理基础。

在教学过程中，要注意培养学生树立科学的自然观和辨证唯物主义世界观，培养学生科学思维和分析解决问题的能力，以及学生的探索精神与创新意识。

二、教学目标1. 学习和理解物理学观察、分析和解决问题的思想方法，培养、提高学生的科学素质,激发对科学的求知欲望及创新精神。

2. 系统地掌握必要的物理学基础知识及其基本规律,能运用经典物理学的理论对力、热、电、磁、光等学科的基本问题作初步的解释、分析和处理。

3. 对物理学的基本概念、基本理论、基本方法能够有比较全面和系统的认识和正确的理解，将微积分知识具体地、灵活地应用于物理问题之中，培养学生分析、解决实际问题的能力，并为后继课程的学习作必要的知识准备。

4. 了解各种理想物理模型，并能够根据物理概念、问题的性质和需要，抓住主要因素，略去次要因素，对所研究的对象进行合理的简化。

5. 了解近代物理学的有关基础知识。

三、学时分配表建议本课程以课堂讲授为主，采用启发式教学法。

教学中可充分利用录像、演示实验及多媒体等手段。

为加强学生对所学内容的理解，掌握解题方法、技巧，教师应推荐相应的参考书，课后留作业，按时辅导答疑。

大学物理1,第2章质点动力学

O
x
mg
tan a1 , arctan a1
g
g
l
m
a1
(2)以小球为研究对象，当小车沿斜面作匀加速运
动时，分析受力如图，建立图示坐标系。
x方向：FT2 sin(α θ) mg sin α ma2
FT 2
y方向：FT2 cos(α θ) mg cos α 0 a2
m
FT2 m 2ga22 sin α a22 g 2
• 强力（strong interaction）
在原子核内（亚微观领域）才表现出来，存在于核子、介子和超子之间的、把原子内的一些质子和中子紧紧束缚在一起的一种力。
其强度是电磁力的百倍，两个相邻质子之间的强力可达104 N 。力程：<10-15 m
• 弱力（weak interaction）
亚微观领域内的另一种短程力。导致衰变放出电子和中微子。两个相邻质子之间的弱力只有10-2 N 左右。
重力（gravity）重力是地球表面物体所受地球引力的一个分量。
G mg
g g0 (1 0.0035cos2 φ)
地理纬度角 g0 是地球两极处的重力加速度。
重力
引力
重力与重力加速度的方向都是竖直向下。
忽略地球自转的影响物体所受的重力就等于它所受的
万有引力：
mg
G
mEm R2
弹力（elastic force）
物体受到外力作用时，它所获得的加速度的大小与合外力的大小成正比，与物体的质量成反比；加速度的
方向与合外力F的方向相同。 F kma
比例系数k与单位制有关，在国际单位制中k＝1
瞬时性：是力F的瞬m时a 作m用d规v律 dt
F

质心质心运动定理

第五章质心刚体质心运动定理ca m F v v =合外质点系的质心加速度由合外力确定，与内力无关。

牛顿定律的独特性质：如果它在某一小尺度范围内是正确的，那么在大尺度范围内也将是正确的。

特殊的质点系——刚体m1l5.1.2 质点系动力学量的分解质心参考系：随质心一起运动的平动参考系，简称质心系。

在质心系中质心静止==c c v r v v常矢量质心系中的运动图象各质点从质心四面散开，或向质心八方汇聚。

质心成为一个运动中心，运动时时刻刻是“各向同性的”。

质点系的动量质点系的动量等于质心的动量c p p v v =质点系相对质心的动量总是为零0=′=′∑ii i v m p vv 质点系中各质点m i 相对质心的运动),(i i v r ′′v v m iO Ci r ′v ir v Cr v 在任一参考系中质点系的动量、动能和角动量与质心运动的关系核反应中的资用能质点系的角动量i c i i c i v v v r r r ′+=′+=v v v v v v ,∑×=iii i v m r L v v v ∑∑∑∑′×′+×⎟⎠⎞⎜⎝⎛′+⎟⎠⎞⎜⎝⎛′×+⎟⎠⎞⎜⎝⎛×=i i i i c i i i i i i c c i i c v m r v r m v m r v m r L v v v v v v v v v ∑′×′=′×=′+=ii i i c c c c v m r L v m r L L L L vv v v v v v v v , ,质点系的角动量可分解成质心角动量与质点系相对质心的角动量之和同一参考点质心为参考点m iOCi r ′v ir v Cr v 其中5.1.3 质心参考系质心系一般是非惯性系，引入平移惯性力ci a m v −在质心系中质点系的动能定理和角动量定理质心系中质点系的动量恒为零，质点系的动量定理不必考虑。

质点组力学

T Ti
2016/8/31 长春大学应用物理系 2
根据质点系的划分，作用于质点的力可分为内力和外力内力：质点组内质点之间相互作用的力该力在质点组内始终是成对出现的，且满足牛顿第三定律，对于整个质点系而言，其内力的矢量和为零。即：
(i ) n n F f ij 0
n
2016/8/31 长春大学应用物理系
内力矩为 17 零？？
为什么内力矩为零？？
r1 f12 r2 f 21 (r2 r1 ) f 21 r12 f 21 r12 f12 0
n
r1
1
f12
o
r12
r2
dpy
d n n e mi viy Fiy dt dt i 1 i 1
dpz d n n e mi viz Fiz dt dt i 1 i 1
对微分式积分,得动量定理的积分表达式为
质点组的动量变化，只与外力有关，（即外力才能改变质点组的动量），而与内力无关，内力只能改变质点系内各质点的动量。
t2 p2 p1 t1 Fdt
冲量定理
2016/8/31
Fdt
冲量元
质点组动量的改变等于合外力对质点组的冲量
长春大学应用物理系 11
二、质心运动定理
2 n n e d ri mi Fi 2 dt i 1 i 1
d mi ri
2 i 1
d mi v i
i 1
n
动量定理微分形式
dt
F
i 1
n
(e) i
说明：质点组动量对时间的微分等于作用于此质点组外力的矢量和。

21质点系的内力和外力质心质心运动定理

前页后页目录 6
2.1 质点系的内力和外力质心质心运动定理
例1 求腰长为a 的匀质等腰直角三角形薄板的质心
位置。P55例题1 y
解：建立如图所示坐标系。根据
对称性，薄板质心就在x轴上。设
dx
薄板的质量面密度为，面积元 o x dm 2xdx
ax
2
质心x坐标
a
xdm
2 2 x2dx
xdm
xc
dm ydm
yc
dm
dl 线分布
dm dl 为质量线密度
面分布
dS
dm dS
为质量面密度
zdm
zc
dm
体分布
dm dV
ቤተ መጻሕፍቲ ባይዱ
dV
为质量体密度
前页后页目录 5
2.1 质点系的内力和外力质心质心运动定理
讨论： 1)匀质规则物体的质心在几何中心。 2)刚体的质心相对自身位置不变。 3)质心和重心是两个不同的概念。物体几何尺寸不大时，质心与重心位置重合。
2.1 质点系的内力和外力质心质心运动定理
2.直角坐标系中质心的位置坐标
N个质点 m1, m2,, mi ,mN
mi ( xi , yi , zi )
xc
mi xi mi
yc
mi yi mi
zc
mi zi mi
前页后页目录 4
2.1 质点系的内力和外力质心质心运动定理
质量连续分布的物体
2.1 质点系的内力和外力质心质心运动定理
2.1 质点系的内力和外力质心质心运动定理
一. 质点系的内力和外力质点系内各个质点之间的相互作用称为内力。质
点系所有内力的矢量和为零。系统外物体对系统内质点的作用称为外力。

2-1质点系的内力和外力质心质心运动定理

作用在系统上的合外力等于系统的总质量乘以质心的加速度系统内各质点的动量的矢量和等于系统质心的速度乘以系统的质量普通物理学21质点系的内力和外力质心质心运动定理设有一质量为2m的弹丸从地面斜抛出去行在最高点处爆炸成质量相等的两个碎片其中一个竖直自由下落另一个水平抛出它们同时落地
第二章运动的守恒量和守恒定律一质心手榴弹质心（红点）的运动轨迹是抛物线
i1
n
i
yi
m
zC
i1
n
i
zi
m'
m'
m'
对质量连续分布的物体：
xC
说明
1 m'
xdm
yC
1 m'
ydm
zC
1 m'
zdm
对密度均匀、形状对称的物体，其质心在其几何中心．
§2-1 质点系的内力和外力质心质心运定律
m' rC
rC m 1 r1 m 1 r 2 m i r i m1 m2 mi

i1
n
m i ri m'
§2-1 质点系的内力和外力质心质心运动定理
普通物理学
对质量离散分布的体系：
m
xC
i1
n
i
xi
yC
m
mg
FN
( C )
(D)保持mg不变.
先加速 mg F N ma 后减速 mg F N ma
F N mg ma mg
F N mg ma mg
普通物理学
其余质点的运动质心的平动
+
绕质心的转动

大学物理2-1质点系的内力和外力 质心 质心运动定理

物理-质心与质心运动定理

大学物理 质心、动量

动量定理 质心运动定理_guys