第九章-结构可靠度的基本概念教案资料
结构可靠度课程

结构可靠度课程在工程领域中,结构安全是非常重要的一个方面。
为了保证结构的安全性,需要结构可靠度的知识。
因此,高校中也设置了结构可靠度课程。
下面将介绍关于该课程的一些基本信息和教学安排。
一、课程简介结构可靠度课程主要是以可靠性理论为基础,涉及到结构在安全性方面的问题。
该课程主要的教学内容包括结构可靠度分析原理、可靠性基本理论、工程结构安全分析、结构抗震可靠分析、结构可靠度设计以及计算机辅助可靠性分析方法等。
此外,该课程还会介绍结构安全方面的现状和风险评估与管理,让学生对结构的安全评估有更为系统的了解。
二、课程教学安排本课程是大学中的选修课程,一般开设在工程、土木等相关专业。
课程教学一般采取讲授与实验相结合的方式进行,既涵盖了理论知识的学习,也侧重于实践能力的提升。
下面将就课程安排进行详细阐述。
1.理论讲授方面课程的理论部分主要由教师讲授,包括可靠度检测、可靠度分析等方面的知识。
同时,教师还会邀请资深的工程师或者研究人员来进行相关的报告或者演讲,让学生对该领域的前沿技术有更加深入的了解。
2.实验方面在本课程中,实验是非常重要的一部分。
通过实验,学生能够更加直观地理解课程理论方面的知识并加深对课程核心概念的理解。
实验主要分为三个环节,即实验准备、实验操作以及实验报告撰写。
在实验准备阶段,学生需要制定实验计划,准备实验所需物品,并与教师沟通确认实验的步骤和方法。
实验操作阶段,学生需要根据实验计划进行实验操作,并记录实验数据和试验结果。
实验报告撰写阶段,学生需要分析实验数据,撰写实验报告,并与教师和同学进行分享和讨论。
三、课程收获通过学习这门课程,学生可以对结构可靠性的重要性有更为深入的认识,并能够使用可靠性计算方法对工程结构进行评估和分析。
此外,学生还能够掌握计算机辅助可靠性分析方法,提高学生的实践能力和实用技能。
总之,结构可靠度课程可以为工程专业学生提供更加系统的工程结构安全知识,帮助他们更好地理解这一领域的重要性并能更好地助力工程结构的可靠性提升。
第9章 结构可靠度分析

g X i
X
( X i Xi )
Z g ( X , X , , X ) 2 Z n g X
1 2 n
则 Z g ( X , X ,, X )
1 2 n
g Z i 1 X i
n
X
X
i
显然 Pf
可靠度指标β:
由β定义的代替失效概率Pf的指标。 β Pf 2.7 3.5×10-3 β与Pf关系 3.2 6.9×10-4 3.7 1.1×10-4 4.2 1.3×10-5
9-23
9.1 结构可靠度基本概念
令:
R S Z 2 2 Z R S
Y Z Z
9-2
9.1 结构可靠度基本概念
(1)、(4)为结构的安全性 (2)为结构的适用性 (3)为结构的耐久性 统称为结构的可靠性
●结构的功能函数
令 Z=R–S R:结构抗力; S:结构荷载效应。
9-3
9.1 结构可靠度基本概念
则有三种情况: (1) Z > 0 结构可靠 (2) Z < 0 结构失效 (3) Z = 0 结构处于极限状态 称 Z=R–S 为结构的功能函数 Z = R – S = 0 为结构极限状态方程 由于影响荷载效应S和结构抗力R都有 很多基本的随机变量,则结构功能函数的 一般形式为
n
2
p f ( )
9-26
9.2 结构可靠度分析的实用方法
情况Ⅱ : 结构功能函数为非线性函数
Z g ( X 1 , X 2 ,, X n )
在各个变量的中心点(均值点)展开成泰勒 级数,仅取线性项
Z g X1 , X 2 ,, X n
结构可靠度结构理论教案
课后自我总结分析
重点分析作用及抗力的概率统计分析。
中南林业科技大学教案(课时备课)
第7次课6学时
课目、课题
结构可靠性理论的应用及其研究进展
教学目的
和要求
目的:掌握结构可靠性理论的应用及结构可靠性理论研究进展。
要求:熟悉结构可靠度理论的应用最新进展及研究趋势。
结构可靠性数学基础
教学目的
和要求
目的:掌握概率密度的性质、随机变量的数字特征、结构可靠性分析常用的概率分布、随机向量、随机变量的函数、随机过程以及数理统计基础。
要求:熟悉随机变量的数学期望与方差等数字特征及其他统计量的计算。
重点
难点
重点:随机变量的数学期望与方差等数字特征及其他统计量的计算。
难点:随机过程的相关概念。
重点
难点
重点:结构可靠性理论的应用。
难点:可靠度理论的应用的研究趋势。。
教学进程(含课堂教学内容、教学方法、辅助手段、师生互动、时间分配、板书设计)
主要内容:结构可靠性理论的应用;
结构可靠性理论研究进展。
教学方法:主要采用课堂讲授方式进行,结合工程实际应用对课堂内容进行综合讲解,中间采用随堂提问的形式对学生进行提问,采用多媒体教学。
重点
难点
重点:结构可靠性基本分析方法中的蒙特卡罗法。
难点:结构可靠性基本分析方法中映射变换法。
教学进程(含课堂教学内容、教学方法、辅助手段、师生互动、时间分配、板书设计)
主要内容:中心点法;
验算点法;
实用分析法;
映射变换法;
蒙特卡罗法;
变量相关情况下结构可靠性分析方法。
结构可靠度概要课件

机理,提高结构可靠性。
探索新型材料和结构的性能特点,研究其 在不同环境下的可靠度变化规律。
多物理场耦合下的结构可靠度
人工智能与结构可靠度的结合
研究结构在多物理场(如温度、压力、振 动等)耦合作用下的性能退化和失效机制。
利用人工智能技术进行结构可靠性分析和 预测,提高预测精度和效率。
03
结构可靠度评估标准
国内外标准对比
国内标准
中国现行结构可靠度设计统一标准《 建筑结构可靠度设计统一标准》 GB50068-2001,规定了建筑结构 可靠度设计的基本原则、要求和计算 方法。
国外标准
如美国的ASCE7-10和欧洲的EC2、 EC3等,与国内标准在可靠度指标、 极限状态定义、荷载组合等方面存在 差异。
绿色可持续发展
在保证结构安全可靠的前提下,注重环保 和可持续发展,降低能耗和资源消耗。
面临的挑战与机遇
挑战
复杂环境和服役条件下的结构可靠性问题,新型材料和结构的性能退化机制,多物理场耦合作用下的性能退化规 律等。
机遇
随着科技的不断进步和工程实践的深入开展,结构可靠度研究将迎来更多的发展机遇和挑战。同时,国家和社会 对结构安全性的重视程度不断提高,为结构可靠度研究提供了广阔的发展空间和应用前景。
结构可靠性增强措施
材料选择与质量控制
01
选用优质材料,加强材料质量控制,提高结构材料的可靠性。
结构设计改进
02
优化结构设计,合理布置结构构件,降低应力集中和疲劳损伤。
施工质量控制
03
严格控制施工过程,确保施工质量符合设计要求,防止施工缺陷。
结构可靠性设计案例分析
案例一
某桥梁结构的可靠性设计分析, 采用有限元模型进行结构分析,
结构可靠度的基本概念
建筑结构设计目标:使得结构在规定的设计使用年限内以适 当的可靠度且经济的方式满足规定的各项功能要求。
第一节 结构可靠度基本概念
●结构的功能要求
四项基本功能:
(1) 能承受在正常施工和正常使用时可能出现的各种作用; (2) 在正常使用时具有良好的工作性能; (3) 在正常维护下具有足够的耐久性能; (4) 在偶然事件发生时(如地震、火灾等)及发生后,仍能保
£
[t ]
Þ
Tmax
£ [t ] ×Wp
M max W
£ [s ]
Þ
M max
£ [s ] ×W
单筋矩形截面 抗弯计算式
0M
1
fcbx
h0
x 2
结构抗力R
荷载效应S 结构抗力R
指结构或结构构件承受荷载效应S的能力
建筑结构设计目标:荷载效应S ≤ 结构抗力R
R≥S 不能绝对满足,只在一定概率意义下满足,即:
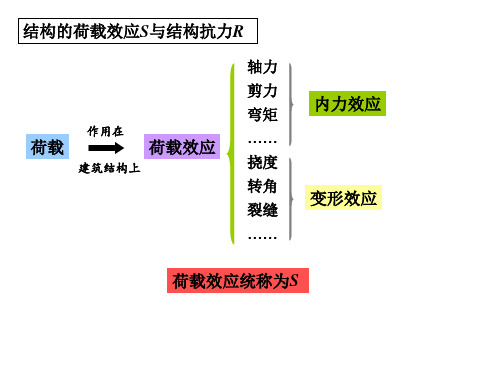
结构的荷载效应S与结构抗力R
作用在
荷载
荷载效应
建筑结构上
轴力 剪力 弯矩 …… 挠度 转角 裂缝 ……
内力效应 变形效应
荷载效应统称为S
结构的荷载效应S与结构抗力R
材料特性
强
轴向拉压杆件 度
安
受扭转杆件
全 校
核
受弯杆件
公 式
构件的几何特征
FN max A
£
[s ]
Þ
FN max
£
[s ] ×
A
Tmax Wp
持必需的整体稳定性。
4
第一节 结构可靠度基本概念
(1)、(4)为结构的安全性 (2)为结构的适用性 (3)为结构的耐久性
结构可靠度理论ppt课件

16
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
17
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
29
3
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
均匀分布随机变量X的取值具有“均匀性” 均匀性特点:均匀分布随机变量X落在(a,b) 内任意子区间的概率只与子区间的长度有关, 而与子区间的位置无关. 可假设有这种特性的随机变量服从均匀分 布.
26
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
图 2.3 可靠度指标的几何意义及验算点
根据前面所 述,将结 构功能函 数 Z 在假 定验算 点 X*= (x1*, x2*,, xn* ) 处运用泰勒 级数展开且只 保留线 性项:
X * Xi
( X * Xi
2
xi*)
由可靠度指标 的几何 意义,验 算点和 可靠度指 标之间 具有如下 关系:
xi* Xi Xi cosi
28
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
24
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
第九章-结构可靠度分析与计算

第二节 结构可靠度基本分析方法
(一)线性功能函数情况 设结构功能函数为线性函数,即
n
Z a0 ai Xi i1
式中 a0、ai ——已知常数(i =1,2,…,n)。 功能函数的统计参数为
n
Z a0 aiXi i1
n
Z (aiXi)2 i1
第二节 结构可靠度基本分析方法
第一节 结构可靠度基本原理 Nhomakorabea结构可靠度: 结构可靠性的概率度量
可靠概率: 失效概率:
结构能完成预定功能的概率(ps) 结构不能完成预定功能的概率(pf)
ps pf 1
失效概率pf 越小,结构的可靠性越高; 失效概率pf 越大,结构的可靠性越低。
习惯上以失效概率pf来度量结构可靠度。
第一节 结构可靠度基本原理
第二节 结构可靠度基本分析方法
(一)两个正态随机变量情况
极限状态方程为
Z g ( R , S ) R S 0
标准化变换,令
R R R R
S S S S
极限状态方程变化为
Z RR SS R S 0
R( R ) S R 2S 2
S RS 0
R 2S 2
R 2S 2
Zg ( X 1 , X 2 , , X n ) i n ( 1 X iX i) X g i
功能函数的统计参数为
第二节 结构可靠度基本分析方法
Z g ( X 1 , X 2 , , X n ) Z
可靠指标为
n(g
i1 Xi
Xi)2
Z g(X1,X2, ,Xn)
Z
n(g
承载的变形。该状态为:
1)整个结构或结构的一部分作为刚体失去平衡(如滑动、 倾覆等);
第9章 结构可靠度分析

时,或结构功能函数为非线性
函数时â
pf
√结构可靠指标很难用基本变
量的统计参数表达â
μZ
Z √则要由失效概率计算可靠指
可靠指标β与失效概率pf的关系
标。
9 - 16
第二节 结构可靠度分析的实用方法
一、中心点法
Ö特点:仅利用基本随机变量的统计参数(均值和方差)计算 结构的可靠度,因此实用方便。
与R相互独立,则
fZ (Z ) = fZ (R, S) = fR (R) × fS (S)
òò 此时有pf = P{Z < 0}= P{R-S < 0}= fR(R) fS(S)dRdS R-S<0
先对R积分,再对S积分,由上式有: 先对S积分,再对R积分,由上式有:
ò ò p f
=
+¥é -¥ êë
÷ö ø
dM=0.05。L为常数,L=4m。采用中心点法计算可靠指标。
P
q
L/2
L/2
简支梁及其受载
9 - 20
第二节 结构可靠度分析的实用方法
解:
mZ
=
mM
-
L 4
mP
-
1 8
L2 m q
= 18 -
4 4
´10
-
1 8
´42´源自2=4kN × m
s P = mPd P = 10´ 0.10 = 1.0kN
< 0}= PîíìsZZ
<
0ýü þ
=
P
ì í î
Z
s
m
Z
Z
< - mZ sZ
ü ý þ
其中:mZ = mR - mS , s Z =
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一节 结构可靠度基本概念
(1) 整个结构或结构的一部分作为刚体失去平衡(如倾覆等); (2) 结构构件或连续因材料强度被超过而破坏(包括疲劳破坏),或
因过度的塑性变形而不适于继续承载; (3) 结构转变为机动体系; (4) 结构或结构构件丧失稳定(如压屈等)。
7
第一节 结构可靠度基本概念
2.正常使用极限状态
(1) 能承受在正常施工和正常使用时可能出现的各种作用; (2) 在正常使用时具有良好的工作性能; (3) 在正常维护下具有足够的耐久性能; (4) 在偶然事件发生时(如地震、火灾等)及发生后,仍能保
持必需的整体稳定性。
3
第一节 结构可靠度基本概念
(1)、(4)为结构的安全性 (2)为结构的适用性 (3)为结构的耐久性
延性结构 脆性结构
目标可靠度指标
重要结构 3.7 4.2
一般结构 3.2 3.7
次要结构 2.7 3.2
第二节 结构概率可靠度的直接设计法
结构概率可靠度设计法
直接设计法 间接设计法
单一系数设计法 多系数设计法
● 直接设计法定义: 直接基于结构可靠度分析理论的设计方法。
●简单示例: 已知µS、δ R 、δS,求µR 。
表10-3 结构设计使用年限分类
类别 设计使用年限(年)
示例
1
5
临时性结构
2
25
易于替换的结构构件
3
50
普通房屋和构筑物
4
100
纪念性建筑和特别重要的建筑结构
功能要求:
结构在规定的设计使用年限内应满足下列功能要求: 1、在正常施工和正常使用时,能承受可能出现的各种作用。 2、在正常使用时具有良好的工作性能。如吊车梁1、风摇晃2 ,水池等。 3、在正常维护下具有足够的耐久性。如材料的使用寿命3 。 4、当发生火灾时,在规定的时间内可保持足够的承载能力。钢结构。 5、在偶然事件发生时(如地震、爆炸等)及发生后,仍能保持必要的 整体稳定性,不出现与起因不相称的破坏后果,防止出现结构的连续倒 塌。
对应于结构或结构构件达到正常使用或耐久性能的某项规 定限值。 (1)影响正常使用或外观的变形; (2)影响正常使用或耐久性能的局部损坏(包括裂缝); (3) 影响正常使用的振动; (4) 影响正常使用的其他特定状态。
8
第一节 结构可靠度基本概念
●结构可靠度
➢ 定义:结构在规定的时间内,在规定的条件下,完成预定功能 的概率。是结构可靠性的概率量度。
公众心理 较安全 安全 很安全
2、结构重要性的影响 一般结构 ps 重要结构 ps↑ 次要结构 ps↓
3、结构破坏性质的影响 ✓ 脆性结构 ps > 延性结构 ps
4、社会经济承受力的影响 ✓ 经济越发达 → ps↑
● 校准法
承认传统设计所具有的可靠度的合理性,通过计算得出的传统设计的 可靠度水平作为参考目标可靠度。
Pf
1.35x10-3
1.5 6.68x10-2
3.5 2.33x10-4
2.0 2.28x10-2
4.0 3.17x10-5
2.5 6.21x10-3
4.5 3.40x10-6
1 5
一、设计要求
R≥S
不能绝对满足,只能在一定概率意义下满足,即:
P {R≥S }=ps
二、目标可靠度
● 可靠度β 的大小对结构设计的影响
●结构的功能函数
令 Z=R–S R:结构抗力; S:结构荷载效应。
统称为结构的可靠性
4
第一节 结构可靠度基本概念
则有三种情况:
(1) Z > 0 结构可靠
(2) Z < 0 结构失效
(3) Z = 0 结构处于极限状态
称
Z=R–S
为结构的功能函数
Z = R – S = 0 为结构极限状态方程
由于影响荷载效应S和结构抗力R都有很多基本的
1 1
第一节 结构可靠度基本概念
●结构可靠指标
➢ 如果R和S为两个相互独立的正态随机变量,则 其中
1 2
令
则 Φ(•):标准正态分布函数
标准正态随机变量
1 3
第一节 结构可靠度基本概念
➢ β与Pf的关系
β越大,Pf越小, Ps越大
1 4
β与Pf的数值关系
β
1.0
Pf
1.59x10-1
β
3.0
ps太大 ps太小
成本高 失效概率大
目标可靠度β 的确定应考虑: 经济与安全的合理平衡
✓ 一般需考虑以下四个因素:
(1) 公众心理 (2) 结构重要性 (3) 结构破坏性质 (4) 社会经济承受力
●各种因素对目标可靠度的影响
1、公众心理的影响
事故 爬山、赛车 飞机旅行
采矿 房屋失火
雷击
一些事故的年死亡率
✓ 规定的时间——一般指结构设计基准期。在同样的条件下,规 定时间越长,结构的可靠度越低。
✓ 规定的条件——指正常设计、正常施工、正常使用条件,排除 人为错误或过失因素。
9
第一节 结构可靠度基本概念
➢ 基本计算公式
可靠度 失效概率
或 如果S与R相互独立,则
1 0
第一节 结构可靠度基本概念
pf R fS(S)d SfR(R )dR
随机变量,则结构功能函数的一般形式为
5
第一节 结构可靠度基本概念
●结构极限状态
✓ 定义:如果整个结构或结构的一部分超过某一特定状态就不能满 足设计规定的某一功能要求,则此特定状态称为该功能的极限状 态。
✓ 两类极限状态——承载能力与正常使用
1.承载能力极限状态
对应于结构或构件达到最大承载能力或不适于继续承载的变形。
由
由上式可解得µR 。 计算繁琐,计算工作量大 除重要工程结构:核反应堆容器、海上采油平台、大坝等宜采用可靠度直接设计法, 大量一般性工程,均常用可靠度间接设计法。
可靠度间接设计法: 采用方便实用的设计表达式,使其具有的可靠度水平与设计目标可靠度尽量
一致或接近。
设计使用年限:
结构在正常设计个年限内,结构只需要进行正常的维护而不需要进行 大修就能够按预期目的使用。如果达不到这个年限则意味着在设计、 施工、使用和维护的某一环节上出现了不正常情况,应查找原因。
年死亡率
事故
5X10-3
汽车旅行
1X10-4
游泳
7X10-4
结构施工
2X10-5
电击
5X10-7
暴风
年死亡率 2.5X10-5 3X10-5 3X10-5 6X10-6 4X10-6
年危险率 10-3 10-4 10-5
50年失效率 5X10-3 5X10-4 5X10-5
可承受人群 胆大的人 一般的人 不再考虑其危险性
第九章-结构可靠度的基本概念
R≥S 不能绝对满足,只在一定概率意义下满足,即:
P{ R ≥S }=Ps Ps----结构可靠概率或结构可靠度
建筑结构设计目标:使得结构在规定的设计使用年限内以适 当的可靠度且经济的方式满足规定的各项功能要求。
第一节 结构可靠度基本概念
●结构的功能要求
四项基本功能:
