波函数满足定态薛定谔方程
15.6 波函数 一维定态薛定谔方程
2
2mE
2
2
, n 1, 2 ,
En n
π
2 2
,
n 1, 2 ,
2ma
n 为主量子数，表明粒子的能量是量子化的。
大学物理 第三次修订本
13
第15章 量子物理基础
波函数
nπ Ψ n x A sin a
2 a
x , n 1, 2 ,
i t Ψ (r , t ) Ψ (r )e
E
定态薛定谔方程
2m 2 2 2 Ψ( r ) 2 E V Ψ(r ) 0 x y z
2 2 2
若粒子在一维空间运动，则
d Ψ x
2
dx
2
2m
大学物理 第三次修订本
o
a
x
势能曲线
11
第15章 量子物理基础
薛定谔方程
d Ψ x
2
dx
2
2mE
2
Ψ x 0
d Ψ x
2
,0 xa
k Ψ x 0
2
令 k
2 mE
2
则
dx
2
方程通解
Ψ x A sin kx B cos kx
Ψ 利用边界条件 x = 0， 0 0 , 则 B = 0 。
物质波波函数是复数，它本身并不代表任 何可观测的物理量。 波函数是怎样描述微观粒子运动状态的？
大学物理 第三次修订本
3
第15章 量子物理基础
1926年德国物理学家玻恩提出了物质波的 统计解释：实物粒子的物质波是一种概率波, t 时刻粒子在空间 r 处附近的体积元 dV 中出现的 概率dW与该处波函数绝对值的平方成正比。
19-(3)波函数 薛定谔方程
1
一 波函数
波函数：描述具有波粒二象性粒子的运动函数。 设一自由粒子，不受外力作用，则粒子作匀速直线运动（设 沿X轴），其动量、能量保持恒定。 X
E const
P const
E h
h p
恒定！ 恒定！
从波动观点看来：这种波只能是单色平面波。
2
自由粒子的波函数 X
波函数：描述具有波粒二象性粒子的运动函数。 注意：波函数一般要用复数表示!
5
二 波函数的统计解释（波恩Born）
代表什么？
粒子的观点 极大值 极小值 中间值 较多电子到达 较少电子到达 介于二者之间 波动的观点 波强度大 波强度小 介于二者之间
b
x
p h
大量粒子的一次性行为和一个粒子多 次性重复性行为是等价的。 统一地看：粒子出现的几率正比
E Ek
Px
2m
i
t
2
2 2
2m x
( 6)
15
2 势场中的薛定谔方程
若粒子处在势场中，势能为U（x、t），总能量：
E Px
2
U ( x , t )(7)
Px
2
2m
E U ( x , t ) ( 8)
2m
将（5）式看成一般情况下的特例：
2
( x , y , z ) U ( x , y , z ) E ( x , y , z )(18)
2
2m
定态薛定谔方程： 2
2m
2
( E U ) 0(19)
19
2
量子力学与统计物理习题解答完整版
量子力学与统计物理习题解答 第一章1. 一维运动粒子处于⎩⎨⎧≤>=-)0(0)0()(x x Axe x xλψ的状态，式中λ>0，求（1）归一化因子A ； （2）粒子的几率密度；（3）粒子出现在何处的几率最大？ 解：（1）⎰⎰∞-∞∞-*=0222)()(dx e x Adx x x x λψψ令 x λξ2=，则323232023202224!28)3(88λλλξξλξλA AA d e A dx ex Ax=⨯=Γ==-∞∞-⎰⎰由归一化的定义1)()(=⎰∞∞-*dx x x ψψ得 2/32λ=A（2）粒子的几率密度xe x x x x P λλψψ2234)()()(-*==（3）在极值点，由一阶导数0)(=dxx dP 可得方程0)1(2=--xe x x λλ 而方程的根0=x ；∞=x ；λ/1=x 即为极值点。
几率密度在极值点的值0)0(=P ；0)(lim =∞→x P x ；24)/1(-=e P λλ由于P(x)在区间(0，1/λ)的一阶导数大于零，是升函数；在区间(1/λ，∞)的一阶导数小于零，是减函数，故几率密度的最大值为24-e λ，出现在λ/1=x 处。
2. 一维线性谐振子处于状态t i x Aet x ωαψ212122),(--=（1）求归一化因子A ；（2）求谐振子坐标小x 的平均值；（3）求谐振子势能的平均值。
解：（1）⎰⎰∞∞--∞∞-*=dx e Adx x222αψψ⎰∞-=02222dx e A xα⎰∞-=222ξαξd e Aαπ2A =由归一化的定义1=⎰∞∞-*dx ψψ得 πα=A （2） ⎰⎰∞∞-∞∞--==dx xe A dx x xP x x222)(α因被积函数是奇函数，在对称区间上积分应为0，故 0=x （3）⎰∞∞-=dx x P x U U )()(⎰∞∞--=dx e kx x 22221απα ⎰∞-=0222dx e x k x απα⎰∞-=222ξξπαξd e k⎥⎦⎤⎢⎣⎡+-=⎰∞-∞-0022221ξξπαξξd e e k⎰∞-=02221ξπαξd e k 2212ππαk=24αk =将2μω=k 、μωα=2代入，可得02141E U ==ω 是总能量的一半，由能量守恒定律U T E +=0可知动能平均值U E U E T ==-=0021和势能平均值相等，也是总能量的一半。
大学物理课件：23-2波函数与薛定谔方程
0.091
例：试求在一维无限深势阱中n=1粒子概率密度的最大值的位置。
解：一维无限深势阱中n=1粒子的概率密度为
1(x)
2
2 a
sin2
a
x
n (x)
d 1(x) 2
dx
4
a2
sin
a
x
cos
a
x0
2 sin n x
aa
因为粒子在阱内，则
sin
a
x
0
cos
a
x
0
a
x
2
由此解得最大值得位置为
在 dV 空间内发现粒子的概率： dP 2 dV *dV
概率密度 表示在某处单位体积内发现粒子的概率. Ψ 2 *
某一时刻在整个空间内发现粒子的概率为:
Ψ
2
dV
1
归一化条件
波函数的标准化条件
1）波函数具有有限性
有限空间内：
Ψ
2
dV
1
2）波函数是连续的
3）波函数是单值的
例：作一维运动的粒子被束缚在 0 x的 a范围内。已知其波函数
移动原子
六、一维简谐振子
微观领域中分子的振
动、晶格的振动、，都
可以近似地用简谐振子模
型来描述 。
一维简谐振子的经典模型
一维简谐振子的势函数：
U (x) 1 kx2 1 m2x2
2
2
k m,
m —— 振子质量， —— 固有频率，x —— 位移
相应的定态薛定谔方程为 ：
2 d2 1 m 2 x2 E
2
2m
d2 dx2
U
x
x
E
x
2
大学物理(下册) 14.6 波函数 薛定谔方程
1.所描述的状态称为 F 的本征态，而上式则 称为本征值方程；
2.波函数的标准条件：单值、有限和连续；
例题 14.6.1 设质量为m的粒子沿x轴方向运动，其势 能为： , x 0,x a Ep u ( x) 0, 0 x a （14.6.15）
无限深势阱：该势能如图所示形如一 无限深的阱，故称无限深势阱，本问 题为求解该一维无限深势阱内粒子的 波函数。
2 2 1 f ( t ) (x, y,z ) 推出： i V (x, y,z ) f (t ) t 2m (x, y,z )
设常量E：
1 f (t ) i E f (t ) t
2
[
2m
V (x, y,z )] (x, y,z ) E (x, y,z )
o
a
x
解：分析 因为势能不随时间变化，故粒子波函数 满足定态薛定谔方程，在势阱内势能为零故其定 态薛定谔方程为：
定态薛定谔方程为：
Ep
k 2mE
d 2 k 0 2 dx
2
其通解为： ( x)
A sin kx B cos kx
o
a
x
由波函数的标准条件：单值、有限和连续可得：
2.定态薛定谔方程 势能函数： V V ( x, y, z ) 波函数可以分离为坐标函数和时间函数的乘积：
(x, y,z,t ) (x, y,z ) f (t )
（14.6.8）
将其代入薛定谔方程式：
2 f (t ) i (x, y,z ) 2 (x, y,z ) f (t ) V (x, y,z ) (x, y,z ) f (t ) t 2m
2
解之得： 定态波函数：
波函数薛定谔方程
(r .t )
0e
i
(
Et
pr )
波函数Ψ是复数，模的平方可表示为
2 *
5
4 、波函数的统计解释: (1)概率密度: 玻恩假定：概率波的波函数Ψ，模的平方
| r,t|2 r,t* r,t
代表 t 时刻，在空间 r 点处单位体积元中发现一个粒子的概 率，称为概率密度。
t 时刻在空间 r 附近体积 dv 内发现粒子的概率为：
为物质波能够干涉)。
薛定谔提出了波函数Ψ(x,y,z,t)所适用的（在非相对论） 动力学方程：
2 2 U x, y, z,t i
2m
t
（１）式中 2 2 2 2 称之为拉普拉斯算符， x2 y 2 z 2
11
（２）U x, y, z, t
表示微观粒子受到的作用势能，它一般的是 r 和 t 的函数， （３） m 是微观粒子的质量。
薛定谔方程既不能由经典理论导出，也不能用严格的逻辑推 理来证明，它的正确与否只能用实验来验证。
1 、一般的薛定谔方程 微观粒子的运动状态用波函数
Ψ(x,y,z,t)描述，薛定谔认为，这 个波函数应该是适用于微观粒子的波 动方程的一个解。
10
•必须能满足德布罗意波公式的要求，
E , h
h
p
•必须是线性微分方程,即其方程的解必须能满足叠加原理 (因
的原理可以证明它的正确性。 从薛定谔方程得到的结论正确与否，需要用实验事实去验证。
薛定谔方程是量子力学的一条基本假设。
14
例 15-23 将波函数在空间各点的振幅同时增大 D 倍,则粒子在 空间的分布概率将
(A)增大Ｄ２倍;(B)增大 2 D 倍;(C)增大 D 倍;(D)不变。
量子力学电子教案波函数和 薛定谔方程
波函数和 薛定谔方程
微观粒子的基本属性不能用经典语言确切描述。
量子力学用波函数描述微观粒子的运动状态，波函数所 遵从的方程——薛定谔方程是量子力学的基本方程。 一、 物质波的波函数及其统计解释
1. 波函数： 概率波的数学表达形式， 描述微观客体的运动状态
(r , t ) ( x, y, z, t )
对屏上电子数分布 作概率性描述
一般 t 时刻,到达空间 r（x,y,z）处某体积dV内的粒子数 ： 2 d N N | | d V
| ( x, y, z, t ) | *
2
dN N dV
| ( x, y, z, t ) |
2
的物理意义:
• t 时刻，出现在空间（x,y,z）点附近单位体积内的 粒子数与总粒子数之比 • t 时刻，粒子出现在空间（x,y,z）点附近单位体积 内的概率 • t 时刻，粒子在空间分布的概率密度
2. 波函数的强度——模的平方 2 波函数与其共轭复数的积 | | * 例：一维自由粒子：
| ( x, t ) | * 0e
2 i ( E t p x x ) i h ( E t p x x )
0e
0
2
3. 波函数的统计解释
1 2
| | | 1 2 | 1 1 * 2 2 * 1 2 * 1 * 2
2 2
干涉项
4、 波函数的归一化条件和标准条件 归一化条件 粒子在整个空间出现的概率为1
|
V
| dV
2
V
dN N dV
即
三维定态薛定谔方程
一般形式薛定谔方程
波函数及薛定谔方程
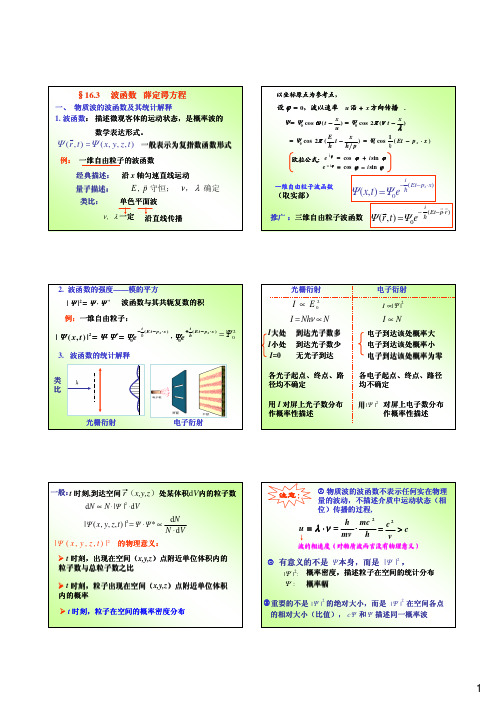
t 时刻，出现在空间（x,y,z）点附近单位体积内的 粒子数与总粒子数之比
t 时刻，粒子出现在空间（x,y,z）点附近单位体积 内的概率
t 时刻，粒子在空间的概率密度分布
注意：
物质波的波函数不表示任何实在物理 量的波动，不描述介质中运动状态（相 位）传播的过程,
NN
标准条件
Ψ是单值、有限、连续的 。
二、薛定谔方程： 是波函数 Ψ所遵从的方程 — 量子力学的基本方程 , 是量子力学的基本假设之一，其正确性由实验检验。
1. 建立 （简单→复杂， 特殊→一般）
一维自由粒子的振幅方程
Ψ (x,t)
=Ψ e−
i ℏ
(
E
t
−
px
⋅
x
)
0
=
Ψ
0e
+
i ℏ
p
x
⋅x
−i Et
2 x
2m
代入
d2ψ ( x) dx2
=
−
px ℏ2
2
ψ
(
x
)*
得
d 2ψ ( x ) dx2
+
2 mE ℏ2
ψ
(x)
=
0
即 一维自由粒子的振幅方程
p
2 x
=
2mE
一维定态薛定谔方程
粒子在力场中运动，且势能不随时间变化
E
=
Ek
+
Ep
=
p
2 x
2m
+U
px2 = 2m(E −U )
代入
d2ψ ( x) dx2
∴ 建立关于振幅函数 ψ(x)的方程 —— 振幅方程
波函数薛定谔方程
✓ 必须能满足德布罗意波公式的要求
E , h
h
p
✓ 必须是线性微分方程,即其方程的解必须能满 足叠加原理 (因为物质波能够干涉)。
第16章 量子物理基础
16–6 波函数 薛定谔方程
8
薛定谔提出了波函数Ψ(x,y,z,t)所适用的（在非相对论） 动力学方程：
i
2
2 V
t
2m
（1）2 2 2 2 称之为拉普拉斯算符
2m
式中Ｅ是粒子的总能量，又称为能量本征值。
第16章 量子物理基础
16–6 波函数 薛定谔方程
11
一维定态薛定谔方程
设微观粒子在外势场中作一维运动，这时该方程为
d2 dx2
(x)
2m
2
(E
V
)
(
x)
0
对于自由粒子，V＝0，在一维情况，并注意 E p2
(非相对论)
2m
i px
(x) 0e
第16章 量子物理基础
16–6 波函数 薛定谔方程
12
3.薛定谔方程的意义
✓ 薛定谔方程在量子力学中的地位与牛顿方程在 经典物理中的地位相当。
✓ 薛定谔方程本身并不是实验规律的总结，也没 有什么更基本的原理可以证明它的正确性。
✓ 从薛定谔方程得到的结论正确与否，需要用实 验事实去验证。薛定谔方程是量子力学的一条基本 假设。
第16章 量子物理基础
16–6 波函数 薛定谔方程
6
二、薛定谔方程
薛定谔（Erwin Schro..dinger， 1887~1961）奥地利物理学家. 1926年建 立了以薛定谔方程为基础的波动力学,并 建立了量子力学的近似方法. 他还对生命 科学作出重大贡献，他的指导思想是 “科学一定是统一的、相通的.”
波函数与薛定谔方程
§2.5
定态薛定谔方程
这里讨论一个极为重要的特殊情况： 假设势能U不显含时间t（经典力学中，在这种势场 中的粒子的机械能是守恒量）。 此时，薛定谔方程可以用分离变量法求其解，令特 解为
(r , t ) (r ) f (t )
代入薛定谔方程
i f t
i t
2
(r , t ) * (r , t )
(1)
几率密度时间变化率
w t * t * t
(2)
将薛定谔方程
i t
2
U
2
i
* t
2
U
2
2m
2m
代入得：
w t i 2m i 2m ( * *)
第二章 波函数与薛定谔方程
2.1 波函数的统计解释 2.2 态迭加原理 2.3 薛定谔方程 2.4 粒子流密度和粒子数守恒 2.5 定态薛定谔方程 2.6 一维无限深势阱 2.7 线性谐振子
§2.1波函数的统计解释
• 一、波函数 • 一般情况下，用一个函数表示描写粒 子的波，并称这个函数为波函数。 (r , t ) ( x, y , z , t ) 波函数的统计解释：波函数在空间某点 的强度（振幅绝对值的平方， (r , t ) 2 ）和 在该点找到粒子的几率成正比。 描写粒子的波称为几率波。 波函数描写粒子的量子状态。
c 1 d
2
令
c则w
2
2
( x, y, z, t ) d 1
满足上式的波函数称为归一化波函数，上式也称为 归一化条件， c 称为归一化常数。
例：给定 ( x)
波函数与薛定谔方程
直到1926年波恩提出统计诠释，大多数物理学家接受
在已知给定的条件下，不可能精确地预知结果，只能预言某些 可能结果的概率 粒子的运动遵守概率定律，但概率本身还是受因果规律支配的 但争论仍在继续：
哥本哈根学派：玻尔、海森伯坚持波函数的概率或统计解释 认为它表明了自然界的最终实质 爱因斯坦不喜欢量子力学的“不完备性” 上帝不是跟宇宙玩掷骰子游戏
满足归一化条件 d 3r 1 的波函数
16
例
17
例
18
续
19
例
20
薛定谔方程引言
21
16-2 薛定谔方程
量子力学基本原理之二： 微观粒子体系的波函数ψ满足
薛定谔方程.
起源： 1926年薛定谔对德布罗意的工作了漂亮又简
洁的说明,-----德拜听后说“要真正研究波动,必须
有波动方程.” 几个星期后,薛定谔找到了这个方程.
也是这个体系的一个可能态。
c11 c2 2 cn n cn n
c1, c2, cn为任意常数 n
波函数遵从叠加原理由实验证实： 以双缝实验为例
1、子弹通过双缝的射击实验 （经典）
子弹
宏观粒子 可以跟踪
a P1
b
P2
P
P P1 P2概率叠加
H
i
t
如果知道了 U ，可列出微分方程，解得Ψ，即找到 Ψ 随时 间变化的规律。
27
定态薛定谔方程：如果粒子所处的势场 U( r ) 与时间无关(即
不显含时间), 可用分离变量法求解.
令
H i
r, t
t r
f
t
第2章 波函数与薛定谔方程
二、波函数的统计解释
电子(微观粒子)到底是什么？ 它既不是经典的粒子，也不是经典的波。它是粒子 和波动两重性矛盾的统一。实际上是粒子“颗粒性” (具有一定的质量和电荷等属性的客体，但不与粒
6
子具有确定轨道相对应，这是由于位置和动量不能 同时具有确定的值，即测不准关系，后讲)与波的 “相干叠加性”(呈现干涉、衍射等现象，但不与 某种实在物理量在空间分布的周期性变化相对应) 的统一。
ˆ i p
3 ˆ 则 p * ( r ) p ( r ) d r
20
可表为
ˆ ) p (，p
动量算符
上式表明，动量平均值与波函数的梯度密切相关 （与波数 k 成正比）。 动能T=p2/2m和角动量L=r×p的平均值也可类似 求出。 一般说来，粒子的力学量A的平均值可如下求出
2
A-1/2称为归一化因子。波函数归一化与否，并 不影响几率分布。
12
注意：1）象平面波等一些理想波函数，它 们不能归一化。对此的归一化问题将在后 边介绍； 2）对于归一化的波函数仍有一个模为1的 因子不定性，即相位（phase）不定性。
e i 1
e
i
2
2
13
三、统计解释对波函数提出的要求
3
一、 波动、粒子两重性矛盾的分析
1 把电子看成是物质波包
包括波动力学的创始人薛定谔、德布罗意等人把 电子波理解为电子的某种实际结构，即看成三维 空间中连续分布的某种物质波包，因而呈现出了 干涉、衍射等现象。波包的大小即电子的大小， 波包的群速度即电子运动的速度。按经典自由粒 子能量，并利用德布罗意关系可得
第二章波函数与薛定谔方程
第二章 波函数与薛定谔方程2.1 设22()exp )2(x x A αψ-=，α为常数, 求归一化常数A . 解：由波函数满足的归一化条件()21x dx ψ+∞-∞=⎰有2222222222()exp 12()x x x x dx A dx A e dx A e dx αααψ+∞+∞+∞+∞---∞-∞-∞-∞-====⎰⎰⎰⎰由积分公式2x e dx +∞--∞=⎰有()()222211x x y e dx ed xe dy ααα+∞+∞+∞----∞-∞-∞===⎰⎰⎰即22221x A e dx A α+∞--∞==⎰，归一化常数A =2.2 设粒子波函数为(,,)x y z ψ ，求在(,)x x dx +范围中找到粒子的概率.解：在(,)x x dx +范围内找到粒子的概率为2(,,)x y z dydz dx ψ+∞+∞-∞-∞⎛⎫⎪⎝⎭⎰⎰.2.3 设在球坐标系中，粒子波函数表为(,,)r ψθϕ，求：(1)在球壳(,)r r dr +中找到粒子的概率；(2)在(,)θϕ方向的立体角d Ω中找到粒子的概率.解：(1)在球壳(,)r r dr +中找到粒子的概率为()22|(,,)|r d r dr ψθϕΩ⎰； (2)在(,)θϕ方向的立体角d Ω中找到粒子的概率()22|(,,)|r r dr d ψθϕΩ⎰.2.4求平面单色波为00()p i x p x ψ⎛⎫⎪⎝⎭=在动量表象中的形式. 解：由坐标表象与动量表象间傅里叶变换式()()121,t (,)e2ipx p x t dx ϕψπ+∞--∞=⎰得单色平面波动量表象中的形式为()()()()001112122111,t ()e e 222ii p x px px p p x dx e dx ϕψπππ⎛⎫ ⎪⎝⎭+∞+∞---∞-∞⎛⎫ ⎪ ⎪⎝⎭==⎰⎰()()001e2i p p xdx p p δπ+∞---∞==-⎰即平面单色波的波函数在动量表象中的表示形式为()()00,p p t p p ϕδ=-.2.5 粒子在0x x =点的量子态为δ函数00()()x x x x ψδ=-，试在动量表象中写出此量子态的形式.解：由坐标表象与动量表象间傅里叶变换式()()121,t (,)e 2i px p x t dx ϕψπ+∞--∞=⎰得δ函数在动量表象中量子态的形式为()()()()00012211211()e e21,t ()2e 2ip i ip x x x x p p x dx x x dx δϕπψππ+∞-----∞+∞∞-===⎰⎰即量子态为δ函数的波函数在动量表象中表示形式为()()00121,t e2i px x p ϕπ-=.2.6 证明从单粒子薛定谔方程得出的粒子速度场是非旋的，即求证0v ∇⨯=，其中/v j ρ=，ρ为概率密度，j 为概率流密度.证明：概率密度为()()(),,,r t r t r t ρψψ*=概率流密度为()()()()(),,,,,2j r t r t r t r t r t mi ψψψψ**⎡⎤⎣⎦=∇-∇根据薛定谔方程式可导出几率守恒方程，并定义几率流密度()()()()()(),,ln ,ln ,2,,2r t r t jv r t r t mi r t r t miψψψψρψψ***⎡⎤⎡⎤⎢⎥⎣⎦⎢⎥⎣⎦∇∇==-=∇-∇()()()()()ln ,ln ,l 2,,n 2r t i m r r t r t t mi ψψψψ**⎡⎤⎣⎦=∇-=∇可见v 正比于一个标量场()(),,r t r t ψψ* 的对数的梯度.梯度场无旋，故v是一个无旋场(0v ∇⨯=).2.7 设粒子在复势场()()()12V r V r iV r =+ 中运动，其中()1V r 和()2V r为实数，证明粒子的概率不守恒，并求出在某一空间体积中粒子概率“丧失”或“增加”的速率.解：根据薛定谔方程及其复数共轭形式()22122i V iV t m ψψψ∂=-∇++∂ (2.7.1)()22122i V iV t mψψψ***∂-=-∇+-∂ (2.7.2)ψ**(2.7.1) -ψ*(2.7.2)得()222222i iV t t m ψψψψψψψψψψ*****⎛⎫ ⎪⎝⎭∂∂+=-∇-∇+∂∂()2222iV mψψψψψψ***=-∇⋅∇-∇+ (2.7.3)即()()222V t mi ψψψψψψψψ****∂+∇⋅∇-∇=∂，可以写为 22j V tρρ∂+∇⋅=∂(2.7.4)其中()()(),,,r t r t r t ρψψ*=，()()()()(),,,,,2j r t r t r t r t r t mi ψψψψ**⎡⎤⎣⎦=∇-∇.上式右边不为零，这意味着粒子的几率不守恒.将上式对空间Ω积分，则得3322Sd r jds d rV t ρρΩΩ∂+=∂⎰⎰⎰ 故某一空间体积中粒子概率“丧失”或“增加”的速率为3322S V d r jds d r t ρρΩΩ∂=-+∂⎰⎰⎰ .2.8 设()()()1212,0E E r c r c r ψψψ=+ ，问(),0r ψ是否为定态，为什么？求(),r t ψ.解：(1)由于定态是体系能量具有确定值的状态，而题中波函数(),0r ψ处于能量1E 的本征态()1E r ψ与能量2E 的本征态()2E r ψ 的叠加状态，故(),0r ψ 不是定态；(2) t 时刻的波函数为()()()121212,i i E t E t E E r t c r e c r eψψψ--=+.2.9 计算1ikr e ψ=和2ikr e r ψ-=相应的概率流密度，并由所得结果说明这两个波函数描述的是怎样传播的波.解：由微商关系式：x y z e e e x y z∂∂∂∇=++∂∂∂ ，r r r e r ∇==，3211r r e r r r ∇=-=-(1)1ψ的概率流密度为：1ikr e r ψ=，1ikr e rψ-*= ()()()2122211ikr ikrikr ikrik ik ikr r r r e r e r ikr e e ikre r e r r rr r r ikr e e r ψ⎛⎫⎪⎝⎭∇-∇-∇-∇-∇=∇===∇= 或()111111ikrikrikr ikr ikr ikr ikr ikr r r r ikr e e ike e e e ike r e r e e e rrr r r r r r ψ⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭-∇=∇=∇+∇=∇+-∇=-= ()()()2212211ikrikr ikr ikr ikr i r r i r k k e r e r ikr e e ikre r e r r rr r r ikr e e r ψ-*------⎛⎫⎪⎝⎭∇-∇+-∇-∇=∇===--∇=+∇ ()()()()()11111,,,,,2j r t r t r t r t r t mi ψψψψ**⎡⎤⎣⎦=∇-∇()()22112ikrikrikr ikr r r ikr e ikr e e e e e mi r r r r --⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫⎢⎥ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦-+=--112r ikr ikr e mi r r ⎛⎫ ⎪⎝⎭--=+2rk e mr =即()12,r k j r t e mr=描述的是沿径向向外传播的球面波； (2) 2ψ的概率流密度为：2ikr e r ψ-=，2ikr e rψ*= ()()()2222211ikr ikrikr ikr ikri r kr ikr e r e r ikr e e ikre r e ikr e e r r r rr r r ψ-------⎛⎫⎪⎝⎭∇-∇+-∇-+∇-∇=∇===-∇= ()()()2222211ikr ikrikr ikrikr ikr r ikr e r e r ikr e e ikre r ik e r r rr r r e r e r ψ*⎛⎫⎪⎝⎭∇-∇-∇-∇=∇====∇∇- ()()()()()22222,,,,,2j r t r t r t r t r t mi ψψψψ**⎡⎤⎣⎦=∇-∇()()22112ikrikr ikr ikrr r ikr e ikr e e e e e mi r r r r --⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫⎢⎥ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦+-=-- ()33112r ikr ikr e mi r r ⎛⎫ ⎪ ⎪⎝⎭-+-=-2rk e mr =-即()22,r k j r t e mr=-描述的是沿径向向内传播的球面波.2.10 粒子在一维势场中运动，若所处的外场均匀但与时间有关，即()(),V x t V t =，试用分离变量法求解一维薛定谔方程.解：由一维薛定谔波动方程()()()222,,,2i x t V x t x t t m x ψψ⎡⎤⎢⎥⎣⎦∂∂=-+∂∂ ， 采用分离变量法求特解，令其特解可表示为()()(),x t x f t ψϕ=，带入一维薛定谔波动方程有()()()()()()()()()()2222i x f t x f t V t x f t t m x ϕϕϕ∂∂=-+∂∂ ()()()()()()()()2222x i f t f t x V t x f t t m xϕϕϕ∂∂=-+∂∂方程两边同时除以()()x f t ϕ可得()()()()()22212f t i x V t f t t m x x ϕϕ∂∂=-+∂∂ ()()()()()22212f t i V t x f t t m x x ϕεϕ∂∂-=-≡∂∂其中ε是既不依赖于t ，也不依赖于x 的常数.(1)此时关于时间部分为：()()()f t i V t f t tε∂-=∂ 方程两边同时对时间t 积分得()()()()()()00000ln tt t t t df i d d V d d i f d V d t f d d ττττετττττε-=⇒-=⎰⎰⎰⎰⎰()()()()00ln ti V d t ti f t V d t f t e ττεττε⎛⎫ ⎪⎝⎭-+⎛⎫ ⎪⎝⎭⎰=-+⇒=⎰(2)关于坐标的部分为：()()()()2222221202d d m x x x m x dx dx εϕεϕϕϕ-=⇒+=此二阶齐次微分方程的解为()x Ae ϕ±=由上述两部分可知()()()()0,t i V d t x t x f t Ae eττεψϕ⎛⎫ ⎪ ⎪⎝⎭-+±⎰==其中A 和ε均为常数，分别由归一化条件和初试条件决定.2.11 粒子在无限深方势阱中(0x a <<)中运动，对处于定态()n x ψ的粒子，证明：2ax =，()222226112a x x n π⎛⎫ ⎪⎝⎭-=-， 0p =，()222n p p mE -=，讨论n →∞的情况，并与经典计算结果比较.解：一维无限深方势阱内(0x a <<)粒子的波函数为()n n x x a πψ⎛⎫⎪⎝⎭=， 能量本征值为22222n n E ma π= .(1) ()()0n n n x n x x x x x dx dx a a ππψψ+∞*-∞⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭==⎰⎰200cos 12sin 1222a a n x a n x x x a dx dx a a ππ⎛⎫⎛⎫⎛⎫- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭==⎰⎰ 0020022cos sin 1111122aaa a n x n x x a a dx dx x a a a n πππ⎛⎫⎛⎫⎛⎫- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭=-=⎰⎰2a=(2)()222202n x a n x x x x dx a a ππ⎛⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪ ⎝⎭⎝⎭⎝⎭⎝-=-⎰22222002212sin 1cos 222a a a n x a n x x dx x dx a a a a ππ⎛⎫⎛⎫⎧⎫⎛⎫⎛⎫⎛⎫ ⎪ ⎪⎨⎬ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎩⎭⎝⎭⎝⎭=-=--⎰⎰ 22220000112112cos cos 4a a a a n x a n xx dx x dx dx x dx a a a a a aππ=--+⎰⎰⎰⎰2222222260132412a a a a n n ππ⎛⎫ ⎪⎝⎭=--+=-(3)()()()(n n i i n x n x p x x dx dx a a ππψψ+∞*-∞⎛⎫⎛⎫-∇-∇ ⎪ ⎪⎝⎭⎝⎭==⎰⎰22022sin cos sin aan n x n x n n x i dx i dx a a a a a πππππ⎛⎫⎛⎫⎛⎫⎪ ⎪⎪⎝⎭⎝⎭⎝⎭-=-=⎰⎰0022022cos cos 222sin aaaa n x i n x n a a a n n x n i dx i a a a ππππππ⎛⎫⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭-==-=-⎰0=(4)()()222222220sin 2sin an n n x x x a n x p p x x dx dx a a ππψψ+∞*-∞⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭∂∂--∂∂-==⎰⎰2222222230022sin sin sin a an n x n a a a a n x n x dx dx a a πππππ⎛⎫⎛⎫⎛⎫⎛⎫ ⎪ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭--==⎰⎰002222223301221cos sin 222a a a n x a n x x a n a n n a a dx πππππ⎧⎫⎛⎫⎛⎫⎛⎫⎪⎪⎨⎬ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎪⎪⎩⎭-==-⎰22222n mE n a π==2.12 考虑质量为m 的粒子被限制在宽度为a 的一维无限深势阱();;0,2,2ax V x a x ⎧⎪⎪⎨⎪⎪⎩<=∞> 中运动，(1)粒子的能级和相应的波函数；(2)粒子处于基态的动量分布. 解：(1)在阱内体系所满足的定态薛定谔方程是2222d E m dx ψψ=- ，2a x < (2.12.1)在阱外，定态薛定谔方程为()2222V x d E m dx ψψψ+=- ，2a x > (2.12.2) (2.12.2)式中，()x V →∞.根据波函数所满足的连续性和有限性条件，只有当0ψ=时，(2.12.2)式才能成立，所以有0ψ=，2ax >(2.12.3) 该条件为解(2.12.1)式时所需的边界条件.为书写简便，引入记号1222mEα⎛⎫⎪⎝⎭= (2.12.4) 则(2.12.1)式简写为2220d dx αψψ+=，2a x <它的解是sin cos A x B x ψαα=+，ax <(2.12.5) 根据ψ的连续性，由(2.12.3)式20a ψ⎛⎫± ⎪⎝⎭=，代入(2.12.5)，有22sin cos 0aaA B αα+=， 22sin cos 0aaA B αα-+=.由此得到2sin 0aA α=，2cos 0aB α=. (2.12.6)A 和B 不能同时为零，否则ψ到处为零，这在物理上是没有意义的.因此，我们得到两组解：(1) 0A =，2cos 0aα= (2.12.7) (2) 0B =，2sin 0aα= (2.12.8)由此可求得22anαπ=，1,2,3,n = (2.12.9)对于第一组解，n 为奇数；对于第二组解，n 为偶数. 0n =对应于ψ恒为零的解，n 等于负整数时解与n 等于相应正整数时解线性相关（仅差一负号），都不取.由(2.12.4)式和(2.12.9)式，得到体系的能量为22222n n E maπ= ，n 为正整数. (2.12.10) 将(2.12.7)式、(2.12.8)式依次代入(2.12.5)式中，并考虑(2.12.9)及(2.12.3)两式，得到一组解的波函数为sin ,20,2n n aA x n x a a x πψ⎧<⎪⎪=⎨⎪>⎪⎩为正偶数 (2.12.11)另一组解的波函数为cos ,20,2n n aB x n x a a x πψ⎧<⎪⎪=⎨⎪>⎪⎩为正奇数 (2.12.12)由归一化条件21dx ψ∞-∞=⎰可得常数A B ==(2)粒子处于基态时1n =，体系的能量为22122E ma π= ，波函数为1x aπψ=，对应于动量空间的波函数为：()()221a a i i px px p x e dx x e dx a πϕψ∞---∞-⎫⎛⎫⎪ ⎪⎪⎝⎭⎭==⎰22c os 2aipx a ap x e dx a π--⎛⎫⎛⎫ ⎪⎪⎝⎭⎝⎭==⎰ 其中积分项2cosaipx a x edx a π--⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭⎰采用两次分部积分求出： 222222cossin sin a i px a a ai ipx px a a x e a a a ix edx x pe dx a a πππππ------⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭=-⎰⎰222sin i ai a p p aipx a i eep a a x e dx a πππ---⎛⎫⎛⎫⎛⎫=++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎰ (I)222222cossincos aipx a a aiipx px a a x e a a a ix edx x pe dx a a πππππ------⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭=---⎰⎰2cos aipx a i a p x e dx aππ--⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭=-⎰ (II) 结合(I)、(II)两式可得2222222222cos 2cos i a i a p p ai px a a ap a e e a p p a x e dx a πππππ---⎛⎫⎪⎛⎫⎛⎫⎛⎫⎝⎭+= ⎪ ⎪ ⎪-⎝⎭⎛⎫⎛⎫⎝⎭⎝⎭- ⎪ ⎪⎝⎭⎝⎭=⎰即()22cos a i px a ap a p x e dx a ππϕ--⎛⎫ ⎪⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭== . 粒子处于基态的动量分布为()222224cos 221ap ap a p p a a p a πππϕπ⎛⎫ ⎪⎝⎭=⎡⎤⎛⎫⎛⎫++ ⎪⎪⎢⎥⎝⎭⎝⎭⎣⎦=2.14 粒子在如图所示的势阱中运动，设粒子处于第n 个束缚态，相应的能级为n E ，如0n V E ，求粒子在阱外出现的概率.解：00E V <<的情况下粒子处于束缚态：在阱外2ax ≥，定态波动方程为 ()022220V d m E dx ψψ--=令β=考虑到束缚态边界条件（x →∞处，()0x ψ→），方程应取如下形式的解(),2,2xx a Ae x x a Be x ββψ-⎧⎪⎪⎨⎪⎪⎩≥=≤-常数A 与B 由归一化条件确定（由于势场具有对称性A B =）.在阱内2ax ≤，定态波动方程表示为22220d mE dx ψψ+= 令k =波函数偶宇称态的解为()cos x C kx ψ ，奇宇称态的解为()sin x D kx ψ . (a) 偶宇称态，波函数()x ψ及其微商()x ψ'在2ax =处是连续的； 22cos cos 2a a x x a xaC kx C k AeAe ββ==--=⇒=()()222cos sin 2xa a x x aAeC kx akC k Ae βββ-==-''-=⇒=-两式相比可得到能级公式为tan 2ka kβ=. 如0n V E ，k β=→=，()2122n ka π+→ ()2222222222+xa a aa a xB A A Aee e e dx Bedx dx x ββββββββψ∞------∞+===⎰⎰⎰阱外带入关系式2cos 2aa C k Ae β-=得()222cos 2C kax dx ψβ=⎰阱外()222221sin 22cos aa C C a ka kdx C kx dx x ψ-+==⎰⎰阱内由于()2122n ka π+→，所以2cos 02ka →，sin 0ka →，粒子出现在阱外的概率远小于粒子出现在阱内的概率()()2222C a dx dx x x ψψ≈≈⎰⎰全空间阱内粒子出现在阱外的概率为()()220222c cos 2=o 2=s =222C k ka V a E dxC a a dxa x x βββψψ⎰⎰全空间阱外22220222221cos 21tan 112ka k k E k V a k ββ⎝⎭====+⎛⎫+ ⎪+⎝⎭=+⎝⎭⎝⎭.2.16 利用厄米多项式的递推关系()()()11220n n n H H nH ξξξξ+--+=，()()12n n H nH ξξ-='，求证()()111()n n n x x x x ψα-+⎤⎥⎥⎦=+，()()11()n n n d x x x dx ψα-+⎤⎥⎥⎦=， 并由此证明()n x ψ态下0x =，2nE V =，0p =，222n p m E T ==. 证明：(1)谐振子波函数()()22n n x H ξψξ-=，其中xξα=，α=关于Hermite 多项式有递推关系()()()11220n n n H H nH ξξξξ+--+=22ξ-得()()()22222211220n n n H H H ξξξξξξ---+--+=()()()2222221102n n n H H H ξξξξξξα---+--+= (*)()()()1120n n n x x xx αψ+--+=由此即得()()111()n n n x x x x ψα-+⎤⎥⎥⎦=(2) 由()()2n n x H ξψξ-=，()()()()()()()()222222x x x n n n n d d d dx dx dx d dx x H x e H x e H x αααψααα---⎫⎫⎛⎫⎪⎪ ⎪=+⎨⎬⎪ ⎪⎪⎭⎝⎭⎭= ()()()()()2222212x x n n x e H x e n H x αααααα---⎫⎛⎫⎪ ⎪=-+⎬⎪⎪⎝⎭⎭(()()()()2222212x x n n x H x n H x ααααα---=-+代入(*)的变形式得()()()222222112n n n H H H ξξξαξξξ---+-=+()(()()()()2222212x x n n n d x dx x H x n H x αααψαα---=-+()()()()22222112122x n n n H H n H x αξξαξξα--+---=-++⎫⎪⎪⎭()()()1112n n n x x x αψ⎫⎪⎪⎭+--=- ()()11n n x x α-+⎤⎥⎥⎦=(3)()()111n n n n nx x dx dx x x ψαψψ+∞+∞**-∞-+-∞⎤⎥⎥⎦==⎰⎰()()11n n n n x x dx dx ψψψψ-++∞+∞**-∞-∞=0=(4)()222222111222n n n n n n V m x m x m x V dx dx dx ωωωψψψψψψ+∞+∞+∞***-∞-∞-∞⎛⎫ ⎪⎝⎭====⎰⎰⎰由(1)得()()111()n n n x x x x ψα-+⎤⎥⎥⎦=+再乘以x 得()()2111()n n n x x x x ψψψα-+⎤⎥⎥⎦=()()()()2211n n n n x x x x αα-+⎫⎤⎤⎪⎥⎥⎪⎥⎦⎦⎤⎥=⎭⎥⎦()()()()2222112n n n n x x x ψα-+⎤⎥⎦=++ ()()()()()222222112n n n n n n x xdx n dx x x x ψψψψα+∞+∞**-∞-∞-+⎧⎫⎤⎨⎬⎩=⎭=⎥⎦+++⎰⎰()()()()222002112n n n n n n x dx n x dx x dx ψψψψψψα+∞+∞**-++∞∞*--∞-∞⎫⎪=++⎬⎪⎩⎭⎰ ()2212n α=+()()222222212111122221112222n n n n E m x m m V ωωωωα=++⎛⎫=+= ⎪⎝⎭==(5)()()11n n n n n n n d d i dx dx i i x dx d p d x x xψψψψψα+∞+∞+∞**-∞-∞-+*-∞--⎤⎛⎫-⎥ ⎪⎝⎭⎥⎦===⎰⎰⎰()()11000n n n n i x x dx dx ψψαψψ-++∞+∞**-∞-∞⎫⎪=-=⎬⎪⎭(6)()()22221121222nn n nnd dm dx m dxxpT dxmx dxαψψψ+∞+∞**-∞--∞+⎧⎫⎤⎪⎪⎥⎨⎬⎥⎪⎪⎛⎫--⎪⎝⎭⎦⎩⎭===⎰⎰()()()() 222 2n nn nn n mx x dx dx x x αααψψ+∞+∞*-*-∞∞+-⎧⎫⎧⎫⎤⎤⎪⎪⎪⎪⎥⎥⎨⎬⎨⎬⎥⎥⎪⎪⎪⎪⎫⎪-⎬⎪⎭⎦⎦⎩⎭⎩⎭=()()()()220022214nn n nnndx dxx xnmx dxψψψψαψψ+∞+∞**-∞+-∞-⎫⎪⎪⎬⎪⎪⎪⎩⎭+∞*-∞+-=-⎰⎰⎰()222111222212144nm nn Enm mωωα⎛⎫⎪⎪⎝⎭⎛⎫⎪⎝⎭+==+=+=2.17 质量为m的粒子处于势阱()220;,1,20;xxxm xVω∞⎧>=≤⎪⎨⎪⎩中，求粒子的可能能量.提示：利用谐振子波函数()nxψ的奇偶性()()()1nn nx xψψ-=-.解：线性谐振子对应于本正函数()()221212122!xn nnx e H xnαααπψ-⎛⎫⎪=⎪⎝⎭，α=的本征值为12nE nω⎛⎫=+⎪⎝⎭.题中0x≤区域，粒子的波函数满足()0xϕ=.0x>区域粒子的波函数满足边界条件()00ϕ=，()0ϕ∞=，由波函数的连续性可知()00ϕ=.由谐振子波函数()nxψ的奇偶性条件()()()1nn nx xψψ-=-，我们得知只有当n取奇数时连续性条件才被满足，故此时粒子的可能能量值为()1321222nE n nωω⎛⎫⎛⎫=++=+⎪ ⎪⎝⎭⎝⎭，0,1,2,n=.相应的本正函数为()()21n nx xϕ+=.()()()222222121011122n n n A x dx A x dx A x dx ψψϕ+∞+∞+∞++-∞====⎰⎰⎰，故A =.2.18 设()1,r t ψ 和()2,r t ψ 是不含时势场()V r中薛定谔方程的两个解，证明对变量变化的全空间积分312d x ψψ*⎰与时间无关，即3120d d x dtψψ*=⎰. 证明：由题意得()1,r t ψ 和()2,r t ψ分别满足薛定谔波动方程()()()()22111,,,2i r t r t V r r t t m ψψψ∂=-∇+∂ (2.18.1) ()()()()22222,,,2i r t r t V r r t t mψψψ∂=-∇+∂ (2.18.2) ()1,r t ψ*⨯ ()2.18.2 - ()2,r t ψ⨯()2.18.1*()()()()()()()()222122112,,,,,,2i r t r t r t r t r t r t t mψψψψψψ***∂=∇-∇∂()()()()()22112,,,,2r t r t r t r t mψψψψ**=∇⋅∇-∇上式对全空间进行积分()()()()()()()()233122112,,,,,,2i r t r t d x r t r t r t r t d x t mψψψψψψ***∂=∇⋅∇-∇∂⎰⎰ ()()()()()22112,,,,2r t r t r t r t ds m ψψψψ**=∇-∇⋅⎰由于无穷远处波函数为零，积分项()()()()()2112,,,,r t r t r t r t ψψψψ**∇-∇⎰ 为零，即()()()132,0,d d x dtr t r t ψψ*= .。
波函数与薛定谔方程
定态Schr dinger方程的解 Schrödinger 2．定态Schr dinger方程的解 ψ ( x) = 0 x > a （3） 有限， 因 ψ(x) 及 E 有限，由（2） 令 （1）
α
2
2 µE = h2
d 2ψ + α 2ψ ( x) = 0 dx 2
从物理考虑， 从物理考虑，粒 （4） 子不能透过无穷 高的势壁。 高的势壁。 （4） 4
◆ 波函数的标准条件
Chapter 2 The wave function and Schrödinger Equation
r r 2 根据Born统计解释， Born统计解释 ω （1）根据Born统计解释， (r , t ) = ψ (r , t ) 是粒子在 t
r 点的几率，这是一个确定的数， 时刻出现在 r 点的几率，这是一个确定的数，所以 r r 的单值函数且有限。 要求 ψ (r , t ) 应是 (r , t ) 的单值函数且有限。
(6)
nπ αn = 2a
（n为奇数） 为奇数）
(7)
(6)和(7)两式统一写成 (6)和(7)两式统一写成
nπ αn = , 2a
2µ E α = 2 h
2
n = 1,2,3, L
（8）
n2π 2 h2 本征能量： 本征能量： En = 8µ a 2
（9）
11
一维无限深势阱（ §2.6 一维无限深势阱（续4）
（3）写出定态波函数 即得到对应第 n 个 本征值 En 的定态波 函数
∞
4.求解定态问题的步骤 4.求解定态问题的步骤
r r Ψ n ( r , t ) = Cnψ n (r ) e
−
i En t h
波函数和薛定谔方程
波函数和薛定谔⽅程波函数和薛定谔⽅程⼀、波函数的统计解释、叠加原理和双缝⼲涉实验微观粒⼦具有波粒⼆象性（德布罗意假设）；德布罗意关系（将描述粒⼦和波的物理量联系在⼀起） k n h p h E ====λων物质波（微观粒⼦—实物粒⼦）引⼊波函数（概率波幅）—描述微观粒⼦运动状态对于微观粒⼦来说，如果不考虑“⾃旋”⼀类的“内禀”态，单值波函数是其物理状态的最详尽描述。
⾄少在⽬前量⼦⼒学框架中，我们不能获得⽐波函数更多的物理信息。
微观粒⼦的状态⽤波函数完全描述——量⼦⼒学中的⼀条基本原理该原理包含三⽅⾯内容：粒⼦的状态⽤波函数表⽰、波函数的统计解释和对波函数性质的要求。
要明确“完全”的含义是什么。
按着波函数的统计解释，波函数统计性的描述体系的量⼦态，若已知单粒⼦（不考虑⾃旋）波函数)(r ψ，则不仅可以确定粒⼦的位置概率分布，⽽且如动量等粒⼦的其它⼒学量的概率分布也均可通过波函数⽽完全确定。
由此可见，只要已知体系的波函数，便可获得该体系的⼀切物理信息。
从这个意义上说，有关体系的全部信息已包含在波函数中，所以说微观粒⼦的状态⽤波函数完全描述。
必须强调指出，波函数给出的有关粒⼦的“信息”本质上是统计性质的。
例如，在适当条件下制备动量为p 的粒⼦，然后测量其空间位置，我们根本⽆法预⾔测量的结果，我们只能知道获得各种可能结果的概率。
很⾃然，⼈们会提出这样的疑问：既然量⼦⼒学只能给出统计结果，那就只需引⼊⼀个概率分布函数（象经典统计⼒学那样），何必假定⼀个复值波函数呢？事实上，引⼊复值波函数的物理基础，乃是量⼦⼒学中的⼜⼀条基本原理——叠加原理。
这条原理告诉我们，两种状态的叠加，绝不是概率相加，数学求和）。
正因如此，在双缝⼲涉实验中，我们才能看见屏上的⼲涉花纹。
实物粒⼦双缝⼲涉实验分析我们⾸先只打开⼀条狭缝，根据粒⼦的波动性，可以预⾔屏上将显⽰波长p / =λ（p 为粒⼦动量）的单缝衍射花纹。
但是，根据粒⼦的微粒性，它们将是⼀个⼀个打上去的，怎样将这两种性质的描述调和起来呢？为此，我们想象将⼊射粒⼦束强度降低，直到只⼀个粒⼦通过狭缝，这时屏上会出现很微弱的衍射花纹吗？当然不会！单个粒⼦只能作为⼀个不可分割的整体打到屏上的⼀个点，从⽽出现⼀个⼩斑点。
波函数 薛定谔方程
玻尔在解释氢原子光谱时就提出了定态的概念雏形.定态也是量子力
学中最重要的概念之一，本节就从薛定谔方程出发，对定态的性质做一些
概括性的讨论.
若势能V(r)与时间无关，则可以设
Ψ(r,t)=Ψ(r)f(t)
（15- 41）
把式（15- 41）代入式（15- 40）,得到
波函数 薛定谔方程
两边同除以Ψ(r)f(t)，就可以分离变量，即
波函数 薛定谔方程
薛定谔方程描述微观粒子运动的一般方程，自然也可以描 15- 36
解，由式（15- 36）可得
（15- 37）
波函数 薛定谔方程
由式（15- 35）可得
波函数 薛定谔方程
（1）这并不是薛定谔方程的证明，薛定谔方程是量子力学的基本 假定，是对大量实验观测结果的概括，它和经典力学中的牛顿三定律一 样，是不能被证明的.
波函数 薛定谔方程
图15- 13 无限深方势阱中的波函数
波函数 薛定谔方程
图15- 14所示为 无限深方势阱中的粒 子分布密度Ψ2(x).容 易看出，当n→∞时， 粒子分布密度会趋于 均匀，即在大量粒子 数条件下，量子力学 将回到经典情况.
图15- 14 无限深方势阱中的粒子分布密度
谢谢观看
波函数 薛定谔方程
若定态波函数能够满足归一化条件，即
则在无限远处，定态波函数必然迅速趋于0，即粒子不可能出现 在无穷远处，也就是粒子被限制在有限的范围内运动，这种状态就称 为束缚态，否则就称为游离态.
波函数 薛定谔方程
在经典情况下，粒子当然也不能出现在阱外，这一点与量子 力学的解并无区别.若是经典粒子，在阱内各处的势场都为零， 因此粒子在阱内均匀分布.在量子力学情况下，容易解得粒子出 现在各处的概率并不相同，随着位置的变化而变化，即粒子分布 是不均匀的.此外，在经典情况下，粒子的能量可以取任意的有 限值，即粒子的能量是可以连续变化的，但在量子力学情况下， 粒子的能量只能取一系列分立值，即能级是量子化的.图15-13所 示为无限深方势阱中的波函数Ψ(x).
第五章波函数与薛定谔方程
第五章波函数与薛定谔方程§5 - 1 波函数的统计诠释一概率波（1）电子双缝衍射和概率波( a )( b )图5 - 1 光( a )和电子( b )的双缝衍射图样●入射电子流的强度很大，即单位时间内有许多电子通过双缝，则底片上很快就出现了图5- 1 ( b )所给出的衍射图样。
●单个电子就具有波动性：即使入射电子流极其微弱，以致电子几乎是单个地通过双缝，短时间内底片上记录下来的只是一些分布不规律的点子，但是只要时间足够长，底片上仍将呈现出有规律的衍射图样，即单个电子就具有波动性。
●实验上所显示出来的电子的波动性，是许多电子在同一个实验中的统计结果；or 是一个在许多次相同实验中的统计结果。
●实验的衍射图样代表了电子在空间r点附近出现的概率的大小，德布罗意波或薛定谔方程中的波函数ψ正是为描写粒子的这种行为而)(r引进的；是刻画粒子在空间概率分布的概率波。
●在量子力学中，波函数)(rψ是最重要的基本概念之一，它可以完全描述一个体系的量子态。
●在经典物理学中并不存在与波函数ψ对应的物理量。
在经典概念下，)(r当相干波源发出来的声波或光波在空间同一区域交叠时，所发生的是周期变化的实在物理量(如位移、压强或电场强度等)的叠加，在合成的强度分布中出现了在非相干叠加(即振幅的平方或强度叠加)时没有的干涉项，正是这一项决定了干涉和衍射现象的发生。
( 2 ) 波函数的概率诠释设衍射波幅用)(r ψ描述，则衍射图样的强度分布用)(r ψ的模方描述 )()(*)(2r r r ψψψ= (5.1)其中：ψ*( r )是ψ ( r )的复共轭。
衍射波强度 | ψ ( r ) |2是刻画电子出现在r 点附近的概率大小的一个量，即 z y x ∆∆∆2)(r ψ (5.2)表示在r 点处的体积元z y x ∆∆∆中找到粒子的概率。
这就是波函数的概率诠释 量子力学的基本原理之一。
结论：波函数ψ( r )：是刻画粒子在空间概率分布的概率波，称为概率波幅或概率幅。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
由此可推得多电子的原子中各壳层所可能有的最 多电子数（见下表）。
原子壳层和分壳层中最多可能容纳的电子数
量子数的意义：
1 主量子数n
氢原子只能处在一些分立的状态，用主量子数，角 量子数，磁量子数来描述, 取值如下
主量子数决定着氢原子的能量，E 与n 的依赖关系与波尔理论相同。
2 角量子数l
角动量有确定值，为
角动量是量子化的，叫轨道角动量。习慣用小写字母表示电子具有某一轨道角动量 的量子态，
3 磁量子数ml 由波函数 Rnl(r)Ylm(,) 描写的定态，不但具有
s 是自旋量子数，只能取1/2。 还假定自旋角动量的空间取向也是量子化的，即 s
在Z方向的分量为：
是自旋磁量子数。 完全描述电子的运动状态，需要四个量子数：
电子自旋及空间取向量子化 z
2
原子的壳层结构
在多电子的原子中，电子的分布是分层次的，电子
的分布层次叫电子壳层。n=1,2,3,4,…,的壳层依次叫 K,L,M,N,…壳层。每一壳层上，对应l=0,1,2,3,…可分 成s,p,d,f…分壳层。电子在壳层中的分布遵从下面两条
l0 1 2 ns pd 1K 2(1s)
34
5
6 Zn
f
gh
i
2
2L 2(2s) 6(2p)
8
3M 2(3s) 6(3p) 10(3d)
18
4N 2(4s) 6(4p) 10(4d) 14(4f)
32
5O 2(5s) 6(5p) 10(5d) 14(5f) 18(5g)
50
6P 2(6s) 6(6p) 10(6d) 14(6f) 18(6g) 22(6h)
为止。下图给出了一些多电子原子结够的示意图。
L
L
K
K
K
2 He
本次课内容
§19-8 量子力学简介（2）
三 薛定谔方程解一维势阱问题 四 对应原理 五 一维方势垒 隧道效应
§19-9 氢原子的量子理论 §19-10 多电子原子中的电子分布
课本 pp266—289； 练习册 第二十单元
§19-8 量子力学简介（2）
定态薛定谔方程
一维定态薛定谔方程
求解定态薛定谔方程，就是在已知势函数的条件下，求出体系可能有的能 量值和波函数。
，于是
即: 由此得到粒子的能量En
En 称为本问题中能量E 的本征值。势阱中的粒子,其能量
是量子化的。
当 n = 1,
E1即基态能级
n 叫作主量子数
势阱中粒子的能级图
E
o
ax
与 E 相对应的本征函数，即本问题的解为：
式中常数Ａ可由归一化条件求得。
得到 最后得到薛定谔方程的解为：
讨论
1 势阱中的粒子的能量不是任意的，只能取分立值，即 能量是量子化的。能量量子化是微观世界特有的现象， 经典粒子处在势阱中能量可取连续的任意值。 电子(m=9.1×10-31千克)：
1921年，施忒恩（O.Stern）和盖拉赫（W.Gerlach）
发现一些处于S 态的原子射线束，在非均匀磁场中一束分
为两束。
S
原子炉 准直屏
N 磁铁
§19-10 多电子原子中的电子分布
1925年，乌仑贝克(G.E.Uhlenbeck)和高德斯密特 (S.A.Goudsmit)提出电子自旋假说。由自旋产生的角动 量 的大小是量子化的，其值为
解：已知无限深势阱中粒子的波函数和能量为
则
多次测量能量(可能测到的值) 能量的平均值
概率各占1/2
§19-9 氢原子的量子理论
一 氢原子定态薛定谔方程的求解
氢原子由一个质子和一个电子组成，电子受质子库仑电场作用而绕核运动 （质子静止）。电子的状态由波函数描述，波函数满足定态薛定谔方程：
这里
，（1）式可写成
确定的能量和角动量的大小，而且具有确定的Lz(角动
量在轴方向的分量)
角动量的分量也只能取分立值。空间取向量子化示意图源自Lz h=m l0.
0
0
0
l=0
l=1
l=2
l=3
二 氢原子中电子的径向几率分布
2p 3p
1s 2s 3s
4p
r
4s
r
3d 4d
r
氢原子中电子的角向几率分布
z
z
y
y
z y
斯特恩-盖拉赫实验
采用球坐标： 球坐标下： （2）式则为： 分离变量，令
代入方程（3）可得： 分离变量得 和
令
，（5）再分离变量式为：
即
和 （5b ）的解是
的单值性要求
（5a ）是勒让德方程，其解是勒让德多项式。为了使
和
时， 为有限，必须限定
（4）是径向方程，可写为：
径向方程用级数法求解。
若E>0,能量连续分布，自由电子情形； 但E<0, （束缚态），波函数标准条件要求
72
7Q 2(7s) 6(7p) 10(7d) 14(7f) 18(7g) 22(7h) 26(7i) 98
2 能量最小原理 原子系统处于正常态时，各个电子趋向于占有最
低能级。能级越低，相应壳层离核越近，首先被电子
填满，其余电子依次向未被占取的最低能级填充，直
到所有 Z 个核外电子分别填入可能占取的最低能级
V (x ) 8 8
三 薛定谔方程解一维势阱问题
质量为m 的粒子在外场中作一维运动，势能函数 为
定态薛定谔方程为：
x=0 x=a
当 x < 0 和 x > a 时，
求解方程（1）
(1)式可写成
令
代入上式得：
此方程的通解为： 由于阱壁无限高，所以
由式（1）得 B = 0 ，波函数为：
由式（2）得
①若势阱宽a=10Å，则 En=0.75neV, 量子化明显； ②若a=1cm,则En=0.75×10-14eV ,量子化不明显。
2 能量为En的粒子在 x-x+dx 内被发现的概率:
波函数
n=4
几率密度分布
n=3
n=2
n=1
0
a0x
a
例题：在阱宽为a 的无限深势阱中,一个粒子的状态为
多次测量其能量。问 每次可能测到的值和相应概率？ 能量的平均值？
基本规律： 1 泡利(W.Pauli)不相容原理
原子中不可能同时有两个或两个以上的电子处于完全 相同的状态（原子中不可能同时有两个或两个以上的电子 具有四个相同的量子数）。
例：基态氦原子核外两电子都处于1s态，其量子态
(n ,l ,ml ,,ms)分别为( 1,0,0,±1/2 )
利用泡利不相容原理可计算各壳层所可能有的最多电子数: