人教版初二数学上册多边形及其内角和练习题(含答案)
数学人教版八年级上册多边形的内角和.3.2-多边形的内角和同步练习(含答案)
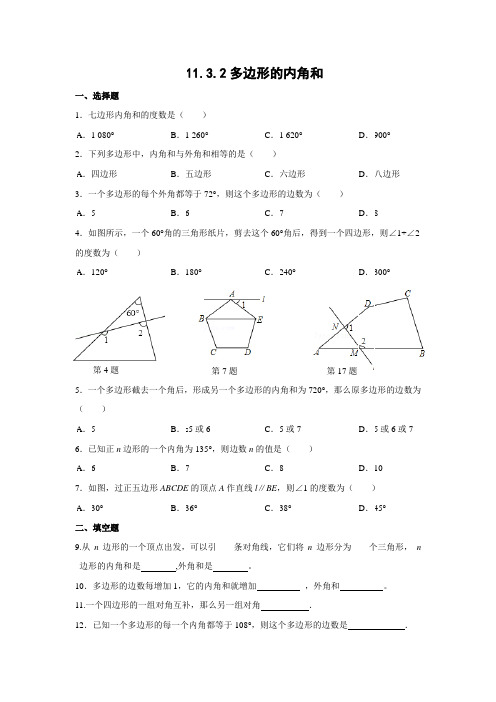
11.3.2多边形的内角和一、选择题1.七边形内角和的度数是( )2.下列多边形中,内角和与外角和相等的是( )3.一个多边形的每个外角都等于72°,则这个多边形的边数为( )4.如图所示,一个60°角的三角形纸片,剪去这个60°角后,得到一个四边形,则∠1+∠2的度数为( )5.一个多边形截去一个角后,形成另一个多边形的内角和为720°,那么原多边形的边数为()6.已知正n 边形的一个内角为135°,则边数n 的值是( )7.如图,过正五边形ABCDE 的顶点A 作直线l ∥BE ,则∠1的度数为( )二、填空题9.从n 边形的一个顶点出发,可以引____条对角线,它们将n 边形分为____个三角形, n 边形的内角和是 ,外角和是 。
10.多边形的边数每增加1,它的内角和就增加 _________,外角和 ________。
11.一个四边形的一组对角互补,那么另一组对角_________ .12.已知一个多边形的每一个内角都等于108°,则这个多边形的边数是 _________ .13.正十二边形每个内角的度数为 _________ .14.如果一个正多边形的一个外角是60°,那么这个正多边形的边数是 _________ .15.若一个多边形内角和等于1260°,则该多边形边数是 _________ .16.一个多边形的内角和是外角和的2倍,则这个多边形的边数为 _________ .17.如图,在四边形ABCD 中,∠A =45°.直线l 与边AB ,AD 分别相交于点M ,N ,则∠1+∠2=_________ .18、已知一个多边形的内角和与外角和的差为1080°,则这个多边形是_____•边形.三、解答题19.一个多边形的内角和是它的外角和的4倍,求这个多边形的边数.20. 已知如图,四边形A B C D 中,B ∠和C ∠的平分线交于点O . 求证:1()2B O C A D ∠=∠+∠.21.•一个多边形截去一个角(不过顶点)后,所形成的一个多边形的内角和是2520°,求原多边形的边数。
八年级数学上册《第十一章 多边形及其内角和》练习题及答案-人教版

八年级数学上册《第十一章多边形及其内角和》练习题及答案-人教版一、选择题1.以下列图形:正三角形、正方形、正五边形、正六边形为“基本图案”可以进行密铺的有( )A.1种B.2种C.3种D.4种2.下列说法中,正确的是( )A.直线有两个端点B.射线有两个端点C.有六边相等的多边形叫做正六边形D.有公共端点的两条射线组成的图形叫做角3.从 7 边形的一个顶点作对角线,把这个 7 边形分成三角形的个数是( )A.7 个B.6 个C.5 个D.4 个4.若一个正多边形的一个外角是36°,则这个正多边形的边数是( )A.10B.9C.8D.65.一个多边形的内角和比它的外角和的3倍少1800,这个多边形的边数是 ( )A.5条B.6条C.7条D.8条6.若正多边形的内角和是540°,则该正多边形的一个外角为( )A.45°B.60°C.72°D.90°7.一个正多边形的外角与它相邻的内角之比为1:4,那么这个多边形的边数为( )A.8B.9C.10D.128.如果一个多边形的每个内角都相等,且内角和为1800°,那么这个多边形的一个外角是( )A.30°B.36°C.60°D.72°9.设四边形的内角和等于a,五边形的外角和等于b,则a与b的关系是( )A.a>bB.a=bC.a<bD.b=a+180°10.把一个多边形纸片沿一条直线截下一个三角形后,变成一个十八边形,则原多边形纸片的边数不可能是( )A.16B.17C.18D.19二、填空题11.形状、大小完全相同的三角形________(填“能”或“不能”)铺满地面;形状、大小完全相同的四边形________(填“能”或“不能”)铺满地面.12.从多边形的一个顶点出发,连接这个点和其他顶点,把多边形分割成16个三角形,则这个多边形的边数是________.13.若从一个多边形的一个顶点出发,最多可以引10条对角线,则它是边形.14.如果一个多边形的各个外角都是40°,那么这个多边形的内角和是.15.如图,已知正五边形ABCDE,AF∥CD,交DB的延长线于点F,则∠DFA=.16.如图,五边形ABCDE是正五边形,若l1平行l2,则∠1-∠2=_______.三、解答题17.求下列图形中x的值:18.我们知道把正三角形、正方形、正六边形合在一起可以铺满平面,若把正十边形、正八边形、正九边形合在一起,能不能铺满地面?为什么?19.一个多边形的内角和是外角和的2倍,则这个多边形是几边形?20.如图,以五边形的每个顶点为圆心,以1为半径画圆,求圆与五边形重合的面积.21.如图,求∠A+∠B+∠C+∠D+∠E+∠F的度数.22.探索问题:(1)如图①,你知道∠BOC=∠B+∠C+∠A的奥秘吗?请你用学过的知识予以证明;(2)如图②﹣1,则∠A+∠B+∠C+∠D+∠E=°;如图②﹣2,则∠A+∠B+∠C+∠D+∠E=°;如图②﹣3,则∠A+∠B+∠C+∠D+∠E=°;(3)如图③,下图是一个六角星,其中∠BOD=70°,则∠A+∠B+∠C+∠D+∠E+∠F=°.参考答案1.C2.D3.C4.A5.C6.C.7.C.8.A.9.B10.A.11.答案为:能,能.12.答案为:18;13.答案为:十三.14.答案为:1260°.15.答案为:36°.16.答案为:72°.17.解:(1)90+70+150+x=360.解得x=50.(2)90+73+82+(180﹣x)=360.解得x=65.(3)x+(x+30)+60+x+(x﹣10)=(5﹣2)×180.解得x=115.18.解:因为正十边形、正八边形、正九边形的一个内角分别为144°,135°,140°它们的和144°+135°+140°>360°所以正十边形、正八边形、正九边形合在一起不能铺满地面19.解:设这个多边形的边数为n∴(n﹣2)•180°=2×360°解得:n=6.故这个多边形是六边形.20.解:(5﹣2)×180°=540°540°÷360°π×12=32π.21.解:连接AF.∵在△AOF和△COD中,∠AOF=∠COD,∴∠C+∠D=∠OAF+∠AFD,∴∠A+∠B+∠C+∠D+∠E+∠F=∠OAF+∠OFA+∠CFE+∠OAB+∠E+∠F=∠BAF+∠AFE+∠E+∠B=360°.22.解:(1)如图①,∠BOC=∠B+∠C+∠A.(2)如图②,∠A+∠B+∠C+∠D+∠E=180°.如图③根据外角的性质,可得∠1=∠A+∠B,∠2=∠C+∠D∵∠1+∠2+∠E=180°∴x=∠A+∠B+∠C+∠D+∠E=180°.如图④,延长EA交CD于点F,EA和BC交于点G根据外角的性质,可得∠GFC=∠D+∠E,∠FGC=∠A+∠B ∵∠GFC+∠FGC+∠C=180°∴x=∠A+∠B+∠C+∠D+∠E=180°.(3)如图⑤,∵∠BOD=70°∴∠A+∠C+∠E=70°∴∠B+∠D+∠F=70°∴∠A+∠B+∠C+∠D+∠E+∠F=70°+70°=140°.。
人教版八年级数学上册练习 多边形及其内角和 同步练习及答案

第11章《三角形》同步练习(§11.3 多边形及其内角和)班级学号姓名得分1.填空:(1)平面内,由____________________________________________________________叫做多边形.组成多边形的线段叫做______.如果一个多边形有n条边,那么这个多边形叫做______.多边形____________叫做它的内角,多边形的边与它的邻边的______组成的角叫做多边形的外角.连结多边形________________的线段叫做多边形的对角线.(2)画出多边形的任何一条边所在直线,如果整个多边形都在______,那么这个多边形称作凸多边形.(3)各个角______,各条边______的______叫做正多边形.2.(1)n边形的内角和等于____________.这是因为,从n边形的一个顶点出发,可以引______条对角线,它们将此n边形分为______个三角形.而这些三角形的内角和的总和就是此n边形的内角和,所以,此n边形的内角和等于180°×______.(2)请按下面给出的思路,进行推理填空.如图,在n边形A1A2A3…A n-1A n内任取一点O,依次连结______、______、______、……、______、______.则它们将此n边形分为______个三角形,而这些三角形的内角和的总和,减去以O为顶点的一个周角就是此多边形的内角和.所以,n边形的内角和=180°×______-( )=( )×180°.3.任何一个凸多边形的外角和等于______.它与该多边形的______无关.4.正n边形的每一个内角等于______,每一个外角等于______.5.若一个正多边形的内角和2340°,则边数为______.它的外角等于______.6.若一个多边形的每一个外角都等于40°,则它的内角和等于______.7.多边形的每个内角都等于150°,则这个多边形的边数为______,对角线条数为______.8.如果一个角的两边分别垂直于另一个角的两边,其中一个角为65°,则另一个角为______度.9.选择题:(1)如果一个多边形的内角和等于它的外角和的两倍,则这个多边形是( ).(A)四边形(B)五边形(C)六边形(D)七边形(2)一个多边形的边数增加,它的内角和也随着增加,而它的外角和( ).(A)随着增加(B)随着减少(C)保持不变(D)无法确定(3)若一个多边形从一个顶点,只可以引三条对角线,则它是( )边形.(A)五(B)六(C)七(D)八(4)如果一个多边形的边数增加1,那么它的内角和增加( ).(A)0°(B)90°(C)180°(D)360°(5)如果一个四边形四个内角度数之比是2∶2∶3∶5,那么这四个内角中( ).(A)只有一个直角(B)只有一个锐角(C)有两个直角(D)有两个钝角(6)在一个四边形中,如果有两个内角是直角,那么另外两个内角( ).(A)都是钝角(B)都是锐角(C)一个是锐角,一个是直角(D)互为补角10.已知:如图四边形ABCD中,∠ABC的平分线BE交CD于E,∠BCD的平分线CF交AB于F,BE、CF相交于O,∠A=124°,∠D=100°.求∠BOF的度数.11.(1)已知:如图1,求∠1+∠2+∠3+∠4+∠5+∠6___________.图1(2)已知:如图2,求∠1+∠2+∠3+∠4+∠5+∠6+∠7+∠8____________.图212.如图,在图(1)中,猜想:∠A+∠B+∠C+∠D+∠E+∠F=______度.请说明你猜想的理由.图1如果把图1成为2环三角形,它的内角和为∠A+∠B+∠C+∠D+∠E+∠F;图2称为2环四边形,它的内角和为∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H;图2则2环四边形的内角和为_____________________________________________度;2环五边形的内角和为________________________________________________度;2环n边形的内角和为________________________________________________度.13.一张长方形的桌面,减去一个角后,求剩下的部分的多边形的内角和.14.一个多边形的内角和与某一个外角的度数总和为1350°,求这个多边形的边数.15.如果一个凸多边形除了一个内角以外,其它内角的和为2570°,求这个没有计算在内的内角的度数.16.小华从点A出发向前走10米,向右转36°,然后继续向前走10米,再向右转36°,他以同样的方法继续走下去,他能回到点A吗?若能,当他走回点A时共走了多少米?若不能,写出理由.参考答案1.略.2.(1)(n -2)×180°,n -3,n -2,n -2.(2)OA 1,OA 2,OA 3……,OA n -1,OA n ,n ,n ,360°,(n -2).3.360°,边数. 4.⋅⨯-n nn oo 360,180)2( 5.十五,24°. 6.1260°. 7.12,54. 8.65°或115°.9.(1)C ,(2)C ,(3)B ,(4)C ,(5)A ,(6)D 10.68°11.(1)360°;(2)360°.12.(1)360°;(2)720°;(3)1080°;(4)2(n -2)×180°.13.180°或360°或540°.14.九.提示:设多边形的边数为n ,某一个外角为α.则(n -2)×180+α =1350. 从而1809071801350)2(αα-+=-=-n . 因为边数n 为正整数,所以α =90,n =9.15.130°.提示:设多边形的边数为n ,没有计算在内的内角为x °.(0<x <180)则(n -2)×180=2570+x . 从而⋅++=-18050142x n 因为边数n 为正整数,所以x =130.16.可以走回到A 点,共走100米.。
人教版初中八年级上册数学《多边形及其内角和》同步练习含答案解析

《11.3 多边形及其内角和》一、选择题:1.一个多边形的外角中,钝角的个数不可能是()A.1个B.2个C.3个D.4个2.不能作为正多边形的内角的度数的是()A.120°B.(128)°C.144°D.145°3.若一个多边形的各内角都相等,则一个内角与一个外角的度数之比不可能是()A.2:1 B.1:1 C.5:2 D.5:44.一个多边形的内角中,锐角的个数最多有()A.3个B.4个C.5个D.6个5.四边形中,如果有一组对角都是直角,那么另一组对角一定()A.都是钝角 B.都是锐角C.是一个锐角、一个钝角 D.互补6.若从一多边形的一个顶点出发,最多可引10条对角线,则它是()A.十三边形 B.十二边形 C.十一边形 D.十边形7.若一个多边形共有十四条对角线,则它是()A.六边形B.七边形C.八边形D.九边形8.一个凸多边形除一个内角外,其余各内角的和为2570°,则这个内角的度数等于()A.90° B.105°C.130°D.120°二、中考题与竞赛题9.若一个多边形的内角和等于1080°,则这个多边形的边数是()A.9 B.8 C.7 D.6三、填空题:10.多边形的内角中,最多有个直角.11.从n边形的一个顶点出发可以引条对角线,这些对角线将这个多边形分成个三角形.12.如果一个多边形的每一个内角都相等,且每一个内角都大于135°,那么这个多边形的边数最少为.13.已知一个多边形的每一个外角都相等,一个内角与一个外角的度数之比为9:2,则这个多边形的边数为.14.每一个内角都是144°的多边形有条边.四、基础训练:15.如图所示,用火柴杆摆出一系列三角形图案,按这种方式摆下去,当摆到20层(N=20)时,需要多少根火柴?16.一个多边形的每一个外角都等于24°,求这个多边形的边数.五、提高训练17.一个多边形的每一个内角都相等,一个内角与一个外角的度数之比为m:n,其中m,n是互质的正整数,求这个多边形的边数(用m,n表示)及n的值.六、探索发现18.从n边形的一个顶点出发,最多可以引多少条对角线?请你总结一下n边形共有多少条对角线.《11.3 多边形及其内角和》参考答案与试题解析一、选择题:1.一个多边形的外角中,钝角的个数不可能是()A.1个B.2个C.3个D.4个【考点】多边形内角与外角.【专题】计算题.【分析】根据n边形的外角和为360°得到外角为钝角的个数最多为3个.【解答】解:∵一个多边形的外角和为360°,∴外角为钝角的个数最多为3个.故选D.【点评】本题考查了多边形的外角和:n边形的外角和为360°.2.不能作为正多边形的内角的度数的是()A.120°B.(128)°C.144°D.145°【考点】多边形内角与外角.【分析】根据n边形的内角和(n﹣2)•180°分别建立方程,求出n,由于n≥3的整数即可得到D 选项正确.【解答】解:A、(n﹣2)•180°=120•n,解得n=6,所以A选项错误;B、(n﹣2)•180°=(128)°•n,解得n=7,所以B选项错误;C、(n﹣2)•180°=144°•n,解得n=10,所以C选项错误;D、(n﹣2)•180°=145°•n,解得n=,不为整数,所以D选项正确.故选D.【点评】本题考查了多边形的内角和定理:n边形的内角和为(n﹣2)•180°.3.若一个多边形的各内角都相等,则一个内角与一个外角的度数之比不可能是()A.2:1 B.1:1 C.5:2 D.5:4【考点】多边形内角与外角.【分析】多边形的外角和是360°,且根据多边形的各内角都相等则各个外角一定也相等,根据选项中的比例关系求出外角的度数,根据多边形的外角和定理求出边数,如果是≥3的正整数即可.【解答】解:A、外角是:180×=60°,360÷60=6,故可能;B、外角是:180×=90°,360÷90=4,故可能;C、外角是:180×=度,360÷=7,故可能;D、外角是:180×=80°.360÷80=4.5,故不能构成.故选D.【点评】本题主要考查了多边形的外角和定理,理解外角与内角的关系是解题的关键.4.一个多边形的内角中,锐角的个数最多有()A.3个B.4个C.5个D.6个【考点】多边形内角与外角.【分析】利用多边形的外角和是360度即可求出答案.【解答】解:因为多边形的外角和是360度,在外角中最多有三个钝角,如果超过三个则和一定大于360度,多边形的内角与相邻的外角互为邻补角,则外角中最多有三个钝角时,内角中就最多有3个锐角.故选A.【点评】本题考查了多边形的内角问题.由于内角和不是定值,不容易考虑,而外角和是360度不变,因而内角的问题可以转化为外角的问题进行考虑.5.四边形中,如果有一组对角都是直角,那么另一组对角一定()A.都是钝角 B.都是锐角C.是一个锐角、一个钝角 D.互补【考点】多边形内角与外角.【分析】由四边形的内角和等于360°,又由有一组对角都是直角,即可得另一组对角一定互补.【解答】解:如图:∵四边形ABCD的内角和等于360°,即∠A+∠B+∠C+∠D=360°,∵∠A=∠C=90°,∴∠B+∠D=180°.∴另一组对角一定互补.故选D.【点评】此题考查了四边形的内角和定理.此题难度不大,解题的关键是注意掌握四边形的内角和等于360°.6.若从一多边形的一个顶点出发,最多可引10条对角线,则它是()A.十三边形 B.十二边形 C.十一边形 D.十边形【考点】多边形的对角线.【分析】根据多边形的对角线的定义可知,从n边形的一个顶点出发,可以引(n﹣3)条对角线,由此可得到答案.【解答】解:设这个多边形是n边形.依题意,得n﹣3=10,∴n=13.故这个多边形是13边形.故选:A.【点评】多边形有n条边,则经过多边形的一个顶点所有的对角线有(n﹣3)条,经过多边形的一个顶点的所有对角线把多边形分成(n﹣2)个三角形.7.若一个多边形共有十四条对角线,则它是()A.六边形B.七边形C.八边形D.九边形【考点】多边形的对角线.【分析】根据多边形对角线公式,可得答案.【解答】解:设多边形为n边形,由题意,得=14,解得n=7,故选:B.【点评】本题考查了多边形的对角线,熟记公式并灵活运用是解题关键.8.一个凸多边形除一个内角外,其余各内角的和为2570°,则这个内角的度数等于()A.90° B.105°C.130°D.120°【考点】多边形内角与外角.【专题】计算题.【分析】可设这是一个n边形,这个内角的度数为x度,利用多边形的内角和=(n﹣2)•180°,根据多边形内角x的范围,列出关于n的不等式,求出不等式的解集中的正整数解确定出n的值,从而求出多边形的内角和,减去其余的角即可解决问题.【解答】解;设这是一个n边形,这个内角的度数为x度.因为(n﹣2)180°=2570°+x,所以x=(n﹣2)180°﹣2570°=180°n﹣2930°,∵0<x<180°,∴0<180°n﹣2930°<180°,解得:16.2<n<17.2,又n为正整数,∴n=17,所以多边形的内角和为(17﹣2)×180°=2700°,即这个内角的度数是2700°﹣2570°=130°.故本题选C.【点评】本题需利用多边形的内角和公式来解决问题.二、中考题与竞赛题9.若一个多边形的内角和等于1080°,则这个多边形的边数是()A.9 B.8 C.7 D.6【考点】多边形内角与外角.【分析】多边形的内角和可以表示成(n﹣2)•180°,依此列方程可求解.【解答】解:设所求正n边形边数为n,则1080°=(n﹣2)•180°,解得n=8.故选:B.【点评】本题考查根据多边形的内角和计算公式求多边形的边数,解答时要会根据公式进行正确运算、变形和数据处理.三、填空题:10.多边形的内角中,最多有 4 个直角.【考点】多边形内角与外角.【分析】由多边形的外角和为360°可求得答案.【解答】解:当内角和90°时,它相邻的外角也为90°,∵任意多边形的外角和为360°,∴360°÷90°=4.故答案为:4.【点评】本题主要考查的是多边形的内角与外角,明确任意多边形的外角和为360°是解题的关键.11.从n边形的一个顶点出发可以引n﹣3 条对角线,这些对角线将这个多边形分成n﹣2 个三角形.【考点】多边形的对角线.【分析】根据n边形对角线的定义,可得n边形的对角线,根据对角线的条数,可得对角线分成三角形的个数.【解答】解从n边形的一个顶点出发可以引n﹣3条对角线,这些对角线将这个多边形分成n﹣2个三角形,故答案为:n﹣3,n﹣2.【点评】本题考查了多边形的对角线,由对角线的定义,可画出具体多边形对角线,得出n边形的对角线.12.如果一个多边形的每一个内角都相等,且每一个内角都大于135°,那么这个多边形的边数最少为9 .【考点】多边形内角与外角.【分析】根据多边形的外角和定理,列出不等式即可求解.【解答】解:因为n边形的外角和是360度,每一个内角都大于135°即每个外角小于45度,就得到不等式:,解得n>8.因而这个多边形的边数最少为9.【点评】本题已知一个不等关系就可以利用不等式来解决.13.已知一个多边形的每一个外角都相等,一个内角与一个外角的度数之比为9:2,则这个多边形的边数为11 .【考点】多边形内角与外角.【分析】先根据多边形的内角和外角的关系,求出一个外角.再根据外角和是固定的360°,从而可代入公式求解.【解答】解:设多边形的一个内角为9x度,则一个外角为2x度,依题意得9x+2x=180°解得x=()°360°÷[2×()°]=11.答:这个多边形的边数为11.【点评】本题考查多边形的内角与外角关系、方程的思想.关键是记住多边形的一个内角与外角互补、及外角和的特征.14.每一个内角都是144°的多边形有10 条边.【考点】多边形内角与外角.【分析】多边形的内角和可以表示成(n﹣2)•180°,因为所给多边形的每个内角均相等,故又可表示成120°n,列方程可求解.此题还可以由已知条件,求出这个多边形的外角,再利用多边形的外角和定理求解.【解答】解:解法一:设所求n边形边数为n,则144°n=(n﹣2)•180°,解得n=10;解法二:设所求n边形边数为n,∵n边形的每个内角都等于144°,∴n边形的每个外角都等于180°﹣144°=36°.又因为多边形的外角和为360°,即36°•n=360°,∴n=10.【点评】本题考查根据多边形的内角和计算公式求多边形的边数,解答时要会根据公式进行正确运算、变形和数据处理.四、基础训练:15.如图所示,用火柴杆摆出一系列三角形图案,按这种方式摆下去,当摆到20层(N=20)时,需要多少根火柴?【考点】规律型:图形的变化类.【分析】关键是通过归纳与总结,得到其中的规律,按规律求解.【解答】解:n=1时,有1个三角形,需要火柴的根数为:3×1;n=2时,有5个三角形,需要火柴的根数为:3×(1+2);n=3时,需要火柴的根数为:3×(1+2+3);…;n=20时,需要火柴的根数为:3×(1+2+3+4+…+20)=630.【点评】此题考查的知识点是图形数字的变化类问题,本题的关键是弄清到底有几个小三角形.16.一个多边形的每一个外角都等于24°,求这个多边形的边数.【考点】多边形内角与外角.【分析】根据多边形外角和为360°及多边形的每一个外角都等于24°,求出多边形的边数即可.【解答】解:设这个多边形的边数为n,则根据多边形外角和为360°,可得出:24×n=360,解得:n=15.所以这个多边形的边数为15.【点评】本题考查了多边形内角与外角,解答本题的关键在于熟练掌握多边形外角和为360°.五、提高训练17.一个多边形的每一个内角都相等,一个内角与一个外角的度数之比为m:n,其中m,n是互质的正整数,求这个多边形的边数(用m,n表示)及n的值.【考点】多边形内角与外角.【分析】设多边形的边数为a,多边形内角和为(a﹣2)180度,外角和为360度得到m:n=180(a ﹣2):360,从而用m、n表示出a的值.【解答】解:设多边形的边数为a,多边形内角和为(a﹣2)180度,外角和为360度,m:n=180(a﹣2):360a=,因为m,n 是互质的正整数,a为整数,所以n=2,故答案为:,2.【点评】本题考查了多边形的内角与外角,解答本题的关键在于熟练掌握多边形内角和与多边形外角和.六、探索发现18.从n边形的一个顶点出发,最多可以引多少条对角线?请你总结一下n边形共有多少条对角线.【考点】多边形的对角线.【分析】从n边形的一个顶点出发,最多可以引n﹣3条对角线,然后即可计算出结果.【解答】解:过n边形的一个顶点可引出n﹣3条对角线;n边形共有条对角线.【点评】本题主要考查的是多边形的对角线,掌握多边形的对角线公式是解题的关键.作者留言:非常感谢!您浏览到此文档。
人教版八年级上册 11.3 多边形及其内角和 同步练习(含答案)

多边形及其内角和同步练习一.选择题1.正多边形的每个内角为135度,则多边形为()A.4B.6C.8D.102.若一个多边形减去一个角后,内角和为720°,则原多边形不可能是几边形()A.四边形B.五边形C.六边形D.七边形3.一个四边形的四个内角度数之比为1:2:4:5,则这个四边形中,最小的内角为()A.30°B.40°C.50°D.60°4.一个正多边形的每个内角的度数都等于相邻外角的2倍,则该正多边形的边数是()A.3B.4C.6D.125.如图,已知一个五边形ABCDE纸片,一条直线将该纸片分割成两个多边形.若这两个多边形内角和分别为m和n,则m+n不可能是()A.540°B.720°C.900°D.1080°6.如图,在五边形ABCDE中,AE∥BC,延长DE至点F,连接BE,若∥A=∥C,∥1=∥3,∥AEF=2∥2,则下列结论正确的是()∥∥1=∥2 ∥AB∥CD ∥∥AED=∥A ∥CD∥DEA.1个B.2个D.4个7.如图,正五边形ABCDE绕点A顺时针旋转后得到正五边形AB′C′D′E′,旋转角为α (0°<α<90°),若DE∥B′C′,则∥α为()A.36°B.54°C.60°D.72°8.如图,在四边形ABCD中,∥DAB的角平分线与∥ABC的外角平分线相交于点P,且∥D+∥C=210°,则∥P=()A.10°B.15°C.30°D.40°9.设BF交AC于点P,AE交DF于点Q.若∥APB=126°,∥AQF=100°,则∥A-∥F=()A.60°B.46°C.26°D.45°10.如图,已知四边形ABCD中,∥C=90°,若沿图中虚线剪去∥C,则∥1+∥2等于()B.135°C.270°D.315°11.如图,在六边形ABCDEF中,若∥A+∥B+∥C+∥D=500°,∥DEF与∥AFE的平分线交于点G,则∥G等于()A.55°B.65°C.70°D.80°12.如图,A,B,C,D,E,F是平面上的6个点,则∥A+∥B+∥C+∥D+∥E+∥F的度数是()A.180°B.360°C.540°D.720°二.填空题13.八边形的内角和为;一个多边形的每个内角都是120°,则它是边形.14.一个多边形,除了一个内角外,其余各角的和为2750°,则内角和是.15.如图,已知在四边形ABCD中,∥A+∥C=135°,∥ADE=125°,则∥B= .16.如图所示,若∥DBE=78°,则∥A+∥C+∥D+∥E= °.17.如图所示,∥A+∥B+∥C+∥D+∥E+∥F+∥G+∥H= °.三.解答题18.(1)已知一个正多边形的每个内角比它的每个外角的4倍多30°,求这个多边形的边数;(2)一个多边形的外角和是内角和的七分之二,求这个多边形的边数.19.如图,在四边形ABCD中,BD∥CD,EF∥CD,且∥1=∥2.(1)求证:AD∥BC;(2)若BD平分∥ABC,∥A=130°,求∥C的度数.20.如图,四边形ABCD中,∥BAD=106°,∥BCD=64°,点M,N分别在AB,BC上,将∥BMN沿MN翻折得∥FMN,若MF∥AD,FN∥DC.求(1)∥F的度数;(2)∥D的度数.21.将纸片∥ABC沿DE折叠使点A落在点A'处【感知】如图∥,点A落在四边形BCDE的边BE上,则∥A与∥1之间的数量关系是;【探究】如图∥,若点A落在四边形BCDE的内部,则∥A与∥1+∥2之间存在怎样的数量关系?并说明理由.【拓展】如图∥,点A落在四边形BCDE的外部,若∥1=80°,∥2=24°,则∥A的大小为.22.已知,在四边形ABCD中,∥A+∥C=160°,BE,DF分别为四边形ABCD的外角∥CBN,∥MDC的平分线.(1)如图1,若BE∥DF,求∥C的度数;(2)如图2,若BE,DF交于点G,且BE∥AD,DF∥AB,求∥C的度数.参考答案1-5:CAACD 6-10:CBBBC 11-12:CB13、1080°;六14、2880°15、170°16、10217、72018、:(1)设这个多边形的每个内角是x°,每个外角是y°,则得到一个方程组得而任何多边形的外角和是360°,则多边形内角和中的外角的个数是360÷30=12,则这个多边形的边数是12边形;(2)设这个多边形的边数为n,依题意得:(n-2)180°=360°,解得n=9,答:这个多边形的边数为9.19、:(1)证明:∵BD⊥CD,EF⊥CD(已知),∴BD∥EF(垂直于同一直线的两条直线平行),∴∠2=∠3(两直线平行,同位角相等).∵∠1=∠2,∴∠1=∠3(等量代换).∴AD∥BC(内错角相等,两直线平行).(2)∵AD∥BC(已知),∴∠ABC+∠A=180°(两直线平行,同旁内角互补).∵∠A=130°(已知),∴∠ABC=50°.∵DB平分∠ABC(已知),∴∠3=25°.∴∠C=90°-∠3=65°.20、:(1)∵MF∥AD,FN∥DC,∠BAD=106°,∠BCD=64°,∴∠BMF=106°,∠FNB=64°,∵将△BMN沿MN翻折,得△FMN,∴∠FMN=∠BMN=53°,∠FNM=∠MNB=32°,∴∠F=∠B=180°-53°-32°=95°;(2)∠F=∠B=95°,∠D=360°-106°-64°-95°=95°.21、:(1)如图,∠1=2∠A.理由如下:由折叠知识可得:∠EA′D=∠A;∵∠1=∠A+∠EA′D,∴∠1=2∠A.(2)如图②,2∠A=∠1+∠2.理由如下:∵∠1+∠A′DA+∠2+∠A′EA=360°,∠A+∠A′+∠A′DA+∠A′EA=360°,∴∠A′+∠A=∠1+∠2,由折叠知识可得:∠A=∠A′,∴2∠A=∠1+∠2.(3)如图③,∵∠1=∠DFA+∠A,∠DFA=∠A′+∠2,∴∠1=∠A+∠A′+∠2=2∠A+∠2,∴2∠A=∠1-∠2=56°,解得∠A=28°.故答案为:∠1=2∠A;28°.22、:(1)过点C作CH∥DF,∵BE∥DF,∴BE∥DF∥CH,∴∠FDC=∠DCH,∠BCH=∠EBC,∴∠DCB=∠DCH+∠BCH=∠FDC+∠EBC,∵BE,DF分别为四边形ABCD的外角∠CBN,∠MDC的平分线,∴∠FDC=∠CDM,∠EBC=∠CBN,∵∠A+∠BCD=160°,∴∠ADC+∠ABC=360°160°=200°,∴∠MDC+∠CBN=160°,∴∠FDC+∠CBE=80°,∴∠DCB=80°;(2)连接GC并延长,同理得∠MDC+∠CBN=160°,∠MDF+∠NBG=80°,∵BE∥AD,DF∥AB,∴∠A=∠MDF=∠DGB=∠NBG=40°,∵∠A+∠BCD=160°,∴∠BCD=160°-40°=120°.。
人教版初中数学初二上册多边形及其内角和同步测试题(解析版)

人教版初中数学初二上册多边形及其内角和同步测试题(解析版)一、选择题(每小题只有一个正确答案)1.在下列4种正多边形的瓷砖图案中不能铺满地面的是()A.B.C.D.2.如图,在正六边形ABCDEF中,若△ACD的面积为12,则该正六边形的面积为()A.30B.36C.48D.603.下列图形中,内角和与外角和相等的多边形是()A.B.C.D.4.要是一个多边形的内角和是外角和的3倍,则这个多边形的边数是( )A.6B.7C.8D.95.如图,边长相等的正五边形和正方形的一边重合,那么∠1的度数是几多() A.30∘B.15∘C.18∘D.20∘6.一个正多边形的内角和为900°,那么从一点引对角线的条数是()A.3 B.4 C.5 D.67.如图,将四边形ABCD去掉一个60°的角得到一个五连形BCDEF,则∠l与∠2的和为()A.60°B.108°C.120°D.240°8.如图所示,∠A+∠B+∠C+∠D+∠E+∠F的度数为) )A.180o B.360o C.540o D.720o二、填空题9.多边形所有外角中,最多有_____个钝角,_____个直角.10.一个正n边形的内角是外角的2倍,则n=_____.11.如图,小亮从点O出发,进步5m后向右转30°,再进步5m后又向右转30°,这样走n次后恰恰回到点O处,小亮走出的这个n边形的每个内角是__________°,周长是___________________m.12.(题文)要是一个正方形被截掉一个角后,得到一个多边形,那么这个多边形的内角和是__________)第 1 页13.如图,五边形ABCDE是正五边形,若l1//l2,则∠1−∠2=__________.三、解答题14.如图,从△ABC的纸片中剪去△CDE,得到四边形ABDE.若∠1+∠2=∠225∘,求纸片中∠C的度数.15.已知在一个十边形中,此中九个内角的和是1320°,求这个十边形另一个内角的度数.16.如图所示,在△ABC中,∠A=60°)BD)CE分别是AC)AB上的高,H是BD和CE的交点,求∠BHC的度数.17.要是一个多边形的各边都相等,且各内角也都相等,那么这个多边形就叫做正多边形,如图,便是一组正多边形,查看每个正多边形中∠α的变化环境,解答下列标题.)1)将下面的表格补充完整:)2)根据纪律,是否存在一个正n边形,使此中的∠α=20°?若存在,直接写出n的值;若不存在,请说明理由.)3)根据纪律,是否存在一个正n边形,使此中的∠α=21°?若存在,直接写出n的值;若不存在,请说明理由.第 1 页参考答案1.C 【剖析】 【剖析】利用一种正多边形的镶嵌应相符一个内角度数能整除360°分别鉴别即可. 【详解】A 、正三角形的每个内角是60°,能整除360°,能密铺,故此选项不相符题意;B 、正方形的每个内角是90°,4个能密铺,故此选项不相符题意;C 、正五边形的每个内角为:180°-360°÷5=108°,不能整除360°,不能密铺,故此选项相符题意;D 、正六边形的每个内角是120°,能整除360°,能密铺,故此选项不相符题意. 故选:C 【点睛】此题主要考察了平面镶嵌知识,表现了学数学用数学的思想.由平面镶嵌的知识可知只用一种正多边形能够铺满地面的是正三角形或正四边形或正六边形. 2.B 【剖析】 【剖析】先由正六边形性质证S △ABC =12S △ACD =12×12,根据正六边形面积=2×四边形ABCD 面积.【详解】 作BH ⊥AC由正六边形性质可知,∠B=∠BCD=120〬, AB=BC=CD, 所以,∠BAC=∠BCA=30〬,所以,∠ACD=120〬-30〬=90〬,BH=12BC=12CD, 所以,S △ABC =12S △ACD =12×12=6,所以,S 正六边形=2×(12+6)=36. 故选:B 【点睛】本题审核知识点:正六边形性质.解题要害点:熟记正六边形性质.3.C【剖析】【剖析】根据多边形的内角和公式(n−2)⋅180°与多边形的外角和定理列式举行谋略即可得解.【详解】设多边形的边数为n,根据题意得,(n−2)⋅180°=360°,解得n=4.故选:C.【点睛】本题考察了多边形的内角和公式与外角和定理,熟记公式与定理是解题的要害.4.C【剖析】【剖析】根据多边形的内角和公式及外角的特性谋略.【详解】多边形的外交和是360°,根据题意得:180°⋅(n−2)=3×360°,解得:n=8.故选:C.【点睛】本题主要考察了多边形内角和公式及外角的特性.求多边形的边数,可以转化为方程的标题来办理.5.C【剖析】【剖析】∠1的度数是正五边形的内角与正方形的内角的度数的差,根据多边形的内角和定理求得角的度数,进而求解.【详解】∵正五边形的内角的度数是1×(5-2)×180°=108°,正方形的内角是90°,5∴∠1=108°-90°=18°.故选:C【点睛】本题考察了多边形的内角和定理、正五边形和正方形的性质,求得正五边形的内角的度数是要害.6.B【剖析】【剖析】n边形的内角和可以表示成(n-2)•180°,设这个多边形的边数是n,就得到关于边数的方程,从而求出边数,再求从一点引对角线的条数.【详解】设这个正多边形的边数是n,则(n-2)•180°=900°,解得:n=7.则这个正多边形是正七边形.所以,从一点引对角线的条数是:7-3=4.故选:B【点睛】本题审核知识点:多边形的内角和.解题要害点:熟记多边形内角和公式.7.D【剖析】【剖析】利用四边形的内角和得到∠B)∠C)∠D的度数,进而让五边形的内角和减去∠B)∠C)∠D的度数即为所求的度数.【详解】∵四边形的内角和为(4−2)×180°)360°)∴∠B)∠C)∠D)360°−60°)300°)∵五边形的内角和为(5−2)×180°)540°)∴∠1)∠2)540°−300°)240°)第 3 页故选:D)【点睛】本题考察多边形的内角和知识,求得∠B)∠C)∠D的度数是办理本题的突破点.8.B【剖析】剖析:根据三角形外角的性质,四边形的内角和谋略即可.详解:∵∠A+∠1+∠D+∠E=360°,∠1=∠B+∠2,∠2=∠C+∠F,∴∠A+∠B+∠C+∠D+∠E+∠F=360°.故选B.点睛:本题考察了多边形内角和公式和三角形外角的性质,三角形的外角即是和它不相邻的两个内角的和,四边形的内角和即是360°.9.34【剖析】【详解】∵多边形的外角和360度,∴外角最多可以有3个钝角;又∵当有4个直角时,四角的和是360度,∴多边形所有外角中,最多有4个直角.故答案为3)4.【点睛】本题主要考察多边形的外角和,多边形的外角和即是360°.10.6【剖析】【剖析】根据正多边形每个内角都相等,外角都相等,正多边形的内角与外角的和即是180°,根据内角是外角的2倍,可设外角为x,则内角为2x,可得:2x+x=180°,解得:x=60°,再根据外角和=6.即是360°,继而可得: n=360°60°【详解】设外角为x,则内角为2x,可得:2x+x=180°,解得:x=60°,=6.所以n=360°60°故答案为:6.【点睛】本题主要考察正多边形内角,外角的干系,办理本题的要害是要熟练掌握正多边形内角和外角的干系.11.150,60【剖析】剖析:回到出发点O点时,所议决的路线正好组成一个外角是30°的正多边形,根据正多边形的性质即可解答.详解:由题意可知小亮的路径是一个正多边形,∵每个外角即是30°)∴每个内角即是150°.∵正多边形的外角和为360°)∴正多边形的边数为360°÷30°=12(边).∴小亮走的周长为5×12=60.点睛:本题主要考察了多边形的内角与外角,牢记多边形的内角与外角概念是解题要害. 12.180°或360°或540°【剖析】剖析: 剪掉一个多边形的一个角,则所得新的多边形的角可能增加一个,也可能不变,也可能减少一个,根据多边形的内角和定理即可求解.详解: n边形的内角和是(n-2)•180°,边数增加1,则新的多边形的内角和是(4+1-2)×180°=540°,所得新的多边形的角不变,则新的多边形的内角和是(4-2)×180°=360°,所得新的多边形的边数减少1,则新的多边形的内角和是(4-1-2)×180°=180°,因而所成的新多边形的内角和是540°或360°或180°.故答案为:540°或360°或180°.点睛:本题主要考察了多边形的内角和的谋略公式,理解:剪掉一个多边形的一个角,则所第 5 页得新的多边形的角可能增加一个,也可能不变,也可能减少一个,是办理本题的要害. 13.72【剖析】剖析:延长AB交l2于点F,根据l1//l2得到∠2=∠3,根据五边形ABCDE是正五边形得到∠FBC=72°,最后根据三角形的外角即是与它不相邻的两个内角的和即可求出.详解:延长AB交l2于点F,∵l1//l2,∴∠2=∠3,∵五边形ABCDE是正五边形,∴∠ABC=108°,∴∠FBC=72°,∠1-∠2=∠1-∠3=∠FBC=72°故答案为:72°.点睛:此题主要考察了平行线的性质和正五边形的性质,正确把握五边形的性质是解题要害. 14.45∘【剖析】【剖析】根据∠1+∠2的度数,再利用四边形内角和定理得出∠A+∠B的度数,即可得出∠C的度数.【详解】因为四边形ABCD的内角和为360∘,且∠1+∠2=225∘.所以∠A+∠B=360∘−225∘=135∘.因为△ABD的内角和为180∘,所以∠C=180∘−(∠A+∠B)=180∘−135∘=45∘.【点睛】此题主要考察了多边形的内角与外角,利用四边形的内角和是360度的实际运用与三角形内角和180度之间的干系是解题要害.15.120°.【剖析】【剖析】n边形的内角和是(n−2)•180°,代入公式就可以求出十边形的内角和,就可以求出另一个内角.【详解】十边形的内角和是(10−2)•180°)1440°)则另一个内角为1440°−1320°)120°)【点睛】此题考察了多边形的内角和,正确印象多边形的内角和公式是办理本题的要害.16.120°.【剖析】【剖析】根据高的定义得∠ADB=∠AEC=90°,于是利用四边形内角和为360°可谋略出∠EHD,然后根据对顶角相等得到∠BHC的度数.【详解】∵BD、CE分别是△ABC边AC、AB上的高,∴∠ADB=∠AEC=90°,而∠A+∠AEH+∠ADH+∠EHD=360°,∴∠EHD=180°﹣60°=120°,∴∠BHC=120°.【点睛】本题考察了四边形的内角和以及三角形高的意义,解答此类题的要害是利用四边形的内角和为360°.17.(1)60°)45°)36°)30°)10°))2)当多边形是正九边形,能使此中的∠α=20°))3)不存在,理由见剖析【剖析】【剖析】(1)根据多边形内角和公式求出多边形的内角和,再根据三角形内角和定理求出即可;(2)根据表中的终于得出纪律,根据纪律得出方程,求出方程的解即可;(3)根据表中的终于得出纪律,根据纪律得出方程,求出方程的解即可.【详解】)1)填表如下:故答案为:60°)45°)36°)30°)10°)第 7 页)2)存在一个正n 边形,使此中的∠α=20°) 理由是:根据题意得:(180n)∘=20°)解得:n=9)即当多边形是正九边形,能使此中的∠α=20°) )3)不存在,理由如下:假设存在正 n 边形使得∠α=21°,得 ∠α=21∘=(180n)∘)解得:n =847,又 n 是正整数,所以不存在正 n 边形使得∠α=21°) 【点睛】本题考察了多边形的内角与外角和等腰三角形的性质,能求出多边形的一个内角的度数是解此题的要害,注意:多边形的内角和=(n-2)×180°.。
八年级上册数学人教版多边形及其内角和 课时练 试题试卷 含答案解析

一、选择题 1. 在如图所示的图形中,凸多边形共有
A. 1 个
B. 2 个
C. 3 个
D. 4 个
2. 若一个多边形的内角和是 900∘,则这个多边形是
A. 五边形
B. 六边形
C. 七边形
D. 八边形
3. 将一个 边形变成 + 1 边形,内角和将
A. 减少 180∘
∴∠
+∠
= 240∘.
∵ , 分别是 ∠ ,∠ 的平分线,
∴∠
=
1 2
∠
,∠
=
1 2
∠
.
∴∠+∠源自=1 2∠
+∠
= 120∘.
∴ ∠ = 180∘ − ∠ + ∠ = 60∘.
8. 在平面内,由一些线段
相接组成的封闭图形叫做多边形;多边形
组
成的角叫做多边形的内角;多边形的边与它的
组成的角叫做多边形的外角.
9. 连接多边形
的两个顶点的线段,叫做多边形的对角线.从 边形 ≥ 4 的一
个顶点出发,可以作
条对角线,这些对角线将 边形分为
个三角形;
边形共有
条对角线.
10. 画出多边形的任何一条边所在直线,如果整个多边形都在这条直线的 个多边形就叫做凸多边形.
,那么这
11.
都相等,
都相等的多边形叫做正多边形.
12. 边形的内角和等于
;多边形的外角和等于
.
13. (1)如图①, =
;如图②, =
;(3)如图③, =
.
14. (1)若一个正多边形的一个外角等于 18∘,则这个正多边形的边数是 (2)已知一个正多边形的内角是 140∘,则这个正多边形的边数是
人教版2023-2024学年八年级上册数学《多边形及其内角》同步练习(含答案)

人教版2023-2024学年八年级上册数学《多边形及其内角》同步练习一、单选题1.一个多边形的每个外角都等于与它相邻的内角,这个多边形是( )边形A .四B .五C .六D .八2.若一个多边形的每个内角都是,那么它的边数是( )140︒A .5B .7C .9D .113.中国古代建筑具有悠久的历史传统和光辉的成就,其建筑艺术也是美术鉴赏的重要对象.如图是中国古代建筑中的一个正八边形的窗户,则它的内角和为( )A .B .C .D .1080︒900︒720︒540︒4.如图,一束平行太阳光照射到正五边形上,若∠1=46°,则∠2的度数为( )A .46°B .108°C .26°D .134°5.如图1是一个2×5长方形方格,用图2所示的1×2的黑色长方形(允许只用一种)去填满,共有( )种不同的方法.A .7B .8C .9D .106.如图,四边形中,与相邻的两外角平分线交ABCD 90,ADC ABC ∠=∠=︒ADC ABC ∠∠、于点若则的度数为( ),E 60,A ∠=︒E ∠A .B .C .D .60 50 40 307.如图,要使一个七边形木架不变形,至少要再钉上木条的根数是( )A .1根B .2根C .3根D .4根8.七边形中,、的延长线相交于点.若图中、、、的ABCDEFG AB ED O 1∠2∠3∠4∠外角的角度和为,则的度数为( )220︒BOD ∠A .B .C .D .30︒35︒40︒45︒9.如图,一个等边三角形纸片,剪去一个角后得到一个四边形,则图中∠α+∠β的度数是( )A .B .C .D .240︒220︒180︒330︒10.如图,直线,将一个含角的直角三角尺按图中方式放置,点E 在AB CD ∥60︒EGF 上,边、分别交于点H 、K ,若,则等于( ).AB GF EF CD 64BEF ∠=︒GHC ∠三、解答题21.若一个多边形的内角和等于它的外角和的24.已知一个正n边形的内角和是正三角形内角和的4倍.(1)求n;(2)用边长相等的正n 边形和正三角形两种地板镶嵌地面,则一个公共顶点处需要正n边形和正三角形的个数分别为x、y,求x和y的关系式.25.如图,小明从点A出发,前进10m后向右转30°,再前进10m后又向右转30°,……,如此反复下去,直到她第一次回到出发点A,他所走的路径构成了一个正多边形.(1)求小明一共走了多少米;(2)求这个正多边形的内角和.答案:1.A2.C3.A4.C5.B6.D7.D8.C9.A10.B11.512.③④13.50°或130°14. 15 60°15.18/十八16. 2 817./36度36︒18./度 144︒1443519. 144 10 144020./度180︒18021.这个多边形是十边形22.(1)15;(2)1523.(1)8(2)360︒24.(1)6n =(2)26x y +=25.(1)小明一共走了120米1800 (2)这个多边形的内角和是.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
11. 3多边形及其内角和
基础过关作业
1. 四边形ABCD中,如果/ A+Z C+Z D=280°,则/ B的度数是()
A . 80°
B . 90°
C . 170°
D . 20°
2. 一个多边形的内角和等于1080。
,这个多边形的边数是
()
A . 9
B . 8
C . 7
D . 6
3. 内角和等于外角和2倍的多边形是()
A .五边形
B .六边形
C .七边形
D .八边形
4. _________________________ 六边形的内角和等于度.
5 .正十边形的每一个内角的度数等于________________ ,每一个外角
的度数等于__________ .
6. 如图,你能数出多少个不同的四边形?
7. 四边形的四个内角可以都是锐角吗?可以都是钝角吗? 可以都是直角吗??为什么?
&求下列图形中x的值:
综合创新作业
9. (综合题)已知:如图,在四边形ABCD中, / A=Z C=90°,
BE平分/ ABC ?DF平分/ ADC BE与DF有怎样的位置关系?为什么?
10. (应用题)有10个城市进行篮球比赛,每个城市均派3
个代表队参加比赛,规定同一城市间代表队不进行比赛,其他代表队都要比赛一场,问按此规定,?所有代表队要
打多少场比赛?
11. (创新题)如图,以五边形的每个顶点为圆心,以1为
半径画圆,求圆与五边形重合的面积.
12. (1)(2005年,南通)已知一个多边形的内角和为540°,则这个多边形为()
A .三角形
B .四边形
C .五边形
D .六边形
(2)(2005年,福建泉州)五边形的内角和等于_______________ 度.
13. (易错题)一个多边形的每一个顶点处取一个外角,这些外角中最多有钝角(?)
A . 1个
B . 2个
C . 3个
D . 4个
培优作业
14 .(探究题)
(1 )四边形有几条对角线?
五边形有几条对角线?
六边形有几条对角线?
猜想并探索:
n边形有几条对角线?
(2)—个n边形的边数增加1,对角线增加多少条?
15.(开放题)如果一个多边形的边数增加1, ?那么这个多
边形的内角和增加多少度?若将n边形的边数增加1倍,
则它的内角和增加多少度?
数学世界
攻其不备
壁虎在一座油罐的下底边沿A处.它发现在自己的正上方一一油罐上
边缘的B?处有一只害虫.壁虎决定捕捉这只害虫.为了不引起害虫的注意,它故意不走直线,而是绕着油罐,沿着一条螺旋路线,从背后对害虫进行突
然袭击如图
7-3-5 .结果,?壁虎的偷袭得到成功,获得了一顿美餐.
AB 请问:壁虎沿着螺旋线爬行是最短的路程吗(线段
除外)?
答案:
1. A 点拨:/ B=360° - (/ A+Z C+Z D ) =360° -280 ° =80°.故选 A .
2. B 点拨:设这个多边形的边数为 n,则(n-2 ) -180=1080.解 得n=8 .
故选B.
3 . B 点拨:设这个多边形的边数为
n ,根据题意,得
(n-2 ) - 180=2 X 360.解得 n=6.故选 B .
4. 720
5. 144° ; 36°
点拨:正十边形每一个内角的度数为:(
10-
2)
180
=144°,
10
每一个外角的度数为:180° -144 ° =36° .
6. 有27个不同的四边形.
7. 解:四边形的四个内角不可以都是锐角,不可以都是钝
角,可以都是直角.
因为四边形的内角和为 360 °,如果四个内角都是锐角或
都是钝角,?
则内角和小于360°或大于360 °,与四边形的内角和为
360。
矛盾.?
所以四个内角不可以都是锐角或都是钝角.
若四个内角都是直角,则四个内角的和等于360。
,与内角和定理相符,
所以四个内角可以都是直角.
&解:(1) 90+70+150+x=360.
解得x=50.
(2)90+73+82+ (180-x ) =360.
解得x=65.
(3)x+ (x+30) +60+x+ (x-10 ) = (5-2 ) X 180.
解得x=115.
9. 解:BE// DF.
理由:I/ A=Z C=90°,
•••/ A+/ C=180°.
•••/ ABC+/ ADC=360 -180 ° =180°.
•••/ ABE』/ ABC / ADF=1 / ADC
2 2
•••/ ABE+/ ADF』(/ ABC+/ ADC =- X 180°=90°.
2 2
又•••/ ABE+/ AEB=90°,
•••/ AEB=/ ADF
••• BE// DF (同位角相等,两直线平行).
10. 解:I n (n-3 )=丄X 10X( 10-3 )=」X 10X 7=35 (场).
2 2 2
答:按此规定,所有代表队要打35场比赛.
点拨:问题类似于求多边形对角线的个数.
11. 解:(5-2)X 180 ° - 360 ° X 12=1.5 .
点拨:不能直接求出扇形的度数,用整体法圆与五边形
重合部分的角度和正好是五边形的内角和.
12. (1) C点拨:设这个多边形的边数为n,
依题意,得(n-2 ) X 180 ° =540 °,解得n=5,故选
C.
(2) 540 点拨:(n-2 ) X 180° = (5-3 )X 180° =540°.
13. C
14 .解:(1)四边形有2条对角线;
五边形有5条对角线;
六边形有9条对角线;
n 边形有垃可条对角线.
2
(2)当n边形的边数增加1时,对角线增加(n-1 )条.
点拨:从n边形的一个顶点出发,向其他顶点共可引
(n-3 )条对角线,n个顶点共可引n (n-3 )条,但这些对
角线每一条都重复了一次,故n边形的对角线条数为血①.
2 15. 180°, n • 180°.
数学世界答案:是最短的路程.可用纸板做一个模型,沿AB
剪开便可看出结论.。
