高中数学 高中圆锥曲线实验及作图
几何画板制作 圆锥曲线的画法
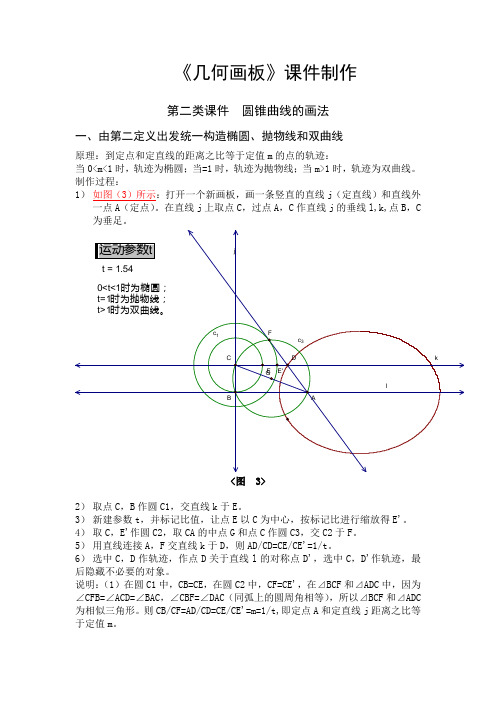
《几何画板》课件制作第二类课件圆锥曲线的画法一、由第二定义出发统一构造椭圆、抛物线和双曲线原理:到定点和定直线的距离之比等于定值m的点的轨迹:当0<m<1时,轨迹为椭圆;当=1时,轨迹为抛物线;当m>1时,轨迹为双曲线。
制作过程:1)如图(3)所示:打开一个新画板,画一条竖直的直线j(定直线)和直线外一点A(定点)。
在直线j上取点C,过点A,C作直线j的垂线l,k,点B,C 为垂足。
<图 3>2)取点C,B作圆C1,交直线k于E。
3)新建参数t,并标记比值,让点E以C为中心,按标记比进行缩放得E'。
4)取C,E'作圆C2,取CA的中点G和点C作圆C3,交C2于F。
5)用直线连接A,F交直线k于D,则AD/CD=CE/CE'=1/t。
6)选中C,D作轨迹,作点D关于直线l的对称点D',选中C,D'作轨迹,最后隐藏不必要的对象。
说明:(1)在圆C1中,CB=CE,在圆C2中,CF=CE',在⊿BCF和⊿ADC中,因为∠CFB=∠ACD=∠BAC,∠CBF=∠DAC(同弧上的圆周角相等),所以⊿BCF和⊿ADC 为相似三角形。
则CB/CF=AD/CD=CE/CE'=m=1/t,即定点A和定直线j距离之比等于定值m。
(2)单击"运动参数t"按钮,比值m 随之改变,这时可以动态地看到,当m 小于1的值逐渐变为1时,轨迹由椭圆变成抛物线;当m 大于1时,轨迹变成双曲线。
二、由第一定义出发,构造椭圆和双曲线及抛物线原理:椭圆(双曲线)——到定点的距离和定直线的距离之和(差)等于定值的点的轨迹;抛物线——到定点的距离和定直线的距离相等的点的轨迹。
制作过程:1.椭圆(或双曲线)的制作:<图 4> <图 5>()()1211221121,2()()x F x F F M F M MN N F M F N MN A B AB F F A F B 作出平面直角坐标系,在轴上任取两点作圆标记圆心的点记为,另一点隐藏。
圆锥曲线准线的几何作图

x2 y2 = 1( a > 0, b > 0 ) 在点 T ( x 0, y 0) 处的 切线 方 a2 b 2 程分别是 x 0x y0y x 0x y0y + 2 = 1 和 2 - 2 = 1。 a2 b a b 4 1 椭圆准线的作图 作法 设 T ( x 0, y 0) ( 非顶点 ) 是 椭圆
x2 y2 + = 1( a > b > 0) 于点 S 、 T , 点 A 1、 A 2 分 别是椭 a 2 b2 圆的 左、 右 顶点 , 连接 A 1 S 、 A 2 T 交于 点 M , 则 过 M
2004 年第 3 期
设 H ( x 0, 0 ) , 又 | T F | =
中学数学教学
2x 0 b2 2a2 , 所以 2 = ,即 a x 0- c b 点, 作
c- a = 2c - a
a- x 0 a2 , 即 x0= 。故直线 MH 为双曲线的 ( 右 ) 准 c 2 a- x 0 线。 4 利用圆锥曲线切线作图 x2 y2 + = 1( a > b > 0) ( 双 a 2 b2 本作法以如下熟知的命题 为基础。 命题 1 曲线 设 T 是椭 圆
x 2 y2 F 22 = 1 ( a > 0, b> 0 ) ) 上一点 ( 非顶点 ) , F 1、 a b 是曲线的两 焦点 , T K 是 ∀ F 1 T F 的 角 平分 线 的垂 线 ( ∀ F 1 TF 的角平分线 ) , 则 T K 是 椭圆 ( 双 曲线 ) 在 T 点处的切线。 命题 2 椭圆 x 2 y2 + = 1 ( a > b> 0 ) 及双曲线 a2 b 2
2
Hale Waihona Puke x2 y2 = 1 ( a > 0 , b > 0 ) 准线 a 2 b2 几何作图的统一的作法。 1 1 椭圆准线的作图 作法 以原点为 圆心 , 以 a 为半 径作 圆 , 交 y 轴 于点 E , 连接 EF ( F 是椭 圆的 左焦点 ) , 作 直线 EH EF 交 x 轴 于点 H , 则 过点 H 且垂 直于 x 轴 的直线 l 即为椭圆的右准线 ( 如下图 1 ) 。 证明 因 为 | OF | = c, | OE | = a, 在 Rt FEH 中 , 由射影定理得 , | OE | 2= | OF | ! | OH | , 所以 | OH | = a2 。故直线 l 为椭圆的右准线。 c
圆锥曲线PPT优秀课件

.
F0 A2 x
其中 a2 b2 c2 , a 0,b c 0 , F0 , F1, F2 是对应的焦点。 B1
(1)若三角形 F0 F1F2 是边长为 1 的等边三角形,求“果圆”的方程;
(2)若
A1 A
B1B
,求
b a
的取值范围;
解:(1)∵F0(c,0)F1(0, b2 c2 ),F2(0, b2 c2 )
①;
∵点 P1, P2 在双曲线上,∴点 P1, P2 的坐标适合方程①。
将 (3, 4
2
),
(
9 4
,
5)
分别代入方程①中,得方程组:
(4 2)2 a2
32 b2
25 a2
(
9)2 4 b2
1
1
将
1 a2
和
1 b2
1
看着整体,解得
a2 1
1 16
1
,
b2 9
∴
a 2 b2
16 即双曲线的标准方程为 y2
9
16
x2 9
1。
点评:本题只要解得 a2 ,b2 即可得到双曲线的方程,没有
必要求出 a,b 的值;在求解的过程中也可以用换元思想, 可能会看的更清楚。
(4) 与双曲线 x 2 y 2 1有共同渐近线, 9 16
且过点 (3,2 3) 。
解析:(4)设所求双曲线方程为 x2 y 2 ( 0) ,
3 m
5 n
1
定义,还要知道椭 圆中一些几何要素
所以,椭圆方程为 y2 x2 1 . 与椭圆方程间的关
10 6
系。
例 2.设椭圆的两个焦点分别为 F1、、F2,过 F2 作椭圆长轴的垂线交椭圆于点 P,若△F1PF2 为
圆锥曲线三个经典实验 (6)

数学实验报告实验序号:3日期:2015年3月28日班级:12组别:123成员:林佳彦林佳佳刘嘉棣郑素萍黄永欣1.实验名称:关于圆锥曲线产生的三个经典实验2.实验目的:沿着历史的轨迹,重走前人发现圆锥曲线的历程。
重现圆锥曲线产生的三个经典实验——梅内克缪斯的割圆锥法、阿波罗尼奥斯的割圆锥法、Dandelin双球实验。
探讨圆锥曲线的种类和各种圆锥曲线产生的条件。
3.实验方法:利用实物、模具观察,利用几何画板课件进行探讨、反思4.实验器材:卡纸、水、橡皮泥、乒乓球、透明软文件夹5.实验过程:(操作步骤、异常情况报告、处理方法)一、梅内克缪斯割圆锥法——最早对圆锥曲线的命名背景:公元前4世纪,希腊著名学者梅内克缪斯首先发现了圆锥曲线.他用平面去截圆锥曲面而得到截痕,并称之为圆锥曲线.当时的圆锥曲面都是通过直角三角形的一条直角边为旋转轴旋转而成的.根据轴三角形顶角的不同,将圆锥曲面分为锐角圆周、钝角圆锥和直角圆锥.Menaechmus用垂直于一条母线的平面去截这三种圆锥面,得到三种不同的截痕。
在锐角圆锥上的截痕定义为椭圆,钝角圆锥上的截痕是双曲线(的一支),在直角圆锥上的截痕是抛物线.值得注意的是,梅内克缪斯虽然推导了圆锥曲线的一些性质,但并没有建立焦点、焦半径的概念.并且当时所使用的旋转体均为直角三角形,得到的均为正圆锥,有一定的局限性.(1)我们小组通过用建立坐标轴的方式,将梅内克缪斯割圆锥法用现在定义的圆锥曲线方程进行验证,发现其与现在的圆锥曲线方程是相符的.即两种定义是相符的,满足了定义的一致性.○1直角圆锥:∵平面DEG⊥平面ABC,平面PVR⊥ABC∴QP⊥平面ABC∴PQ⊥RV又∵RV是直径,根据射影定理∴PO²=RO×OV∵△HDG∽DOV∴DO OV DO DG=OV=HD DG HD∙⇒且RO=HD∴PO2=RO×OV=HD×DO DGHD∙=DO×DG若我们建立以D为圆心,DF为X轴的直角坐标系,P点坐标为(x,y)则得到曲线方程为:2y DG x=∙,其中DG由点D的位置决定,是一个常数这正好符合我们现代解析几何中的抛物线的方程。
高中数学 第二章 圆锥曲线与方程 2.1.2 由曲线求它的

• 通过这节课,对知识有什么新认识? • 加深理解了什么方法?
2013 海淀二模理 14.在平面直角坐标系中,动点 P(x, y) 到两条坐标轴的距离之和等于它到点 (1,1) 的距 离,记点 P 的轨迹为曲线W .
(I) 给出下列三个结论:
①曲线W 关于原点对称; ②曲线W 关于直线 y x 对称; ③曲线W 与 x 轴非负半轴, y 轴非负半轴围成的封闭图形的面积小于 1 ;
距离之积等于常数a 2,
(1)曲线C过坐标原点;
(2)曲线C 关于坐标原点对称;
(3)点P是曲线C
上点,则F1PF2的面积不大于
1 2
a 2。
ቤተ መጻሕፍቲ ባይዱ
以上结论正确的是_____________
、
如:(1)曲线C范围是什么? (2)曲线C是否关于x轴或者y轴对称?
(3)若a=0,则曲线C表示的是什么?
课堂小结:
请你分析曲线x3 y2 1的几何性质?
你能画出曲线x3 y2 1的图像吗?
例、题1:乔凡尼多美尼科 卡西尼是一位意大利出生的法国籍 天文学家和水利工程师,他是第一个发现土星的人。
1675年,他在研究土星及其卫星的运行规律时,发现了
一条平面曲线方程,满足以下条件:
曲线C上任意一个动点P到两个定点F1 1, 0、F2 1, 0
2
其中,所有正确结论的序号是_____;
(Ⅱ)曲线W 上的点到原点距离的最小值为______.
分析x2 y3 1性质和图像
平面解析几何研究的两个主要问题:
(1)根据已知条件求出曲线的方程; (2)通过方程研究曲线的几何性质。
由曲线的方程研究曲线的几何性质
你能说出椭圆 x2 y2 1的哪些几何性质? 2
高中数学第二章圆锥曲线与方程2.3.2双曲线的简单几何性质课件新人教A版选修2

高中数学第二章圆锥曲线与方程2.3.2双曲线的简单几何性质课件新人教A 版选修2
2.线的草图,首先在坐标系中画出渐近线 y=±32x,顶 点-23,0,23,0,然后算出双曲线在第一象限内一点的坐标, 比如取 y=1,算出 x=232≈0.94,可知点(0.94,1),(0.94,-1) 在双曲线上,将三点(0.94,-1),(23,0),(0.94,1)依次连成光滑 曲线并让它随 x 的增大逐步接近渐近线,画出位于第一、四象限 内双曲线的一支.最后由对称性可画出位于第二、三象限内双曲 线的另一支,得双曲线的草图如图所示.
(2a,- 3b),代入直线方程得- 3b=ba(2a-c),化简可得离心 率 e=ac=2+ 3.
【答案】 2+ 3
法二:∵渐近线 y=12x 过点(4,2),而 3<2, ∴点(4, 3)在渐近线 y=12x 的下方, 在 y=-12x 的上方(如图). ∴双曲线的焦点在 x 轴上,
休息时间到啦
同学们,下课休息十分钟。现在是休息时间,你 们休息一下眼睛,
看看远处,要保护好眼睛哦~站起来动一动,久坐 对身体不好哦~
结束语
同学们,你们要相信梦想是价值的源泉,相信成 功的信念比成功本身更重要,相信人生有挫折没 有失败,相信生命的质量来自决不妥协的信念, 考试加油!奥利给~
【解析】 如图所示,不妨设与渐近线平行的直线 l 的斜率
为ba,又直线 l 过右焦点 F(c,0),则直线 l 的方程为 y=ba(x-c).因 为点 P 的横坐标为 2a,代入双曲线方程得4aa22-by22=1,化简得 y =- 3b 或 y= 3b(点 P 在 x 轴下方,故舍去),故点 P 的坐标为
数学苏教版选修2-121圆锥曲线(课件)

例1.已知条件p:平面上的动点M到两定点F1,F2
的距离之和为常数2a> |F1F2| ;条件Q:动点M的
轨迹以F1,F2为焦点的椭圆,则P是Q的(C)条件
A.充分不必要
B。必要不充分
C.充要
D.既不充分也不必要
例2.如图:一圆形纸片的圆心为O,F是圆内一定点,M
MF1 + MF2 =MP + MQ = PQ=定值
V
Q O2
F2 F1
M
O1
P
椭圆的定义:
平面内到两定点 F1,F2的距离和等于常数(大于 F1F2) 的点的轨迹叫做椭圆,两个定点 F1,F2叫做椭圆的焦 点,两焦点间的距离叫做椭圆的焦距。
可以用数学表达式来体现:
设平面内的动点为M,有MF1 MF2 2a
是圆周上一动点,把纸片折叠使M与F重合,然后抹平
纸 片 , 折 痕 为 CD , 设 CD 与 OM 交 于 P , 则 点 P 的 轨 迹 是
(A )
D M
A.椭圆
B.双曲线
C.抛物线
D.圆
O
C
F
例3.一动圆过定点A(-4,0) ,且与定圆 B:(x-4曲线右支 )
看PF1和PF2谁大,偏向小 的一边。
抛物线的定义 :
平面内到一个定点F和一条定直线L(F不在L 上)的距离相等的点轨迹叫做抛物线,定点F叫做 抛物线的焦点,定直线L叫做抛物线的准线
可以用数学表达式来体现: 设平面内的动点为M ,有 MF=d(d为动点M到
直线L的距离)
说明:
1、椭圆、双曲线、抛物线统称为圆锥曲线
变式:过点A(3,0)且与y轴相切的动圆
圆锥曲线的基本概念与图像

确定圆锥曲线的类型和参数
绘制圆锥曲线的常用方法
极坐标法:将圆锥曲线转换为极坐标形式,然后绘制出曲线的图像。
数值法:通过数值计算的方法,近似地绘制出圆锥曲线的图像。
直接法:根据圆锥曲线的定义和性质,直接绘制出曲线的图像。
参数法:通过引入参数方程,将圆锥曲线表示为参数方程,然后绘制出曲线的图像。
绘制圆锥曲线的注意事项
圆锥曲线的焦点与准线
焦点:圆锥曲线上的点到曲线的两个焦点的距离之和等于常数
准线:与圆锥曲线的母线平行的直线,与曲线相交于焦点
圆锥曲线的离心率
定义:圆锥曲线的离心率是用来描述圆锥曲线形状的一个重要参数,定义为焦距与轴线长度之比。
单击此处添加标题
单击此处添加标题
计算方法:离心率可以通过圆锥曲线的标准方程进行计算,也可以通过图形直观地测量得出。
圆锥曲线在三维空间中的形态和性质
圆锥曲线在解决实际问题中的应用
圆锥曲线在解决几何问题中的优势和局限性
05
圆锥曲线在物理中的应用
圆锥曲线在光学中的应用
椭圆和抛物线的光学性质
双曲线的光学性质
圆锥曲线在光学仪器中的应用
圆锥曲线在光波导中的应用
圆锥曲线在力学中的应用
抛物线在射程运动中的应用
圆锥曲线在碰撞与动量守恒定律中的应用
特性:渐近线的斜率等于圆锥曲线在顶点处的切线斜锥曲线的类型,渐近线可分为水平渐近线、竖直渐近线、斜渐近线等
03
圆锥曲线的图像绘制
绘制圆锥曲线的基本步骤
使用绘图软件或手动画图,连接点形成曲线
根据参数方程计算曲线上点的坐标
建立坐标系,确定坐标轴
抛物线在几何问题中的应用:抛物线的性质,如所有从焦点出发的线段都与抛物线相切,使得它在解决与焦点、准线和切线相关的问题中非常有用。
