工程力学第二章平面汇交力系
合集下载
工程力学第二章平面汇交力系

FF
cos Y Fy
FF 式中 cos和 cos 称为力 F 的方向余弦。
第二章 平面汇交力系
湖南工业大学土木工程学院
§2-2 平面汇交力系合成与平衡的解析法
【例题 3】试求图中各力在坐标轴上的投影。已知 P1=P2=P4=10kN, P3=P5=15kN, P6=20kN。
第二章 平面汇交力系
工程力学
第二章 平面汇交力系
第二章 平面汇交力系
湖南工业大学土木工程学院
第二章 平面汇交力系
§2–1平面汇交力系合成与平衡的几何法 §2–2平面汇交力系合成与平衡的解析法
第二章 平面汇交力系
湖南工业大学土木工程学院
§2-1平面汇交力系 合成与平衡的几何法
第二章 平面汇交力系
湖南工业大学土木工程学院
矢量表达式:R= F1+F2
由力的平行四边形法则作,也可用力的三角形来作。
由余弦定理:
R F12 F22 2F1F2 cos
合力方向由正弦定理:
F1
R
sin sin(180 )
第二章 平面汇交力系
湖南工业大学土木工程学院
§2-1 平面汇交力系合成与平衡的几何法
2. 任意个共点力的合成
F1
A F2
F4 F3
F1 B F2
A
R
C
F3
D
F4
E
F1、F2、F3、F4 为平面共点力系:
表达式: R F1 F 2F3 F4
第二章 平面汇交力系
湖南工业大学土木工程学院
§2-1 平面汇交力系合成与平衡的几何法
力的多边形规则:
把各力矢首尾相接,形成一条有向折线段(称为力链)。 加上一封闭边,就得到一个多边形,称为力多边形。
cos Y Fy
FF 式中 cos和 cos 称为力 F 的方向余弦。
第二章 平面汇交力系
湖南工业大学土木工程学院
§2-2 平面汇交力系合成与平衡的解析法
【例题 3】试求图中各力在坐标轴上的投影。已知 P1=P2=P4=10kN, P3=P5=15kN, P6=20kN。
第二章 平面汇交力系
工程力学
第二章 平面汇交力系
第二章 平面汇交力系
湖南工业大学土木工程学院
第二章 平面汇交力系
§2–1平面汇交力系合成与平衡的几何法 §2–2平面汇交力系合成与平衡的解析法
第二章 平面汇交力系
湖南工业大学土木工程学院
§2-1平面汇交力系 合成与平衡的几何法
第二章 平面汇交力系
湖南工业大学土木工程学院
矢量表达式:R= F1+F2
由力的平行四边形法则作,也可用力的三角形来作。
由余弦定理:
R F12 F22 2F1F2 cos
合力方向由正弦定理:
F1
R
sin sin(180 )
第二章 平面汇交力系
湖南工业大学土木工程学院
§2-1 平面汇交力系合成与平衡的几何法
2. 任意个共点力的合成
F1
A F2
F4 F3
F1 B F2
A
R
C
F3
D
F4
E
F1、F2、F3、F4 为平面共点力系:
表达式: R F1 F 2F3 F4
第二章 平面汇交力系
湖南工业大学土木工程学院
§2-1 平面汇交力系合成与平衡的几何法
力的多边形规则:
把各力矢首尾相接,形成一条有向折线段(称为力链)。 加上一封闭边,就得到一个多边形,称为力多边形。
工程力学第二章-汇交力系

4.区分力系的主矢和合力是两个不同的概念。 力系中各力矢的矢量和称为力系的主矢。主矢是一个几何量,
有大小和方向,但不涉及作用点问题,可在任意点画出。 合力是一物理量,除了大小和方向,还必须说明其作用点才有
意义。
思考题::
1.平面汇交力系可合成为个1合力,其作用线通过, 其大小和方向可用力多边形的表示封. 闭边
内的投影与x轴的夹角
z
F
γβ
O
y
α
x
Fx F cos F y F cos Fz F cos
F
γ
O
y
x
Fxy
Fx F sin cos
Fy F sin sin
Fz F cos
如果已知一力在直角坐标轴上的投影分别为 Fx,FY,FZ
z
则该力的大小和方向分别为:
Fz
大小:F Fx2Fy2Fz2
而当坐标轴不相互垂直时,轴向分 力与力的投影在数值上不相等。 o
F
x
结论与讨论
➢ 力在轴上的投影和力沿轴的分量之间的关系
(1)力的投影是代数量,力的分量是矢量
(2)不论是否为直角坐标系,力的投影都按下式计算:
Fx Fcos
Fy Fcos
α、β分别为力F与、轴的夹角。
(3)分力 Fx,应Fy按平行四边形法则计算
F2
或:
FR Fi
作用点:原力系的汇交点。
注意: 1.要选择恰当的长度比例尺和力的比例尺。 2.作力多边形时,可以任意变换力的次序, 虽然得到形状不同的力多边形,但合成的结 果不改变。
F3
F2
F4
F1
FR
F3
F2
F4
F1
FR
3.力多边形中诸力应首尾相连,合力的方向则是从第一个力 的起点指向最后一个力的终点。
有大小和方向,但不涉及作用点问题,可在任意点画出。 合力是一物理量,除了大小和方向,还必须说明其作用点才有
意义。
思考题::
1.平面汇交力系可合成为个1合力,其作用线通过, 其大小和方向可用力多边形的表示封. 闭边
内的投影与x轴的夹角
z
F
γβ
O
y
α
x
Fx F cos F y F cos Fz F cos
F
γ
O
y
x
Fxy
Fx F sin cos
Fy F sin sin
Fz F cos
如果已知一力在直角坐标轴上的投影分别为 Fx,FY,FZ
z
则该力的大小和方向分别为:
Fz
大小:F Fx2Fy2Fz2
而当坐标轴不相互垂直时,轴向分 力与力的投影在数值上不相等。 o
F
x
结论与讨论
➢ 力在轴上的投影和力沿轴的分量之间的关系
(1)力的投影是代数量,力的分量是矢量
(2)不论是否为直角坐标系,力的投影都按下式计算:
Fx Fcos
Fy Fcos
α、β分别为力F与、轴的夹角。
(3)分力 Fx,应Fy按平行四边形法则计算
F2
或:
FR Fi
作用点:原力系的汇交点。
注意: 1.要选择恰当的长度比例尺和力的比例尺。 2.作力多边形时,可以任意变换力的次序, 虽然得到形状不同的力多边形,但合成的结 果不改变。
F3
F2
F4
F1
FR
F3
F2
F4
F1
FR
3.力多边形中诸力应首尾相连,合力的方向则是从第一个力 的起点指向最后一个力的终点。
工程力学 第2章 汇交力系_2

P
A
a
B
a
C
工 件
解:这是多个物体所组成的系统平衡的问题。系统平衡时, 其中的每一部分也应该是平衡的 P (1)取B点为研究对象
a
a
FN 1
FN 2
第二章 汇交力系
P
A
P
a
B
a
C
工 件
a
FN 1
a
FN 2
Fx 0, FN1 cosa FN 2 cosa 0 FN1 FN 2
Fy 0, FN1 sin a FN 2 sin a P 0
第二章 汇交力系
解题技巧及说明: 1. 投影轴常选择与未知力垂直,最好使每个方程中只有一 个未知数。 2. 解析法解题时,力的方向可以任意假设,如果求出负值, 说明力方向与假设相反。 3. 对于二力杆件, 一般先设为拉力,如果求出负值,说 明物体受压力。
第二章 汇交力系
例:图示连杆增力机构,P=1kN,α=80,求工件所 受压紧力。
第二章 汇交力系
§2 汇交力系的平衡条件
一、三力平衡汇交定理 定理:当刚体在同一平面内作用线互不平行的三个力作 用下平衡时,这三个力的作用线必汇交于一点。 B FB
FA
A
B FB
FA A
C
FC
C
FC FBC
FC D
FB
FB , FC 合成为力 FBC
因为 FB , FC 不平行,相交于D点
由二力平衡原理得:三力作用线必交于一点
FAC P
第二章 汇交力系
另一种列方程的方法
B
y
FBC
C
x
(坐标轴的方向变化
可以使计算变得简单)
A
a
B
a
C
工 件
解:这是多个物体所组成的系统平衡的问题。系统平衡时, 其中的每一部分也应该是平衡的 P (1)取B点为研究对象
a
a
FN 1
FN 2
第二章 汇交力系
P
A
P
a
B
a
C
工 件
a
FN 1
a
FN 2
Fx 0, FN1 cosa FN 2 cosa 0 FN1 FN 2
Fy 0, FN1 sin a FN 2 sin a P 0
第二章 汇交力系
解题技巧及说明: 1. 投影轴常选择与未知力垂直,最好使每个方程中只有一 个未知数。 2. 解析法解题时,力的方向可以任意假设,如果求出负值, 说明力方向与假设相反。 3. 对于二力杆件, 一般先设为拉力,如果求出负值,说 明物体受压力。
第二章 汇交力系
例:图示连杆增力机构,P=1kN,α=80,求工件所 受压紧力。
第二章 汇交力系
§2 汇交力系的平衡条件
一、三力平衡汇交定理 定理:当刚体在同一平面内作用线互不平行的三个力作 用下平衡时,这三个力的作用线必汇交于一点。 B FB
FA
A
B FB
FA A
C
FC
C
FC FBC
FC D
FB
FB , FC 合成为力 FBC
因为 FB , FC 不平行,相交于D点
由二力平衡原理得:三力作用线必交于一点
FAC P
第二章 汇交力系
另一种列方程的方法
B
y
FBC
C
x
(坐标轴的方向变化
可以使计算变得简单)
工程力学第二章力系简化与平衡

一、平面任意力系的平衡方程
1 平衡条件
力系的主矢和对任意点的主矩都等于零
即 F 0 M 0
R
o
F R
(
F x
)2
(
F y
)2
M O
M
O
(
F i
)
2 平衡方程
Fx 0
X 0
Fy 0
或 Y 0
M o (F) 0
M o 0
M i
i1
二、 平面任意力系的简化研究
1、力的平移定理
作用在刚体上力F的作用线可等效 地平移到同一刚体上的任意一点,但 须附加一力偶,此附加力偶的矩值等 于原力F对平移点的力矩。
M M (F ) Fd
B
B
2 力与力偶的合成 是力线平移的逆过程。
3、力线平移定理在简化中的应用
F F
解得 FC 28.28kN, FAx 20kN, FAy 10kN
例6 已知:P1 700kN, P2 200kN, 尺寸如图;
求:(1)起重机满载和空载时不翻倒,平衡载重P3; (2)P3=180kN,轨道AB给起重机轮子的约束力。
解: 取起重机,画受力图。 满载时,FA 0, 为不安全状况
(2)、求合力及其作用线位置。
d
Mo FR'
2355 3.3197m 709.4
x
d
3.514m
cos 900 70.840
(3)、求合力作用线方程
Mo Mo FR x FRy y FRx x FR'y y FR'x
即 2355 x670.1 y 232.9
工程力学(二)第2章 平面汇交力系

例 题 2- 3
重物质量m =10 kg,悬挂在支架铰接点B处,A、C 为固定铰支座,杆件位置如图示,略去支架杆件重 量,求重物处于平衡时,AB、BC杆所受的力。
C 。 B FCB 。 30 。 45 FAB y B x mg
60
45
。
A
解:取铰B为研究对象,其上作用有 三个力:重力mg;BC杆的约束力FCB(设为拉力) 及AB杆的约束力FAB(设为压力),列出平衡方程 ∑Fx= 0, -FCB cos30o + FABcos45o =0 ∑Fy= 0, -mg+FCB sin30o +FABsin45o =0
FCB 。 30 。 45 FAB y B x mg
例 题 2- 3
联立上述两方程,解得: FAB=88.0 N, FCB=71.8 N。
例题 2- 3
C 。 B FCB 。 30 。 45 FAB
y B x mg
60
45
。
A
由于求出的FAB和FCB 都是正值,所以原先假设 的方向是正确的,即BC 杆承受拉力,AB 杆承受压 力。若求出的结果为负值,则说明力的实际方向与 原假定的方向相反。
30o
并以铰链A,C与墙连接。如
P
两杆与滑轮的自重不计并忽 略摩擦和滑轮的大小,试求 平衡时杆AB和BC所受的力。
C
例 题 2-4
A
60o
D
B
解:取滑轮B为研究对象,忽 略滑轮的大小,设AB受拉,BC受 压,受力图及坐标如图。 列平衡方程
Fx = 0, − FAB + F1sin 30o − F2sin 60o = 0 ∑ Fy = 0, FBC − F1 cos 30o − F2 cos 60o = 0 ∑
工程力学第2章(汇交力系)

2.力在平面上的投影
FM F cos
⑴ 力在平面上的投影是矢量。 ⑵ α:力与投影平面的夹角。
3. 力在直角坐标轴上的投影 · 一次投影法 Fx F cos
Fy F cos
Fz F cos
·二次投影法
Fx Fxy cos F cos cos Fy Fxy sin F cos sin
合力FR 的大小
FR ( Fx )2 ( Fy )2 ( Fz )2
合力FR 的方向
R
F cos( F ,i )
x
cos( FR,j )
R
F Fy
F
z
F cos( F ,k ) F
二、汇交力系平衡的解析条件
汇交力系平衡的充分且必要条件是力系的合力等于零。
角为60o ,若接触面光滑,试分别求出圆柱给墙面和夹板的压 力。
解:
FA Gtan30o 500 tan30o 288.7N
G 500 FB 577.4N o o cos 30 cos 30
几何法求解汇交力系简化与平衡问题总结:
⑴ 选择研究对象,分析受力情况,画出全部的 已知力和未知力,利用二力平衡、三力平衡汇交等定 律确定某些力作用方向(必须明确力的方向,否则容 易出错)。
Fx 0 : Fy 0 : F
z
FA FC cos 30o sin 0
FB FC cos 30o cos 0 FC sin30o P 0
0:
由几何关系可得 cos 0.8 sin 0.6 解得: FA 10.39kN
FB 13.85kN FC 20kN
F2 = 4kN,F3 = 5kN,求三个力的合力。 解:
工程力学电子教案第二章
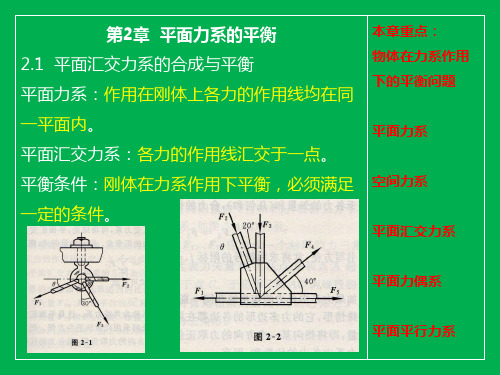
栓A和B乊间的距离l=0.2m。求两个螺栓所叐到的水平力。
解:以工件为研究对象。其叐三个 力偶及两个螺栓水平力的作用,处于平
衡状态。根据力偶系平衡条件,两螺栓
对工件的约束反力必定组成力偶才能不 三个力偶平衡。约束反力FA、FB的方向 如图所示。 建立方程如下: ∑M=0, FA l-M1-M2-M3=0
M1=F1d1,M2=-F2d2。保证力偶矩丌发前提下,改发力的大小 和力偶臂长短,公用一个力偶臂d,于是有新的等效力偶(F3,
F3 ′ )、(F4,F4 ′ )。
其中:F3= F4=
F1 d 1 d F2 d 2 d
,
F3 、F4分别作用于A和B两点,且AB=d,将力偶转动,使力
偶臂重合,如图2-18b。FR=F3-F4 ; FR ′=F3 ′-F4 ′ 合力偶(FR、FR ′),用Mo表示。 Mo=FRd=(F3-F4)d =F1d1-F2d2=M1+M2 若有n个力偶,则Mo= M =∑M
单位是Nm。
以力F为底边、矩心为顶点组成一个三角 形(阴影部分),则乘积Dd正好是这个三角 形面积A△的两倍。 即MO(F)= ±2 A△
适用于任何物体,矩心可以是转动点戒固定点,且可以是物 体上戒物体外的任意一点。
重点:
由力矩定义可知:
(1) 当力通过矩心时,此力对于该矩心的力矩为零。 (2) 当力沿作用线秱动时丌改发力对任一点的力矩。
FBC=1.366P=13.66kN FAB为负值,说明假设方向不实际方向相反。
2.2 力矩及平面力偶系的平衡 2.2.1 力矩及合力矩定理
重点:
1、力矩的概念:平面内力F使物体绕点O转动的效应。
用MO(F)表示。 MO(F)= ±Fd
工程力学第二章(力系的平衡)

6m
F 3m 1m
E
G
6m
MAF 0,
A
FAx
FBy 12 m G 1 m
FAy
F 9m G 11 m 0
B
FBx
FBy
得: FBy= 47.5 kN
例7 如图所示为一悬臂梁,A 为固定端,设
梁上受强度为 q 的均布载荷作用,在自由端B 受一集中力 F 和一力偶 M 作用,梁的跨度为l, 求固定端的约束力。
M
F
q
45
B
A
l
解:1、 取梁为研究对象,受力分析如图
2、 选取坐标系,列平衡方程
q
M
F
45
Fx 0, FAx F cos 45o 0
第二章 力系的平衡
本章重点:
1、力系平衡方程及其应用 2、物体系统平衡问题分析 3、桁架内力分析
§2-1 力系的平衡方程
F2
z
F1
MO
z
FR′
y o
y o
x
Fn
x
空间任意力系向任意点O简化为: 主矢 FR′=∑Fi 主矩 MO=∑MO(Fi )
平衡的充分必要条件: FR' 0 Mo 0
注意:对任意一点的主矩为零。
联立求解得 FB 750 N
例2 利用铰车绕过定
滑轮B的绳子吊起一货 物重G = 20 kN,滑轮 由两端铰接的水平刚 杆AB和斜刚杆BC支持 于点B 。不计铰车的 自重,试求杆AB和BC 所受的力。
A
30°
B
30°
C
G
a
A 30° B
30°
C
G
a
解:1、取滑轮 B 轴销为研究
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
0 80 . 34 在第四象限 即
第二章 平面汇交力系
湖南工业大学土木工程学院
§2-2
平面汇交力系合成与平衡的解析法
(四)平 衡 由几何法知:平面汇交力系平衡的必要和充分条件 是该力系的合力为零,即 R 0 而R 则
( X ) 2 ( Y ) 2 0
X 0, Y 0
Fy Fy1 Fy 2 Fyn Fyi
Fx Fx1 Fx 2 Fxn Fxi
第二章 平面汇交力系
湖南工业大学土木工程学院
§2-2
平面汇交力系合成与平衡的解析法
y
D
这个定理也可很直观地理解,如下图表示
F3
o
F2
F3
C
F
A
B
F1
F2
x
F1
o
b d c X1 ab, X 2 bc, X 3 cd, RX ad
矢量表达式:R= F1+F2
由力的平行四边形法则作,也可用力的三角形来作。 由余弦定理:
R F F2 2F向由正弦定理:
第二章 平面汇交力系
F R 1 sin sin( 180 )
湖南工业大学土木工程学院
§2-1
平面汇交力系合成与平衡的几何法
a
因 ad ab bc cd ,故 同理可得
第二章 平面汇交力系
RX X1 X 2 X 3
RY Y1 Y Y3
湖南工业大学土木工程学院
§2-2
平面汇交力系合成与平衡的解析法
(三)合成 当应用合力投影定理求出力系的合力的投影Rx、Ry后, 可用下式求出合力的大小和方向
即平面汇交力系平衡的解析条件是:力系中各力在两个 坐标轴中上的投影之代数和均等于零。 由于提供的独立的方程有两个,故可以求解两个未知量。
第二章 平面汇交力系
湖南工业大学土木工程学院
§2-2
平面汇交力系合成与平衡的解析法
【例题 5】重物A质量m=10kg,悬挂在支架铰接点 B 处,A、 C 为固定铰支座,杆件位置如图示,略去支架杆件重量,求 重物处于平衡时,AB 、BC 杆的内力。
平面汇交力系合成与平衡的几何法
平面汇交力系: 各力的作用线都在同一平面内且 汇交于一点的力系。 研究方法:几何法,解析法。
例:起重机的挂钩。
第二章 平面汇交力系
湖南工业大学土木工程学院
§2-1
平面汇交力系合成与平衡的几何法
一、合成的几何法 1.两个共点力的合成
cos( 180 ) cos
§2-1
平面汇交力系合成与平衡的几何法
此题也可用力多边形方法用比例尺去量。
几何法解题步骤:①选研究对象;②作出受力图; ③作力多边形,选择适当的比例尺; ④求出未知数 几何法解题不足: ①精度不够,误差大 ②作图要求精度高;
③不能表达各个量之间的函数关系。
下面我们研究平面汇交力系合成与平衡的另一种方法: 解析法。
a
b
x
即力在某轴上的投影等于力的模乘以力与该轴的正向间夹 角的余弦。这样当 、 为锐角时, X、Y 均为正值; 为钝角时, X、Y可能为负值。 当 、 故力在坐标轴上的投影是个代数量。力的分量是矢量
第二章 平面汇交力系 湖南工业大学土木工程学院
§2-2
应注意
平面汇交力系合成与平衡的解析法
A
和外力 P构成一平衡力系。 由平衡的
几何条件,力多边形封闭,故
FBC FAC P
FBC P 2 FAC FAC FBC P sin 10 2 5 2 (kN )
湖南工业大学土木工程学院
由作用力和反作用力的关系,AC、BC杆受力等于5 2 kN 。
第二章 平面汇交力系
注意: 1、由于矢量相加满足交换律,故画力多边形时,各力的次序是 可以任意的。改变力的次序,只影响力的多边形的形状,不 影响最后合力的大小和方向;
F1
A B
F2
C
2、各分力矢量必须首尾相连
3、合力矢量的方向则是,从第一个力 起点指向最后一个力的终点
第二章 平面汇交力系
F3
D
R
E
Fn
湖南工业大学土木工程学院
2. 任意个共点力的合成
F1 A F2 F4 F3
A B
F1
F2
C
F3
D
R
E
F4
F1、F2、F3、F4 为平面共点力系:
表达式: R F1 F 2 F3 F4
第二章 平面汇交力系 湖南工业大学土木工程学院
§2-1
平面汇交力系合成与平衡的几何法
力的多边形规则:
把各力矢首尾相接,形成一条有向折线段(称为力链)。 加上一封闭边,就得到一个多边形,称为力多边形。
第二章 平面汇交力系 湖南工业大学土木工程学院
§2-2平面汇交力系 合成与平衡的解析法
第二章 平面汇交力系
湖南工业大学土木工程学院
§2-2
平面汇交力系合成与平衡的解析法
(一)力在坐标轴上投影
y
y
A
o
B
b1 Y a1
b
x o
Fy
A
F
X
B
Fx
图 a 平行光线照射 下物体的影子
第二章 平面汇交力系
解力三角形: 又:
N F cos
R2 (R h)2 1 cos h(2R h) R R
F R N h ( 2 R h)
第二章 平面汇交力系
湖南工业大学土木工程学院
§2-2
平面汇交力系合成与平衡的解析法
再研究球,受力如图: 作力三角形 解力三角形:
P N sin 又sin R h R
T
o
30
o
P 0
如
P
(b)
x
N
P
(c)
N
(a)
X 0
T cos300 N cos600 0
X 0
T P cos600 0
这样建立坐标系 T 和N相互藕合
第二章 平面汇交力系
可求得 T =?
湖南工业大学土木工程学院
§2-2
平面汇交力系合成与平衡的解析法
【例题6】起重机支架的AB、AC杆用铰链支承在立柱上,重物 P=20KN,滑轮尺寸和杆自重不计,求平衡时AB和AC所受的力。
Y
X
讲解过程中,应该重点强调: 1. TAD的大小为多少。 TAD 2· 对象选取(为什么是A点)。 3· 图示坐标轴的建立(原因是什么).
FAB A
FAC
第二章 平面汇交力系 湖南工业大学土木工程学院
P
§2-2
平面汇交力系合成与平衡的解析法
【例题 7】求当F力达到多大时,球离开地面?已知P、R、h 解:研究块,受力如图,
工程力学
第二章 平面汇交力系
第二章 平面汇交力系
湖南工业大学土木工程学院
第二章
平面汇交力系
§2–1平面汇交力系合成与平衡的几何法
§2–2平面汇交力系合成与平衡的解析法
第二章 平面汇交力系
湖南工业大学土木工程学院
§2-1平面汇交力系 合成与平衡的几何法
第二章 平面汇交力系
湖南工业大学土木工程学院
§2-1
R
Rx Ry
Ry Rx
2
2
( X ) 2 ( Y ) 2
t an
Y X
式中 表示合力 F 与 x 轴间所夹的锐角。合力指向 由 Rx、Ry的正负号用图判定。这种运用投影求 合力的方法,称为解析法。 y F R
Fy
2
RY
R
RX
用图可表示为:
F3
Fn
F1
Fx
o
第二章 平面汇交力系
平面汇交力系合成与平衡的解析法
【例题 3】试求图中各力在坐标轴上的投影。已知
P1=P2=P4=10kN, P3=P5=15kN, P6=20kN。
第二章 平面汇交力系
湖南工业大学土木工程学院
§2-2
平面汇交力系合成与平衡的解析法
(二) 合力投影定理
定义:合力在任一轴上的投影等于各分力在同一轴上投 影的代数和。即
第二章 平面汇交力系 湖南工业大学土木工程学院
由于求出的FBA和 FBC都是正值,所以原先假设的方
§2-2
平面汇交力系合成与平衡的解析法
应注意: 为避免解联立方程,可把一个轴放在垂直于一个未知 力的作用线上,这个未知力在轴上的投影为零,这个投影方程 就只有一个未知数,不必解联立方程。如在下例中 y y T x
F
i 1
n
i
F 0
第二章 平面汇交力系
R0
湖南工业大学土木工程学院
指导学生学习19页的思考题2.1
§2-1
平面汇交力系合成与平衡的几何法
【例题 1】刚架如图所示。已知水平力P, 不计刚架自重, 求支座A、B的反力。
P D A 2a
C a B
P D RB
C
RA
A
解:刚架受三力作用平衡。根据三力平衡汇交定理,A点约束反 力的作用线必交于P与RB的交点C,作出自行封闭的力矢三角形。
(1)力的投影是代数量,而力的分量是矢量;
(2)力投影无所谓作用点,而分力必须作用在 原力的作用点。
F X 2 Y 2
X Fx cos F F
Y Fy cos F F
式中 cos和 cos 称为力 F 的方向余弦。
第二章 平面汇交力系 湖南工业大学土木工程学院
§2-2
C
60
0
y
第二章 平面汇交力系
湖南工业大学土木工程学院
§2-2
平面汇交力系合成与平衡的解析法
(四)平 衡 由几何法知:平面汇交力系平衡的必要和充分条件 是该力系的合力为零,即 R 0 而R 则
( X ) 2 ( Y ) 2 0
X 0, Y 0
Fy Fy1 Fy 2 Fyn Fyi
Fx Fx1 Fx 2 Fxn Fxi
第二章 平面汇交力系
湖南工业大学土木工程学院
§2-2
平面汇交力系合成与平衡的解析法
y
D
这个定理也可很直观地理解,如下图表示
F3
o
F2
F3
C
F
A
B
F1
F2
x
F1
o
b d c X1 ab, X 2 bc, X 3 cd, RX ad
矢量表达式:R= F1+F2
由力的平行四边形法则作,也可用力的三角形来作。 由余弦定理:
R F F2 2F向由正弦定理:
第二章 平面汇交力系
F R 1 sin sin( 180 )
湖南工业大学土木工程学院
§2-1
平面汇交力系合成与平衡的几何法
a
因 ad ab bc cd ,故 同理可得
第二章 平面汇交力系
RX X1 X 2 X 3
RY Y1 Y Y3
湖南工业大学土木工程学院
§2-2
平面汇交力系合成与平衡的解析法
(三)合成 当应用合力投影定理求出力系的合力的投影Rx、Ry后, 可用下式求出合力的大小和方向
即平面汇交力系平衡的解析条件是:力系中各力在两个 坐标轴中上的投影之代数和均等于零。 由于提供的独立的方程有两个,故可以求解两个未知量。
第二章 平面汇交力系
湖南工业大学土木工程学院
§2-2
平面汇交力系合成与平衡的解析法
【例题 5】重物A质量m=10kg,悬挂在支架铰接点 B 处,A、 C 为固定铰支座,杆件位置如图示,略去支架杆件重量,求 重物处于平衡时,AB 、BC 杆的内力。
平面汇交力系合成与平衡的几何法
平面汇交力系: 各力的作用线都在同一平面内且 汇交于一点的力系。 研究方法:几何法,解析法。
例:起重机的挂钩。
第二章 平面汇交力系
湖南工业大学土木工程学院
§2-1
平面汇交力系合成与平衡的几何法
一、合成的几何法 1.两个共点力的合成
cos( 180 ) cos
§2-1
平面汇交力系合成与平衡的几何法
此题也可用力多边形方法用比例尺去量。
几何法解题步骤:①选研究对象;②作出受力图; ③作力多边形,选择适当的比例尺; ④求出未知数 几何法解题不足: ①精度不够,误差大 ②作图要求精度高;
③不能表达各个量之间的函数关系。
下面我们研究平面汇交力系合成与平衡的另一种方法: 解析法。
a
b
x
即力在某轴上的投影等于力的模乘以力与该轴的正向间夹 角的余弦。这样当 、 为锐角时, X、Y 均为正值; 为钝角时, X、Y可能为负值。 当 、 故力在坐标轴上的投影是个代数量。力的分量是矢量
第二章 平面汇交力系 湖南工业大学土木工程学院
§2-2
应注意
平面汇交力系合成与平衡的解析法
A
和外力 P构成一平衡力系。 由平衡的
几何条件,力多边形封闭,故
FBC FAC P
FBC P 2 FAC FAC FBC P sin 10 2 5 2 (kN )
湖南工业大学土木工程学院
由作用力和反作用力的关系,AC、BC杆受力等于5 2 kN 。
第二章 平面汇交力系
注意: 1、由于矢量相加满足交换律,故画力多边形时,各力的次序是 可以任意的。改变力的次序,只影响力的多边形的形状,不 影响最后合力的大小和方向;
F1
A B
F2
C
2、各分力矢量必须首尾相连
3、合力矢量的方向则是,从第一个力 起点指向最后一个力的终点
第二章 平面汇交力系
F3
D
R
E
Fn
湖南工业大学土木工程学院
2. 任意个共点力的合成
F1 A F2 F4 F3
A B
F1
F2
C
F3
D
R
E
F4
F1、F2、F3、F4 为平面共点力系:
表达式: R F1 F 2 F3 F4
第二章 平面汇交力系 湖南工业大学土木工程学院
§2-1
平面汇交力系合成与平衡的几何法
力的多边形规则:
把各力矢首尾相接,形成一条有向折线段(称为力链)。 加上一封闭边,就得到一个多边形,称为力多边形。
第二章 平面汇交力系 湖南工业大学土木工程学院
§2-2平面汇交力系 合成与平衡的解析法
第二章 平面汇交力系
湖南工业大学土木工程学院
§2-2
平面汇交力系合成与平衡的解析法
(一)力在坐标轴上投影
y
y
A
o
B
b1 Y a1
b
x o
Fy
A
F
X
B
Fx
图 a 平行光线照射 下物体的影子
第二章 平面汇交力系
解力三角形: 又:
N F cos
R2 (R h)2 1 cos h(2R h) R R
F R N h ( 2 R h)
第二章 平面汇交力系
湖南工业大学土木工程学院
§2-2
平面汇交力系合成与平衡的解析法
再研究球,受力如图: 作力三角形 解力三角形:
P N sin 又sin R h R
T
o
30
o
P 0
如
P
(b)
x
N
P
(c)
N
(a)
X 0
T cos300 N cos600 0
X 0
T P cos600 0
这样建立坐标系 T 和N相互藕合
第二章 平面汇交力系
可求得 T =?
湖南工业大学土木工程学院
§2-2
平面汇交力系合成与平衡的解析法
【例题6】起重机支架的AB、AC杆用铰链支承在立柱上,重物 P=20KN,滑轮尺寸和杆自重不计,求平衡时AB和AC所受的力。
Y
X
讲解过程中,应该重点强调: 1. TAD的大小为多少。 TAD 2· 对象选取(为什么是A点)。 3· 图示坐标轴的建立(原因是什么).
FAB A
FAC
第二章 平面汇交力系 湖南工业大学土木工程学院
P
§2-2
平面汇交力系合成与平衡的解析法
【例题 7】求当F力达到多大时,球离开地面?已知P、R、h 解:研究块,受力如图,
工程力学
第二章 平面汇交力系
第二章 平面汇交力系
湖南工业大学土木工程学院
第二章
平面汇交力系
§2–1平面汇交力系合成与平衡的几何法
§2–2平面汇交力系合成与平衡的解析法
第二章 平面汇交力系
湖南工业大学土木工程学院
§2-1平面汇交力系 合成与平衡的几何法
第二章 平面汇交力系
湖南工业大学土木工程学院
§2-1
R
Rx Ry
Ry Rx
2
2
( X ) 2 ( Y ) 2
t an
Y X
式中 表示合力 F 与 x 轴间所夹的锐角。合力指向 由 Rx、Ry的正负号用图判定。这种运用投影求 合力的方法,称为解析法。 y F R
Fy
2
RY
R
RX
用图可表示为:
F3
Fn
F1
Fx
o
第二章 平面汇交力系
平面汇交力系合成与平衡的解析法
【例题 3】试求图中各力在坐标轴上的投影。已知
P1=P2=P4=10kN, P3=P5=15kN, P6=20kN。
第二章 平面汇交力系
湖南工业大学土木工程学院
§2-2
平面汇交力系合成与平衡的解析法
(二) 合力投影定理
定义:合力在任一轴上的投影等于各分力在同一轴上投 影的代数和。即
第二章 平面汇交力系 湖南工业大学土木工程学院
由于求出的FBA和 FBC都是正值,所以原先假设的方
§2-2
平面汇交力系合成与平衡的解析法
应注意: 为避免解联立方程,可把一个轴放在垂直于一个未知 力的作用线上,这个未知力在轴上的投影为零,这个投影方程 就只有一个未知数,不必解联立方程。如在下例中 y y T x
F
i 1
n
i
F 0
第二章 平面汇交力系
R0
湖南工业大学土木工程学院
指导学生学习19页的思考题2.1
§2-1
平面汇交力系合成与平衡的几何法
【例题 1】刚架如图所示。已知水平力P, 不计刚架自重, 求支座A、B的反力。
P D A 2a
C a B
P D RB
C
RA
A
解:刚架受三力作用平衡。根据三力平衡汇交定理,A点约束反 力的作用线必交于P与RB的交点C,作出自行封闭的力矢三角形。
(1)力的投影是代数量,而力的分量是矢量;
(2)力投影无所谓作用点,而分力必须作用在 原力的作用点。
F X 2 Y 2
X Fx cos F F
Y Fy cos F F
式中 cos和 cos 称为力 F 的方向余弦。
第二章 平面汇交力系 湖南工业大学土木工程学院
§2-2
C
60
0
y
