Newton迭代法求解非线性方程
求解非线性方程的三种新的迭代法

求解非线性方程的三种新的迭代法
迭代法是一种通过迭代逼近的方式来求解方程的方法。
它的基本思想是通过不断逼近
方程的解,使得逼近值与真实解的差距越来越小,最终得到方程的解。
下面介绍三种新的迭代法:牛顿迭代法,弦截法和切线法。
一、牛顿迭代法
牛顿迭代法是一种通过利用函数导数的信息来逼近方程解的方法。
它的迭代公式为:
x_(n+1) = x_n - f(x_n)/f'(x_n)
x_n表示第n次迭代得到的逼近解,f(x_n)表示在x_n处的函数值,f'(x_n)表示在x_n 处的导数值。
牛顿迭代法的优点是收敛速度快,通常是二阶收敛,但其缺点是需要计算函数的导数,如果导数计算困难或者导数为零的情况下,该方法可能不适用。
二、弦截法
三、切线法
切线法的优点和牛顿迭代法类似,但其缺点是需要计算函数的导数,且对于初始逼近
解的选择比较敏感。
牛顿迭代法、弦截法和切线法都是三种常用的非线性方程迭代法。
它们各自有着优点
和缺点,适用的领域和条件也不尽相同。
在实际问题中,需要根据具体情况选择合适的方
法来求解非线性方程。
非线性方程求解

⾮线性⽅程求解基于MATLAB的⾮线性⽅程的五种解法探讨摘要:本⽂利⽤matlab软件对⾮线性⽅程解法中的⼆分法、简单迭代法、⽜顿法、割线法以及Steffensen法的数值分析⽅法的算法原理及实现⽅法进⾏了探讨。
对f x x x=+-()2ln2的零点问题,分别运⽤以上五种不同的⽅法进⾏数值实验,⽐较⼏种解法的优缺点并进⾏初步分析评价。
关键词:⼆分法、简单迭代法、⽜顿法、割线法、Steffensen法1、引⾔在很多实际问题中,经常需要求⾮线性⽅程f(x) =0的根。
⽅程f(x) =0的根叫做函数f(x)的零点。
由连续函数的特性知:若f(x)在闭区间[a,b ]上连续,且()()0f a f b<.则f(x) =0在开区间(a,b)内⾄少有⼀个实根。
这时称[a,b]为⽅程f(x) =0的根的存在区间。
本⽂主要对⾮线性⽅程的数值解法进⾏分析,并介绍了⾮线性⽅程数值解法的五种⽅法。
并设=+-.f x x x()2ln2f x在[1,2]上的图形,如图1:. 显然,函数在[1,2]之间有⼀个零点。
⾸先画出()2、计算机配置操作系统Windows 7 旗舰版内存2GB处理器AMD 4核 A6-3400M APU 1.4GHz图.13、⼆分法⼆分法的基本思想是将⽅程根的区间平分为两个⼩区间,把有根的⼩区间再平分为两个更⼩的区间,进⼀步考察根在哪个更⼩的区间内。
如此继续下去,直到求出满⾜精度要求的近似值。
设函数()f x 在区间[a,b ]上连续,且f(a)·f(b) <0,则[a,b ]是⽅程f(x) =0的根的存在区间,设其内有⼀实根,记为x*。
取区间[a,b ]的中点()2k a b x +=并计算1()f x ,则必有下列三种情况之⼀成⽴: (1) 1()f x =0,x1就是⽅程的根x*;(2)()f a .1()f x <0,⽅程的根x*位于区间[a, 1x ]之中,此时令111,a a b x ==; (3)1()f x .()f b <0,⽅程的根x*位于区间[1x ,b ]之中,此时令11a x =,1b b =。
非线性方程求根—牛顿迭代法(新)

非线性方程求根——牛顿迭代法一、牛顿迭代法的基本思想基本思想:将非线性方程逐步归结为某种线性方程求解。
设方程f (x )=0有近似根x k (f `(x k )≠0),将f (x )在x k 展开:(ξ在x 和x k 之间)2()()()()()()2!k k k k f f x f x f x x x x x ξ'''=+-+-()()()()k k k f x f x f x x x '≈+-可设记该线性方程的根为x k +1,则()()()0k k k f x f x x x '+-=1()()k k k k f x x x f x +=-'故f (x )=0可近似表示为即为Newton 法迭代格式。
(k =0,1,……)例:用Newton 迭代法求方程310x x --=在x 0=1.5附近的近似实根。
解:32()1,()31f x x x f x x '=--=-迭代公式为312131kk k k k x x x x x +--=--计算步骤如下:(1)取初值x 0=1.5;(2)按照迭代公式计算x 1;(3)若|x 1-x 0|<=0.00001,终止迭代;否则,x 0=x 1;转(2);(4)输出迭代次数和近似根.二、牛顿迭代法的实现MATLAB求解程序设计:方程及一阶导数函数:function[fun,dfun]=fun0(x)fun=x^3-x-1;%求原函数的值dfun=3*x^2-1;%求一阶导数的值计算主程序:clearx0=1.5;[fun,dfun]=fun0(x0);x1=x0-fun/dfun;i=1;while abs(x1-x0)>1e-5x0=x1;[fun,dfun]=fun0(x0);x1=x0-fun/dfun;i=i+1;enddisp('the solution is x1=')x1disp('the iter time is ')i计算结果为:the solution is x1=x1 =1.3247the iter time isi =4可见经过4次迭代即到达要求的精度,原方程的一个近似实数根为1.3247.三、牛顿迭代法的收敛性牛顿迭代法的迭代函数:)()()(x f x f x x '-=ϕ222)]([)()()]([)()()]([1)(x f x f x f x f x f x f x f x '''='''-'-='ϕ设f (x *)=0,f `(x *)≠0,则ϕ`(x *)=0,故Newton 迭代法在x *附近至少平方收敛。
解非线性方程的牛顿迭代法及其应用

解非线性方程的牛顿迭代法及其应用一、本文概述非线性方程是数学领域中的一个重要研究对象,其在实际应用中广泛存在,如物理学、工程学、经济学等领域。
求解非线性方程是一个具有挑战性的问题,因为这类方程往往没有简单的解析解,需要通过数值方法进行求解。
牛顿迭代法作为一种古老而有效的数值求解方法,对于求解非线性方程具有重要的应用价值。
本文旨在介绍牛顿迭代法的基本原理、实现步骤以及在实际问题中的应用。
我们将详细阐述牛顿迭代法的基本思想,包括其历史背景、数学原理以及收敛性分析。
我们将通过具体实例,展示牛顿迭代法的计算步骤和实际操作过程,以便读者能够更好地理解和掌握该方法。
我们将探讨牛顿迭代法在各个领域中的实际应用,包括其在物理学、工程学、经济学等领域中的典型应用案例,以及在实际应用中可能遇到的问题和解决方法。
通过本文的介绍,读者可以深入了解牛顿迭代法的基本原理和应用技巧,掌握其在求解非线性方程中的实际应用方法,为进一步的研究和应用提供有力支持。
二、牛顿迭代法的基本原理牛顿迭代法,又称为牛顿-拉夫森方法,是一种在实数或复数域上近似求解方程的方法。
其基本原理是利用泰勒级数的前几项来寻找方程的根。
如果函数f(x)在x0点的导数f'(x0)不为零,那么函数f(x)在x0点附近可以用一阶泰勒级数来近似表示,即:这就是牛顿迭代法的基本迭代公式。
给定一个初始值x0,我们可以通过不断迭代这个公式来逼近f(x)的根。
每次迭代,我们都用当前的近似值x0来更新x0,即:这个过程一直持续到满足某个停止条件,例如迭代次数达到预设的上限,或者连续两次迭代的结果之间的差小于某个预设的阈值。
牛顿迭代法的收敛速度通常比线性搜索方法快,因为它利用了函数的导数信息。
然而,这种方法也有其局限性。
它要求函数在其迭代点处可导,且导数不为零。
牛顿迭代法可能不收敛,如果初始点选择不当,或者函数有多个根,或者根是重根。
因此,在使用牛顿迭代法时,需要谨慎选择初始点,并对迭代过程进行适当的监控和调整。
牛顿迭代法求解非线性方程组的解

10 简化牛顿法 简化牛顿法又称平行弦法,其迭代公式为
xk1 xk Cf (xk ),C 0, k 0,1,
(4-7)
从不动点迭代法的角度看,简化牛顿法的迭代函数(x) x Cf (x) ,下面讨论简
化牛顿法的收敛性。
若| '(x) ||1 Cf '(x) | 1 ,即取 0 Cf ' (x) 2 .在根 x* 附近成立,则迭代法
x k 的点 Pk 引切线,并将该切线与 x 轴的交点的横坐标 x k1 作为 x* 的新的近似值。 注意到切线方程为
y f (xk ) f '(xk )(x xk )
(4-4)
这样求得的值 x k1 比满足 f (xk ) f '(xk )(x xk ) 0 ,从而就是牛顿公式
x
k 1
| f (xk1) || f (xk ) |
(4-8)
满足此要求的算法称为下山法。
将牛顿法和下山法一起使用时,即在下山法保证函数值稳定下降的前提下,
用牛顿法加快收敛速度。为此,为此将牛顿法的计算结果
xk 1
xk
f (xk ) f ' (xk )
(4-9)
与前一步的近似值 xk 的适当加权平均作为新的改进值
代法中所遇到的 jacobi 矩阵难求的问题。
关键词:非线性方程组、牛顿迭代法、MATLAB、 jacobi 矩阵
一、前言 非线性方程组在实际问题中经常出现,并且在科学与工程计算中的地位越来
越来重要,很多常见的线性模型都是在一定条件下由非线性问题简化得到的,为 得到更符合实际的解答,往往需要直接研究非线性模型,然而从线性到非线性是 一个质的飞跃,方程的性质的不同,所以求解方法也有很大差别。本文主要介绍 关于非线性方程及方程组的数值解法,先分析非线性方程的数值解法,然后再延 伸到方程组的解法。
非线性方程组求解的牛顿迭代法用MATLAB实现

非线性方程组求解的牛顿迭代法用MATLAB实现首先,我们需要定义非线性方程组。
假设我们要求解方程组:```f1(x1,x2)=0f2(x1,x2)=0```其中,`x1`和`x2`是未知数,`f1`和`f2`是非线性函数。
我们可以将这个方程组表示为向量的形式:```F(x)=[f1(x1,x2);f2(x1,x2)]=[0;0]```其中,`F(x)`是一个列向量。
为了实现牛顿迭代法,我们需要计算方程组的雅可比矩阵。
雅可比矩阵是由方程组的偏导数组成的矩阵。
对于方程组中的每个函数,我们可以计算其对每个变量的偏导数,然后将这些偏导数组成一个矩阵。
在MATLAB中,我们可以使用`jacobi`函数来计算雅可比矩阵。
以下是一个示例函数的定义:```matlabfunction J = jacobi(x)x1=x(1);x2=x(2);J = [df1_dx1, df1_dx2; df2_dx1, df2_dx2];end```其中,`x`是一个包含未知数的向量,`df1_dx1`和`df1_dx2`是`f1`对`x1`和`x2`的偏导数,`df2_dx1`和`df2_dx2`是`f2`对`x1`和`x2`的偏导数。
下一步是实现牛顿迭代法。
牛顿迭代法的迭代公式为:```x(k+1)=x(k)-J(x(k))\F(x(k))```其中,`x(k)`是第`k`次迭代的近似解,`\`表示矩阵的求逆操作。
在MATLAB中,我们可以使用如下代码来实现牛顿迭代法:```matlabfunction x = newton_method(x_initial)max_iter = 100; % 最大迭代次数tol = 1e-6; % 收敛阈值x = x_initial; % 初始解for k = 1:max_iterF=[f1(x(1),x(2));f2(x(1),x(2))];%计算F(x)J = jacobi(x); % 计算雅可比矩阵 J(x)delta_x = J \ -F; % 计算增量 delta_xx = x + delta_x; % 更新 xif norm(delta_x) < tolbreak; % 达到收敛条件,停止迭代endendend```其中,`x_initial`是初始解的向量,`max_iter`是最大迭代次数,`tol`是收敛阈值。
用Matlab编写二分法和Newton迭代法求解非线性函数
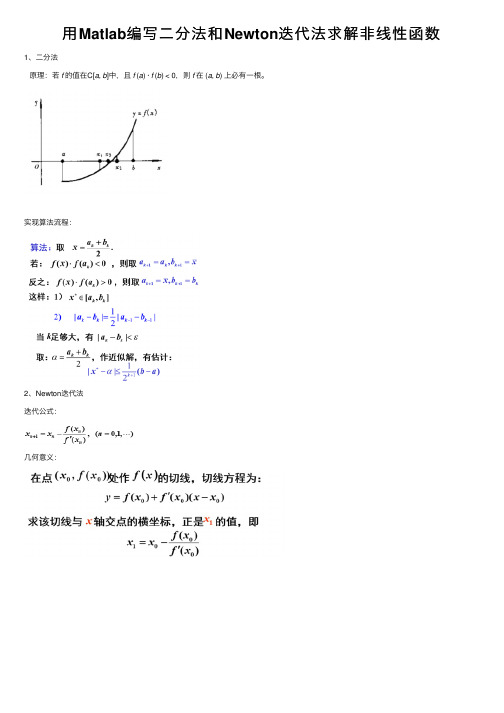
⽤Matlab编写⼆分法和Newton迭代法求解⾮线性函数1、⼆分法原理:若f的值在C[a, b]中,且f (a) · f (b) < 0,则f在 (a, b) 上必有⼀根。
实现算法流程:2、Newton迭代法迭代公式:⼏何意义:3、求解问题⽤Newton法和⼆分法求的解。
4、代码实现1 clear;close;clc2 a=0;b=1;%根区间3 e=10^(-6);%根的容许误差4 [X , N]=dichotomy(e,a,b);%⼆分法5 p0=0.5;%初始值6 N=15;%迭代次数7 [X1]=Newdon(p0,e,N);%Newton迭代法89 function [X , N]=dichotomy(deta,a,b)10 % 函数dichotomy:⼆分法11 %输⼊值:12 %fun:⽅程函数13 %deta:根的容许误差14 %有根区间:[a,b]15 %输出值16 %X:求解到的⽅程的根17 %N:总的迭代次数18 N=1+fix(log2((b-a)/deta));%由公式7.2求得,取整数|X_N-X*|<=(b-a)/2^N<deta,求N19 n=1;20 f1=myfunction(a);21 f2=myfunction(b);22if (f1*f2>0)23 disp('根不在输⼊的区间⾥,请重新输⼊区间');24else25while n <= N26 x=(a+b)/2;27if myfunction(a)*myfunction(x)>028 a=x;29else30 b=x;31 end32 n=n+1;33 end34 X=x;35 fprintf('第%d次⼆分法求出的⽅程的根:\n',N);36 fprintf('X=\n');37 disp(X);38 end39 end4041 function [P]=Newdon(p0,TOL,N)42 %求⽅程组的解43 %输⼊参数44 %初始值:p045 %误差容限:TOL46 %最⼤迭代次数:N47 %输出参数:48 %⽅程近似解:p49 %或失败信息“Method failed”50 format long;51 n=1;%初始迭代次数52 syms x;53while n<=N54if abs(subs(diff(myfunction(x)),x,p0))<TOL55 P=p0;56break;57else58if subs(diff(myfunction(x),2),x,p0)==059 disp('Method failed');60break;61else62 p=p0-myfunction(p0)/subs(diff(myfunction(x)),x,p0);63 p=eval(p);%将exp的值转为⼩数值64if(abs(p-p0)<TOL)65 P=p;66break;67else68 p0=p;69 end70 end71 end72 n=n+1;73 end74 % P=vpa(P,10);%将分数转为⼩数并保留8位⼩数75 fprintf('第%d次NeWton迭代法求出的⽅程的根:\n',N);76 fprintf('P=\n');77 disp(P);78 end7980 function f=myfunction(x)81 f=x*exp(x)-1;82 end5、求解结果。
newton迭代法11-12

若f(a)f(x0)<0 成立,则根必在区间(a, x0)内,取a1=a,b1= x0;否则 必在区间(x0,b)内,取a1= x0,b1=b,
这样,得到新区间(a1,b1),其长度为[a,b]的一半,如此继续下去,进 行k次等分后,得到一组不断缩小的区间,[a,b],[a1,b1],......[ak,bk].
( x*)
2!
( x x*) 2
( p1) ( x*)
( p 1)!
( x x*)p1
( p ) ( x*)
p!
( x x*)p
如果( x*) ( x*) ( p1) ( x*) 0
而 ( p ) ( x*) 0
解三:迭代格式 xk+1=(xk3-5)/2 令x0=2.5,得迭代序列: x1=5.3125, x2=72.46643066, X3=190272.0118, x4=3.444250536 1016, x5=2.042933398 1046, 计算x6时溢出
同样的方程不同的迭代格式有不同的结果 迭代函数的构造有关
L Lk xk x * xk xk 1 x1 x0 1 L 1 L
xk x * x * xk 1 xk xk 1 g'( ) xk x * xk xk+1
因此: 1 xk x * xk xk+1 1 L
证毕.
定理1指出,
例1 用简单迭代法求区间(2,3)内方程x3-2x-5=0的根 lim x 解一 将方程两边同加2x+5,再开三次方,得式同解方程 x= 3 2 x 5 作迭代格式 xk+1= 3 2 xk 5 , k=0,1,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Newton迭代法求解非线性方程一、 Newton 迭代法概述构造迭代函数的一条重要途径是用近似方程来代替原方程去求根。
因此,如果能将非线性方程f (x )=0用线性方程去代替,那么,求近似根问题就很容易解决,而且十分方便。
牛顿(Newton)法就是一种将非线性方程线化的一种方法。
设k x 是方程f (x )=0的一个近似根,把如果)(x f 在k x 处作一阶Taylor 展开,即:)x x )(x ('f )x (f )x (f k k k -+≈ (1-1)于是我们得到如下近似方程:0)x x )(x ('f )x (f k k k =-+ (1-2)设0)('≠k x f ,则方程的解为:x ̅=x k +f(x k )f(x k )́ (1-3)取x ~作为原方程(1.1)的新近似根1+k x ,即令: )x ('f )x (f x x k k k 1k -=+, k=0,1,2,… (1-4) 上式称为牛顿迭代格式。
用牛顿迭代格式求方程的根的方法就称为牛顿迭代法,简称牛顿法。
牛顿法具有明显的几何意义。
方程:)x x )(x ('f )x (f y k k k -+= (1-5) 是曲线)x (f y =上点))x (f ,x (k k 处的切线方程。
迭代格式(1-4)就是用切线式(1-5)的零点来代替曲线的零点。
正因为如此,牛顿法也称为切线法。
牛顿迭代法对单根至少是二阶局部收敛的,而对于重根是一阶局部收敛的。
一般来说,牛顿法对初值0x 的要求较高,初值足够靠近*x 时才能保证收敛。
若要保证初值在较大范围内收敛,则需对)x (f 加一些条件。
如果所加的条件不满足,而导致牛顿法不收敛时,则需对牛顿法作一些改时,即可以采用下面的迭代格式:)x ('f )x (f x x k k k 1k λ-=+,⋯=,2,1,0k (1-6)上式中,10<λ<,称为下山因子。
因此,用这种方法求方程的根,也称为牛顿下山法。
牛顿法对单根收敛速度快,但每迭代一次,除需计算)x (f k 之外,还要计算)x ('f k 的值。
如果)x (f 比较复杂,计算)x ('f k 的工作量就可能比较大。
为了避免计算导数值,我们可用差商来代替导数。
通常用如下几种方法: 1. 割线法 如果用1k k 1k k x x )x (f )x (f ----代替)x ('f k ,则得到割线法的迭代格式为:)x (f )x (f )x (f x x x x k 1k k 1k k k 1k --+---= (1-7)2. 拟牛顿法 如果用)x (f ))x (f x (f )x (f k 1k k k ---代替)x ('f k ,则得到拟牛顿法的迭代格式为:))x (f x (f )x (f )x (f x x 1k k k k 2k 1k -+---= (1-8) 3. Steffenson 法如果用)x (f )x (f ))x (f x (f k k k k -+代替)x ('f k ,则得到拟牛顿法的迭代格式为:)x (f ))x (f x (f )x (f x x k k k k 2k 1k -+-=+ (1-9) 二、 算法分析1. 割线法割线法的迭代公式为:)x (f )x (f )x (f x x x x k 1k k 1k k k 1k --+---=,k=0,1,2,…割线法是超线性收敛,其程序流程图为:2. 拟牛顿法牛顿拟迭代法迭代公式为:))x (f x (f )x (f )x (f x x 1k k k k 2k 1k -+---= (1) 对单根条件下,牛顿拟迭代法平方收敛,牛顿拟迭代法程序框图如下所示:(2) 对重根条件下,此时迭代公式修改为:))x (f x (f )x (f )x (f mx x 1k k k k 2k 1k -+---=,m 为根的重数 此时,牛顿迭代法至少平方收敛。
3. Steffenson 法Steffenson 迭代法程序流程图与牛顿拟迭代法类似。
三、 牛顿法的程序给定初值0p ,用牛顿法格式)p ('f )p (f p p 1k 1k 1k k ---=,⋯=,2,1k ,求解非线性方程0)x (f =。
*********************************************************************function [p1,err,k,y] = newton(f1041,df1041,p0,delta,max1) % f1041是非线性函数。
% df1041是f1041的微商。
% p0是初始值。
% delta 是给定允许误差。
% max1是迭代的最大次数。
% p1是牛顿法求得的方程的近似解。
% err 是p0的误差估计。
% k 是迭代次数。
% y = f(p1)p0, feval('f1041',p0) for k = 1:max1p1 = p0 - feval('f1041', p0)/feval('df1041', p0); err = abs(p1-p0); p0 = p1;p1, err, k, y = feval('f1041', p1) if (err < delta) | (y == 0),break, endp1, err, k, y = feval('f1041', p1) end*********************************************************************四、程序实例与计算结果例 用上述程序求方程0233=+-x x 的一个近似解,给定初值为1.2,误差界为610-。
解:先用m文件先定义二个名为f1041.m和df1041.m的函数文件。
function y = f1041(x)y = x^3 – 3*x + 2;function y=df1041(x)y=3*x^2-3;建立一个主程序prog1041.mclearnewton('f1041','df1041',1.2, 10^(-6), 18) 然后在MATLAB命令窗口运行上述主程序,即:>> prog1041计算结果如下:p0 = 1.2000 ans = 0.1280 p1 = 1.1030 err = 0.0970 k = 1y = 0.0329 p1 = 1.1030 err = 0.0970 k = 1y = 0.0329 p1 = 1.0524 err = 0.0507 k = 2y = 0.0084 p1 = 1.0524 err = 0.0507 k = 2y = 0.0084 p1 = 1.0264 err = 0.0260 k = 3y = 0.0021p1 = 1.0264 err = 0.0260 k = 3y = 0.0021p1 = 1.0133 err = 0.0131 k = 4y = 5.2963e-004 p1 = 1.0133 err = 0.0131 k = 4y = 5.2963e-004 p1 = 1.0066 err = 0.0066 k = 5y = 1.3270e-004p1 = 1.0066 err = 0.0066k = 5y = 1.3270e-004 p1 = 1.0033 err = 0.0033k = 6y = 3.3211e-005 p1 = 1.0033 err = 0.0033k = 6y = 3.3211e-005 p1 = 1.0017 err = 0.0017k = 7y = 8.3074e-006 p1 = 1.0017 err = 0.0017k = 7y = 8.3074e-006 p1 = 1.0008 err = 8.3157e-004 k = 8y = 2.0774e-006 p1 = 1.0008 err = 8.3157e-004 k = 8y = 2.0774e-006 p1 = 1.0004 err = 4.1596e-004 k = 9y = 5.1943e-007 p1 = 1.0004 err = 4.1596e-004 k = 9y = 5.1943e-007 p1 = 1.0002 err = 2.0802e-004 k = 10y = 1.2987e-007 p1 = 1.0002 err = 2.0802e-004 k = 10y = 1.2987e-007 p1 = 1.0001 err = 1.0402e-004 k = 11y = 3.2468e-008 p1 = 1.0001 err = 1.0402e-004 k = 11y = 3.2468e-008 p1 = 1.0001 err = 5.2014e-005 k = 12y = 8.1170e-009 p1 = 1.0001 err = 5.2014e-005 k = 12y = 8.1170e-009p1 = 1.0000 err = 2.6008e-005 k = 13y = 2.0293e-009 p1 = 1.0000 err = 2.6008e-005 k = 13y = 2.0293e-009 p1 = 1.0000 err = 1.3004e-005 k = 14y = 5.0732e-010 p1 = 1.0000 err = 1.3004e-005 k = 14y = 5.0732e-010 p1 = 1.0000 err = 6.5020e-006 k = 15y = 1.2683e-010 p1 = 1.0000 err = 6.5020e-006 k = 15 y = 1.2683e-010 p1 = 1.0000 err = 3.2510e-006 k = 16y = 3.1708e-011 p1 = 1.0000 err = 3.2510e-006 k = 16y = 3.1708e-011 p1 = 1.0000 err = 1.6255e-006 k = 17y = 7.9270e-012 p1 = 1.0000 err = 1.6255e-006 k = 17y = 7.9270e-012 p1 = 1.0000 err = 8.1277e-007 k = 18y = 1.9817e-012 ans = 1.0000这说明,经过18次迭代得到满足精度要求的值。
