C++实现 牛顿迭代 解非线性方程组
牛顿法及基于牛顿算法下的Steffensen加速法求解非线性方程组方法例题及答案
1. 非线性方程组求解1.分别用牛顿法,及基于牛顿算法下的Steffensen 加速法。
(1) 求ln(sin )x x +的根。
初值0x 分别取0.1,1,1.5,2,4进行计算。
(2) 求sin =0x 的根。
初值0x 分别取1,1.4,1.6,1.8,3进行计算。
分析其中遇到的现象与问题。
(1)牛顿法牛顿法实质上是一种线性化方法,其基本思想是将非线性方程()0f x =逐步归结为某种线性方程来求解。
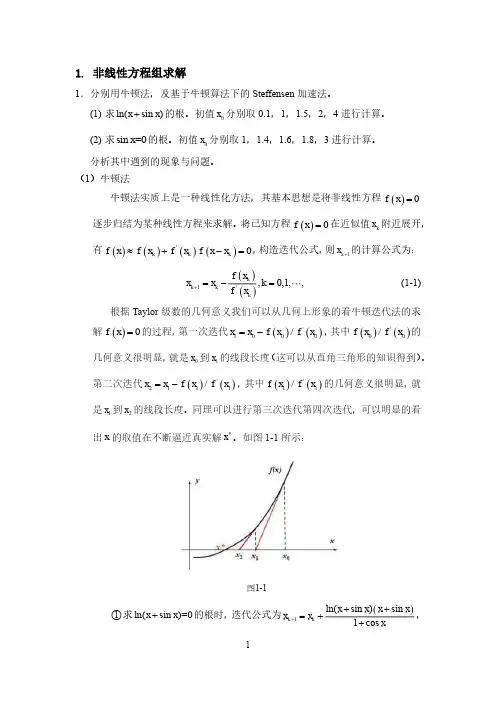
将已知方程()0f x =在近似值k x 附近展开,有()()()()'0k k k f x f x f x f x x ≈+-=,构造迭代公式,则1k x +的计算公式为:()()1',0,1,,k k k k f x x x k f x +=-= (1-1)根据Taylor 级数的几何意义我们可以从几何上形象的看牛顿迭代法的求解()0f x =的过程,第一次迭代()()'1000/x x f x f x =-,其中()()'00/f x f x 的几何意义很明显,就是0x 到1x 的线段长度(这可以从直角三角形的知识得到)。
第二次迭代()()'2111/x x f x f x =-,其中()()'11/f x f x 的几何意义很明显,就是1x 到2x 的线段长度。
同理可以进行第三次迭代第四次迭代,可以明显的看出x 的取值在不断逼近真实解*x 。
如图1-1所示:图1-1○1求ln(sin )=0x x +的根时,迭代公式为()1ln(sin )sin 1cos k k x x x x x x x+++=++,0示。
计算结果见附录1表F.1-1所示。
初值取1.5,2,4进行计算时结果不收敛。
表 1-1 牛顿法计算结果○2求sin =0x 的根时,迭代公式为1cos k k x x x+=+,初值0x 分别取1、1.4、1.6、1.8、3计算时结果收敛,误差小于510-时,近似解如表1-2所示。
求解非线性方程的三种新的迭代法

求解非线性方程的三种新的迭代法
迭代法是一种通过迭代逼近的方式来求解方程的方法。
它的基本思想是通过不断逼近
方程的解,使得逼近值与真实解的差距越来越小,最终得到方程的解。
下面介绍三种新的迭代法:牛顿迭代法,弦截法和切线法。
一、牛顿迭代法
牛顿迭代法是一种通过利用函数导数的信息来逼近方程解的方法。
它的迭代公式为:
x_(n+1) = x_n - f(x_n)/f'(x_n)
x_n表示第n次迭代得到的逼近解,f(x_n)表示在x_n处的函数值,f'(x_n)表示在x_n 处的导数值。
牛顿迭代法的优点是收敛速度快,通常是二阶收敛,但其缺点是需要计算函数的导数,如果导数计算困难或者导数为零的情况下,该方法可能不适用。
二、弦截法
三、切线法
切线法的优点和牛顿迭代法类似,但其缺点是需要计算函数的导数,且对于初始逼近
解的选择比较敏感。
牛顿迭代法、弦截法和切线法都是三种常用的非线性方程迭代法。
它们各自有着优点
和缺点,适用的领域和条件也不尽相同。
在实际问题中,需要根据具体情况选择合适的方
法来求解非线性方程。
C++二元非线性方程组

二元非线性方程牛顿迭代法C++代码。
小弟需要解一个二元非线性方程组,虽然说matlab的解法是一两个代码的事,但是我的情况是需要在C++ 里面实现。
由于自己不熟悉C++代码和牛顿迭代法的解法,小弟最近在网上找了一些资料。
发现很多有问题的例子,纯粹是在误导别人,浪费别人的时间。
于是小弟自己在看了解法(牛顿迭代法)的基础上,自己通过C++ 语言实现了一些简单方程组的解法,分享给给大家。
1. 非线性方程组的解法原理我在网上找了一个资料,应该是中南大学计算机学院的教程,如下:注意,他这里的例子第二个方程应该是,x1*x2*x2+x1-10*x2+8经过观察,我发现其实对于2元方程来说:f(x1,x2)和g(x1,x2)。
牛顿迭代法里面的迭代量(Δx 1 和Δx 2) 可以如下表示。
(我看到网上很多例子用矩阵来表示,我表示看不太懂,而且根据网上贴出来的程序,发现有错误。
而我发现对于2元方程来说,用下面的表示方法更直观,更简单。
2元方程并不需要再学习矩阵的相关知识。
)()()()221121211,,,x x x f x x x f x x f x ∂∂+∂∂-=∆ ()()()221121212,x x x x g x ∂+∂-=∆2. 代码(运行环境, VS 2010, WIN 7 64)// Nonlinear.cpp : Defines the entry point for the console application.//#include"stdafx.h"#include<math.h>#include<iostream>using namespace std;int _tmain(int argc, _TCHAR* argv[]){double x1,x2; //变量x1,x2;double x1_0,x2_0; //变量x1,x2迭代前的值double x1_1,x2_1; //变量x1,x2迭代后的值double delta_x1,delta_x2; //变量double function_F,function_G; //方程f(x1,x2) 和g(x1,x2)double F_x1,F_x2; //方程f的偏导double G_x1,G_x2; //方程g的偏导double Error=1e-10; //给定的误差double Error_cout; //用来计算的误差int Steps; //运行步骤int Max_Steps=100000; //最大运行步骤x1 = 0.5;x2 = 0.5; //初始化初值x1_0 = x1;x2_0 = x2;for(Steps=1;Steps<=Max_Steps;Steps++){// 方程组, f(x1,x2), g(x1,x2)function_F = x1_0*x1_0-10.0*x1_0+x2_0*x2_0+8.0; // 10.0的意思是double类型,10 是指整数类型function_G = x1_0*x2_0*x2_0+x1_0-10.0*x2_0+8.0;// 偏导,F_x1 = 2.0*x1_0-10.0;F_x2 = 2.0*x2_0;G_x1 = x1_0*x1_0+1.0;G_x2 = 2.0*x1_0*x2_0-10.0;// 迭代delta_x1 = -function_F/(F_x1+F_x2);delta_x2 = -function_G/(G_x1+G_x2);x1_1 = x1_0 + delta_x1;x2_1 = x2_0 + delta_x2;x1_0 = x1_1; //迭代,将新计算的变量赋值给原始变量x2_0 = x2_1;Error_cout = fabs(delta_x1)+fabs(delta_x2);if(Error_cout<Error)break; //当迭代到某个次数时,变量变化不大的时候就不运行了}printf(" Run steps is %d\n",Steps);printf(" x1 is %lf\n",x1_0);printf(" x2 is %lf\n",x2_0);return 0;}运行结果为:当然,对于有些方程用这个方法是解不了的,大家可以查一下阻尼牛顿法!。
c++ 牛顿迭代法解方程组

c++ 牛顿迭代法解方程组牛顿迭代法是一种求解方程的数值方法,它通过迭代逼近的方式,不断接近方程的解。
首先,我们需要定义要解的方程组。
假设我们要求解的方程组为:f1(x1, x2, ..., xn) = 0f2(x1, x2, ..., xn) = 0...fn(x1, x2, ..., xn) = 0其中,f1, f2, ..., fn是方程组中的各个方程,x1, x2, ..., xn是方程组的未知数。
接下来,我们可以利用牛顿迭代法来求解这个方程组。
具体步骤如下:1. 首先,我们需要给出方程组的初始猜测解。
设初始解为x^(0) = (x1^(0), x2^(0), ..., xn^(0))。
2. 然后,我们计算方程组在初始解处的Jacobi矩阵J^(0),即:J^(0) = [[∂f1/∂x1, ∂f1/∂x2, ..., ∂f1/∂xn],[∂f2/∂x1, ∂f2/∂x2, ..., ∂f2/∂xn],...[∂fn/∂x1, ∂fn/∂x2, ..., ∂fn/∂xn]]其中,∂f/∂x表示方程f对未知数x的偏导数。
3. 接下来,我们计算方程组在初始解处的函数值向量F^(0),即:F^(0) = [f1(x1^(0), x2^(0), ..., xn^(0)),f2(x1^(0), x2^(0), ..., xn^(0)),...fn(x1^(0), x2^(0), ..., xn^(0))]4. 然后,我们可以利用牛顿迭代公式来更新解,即:x^(k+1) = x^(k) - (J^(k))^(-1) * F^(k)其中,x^(k)表示第k次迭代的解,J^(k)表示第k次迭代的Jacobi矩阵,F^(k)表示第k次迭代的函数值向量。
5. 将更新后的解x^(k+1)代入方程组,并重新计算Jacobi矩阵和函数值向量。
6. 重复步骤4和步骤5,直到满足迭代停止的条件。
常见的迭代停止条件有:达到最大迭代次数、解的变化小于某个阈值、函数值的范数小于某个阈值等。
c++ 牛顿迭代法解方程组

c++ 牛顿迭代法解方程组牛顿迭代法(Newton's Method)是一种用于解方程的迭代算法,可以用于解非线性方程组。
下面是使用 C++ 实现牛顿迭代法解方程组的示例:#include <iostream>#include <cmath>// 定义方程组中的函数double f1(double x, double y) {return x * x + y * y - 1;}double f2(double x, double y) {return x - y * y;}// 定义方程组中的偏导数double df1_dx(double x, double y) {return 2 * x;}double df1_dy(double x, double y) {return 2 * y;}double df2_dx(double x, double y) {return 1;}double df2_dy(double x, double y) {return -2 * y;}// 牛顿迭代法解方程组void newtonIteration(double x0, double y0, int maxIterations) { double epsilon = 1e-6; // 迭代精度double x = x0;double y = y0;for (int i = 0; i < maxIterations; i++) {double det = df1_dx(x, y) * df2_dy(x, y) - df1_dy(x, y) * df2_dx(x, y);double dx = (-f1(x, y) * df2_dy(x, y) + f2(x, y) * df1_dy(x, y)) / det;double dy = (f1(x, y) * df2_dx(x, y) - f2(x, y) * df1_dx(x, y)) / det;x += dx;y += dy;if (std::abs(dx) < epsilon && std::abs(dy) < epsilon) { std::cout << "Converged to solution: x = " << x << ", y = " << y << std::endl;return;}}std::cout << "Iteration did not converge to a solution" << std::endl;}int main() {double initialX = 0.5;double initialY = 0.5;int maxIterations = 100;newtonIteration(initialX, initialY, maxIterations);return 0;}在上述示例中,我们定义了一个方程组,包含两个方程 f1(x, y) = x^2 + y^2 - 1和f2(x, y) = x - y^2。
牛顿迭代法求解非线性方程组的代码

牛顿迭代法求解非线性方程组非线性方程组如下:221122121210801080x x x x x x x ⎧-++=⎪⎨+-+=⎪⎩ 给定初值()00.0T x =,要求求解精度达到0.000011.首先建立函数()F X ,方程编程如下,将F.m 保存到工作路径中: function f=F(x)f(1)=x(1)^2-10*x(1)+x(2)^2+8;f(2)=x(1)*x(2)^2+x(1)-10*x(2)+8;f=[f(1),f(2)] ;2.建立函数()DF X ,用于求方程的jacobi 矩阵,将DF.m 保存到工作路径中:function df=DF(x)df=[2*x(1)-10,2*x(2);x(2)^2+1,2*x(1)*x(2)-10]; %jacobi 矩阵是一阶偏导数以一定方式排列成的矩阵。
3.编程牛顿迭代法解非线性方程组,将newton.m 保存在工作路径中:clear,clc;x=[0,0]';f=F(x);df=DF(x);fprintf('%d %.7f %.7f\n',0,x(1),x(2));N=4;for i=1:Ny=df\f';x=x-y;f=F(x);df=DF(x);fprintf('%d %.7f %.7f\n',i,x(1),x(2));if norm(y)<0.0000001break;elseendendezplot('x^2-10*x+y^2+8',[-6,6,-6,6]);hold onezplot('x*y^2+x-10*y+8',[-6,6,-6,6]);运行结果如下:0 0.0000000 0.00000001 0.8000000 0.88000002 0.9917872 0.99171173 0.9999752 0.99996854 1.0000000 1.0000000友情提示:范文可能无法思考和涵盖全面,供参考!最好找专业人士起草或审核后使用,感谢您的下载!。
C语言求解非线性方程、线性方程组代码
本文档提供了牛顿法、列主元素消去法、LU分解法三类求解方程的代码,对应非线性方程及线性方程组。
利用C语言编写,采用txt文件输入、输出方式。
/*牛顿法求解非线性方程*/#include<stdio.h>#include<math.h>#include<stdlib.h>float f(float x) /* 定义函数f(x) */{ return 2*x*x+2*x+1-exp(2*x); }float f1(float x) /* 定义函数f(x)的导数f1(x) */{ return 4*x+2-2*exp(2*x); }main(){float x0,x1,eps; /*定义初值和迭代精度*/FILE *fp1,*fp2;if((fp1=fopen("in.txt","r"))==NULL){printf("Can't open this file!\n");exit(0);}fscanf(fp1,"%f %f",&x1,&eps);do{x0=x1;if(fabs(f(x0))<=eps) x1=x0;elsex1=x0-f(x0)/f1(x0); /*牛顿迭代*/}while(fabs(f(x1))>eps); /*循环条件*/fp2=fopen("out.txt","w");fprintf(fp2,"%e",x1);fclose(fp1);fclose(fp2);}/*列主元素消去法求解线性方程组*/#include<stdio.h>#include<math.h>#include<stdlib.h>#define N 3void main(){ int i,j,k,mi; /*定义变量类型*/ float max,temp;float a[N][N],b[N],x[N],r[N][N+1];FILE *fp1; /*输入系数矩阵及列向量b*/ if((fp1=fopen("in.txt","r"))==NULL){printf("Can't open this file!\n");exit(0);}for(i=0;i<N;i++)for(j=0;j<N+1;j++)fscanf(fp1,"%f",&r[i][j]);fclose(fp1);for(i=0;i<N;i++)for(j=0;j<N;j++)a[i][j]=r[i][j];for(i=0;i<N;i++)b[i]=r[i][N];for(j=0;j<N-1;j++) /*找出列主元素并交换*/{for(i=j+1,mi=j,max=fabs(a[j][j]);i<N;i++)if(fabs(a[i][j])>max){mi=i;max=fabs(a[i][j]);}if(j<mi){temp=b[j];b[j]=b[mi];b[mi]=temp;for(k=j;k<N;k++){temp=a[j][k];a[j][k]=a[mi][k];a[mi][k]=temp;}}for(i=j+1;i<N;i++){temp=-a[i][j]/a[j][j];b[i]+=b[j]*temp;for(k=j;k<N;k++)a[i][k]+=a[j][k]*temp;}}x[N-1]=b[N-1]/a[N-1][N-1]; /*消去求解*/ for(i=N-2;i>=0;i--){x[i]=b[i];for(j=i+1;j<N;j++)x[i]-=a[i][j]*x[j];x[i]/=a[i][i];}FILE *fp2;fp2=fopen("out.txt","w");for(i=0;i<N;i++)fprintf(fp2,"x[%d]=%f\n",i+1,x[i]);fclose(fp2);}/*线性方程组的LU分解法*/#include<stdio.h>#include<math.h>#include<stdlib.h>#define N 3void main(){ int i,j,k,n;float temp;float a[N][N],b[N],x[N],y[N],L[N][N],U[N][N],r[N][N+1];FILE *fp1;if((fp1=fopen("in.txt","r"))==NULL){printf("Can't open this file!\n");exit(0);}for(i=0;i<N;i++)for(j=0;j<N+1;j++)fscanf(fp1,"%f",&r[i][j]);fclose(fp1);for(i=0;i<N;i++)for(j=0;j<N;j++)a[i][j]=r[i][j];for(i=0;i<N;i++)b[i]=r[i][N];for(i=0;i<N;i++) /*矩阵分解*/{U[0][i]=a[0][i];L[i][i]=1.0;L[i][0]=a[i][0]/a[0][0];for(j=i+1;j<N;j++){ L[i][j]=0;U[j][i]=0;}}for(i=1;i<N;i++){for(j=i;j<N;j++){temp=0;for(k=0;k<i;k++)temp=temp+L[i][k]*U[k][j];U[i][j]=a[i][j]-temp;}for(j=i;j<N;j++){temp=0;for(k=0;k<i;k++)temp=temp+L[j][k]*U[k][i];L[j][i]=(a[j][i]-temp)/U[i][i];}}y[0]=b[0]; /*解该线性方程组*/ for(i=1;i<N;i++){temp=0;for(j=0;j<i;j++)temp=temp+L[i][j]*y[j];y[i]=b[i]-temp;}x[N-1]=y[N-1]/U[N-1][N-1];for(i=N-2;i>=0;i--){x[i]=y[i];for(j=i+1;j<N;j++)x[i]-=U[i][j]*x[j];x[i]/=U[i][i];}FILE *fp2;fp2=fopen("out.txt","w");for(i=0;i<N;i++)fprintf(fp2,"x[%d]=%f\n",i+1,x[i]);fclose(fp2);}。
牛顿迭代法求根c语言
牛顿迭代法求根c语言牛顿迭代法是一种常用的数值计算方法,其可以用来求解非线性方程的根。
本文将介绍牛顿迭代法的基本原理和实现方法,并提供一些使用C语言实现牛顿迭代法求根的示例代码。
一、牛顿迭代法的原理在介绍牛顿迭代法的原理之前,我们先来看一个简单的例子。
假设我们要求解方程f(x) = 0的近似根,其中f(x)是一个可导函数。
我们可以通过利用切线来逼近方程f(x) = 0的根。
具体地,我们可以选择一个起始点x0,然后在x0处取得f(x0)的切线,将其延长到x轴上的交点x1,那么x1就是f(x) = 0的一个近似根。
可以通过数学方法得到x1的表达式:x1 = x0 - f(x0) / f'(x0)其中f'(x0)表示函数f(x)在x0处的导数。
换句话说,我们使用f(x)在x0处的切线来近似替代f(x)的图形,直到得到f(x) = 0的一个近似根为止。
这就是牛顿迭代法的基本思想。
牛顿迭代法的具体步骤如下:1. 选择一个起始点x0;2. 使用f(x)在x0处的切线来近似替代f(x)的图形;3. 在切线上取得x轴的交点x1; 4. 将x1作为新的起始点,重复步骤2和3,直到得到近似根。
二、牛顿迭代法的实现牛顿迭代法的实现过程比较简单,但需要注意一些细节。
具体实现可以分为以下几个步骤:1. 定义一个函数f(x),表示待求解的方程;2. 定义一个函数f_prime(x),表示函数f(x)在x处的导数;3. 定义一个起始点x0;4. 通过牛顿迭代公式计算出x1; 5. 将x1作为新的起始点,重复步骤4,直到满足精度要求为止。
下面,我们提供一段使用C语言实现牛顿迭代法求根的代码示例:```c #include<stdio.h> #include<math.h>#define EPSILON 0.0001double f(double x) { // 表示待求解的非线性方程 return x*x*x - x*x + 2; }double f_prime(double x) { // 表示f(x)在x 处的导数 return 3*x*x - 2*x; }double newton_raphson(double x) { // 牛顿迭代法求根 double x0 = x;while (1) { double x1 = x0 - f(x0) / f_prime(x0);if (fabs(x1 - x0) < EPSILON) return x1;x0 = x1; } }int main() { double x = 0;printf("The root is: %lf\n",newton_raphson(x));return 0; } ```代码中,定义了非线性方程f(x)和它在x处的导数f_prime(x),然后利用牛顿迭代法计算出方程的近似根。
解非线性方程组的牛顿法
考虑非线性方程组
f1(x1, x2, , xn ) 0,
f2(x1, x2, , xn ) 0,
fn (x1, x2, , xn ) 0. 利用向量记号写为
F (X ) O. 这里F (X )是定义在某区域D Rn上向量值函数. 若存在 X* D, 使得F (X*) O, 则称X*为非线性方程组的解.
.
逐次迭代得结果.
Step 5 Set x x y
Step 6 If y TOL then OUTPUT(x)
Step7 Set k k 1
STOP.
Step8 OUTPUT (‘Maximum number of iterations exceeded’) STOP.
为了说明上述算法,我们可以看看下面的例子。设
s1
145 272
,
145 272
T
.
x2 x1 s1 0.092,3.092 T .
显然,我们只经过两步计算,所得到的 x2就已经非常靠近 解 0,3T .
例1 用牛顿法求解方程组
k x (k) 0 (1.5, 1.0)T
f1( f2(
x1 x1
,x2 ,x2
) )
x1 2 x12
定理 2 设G : D Rn Rn在D内有一不动点X *且G在X *可导,
(G(X*)) 1, 则存在开球 S S( X*, ) D, 对X (0) S, 迭代序列{X (k)}
收敛于X *.
牛顿迭代公式:
X (k1) X (k) F( X (k) ) 1 F ( X (k) ),
其中
f1
F
(
X
(k
)
)
非线性方程的求解方法
非线性方程的求解方法非线性方程是数学中的基本概念,对于许多科学领域而言,非线性方程的求解具有重要的意义。
然而,与线性方程相比,非线性方程的求解方法较为复杂,因此需要掌握一些有效的解法。
本文将介绍几种非线性方程的求解方法。
一、牛顿迭代法牛顿迭代法也叫牛顿-拉夫逊迭代法,是一种求解非线性方程的有效方法。
该方法的基本思路是,选择一个初始值,通过迭代计算不断逼近非线性方程的根。
牛顿迭代法的公式为:$$x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)}$$其中,$f(x)$表示非线性方程,$f'(x)$表示$ f(x) $的一阶导数。
牛顿迭代法的优点在于速度快,迭代次数少,但其局限性在于收敛性受初始点选取的影响较大。
二、割线法割线法(Secant method)也是一种求解非线性方程的有效方法。
与牛顿迭代法不同,割线法使用的是两个初始值,并根据两点间的连线与$ x $轴的交点来作为新的近似根。
割线法的公式为:$$x_{n+1}=x_n-\frac{f(x_n)(x_n-x_{n-1})}{f(x_n)-f(x_{n-1})}$$割线法的优势是不需要求解导数,但其缺点在于需要两次迭代才能得到下一个近似根,因此计算量较大。
三、二分法二分法(Bisection method)是求解非线性方程的另一种有效方法。
该方法的基本思路是找到非线性方程的一个区间,使函数值在该区间内的符号相反,然后通过逐步缩小区间,在区间内不断逼近非线性方程的根。
二分法的公式为:$$x_{n+1}=\frac{x_n+x_{n-1}}{2}$$其中,$x_n$和$x_{n-1}$是区间的端点。
二分法的优点在于收敛性稳定,但其缺点在于迭代次数较多,因此计算量也较大。
四、弦截法弦截法(Regula Falsi method)也是一种求解非线性方程的有效方法。
它和二分法类似,都是通过缩小根所在的区间来逼近根。
不同之处在于,弦截法不是以区间中点为迭代点,而是以区间两个端点之间的连线与$ x $轴的交点为迭代点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
C++实现牛顿迭代解非线性方程组(二元二次为例)
求解{0=x*x-2*x-y+0.5;
0=x*x+4*y*y-4;
}的方程
#include<iostream>
#include<cmath>
#define N 2 // 非线性方程组中方程个数、未知量个数#define Epsilon 0.0001 // 差向量1范数的上限
#define Max 100 // 最大迭代次数
using namespace std;
const int N2=2*N;
int main()
{
void ff(float xx[N],float yy[N]); //计算向量函数的因变量向量yy[N]
void ffjacobian(float xx[N],float yy[N][N]); //计算雅克比矩阵yy[N][N]
void inv_jacobian(float yy[N][N],float inv[N][N]); //计算雅克比矩阵的逆矩阵inv
void newdundiedai(float x0[N], float inv[N][N],float y0[N],float x1[N]);
//由近似解向量x0 计算近似解向量x1
float x0[N]={2.0,0.25},y0[N],jacobian[N][N],invjacobian[N][N],x1[N],errornorm;
int i,j,iter=0;
//如果取消对x0的初始化,撤销下面两行的注释符,就可以由键盘x读入初始近似解向量for( i=0;i<N;i++)
cin>>x0[i];
cout<<"初始近似解向量:"<<endl;
for (i=0;i<N;i++)
cout<<x0[i]<<" ";
cout<<endl;cout<<endl;
do
{
iter=iter+1;
cout<<"第"<<iter<<" 次迭代开始"<<endl; //计算向量函数的因变量向量y0
ff(x0,y0); //计算雅克比矩阵jacobian
ffjacobian(x0,jacobian); //计算雅克比矩阵的逆矩阵invjacobian inv_jacobian(jacobian,invjacobian); //由近似解向量x0 计算近似解向量x1 newdundiedai(x0, invjacobian,y0,x1); //计算差向量的1范数errornorm
errornorm=0;
for (i=0;i<N;i++)
errornorm=errornorm+fabs(x1[i]-x0[i]);
if (errornorm<Epsilon) break;
for (i=0;i<N;i++)
x0[i]=x1[i];
} while (iter<Max);
return 0;
}
void ff(float xx[N],float yy[N]) //调用函数
{float x,y;
int i;
x=xx[0];
y=xx[1];
yy[0]=x*x-2*x-y+0.5;
yy[1]=x*x+4*y*y-4; //计算初值位置的值
cout<<"向量函数的因变量向量是:"<<endl;
for( i=0;i<N;i++)
cout<<yy[i]<<" ";
cout<<endl;
cout<<endl;
}
void ffjacobian(float xx[N],float yy[N][N])
{
float x,y;
int i,j;
x=xx[0];
y=xx[1];
//jacobian have n*n element //计算函数雅克比的值yy[0][0]=2*x-2;
yy[0][1]=-1;
yy[1][0]=2*x;
yy[1][1]=8*y;
cout<<"雅克比矩阵是:"<<endl;
for( i=0;i<N;i++)
{for(j=0;j<N;j++)
cout<<yy[i][j]<<" ";
cout<<endl;
}
cout<<endl;
}
void inv_jacobian(float yy[N][N],float inv[N][N]) {float aug[N][N2],L;
int i,j,k;
cout<<"开始计算雅克比矩阵的逆矩阵:"<<endl; for (i=0;i<N;i++)
{ for(j=0;j<N;j++)
aug[i][j]=yy[i][j];
for(j=N;j<N2;j++)
if(j==i+N) aug[i][j]=1;
else aug[i][j]=0;
}
for (i=0;i<N;i++)
{ for(j=0;j<N2;j++)
cout<<aug[i][j]<<" ";
cout<<endl;
}
cout<<endl;
for (i=0;i<N;i++)
{
for (k=i+1;k<N;k++)
{L=-aug[k][i]/aug[i][i];
for(j=i;j<N2;j++)
aug[k][j]=aug[k][j]+L*aug[i][j];
}
}
for (i=0;i<N;i++)
{ for(j=0;j<N2;j++)
cout<<aug[i][j]<<" ";
cout<<endl;
cout<<endl;
for (i=N-1;i>0;i--)
{
for (k=i-1;k>=0;k--)
{L=-aug[k][i]/aug[i][i];
for(j=N2-1;j>=0;j--)
aug[k][j]=aug[k][j]+L*aug[i][j];
}
}
for (i=0;i<N;i++)
{ for(j=0;j<N2;j++)
cout<<aug[i][j]<<" ";
cout<<endl;
}
cout<<endl;
for (i=N-1;i>=0;i--)
for(j=N2-1;j>=0;j--)
aug[i][j]=aug[i][j]/aug[i][i];
for (i=0;i<N;i++)
{ for(j=0;j<N2;j++)
cout<<aug[i][j]<<" ";
cout<<endl;
for(j=N;j<N2;j++)
inv[i][j-N]=aug[i][j];
}
cout<<endl;
cout<<"雅克比矩阵的逆矩阵:"<<endl; for (i=0;i<N;i++)
{ for(j=0;j<N;j++)
cout<<inv[i][j]<<" ";
cout<<endl;
cout<<endl;
}
void newdundiedai(float x0[N], float inv[N][N],float y0[N],float x1[N]) {
int i,j;
float sum=0;
for(i=0;i<N;i++)
{ sum=0;
for(j=0;j<N;j++)
sum=sum+inv[i][j]*y0[j];
x1[i]=x0[i]-sum;
}
cout<<"近似解向量:"<<endl;
for (i=0;i<N;i++)
cout<<x1[i]<<" ";
cout<<endl;cout<<endl;
}。
