用牛顿法求解非线性方程教学内容
牛顿法及基于牛顿算法下的Steffensen加速法求解非线性方程组方法例题及答案
1. 非线性方程组求解1．分别用牛顿法，及基于牛顿算法下的Steffensen 加速法。
(1) 求ln(sin )x x +的根。
初值0x 分别取0.1，1，1.5，2，4进行计算。
(2) 求sin =0x 的根。
初值0x 分别取1，1.4，1.6，1.8，3进行计算。
分析其中遇到的现象与问题。
（1）牛顿法牛顿法实质上是一种线性化方法，其基本思想是将非线性方程()0f x =逐步归结为某种线性方程来求解。
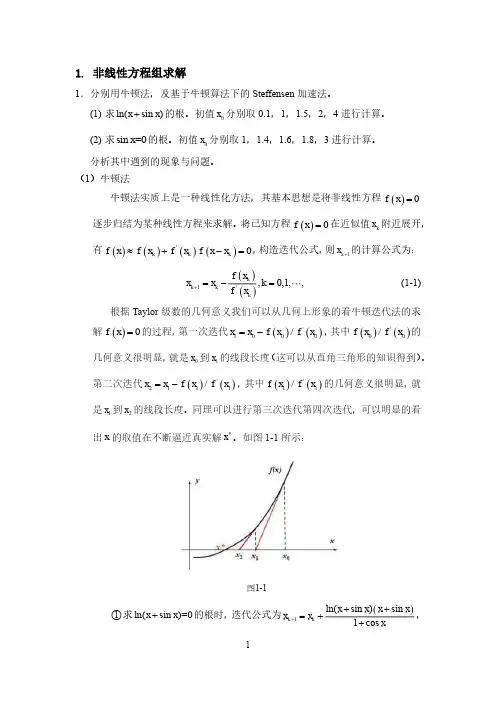
将已知方程()0f x =在近似值k x 附近展开，有()()()()'0k k k f x f x f x f x x ≈+-=，构造迭代公式，则1k x +的计算公式为：()()1',0,1,,k k k k f x x x k f x +=-= (1-1)根据Taylor 级数的几何意义我们可以从几何上形象的看牛顿迭代法的求解()0f x =的过程，第一次迭代()()'1000/x x f x f x =-，其中()()'00/f x f x 的几何意义很明显，就是0x 到1x 的线段长度（这可以从直角三角形的知识得到）。
第二次迭代()()'2111/x x f x f x =-，其中()()'11/f x f x 的几何意义很明显，就是1x 到2x 的线段长度。
同理可以进行第三次迭代第四次迭代，可以明显的看出x 的取值在不断逼近真实解*x 。
如图1-1所示：图1-1○1求ln(sin )=0x x +的根时，迭代公式为()1ln(sin )sin 1cos k k x x x x x x x+++=++，0示。
计算结果见附录1表F.1-1所示。
初值取1.5，2，4进行计算时结果不收敛。
表 1-1 牛顿法计算结果○2求sin =0x 的根时，迭代公式为1cos k k x x x+=+，初值0x 分别取1、1.4、1.6、1.8、3计算时结果收敛，误差小于510-时，近似解如表1-2所示。
求解非线性方程组的非精确牛顿法
求解非线性方程组的非精确牛顿法摘要:在经典牛顿法的基础上,给出了求解非线性方程组的非精确牛顿法。
在一定的条件下,证明了该算法的超线性收敛性,并且这个收敛性是二阶的。
关键词:非线性方程组;非精确牛顿法;收敛性对于无约束问题： minf(x) (1) 其中x∈Rn,f∶Rn→R是一个连续可微函数。
求解无约束优化问题方法大都属于迭代法,这类算法特点是:每一次迭代都要求函数值有所下降,因此人们称这类算法为下降法。
当下降方向取为负梯度时,此时函数值下降量最大,人们称它为最速下降法。
它是无约束最优化问题中最简单的方法,它具有全局收敛性,并且存储最较少,因此它适合于解决大型优化问题。
但它的缺点是收敛速度慢,在最优点处附近容易产生锯齿现象,为了改善收敛速度,人们提出了牛顿法。
牛顿法的基本思想是,在极小点附近用二阶Taylor多项式近似目标函数f(x),进而求出极小点的估计值。
设f(x)是二次可微实函数,x∈Rn。
又设x(k)是f(x)的极小点的一个估计,把f(x)在x(k)展成Taylor级数,并取二阶近似：f(x)≈Φ(x)=f(x(k))+ f(x(k))T(x-x(k))+12(x-x(k))T 2f(x(k))(x-x(k)) (2) 令Φ(x)=0,可得:x(k+1)=x(k)- 2f(x(k))-1 f(x(k)) (3)运用牛顿法时,初点的选择十分重要。
如果初始点靠近极小点,则可能很快收敛;如果初始点远离极小点,迭代产生的点列可能不收敛于极小点。
为了克服这个缺点,可以改进迭代公式(3):x(k+1)=x(k)+λkd(k)(4)其中d(k)=- 2f(x(k))-1 f(x(k))为牛顿方向,λk是由一维搜索得到的步长,即满足：f(x(k)+λkd(k))=minλf(x(k)+λd(k)) 这样修改后的算法称为阻尼牛顿法。
由于阻尼牛顿法含有一维搜索,因此每次迭代目标函数值一般有所下降(绝不会上升)。
解非线性方程的牛顿迭代法及其应用
解非线性方程的牛顿迭代法及其应用一、本文概述非线性方程是数学领域中的一个重要研究对象，其在实际应用中广泛存在，如物理学、工程学、经济学等领域。
求解非线性方程是一个具有挑战性的问题，因为这类方程往往没有简单的解析解，需要通过数值方法进行求解。
牛顿迭代法作为一种古老而有效的数值求解方法，对于求解非线性方程具有重要的应用价值。
本文旨在介绍牛顿迭代法的基本原理、实现步骤以及在实际问题中的应用。
我们将详细阐述牛顿迭代法的基本思想，包括其历史背景、数学原理以及收敛性分析。
我们将通过具体实例，展示牛顿迭代法的计算步骤和实际操作过程，以便读者能够更好地理解和掌握该方法。
我们将探讨牛顿迭代法在各个领域中的实际应用，包括其在物理学、工程学、经济学等领域中的典型应用案例，以及在实际应用中可能遇到的问题和解决方法。
通过本文的介绍，读者可以深入了解牛顿迭代法的基本原理和应用技巧，掌握其在求解非线性方程中的实际应用方法，为进一步的研究和应用提供有力支持。
二、牛顿迭代法的基本原理牛顿迭代法，又称为牛顿-拉夫森方法，是一种在实数或复数域上近似求解方程的方法。
其基本原理是利用泰勒级数的前几项来寻找方程的根。
如果函数f(x)在x0点的导数f'(x0)不为零，那么函数f(x)在x0点附近可以用一阶泰勒级数来近似表示，即：这就是牛顿迭代法的基本迭代公式。
给定一个初始值x0，我们可以通过不断迭代这个公式来逼近f(x)的根。
每次迭代，我们都用当前的近似值x0来更新x0，即：这个过程一直持续到满足某个停止条件，例如迭代次数达到预设的上限，或者连续两次迭代的结果之间的差小于某个预设的阈值。
牛顿迭代法的收敛速度通常比线性搜索方法快，因为它利用了函数的导数信息。
然而，这种方法也有其局限性。
它要求函数在其迭代点处可导，且导数不为零。
牛顿迭代法可能不收敛，如果初始点选择不当，或者函数有多个根，或者根是重根。
因此，在使用牛顿迭代法时，需要谨慎选择初始点，并对迭代过程进行适当的监控和调整。
利用牛顿迭代法求解非线性代数方程组
xi k 1
xi k
xi k i 1,2, , n
（3-7 ）
则式（ 3-6 ）可写为
xk
F' xk
1
F
xk
（3-8 ）
或
xk 1
xkHale Waihona Puke F' xk1
F
xk
（3-9 ）
称式（ 3-9 ）为求解非线性方程组（ 3-2 ）的牛顿迭代法，而线性方程
组（ 3-4 ）称为牛顿方程组。
三、 算法描述
（1） 在真实根 x 附近选取一个近似根 x1；
x
(4 2
)
1.6615
所以取迭代次数为 3，且可取（1.2343 ，1.6615 ）为非线性方程组（4-1 ）
的近似解。
五、心得体会：
通过学习，我们认识到牛顿迭代法是求解非线性代数方程组的一
种简单而有效的方法。 我们通过将非线性代数方程组的系数矩阵求导
来使方程组线性化， 从而求得方程组的近似解。 牛顿迭代法的优点是
（3-3 ）
F x 0 成为向量函数。
设
x1k
,
x
k 2
,
,
x
k n
是方程组（ 3-2 ）的一组近似解，把它的左端
在
x1k
,
x
k 2
,
, xnk 处用多元函数的泰勒展式展开，然后取线性部
分，便得方程组（ 3-2 ）得近似方程组
f1 x1k , x2k , , xnk f 2 x1k , x2k , , xnk
收敛速度快，但每次都要求导，求逆，计算量大。
在这段学习的过程中，感谢王老师给予我们耐心而清晰的讲解，
使我们掌握了一些数值分析的基本方法， 学有收获。 我感到这些数学
newton迭代法11-12
若f(a)f(x0)<0 成立,则根必在区间(a, x0)内,取a1=a,b1= x0;否则 必在区间(x0,b)内,取a1= x0,b1=b,
这样,得到新区间(a1,b1),其长度为[a,b]的一半,如此继续下去,进 行k次等分后,得到一组不断缩小的区间,[a,b],[a1,b1],......[ak,bk].
( x*)
2!
( x x*) 2
( p1) ( x*)
( p 1)!
( x x*)p1
( p ) ( x*)
p!
( x x*)p
如果( x*) ( x*) ( p1) ( x*) 0
而 ( p ) ( x*) 0
解三：迭代格式 xk+1=(xk3-5)/2 令x0=2.5,得迭代序列: x1=5.3125, x2=72.46643066, X3=190272.0118, x4=3.444250536 1016， x5=2.042933398 1046, 计算x6时溢出
同样的方程不同的迭代格式有不同的结果 迭代函数的构造有关
L Lk xk x * xk xk 1 x1 x0 1 L 1 L
xk x * x * xk 1 xk xk 1 g'( ) xk x * xk xk＋1
因此： 1 xk x * xk xk＋1 1 L
证毕.
定理1指出,
例1 用简单迭代法求区间(2,3)内方程x3-2x-5=0的根 lim x 解一 将方程两边同加2x+5,再开三次方，得式同解方程 x= 3 2 x 5 作迭代格式 xk+1= 3 2 xk 5 , k=0,1,
牛顿法非线性方程求解
《MATLAB 程序设计实践》课程考核１. 编程实现以下科学计算算法，并举一例应用之。
（参考书籍《精通ＭＡT ＬＡＢ科学计算》，王正林等著，电子工业出版社，２００９ 年）“牛顿法非线性方程求解”解：弦截法本质是一种割线法，它从两端向中间逐渐逼近方程的根；牛顿法本质上是一种切线法，它从一端向一个方向逼近方程的根，其递推公式为：-=+n n x x 1)()('n n x f x f初始值可以取)('a f 和)('b f 的较大者，这样可以加快收敛速度。
和牛顿法有关的还有简化牛顿法和牛顿下山法。
在MA TLAB 中编程实现的牛顿法的函数为：NewtonRoot 。
功能：用牛顿法求函数在某个区间上的一个零点。
调用格式：root=NewtonRoot )(```eps b a f 其中，f 为函数名； a 为区间左端点； b 为区间右端点 eps 为根的精度；root 为求出的函数零点。
，牛顿法的matlab程序代码如下：function root=NewtonRoot(f,a,b,eps)%牛顿法求函数f在区间[a,b]上的一个零点%函数名:f%区间左端点:a%区间右端点:b%根的精度:eps%求出的函数零点:rootif(nargin==3)eps=1.0e-4;endf1=subs(sym(f),findsym(sym(f)),a);f2=subs(sym(f),findsym(sym(f)),b);if (f1==0)root=a;endif (f2==0)root=b;endif (f1*f2>0)disp('两端点函数值乘积大于0 ！');return;elsetol=1;fun=diff(sym(f)); %求导数fa=subs(sym(f),findsym(sym(f)),a);fb=subs(sym(f),findsym(sym(f)),b);dfa=subs(sym(fun),findsym(sym(fun)),a);dfb=subs(sym(fun),findsym(sym(fun)),b);if(dfa>dfb) %初始值取两端点导数较大者root=a-fa/dfa;elseroot=b-fb/dfb;endwhile(tol>eps)r1=root;fx=subs(sym(f),findsym(sym(f)),r1);dfx=subs(sym(fun),findsym(sym(fun)),r1); %求该点的导数值 root=r1-fx/dfx; %迭代的核心公式tol=abs(root-r1);endend例：求方程3x^2－exp（x）＝0的一根解：在MATLAB命令窗口输入：>> r=NewtonRoot('3*x^2-exp(x)',3,4)输出结果：X=3.7331流程图：2、编程解决以下科学计算问题1）二自由度可解耦系统的振动模态分析。
解非线性方程组的牛顿迭代法
为克服这两个缺点，通常可用下述方法.
（1） 简化牛顿法，也称平行弦法.
xk 1 xk Cf ( xk )
其迭代公式为 （4.7）
C 0,1 ,.
迭代函数 ( x) x Cf ( x).
若在根 x * 附近成立 ( x) 1 Cf ( x) 1 ，即取 0 Cf ( x) 2，则迭代法（4.7）局部收敛.
8
xk
C 2 C
q2
k
1 q
2k
.
对任意 x0 0，总有 q 1，故由上式推知，当 k 时 xk C ，即迭代过程恒收敛. 例8 解 求 115 .
表7 6 计算结果 k 0 1 2 3 4 xk 10 10.750000 10.723837 10.723805 10.723805
f ( x) , f ( x)
由于
( x)
f ( x) f ( x) . 2 [ f ( x)]
假定 x *是 f ( x) 的一个单根，即 f ( x*) 0, f ( x*) 0 ， 则由上式知 ( x*) 0 ，于是依据定理4可以断定，牛顿法 在根 x *的邻近是平方收敛的.
准备 迭代
x0 ，计算 f 0 f ( x0 ), 选定初始近似值
步骤2
按公式
x1 x0 f 0 / f 0
迭代一次，得新的近似值 x1，计算 f1 f ( x1 ), f1 f ( x1 ). 步骤3 控制
x1 满足 1 如果
f1 2 ，则终 或
5
止迭代，以 x1作为所求的根；否则转步骤4. 允许误差，而
3
又因
( x*)
f ( x*) , f ( x*)
牛顿法解非线性方程组
一、求根方法原理把非线性函数f(x)=0在x0处展开成泰勒级数取其线性部分，作为非线性方程的近似方程，则有 , 设，则其解为,再把f(x)在x1处展开为泰勒级数，取其线性部分为的近似方程，若，则得，如此继续下去，得到牛顿法的迭代公式：，通过迭代，这个式子必然在的时候收敛。
整个过程如下图：牛顿法收敛很快，而且可求复根，缺点是对重根收敛较慢，要求函数的一阶导数存在。
二、求解步骤1. 选取一个接近函数零点的自变量 x 值作为起始点。
2. 使用如下的迭代公式更新近似解。
3. 如果得出的解满足误差要求，终止迭代，所得的值即视为方根根的近似解。
三、自定的非线性方程使用牛顿迭代法近似求解如下方程在[-1, 1]之间的根：四、源程序代码clear, close allclcf = @(x) cos(x) -x.^3;f_prime = @(x) -sin(x) -3*x.^2;error = 1; %初始化误差变量iter = 0; %初始化迭代次数变量max_iter = 5000; %定义最大允许迭代次数tol = 1e-8; %定义循环终止误差x0 = 0.5; %初始值while error > tol && iter <= max_iterx = x0 - f(x0)/f_prime(x0); %更新x的值error = abs((x-x0)/x0); %计算相对误差iter = iter +1; %更新迭代次数x0 = x; %计算出的x赋值给x0，继续迭代，直到达到误差条件。
end五、上机运行结果截图六、结论1.迭代法是求解非线性方程组的一种很好的方法，它可以反复校验根的近似值，直到得出符合精度的解。
从几何角度上来解释可以解释为两个函数的无限逼近2.我们为了加快迭代的速度，引入了牛顿法，牛顿法的收敛速度很快，但是其收敛性取决于牛顿法的取值。
3.。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2.2790
2.2790
2.2790
2.2790
2.2790
2.2790
2.2790
从上述的运算结果可以看出，迭代公式1、2、4不收敛，3虽然收敛，但与其他迭代法的结果差异太大，对5和6分别用埃特金加速和斯特芬森迭代得到结果如下：
对于5埃特金加速结果：
B =
2.0000
2.2804
2.2791
(a) , (b) , (c) ,
(d) (e) , (f) .
2.对每一种迭代格式，编制一个程序进行运算，观察每种格式的敛散情况；用事后误差估计 来控制迭代次数，并且输出迭代的次数；观察不同初值的结果.
3.从理论上分析各种格式的收敛性及收敛阶.
4.将收敛较慢的一种格式分别用Atken方法及Steffsen方法加速，通过输出结果了解加速效果.
2.2790
2.2790
2.2790
2.2790
2.2790
2.2790
2.2790
2.2790
2.2790
2.2790
2.2790
2.2790
2.2790
2.2790
2.2790
2.2790
0
斯特芬森迭代结果：
x =
2.0000
2.1547
2.2792
2.2790
2.2790
2.2790
2.2790
2.埃特金加速收敛方法
设 是根 的某个近似值，用迭代一次得 ，
而由微分中值定理，有
其中 介于 和 之间。
假设 改变不大，近似地取某个近似值L，则有
若将校正值 再迭代一次，又得 由于
将它与前面的式子联立，消去未知的L，有
由此推知
，
记
称为埃特金加速方法。
3.斯特芬森迭代法
将埃特金加速技巧与不动点迭代结合，则可得到如下的迭代法
1.0e+142 *
0.0000
0.0000
-0.0000
-0.0000
-0.0000
-0.0000
-0.0000
-0.0000
-0.0000
-1.4947
-Inf
-Inf
-Inf
-Inf
-Inf
-Inf
-Inf
-Inf
-Inf
-Inf
迭代公式3：
x3 =
2.0000
3.3166
3.8665
4.0743
2.2790
2.2790
2.2790
2.2790
2.2790
2.2790
2.2790
2.2790
2.2790
2.2790
2.2790
2.2790
2.2790
对于6埃特金加速结果：
B =
2.0000
2.2878
2.2790
2.2790
2.2790
2.2790
斯特芬森迭代结果：
x =
2.0000
2.1544
3探索不同方式改写方程的收敛程度
【理论概述与算法描述】
1.牛顿法
设已知方程f(x)=0有近似根xk,将函数f(x)在点xk展开，有
f(x)=f(xk)+f’(xk)(x-xk),
于是方程可表示为
f(xk)+f’(xk)(x-xk)=0,
这是个线性方程，记其根为x(k+1),
则x(k+1)=xk-f(xk)/f’(xk),这就是牛顿迭代法求根.
用牛顿法求解非线性方程
实验
一、
1.掌握常用的非线性方程求根算法（二分法、不动点迭代法与Newton法）及加速技术（Aitken加速与Steffsen加速）.
2.会编写计算机程序实现给定迭代函数的迭代算法及其加速；掌握迭代算法的精度控制方法.
二、
求代数方程 的实根.
三、
1．方程有一个实根： .将方程以下面六种不同方式等价地改写，构造迭代格式，计算 :
-22.5018
0.0099
-1.6667
-22.5185
0.0099
-1.6667
-22.5185
0.0099
-1.6667
-22.5185
0.0099-1.6667来自-22.5185迭代公式5：
x5 =
2.0000
2.3452
2.2654
2.2819
2.2784
2.2791
2.2790
2.2790
即为斯特芬森迭代法
【实验问题】
1.求代数方程 的实根.
2．方程有一个实根： .将方程以下面六种不同方式等价地改写，构造迭代格式，计算 :
(a) , (b) , (c) ,
(d) (e) , (f) .
3.对每一种迭代格式，编制一个程序进行运算，观察每种格式的敛散情况；用事后误差估计 来控制迭代次数，并且输出迭代的次数；观察不同初值的结果.
4.从理论上分析各种格式的收敛性及收敛阶.
5.将收敛较慢的一种格式分别用Atken方法及Steffsen方法加速，通过输出结果了解加速效果.
6.将一种不收敛的方法用Steffsen方法加速得到收敛的迭代.
【实验过程与结果】
1.用matlab编程计算代数方程的根
2.分别编写6个迭代法编程，对结果进行分析
2.2838
2.2790
2.2790
从以上结果可以看出，埃特金加速方法和斯特芬森迭代法确实可以加快收敛速度，且在此题的情况下，两种方法的加速效果差不多，但埃特金加速方法较斯特芬森迭代法来说更为简单易理解，运算步骤也少一些，因此对于此题，我们可以选用埃特金加速方法。
【结果分析、讨论与结论】
迭代公式1：
x1 =
2.0000
1.5000
2.0000
1.5000
2.0000
1.5000
2.0000
1.5000
2.0000
1.5000
2.0000
1.5000
2.0000
1.5000
2.0000
1.5000
2.0000
1.5000
2.0000
1.5000
迭代公式2：
x2 =
5.将一种不收敛的方法用Steffsen方法加速得到收敛的迭代.
附录一：
《数值分析》实验报告（模板）
【实验课题】用牛顿迭代法求非线性方程根
【实验目标】
明确实验目标
1.掌握常用的非线性方程求根算法（二分法、不动点迭代法与Newton法）及加速技术（Aitken加速与Steffsen加速）.
2.会编写计算机程序实现给定迭代函数的迭代算法及其加速；掌握迭代算法的精度控制方法.
2.2790
2.2790
2.2790
2.2790
2.2790
2.2790
2.2790
2.2790
2.2790
2.2790
2.2790
2.2790
迭代公式6：
x6 =
2.0000
2.3333
2.2806
2.2790
2.2790
2.2790
2.2790
2.2790
2.2790
2.2790
2.2790
2.2790
4.1500
4.1773
4.1871
4.1906
4.1919
4.1923
4.1925
4.1926
4.1926
4.1926
4.1926
4.1926
4.1926
4.1926
4.1926
4.1926
迭代公式4：
x4 =
2.0000
5.0000
0.2273
-1.6959
-40.3095
0.0031
-1.6667