牛顿法非线性方程求解
非线性方程求解

⾮线性⽅程求解基于MATLAB的⾮线性⽅程的五种解法探讨摘要:本⽂利⽤matlab软件对⾮线性⽅程解法中的⼆分法、简单迭代法、⽜顿法、割线法以及Steffensen法的数值分析⽅法的算法原理及实现⽅法进⾏了探讨。
对f x x x=+-()2ln2的零点问题,分别运⽤以上五种不同的⽅法进⾏数值实验,⽐较⼏种解法的优缺点并进⾏初步分析评价。
关键词:⼆分法、简单迭代法、⽜顿法、割线法、Steffensen法1、引⾔在很多实际问题中,经常需要求⾮线性⽅程f(x) =0的根。
⽅程f(x) =0的根叫做函数f(x)的零点。
由连续函数的特性知:若f(x)在闭区间[a,b ]上连续,且()()0f a f b<.则f(x) =0在开区间(a,b)内⾄少有⼀个实根。
这时称[a,b]为⽅程f(x) =0的根的存在区间。
本⽂主要对⾮线性⽅程的数值解法进⾏分析,并介绍了⾮线性⽅程数值解法的五种⽅法。
并设=+-.f x x x()2ln2f x在[1,2]上的图形,如图1:. 显然,函数在[1,2]之间有⼀个零点。
⾸先画出()2、计算机配置操作系统Windows 7 旗舰版内存2GB处理器AMD 4核 A6-3400M APU 1.4GHz图.13、⼆分法⼆分法的基本思想是将⽅程根的区间平分为两个⼩区间,把有根的⼩区间再平分为两个更⼩的区间,进⼀步考察根在哪个更⼩的区间内。
如此继续下去,直到求出满⾜精度要求的近似值。
设函数()f x 在区间[a,b ]上连续,且f(a)·f(b) <0,则[a,b ]是⽅程f(x) =0的根的存在区间,设其内有⼀实根,记为x*。
取区间[a,b ]的中点()2k a b x +=并计算1()f x ,则必有下列三种情况之⼀成⽴: (1) 1()f x =0,x1就是⽅程的根x*;(2)()f a .1()f x <0,⽅程的根x*位于区间[a, 1x ]之中,此时令111,a a b x ==; (3)1()f x .()f b <0,⽅程的根x*位于区间[1x ,b ]之中,此时令11a x =,1b b =。
高斯牛顿法手算例题

高斯牛顿法手算例题高斯-牛顿法是一种用于求解非线性方程组的迭代数值方法。
它通过不断迭代来逼近方程组的解。
我将通过一个手算例题来演示高斯-牛顿法的应用。
假设我们要解决以下非线性方程组:f1(x, y) = x^2 + y^2 25 = 0。
f2(x, y) = x y 9 = 0。
我们首先需要计算方程组的雅可比矩阵,即关于变量x和y的偏导数矩阵:J = |2x 2y|。
|y x |。
接下来,我们选择一个初始解向量,例如(x0, y0) = (1, 1)。
然后,我们可以使用以下公式进行迭代:(xn+1, yn+1) = (xn, yn) (J^T J)^(-1) J^T f(xn, yn)。
其中,^T表示矩阵的转置,^(-1)表示矩阵的逆,f(xn, yn)是方程组的函数向量。
现在,让我们开始手算迭代过程:首先,计算f(x0, y0)和J在(x0, y0)处的值:f(x0, y0) = (1^2 + 1^2 25, 11 9) = (-22, -8)。
J = |21 21|。
|1 1 |。
接下来,我们需要计算(J^T J)^(-1) J^T的值。
首先计算J^T J:J^T J = |2 1| |2 2| = |8 4|。
|1 1| |2 2| |4 4|。
然后计算其逆矩阵:(J^T J)^(-1) = (1/(84-44)) |2 -1| = (1/8) |1 -1|。
|-1 2 | |-12 |。
最后,计算(J^T J)^(-1) J^T:(J^T J)^(-1) J^T = (1/8) |1 -1| |2 1| = (1/8) |21|。
|-1 2 | |1 1| |-1 2|。
现在,我们可以将这些值代入迭代公式中:(x1, y1) = (1, 1) (1/8) |2 1| |-22|。
|-1 2 | |-8 |。
(x1, y1) = (1, 1) (1/8) |2 1| |-22| = (1, 1) (1/8)|18|。
数值分析非线性方程的数值解法

数值分析非线性方程的数值解法数值分析是一种应用数学方法来分析和解决数学问题的领域。
非线性方程是数值分析中一类重要的问题,其解法包括了迭代法、牛顿法、割线法等。
本文将详细介绍这些数值解法及其原理和应用。
一、迭代法迭代法是解非线性方程的一种常用数值方法。
该方法的基本思想是通过不断迭代逼近方程的根,直到达到所需精度或满足停止准则为止。
迭代法的求根过程如下:1.选择适当的初始值x0。
2. 利用迭代公式xn+1 = g(xn),计算下一个近似根。
3.重复步骤2,直到满足停止准则为止。
常用的迭代法有简单迭代法、弦截法和牛顿法。
简单迭代法的迭代公式为xn+1 = f(xn),其中f(x)为原方程的一个改写形式。
该方法的收敛性要求函数f(x)在解附近有收敛性且导数在一个区间内收敛。
弦截法的迭代公式为xn+1 = xn - f(xn) * (xn-xn-1) / (f(xn)-f(xn-1))。
该方法通过连接两个点上的函数值的割线来逼近方程的根。
牛顿法的迭代公式为xn+1 = xn - f(xn) / f'(xn),其中f'(x)为f(x)的导数。
该方法通过用切线来逼近方程的根。
二、牛顿法牛顿法是解非线性方程的一种常用迭代法。
该方法通过使用方程的导数来逼近方程的根。
迭代过程如下:1.选择适当的初始值x0。
2. 利用迭代公式xn+1 = xn - f(xn) / f'(xn),计算下一个近似根。
3.重复步骤2,直到满足停止准则为止。
牛顿法的收敛速度较快,但要求方程的导数存在且不为0。
三、割线法割线法是解非线性方程的另一种常用迭代法。
该方法通过连接两个点上的函数值的割线来逼近方程的根。
迭代过程如下:1.选择适当的初始值x0和x12. 计算下一个近似根xn+1 = xn - f(xn) * (xn-xn-1) / (f(xn)-f(xn-1))。
3.重复步骤2,直到满足停止准则为止。
割线法的收敛速度介于简单迭代法和牛顿法之间。
非线性方程求解

非线性方程求解在数学中,非线性方程是一种函数关系,其表达式不能通过一次函数处理得到。
与线性方程不同,非线性方程的解决方案往往更具挑战性,因为它涉及到更复杂的计算过程。
尤其在实际应用中,非线性方程的求解是一个非常重要的问题。
本文将讨论几种常用的非线性方程求解方法。
二分法二分法,也称为折半法,是一种基本的求解非线性方程的方法之一。
它的核心思想是将区间一分为二并判断方程在哪一半具有根。
不断这样做直到最终解得精度足够高为止。
下面是利用二分法求解非线性方程的流程:1. 设定精度值和区间范围2. 取区间的中点并计算函数值3. 如果函数值为0或函数值在给定精度范围内,返回中点值作为精确解4. 如果函数值不为0,则判断函数值的正负性并缩小区间范围5. 重复步骤2-4直到满足给定精度为止当然,这种方法并不总是能够找到方程的解。
在方程存在多个解或者区间范围不合适的情况下,二分法可能会导致求解失败。
但它是一种很好的起点,同时也是更复杂的求解方法中的一个重要组成部分。
牛顿迭代法牛顿迭代法是一种更复杂的求解非线性方程的方法。
它利用泰勒级数和牛顿迭代公式,通过不断迭代来逼近根的位置。
下面是利用牛顿迭代法求解非线性方程的流程:1. 先取一个近似值并计算函数值2. 求出函数的导数3. 利用牛顿迭代公式,计算下一个近似根4. 检查下一个近似根的精度是否满足条件,如果满足,返回当前近似根5. 如果精度不满足,则将新的近似根带入公式,重复步骤2-5当然,牛顿迭代法的收敛性并不总是保证的。
如果迭代过程太过温和,它可能无法收敛到精确解。
如果迭代过程过于暴力,则会出现发散现象,使得求解变得不可能。
其他方法此外,还有一些其他的求解非线性方程的方法,例如黄金分割法、逆二次插值法、牛顿切线法等等。
其中每一种方法都有其优缺点,不同的情况下,不同的方法都可能比其他方法更加适合。
结论总体来说,求解非线性方程的方法非常复杂。
无论是哪种方法,都需要一定的数学基础和计算机知识。
Ansys Workbench非线性分析 牛顿辛普森法过程
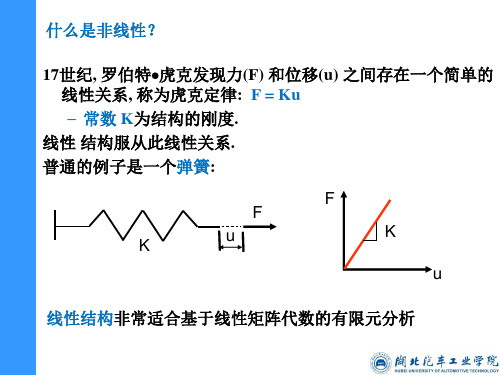
然而, 相当多的结构在力和位移之间没有线性关系 因为此类结构的 F-u 图不是直线, 这样的结构称为非线性结构 . – 刚度不再是一个常数K; 它成为施加载荷的函数, KT (切 线刚度). 普通的例子是韧性金属的拉伸试验:
载荷位移曲线
Fa Fnr
R
下一次迭代用刚度矩阵
u0 △ u u1
u0: 所设初始位移值
u
位移
KT :切向刚度
u1: 下次迭代位移值
R F a F nr
收敛: Newton-Raphson法需要一个收敛的度量以决定 何时结束迭代。给定节点Fa,节点力Fnr ,在一个体 中,节点载荷必须与节点力平衡
高级接触选项包括: 自动探测尺寸 Auto detection dimension and slider 非对称接触Asymmetric contact 接触结果工具Contact results tool 接触算法contact formulations Pinball 控制
膜片弹簧接触设置
带支撑环的膜片弹簧边界条件及求解设置
3 2 F1 269.991 2981 1 9238 1
膜片弹簧大端载荷-位移曲线
3 2 F1 269.991 2981 1 9238 1
注:膜片弹簧载荷挠度曲线为非线性,是由于大变形引起 的几何非线性,但材料始终发生的是弹性变形,没有发生 塑性变形
回忆材料力学中低碳钢力学性能试验
最优化理论与方法——牛顿法

牛顿法牛顿法作为求解非线性方程的一种经典的迭代方法,它的收敛速度快,有内在函数可以直接使用。
结合着matlab 可以对其进行应用,求解方程。
牛顿迭代法(Newton Newton’’s s method method )又称为牛顿-拉夫逊方法(Newton-Raphson method ),它是牛顿在17世纪提出的一种在实数域和复数域上近似求解方程的方法,其基本思想是利用目标函数的二次Taylor 展开,并将其极小化。
牛顿法使用函数()f x 的泰勒级数的前面几项来寻找方程()0f x =的根。
牛顿法是求方程根的重要方法之一,其最大优点是在方程()0f x =的单根附近具有平方收敛,而且该法还可以用来求方程的重根、复根,此时非线性收敛,但是可通过一些方法变成线性收敛。
收敛。
牛顿法的几何解释:牛顿法的几何解释:方程()0f x =的根*x 可解释为曲线()y f x =与x 轴的焦点的横坐标。
如下图:轴的焦点的横坐标。
如下图:设k x 是根*x 的某个近似值,过曲线()y f x =上横坐标为k x 的点k P 引切线,并将该切线与x 轴的交点轴的交点 的横坐标1k x +作为*x 的新的近似值。
鉴于这种几何背景,牛顿法亦称为切线法。
牛顿法亦称为切线法。
2 牛顿迭代公式:(1)最速下降法:x-d gk k×Gg sks×GGd 101x x x -(1)令k k G v I k G -=+,其中:,其中:0k v =,如果k G 正定;0,k v >否则。
否则。
(2)计算_k G 的Cholesky 分解,_T k k k k G L D L =。
(3)解_k k G d g =-得k d 。
(4)令1k k k x x d +=+牛顿法的优点是收敛快,缺点一是每步迭代要计算()()'k k f x f x 及,计算量较大且有时()'k fx 计算较困难,二是初始近似值0x 只在根*x附近才能保证收敛,如0x 给的不合适可能不收敛。
二维一般牛顿法

二维一般牛顿法
在数值计算中,当需要求解非线性方程组时,二维一般牛顿法是一种常用的迭代算法。
它是一种高效的求解非线性问题的方法。
二维一般牛顿法的基本思想是采用局部线性逼近的方式,将非线性问题转化为线性问题,然后通过一系列迭代求解线性问题,最终得到非线性方程组的解。
具体来说,该算法的迭代公式为:
x(k+1) = x(k) - [J(x(k))]^(-1) * F(x(k))
其中,x(k)表示第k次迭代时的解向量,J(x(k))为x(k)点处的雅可比矩阵,F(x(k))为x(k)点处的函数值向量。
在实际应用中,二维一般牛顿法通常需要进行多次迭代才能达到精度要求。
因此,在每一次迭代中,需要对雅可比矩阵进行求解,这通常是一个比较耗时的过程。
为了提高计算效率,可以采用一些优化方法,比如预处理技术、加速技术等。
二维一般牛顿法的优点在于其收敛速度较快,而且对初始值的选取不敏感。
但是,该方法也存在一些缺点。
比如,当函数值存在极小值或者收敛点时,该方法容易陷入局部极小值,从而无法得到全局最优解。
因此,在实际应用中,需要根据具体问题的特点选择合适的求解方
法。
对于一些存在多个局部极小值的问题,可以采用遗传算法、模拟退火等全局优化算法来求解。
二维一般牛顿法是一种常用的非线性方程组求解方法,其优点在于收敛速度快、对初始值不敏感,但也存在一些缺点。
在实际应用中,需要根据问题的特点选择合适的求解方法,以获得更好的结果。
解一元三次方程

解一元三次方程一元三次方程是指只含有一个未知数,并且未知数的最高次数为3的方程。
解一元三次方程的方法有多种,下面将介绍其中两种常用的方法:牛顿法和因式分解法。
一、牛顿法牛顿法是一种利用切线逼近函数零点的方法,适用于非线性方程求解。
对于一元三次方程,我们可以利用牛顿法进行求解。
设给定的一元三次方程为:ax^3 + bx^2 + cx + d = 0,其中a、b、c、d为已知系数,x为未知数。
牛顿法的迭代公式为:x_(n+1) = x_n - f(x_n)/f'(x_n),其中x_n为第n次迭代的近似解,f(x_n)为方程在x_n处的函数值,f'(x_n)为方程在x_n处的导数值。
具体步骤如下:1. 初始化近似解x_0,通常选择一个离根比较近的值。
2. 计算方程在x_n处的函数值f(x_n)和导数值f'(x_n)。
3. 根据迭代公式计算新的近似解x_(n+1)。
4. 判断|x_(n+1) - x_n|是否小于给定的精度要求,若满足则停止迭代,否则继续迭代。
5. 重复步骤2-4,直到满足精度要求。
二、因式分解法因式分解法是一种将三次方程分解为一次和二次方程的乘积的方法,然后求解得到方程的根。
对于给定的一元三次方程:ax^3 + bx^2 + cx + d = 0,我们可以根据不同的情况来进行因式分解。
1. 若方程有一个实数根x_1,则可以通过除以(x − x_1)得到一个二次方程:(ax^2 + (b − ax_1)x + c − bx_1) = 0。
接下来,我们可以使用求解二次方程的方法来求解这个二次方程的根x_2和x_3。
2. 若方程有三个实数根x_1、x_2和x_3,则可以通过因式分解得到:(x − x_1)(x −x_2)(x − x_3) = 0。
这样,我们可以根据已知的三个根来得到方程的因式分解形式。
需要注意的是,当方程没有实数根时,我们可能需要考虑复数解的情况。
综上所述,解一元三次方程的方法有牛顿法和因式分解法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《MATLAB 程序设计实践》课程考核
---第37-38页
题1
: 编程实现以下科学计算算法,并举一例应用之。(参考书籍《精
通MATLAB科学计算》,王正林等著,电子工业出版社,2009
年)
“牛顿法非线性方程求解”
弦截法本质是一种割线法,它从两端向中间逐渐逼近方程的根;牛顿法本质上是一种切线法,
它从一端向一个方向逼近方程的根,其递推公式为:
nnxx
1
)()('nnxf
xf
初始值可以取)('af和)('bf的较大者,这样可以加快收敛速度。
和牛顿法有关的还有简化牛顿法和牛顿下山法。
在MATLAB中编程实现的牛顿法的函数为:NewtonRoot。
功能:用牛顿法求函数在某个区间上的一个零点。
调用格式:root=NewtonRoot)(```epsbaf
其中,f为函数名;
a
为区间左端点;
b
为区间右端点
eps为根的精度;
root为求出的函数零点。
,
牛顿法的matlab程序代码如下:
function root=NewtonRoot(f,a,b,eps)
%牛顿法求函数f在区间[a,b]上的一个零点
%函数名:f
%区间左端点:a
N
Y
输入参数值
nargin==3
f1==0
eps=1.0e-4
结束
f2==0
f1*f2>0
两端点函数值乘
积大于0 !
Y
N
dfa>dfb
Y
N
N
N
Y
Y
开始
tol>eps
Y
输出结果
N
流程图:
root=a
root=b
root=a-fa/dfa
root=b-fb/dfb
root=r1-fx/dfx
%区间右端点:b
%根的精度:eps
%求出的函数零点:root
if(nargin==3)
eps=1.0e-4;
end
f1=subs(sym(f),findsym(sym(f)),a);
f2=subs(sym(f),findsym(sym(f)),b);
if (f1==0)
root=a;
end
if (f2==0)
root=b;
end
if (f1*f2>0)
disp('两端点函数值乘积大于0 !');
return;
else
tol=1;
fun=diff(sym(f)); %求导数
fa=subs(sym(f),findsym(sym(f)),a);
fb=subs(sym(f),findsym(sym(f)),b);
dfa=subs(sym(fun),findsym(sym(fun)),a);
dfb=subs(sym(fun),findsym(sym(fun)),b);
if(dfa>dfb) %初始值取两端点导数较大者
root=a-fa/dfa;
else
root=b-fb/dfb;
end
while(tol>eps)
r1=root;
fx=subs(sym(f),findsym(sym(f)),r1);
dfx=subs(sym(fun),findsym(sym(fun)),r1); %求该点的导数值
root=r1-fx/dfx; %迭代的核心公式
tol=abs(root-r1);
end
end
例:求方程3x^2-exp(x)=0的一根
解:在MATLAB命令窗口输入:
>> r=NewtonRoot('3*x^2-exp(x)',3,4)
输出结果:
X=3.7331
2、编程解决以下科学计算问题
1) 二自由度可解耦系统的振动模态分析,二自由度振动系统如图所示,其一般方程为:
0)12(2)12(2220221)21(221)21(11........xxKxxcxm
xKxKKxcxccxm
可写成矩阵形式:0...KxxCxM
设C=0,即无阻尼情况,则系统可解耦为两种独立的振动模态。
输入参数值
结束
开始
流程图:
构成参数矩阵
设定初始条件
i=1:round(tf/dt)+1
循环计算矩阵指数
绘制图象
系统解耦的振动模态的MATLAB代码如下:
function erziyoudu()
%输入各原始参数
m1=input('m1=');m2=input('m2='); %质量
k1=input('k1=');k2=input('k2='); %刚度
%输入阻尼系数
c1=input('c1=');c2=input('c2=');
%给出初始条件及时间向量
x0=[1;0];
xd0=[0;-1];
tf=50; %步数
dt=0.1; %步长
%构成二阶参数矩阵
M=[m1,0;0,m2];
K=[k1+k2,-k2;-k2,k2];
C=[c1+c2,-c2;-c2,c2];
%构成四阶参数矩阵
A=[zeros(2,2),eye(2);-M\K,-M\C];
%四元变量的初始条件
y0=[x0;xd0];
%设定计算点,作循环计算
for i=1:round(tf/dt)+1
t(i)=dt*(i-1);
y(:,i)=expm(A*t(i))*y0;%循环计算矩阵指数
end
%按两个分图绘制x1、x2曲线
subplot(2,1,1),plot(t,y(1,:)),grid
xlabel('t'),ylabel('y');
subplot(2,1,2),plot(t,y(2,:)),grid
xlabel('t'),ylabel('y');
运行M文件,依下图所示在MATLAB命令窗口中输入数据:
即可得出该振动的两种模态
2)用GUI方式解下列PDE:
;0,4sin0),3(30,40,030402222yyxxuxu
uyyu
yx
yux
u
解:第一步,在MATLAB命令窗口输入命令pdetool打开工具箱,调整x坐标范围为[0 4],y
坐标范围为[0 3].通过options选项的Axes Linits设定如下图所示。
第二步,设定矩形区域。点击工具箱栏中的按钮“”,拖动鼠标画出一矩形,并双击该
矩形,设定矩形大小,如下图所示。
第三步,设边界条件。点击工具栏中的按钮“”,并双击矩形区域的相应的边线在弹出
的对话框中设定边界条件。如下图所示,分别为各边框的边界条件。
第四步,设定方程。单机工具栏中的按钮“”,在PDE模式下选择方程类型,如下图
所示,并在其中设定参数。
第五步,单击工具栏中的按钮“”,拆分区域为若干子区域,如下图所示。
第六步,单击工具栏中的按钮“”,将子区域细化,从而保证结果更精确,如下图所
示。
第七步,单击工具栏中的按钮“”,设置所画曲线的特性,如下图所示,并作出其解
的三维图。
第八步,单击图2-8在标出的“plot”按钮,或单击工具栏中的按钮“”,可作出解的
三维图,如下图所示。
简要流程图:
开始
绘制要求区域图
设置边界条件
设置方程参数
剖分网格
作出解的三维图
结束
