matlab程序设计实践-牛顿法解非线性方程
matlab牛顿拉夫逊法与快速分解法的实现
一、概述MATLAB是一种强大的数学软件工具，它提供了许多优秀的数值计算和数据分析功能。
其中，牛顿拉夫逊法和快速分解法是两种常用的数值计算方法，它们在解决非线性方程组和矩阵分解等问题中具有重要的应用价值。
本文将介绍如何在MATLAB中实现这两种方法，并对它们的优缺点进行详细分析。
二、牛顿拉夫逊法的实现1. 算法原理牛顿拉夫逊法是一种用于求解非线性方程组的迭代算法。
它利用函数的一阶和二阶导数信息来不断逼近方程组的解，直到满足精度要求为止。
算法原理可以用以下公式表示:公式1其中，x表示解向量，F(x)表示方程组的函数向量，J(x)表示方程组的雅可比矩阵，δx表示解的更新量。
通过不断迭代更新x，最终得到方程组的解。
2. MATLAB代码实现在MATLAB中，可以通过编写函数来实现牛顿拉夫逊法。
以下是一个简单的示例代码：在这段代码中，首先定义了方程组的函数向量和雅可比矩阵，然后利用牛顿拉夫逊法进行迭代更新，直到满足精度要求为止。
通过这种方式，就可以在MATLAB中实现牛顿拉夫逊法，并应用于各种实际问题。
三、快速分解法的实现1. 算法原理快速分解法是一种用于矩阵分解的高效算法。
它利用矩阵的特定性质，通过分解为更小的子问题来加速计算过程。
算法原理可以用以下公式表示:公式2其中，A表示要分解的矩阵，L和U分别表示矩阵的下三角和上三角分解。
通过这种分解方式，可以将原始矩阵的计算量大大减小，提高求解效率。
2. MATLAB代码实现在MATLAB中，可以利用内置函数来实现快速分解法。
以下是一个简单的示例代码：在这段代码中，利用MATLAB内置的lu函数进行LU分解，得到矩阵的下三角和上三角分解。
通过这种方式，就可以在MATLAB中实现快速分解法，并应用于各种矩阵计算问题。
四、方法比较与分析1. 算法复杂度牛顿拉夫逊法和快速分解法在计算复杂度上有所不同。
牛顿拉夫逊法的迭代次数取决于所求解问题的非线性程度，通常需要较多的迭代次数。
牛顿迭代法解非线性方程组（MATLAB版）
⽜顿迭代法解⾮线性⽅程组（MATLAB版）⽜顿迭代法，⼜名切线法，这⾥不详细介绍，简单说明每⼀次⽜顿迭代的运算：⾸先将各个⽅程式在⼀个根的估计值处线性化（泰勒展开式忽略⾼阶余项），然后求解线性化后的⽅程组，最后再更新根的估计值。
下⾯以求解最简单的⾮线性⼆元⽅程组为例（平⾯⼆维定位最基本原理），贴出源代码：1、新建函数fun.m，定义⽅程组1 function f=fun(x);2 %定义⾮线性⽅程组如下3 %变量x1 x24 %函数f1 f25 syms x1 x26 f1 = sqrt((x1-4)^2 + x2^2)-sqrt(17);7 f2 = sqrt(x1^2 + (x2-4)^2)-5;8 f=[f1 f2];2、新建dfun.m，求出⼀阶微分⽅程1 function df=dfun(x);2 f=fun(x);3 df=[diff(f,'x1');diff(f,'x2')]; %雅克⽐矩阵3、建⽴newton.m，执⾏⽜顿迭代过程1 clear;clc2 format;3 x0=[0 0]; % 迭代初始值4 eps = 0.00001; % 定位精度要求5for i = 1:106 f = double(subs(fun(x0),{'x1''x2'},{x0(1) x0(2)}));7 df = double(subs(dfun(x0),{'x1''x2'},{x0(1) x0(2)})); % 得到雅克⽐矩阵8 x = x0 - f/df;9if(abs(x-x0) < eps)10break;11 end12 x0 = x; % 更新迭代结果13 end14 disp('定位坐标：');15 x16 disp('迭代次数：');17 i结果如下：定位坐标：x =0.0000 -1.0000迭代次数：i =4。
matlab实验一：非线性方程求解-牛顿法
matlab实验一：非线性方程求解-牛顿法实验一:非线性方程求解程序1：二分法：syms f x;f=input（'请输入f（x)='）;A=input（’请输入根的估计范围[a,b］=’）;e=input（'请输入根的误差限e=’);while (A（2)—A（1)）>ec=(A（1）+A(2)）/2；x=A（1）；f1=eval（f)；x=c；f2=eval（f）；if (f1＊f2）〉0A(1)=c；elseA(2)=c;endendc=（A(1)+A（2）)/2；fprintf(’c=％。
6f\na=%.6f\nb=%.6f\n'，c，A)用二分法计算方程：1．请输入f（x）=sin（x)—x^2/2请输入根的估计范围[a，b］=[1,2］请输入根的误差限e=0。
5e-005c=1.404413a=1。
404411b=1.4044152．请输入f(x)=x^3—x-1请输入根的估计范围［a，b］=[1，1.5]请输入根的误差限e=0.5e-005c=1。
324717a=1。
324715b=1。
324718程序2：newton法：syms f x；f=input（’请输入f（x)=');df=diff(f);x0=input('请输入迭代初值x0=’)；e1=input('请输入奇异判断e1=’）;e2=input（'请输入根的误差限e2='）；N=input（'请输入迭代次数限N=’)；k=1；while （k〈N）x=x0；if abs（eval（f）)〈e1 fprintf(’奇异！\nx=％。
6f\n迭代次数为:％d\n’,x0，k）breakelsex1=x0—eval(f)/eval(df）;if abs（x1-x0)<e2fprintf（'x=%。
6f\n迭代次数为:％d\n’，x1,k）breakelsex0=x1；k=k+1;endendendif k〉=Nfprintf（'失败\n'）end用newton法计算方程:1．请输入f(x）=x*exp（x)—1请输入迭代初值x0=0。
matlab牛顿迭代法求方程
一、引言在数值计算中，求解非线性方程是一项常见的任务。
牛顿迭代法是一种常用且有效的方法，它通过不断逼近函数的零点来求解方程。
而在MATLAB中，我们可以利用其强大的数值计算功能来实现牛顿迭代法，快速求解各种非线性方程。
二、牛顿迭代法原理与公式推导1. 牛顿迭代法原理牛顿迭代法是一种利用函数的导数信息不断逼近零点的方法。
其核心思想是利用当前点的切线与x轴的交点来更新下一次迭代的值，直至逼近方程的根。
2. 公式推导与迭代过程假设要求解方程f(x)=0，在初始值x0附近进行迭代。
根据泰勒展开，对f(x)进行一阶泰勒展开可得：f(x) ≈ f(x0) + f'(x0)(x - x0)令f(x)≈0，则有：x = x0 - f(x0)/f'(x0)将x带入f(x)的表达式中，即得到下一次迭代的值x1：x1 = x0 - f(x0)/f'(x0)重复以上过程，直至达到精度要求或者迭代次数上限。
三、MATLAB中的牛顿迭代法实现1. 编写函数在MATLAB中，我们可以编写一个函数来实现牛顿迭代法。
需要定义原方程f(x)的表达式，然后计算其一阶导数f'(x)的表达式。
按照上述推导的迭代公式，编写循环语句进行迭代计算，直至满足精度要求或者达到最大迭代次数。
2. 调用函数求解方程在编写好牛顿迭代法的函数之后，可以通过在MATLAB命令窗口中调用该函数来求解具体的方程。
传入初始值、精度要求和最大迭代次数等参数，即可得到方程的近似根。
四、牛顿迭代法在工程实践中的应用1. 求解非线性方程在工程领域，很多问题都可以转化为非线性方程的求解问题，比如电路分析、控制系统设计等。
利用牛顿迭代法可以高效地求解这些复杂方程，为工程实践提供了重要的数值计算手段。
2. 优化问题的求解除了求解非线性方程外，牛顿迭代法还可以应用于优化问题的求解。
通过求解目标函数的导数等于0的方程，可以找到函数的极值点，从而解决各种优化问题。
非线性方程组求解的牛顿迭代法用MATLAB实现
非线性方程组求解的牛顿迭代法用MATLAB实现首先，我们需要定义非线性方程组。
假设我们要求解方程组：```f1(x1,x2)=0f2(x1,x2)=0```其中，`x1`和`x2`是未知数，`f1`和`f2`是非线性函数。
我们可以将这个方程组表示为向量的形式：```F(x)=[f1(x1,x2);f2(x1,x2)]=[0;0]```其中，`F(x)`是一个列向量。
为了实现牛顿迭代法，我们需要计算方程组的雅可比矩阵。
雅可比矩阵是由方程组的偏导数组成的矩阵。
对于方程组中的每个函数，我们可以计算其对每个变量的偏导数，然后将这些偏导数组成一个矩阵。
在MATLAB中，我们可以使用`jacobi`函数来计算雅可比矩阵。
以下是一个示例函数的定义：```matlabfunction J = jacobi(x)x1=x(1);x2=x(2);J = [df1_dx1, df1_dx2; df2_dx1, df2_dx2];end```其中，`x`是一个包含未知数的向量，`df1_dx1`和`df1_dx2`是`f1`对`x1`和`x2`的偏导数，`df2_dx1`和`df2_dx2`是`f2`对`x1`和`x2`的偏导数。
下一步是实现牛顿迭代法。
牛顿迭代法的迭代公式为：```x(k+1)=x(k)-J(x(k))\F(x(k))```其中，`x(k)`是第`k`次迭代的近似解，`\`表示矩阵的求逆操作。
在MATLAB中，我们可以使用如下代码来实现牛顿迭代法：```matlabfunction x = newton_method(x_initial)max_iter = 100; % 最大迭代次数tol = 1e-6; % 收敛阈值x = x_initial; % 初始解for k = 1:max_iterF=[f1(x(1),x(2));f2(x(1),x(2))];%计算F(x)J = jacobi(x); % 计算雅可比矩阵 J(x)delta_x = J \ -F; % 计算增量 delta_xx = x + delta_x; % 更新 xif norm(delta_x) < tolbreak; % 达到收敛条件，停止迭代endendend```其中，`x_initial`是初始解的向量，`max_iter`是最大迭代次数，`tol`是收敛阈值。
用Matlab编写二分法和Newton迭代法求解非线性函数
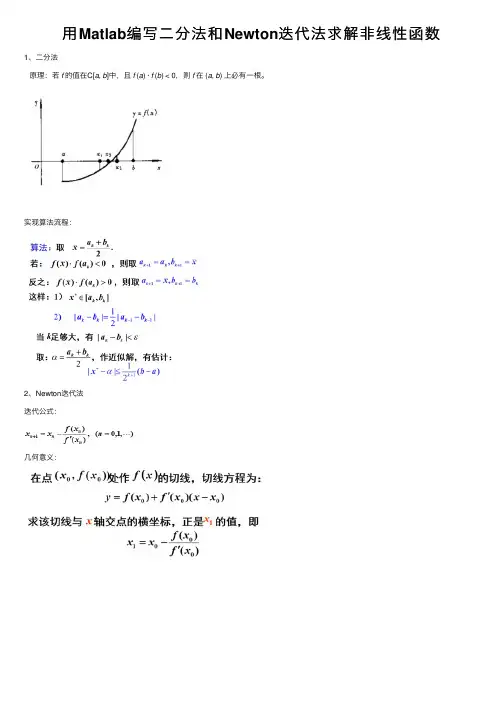
⽤Matlab编写⼆分法和Newton迭代法求解⾮线性函数1、⼆分法原理：若f的值在C[a, b]中，且f (a) · f (b) < 0，则f在 (a, b) 上必有⼀根。
实现算法流程：2、Newton迭代法迭代公式：⼏何意义：3、求解问题⽤Newton法和⼆分法求的解。
4、代码实现1 clear;close;clc2 a=0;b=1;%根区间3 e=10^(-6);%根的容许误差4 [X , N]=dichotomy(e,a,b);%⼆分法5 p0=0.5;%初始值6 N=15;%迭代次数7 [X1]=Newdon(p0,e,N);%Newton迭代法89 function [X , N]=dichotomy(deta,a,b)10 % 函数dichotomy:⼆分法11 %输⼊值：12 %fun:⽅程函数13 %deta:根的容许误差14 %有根区间：[a,b]15 %输出值16 %X:求解到的⽅程的根17 %N:总的迭代次数18 N=1+fix(log2((b-a)/deta));%由公式7.2求得,取整数|X_N-X*|<=(b-a)/2^N<deta,求N19 n=1;20 f1=myfunction(a);21 f2=myfunction(b);22if (f1*f2>0)23 disp('根不在输⼊的区间⾥，请重新输⼊区间');24else25while n <= N26 x=(a+b)/2;27if myfunction(a)*myfunction(x)>028 a=x;29else30 b=x;31 end32 n=n+1;33 end34 X=x;35 fprintf('第%d次⼆分法求出的⽅程的根:\n',N);36 fprintf('X=\n');37 disp(X);38 end39 end4041 function [P]=Newdon(p0,TOL,N)42 %求⽅程组的解43 %输⼊参数44 %初始值：p045 %误差容限:TOL46 %最⼤迭代次数:N47 %输出参数：48 %⽅程近似解：p49 %或失败信息“Method failed”50 format long;51 n=1;%初始迭代次数52 syms x;53while n<=N54if abs(subs(diff(myfunction(x)),x,p0))<TOL55 P=p0;56break;57else58if subs(diff(myfunction(x),2),x,p0)==059 disp('Method failed');60break;61else62 p=p0-myfunction(p0)/subs(diff(myfunction(x)),x,p0);63 p=eval(p);%将exp的值转为⼩数值64if(abs(p-p0)<TOL)65 P=p;66break;67else68 p0=p;69 end70 end71 end72 n=n+1;73 end74 % P=vpa(P,10);%将分数转为⼩数并保留8位⼩数75 fprintf('第%d次NeWton迭代法求出的⽅程的根:\n',N);76 fprintf('P=\n');77 disp(P);78 end7980 function f=myfunction(x)81 f=x*exp(x)-1;82 end5、求解结果。
牛顿法解非线性方程(MATLAB和C++)
41 end
42 time = toc;
43
44 fprintf('\nIterated times is %g.\n', times);
45 fprintf('Elapsed time is %g seconds.\n', time);
46
47 root = x_iter;
48
49 % subfunction
5
6 // 功能描述：求解非线性方程根，并输出最终解 7 // 迭代式：x(k+1) = x(k) - f(x(k))/df(x(k)). 8 // 使用：修改标出的“修改”部分即可自定义参数
9
10 // 输入：函数 fun，函数导数 dfun，初值 x0，
4
11 // 最大迭代次数 maxiter，停止精度 tol 12 // 输出：迭代数值解 x_iter2
2
Listing 1: MATLAB EXAMPLE 1 % 2013/11/20 15:14:38
2
3 f = @(x)x^2 − 2; 4 df = @(x)2*x; 5 x0 = 3; 6 root = newton(f, df, x0);
C++ 以 C++ 实现的方法并未编写成为一般可调用的方法，而作为一个独立的 文件（包含一个实例），修改部分即可求解对应的方程。具体参照 cpp 文件内 注释。
A 附录
A.1 MATLAB
Listing 2: MATLAB CODE 1 function root = newton(f, df, x0, maxiter, tol) 2 %NEWTON Newton's method for nonlinear equations. 3% 4 % NEWTON's method: x(k+1) = x(k) - f(x(k))/f'(x(k)). 5% 6 % Inputs 7 % f - nonlinear equation. 8 % df - derivative of f(x). 9 % x0 - initial value. 10 % maxiter - maximum iterated times. 11 % tol - precision. 12 % 13 % Outputs 14 % root - root of f(x) = 0.
牛顿下山法求非线性方程组解
《MATLAB 程序设计实践》课程考核1、编程实现以下科学计算算法，并举一例应用之。
（参考书籍《精通ＭＡＬＡＢ科学计算》，王正林等著，电子工业出版社，２００９年）“牛顿下山法求非线性方程组解”解：算法说明：牛顿下山法的迭代公式：())()(11n n n n x F x F w x x -+-=w 的取值范围为10≤w ，为了保证收敛，还要求w 的取值使得：())(1n n x F x F +可以用作次减半法来确定w 。
为了减少计算量，还可以用差商来代替偏导数。
在MA TLAB 中编程实现的非线形方程组的牛顿下山法的函数：mulDNewton 。
功能：用牛顿下山法求非线形方程组的一个解。
调用格式：[]),0(,eps x mulDNewton n r = 其中， x0为初始迭代向量Eps 为迭代精度；r 为求出的解向量n 为迭代步数。
牛顿下山法的MATLAB 代码如下：function [r,n]=mulDNewton(x0,eps) %牛顿下山法求非线形方程组的一个解 %初始迭代向量：x0 %迭代精度：eps %解向量： r %迭代步数：n if nargin==1 eps=1.0e-4;%输入的自变量的数目为1个时，精度定为eps=1.0e-4 endr=x0-myf(x0)/dmyf(x0); %当n=1时，取w=1 n=1; tol=1;%初始n 和tol 的值 while tol>eps x0=r; ttol=1; %初始ttol 的值 w=1;%初始w 的值，w 就是下山因子alpha F1=norm(myf(x0)); while ttol>=0r=x0-w*myf(x0)/dmyf(x0); ttol=norm(myf(r))-F1; w=w/2; endtol=norm(r-x0); n=n+1; if (n>100000)disp('迭代步数太多，可能不收敛！'); return ; end end举例说明：牛顿下山法求下面方程组⎩⎨⎧=--=-+0sin 1.0cos 5.00)cos(1.0sin 5.02211211x x x x x x x 的根，其初始迭代值取（0,0）。
牛顿法matlab程序及例题
牛顿法matlab程序及例题牛顿法是一种求解非线性方程组的常用方法，它的基本思想是通过迭代逐步逼近方程组的根。
在matlab中，可以通过编写相应的程序来实现牛顿法，并且可以通过一些例题来深入理解其应用。
下面是一份牛顿法的matlab程序：function [x, fval, exitflag, output] = mynewton(fun, x0, tol, maxiter)% fun：非线性方程组的函数句柄% x0：初始点% tol：允许误差% maxiter：最大迭代次数x = x0;fval = feval(fun, x);iter = 0;output = [];while norm(fval) > tol && iter < maxiteriter = iter + 1;J = myjacobian(fun, x);dx = - J fval;x = x + dx;fval = feval(fun, x);output = [output; [x', norm(fval)]];endif norm(fval) <= tolexitflag = 0; % 成功求解elseexitflag = 1; % 未能求解end% 计算雅可比矩阵function J = myjacobian(fun, x)n = length(x);fval = feval(fun, x);J = zeros(n);h = sqrt(eps); % 微小的增量for j = 1:nxj = x(j);x(j) = xj + h;fval1 = feval(fun, x);x(j) = xj - h;fval2 = feval(fun, x);x(j) = xj;J(:, j) = (fval1 - fval2) / (2 * h);end接下来，我们可以通过一个例题来演示牛顿法的应用。
非线性方程的数值解法牛顿下山法matlab
非线性方程的数值解法——计算物理实验作业九陈万 物理学2013级 130********● 题目：用下列方法求0133=--=x x f(x)在20=x 附近的根。
根的准确值 87938524.1*=x ,要求计算结果精确到四位有效数字。
（1）用牛顿法；（2）用弦截法，取；9.1,210==x x● 主程序：clearclc;%----------------初值设定-------------------x0 = 2;x1 = 1.9;eps = 0.00001;N = 50;%----------------迭代求解-------------------Newton(x0,eps,N);Newton_downhill(x0,eps,N);Secant_Method(x0,x1,eps,N);● 子程序：f(x)function [y]=f(x)y = x^3-3*x-1; %函数f(x)End● 程序一：牛顿法function Newton(x0,eps,N)% 牛顿法% x0是迭代初值，eps是精度，N是迭代上限format long;k = 1;while(1)ff = (f(x0+0.1*eps)-f(x0))/(0.1*eps);if ff == 0disp('分母为零，请重新选择初始迭代值')break;elsex1=x0-f(x0)/ff ;if abs(x1-x0)<epsdisp('满足精度要求的根是：')disp(x1)break;elseif k>=Ndisp('迭代失败，请检查程序是否有误')breakelsek = k+1;x0 = x1;endendend程序二：弦截法function Secant_Method(x0,x1,eps,N)% 弦截法% x0,x1是迭代初值，eps是精度，N是迭代上限format long;k = 1;while(1)if f(x0)==0disp('满足精度要求的解是：')disp(x0)elseif f(x1)==0disp('满足精度要求的解是：')disp(x1)break;elseif abs(f(x1)-f(x0))==0disp('分母为零，请重新选择初始迭代值')break;elsex2 = x1-f(x1)*(x1-x0)/(f(x1)-f(x0));if abs(x2-x1)<epsdisp('满足精度要求的解是：')disp(x2)break;elseif k>=Ndisp('迭代失败，请检查程序是否有误')break;elsek = k+1;x0 = x1;x1 = x2;endendend程序三：牛顿下山法function Newton_downhill(x0,eps,N)% 牛顿下山法% x0是迭代初值，eps是精度，N是迭代上限format long;k = 1;while(1)lamda = 1;ff = (f(x0+0.1*eps)-f(x0))/(0.1*eps);if ff == 0disp('分母为零，请重新选择初始迭代值')elsewhile(1)x1 = x0-lamda*f(x0)/ff ;if f(x1)>=f(x0)lamda = 0.5*lamda;elsebreak;endendif abs(x1-x0)<epsdisp('牛顿下山法满足精度要求的根是：')disp(x1)break;elseif k>=Ndisp('迭代失败，请检查程序是否有误')breakelsek = k+1;x0 = x1;endendendend●程序运行结果：牛顿法：满足精度要求的根是：1.879385241571819弦截法：满足精度要求的解是：1.879385241572444●分析讨论：从运行结果来看，牛顿法与弦截法的结果与给定准确值完全相等；从运行时间上看速度都相当快。
matlab程序设计实践-牛顿法解非线性方程
matlab程序设计实践-⽜顿法解⾮线性⽅程中南⼤学MATLAB程序设计实践学长有爱奉献，下载填上信息即可上交，没有下载券的⾃⾏百度。
所需m⽂件照本⽂档做即可，即新建（FILE）→脚本（NEW-Sscript）→复制本⽂档代码→运⾏（会跳出保存界⾯，⽂件名默认不要修改，保存）→结果。
第⼀题需要把数据⽂本⽂档和m⽂件放在⼀起。
全部测试⽆误，放⼼使⽤。
本⽂档针对做⽜顿法求⾮线性函数题⽬的同学，当然第⼀题都⼀样，所有⼈都可以⽤。
←记得删掉这段话班级：学号：姓名：⼀、《MATLAB程序设计实践》Matlab基础表⽰多晶体材料织构的三维取向分布函数（f＝f（φ1，φ，φ2））是⼀个⾮常复杂的函数，难以精确的⽤解析函数表达，通常采⽤离散空间函数值来表⽰取向分布函数，是三维取向分布函数的⼀个实例。
由于数据量⾮常⼤，不便于分析，需要借助图形来分析。
请你编写⼀个matlab程序画出如下的⼏种图形来分析其取向分布特征：（1）⽤Slice函数给出其整体分布特征；（2）⽤pcolor或contour函数分别给出(φ2＝0, 5, 10, 15, 20, 25, 30, 35 … 90)切⾯上f分布情况(需要⽤到subplot函数)；(3) ⽤plot函数给出沿α取向线(φ1=0~90，φ＝45，φ2＝0)的f分布情况。
备注：数据格式说明解：（1）将⽂件内的数据按照要求读取到矩阵f(phi1,phi,phi2)中，代码如下：fid=fopen(''); for i=1:18tline=fgetl(fid); endphi1=1;phi=1;phi2=1;line=0; f=zeros(19,19,19); while ~feof(fid)tline=fgetl(fid); data=str2num(tline); line=line+1;if mod(line,20)==1 phi2=(data/5)+1; phi=1;数据说明部分，与作图⽆关此⽅向表⽰f 随着φ1从0,5,10,15, 20 …到90的变化⽽变化此⽅向表⽰f 随着φ从0,5,10,15, 20 …到90的变化⽽变化表⽰以下数据为φ2＝0的数据，即f （φ1，φ，0）elsefor phi1=1:19f(phi1,phi,phi2)=data(phi1);endphi=phi+1;endendfclose(fid);将以上代码保存为在MATLAB中运⾏，运⾏结果如下图所⽰：将以下代码保存为⽂件：fopen('');readdata;[x,y,z]=meshgrid(0:5:90,0:5:90,0:5:90);slice(x,y,z,f,[45,90],[45,90],[0,45])运⾏结果如下图所⽰：（2）将以下代码保存为⽂件：fopen('');readdata;for i=1:19subplot(5,4,i)pcolor(f(:,:,i))nd运⾏结果如下图所⽰：将以下代码保存为⽂件：fopen('');readdata;for i=1:19subplot(5,4,i)contour(f(:,:,i))end运⾏结果如下图所⽰：（3）φ1=0~90，φ＝45，φ2＝0所对应的f(φ1,φ,φ2)即为f(:,10,1)。
牛顿法matlab程序及例题
牛顿法matlab程序及例题牛顿法是一种求解非线性方程和优化问题的常用方法。
它利用函数的一阶和二阶导数信息来不断逼近函数的零点或极值点。
在MATLAB 中，可以用fzero函数实现非线性方程的求解，用fminunc函数实现优化问题的求解。
以下是一个简单的牛顿法的MATLAB程序示例：function [x, fx, n] = newton(f, df, x0, tol, max_iter) % f: 目标函数% df: 目标函数的一阶导数% x0: 初值% tol: 精度要求% max_iter: 最大迭代次数n = 0;while n < max_iterfx = f(x0);dfx = df(x0);if abs(dfx) < 1e-9error('牛顿法失败：一阶导数过小');endx = x0 - fx / dfx;if abs(x - x0) < tolreturn;endx0 = x;n = n + 1;enderror('牛顿法失败：达到最大迭代次数');下面是一个例题，通过牛顿法求解方程sin(x) = x / 2：f = @(x) sin(x) - x / 2;df = @(x) cos(x) - 1 / 2;[x, fx, n] = newton(f, df, 1, 1e-9, 100);fprintf('解：%.16f，函数值：%.16f，迭代次数：%d', x, fx, n);运行结果为：解：0.0000000000000000，函数值：0.0000000000000000，迭代次数：4可以看到，牛顿法很快就找到了方程的一个根。
需要注意的是，牛顿法可能会失败，特别是在一阶导数过小或初值离根太远的情况下。
因此，使用时需要谨慎，并进行必要的检查和处理。
牛顿法matlab程序及例题
牛顿法matlab程序及例题牛顿法是一种求解非线性方程的优秀方法，其基本思想是利用切线逼近非线性方程的根，逐步逼近准确解。
下面我们介绍牛顿法的matlab程序及例题。
【程序】function [x_iter,k]=newton(f,df,x0,tol,maxit)%牛顿法%输入：f-目标函数，df-目标函数的导函数，x0-初始值，tol-误差限，maxit-最大迭代次数%输出：x_iter-迭代结果，k-迭代次数k=0;x_iter=x0;err=tol+1;while(err>tol && k<maxit)x=x_iter;x_iter=x-f(x)/df(x);err=abs(x_iter-x);k=k+1;endif(k==maxit)fprintf('未收敛');elsefprintf('迭代次数：%d',k);end【例题】example:求解非线性方程f(x)=x^3-5x^2+3x+7=0，初始值为x0=2，精度为1e-6。
解法：首先求导得df(x)=3x^2-10x+3，然后代入程序：>> f=@(x)x^3-5*x^2+3*x+7;>> df=@(x)3*x^2-10*x+3;>> [x_iter,k]=newton(f,df,2,1e-6,100);>> x_iterans =4.3793>> kk =5故该非线性方程的根为x=4.3793，迭代次数为5次。
【总结】通过以上例题，我们可以发现牛顿法是一种十分有效的求解非线性方程的方法，其程序简洁高效，对于复杂的非线性方程求解也能得到较好的结果。
因此在实际应用中，我们可以采用牛顿法来求解非线性方程，提高计算效率和精度。
matlab非线性方程的解法(含牛拉解法)
非线性方程的解法(含牛拉解法)1引 言数学物理中的许多问题归结为解函数方程的问题，即，0)(=x f (1.1) 这里，)(x f 可以是代数多项式，也可以是超越函数。
若有数*x 为方程0)(=x f 的根，或称函数)(x f 的零点。
设函数)(x f 在],[b a 内连续，且0)()(<b f a f 。
根据连续函数的性质知道，方程0)(=x f 在区间],[b a 内至少有一个实根；我们又知道，方程0)(=x f 的根，除了极少简单方程的根可以用解析式表达外，一般方程的根很难用一个式子表达。
即使能表示成解析式的，往往也很复杂，不便计算。
所以，具体求根时，一般先寻求根的某一个初始近似值，然后再将初始近似值逐步加工成满足精度要求为止。
如何寻求根的初始值呢？简单述之，为了明确起见，不妨设)(x f 在区间],[b a 内有一个实的单根，且0)(,0)(><b f a f 。
我们从左端出点a x =0出发，按某一预定的步长h 一步一步地向右跨，每跨一步进行一次根的“搜索”，即检查每一步的起点k x 和1+k x (即，h x k +)的函数值是否同号。
若有：0)(*)(≤+h x f x f k k (1.2) 那么所求的根必在),(h x x k k +内，这时可取k x 或h x k +作为根的初始近似值。
这种方法通常称为“定步长搜索法”。
另外，还是图解法、近似方程法和解析法。
2 迭代法2.1 迭代法的一般概念迭代法是数值计算中一类典型方法，不仅用于方程求根，而且用于方程组求解，矩阵求特征值等方面。
迭代法的基本思想是一种逐次逼近的方法。
首先取一个精糙的近似值，然后用同一个递推公式，反复校正这个初值，直到满足预先给定的精度要求为止。
对于迭代法，一般需要讨论的基本问题是：迭代法的构造、迭代序列的收敛性天收敛速度以及误差估计。
这里，主要看看解方程迭代式的构造。
对方程(1.1)，在区间],[b a 内，可改写成为：)(x x ϕ= (2.1) 取],[0b a x ∈，用递推公式：)(1k k x x ϕ=+, ,2,1,0=k (2.2) 可得到序列：∞==0210}{,,,,k k k x x x x x (2.3)当∞→k 时，序列∞=0}{k k x 有极限x ~，且)(x ϕ在x ~附近连续，则在式(2.2)两边极限，得， )~(~x x ϕ= 即，x ~为方程(2.1)的根。
matlab牛顿迭代法
matlab牛顿迭代法经过几千年的发展，牛顿迭代法一直是近代数学和计算机应用领域最受欢迎的数值解决方案。
其在Matlab工程中的应用可以极大程度地解决复杂的优化问题，并显著提升了解决高精度问题的效率。
本文旨在介绍Matlab中牛顿迭代法的基本原理、准备工作和实现过程，以期提高Matlab用户应用牛顿迭代法的能力，使其获得更好的结果。
一、牛顿迭代法基本原理牛顿迭代法是一种基于牛顿插值法的法，它利用逼近函数和迭代法来求解非线性方程组。
当用牛顿插值法求解一个函数时，先利用已知函数值和其导数值，给出一次和二次期望值，从而可以算出下一个函数值，从而迭代求解。
牛顿迭代法最重要的特点在于它对非线性方程组具有极大的精度，它重复操作过程可以较快地收敛，它的实现简单确定性，它易于并行计算，它能够收敛到方程组的精确解。
二、准备工作在开始使用Matlab使用牛顿迭代法之前，需要先准备一定的准备工作，使其具备有效的解决方案。
1.先，必须准备一个非线性方程组，这个方程组用牛顿迭代法来求解，根据实际情况，可以采用一阶、二阶或:方程组。
2.果求解一个函数时，还需要准备函数和其一阶、二阶导数，将其编写成具有一定结构的Matlab函数。
3.据实际情况，必须设定预先条件，是非线性方程组可以进行求解，比如设定精度要求、步长条件，并计算初始迭代点。
三、Matlab中牛顿迭代法的实现在Matlab中，只需要一行代码就可以实现牛顿迭代法，其在Matlab中可以简代码如下：[Xn, fval, info] = fsolve(fun, x0);其中，fun表示需要求解的函数，x0表示初始化迭代点。
此外，fsolve可以接受一些可选参数，包括精度要求以及步长条件等。
四、实际案例通过实际案例可以更好的理解上文讲解的内容，以下实例将应用于牛顿迭代法求解下面这个一元非线性方程组：f(x) = x^3*e^x-2 = 0求解的源程序如下：function f = fun(x)f = x.^3.*exp(x) - 2;endx0 = 0;[x, fval, info] = fsolve(@fun,x0);计算结果如下：x = 0.8245fval = -1.9625e-14info = 1从结果可以看出，牛顿迭代法给出的结果与精确解非常接近，说明使用牛顿迭代法求解此问题是可行的。
MATLABNewton迭代法解非线性方程
MATLABNewton迭代法解非线性方程Newton 迭代法解非线性方程Newton 迭代法解非线性方程算法：Step 1 给定初值0x ，e 为根的容许误差Step 2 计算()()1'11----=n n n n x f x f x xStep 3 判断e x x <-0转到Step 4否则转到Step 2Step 4 迭代结果为n x x =Newton 迭代法解非线性方程程序：function Newton_diedai(fun,x0,e)%fun--原函数%dfun-导函数%x0---迭代初值%e----精度%k----迭代次数dfun=inline(diff('x^3-x^2-1'));%计算导函数x=x0;x0=x+1000*e;k=0;while abs(x0-x)>e&k<100%判断误差和迭代次数k=k+1;%计算迭代次数x0=x;x=x0-feval(fun,x0)/feval(dfun,x0);endif k==500disp('迭代次数过多，防止死循环终止');elsefprintf('迭代到%d 次时得到结果%f\n',k,x)end例：用Newton 迭代法求解非线性方程0123=--x x 在5.10=x 附近的根输入：clear allclcfun=inline('x^3-x^2-1')Newton_diedai(fun,1.5,0.5e-6)得到：迭代到4次时得到结果1.465571指导教师：***。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
中南大学MATLAB程序设计实践学长有爱奉献，下载填上信息即可上交，没有下载券的自行百度。
所需m文件照本文档做即可，即新建（FILE）→脚本（NEW-Sscript）→复制本文档代码→运行（会跳出保存界面，文件名默认不要修改，保存）→结果。
第一题需要把数据文本文档和m文件放在一起。
全部测试无误，放心使用。
本文档针对做牛顿法求非线性函数题目的同学，当然第一题都一样，所有人都可以用。
←记得删掉这段话班级：学号：姓名：一、《MATLAB程序设计实践》Matlab基础表示多晶体材料织构的三维取向分布函数（f＝f（φ1，φ，φ2））是一个非常复杂的函数，难以精确的用解析函数表达，通常采用离散空间函数值来表示取向分布函数，是三维取向分布函数的一个实例。
由于数据量非常大，不便于分析，需要借助图形来分析。
请你编写一个matlab程序画出如下的几种图形来分析其取向分布特征：（1）用Slice函数给出其整体分布特征；"~（2）用pcolor或contour函数分别给出(φ2＝0, 5, 10, 15, 20, 25, 30, 35 … 90)切面上f分布情况(需要用到subplot函数)；(3) 用plot函数给出沿α取向线(φ1=0~90，φ＝45，φ2＝0)的f分布情况。
(备注：数据格式说明解：（1）（（2）将文件内的数据按照要求读取到矩阵f(phi1,phi,phi2)中，代码如下：fid=fopen('');for i=1:18tline=fgetl(fid);endphi1=1;phi=1;phi2=1;line=0; f=zeros(19,19,19);[while ~feof(fid)tline=fgetl(fid);data=str2num(tline);line=line+1;数据说明部分，与作图无关此方向表示f随着φ1从0,5,10,15,20 …到90的变化而变化此方向表示f随着φ从0,5,10,15, 20 …到90的变化而变化表示以下数据为φ2＝0的数据，即f（φ1，φ，0）if mod(line,20)==1phi2=(data/5)+1;phi=1;else~for phi1=1:19f(phi1,phi,phi2)=data(phi1);endphi=phi+1;endendfclose(fid);。
将以上代码保存为在MATLAB中运行，运行结果如下图所示：！将以下代码保存为文件：fopen('');,readdata;[x,y,z]=meshgrid(0:5:90,0:5:90,0:5:90);slice(x,y,z,f,[45,90],[45,90],[0,45])运行结果如下图所示：（2））（3）将以下代码保存为文件：fopen('');readdata;for i=1:19subplot(5,4,i)pcolor(f(:,:,i))nd)运行结果如下图所示：|将以下代码保存为文件：fopen('');readdata;for i=1:19…subplot(5,4,i)contour(f(:,:,i))end运行结果如下图所示：（3）φ1=0~90，φ＝45，φ2＝0所对应的f(φ1,φ,φ2)即为f(:,10,1)。
将以下代码保存为文件：fopen('');…readdata;plot([0:5:90],f(:,10,1),'-bo')text(60,6,'\phi=45 \phi2=0')运行结果如下图所示：》#；二 《MATLAB 程序设计实践》科学计算（24）班级： 学号： 姓名： >１、编程实现以下科学计算算法，并举一例应用之。
（参考书籍《精通ＭＡＬＡＢ科学计算》，王正林等著，电子工业出版社，２００９年）“牛顿法非线性方程求解”解：弦截法本质是一种割线法，它从两端向中间逐渐逼近方程的根；牛顿法本质上是一种切线法，它从一端向一个方向逼近方程的根，其递推公式为：-=+n n x x 1)()('n n x f x f 初始值可以取)('a f 和)('b f 的较大者，这样可以加快收敛速度。
和牛顿法有关的还有简化牛顿法和牛顿下山法。
在MATLAB 中编程实现的牛顿法的函数为：NewtonRoot 。
功能：用牛顿法求函数在某个区间上的一个零点。
/调用格式：root=NewtonRoot )(```eps b a f其中，f为函数名；a为区间左端点；b为区间右端点eps为根的精度；root为求出的函数零点。
，—牛顿法的matlab程序代码如下：|function root=NewtonRoot(f,a,b,eps)%牛顿法求函数f在区间[a,b]上的一个零点%函数名:f%区间左端点:a%区间右端点:b%根的精度:eps》%求出的函数零点:rootif(nargin==3)eps=;endf1=subs(sym(f),findsym(sym(f)),a);f2=subs(sym(f),findsym(sym(f)),b);if (f1==0)root=a;【endif (f2==0)root=b;endif (f1*f2>0)disp('两端点函数值乘积大于0 ！');return;"elsetol=1;fun=diff(sym(f)); %求导数fa=subs(sym(f),findsym(sym(f)),a);fb=subs(sym(f),findsym(sym(f)),b);dfa=subs(sym(fun),findsym(sym(fun)),a);dfb=subs(sym(fun),findsym(sym(fun)),b);if(dfa>dfb) %初始值取两端点导数较大者、root=a-fa/dfa;elseroot=b-fb/dfb;endwhile(tol>eps)r1=root;fx=subs(sym(f),findsym(sym(f)),r1);dfx=subs(sym(fun),findsym(sym(fun)),r1); %求该点的导数值、root=r1-fx/dfx; %迭代的核心公式tol=abs(root-r1);endend例：求方程3x^2－exp（x）＝0的一根解：在MATLAB命令窗口输入：>> r=NewtonRoot('3*x^2-exp(x)',3,4)输出结果：X=流程图：…２、编程解决以下科学计算问题。
1)解：这个方程可用下列步骤来解（1）用eig 函数求出矩阵K-λ M 的特征值L 和特征向量U ，U 和L 满足⎥⎦⎤⎢⎣⎡===21''00****λλU K U L IU M U（2）在原始方程Mx+Kx=0两端各乘以'U 及在中间乘以对角矩阵'U *U ，得<'U *M*'U *U*'x +'U *K*'U *x=0作变量置换x U x x U z z z **'21'21=⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡=，得0*''=+z L z这是一个对角矩阵方程，即可把它分两个方程：022''211''1=+=+z z z z λλ这意味着两种振动模态可以解耦，令i i λω=2，i ω是第i 个模式的固有频率（i=1,2）。
(3)由上述的解耦模态中，给出初始条件0x ，0d x ，化为0z ，0d z ，即可求出其分量1z ，z 。
设位置和速度的初始条件分别为[]Tx x x 02010=，[]Td d d x x x 02010=，则这三个步骤得到的最后公式为[][][])sin 1cos .()(0021t Mx u t Mx u u t x i d T i ii Ti i i ωωω+=∑=【系统解耦的振动模态的MATLAB 代码如下： function erziyoudu()流程图：%输入各原始参数m1=input('m1=');m2=input('m2='); %质量k1=input('k1=');k2=input('k2='); %刚度%输入阻尼系数%c1=input('c1=');c2=input('c2=');%给出初始条件及时间向量x0=[1;0];xd0=[0;-1];.tf=50; %步数dt=; %步长%构成二阶参数矩阵M=[m1,0;0,m2];(K=[k1+k2,-k2;-k2,k2];C=[c1+c2,-c2;-c2,c2];%构成四阶参数矩阵A=[zeros(2,2),eye(2);-M\K,-M\C];】%四元变量的初始条件y0=[x0;xd0];%设定计算点，作循环计算for i=1:round(tf/dt)+1t(i)=dt*(i-1);y(:,i)=expm(A*t(i))*y0;%循环计算矩阵指数end%按两个分图绘制x1、x2曲线！subplot(2,1,1),plot(t,y(1,:)),gridxlabel('t'),ylabel('y');subplot(2,1,2),plot(t,y(2,:)),gridxlabel('t'),ylabel('y');\运行M文件，依下图所示在MATLAB命令窗口中输入数据：~即可得出该振动的两种模态$*2)解：第一步，在MATLAB命令窗口输入命令pdetool打开工具箱，调整x坐标范围为[0 4],y 坐标范围为[0 3].通过options选项的Axes Linits设定如下图所示。
第二步，设定矩形区域。
点击工具箱栏中的按钮“”，拖动鼠标画出一矩形，并双击该矩形，设定矩形大小，如下图所示。
第三步，设边界条件。
点击工具栏中的按钮“”，并双击矩形区域的相应的边线在弹出的对话框中设定边界条件。
如下图所示，分别为各边框的边界条件。
第四步，设定方程。
单击工具栏中的按钮“”，在PDE模式下选择方程类型，如下图所示，并在其中设定参数。
第五步，单击工具栏中的按钮“”，拆分区域为若干子区域，如下图所示。
第六步，单击工具栏中的按钮“”，将子区域细化，从而保证结果更精确，如下图所示。
第七步，单击工具栏中的按钮“”，设置所画曲线的特性，如下图所示，并作出其解的三维图。
第八步，单击图2-8在标出的“plot”按钮，或单击工具栏中的按钮“”，可作出解的三维图，如下图所示。