材料力学内力图绘制详解.pdf
材料力学内力图绘制详细讲解
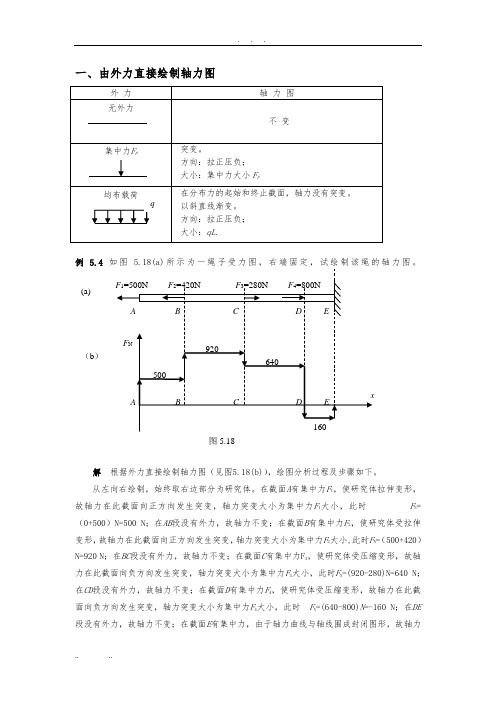
一、由外力直接绘制轴力图例 5.4 力图。
解 根据外力直接绘制轴力图(见图5.18(b)),绘图分析过程及步骤如下。
从左向右绘制,始终取右边部分为研究体。
在截面A 有集中力F 1,使研究体拉伸变形,故轴力在此截面向正方向发生突变,轴力突变大小为集中力F 1大小,此时 F N =(0+500)N=500 N ;在AB 段没有外力,故轴力不变;在截面B 有集中力F 2,使研究体受拉伸变形,故轴力在此截面向正方向发生突变,轴力突变大小为集中力F 2大小,此时F N =(500+420)N=920 N ;在BC 段没有外力,故轴力不变;在截面C 有集中力F 3,使研究体受压缩变形,故轴力在此截面向负方向发生突变,轴力突变大小为集中力F 3大小,此时F N =(920-280)N=640 N ;在CD 段没有外力,故轴力不变;在截面D 有集中力F 4,使研究体受压缩变形,故轴力在此截面向负方向发生突变,轴力突变大小为集中力F 4大小,此时 F N =(640-800)N =-160 N ;在DE 段没有外力,故轴力不变;在截面E 有集中力,由于轴力曲线与轴线围成封闭图形,故轴力(b )(a)突变为0。
例5.5有一根阶梯轴受力如图5.19(a)所示,试绘制阶梯轴的轴力图。
图5.19解从右向左绘制,始终取左变部分为研究体。
根据外力直接绘制轴力图(见图5.19(b)),绘图分析过程及步骤如下:在截面A有集中力F1,使研究体压缩变形,故轴力在此截面向负方向发生突变,轴力突变大小为集中力F1大小,此时F N=(0-10)kN=-10 kN;在AB段有均匀分布载荷,使研究体受拉伸变形,故轴力以斜直线规律向正方向渐变,轴力渐变大小为均匀分布载荷大小,此时F N=(-10+10×2)kN=10 kN;在截面B没有力,故此截面轴力没有变化;在BC段没有外力,故轴力不变;在截面C有集中力F2,使研究体受拉伸变形,故轴力在此截面向正方向发生突变,轴力突变大小为集中力F2大小,此时F N=(10+10)kN=20 kN;在CD段没有外力,故轴力不变;在截面D有集中力,由于轴力曲线与轴线围成封闭图形,故轴力突变为0.二、由外力直接绘制扭矩图外力扭矩图无外力不变集中力F P突变。
材料力学第3讲-绘制梁内力图的基本方法

用函数关系表示沿梁轴线各横截面上剪力和弯矩的变化规律, 分别称作剪力方程和弯矩方程.
①剪力方程(Shear- force equation)
FS= FS(x)
②弯矩方程(Bending-moment equation)
构件受弯时,横截面上其作用面垂直于截
面的内力偶矩.
FRAy
m
m
FS M
C
②剪力(Shear force) FS
构件受弯时,横截面上其作用线平行于截面 的内力.
M C
FS
F B
FRB
F FRB
2)梁的内力的正负号规定 (Sign convention for internal force)
m FS
①剪力的正负号规定
左侧梁段 顺时针转向的外力偶引起正值的弯矩 逆时针转向的外力偶引起负值的弯矩
右侧梁段 逆时针转向的外力偶引起正值的弯矩 顺时针转向的外力偶引起负值的弯矩
【例题2-3-4】轴的计例算简图如图所示,已知 F1 = F2 = F = 60kN, a = 230mm,b = 100 mm 和c = 1000 mm. 求 C 、D 点处横截面
M= M(x)
2)剪力图和弯矩图(Shear-force & bending-moment diagrams)
以平行于梁轴的横坐标x表示横截面的位置,以纵坐标表示相
应截面上的剪力和弯矩.这种图线分别称为剪力图和弯矩图 FS(x)
x O
O
x
FS 图的坐标系
M(x) M 图的坐标系
剪力图为正值画在 x 轴上侧,负值画在x 轴下侧
材料力学 弯曲内力图(2)

集中力偶
m C
Q
图 特 征
水平直线
Q Q Q
斜直线
Q x x
自左向右突变
Q Q 1 C x
无变化
Q C x
x
Q>0 Q<0
x
斜直线 M M2 图 x 与 x x x x x 特 m 征 M 反 M M1 M M M M 增函数 降函数 坟状 盆状 折向与P反向 向 M1 - M 2 = m
160
kNm
130
210
340
280
4.9 å m = 0
Ai
例题 &
解:(1)求支反力:
m=160kN
P=20kN q=20kN/m
A
ÞLeabharlann D B E
1 R = ( 20 ´ 12 + 20 ´ 10 ´ 7 - 160 ) = 148 kN ( -) B 10 å m Bi = 0 Þ 1 Y = ( 160 + 20 ´ 10 ´ 3 - 20 ´ 2 ) = 72 kN ( -) A 10 校核 : å Y OK ! ) i = Y A + R B - 20 ´ 10 - 20 = 0 (
(+) O
9a / 4
4a 4a
a F By 3
qa
= qa 4 当FS = 0时; x = 9a / 4; M max = 81qa 2 / 32
x 3.建立坐标系建立
()
7qa / 4
O
81 qa 2 / 32
qa
FS-x和M-x坐标系
4.确定控制面上的剪 x 力值,并将其标在 FS-x中。 5.确定控制面上的 弯矩值,并将其标在 M-x中。
材料力学基本第二章 内力与内力图

CB段: BA段:
FN x1 0
FQ x1 F
M x1 Fx1
FN x2 F
FQ x2 0
M x2 F a
0 x1 a
0 x1 a
0 x1 a 0 x2 l
0 x2 l
0 x2 l
2.绘制剪力图和弯矩图
五、平面曲杆的内力图
平面曲杆:轴线为平面曲线的杆件。 内力的符号规定为:弯矩以使曲杆轴线曲率增加者为正,轴力和剪力的符 号规定与前面的相同。
2.6 结论与讨论
结
结论
论 与
• 一个重要概念
讨 论
• 三个微分方程
结
• 一套方法
论
讨论
结
论
与
比较前面三个梁的受力、剪力
讨 论
和弯矩图的相同 之处和不同
之处,从中能得到什么重要结
讨
论?
论
FQ
结
论
与
讨
FQ
论
讨
FQ
论
确定控
结 论 与 讨
制面上剪力 和弯矩有几 种方法?怎
论 样确定弯矩
图上极值点
讨 处的弯矩数
4. 在梁的某一截面上剪力为零,则在这一截面上弯矩有极值。
5. 在梁的某一截面上若作用有集中力,则此处剪力图有突变,突变的值 恰好等于集中力的数值。
6. 在梁的某一截面上若作用有集中力偶,则剪力图不发生变化,但此处 弯矩图会发生突变,突变的值恰好等于集中力偶的数值。
二、剪力、弯矩与载荷集度之间的积分关系
AD段 MeD T3 0
C
d) T3
D
T /Nm
T3 MeD 1018.6 N m e)
1018.6 (+)
材料力学--第2章杆件的内力与内力图

轴力图的画法
画轴力图的步骤:求约束反力、求控制截面上的轴 力、画轴力图。 求任一横截面轴力的简便方法:任一横截面上的轴 力等于该截面一侧杆件上所有外力(包括反力)的代数和; 外力背离截面产生拉力,外力指向截面产生压力。 在分布轴向外力作用下,轴力图为斜直线或曲线。 没有分布轴向外力作用时,整个杆件轴力图为平行于杆件
外加扭力矩Me确定后,应用截面法可以确定横截面上 的内力──扭矩,圆轴两端受外加扭力矩Me作用时,横截 面上将产生分布剪应力,这些剪应力将组成对横截面中心 的合力矩,称为扭矩(twist moment),用Mx表示。
Me Me
Me
Mx
n
- 右手螺旋定则
第2章 杆件的内力和内力图
◎ 扭矩与扭矩图
如果只在轴的两个端截面作用有外力偶矩,则沿轴线 方向所有横截面上的扭矩都是相同的,并且都等于作用在 轴上的外力偶矩。 当轴的长度方向上有两个以上的外力偶矩作用时,轴
D
E
2
FA
40kN
FN2
F
x
0, FN2 FA 40 0, FN2 50kN(拉)
第2章 杆件的内力和内力图
求CD段内的轴力
◎ 轴力与轴力图
FA
A
40kN B
55kN
25kN
20kN
C
3
D
E
FN3
25kN
20kN
F
x
0, FN3 25 20 0, FN3 5kN(压)
第2章 杆件的内力和内力图
同理,求得AB、 BC、CD段内力分 别为: FN2 B FB FN3 C FC C FC FN4 FN 2F 5F
◎ 轴力与轴力图
任务十五梁的内力图绘制

任务十五
梁的内力图绘制
任务十五
梁的内力图绘制
3、利用内力方程画内力图
AB段:坐标原点取在左端A点处,距原点A为x1处的任意截面, 其剪力方程和弯矩方程为
Q(x1)=RA-qx1=1.5qa-qx1(0<x1<4a) M(x1)=RAx1-qx21/2=3qa/2x1-q/2x12 (0≤x1≤4a) BC段:坐标原点取在右端C点处,距原点C为x2处的任意截面, 其剪力方程和弯矩方程为 Q(x2)=qx2(0≤x2<2a)
x=a,MC=Pab/l
x=l,MB=0
任务十五
梁的内力图绘制
3、利用内力方程画内力图
从所作的内力图知,若a>b,则在CB段任一截面上的剪力值都 相等且比AC段的要大,其值|Qmax|=Pa/l,最大弯矩发生在集中力 P作用的截面上,其值|Mmax|=Pab/l 如果集中力P作用在梁的跨中,即a=b=l/2 |Qmax|=P/2 |Mmax|=Pl/4
为了形象地表示剪力和弯矩沿梁轴的变化规律,把剪 力方程和弯矩方程用其图像表示,称为剪力图和弯矩图。 剪力图和弯矩图的画法与轴力图、扭矩图很相似,用平 行于梁轴的横坐标x表示梁横截面的位置,用垂直于梁轴 的纵坐标表示相应截面的剪力和弯矩。 在土建工程中,习惯上将正剪力画在x轴上方,负剪 力画在x轴的下方;正弯矩画在x轴下方,负弯矩画在x轴 的上方,即把弯矩图画在梁受拉的一侧。
材料力学第4讲-利用微分关系绘制梁内力图

在CD和DB段,剪力为负值,弯矩图
1.7 为向下倾斜的直线.
最大弯矩发生在剪力改变正、负号的 C
截面处.说明剪力图和弯矩图是正确的.
27 +
例题3-4-2 一简支梁受均布荷载作用,其集度 q=100kN/m ,如图 所示.试用简
易法作此梁的剪力图和弯矩图. 解:(1) 计算梁的支反力
FRA FRB 0.5 100 1.6 80kN
(1)梁的载荷集度函数、剪力函数和弯矩函数之间的 微分关系
(2)利用微分关系的绘制简单梁的内力图 (3)利用微分关系绘制多跨静定的内力图 (4)根据梁的内力图反推梁的荷载图 2.5 应用叠加原理绘制梁的内力图(待学习) 2.6 刚架和组合变形杆件的内力分析(待学习)
2.4 利用微分关系绘制梁的内力图
dFS ( x) q( x) dx
dM ( x) dx
FS
(
x)
(3)内力的极值点位置的判断 1)最大剪力可能发生在集中力所在截面的一侧;或
发生在剪力图有转折的截面处或杆件的端部.
2)梁上最大弯矩 Mmax可能发生在均布荷载作用区段 内FS(x) = 0 的截面上; 或发生在杆件中部弯矩发生
转折或突变处,或发生在杆件的端部。
将梁分为 AC、CD、DB 三段.
AC和DB上无荷载,CD 段有向下的
均布荷载.
(2)剪力图 AC段 水平直线
FSA右 FRA 80kN
CD段 向右下方的斜直线
FRA
A C
0.2 1
FS
(kN)
80
q
FRB
B
D
1.6
2
+
FSC FRA 80kN
FSD FRB 80kN
材料力学内力图绘制详解
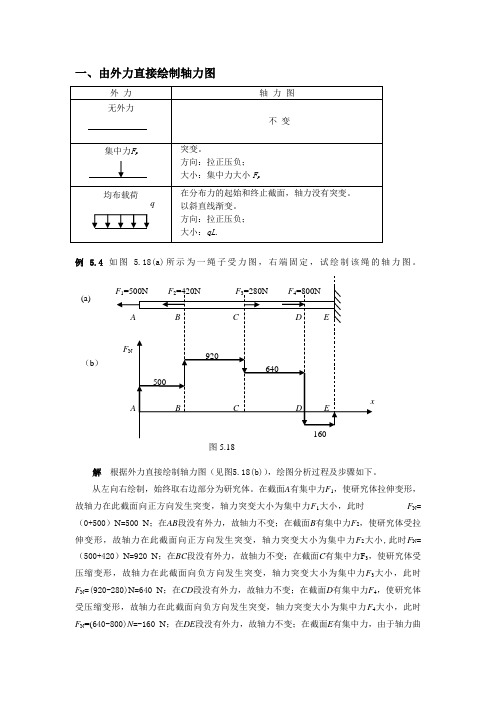
一、由外力直接绘制轴力图例 5.4 如图 5.18(a)所示为一绳子受力图,右端固定,试绘制该绳的轴力图。
解 根据外力直接绘制轴力图(见图5.18(b)),绘图分析过程及步骤如下。
从左向右绘制,始终取右边部分为研究体。
在截面A 有集中力F 1,使研究体拉伸变形,故轴力在此截面向正方向发生突变,轴力突变大小为集中力F 1大小,此时 F N =(0+500)N =500 N ;在AB 段没有外力,故轴力不变;在截面B 有集中力F 2,使研究体受拉伸变形,故轴力在此截面向正方向发生突变,轴力突变大小为集中力F 2大小,此时F N =(500+420)N =920 N ;在BC 段没有外力,故轴力不变;在截面C 有集中力F 3,使研究体受压缩变形,故轴力在此截面向负方向发生突变,轴力突变大小为集中力F 3大小,此时F N =(920-280)N =640 N ;在CD 段没有外力,故轴力不变;在截面D 有集中力F 4,使研究体受压缩变形,故轴力在此截面向负方向发生突变,轴力突变大小为集中力F 4大小,此时 F N =(640-800)N =-160 N ;在DE 段没有外力,故轴力不变;在截面E 有集中力,由于轴力曲(b )(a)线与轴线围成封闭图形,故轴力突变为0。
例5.5有一根阶梯轴受力如图5.19(a)所示,试绘制阶梯轴的轴力图。
图5.19解从右向左绘制,始终取左变部分为研究体。
根据外力直接绘制轴力图(见图5.19(b)),绘图分析过程及步骤如下:在截面A有集中力F1,使研究体压缩变形,故轴力在此截面向负方向发生突变,轴力突变大小为集中力F1大小,此时F N=(0-10)kN=-10 kN;在AB段有均匀分布载荷,使研究体受拉伸变形,故轴力以斜直线规律向正方向渐变,轴力渐变大小为均匀分布载荷大小,此时F N=(-10+10×2)kN=10 kN;在截面B没有力,故此截面轴力没有变化;在BC段没有外力,故轴力不变;在截面C有集中力F2,使研究体受拉伸变形,故轴力在此截面向正方向发生突变,轴力突变大小为集中力F2大小,此时F N=(10+10)kN=20 kN;在CD段没有外力,故轴力不变;在截面D有集中力,由于轴力曲线与轴线围成封闭图形,故轴力突变为0.二、由外力直接绘制扭矩图制其内力图。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(a)
F1=500N F2=420N
A
B
F3=280N C
F4=800N DE
FN (b)
920 640
500
A
B
C
x DE
-160 图 5.18
解 根据外力直接绘制轴力图(见图5.18(b)),绘图分析过程及步骤如下。
从左向右绘制,始终取右边部分为研究体。在截面A有集中力F1,使研究体拉伸变形,
故轴力在此截面向正方向发生突变,轴力突变大小为集中力F1大小,此时
2
二、由外力直接绘制扭矩图
外力 无外力
扭矩图 不变
集中力FP
突变。 方向:右手螺旋法则,四指指向外力偶方向,拇指离开为正; 大小:集中力偶大小 FP
均布力偶 Mq
在分布力的起始和终止截面,扭矩没有突变。 以斜直线渐变。
方向:右手螺旋法则,四指指向外力偶方向,拇指离开为正;
大小:Mq
例5.7 如图5.24(a)所示圆轴,左端固定、右端自由,受到三个集中力偶作用,试绘
例5.11 如图5.29(a)所示外伸梁,试计算其内力并画出内力图。
图5.29
解 (1)先求支座反力。取整段梁研究,其受力如图5.29(a),由平衡条件得
中力偶M3大小 M x = (−1+ 3) = 2 kN • m ;在CD段有无外载荷,故扭矩不变;在截面D有集
中力,由于扭矩曲线与轴线围成封闭图形,故扭矩突变为零。扭矩图如图5.25(b)所示。
3
三、由外力直接绘制剪力图和弯矩图
载荷 无外力
集中力
剪力、弯矩与分布载荷间的关系
Fe图
M图
FQ=0,M不变;FQ≠0,M 以斜
直线变化,从起始点到终点,大
不变
小为FQ与x轴围成的面积,变化方 向FQ为正,向正向渐变,否则向
负向渐变
突变,方向与FP相同, 大小为FP
无变化
集中力偶M
均布载荷 q
不变
突变,突变大小为M,突变方向
力偶
(顺时针方向时)为
正向;力偶
(逆时针方向
时)为负向
以斜直线渐变,方向 以抛物线渐变,FQ=0处,为极值,
一、由外力直接绘制轴力图
外力 无外力
轴力图 不变
集中力FP
均布载荷 q
突变。 方向:拉正压负; 大小:集中力大小 FP
在分布力的起始和终止截面,轴力没有突变。 以斜直线渐变。 方向:拉正压负; 大小:qL.
例 5.4 如 图 5.18(a) 所 示 为 一 绳 子 受 力 图 , 右 端 固 定 , 试 绘 制 该 绳 的 轴 力 图 。
AB段无外载荷,故扭矩不变;在截面B有集中力偶M2,变形方向由右手螺旋法则判断,拇指 指向截面,故扭矩在此截面向负方向发生突变,扭矩突变大小为集中力偶 M2大小此时
Mx=1-2=-1 kN • m ;在BC段无外载荷,故扭矩不变;在截面C有集中力偶M3,变形方向由
右手螺旋法则判断,拇指背离截面,故扭矩在此截面向正方向发生突变,扭矩突变大小为集
与q一致,大小为ql
按面积计算M值变化大小
例5.10 如图5.28(a)所示,简支梁AB,在C点承受集中载荷F=6 kN作用,跨度l=3 m,
a = 2 m ,试绘制梁的内力图。
4
解 (1)求支座反力。取整段梁为研究对象,受力分析如图5.28(b),由平衡条件得
MA (F) = 0 FB l − F a = 0
FA • a = 4 kN • m ;在截面C有一向下的集中载荷F,故在此截面剪力向下突变F,弯矩
没有变化;在CB段没有外力,故剪力在该段没有变化,由剪力小于零,则该段弯矩以斜直
5
线规律 向负向变化,从截面 C到 截面B弯矩变化大小为 CB段剪力与 x轴围成的 面积即
FB • (l − a) = 4 kN • m 变为0。
FN=(640-800)N=-160 N;在DE段没有外力,故轴力不变;在截面E有集中力,由于轴力曲
1
线与轴线围成封闭图形,故轴力突变为0。 例5.5 有一根阶梯轴受力如图5.19(a)所示,试绘制阶梯轴的轴力图。
图 5.19 解 从右向左绘制,始终取左变部分为研究体。根据外力直接绘制轴力图(见图 5.19(b)),绘图分析过程及步骤如下: 在截面A有集中力F1,使研究体压缩变形,故轴力在此截面向负方向发生突变,轴力突 变大小为集中力F1大小,此时FN=(0-10)kN=-10 kN;在AB段有均匀分布载荷,使研究体 受拉伸变形,故轴力以斜直线规律向正方向渐变,轴力渐变大小为均匀分布载荷大小,此时 FN=(-10+10×2)kN=10 kN;在截面B没有力,故此截面轴力没有变化;在BC段没有外力, 故轴力不变;在截面C有集中力F2,使研究体受拉伸变形,故轴力在此截面向正方向发生突 变,轴力突变大小为集中力F2大小,此时FN=(10+10)kN=20 kN;在CD段没有外力,故轴 力不变;在截面D有集中力,由于轴力曲线与轴线围成封闭图形,故轴力突变为0.
FN=
(0+500)N=500 N;在AB段没有外力,故轴力不变;在截面B有集中力F2,使研究体受拉 伸变形,故轴力在此截面向正方向发生突变,轴力突变大小为集中力 F2大小,此时FN= (500+420)N=920 N;在BC段没有外力,故轴力不变;在截面C有集中力F3,使研究体受
压缩变形,故轴力在此截面向负方向发生突变,轴力突变大小为集中力F3大小,此时 FN=(920-280)N=640 N;在CD段没有外力,故轴力不变;在截面D有集中力F4,使研究体 受压缩变形,故轴力在此截面向负方向发生突变,轴力突变大小为集中力 F4大小,此时
制其内力图。
图5.25 解 从右向左绘制,始终取左部分为研究体。根据外力偶直接绘制扭矩图,绘制分析过 程及步骤如下: 在截面A有集中力偶M1,变形方向由右手螺旋法则判断,拇指背离截面,故扭矩在此截
面向正方向发生突变,扭矩突变大小为集中力偶M1大小,此时 Mx = (0 +1) =1 kN• m ;在
解得
FB = 4 kN
Fy = 0 FA + FB − F = 0
解得
FA = 2 kN
(2)由外力直接绘制内力图。 从A截面开始,有一向上的集中力FA,故在此截面剪力向上突变,突变大小等于FA,弯 矩没有变化;AC段没有外力,故剪力在该段没有变化,由于剪力大于零,故在该段弯矩以 斜直线规律向正向变化,从截面A到截面C弯矩变化大小为AC段剪力与x轴围成的面积即
