材料力学内力图绘制详解
材料力学专题一梁的内力和内力图

专题一 梁的内力和内力图例1求图1(a)所示梁截面 A 、C 的剪力和弯矩。
解:1)求反力kN 5=A F ,kN 4=B F2)求A 左截面的内力,如图(a)所示。
0=∑i Y , 0=+左SA p F F ,kN 3-=左SA F0=∑O M ,02=+⨯左A p M F , m kN 6⋅-=左A M3)求A 右截面的内力,如图(b)所示。
0=∑i Y ,0=+--A SA p F F F 左,kN 2=左SA F0=∑O M ,02=+⨯右A p M F , m kN 6⋅-=右A M4)求C 左截面的内力,如图(c)所示。
0=∑i Y ,02=-⨯--左SC P A F q F F ,0=左SC F0=∑O M ,01224=+⨯⨯+⨯-⨯左C A p M q F F ,=左C M m kN 4⋅-=5)求C 右截面的内力,如图(d)所示。
0=∑i Y ,02=-⨯--右SC P A F q F F ,0235=--=右SC F 0=∑O M ,012241=++⨯⨯+⨯-⨯右C A p M M q F F ,=右C M m kN 6⋅-=【小结】①求指定截面上的内力时,既可取梁的左段为脱离体,也可取右段为脱离体,两者计算结果一致。
一般取外力比较简单的一段进行分析。
②在解题时,通常假设截面上把内力为正,若最后计算结果是正,则表示假设的内力方向(转向)与实际是相同的,否则是相反的。
③该题也可以不画受力图,不写平衡方程而由前面的结论直接求得结果。
图1(a)(b)(c)(d) (e)例2试计算图2所示各梁指定截面(标有细线者)的剪力与弯矩。
解:(a)取A +截面左段研究,, 0SA A F F M ++==取C 截面左段研究,, 2SC C Fl F F M == 取B -截面左段研究, , SB BF F M Fl ==(b) 求A 、B 处约束反力如图(d)所示,l M F F e B A /==取A +截面左段研究,, e SA A A e M F F M M l++=-=-=取C 截面左段研究,, 22e e SC A A e A M Ml F F M M F l +=-=-=-⨯=取B 截面右段研究,, 0e SB B B MF F M l=-=-=(c) 求A 、B 处约束反力 取A +截面右段研究,233, 22248SA A l ql l l ql F q M q ++=⨯==-⨯⨯=-取C -截面右段研究,2, 22248SC C l ql l l ql F q M q --=⨯==-⨯⨯=-取C +截面右段研究,2, 22248SC C l ql l l ql F q M q ++=⨯==-⨯⨯=-取B -截面右段研究,0, 0SB B F M --==图2 (b) (a) qB (c) B图(d)例3试写出图3所示梁的内力方程,并画出剪力图和弯矩图。
计算内力与画内力图的技巧

OCCUPATION2012 0926交流E XPERIENCE计算内力与画内力图的技巧余瀚欣 夏志娟 韩美娥 余茂武在材料力学四种基本变形的学习中,计算内力与画内力图是各种基本变形强度与刚度计算的基础。
一般情况下构件不同截面上的内力是不同的,内力随横截面位置而变化。
由于在进行强度与刚度计算时,需要知道各横截面上内力的最大值以及所在截面位置即危险面,因此必须知道内力随截面变化的规律。
为了便于形象直观地看到内力的变化规律,通常是将内力沿构件轴线的变化用图形来表示,这种图形称为内力图。
计算内力画内力图,是每位学者都觉得很头疼的事,而职业院校的学生由于基础相对薄弱学起来就更难,因此对其技巧的探索与研究势在必行。
有不少从教者做了很大的努力,总结不少好的方法,但相比本文介绍的方法还是麻烦了点。
本文介绍的方法简便易行,学生易于接受,增强了学习的主动性和积极性。
下面以三种不同的方法计算扭转变形时的内力、画内力图为例,通过比较说明第三种方法的可行性、简便性与实用性。
例:一传动轴如图1所示。
已知其上作用有外力偶m 1=100Nm,m 2=50Nm,m 3=20KNm,m 4=30Nm,试求轴的扭矩,并画出扭矩图。
一、第一种方法:截面法1.计算轴各段扭矩(见图1)AB 段:Σm x =0,m 2+M n 1=0,M n 1=-m 2=-50Nm (取截面以左分析)BC 段:Σm x =0,m 2+m 3+M n 2=0,M n 2=-m 2-m 3=-70Nm (取截面以左分析)CD 段:Σm x =0,m 4-M n 3=0,M n 3=+m 4=-30Nm (取截面以右分析)1-1,2-2截面扭矩计算出现负值,说明图1中b )、c )中的假设的扭矩转向与实际相反,实际扭矩矢量方向与横截面的外法线方向相反。
按扭矩正负符号规定,该扭矩为负。
3-3截面扭矩计算出现正值,说明图1d )中的假设的扭矩转向与实际相同,实际扭矩矢量方向与横截面的外法线方向相同。
材料力学基本第二章 内力与内力图

CB段: BA段:
FN x1 0
FQ x1 F
M x1 Fx1
FN x2 F
FQ x2 0
M x2 F a
0 x1 a
0 x1 a
0 x1 a 0 x2 l
0 x2 l
0 x2 l
2.绘制剪力图和弯矩图
五、平面曲杆的内力图
平面曲杆:轴线为平面曲线的杆件。 内力的符号规定为:弯矩以使曲杆轴线曲率增加者为正,轴力和剪力的符 号规定与前面的相同。
2.6 结论与讨论
结
结论
论 与
• 一个重要概念
讨 论
• 三个微分方程
结
• 一套方法
论
讨论
结
论
与
比较前面三个梁的受力、剪力
讨 论
和弯矩图的相同 之处和不同
之处,从中能得到什么重要结
讨
论?
论
FQ
结
论
与
讨
FQ
论
讨
FQ
论
确定控
结 论 与 讨
制面上剪力 和弯矩有几 种方法?怎
论 样确定弯矩
图上极值点
讨 处的弯矩数
4. 在梁的某一截面上剪力为零,则在这一截面上弯矩有极值。
5. 在梁的某一截面上若作用有集中力,则此处剪力图有突变,突变的值 恰好等于集中力的数值。
6. 在梁的某一截面上若作用有集中力偶,则剪力图不发生变化,但此处 弯矩图会发生突变,突变的值恰好等于集中力偶的数值。
二、剪力、弯矩与载荷集度之间的积分关系
AD段 MeD T3 0
C
d) T3
D
T /Nm
T3 MeD 1018.6 N m e)
1018.6 (+)
材料力学--第2章杆件的内力与内力图

轴力图的画法
画轴力图的步骤:求约束反力、求控制截面上的轴 力、画轴力图。 求任一横截面轴力的简便方法:任一横截面上的轴 力等于该截面一侧杆件上所有外力(包括反力)的代数和; 外力背离截面产生拉力,外力指向截面产生压力。 在分布轴向外力作用下,轴力图为斜直线或曲线。 没有分布轴向外力作用时,整个杆件轴力图为平行于杆件
外加扭力矩Me确定后,应用截面法可以确定横截面上 的内力──扭矩,圆轴两端受外加扭力矩Me作用时,横截 面上将产生分布剪应力,这些剪应力将组成对横截面中心 的合力矩,称为扭矩(twist moment),用Mx表示。
Me Me
Me
Mx
n
- 右手螺旋定则
第2章 杆件的内力和内力图
◎ 扭矩与扭矩图
如果只在轴的两个端截面作用有外力偶矩,则沿轴线 方向所有横截面上的扭矩都是相同的,并且都等于作用在 轴上的外力偶矩。 当轴的长度方向上有两个以上的外力偶矩作用时,轴
D
E
2
FA
40kN
FN2
F
x
0, FN2 FA 40 0, FN2 50kN(拉)
第2章 杆件的内力和内力图
求CD段内的轴力
◎ 轴力与轴力图
FA
A
40kN B
55kN
25kN
20kN
C
3
D
E
FN3
25kN
20kN
F
x
0, FN3 25 20 0, FN3 5kN(压)
第2章 杆件的内力和内力图
同理,求得AB、 BC、CD段内力分 别为: FN2 B FB FN3 C FC C FC FN4 FN 2F 5F
◎ 轴力与轴力图
材料力学第4讲-利用微分关系绘制梁内力图

在CD和DB段,剪力为负值,弯矩图
1.7 为向下倾斜的直线.
最大弯矩发生在剪力改变正、负号的 C
截面处.说明剪力图和弯矩图是正确的.
27 +
例题3-4-2 一简支梁受均布荷载作用,其集度 q=100kN/m ,如图 所示.试用简
易法作此梁的剪力图和弯矩图. 解:(1) 计算梁的支反力
FRA FRB 0.5 100 1.6 80kN
(1)梁的载荷集度函数、剪力函数和弯矩函数之间的 微分关系
(2)利用微分关系的绘制简单梁的内力图 (3)利用微分关系绘制多跨静定的内力图 (4)根据梁的内力图反推梁的荷载图 2.5 应用叠加原理绘制梁的内力图(待学习) 2.6 刚架和组合变形杆件的内力分析(待学习)
2.4 利用微分关系绘制梁的内力图
dFS ( x) q( x) dx
dM ( x) dx
FS
(
x)
(3)内力的极值点位置的判断 1)最大剪力可能发生在集中力所在截面的一侧;或
发生在剪力图有转折的截面处或杆件的端部.
2)梁上最大弯矩 Mmax可能发生在均布荷载作用区段 内FS(x) = 0 的截面上; 或发生在杆件中部弯矩发生
转折或突变处,或发生在杆件的端部。
将梁分为 AC、CD、DB 三段.
AC和DB上无荷载,CD 段有向下的
均布荷载.
(2)剪力图 AC段 水平直线
FSA右 FRA 80kN
CD段 向右下方的斜直线
FRA
A C
0.2 1
FS
(kN)
80
q
FRB
B
D
1.6
2
+
FSC FRA 80kN
FSD FRB 80kN
材料力学内力图绘制详解
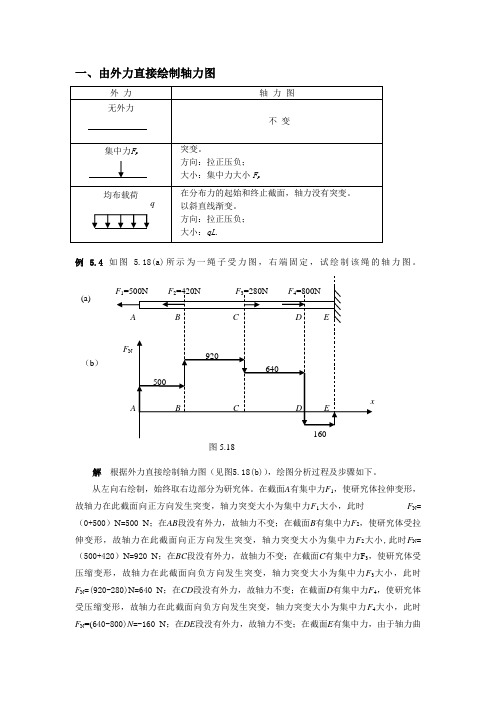
一、由外力直接绘制轴力图例 5.4 如图 5.18(a)所示为一绳子受力图,右端固定,试绘制该绳的轴力图。
解 根据外力直接绘制轴力图(见图5.18(b)),绘图分析过程及步骤如下。
从左向右绘制,始终取右边部分为研究体。
在截面A 有集中力F 1,使研究体拉伸变形,故轴力在此截面向正方向发生突变,轴力突变大小为集中力F 1大小,此时 F N =(0+500)N =500 N ;在AB 段没有外力,故轴力不变;在截面B 有集中力F 2,使研究体受拉伸变形,故轴力在此截面向正方向发生突变,轴力突变大小为集中力F 2大小,此时F N =(500+420)N =920 N ;在BC 段没有外力,故轴力不变;在截面C 有集中力F 3,使研究体受压缩变形,故轴力在此截面向负方向发生突变,轴力突变大小为集中力F 3大小,此时F N =(920-280)N =640 N ;在CD 段没有外力,故轴力不变;在截面D 有集中力F 4,使研究体受压缩变形,故轴力在此截面向负方向发生突变,轴力突变大小为集中力F 4大小,此时 F N =(640-800)N =-160 N ;在DE 段没有外力,故轴力不变;在截面E 有集中力,由于轴力曲(b )(a)线与轴线围成封闭图形,故轴力突变为0。
例5.5有一根阶梯轴受力如图5.19(a)所示,试绘制阶梯轴的轴力图。
图5.19解从右向左绘制,始终取左变部分为研究体。
根据外力直接绘制轴力图(见图5.19(b)),绘图分析过程及步骤如下:在截面A有集中力F1,使研究体压缩变形,故轴力在此截面向负方向发生突变,轴力突变大小为集中力F1大小,此时F N=(0-10)kN=-10 kN;在AB段有均匀分布载荷,使研究体受拉伸变形,故轴力以斜直线规律向正方向渐变,轴力渐变大小为均匀分布载荷大小,此时F N=(-10+10×2)kN=10 kN;在截面B没有力,故此截面轴力没有变化;在BC段没有外力,故轴力不变;在截面C有集中力F2,使研究体受拉伸变形,故轴力在此截面向正方向发生突变,轴力突变大小为集中力F2大小,此时F N=(10+10)kN=20 kN;在CD段没有外力,故轴力不变;在截面D有集中力,由于轴力曲线与轴线围成封闭图形,故轴力突变为0.二、由外力直接绘制扭矩图制其内力图。
材料力学第4讲-利用微分关系绘制梁内力图

求支座反力的顺序;中间铰接处和刚接处剪力图和弯矩图的特点。
(4)根据梁的内力图反推梁的荷载图
内力图与荷载图的对应关系;微分关系的应用。
2.4(1)梁的荷载集度函数、剪力 函数和弯矩函数之间的微分关系
设梁上作用有任意分布荷载,
其集度 q = q (x) 规定 q (x)向上为正. 将 x 轴的坐标原点取在梁的左端. 假想地用坐标为 x 和 x+dx的两
算出截面C上的剪力为 (3-
24)kN=-5kN,即可确定这条
4m
斜直线(如图所示). FS/kN 3
M=10kN·m C 2m
F=2kN FRB
B
D
2m
2
x
截面C和B之间梁上无分布载荷,
剪力图为水平线.
5
截面B上有一集中力FRB,从B的左侧到B得右侧,建立了图发生突然变化, 变化的数值即等于FRB.故FRB右侧截面上的剪力为(-5+7)kN=2kN.
x1
等号右边积分的几何意义是x1 , x2两横截面间分布荷载图的面积.
dM ( x) dx
FS
(
x)
若横截面x= x1,x=x2 间无集中力偶作用则得
M ( x2 ) M ( x1 )
x2 x1
FS
(
x
)dx
等号右边积分的几何意义是 x1 , x2两个横截面间剪力图的面积.
例题3-4-1 一简支梁受两个力F作用,如图所示.已知 F= 25.3kN,
dFS ( x) q( x) dx
dM ( x) dx
FS
(
x)
(3)内力的极值点位置的判断 1)最大剪力可能发生在集中力所在截面的一侧;或
【材料力学课件】平面刚架和曲杆的内力图

5-5 平面刚架和曲杆的内力图杆系结构若在结点处为刚性连接,则这种结构称为刚架。
各杆连接处称为刚结点。
刚架变形时,刚结点处各杆轴线之间的夹角保持不变。
★请看动画演示→★请看动画演示→平面刚架各杆的内力,除了剪力和弯矩外,还有轴力。
作刚架内力图的方法和步骤与梁相同,但因刚架是由不同取向的杆件组成,习惯上按下列约定:弯矩图,画在各杆的受拉一侧,不注明正、负号。
剪力图及轴力图,可画在刚架轴线的任一侧(通常正值画在刚架外侧),但须注明正负号;剪力和轴力的正负号仍与前述规定相同。
,(2)画BC杆的内力图由于AB及BC杆中间没有作用集中力及分布载荷,只需求出各杆端点的内力即可画出内力图。
对于BC杆,1截面的内力(考虑右半部分杆件):轴力剪力弯矩剪力的正负号仍与梁中规定相同,可以看出,不论从杆件的上方或下方来观察此杆件,1截面的剪力都是正的。
2截面的内力(考虑右半部分杆件),,(上边受拉)根据1、2截面所求得的内力,可画出其内力图如图5-14b、c、d所示。
作轴力 N 图及剪力 Q 图时,内力图画在杆件哪一边都可以,但须注明正负号。
对于弯矩 M ,由于从不同方向观察会得到不同的正负号,故规定将 M 图画在杆件受拉的一边,但不标正负号。
(3)画AB杆的内力图对于AB杆,3截面的内力(考虑上半部刚架),,(左边受力)4截面的内力(考虑上半部刚架),,(左边受力)(4)对刚结点的平衡进行校核画出整个刚架的内力图后,一般应校核刚结点处是否满足平衡条件。
根据所绘的内力图,可画出刚结点的受力图如图5-15所示,按刚结点的平衡条件可得,,由此可见,对于图5-15所示连接两相互垂直杆件的刚结点,若结点上没有作用载荷,则一杆的剪力绝对值应等于另一杆的轴力绝对值,两杆在刚结点处的弯矩值相等,且受拉边也相同。
对于连接两根以上杆件的刚结点(图5-16a)或结点上作用载荷的刚结点,平衡条件仍必须满足。
例如对于图5-16b所示在结点处作用外力偶m的刚结点,力矩平衡条件应为,由于中间无集中载荷,只需求出端截面的内力值即可画内力图。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、由外力直接绘制轴力图
例 5.4 如图 5.18(a)所示为一绳子受力图,右端固定,试绘制该绳的轴力图。
解 根据外力直接绘制轴力图(见图5.18(b)),绘图分析过程及步骤如下。
从左向右绘制,始终取右边部分为研究体。
在截面A 有集中力F 1,使研究体拉伸变形,
故轴力在此截面向正方向发生突变,轴力突变大小为集中力F 1大小,此时 F N =(0+500)N =500 N ;在AB 段没有外力,故轴力不变;在截面B 有集中力F 2,使研究体受拉伸变形,故轴力在此截面向正方向发生突变,轴力突变大小为集中力F 2大小,此时F N =(500+420)N =920 N ;在BC 段没有外力,故轴力不变;在截面C 有集中力F 3,使研究体受压缩变形,故轴力在此截面向负方向发生突变,轴力突变大小为集中力F 3大小,此时F N =(920-280)N =640 N ;在CD 段没有外力,故轴力不变;在截面D 有集中力F 4,使研究体受压缩变形,故轴力在此截面向负方向发生突变,轴力突变大小为集中力F 4大小,此时 F N =(640-800)N =-160 N ;在DE 段没有外力,故轴力不变;在截面E 有集中力,由于轴力曲
(b )
(a)
线与轴线围成封闭图形,故轴力突变为0。
例5.5有一根阶梯轴受力如图5.19(a)所示,试绘制阶梯轴的轴力图。
图5.19
解从右向左绘制,始终取左变部分为研究体。
根据外力直接绘制轴力图(见图5.19(b)),绘图分析过程及步骤如下:
在截面A有集中力F1,使研究体压缩变形,故轴力在此截面向负方向发生突变,轴力突变大小为集中力F1大小,此时F N=(0-10)kN=-10 kN;在AB段有均匀分布载荷,使研究体受拉伸变形,故轴力以斜直线规律向正方向渐变,轴力渐变大小为均匀分布载荷大小,此时F N=(-10+10×2)kN=10 kN;在截面B没有力,故此截面轴力没有变化;在BC段没有外力,故轴力不变;在截面C有集中力F2,使研究体受拉伸变形,故轴力在此截面向正方向发生突变,轴力突变大小为集中力F2大小,此时F N=(10+10)kN=20 kN;在CD段没有外力,故轴力不变;在截面D有集中力,由于轴力曲线与轴线围成封闭图形,故轴力突变为0.
二、由外力直接绘制扭矩图
外力扭矩图
无外力
不变
集中力F P突变。
方向:右手螺旋法则,四指指向外力偶方向,拇指离开为正;
大小:集中力偶大小F P
均布力偶在分布力的起始和终止截面,扭矩没有突变。
以斜直线渐变。
方向:右手螺旋法则,四指指向外力偶方向,拇指离开为正;
大小:M q
制其力图。
图5.25
解从右向左绘制,始终取左部分为研究体。
根据外力偶直接绘制扭矩图,绘制分析过程及步骤如下:
在截面A有集中力偶M1,变形方向由右手螺旋法则判断,拇指背离截面,故扭矩在此截面向正方向发生突变,扭矩突变大小为集中力偶M1大小,此时m
kN
1
)1
0(•
=
+
=
x
M;在AB段无外载荷,故扭矩不变;在截面B有集中力偶M2,变形方向由右手螺旋法则判断,拇指指向截面,故扭矩在此截面向负方向发生突变,扭矩突变大小为集中力偶M2大小此时M x=1-2=-1m
kN•;在BC段无外载荷,故扭矩不变;在截面C有集中力偶M3,变形方向由右手螺旋法则判断,拇指背离截面,故扭矩在此截面向正方向发生突变,扭矩突变大小为集中力偶M3大小m
kN
2
)3
1
(•
=
+
-
=
x
M;在CD段有无外载荷,故扭矩不变;在截面D有集中力,由于扭矩曲线与轴线围成封闭图形,故扭矩突变为零。
扭矩图如图5.25(b)所示。
M q
三、由外力直接绘制剪力图和弯矩图
剪力、弯矩与分布载荷间的关系
例5.10如图5.28(a)所示,简支梁AB,在C点承受集中载荷F=6 kN作用,跨度l=3 m,a,试绘制梁的力图。
2
m
解 (1)求支座反力。
取整段梁为研究对象,受力分析如图5.28(b),由平衡条件得
0)(A =∑F M ⇒0B =⋅-⋅a F l F
解得
kN 4B =F
0=∑y F ⇒0B A =-+F F F
解得
kN 2A =F
(2)由外力直接绘制力图。
从A 截面开始,有一向上的集中力F A ,故在此截面剪力向上突变,突变大小等于F A ,弯矩没有变化;AC 段没有外力,故剪力在该段没有变化,由于剪力大于零,故在该段弯矩以斜直线规律向正向变化,从截面A 到截面C 弯矩变化大小为AC 段剪力与x 轴围成的面积即
m kN 4A •=•a F ;在截面C 有一向下的集中载荷F ,故在此截面剪力向下突变F ,弯矩
没有变化;在CB 段没有外力,故剪力在该段没有变化,由剪力小于零,则该段弯矩以斜直
线规律向负向变化,从截面C 到截面B 弯矩变化大小为CB 段剪力与x 轴围成的面积即
m kN 4)(B •=-•a l F 变为0。
例5.11 如图5.29(a)所示外伸梁,试计算其力并画出力图。
图5.29
解 (1)先求支座反力。
取整段梁研究,其受力如图5.29(a),由平衡条件得
∑=-⋅+⋅⇒=020)(2
A B AB q AB F BC F F M
∑=⋅--+⇒=00B A y
AB q F F F F
解得
kN 35,kN 15B A ==F F
(2)由外力直接绘制力图。
从截面A 开始,有一向上的集中力F A ,故在此截面剪力向上突变,突变大小等于F A ,弯
矩没有变化;AB 段有向下的均布力系,故剪力在该段以斜直线规律向下渐渐变化,从截面A 到截面B 剪力值变化q AB ⋅,弯矩以开口向上的抛物线规律渐渐变化,在剪力为零的截面D
弯矩为极值,从截面A 到截面D 变化值为小三角形面积
m kN 625.52
251515
215•=+⨯
⨯,从截面D 到截面B 变化大三角形面积
m kN 625.152
251525
225•=+⨯
⨯;在截面B 有一向上的集中力F B ,故在该截面剪力向上突变,突变大小等于F B 的大小,弯矩没有变化;BC 段没有外力,故剪力在该段没有变化,由于剪力大于零,故该段弯矩以斜直线规律向正向变化,从截面C 到截面B 弯矩变化大小为BC 段剪力与x 轴围成的面积。
所绘力图如图5.29(b)、(c)所示。
(3)检查图形是否封闭。
例5.12 如图5.30(a)所示外伸梁,集中力F =10 kN ,均布载荷集度q =10 kN /m ,试利用剪力、弯矩与载荷集度的微分关系绘制出梁的剪力图、弯矩图。
图5.30
解:(1)求A 处约束力。
取整体研究,受力如图5.30(a),建立平衡方程。
0)(A
=∑F M
⇒05.2D =⨯⋅-⋅-⋅BD q AC F AD F
解得
kN 5.17D =F
∑=+⋅--⇒=010D A y
F q F F F
解得
kN 5.2A =F
(2)由外力直接绘制力图。
从截面A 开始,有一向上的集中力F A ,故在此截面剪力向上突变,突变大小等于F A ,弯矩没有变化;AC 段没有外力,故剪力在该段没有变化,由于剪力大于零,则该段弯矩以斜直线规律向正向变化,从截面C 到截面B 弯矩变化大小为AC 段剪力与x 轴围成的面积;截面C 有一向下的集中力F ,故在此截面剪力向下突变,突变大小等于F 的大小,弯矩没有变化;CD 段没有外力,故剪力在该段没有变化,由于剪力小于零,则该段弯矩以斜直线规律向负向变化,从截面C 到截面D 弯矩变化大小为CD 段剪力与x 轴围成的面积; 截面D 有一向上的集中力F D ,故在此截面剪力向上突变F D ,弯矩没有变化;DB 段有向下的均布力系,故剪力在该段以斜直线规律向下渐渐变化,从截面D 到截面B 剪力值变化DB q ⋅,弯矩以开口向上的抛物线规律渐渐变化,在剪力为零的截面D 弯矩为极值,从截面D 到截面B 变化大小为小三角形面积。
(3)检查图形是否封闭。
