高数 平面曲线的曲率 知识点与例题精讲课件
第七节平面曲线的曲率
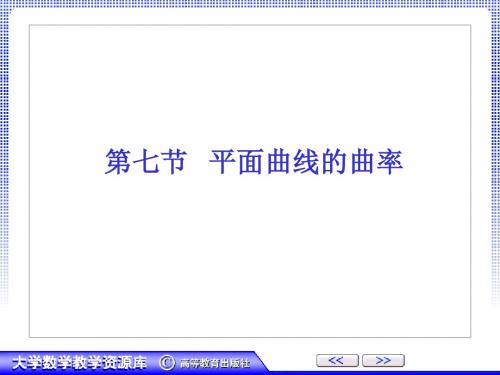
为半径的圆为 L 在点 M 的曲率圆.
为曲率半径.
二、曲率
1.曲率就是曲线在某点处的弯曲程度.如路 弯度大,车子离心率越大;梁一般在弯的最厉害 的地方断裂;……圆的半径越小弯的越厉害,于 是 2. 定义: 1 k
2 y 0 . 4 x 例3 一工件内表面截线为 ,用砂轮磨 削其内表面,半径多大合适? 解:砂轮半径 抛物 y 线上各点处曲率半径 2 y 0 . 4 x 的最小者,才不会破 坏工件内表面, 由例2 知抛物线在顶点处曲 曲率半径最小. 率最大, y 0.8 x , y 0.8 x O 0.8 k (0,0) 0.8 , 32 (1 0) 1 k 1.25 , 所以砂轮半径不能大于1.25.
( x0 a ) [ f ( x0 ) ] f ( x0 ) 0
(5)
(6)
1 [ f ( x0 )]2 [ f ( x0 ) ] f ( x0 ) 0
从(6)式解出:
1 [ f ( x0 )]2 f ( x0 ) f ( x0 )
第七节 平面曲线的曲率
讲解方法一:
一、曲率圆
1、实际问题: 一质点作曲线运动, 考察 y 运动在某点 M ( x0 , f ( x0 )) 处的情形. 局部情形时, 可用圆周曲线来替代这点 附近的曲线 L , 这样就可 以用圆周运动的知识来析 o 这点处的曲线运动.
D
y f ( x)
L
M
x0
x
再代入(5)式解出:
1 [ f ( x 0 )] x 0 f ( x 0 ) f ( x0 )
代入(2)式解出:
《高等数学曲率》课件

曲率与生物形态
在自然界中,许多生物形态都呈现出 曲率的特点。例如,鸟类的飞行轨迹 、河流的流向、植物的生长方式等都 与曲率密切相关。通过研究这些生物 形态的曲率特点,可以更好地理解自 然界的规律和原理。
VS
曲率在生物形态中的应用还体现在仿 生学领域。通过模仿自然界中生物的 形态和运动方式,可以创造出更加高 效、环保和可持续的交通工具、建筑 材料等。例如,仿生学中的“蜂巢” 结构就是利用了曲率的特点,具有很 好的抗压和抗震性能。
曲率与建筑设计
在建筑设计中,曲率也被广泛应用。通过合理利用曲率,可以创造出更加美观、舒适和功能性的建筑。例如,在建筑设计时 可以利用曲率来优化建筑的外观和结构,提高建筑的稳定性和安全性。
曲率还可以用于建筑内部的布局和空间设计。例如,利用曲率可以将建筑的内部空间划分为不同的区域,提高建筑的实用性 和舒适性。
曲率研究展望
曲率与几何拓扑关系
未来研究可以探索曲率与几何拓扑之间的关系,例如研究 曲率在曲面分类中的作用,以及曲率在流形学习等方面的 应用。
高维空间曲率研究
随着高维几何的发展,对高维空间中曲率的研究也日益重 要,未来可以进一步探讨高维空间中曲率的性质和计算方 法。
数值计算与模拟
随着计算机技术的发展,数值计算和模拟已经成为研究曲 率的重要手段,未来可以借助更先进的计算方法和模拟技 术,对曲率进行更精确和深入的研究。
03
曲率应用
曲率在几何学中的应用
曲率在几何学中有着广泛的应用,它描述了曲线在某一点的 弯曲程度。在平面几何中,曲率用于描述曲线在某一点的弯 曲程度,而在球面几何中,曲率则用于描述曲面在某一点的 弯曲程度。
在几何学中,曲率的概念可以帮助我们更好地理解空间中的 几何形状,以及它们之间的相互关系。例如,在研究行星运 动时,曲率的概念可以帮助我们理解行星轨道的形状和大小 。
高数 平面曲线积分 知识点与例题精讲

若 P Q
y
y x
则 B( x1 , y1 ) Pdx Qdy A( x0 , y0 )
A( x0 , y0 )
o
x1 x0
P
(
x,
y0
)dx
y1Q(
y0
x1
,
y)dy
或
y1Q (
y0
x0
,
y
)dy
x1 x0
机动 目录 上页 下页 返回 结束
取圆弧 AB : x cos , y sin ( : 0 )
2
2
2
W
AB
k r2
(
y
d
x
xdy)
y A
L
k
2
o
Bx
思考: 积分路径是否可以取 AO OB ? 为什么?
注意, 本题只在不含原点的单连通区域内积分与路径
无关 !
Q x
o
( x 0 ) (1,0)
x
( x,0 )
由定理 2 可知存在原函数
x 1
0
dx
x
y 0
dy x2 y2
机动 目录 上页 下页 返回 结束
或
y 0
1
d
y y
2
arctan x
2
y
y (1, y) (x, y) o (1,0) ( x,0 ) x
有关定理的说明:
(1) 开区域G 是一个单连通域.
(2) 函数 P( x, y), Q( x, y) 在G 内具有一阶连
曲线的曲率PPT课件

s( x) lim s lim x0 x0
(x)2 (y)2 ( x )2
x lim
1 ( y )2
1 ( y)2,
x0
x
.
, lim M M 1 x0 M M
4
ds 1 ( y)2dx
或
ds (dx)2 (dy)2 .
几何意义:
y
ds MT
dx cos ;
ds
O
dy sin .
.
12
由此可得曲率中心公式
y
D( , )
x y(1 y2) ,
y
y 1 y2 .
CR
T
M(x, y)
y
O
x
当点 M (x, y) 沿曲线 C : y f ( x) 移动时, 相应
的曲率中心的轨迹 G 称为曲线 C 的渐屈线, 曲线 C
称为曲线G 的渐伸线 .
.
13
二、典型例题
A
M
M0
有向弧段M0M的值 s .
O a x0 x b x
.
2
弧的定义
y y f (x) B
有向弧段M0M的值 s (简称弧 s)
A
M
M0
规定为:
s 的大小等于弧M0M的长度, O a x0 x b x
当弧M0M的方向与曲线的正方向一致时, s > 0, 相反时, s < 0.
显然, s 是个代数量, 且是x的单调增函数 s(x).
3
2a
3.
(1 y2 )2 [1 (2ax b)2]2
显然,
当x b 时, 2a
K最大.
又
Q
(
b 2a
,
第03章06节平面曲线的曲率
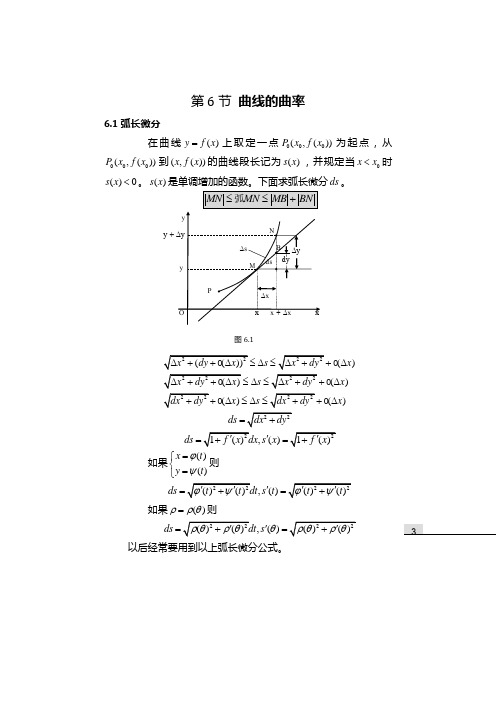
第6节 曲线的曲率6.1弧长微分在曲线()y f x =上取定一点000(,())P x f x 为起点,从000(,())P x f x 到(,())x f x 的曲线段长记为()s x ,并规定当0x x <时()0s x <。
()s x 是单调增加的函数。
下面求弧长微分ds 。
()()()()s x s x x s x ≤∆≤∆≤∆≤∆∆≤∆≤∆ds =,()ds s x '== 如果()()xt y t ϕψ=⎧⎨=⎩则,()ds s t '==如果()ρρθ=则,()ds s θ'==以后经常要用到以上弧长微分公式。
图6.1y +离 散数 学6.2曲线的曲率这节讨论曲线的曲率,也就是曲线的弯曲程度。
设曲线()y f x =在()00,()x f x 的切线0L 与x 轴正向的夹角为0θ,在()00,()x x f x x +∆+∆的切线x L ∆与x 轴正向的夹角为x θ∆。
经过x ∆,切线的夹角变化了0x θθθ∆∆=-设()00,()x f x 和()00,()x x f x x +∆+∆之间曲线的长为s ∆。
容易想见,()00,()x f x 和()00,()x x f x x +∆+∆之间曲线的曲率(弯曲程度)与θ∆成正比,与s ∆成反比,平均曲率()k x sθ∆∆=∆ 让0x ∆→求极限,就得到曲线()y f x =在()00,()x f x 的曲率(弯曲程度)000()lim ()limx x d k x k x s dsθθ∆→∆→∆=∆==∆ 下面我们求出d dsθ从而得到求曲率的计算公式。
用x 作参数 ()()s s x x θθ=⎧⎨=⎩()()2222tan ()1()cos 1tan ()1()()()1()f x d f x dx d f x dx f x d f x dxd f x dx f x θθθθθθθ'=''=''+='''+=''='+第1章集 合322()1()d f x d ds dxdxds f x θθ''=='⎡⎤+⎣⎦003220()()1()f x k x f x ''='⎡⎤+⎣⎦例子:求半径为r 的圆上一点的曲率。
高等数学导数应用(三)曲率PPT课件

目录
• 曲率定义与计算 • 导数与曲率的关系 • 曲率在实际问题中的应用 • 曲率的应用案例分析 • 总结与展望
01
曲率定义与计算
曲率的定义
曲率是描述曲线在某一点弯曲程 度的量,定义为曲线在该点处切
线的斜率的变化率。
在二维平面上,曲线的曲率等于 其上任一点处切线的斜率的导数。
导数的性质
导数具有连续性、可导性、可积性等 性质,这些性质在研究函数的形态、 单调性、极值等问题中具有重要作用。
导数与曲率的关系
导数与曲率的关系
曲率是描述曲线在某一点弯曲程度的 量,与函数在该点的导数密切相关。 曲率等于函数在该点的导数的绝对值 。
导数与曲率的几何意义
在几何上,导数表示曲线在某一点的 切线斜率,而曲率表示该点附近曲线 的弯曲程度。因此,导数和曲率共同 决定了曲线在该点的形态。
在几何图形中,曲率的应用非常广泛,如圆、椭圆、 抛物线、双曲线等。
曲率决定了图形的形状和性质,如圆的曲率处处相等 且为常数,而抛物线的曲率只在顶点处为0。
在工程和科学研究中,曲率的应用也非常重要,如分 析机械零件的应力分布、研究光的传播路径等。
的定义
导数是函数在某一点的变化率,表示 函数在该点的切线斜率。
05
总结与展望
总结高等数学导数应用(三)曲率的主要内容
曲率的概念
曲率是描述曲线弯曲程度的量,对于二维平面上的曲 线,曲率等于切线方向的转动角速度。
导数与曲率的关系
曲率是函数二阶导数的几何意义,即曲率等于函数二 阶导数的值。
曲率的应用
曲率在几何、物理、工程等领域有着广泛的应用,如 分析机械零件的应力分布、预测股价波动等。
《平面曲线的曲率》课件

二次曲线的曲率
二次曲线的曲率公式:K = 1/r,其中r是曲线的半径 曲率与二次曲线的形状关系:曲率越大,曲线的弯曲程度越大 曲率与二次曲线的切线关系:曲率等于切线斜率与半径的比值 曲率与二次曲线的弧长关系:曲率等于弧长与半径的比值
高次曲线的曲率
高次曲线:指次数大于2的曲线,如三次曲线、四次曲线等
YOUR LOGO
20XX.XX.XX
平面曲线的曲率
,
汇报人:
目 录
01 单 击 添 加 目 录 项 标 题 02 平 面 曲 线 的 曲 率 定 义 03 平 面 曲 线 曲 率 的 应 用 04 平 面 曲 线 曲 率 的 性 质 05 平 面 曲 线 曲 率 的 计 算 方 法 06 平 面 曲 线 曲 率 的 实 例 分 析
航线规划:利用曲率信息规划最 优航线
添加标题
添加标题
添加标题
添加标题
避障:根据曲率变化判断障碍物 位置和距离
船舶性能评估:通过曲率变化评 估船舶性能和稳定性
平面曲线曲率的性
04
质
曲率的几何意义
曲率是描述曲线 弯曲程度的量
曲率越大,曲线 弯曲程度越大
曲率是曲线在某 一点的切线方向 与曲线在该点的 法线方向的夹角
曲率半径
曲率半径:描述平面曲线弯曲程度的量
公式:R=1/k,其中k为曲率
应用:在工程、物理、数学等领域有广泛应用 特点:曲率半径越大,曲线弯曲程度越小;曲率半径越小,曲线弯 曲程度越大。
曲率的意义
曲率是描述曲线 弯曲程度的量
曲率越大,曲线 弯曲程度越大
曲率是描述曲线 形状的重要参数
曲率在工程、物 理、数学等领域 有广泛应用
பைடு நூலகம்
高等数学课件3-5曲率

高等数学课件3-5曲率
汇报人:
目录
01 02 03 04 05 06
添加目录项标题
曲率的概念
曲率在高等数学中的意义
高等数学课件3-5曲率的讲解重点 如何理解高等数学课件3-5曲率的
意义 如何应用高等数学课件3-5曲率解
决实际问题
01
添加目录项标题
02
曲率的概念
曲率的定义
曲率是描述曲线 弯曲程度的量
曲率越大,曲线 弯曲程度越大
曲率是曲线在某 一点的切线方向 与该点处曲线的 法线方向之间的 夹角
曲率是曲线在某 一点的切线方向 与该点处曲线的 法线方向之间的 夹角
曲率的计算方法
曲率公式:k = 1/r,其中k为曲率,r 为半径
曲率圆:曲率半径的圆,曲率中心为 圆心,曲率半径为半径
曲率半径:r = 1/k,其中k为曲率
曲率在曲线和曲面中的应用
曲率是描述曲 线或曲面弯曲
程度的量
曲率越大,曲 线或曲面的弯
曲程度越大
曲率在微分几 何、拓扑学、 物理等领域有
广泛应用
曲率可以帮助 我们理解和分 析曲线和曲面 的性质,如长 度、面积、体
积等
曲率在微积分学中的应用
曲率是描述曲线弯曲程度的重要 参数
曲率在微积分学中用于求解曲线 的弧长、面积等问题
利用曲率进行创新和设计
曲率在工程设计中的应用:如 桥梁、建筑、机械等
曲率在艺术设计中的应用:如 雕塑、绘画、平面设计等
曲率在科学研究中的应用:如 物理、化学、生物等
曲率在商业设计中的应用:如 产品包装、广告设计等
感谢观看
汇报人:
添加标题
添加标题
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
6
3
[1 ( y)2 ]2 (4sin2 t 9cos2 t )2
6
3
(4 5cos2 t )2
3
要使k 最大, 必有 (4 5cos2 t)2 最小,
t , 3 此时k 最大,
22
练习题
一、 填空题:
1、 曲率处处为零的曲线为________;曲率处处相等的
曲线为__________.
M M s
注意: 直线上任意点处的曲率为 0 !
机动 目录 上页 下页 返回 结束
例1. 求半径为R 的圆上任意点处的曲率 .
解: 如图所示 , s R
K lim 1 s0 s R
M
s
R M
可见: R 愈小, 则K 愈大 , 圆弧弯曲得愈厉害 ;
3.曲线上一点处的曲率圆弧可近似代替该点附 近曲线弧(称为曲线在该点附近的二次近似).
例4. 设一工件内表面的截痕为一椭圆, 现要用砂轮磨 削其内表面 , 问选择多大的砂轮比较合适?
解: 设椭圆方程为
由例3可知, 椭圆在
y
处曲率最大 ,
即曲率半径最小, 且为
R
(a2
sin
2
t
b2
cos 2
t
3
又( b , b2 4ac)为抛物线的顶点, 2a 4a
抛物线在顶点处的曲率最大.
例3. 求椭圆
在何处曲率最大?
解: x a sin t ;
y b cos t ; 故曲率为
x a cos t y b sin t
x 表示对参 数 t 的导数
K
(
x y xy x 2 y 2 )32
K
(1
y y2 )32
当 y 1 时, 有曲率近似计算公式 K y
机动 目录 上页 下页 返回 结束
说明:
(1)
若曲线由参数方程
x y
x(t) y(t )
给出,
则
x y xy K ( x 2 y 2 )32
(2) 若曲线方程为 x ( y),则
六、曲线上曲率最大的点称为此曲线的顶点,试求指 数曲线 y e x 的顶点,并求在该点处的曲率半径 .
练习题答案
一、1、直线. 圆; 2 、2, 1 ; 2
二、k cos x , sec x .
三、k 2 . 3a sin 2t0
五、( ,1)处曲率半径有最小值 1. 2
六. ( 1 ln 2, 1 ), 3 3 .
曲率半径
R
1 K
(1 y2 )32 y
机动 目录 上页 下页 返回 结束
思考与练习
1. 曲线在一点处的曲率圆与曲线有何密切关系? 答: 有公切线 ; 凹向一致 ; 曲率相同.
2. 求双曲线
的曲率半径 R , 并分析何处 R 最小?
解:
y
1 x2
,
y
2 x3
,
则
y
1
R
(1
2、抛 物 线 y x 2 4x 3 在 (2,-1) 处 的 曲 率 为 ________;曲率半径为_________.
3、曲 线 y ln( x 1 x 2 ) 在 (0,0) 处 的 曲 率 为 ___________.
二、 求曲线 y ln(sec x) 在点( x, y) 处的曲率及曲率半
若曲线由参数方程表示:
x y
x(t) y(t )
则弧长微分公式为 ds x 2 y 2 d t y
几何意义: ds MT
dx cos ; dy sin
ds
ds
T
M dy
dx
o x x dx x
机动 目录 上页 下页 返回 结束
二、曲率及其计算公式
径.
三、
求曲线 x y
a cos3 a sin3
t t
在t
t0 处的曲率
.
四、 证 明 曲 线 y a cosh x 在 任 何 一 点 处 曲 率 半 径 为 a
y2 . a
五、曲线弧 y sin x (0 x ) 上哪一点处的曲率半 径最小?求出该点处的曲率半径 .
x
MM MM
(x)2 (y)2 x
oa
x
x
xb
x
M M 1 (y )2
MM
x
s( x) lim s 1 ( y)2 x0 x
lim M M 1 x0 M M
机动 目录 上页 下页 返回 结束
ds 1 ( y)2dx 或 ds (dx)2 (d y)2
曲率是描述曲线局部性质(弯曲程度)的量.
1
2
M2 S2 M3
S1
M1
弧段弯曲程度 越大转角越大
S1
M
M
N
S2 N
转角相同弧段越 短弯曲程度越大
在光滑弧上自点 M 开始取弧段, 其长为s , 对应切线
转角为 , 定义
弧段 s上的平均曲率
K s
点 M 处的曲率 K lim d s0 s ds
令 f (t) 0, 得 t 0, , , 3 , 2
2
2
计算驻点处的函数值:
t
02
3 2
2
f (t) b2 a2 b2 a2 b2
设0 b a , 则 t 0 , , 2时
y
f (t)取最小值 , 从而 K 取最大值 .
b
这说明椭圆在点( a , 0 ) 处曲率 a
)2
ab
t0
o
x
显然, 砂轮半径不超过 时, 才不会产生过量磨损 ,
或有的地方磨不到的问题.
例3 目录 上页 下页 返回 结束
内容小结
1. 弧长微分 ds 1 y2 dx 或 ds (dx)2 (d y)2
2. 曲率公式 3. 曲率圆
K
d ds
y (1 y2 )3.
ax
最大.
b
机动 目录 上页 下页 返回 结束
三、 曲率圆与曲率半径
设 M 为曲线 C 上任一点 , 在点 y
D( , )
M 处作曲线的切线和法线, 在曲线
的凹向一侧法线上取点 D 使
C
R
T
M (x, y)
DM R 1
o
x
K
把以 D 为中心, R 为半径的圆叫做曲线在点 M 处的
曲率圆( 密切圆 ) ,R 叫做曲率半径, D 叫做曲率中心.
在点M 处曲率圆与曲线有下列密切关系:
(1) 有公切线; (2) 凹向一致; (3) 曲率相同 .
机动 目录 上页 下页 返回 结束
注意:
1.曲线上一点处的曲率半径与曲线在该点处的 曲率互为倒数.
即 R 1,k 1 . kR
2.曲线上一点处的曲率半径越大,曲线在该点 处的曲率越小(曲线越平坦);曲率半径越小,曲 率越大(曲线越弯曲).
第4.7 节 平面曲线的曲率
主要内容: 一、 弧微分 二、 曲率及其计算公式 三、 曲率圆与曲率半径
机动 目录 上页 下页 返回 结束
一、 弧微分
设
在(a , b)内有连续导数, 其图形为 AB,
弧长 s AM s( x)
s x
MM MM
MM x
y
y
f (x) M
B
A M y
y2 )32 (1
1 x4
3
)
2
y
2 x3
1 2
(
x2
3
1 x2
)
2
2
o
1
x
显然 R x1 2 为最小值. 利用 a2 b2 2ab
机动 目录 上页 下页 返回 结束
思考题
椭圆 x 2cos t, y 3sin t上哪些点处
曲率最大?
思考题解答
k | y | 3
K
(1
x
x
2
3
)
2
y
K
(1
y
2
3
)
2
机动 目录 上页 下页 返回 结束
例2 抛物线 y ax2 bx c 上哪一点的曲率最大?
解 y 2ax b, y 2a,
k
2a 3.
[1 (2ax b)2 ]2
显然, 当x b 时, k最大. 2a
ab
(a2
sin
2
t
b2
cos
2
t
3
)
2
K 最大
f (t ) a2 sin2 t b2 cos2 t 最小
求驻点: f (t ) 2a2 sin t cos t 2bcos t sin t (a2 b2 )sin 2 t
机动 目录 上页 下页 返回 结束
f (t ) (a2 b2 )sin 2 t
R 愈大, 则K 愈小 , 圆弧弯曲得愈小 .
机动 目录 上页 下页 返回 结束
曲率K 的计算公式
设曲线弧 y f ( x) 二阶可导, 则由
tan y (设 )
2
2
得 arctan y
d (arctan y)dx
K d ds
又 故曲率计算公式为
