平面曲线的曲率
第七节平面曲线的曲率
为半径的圆为 L 在点 M 的曲率圆.
为曲率半径.
二、曲率
1.曲率就是曲线在某点处的弯曲程度.如路 弯度大,车子离心率越大;梁一般在弯的最厉害 的地方断裂;……圆的半径越小弯的越厉害,于 是 2. 定义: 1 k
2 y 0 . 4 x 例3 一工件内表面截线为 ,用砂轮磨 削其内表面,半径多大合适? 解:砂轮半径 抛物 y 线上各点处曲率半径 2 y 0 . 4 x 的最小者,才不会破 坏工件内表面, 由例2 知抛物线在顶点处曲 曲率半径最小. 率最大, y 0.8 x , y 0.8 x O 0.8 k (0,0) 0.8 , 32 (1 0) 1 k 1.25 , 所以砂轮半径不能大于1.25.
( x0 a ) [ f ( x0 ) ] f ( x0 ) 0
(5)
(6)
1 [ f ( x0 )]2 [ f ( x0 ) ] f ( x0 ) 0
从(6)式解出:
1 [ f ( x0 )]2 f ( x0 ) f ( x0 )
第七节 平面曲线的曲率
讲解方法一:
一、曲率圆
1、实际问题: 一质点作曲线运动, 考察 y 运动在某点 M ( x0 , f ( x0 )) 处的情形. 局部情形时, 可用圆周曲线来替代这点 附近的曲线 L , 这样就可 以用圆周运动的知识来析 o 这点处的曲线运动.
D
y f ( x)
L
M
x0
x
再代入(5)式解出:
1 [ f ( x 0 )] x 0 f ( x 0 ) f ( x0 )
代入(2)式解出:
最新24-平面曲线的曲率汇总

解
x 0 1 , y0 1 ,
y x 1 2 xx 1 2 , yx12, 在点(1,1)处的曲率半径为
R
(1
y2
)
3 2
(122)23 125
y
2
2
曲率中心为
x0
y(1y2) y
12(122)4 2
y0
1 y2 y
1122 2
7 2
曲率中D(心 4, : 7). 2
曲率圆的方程为
(x4)2(y7)2125 24
在M 点 处可用一个相应的圆来描述曲线的弯曲程度
曲率中心的坐标
设曲y 线 f(x )方 ,f(x )程 存为 在
f(x0)0,则曲线在点 M(x0, y0)处的曲率
中心 D(, )的坐标为
x0
y(1y2), y
y0
1 y2 y
,
式 y 与 中 y 是 y f(x )在 M 处 点的 .
求抛 yx2 物 在(1 线 ,点 1 )处的 例5 曲率半径、曲率中心和曲率圆方程 .
,
2
,
3,
2
因a为 b, 故在各象限中
dk
d
的符号依次为
Ⅰ
Ⅱ
Ⅲ
Ⅳ
+
+
由此当 可得:2当 , 32时 0,,k时 取 ,k最 取小 km最 in 值 kab大 m2ax b值 a2
在有些实际问题中 , 若 |y|1 , 则可 k|y 取 |.
k 1, R5. 5
O
M
O
M
曲率圆 曲率半径 曲率中心 曲率半径曲1率
24-平面曲线的曲率
例1 求半径为 R 的圆上任意一点处的曲率 .
曲线的曲率曲率半径

.
O点处抛物线轨道的曲率半径
y
x0
x 2000
x0
0,
y
x0
1. 2000
得曲率为
k
x x0
1. 2000
曲率半径为 2000 米.
F 70 4002 5600(牛) 571.4(千克), 2000
Q 70(千克力) 571.4(千克力),
641.5(千克力).
即:飞行员对座椅的压力为641.5千克力.
§2-8
曲线的曲率.曲率半径
一、平面曲线的曲率及其计算公式
曲率是描述曲线局部性质(弯曲程度)的量.
1
2
M2 S2 M3
S1
M1
弧段弯曲程度 越大转角越大
S1
M
M
N
S2 N
转角相同弧段越 短弯曲程度越大
y
M0 是基点. MM s ,
C
M.
M M 切线转角为 .
S
. M0 S M
)
定义
o
x
弧段MM的平均曲率为K .
s
曲线C在点M处的曲率 K lim s0 s
在 lim d 存在的条件下,
s0 s ds
K
d .
ds
注意: (1) 直线的曲率处处为零; (2) 圆上各点处的曲率等于半径的倒数, 对于半径为R的圆周 Δ S = RΔθ
1
s R
(3)曲率的倒数称为 曲率半径 = 1/K
1 cos t
sin3 t
2
y
1 4a
1 sin4
t
,
代入公式K
(1
y y2 )3/ 2
1 4a sin
t
高数 平面曲线的曲率 知识点与例题精讲课件

6
3
[1 ( y)2 ]2 (4sin2 t 9cos2 t )2
6
3
(4 5cos2 t )2
3
要使k 最大, 必有 (4 5cos2 t)2 最小,
t , 3 此时k 最大,
22
练习题
一、 填空题:
1、 曲率处处为零的曲线为________;曲率处处相等的
曲线为__________.
M M s
注意: 直线上任意点处的曲率为 0 !
机动 目录 上页 下页 返回 结束
例1. 求半径为R 的圆上任意点处的曲率 .
解: 如图所示 , s R
K lim 1 s0 s R
M
s
R M
可见: R 愈小, 则K 愈大 , 圆弧弯曲得愈厉害 ;
3.曲线上一点处的曲率圆弧可近似代替该点附 近曲线弧(称为曲线在该点附近的二次近似).
例4. 设一工件内表面的截痕为一椭圆, 现要用砂轮磨 削其内表面 , 问选择多大的砂轮比较合适?
解: 设椭圆方程为
由例3可知, 椭圆在
y
处曲率最大 ,
即曲率半径最小, 且为
R
(a2
sin
2
t
b2
cos 2
t
3
又( b , b2 4ac)为抛物线的顶点, 2a 4a
抛物线在顶点处的曲率最大.
例3. 求椭圆
在何处曲率最大?
解: x a sin t ;
y b cos t ; 故曲率为
x a cos t y b sin t
x 表示对参 数 t 的导数
K
(
x y xy x 2 y 2 )32
平面曲线的曲率

( b , b2 4ac)
曲率表征曲线局部性质〔弯曲程度〕的量 砂轮的曲率应不小于抛物线顶点的曲率0.
2a 4a
K 2a
例2、设工件外表的截线为抛物线 y 0.4x2. 现在要用砂轮磨削其内外表.问用直径多大的砂轮 才比较适宜?
注: 直线上任意点处的曲率为 0 !
例2、设工件外表的截线为抛物线 y 0.
y 2a 思考:直线任意点处的曲率是多少?
K 注: 直线上任意点处的曲率为 0 !
现砂在轮要 的用曲砂率轮应磨不削小其于内抛外物表线顶. 点的曲率0.2
3 2
1y 1(2axb) 思考:直线任意点处的曲率是多少?
3 22
y
d
( 1
y2
)dx
0
故曲率计算公式为
y K (1 y2 )32
C:yf(x)
M
x
K d .
ds
例1 抛物线 yax2bxc在哪个点曲率最大?
1、引例:弯曲程度与哪些因素有关?
解: y2axb 砂轮的曲率应不小于抛物线顶点的曲率0.
例如:求半径为R 的圆上任意点处的曲率。
y 2a
25单位长 即直径不得超过2.
C
弧段 M M 平均曲率
K s
点 M 处的曲率
K lim d
s0 s
ds
M
s
M0 M
0
x
例如:求半径为R 的圆上任意点处的曲率。
M s
R M
思考:直线任意点处的曲率是多少?
注: 直线上任意点处的曲率为 0 !
二、曲率的计算公式
设曲线弧 y f (x)
谢金云(2)《平面曲线的曲率》教案和说课设计

平面曲线的曲率第一部分:教案(P1-6)第二部分:说课稿(P7-11)2009年12月《平面曲线的曲率》教案课题:平面曲线的曲率课时:2课时(90分钟)教学目标:认知目标:1、理解曲率的概念和曲率公式的实际应用;2、了解曲率圆和曲率半径的概念;3、掌握曲率计算公式的推导过程及公式的实际应用,真正体会微积分和导数在数学中的重要地位。
能力目标:激发学生的数学学习兴趣,加强数学建模的能力,掌握归纳总结的数学思想方法,培养学生联系实际学习的意识,增进数学应用的眼光,提高学生的主观能动性情感目标:培养学生勇于探索、大胆应用的数学精神,培养团结协作的意识。
教学重点:曲率的概念,曲率计算公式的实际应用。
教学难点:利用曲率计算公式解决实际应用问题。
教学方法:引导探究法(Enlightment)、分层次教学法(Delamination)、任务驱动法(Assignment)。
教学工具:木杆、多媒体课件教学。
教学过程:一、引入:前面我们已经学习了导数的应用,例如函数极值、最值的求解,函数单调性的判断及函数图像的描绘等,我们体会了导数的重要性,曾有人说微积分和导数是最伟大的人类心智成就之一,足以可见它们在人类生产生活中的应用之广泛,今天我们要继续学习导数的另一个应用——“平面曲线的曲率”,这个内容虽然是个选修内容,可是对于我们工程机械专业的学生来说是个不得不学的内容,所以我们接下来就来探讨有关平面曲线的曲率的问题。
二、新课讲解:(一)引入课题:(5分钟)操作实验,并布置任务。
感性认识“直”——“弯”——“最弯之处”:取一根笔直的木杆,当它放置于桌面上时,它很明显时直的,没有弯曲。
当它的两端各受另一个向上的外力时,它马上会开始弯曲,在这个过程中,有的地方弯曲程度大,有的地方弯曲程度小,随着力度的增大,竹片会断裂,很明显我们可以得出结论:断裂处就是弯曲得最厉害的地方。
当然弯曲的时木杆,断裂了也没什么关系,但若是因荷载作用而弯曲变形的船体结构中的钢梁,我们是不能让它们断裂的,所以我们必须找到那个最容易断裂的地方,然后给它加固,或者我们要采取一些什么样的措施来防止因为弯曲而容易断裂的铁路铁轨的问题呢?在数学领域里,我们用曲率来描述曲线的弯曲程度,因此今天我们就来探讨“平面曲线的曲率”的问题。
平面曲线的弧长与曲率

O
ax
π
因此 s 4 2 x2(t ) y2(t )dt 0
π
4 2
3a cos2 t sin t
2
3a sin2 t cos t
2
dt
0
12a
π 2
sin
t
cos
tdt
12a
sin2
t
π 2
6a.
0
20
数学分析 第十章 定积分的应用
高等教育出版社
§3 平面曲线的弧长曲率
平面曲线的弧长
n
故 lim T 0 i1
x2(i ) y2(i )Δti
数学分析 第十章 定积分的应用
高等教育出版社
x2(t) y2(t) dt.
§3 平面曲线的弧长曲率
平面曲线的弧长
由第一章§1习题 6 可知
*平面曲线的曲率
x2(i ) y2(i ) x2(i ) y2(i ) y(i ) y(i ) . 又y(t)在[ , ]上连续,从而在[ , ]上一致连续,
b2
ab sin2 t
b2
32.
当 a b 0 时, 在 t 0, π 处曲率最大, 在 t π ,
3π 2
处曲率最小,
Kmax
a b2
, Kmin
b a2
.
2
数学分析 第十章 定积分的应用
高等教育出版社
§3 平面曲线的弧长曲率
平面曲线的弧长
*平面曲线的曲率
由例1可得,若
a
b
R,
则各点处曲率相等,
数学分析 第十章 定积分的应用
高等教育出版社
§3 平面曲线的弧长曲率
平面曲线的弧长
*平面曲线的曲率
第03章06节平面曲线的曲率
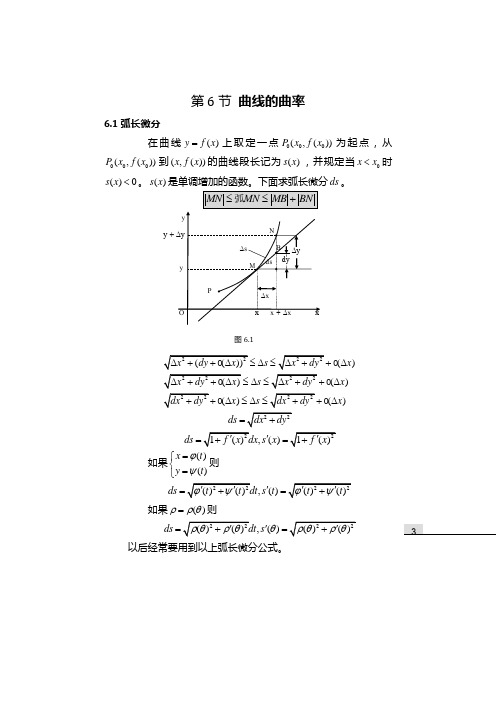
第6节 曲线的曲率6.1弧长微分在曲线()y f x =上取定一点000(,())P x f x 为起点,从000(,())P x f x 到(,())x f x 的曲线段长记为()s x ,并规定当0x x <时()0s x <。
()s x 是单调增加的函数。
下面求弧长微分ds 。
()()()()s x s x x s x ≤∆≤∆≤∆≤∆∆≤∆≤∆ds =,()ds s x '== 如果()()xt y t ϕψ=⎧⎨=⎩则,()ds s t '==如果()ρρθ=则,()ds s θ'==以后经常要用到以上弧长微分公式。
图6.1y +离 散数 学6.2曲线的曲率这节讨论曲线的曲率,也就是曲线的弯曲程度。
设曲线()y f x =在()00,()x f x 的切线0L 与x 轴正向的夹角为0θ,在()00,()x x f x x +∆+∆的切线x L ∆与x 轴正向的夹角为x θ∆。
经过x ∆,切线的夹角变化了0x θθθ∆∆=-设()00,()x f x 和()00,()x x f x x +∆+∆之间曲线的长为s ∆。
容易想见,()00,()x f x 和()00,()x x f x x +∆+∆之间曲线的曲率(弯曲程度)与θ∆成正比,与s ∆成反比,平均曲率()k x sθ∆∆=∆ 让0x ∆→求极限,就得到曲线()y f x =在()00,()x f x 的曲率(弯曲程度)000()lim ()limx x d k x k x s dsθθ∆→∆→∆=∆==∆ 下面我们求出d dsθ从而得到求曲率的计算公式。
用x 作参数 ()()s s x x θθ=⎧⎨=⎩()()2222tan ()1()cos 1tan ()1()()()1()f x d f x dx d f x dx f x d f x dxd f x dx f x θθθθθθθ'=''=''+='''+=''='+第1章集 合322()1()d f x d ds dxdxds f x θθ''=='⎡⎤+⎣⎦003220()()1()f x k x f x ''='⎡⎤+⎣⎦例子:求半径为r 的圆上一点的曲率。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
极坐标方程 ( ),
K
Yunnan University
2 2 2
( 2 )
3 2 2
, ( ( )).
§4. 平面曲线的曲率 四、曲率半径与曲率圆
1 1 , R . 对半径为 R 的圆, R K Def : 曲线上一点的曲率的倒数称为曲线在该点的 K
切线:y = 0 ,
1 2 ( x0 0) ( y0 0) min , 4
2
法线: x = 0 .
1 1 而圆心( x0 , y0 )在法线上, 故 x0 0, y0 (舍y0 ). 2 2 于是, y x2在(0,0)点处的曲率圆方程: 1 2 1 2 x (y ) . 2 4
§4. 平面曲线的曲率
关于 ds 的具体表示式:
y f ( x)(a x b),f ( x)在[a, b]连续,则 ⑴ 弧的方程为
ds 1 f 2 ( x)dx.
⑵ 弧的方程为x (t ),y (t ), t , (t )与 (t )
K
Yunnan University
y (1 y2 )
3 2
.
§4. 平面曲线的曲率
参数方程 x (t ), y (t ),
K
( 2 )
3 2 2
,
(t ) , (t )
§4. 平面曲线, 其弯曲程度一般不同. 例如:
A
1
A'
B
2
A
s
B
A'
s
B'
B
AB AB s. 1 2 .
Yunnan University
§4. 平面曲线的曲率
结论: 曲线的弯曲程度与其 切线方向变化的夹角 的大小及其弧长 s 有关.
曲率半径,记作
1 . K
·
A
o
曲率中心
几何意义: 如图,在A点作曲线的法线,并在曲线凹的一侧的法线上取
A
一点O,使得 OA= (曲线在A点的曲率半径). 以O为圆心,
为半径作一个圆,称之为曲线在A点的曲率圆.
Yunnan University
§4. 平面曲线的曲率 曲率圆与曲线在A点具有以下关系: ⑴ 有共同的切线,即圆与曲线在点 A 相切;
A
A R O
o
x
1 K . s R R
Yunnan University
B
§4. 平面曲线的曲率
对于直线, 其切线方向不变, 即 0 , 有
K 0, s
故“直线不曲” .
同一条曲线的不同点处, 曲线弯曲的程度可能不同.
Def : 曲线在 A 点的曲率为
A
s
·
B B'
o
A'
· s
s s 相同.
Yunnan University
§4. 平面曲线的曲率
将
K s
y
B
s
称为曲线段 AB 的平均曲率,它 刻画了一段曲线的平均弯曲程度. 对于半径为R的圆, 任意弧段 AB = s = R , 有
§4. 平面曲线的曲率 三、曲率的计算
先计算 d , 考虑曲线 y f ( x) 在 M 点的切线, 有
t an y,
两边求微分,得
i.e. arctany.
dy y d dx. 2 2 1 y 1 y
d 把ds和d 代入 K 中得曲率的计算公式: ds
d K lim . s 0 s ds
其中 s 为点A及其邻点B之间弧长, 为AB上切线 方向变化的角度. 曲率刻画了曲线在一点的弯曲程度.
Yunnan University
§4. 平面曲线的曲率 二、弧长的微分 ds y
M ( x, y)
M
s
如图,设曲线的弧长 s 由点 A 起算. 任取 MN = s ,有
在[ , ]连续,且不全为 0,则
ds 2 (t ) 2 (t )dt.
⑶ 弧的方程为 ( )(极坐标方程)( ), ( )
在[ , ]连续, 则
ds 2 ( ) 2 ( )d .
Yunnan University
2
y x2
O1
O
自原点逐渐上升 (| x | 增大),
A
K 逐渐减小, 逐渐增大 .
Yunnan University
x
§4. 平面曲线的曲率
求 y x 2 的最小曲率半径时的曲率圆的方程.
设曲率圆圆心 ( x0 , y0 ), 则
2
又在(0,0)处, y 0, y 2, 故
§4. 平面曲线的曲率
MN MN,用MN代替MN,再令x 0,得
ds 2 dy 2 ( ) 1 ( ) , dx dx
从而即得 弧长微分的公式
ds 1 y dx,
2
或
ds dx dy , ds dx dy .
2 2 2 2 2
Yunnan University
⑵ 有相同的曲率;
⑶ 圆和曲线在点 A 具有相同的一阶和二阶导数. 表明:讨论 y = f (x) 在某点 x 的性质时,若此性质仅 与 x , y , y , y 有关,则只要讨论曲线在 x 点的曲率圆 的性质,即可知这曲线在 x 点附近的性质.
Yunnan University
§4. 平面曲线的曲率
N ( x x, y y)
x
y
MN x2 y 2 , 由此
2
2
A o x
x x
x
2 MN y 1 . x x 当 x 充分小时,在一些假定之下( 如曲线有连续导数 ),
Yunnan University
2 y x 例1. 求抛物线 上任一点处的曲率和曲率半径.
解: y 2 x, y 2.
2 3/ 2 ( 1 4 x ) 2 1 K , . 2 3/ 2 (1 4 x ) K 2
在点(0,0), K max 2, min
1 . 2
O2
y
随着曲线 y x
