武汉 中考数学(反比例函数提高练习题)压轴题训练
中考数学——反比例函数的综合压轴题专题复习附答案解析

一、反比例函数真题与模拟题分类汇编(难题易错题)1.在平面直角坐标系内,双曲线:y= (x>0)分别与直线OA:y=x和直线AB:y=﹣x+10,交于C,D两点,并且OC=3BD.(1)求出双曲线的解析式;(2)连结CD,求四边形OCDB的面积.【答案】(1)解:过点A、C、D作x轴的垂线,垂足分别是M、E、F,∴∠AMO=∠CEO=∠DFB=90°,∵直线OA:y=x和直线AB:y=﹣x+10,∴∠AOB=∠ABO=45°,∴△CEO∽△DEB∴= =3,设D(10﹣m,m),其中m>0,∴C(3m,3m),∵点C、D在双曲线上,∴9m2=m(10﹣m),解得:m=1或m=0(舍去)∴C(3,3),∴k=9,∴双曲线y= (x>0)(2)解:由(1)可知D(9,1),C(3,3),B(10,0),∴OE=3,EF=6,DF=1,BF=1,∴S四边形OCDB=S△OCE+S梯形CDFE+S△DFB= ×3×3+ ×(1+3)×6+ ×1×1=17,∴四边形OCDB的面积是17【解析】【分析】(1)过点A、C、D作x轴的垂线,垂足分别是M、E、F,由直线y=x和y=﹣x+10可知∠AOB=∠ABO=45°,证明△CEO∽△DEB,从而可知 = =3,然后设设D(10﹣m,m),其中m>0,从而可知C的坐标为(3m,3m),利用C、D在反比例函数图象上列出方程即可求出m的值.(2)求分别求出△OCE、△DFB△、梯形CDFE的面积即可求出答案.2.如图.一次函数y=x+b的图象经过点B(﹣1,0),且与反比例函数(k为不等于0的常数)的图象在第一象限交于点A(1,n).求:(1)一次函数和反比例函数的解析式;(2)当1≤x≤6时,反比例函数y的取值范围.【答案】(1)解:把点B(﹣1,0)代入一次函数y=x+b得: 0=﹣1+b,∴b=1,∴一次函数解析式为:y=x+1,∵点A(1,n)在一次函数y=x+b的图象上,∴n=1+1,∴n=2,∴点A的坐标是(1,2).∵反比例函数的图象过点A(1,2).∴k=1×2=2,∴反比例函数关系式是:y=(2)解:反比例函数y= ,当x>0时,y随x的增大而减少,而当x=1时,y=2,当x=6时,y= ,∴当1≤x≤6时,反比例函数y的值:≤y≤2【解析】【分析】(1)根据题意首先把点B(﹣1,0)代入一次函数y=x+b求出一次函数解析式,又点A(1,n)在一次函数y=x+b的图象上,再利用一次函数解析式求出点A的坐标,然后利用代入系数法求出反比例函数解析式,(2)根据反比例函数的性质分别求出当x=1,x=6时的y值,即可得到答案.3.如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数y= (k>0,x>0)的图象上,点D的坐标为(,2).(1)求k的值;(2)若将菱形ABCD沿x轴正方向平移,当菱形的一个顶点恰好落在函数y= (k>0,x >0)的图象上时,求菱形ABCD平移的距离.【答案】(1)解:作DE⊥BO,DF⊥x轴于点F,∵点D的坐标为(,2),∴DO=AD=3,∴A点坐标为:(,5),∴k=5 ;(2)解:∵将菱形ABCD向右平移,使点D落在反比例函数y= (x>0)的图象上D′,∴DF=D′F′=2,∴D′点的纵坐标为2,设点D′(x,2)∴2= ,解得x= ,∴FF′=OF′﹣OF= ﹣ = ,∴菱形ABCD平移的距离为,同理,将菱形ABCD向右平移,使点B落在反比例函数y= (x>0)的图象上,菱形ABCD平移的距离为,综上,当菱形ABCD平移的距离为或时,菱形的一个顶点恰好落在函数图象上.【解析】【分析】(1)根据菱形的性质和D的坐标即可求出A的坐标,代入求出即可;(2)B和D可能落在反比例函数的图象上,根据平移求出即可.4.已知反比例函数y= 的图象经过点A(﹣,1).(1)试确定此反比例函数的解析式;(2)点O是坐标原点,将线段OA绕O点顺时针旋转30°得到线段OB.判断点B是否在此反比例函数的图象上,并说明理由;(3)已知点P(m, m+6)也在此反比例函数的图象上(其中m<0),过P点作x轴的垂线,交x轴于点M.若线段PM上存在一点Q,使得△OQM的面积是,设Q点的纵坐标为n,求n2﹣2 n+9的值.【答案】(1)解:由题意得1= ,解得k=﹣,∴反比例函数的解析式为y=﹣(2)解:过点A作x轴的垂线交x轴于点C.在Rt△AOC中,OC= ,AC=1,∴OA= =2,∠AOC=30°,∵将线段OA绕O点顺时针旋转30°得到线段OB,∴∠AOB=30°,OB=OA=2,∴∠BOC=60°.过点B作x轴的垂线交x轴于点D.在Rt△BOD中,BD=OB•sin∠BOD= ,OD= OB=1,∴B点坐标为(﹣1,),将x=﹣1代入y=﹣中,得y= ,∴点B(﹣1,)在反比例函数y=﹣的图象上(3)解:由y=﹣得xy=﹣,∵点P(m, m+6)在反比例函数y=﹣的图象上,其中m<0,∴m( m+6)=﹣,∴m2+2 m+1=0,∵PQ⊥x轴,∴Q点的坐标为(m,n).∵△OQM的面积是,∴OM•QM= ,∵m<0,∴mn=﹣1,∴m2n2+2 mn2+n2=0,∴n2﹣2 n=﹣1,∴n2﹣2 n+9=8.【解析】【分析】(1)由于反比例函数y= 的图象经过点A(﹣,1),运用待定系数法即可求出此反比例函数的解析式;(2)首先由点A的坐标,可求出OA的长度,∠AOC的大小,然后根据旋转的性质得出∠AOB=30°,OB=OA,再求出点B的坐标,进而判断点B是否在此反比例函数的图象上;(3)把点P(m, m+6)代入反比例函数的解析式,得到关于m的一元二次方程;根据题意,可得Q点的坐标为(m,n),再由△OQM的面积是,根据三角形的面积公式及m<0,得出mn的值,最后将所求的代数式变形,把mn的值代入,即可求出n2﹣2 n+9的值.5.已知:如图,正比例函数y=ax的图象与反比例函数y= 的图象交于点C(3,1)(1)试确定上述比例函数和反比例函数的表达式;(2)根据图象回答,在第一象限内,当x取何值时,反比例函数的值大于正比例函数的值?(3)点D(m,n)是反比例函数图象上的一动点,其中0<m<3,过点C作直线AC⊥x 轴于点A,交OD的延长线于点B;若点D是OB的中点,DE⊥x轴于点E,交OC于点F,试求四边形DFCB的面积.【答案】(1)解:将点C(3,1)分别代入y= 和y=ax,得:k=3,a= ,∴反比例函数解析式为y= ,正比例函数解析式为y= x;(2)解:观察图象可知,在第二象限内,当0<x<3时,反比例函数值大于正比例函数值;(3)解:∵点D(m,n)是OB的中点,又在反比例函数y= 上,∴OE= OA= ,点D(,2),∴点B(3,4),又∵点F在正比例函数y= x图象上,∴F(,),∴DF= 、BC=3、EA= ,∴四边形DFCB的面积为 ×( +3)× = .【解析】【分析】(1)利用待定系数法把C坐标代入解析式即可;(2)须数形结合,先找出交点,在交点的左侧与y轴之间,反比例函数值大于正比例函数值.(3)求出DF、BC、EA,代入梯形面积公式即可.6.已知点P在一次函数y=kx+b(k,b为常数,且k<0,b>0)的图象上,将点P向左平移1个单位,再向上平移2个单位得到点Q,点Q也在该函数y=kx+b的图象上.(1)k的值是________;(2)如图,该一次函数的图象分别与x轴、y轴交于A,B两点,且与反比例函数y=图象交于C,D两点(点C在第二象限内),过点C作CE⊥x轴于点E,记S1为四边形CEOB的面积,S2为△OAB的面积,若 = ,则b的值是________.【答案】(1)﹣2(2)3【解析】【解答】解:(1)设点P的坐标为(m,n),则点Q的坐标为(m﹣1,n+2),依题意得:,解得:k=﹣2.故答案为:﹣2.(2)∵BO⊥x轴,CE⊥x轴,∴BO∥CE,∴△AOB∽△AEC.又∵ = ,∴ = = .令一次函数y=﹣2x+b中x=0,则y=b,∴BO=b;令一次函数y=﹣2x+b中y=0,则0=﹣2x+b,解得:x= ,即AO= .∵△AOB∽△AEC,且 = ,∴.∴AE= AO= b,CE= BO= b,OE=AE﹣AO= b.∵OE•CE=|﹣4|=4,即 b2=4,解得:b=3 ,或b=﹣3 (舍去).故答案为:3 .【分析】(1)设出点P的坐标,根据平移的特性写出Q点的坐标,由点P,Q均在一次函数y=kx+b(k,b为常数,且k<0,b>0)的图象上,即可得出关于k,m,n,b的四元次一方程组,两式作差即可求出k的值;(2)由BO⊥x轴,CE⊥x轴,找出△AOB∽△AEC.再由给定图形的面积比即可求出==,根据一次函数的解析式可以用含b的式子表示出OA,OB,由此即可得出线段CE,AE 的长,利用OE=AE﹣AO求出OE的长,再借助反比例函数K的几何意义得出关于b的一元二次方程,解方程即可得出结论。
中考数学压轴题反比例函数综合题专题练习

中考数学压轴题反比例函数综合题专题练习1、反比例函数y=(k为常数,且k≠0)的图象经过点A(1,3)、B(3,m).(1)求反比例函数的解析式及B点的坐标;(2)在x轴上找一点P,使P A+PB的值最小,求满足条件的点P的坐标.2、如图,一次函数y1=k1x+b的图象与反比例函数y2=(x>0)的图象交于A、B两点,与y轴交于C点,已知A点坐标为(2,1),C点坐标为(0,3)(1)求一次函数和反比例函数的解析式;(2)在x轴上找一点P,使得△PAB的周长最小,请求出点P的坐标.3、如图,反比例函数图象在第一象限的分支上有一点C(1,3),过点C的直线y=kx+b〔k<0〕与x轴交于点A.(1)求反比例函数的解析式;(2)当直线与反比例函数的图象在第一象限内的另一交点的横坐标为3时,求△COD的面积.4、如图,已知反比例函数y=的图象与一次函数y=x+b的图象交于点A(1,4),点B(﹣4,n).(1)求n和b的值;(2)求△OAB的面积;(3)直接写出一次函数值大于反比例函数值的自变量x的取值范围.5、若反比例函数过面积为9的正方形AMON的顶点A,且过点A的直线y2=mx﹣n的图象与反比例函数的另一交点为B(﹣1,a)(1)求出反比例函数与一次函数的解析式;(2)求△AOB的面积.6、如图,在平面直角坐标系xOy中,正方形ABCO的对角线BO在x轴上,若正方形ABCO的边长为2,点B在x负半轴上,反比例函数y=的图象经过C点.(1)求该反比例函数的解析式;(2)当函数值y>﹣2时,请直接写出自变量x的取值范围;(3)若点P是反比例函数上的一点,且△PBO的面积恰好等于正方形ABCO的面积,求点P的坐标.7、如图,已知反比例函数y=的图象与一次函数y=x+b的图象交于点A(1,4),点B(﹣4,n).(1)求n和b的值;(2)求△OAB的面积;(3)直接写出一次函数值大于反比例函数值的自变量x的取值范围.8、如图,一次函数y=kx+b(k≠0)的图象与反比例函数y=(m≠0)的图象交于点A、B,与y轴交于点C.过点A作AD⊥x轴于点D,AD=2,∠CAD=45°,连接CD,已知△ADC的面积等于6.(1)求一次函数和反比例函数的解析式;(2)若点E是点C关于x轴的对称点,求△ABE的面积.9、如图所示,在平面直角坐标系中,一次函数y=ax+1(a≠0)与反比例函数y =(k≠0)的图象交于A、D两点,AB⊥x轴于点B,tan∠AOB=,△AOB的面积为3.(1)求反比例函数和一次函数的解析式;(2)求△AOD的面积;(3)当x为何值时,一次函数值不小于反比例函数值.10、在平面直角坐标系中,一次函数y =﹣x +b 的图象与反比例函数y =(k ≠0)图象交于A 、B 两点,与y 轴交于点C ,与x 轴交于点D ,其中A 点坐标为(﹣2,3).(1)求一次函数和反比例函数解析式.(2)若将点C 沿y 轴向下平移4个单位长度至点F ,连接AF 、BF ,求△ABF 的面积.(3)根据图象,直接写出不等式﹣x +b >的解集.11、如图,在平面直角坐标系xOy 中,一次函数1y ax b (a ,b 为常数,且0a ≠)与反比例函数2m y x=(m 为常数,且0m ≠)的图象交于点A (﹣2,1)、B (1,n ).(1)求反比例函数和一次函数的解析式;(2)连结OA 、OB ,求△AOB 的面积;(3)直接写出当120y y <<时,自变量x 的取值范围.12、如图,已知A(﹣4,a),B(﹣1,2)是一次函数y1=kx+b与反比例函数y2=(m<0)图象的两个交点,AC⊥x轴于C.(1)求出k,b及m的值.(2)根据图象直接回答:在第二象限内,当y1>y2时,x的取值范围是.(3)若P是线段AB上的一点,连接PC,若△PCA的面积等于,求点P坐标.13、如图,在平面直角坐标系xOy中,B(3,﹣1)是反比函数y=图象上的一点,过B点的一次函数y=﹣x+b与反比例函数交于另一点A.(1)求一次函数和反比例函数的表达式;(2)求△AOB面积;(3)在A点左边的反比例函数图象上求点P,使得S△POA:S△AOB=3:2.14、如图,在平面直角坐标系中有Rt△ABC,已知∠CAB=90°,AB=AC,A(﹣2,0),B(0,1).(1)求点C的坐标;(2)将△ABC沿x轴正方向平移,在第一象限内B,C两点的对应点B′,C′恰好落在某反比例函数图象上,求该反比例函数的解析式;(3)若把上一问中的反比例函数记为y1,点B′,C′所在的直线记为y2,请直接写出在第一象限内当y1<y2时x的取值范围.。
中考数学(反比例函数提高练习题)压轴题训练含答案解析

中考数学(反比例函数提高练习题)压轴题训练含答案解析一、反比例函数1.如图,已知抛物线y=﹣x2+9的顶点为A,曲线DE是双曲线y= (3≤x≤12)的一部分,记作G1,且D(3,m)、E(12,m﹣3),将抛物线y=﹣x2+9水平向右移动a个单位,得到抛物线G2.(1)求双曲线的解析式;(2)设抛物线y=﹣x2+9与x轴的交点为B、C,且B在C的左侧,则线段BD的长为________;(3)点(6,n)为G1与G2的交点坐标,求a的值.(4)解:在移动过程中,若G1与G2有两个交点,设G2的对称轴分别交线段DE和G1于M、N两点,若MN<,直接写出a的取值范围.【答案】(1)把D(3,m)、E(12,m﹣3)代入y= 得,解得,所以双曲线的解析式为y= ;(2)2(3)解:把(6,n)代入y= 得6n=12,解得n=2,即交点坐标为(6,2),抛物线G2的解析式为y=﹣(x﹣a)2+9,把(6,2)代入y=﹣(x﹣a)2+9得﹣(6﹣a)2+9=2,解得a=6± ,即a的值为6± ;(4)抛物线G2的解析式为y=﹣(x﹣a)2+9,把D(3,4)代入y=﹣(x﹣a)2+9得﹣(3﹣a)2+9=4,解得a=3﹣或a=3+ ;把E(12,1)代入y=﹣(x﹣a)2+9得﹣(12﹣a)2+9=1,解得a=12﹣2 或a=12+2 ;∵G1与G2有两个交点,∴3+ ≤a≤12﹣2 ,设直线DE的解析式为y=px+q,把D(3,4),E(12,1)代入得,解得,∴直线DE的解析式为y=﹣ x+5,∵G2的对称轴分别交线段DE和G1于M、N两点,∴M(a,﹣ a+5),N(a,),∵MN<,∴﹣ a+5﹣<,整理得a2﹣13a+36>0,即(a﹣4)(a﹣9)>0,∴a<4或a>9,∴a的取值范围为9<a≤12﹣2 .【解析】【解答】解:(2)当y=0时,﹣x2+9=0,解得x1=﹣3,x2=3,则B(﹣3,0),而D(3,4),所以BE= =2 .故答案为2 ;【分析】(1)把D(3,m)、E(12,m﹣3)代入y= 得关于k、m的方程组,然后解方程组求出m、k,即可得到反比例函数解析式和D、E点坐标;(2)先解方程﹣x2+9=0得到B(﹣3,0),而D(3,4),然后利用两点间的距离公式计算DE的长;(3)先利用反比例函数图象上点的坐标特征确定交点坐标为(6,2),然后把(6,2)代入y=﹣(x ﹣a)2+9得a的值;(4)分别把D点和E点坐标代入y=﹣(x﹣a)2+9得a的值,则利用图象和G1与G2有两个交点可得到3+ ≤a≤12﹣2 ,再利用待定系数法求出直线DE的解析式为y=﹣ x+5,则M(a,﹣ a+5),N(a,),于是利用MN<得到﹣ a+5﹣<,然后解此不等式得到a<4或a>9,最后确定满足条件的a的取值范围.2.如图1,已知一次函数y=ax+2与x轴、y轴分别交于点A,B,反比例函数y= 经过点M.(1)若M是线段AB上的一个动点(不与点A、B重合).当a=﹣3时,设点M的横坐标为m,求k与m之间的函数关系式.(2)当一次函数y=ax+2的图象与反比例函数y= 的图象有唯一公共点M,且OM= ,求a的值.(3)当a=﹣2时,将Rt△AOB在第一象限内沿直线y=x平移个单位长度得到Rt△A′O′B′,如图2,M是Rt△A′O′B′斜边上的一个动点,求k的取值范围.【答案】(1)解:当a=﹣3时,y=﹣3x+2,当y=0时,﹣3x+2=0,x= ,∵点M的横坐标为m,且M是线段AB上的一个动点(不与点A、B重合),∴0<m<,,DANG则,﹣3x+2= ,当x=m时,﹣3m+2= ,∴k=﹣3m2+2m(0<m<)(2)解:由题意得:,ax+2= ,ax2+2x﹣k=0,∵直线y=ax+2(a≠0)与双曲线y= 有唯一公共点M时,∴△=4+4ak=0,ak=﹣1,∴k=﹣,则,解得:,∵OM= ,∴12+(﹣)2=()2,a=±(3)解:当a=﹣2时,y=﹣2x+2,∴点A的坐标为(1,0),点B的坐标为(0,2),∵将Rt△AOB在第一象限内沿直线y=x平移个单位得到Rt△A′O′B′,∴A′(2,1),B′(1,3),点M是Rt△A′O′B′斜边上一动点,当点M′与A′重合时,k=2,当点M′与B′重合时,k=3,∴k的取值范围是2≤k≤3【解析】【分析】(1)当a=﹣3时,直线解析式为y=﹣3x+2,求出A点的横坐标,由于点M的横坐标为m,且M是线段AB上的一个动点(不与点A、B重合)从而得到m的取值范围,由﹣3x+2= ,由X=m得k=﹣3m2+2m(0<m<);(2)由ax+2= 得ax2+2x﹣k=0,直线y=ax+2(a≠0)与双曲线y= 有唯一公共点M时,△=4+4ak=0,ak=﹣1,由勾股定理即可;(3)当a=﹣2时,y=﹣2x+2,从而求出A、B两点的坐标,由平移的知识知A′,B′点的坐标,从而得到k的取值范围。
反比例函数大题(二大题型)—2024年中考数学压轴题专项训练(全国通用)解析版

反比例函数大题(二大题型)通用的解题思路:题型一.反比例函数与一次函数的交点问题反比例函数与一次函数的交点问题(1)求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解,若方程组有解则两者有交点,方程组无解,则两者无交点.(2)判断正比例函数y =k 1x 和反比例函数y =在同一直角坐标系中的交点个数可总结为:①当k 1与k 2同号时,正比例函数y =k 1x 和反比例函数y =在同一直角坐标系中有2个交点;②当k 1与k 2异号时,正比例函数y =k 1x 和反比例函数y =在同一直角坐标系中有0个交点. 题型二.反比例函数综合题(1)应用类综合题能够从实际的问题中抽象出反比例函数这一数学模型,是解决实际问题的关键一步,培养了学生的建模能待定系数法和其他学科中的知识.(2)数形结合类综合题利用图象解决问题,从图上获取有用的信息,是解题的关键所在.已知点在图象上,那么点一定满足这个函数解析式,反过来如果这点满足函数的解析式,那么这个点也一定在函数图象上.还能利用图象直接比较函数值或是自变量的大小.将数形结合在一起,是分析解决问题的一种好方法.题型一.反比例函数与一次函数的交点问题(共25小题)1.(2024•新北区校级模拟)如图,双曲线1k y x =与直线232y x =交于A ,B 两点.点(2,)A a 和点(,3)B b −在双曲线上,点C 为x 轴正半轴上的一点.(1)求双曲线1k y x =的表达式和a ,b 的值; (2)请直接写出使得12y y >的x 的取值范围;(3)若ABC ∆的面积为12,求此时C 点的坐标.【分析】(1)把点(2,)A a 和点(,3)B b −代入232y x =,求出a 与b 的值,再将A 点坐标代入1k y x=,即可求出反比例函数解析式;(2)根据A 与B 横坐标,利用图象求出反比例函数值大于一次函数值时x 的范围即可;(3)根据12ABC AOC BOC S S S ∆∆∆=+=,求出OC 的长,进而得到此时C 点的坐标.【解答】解:(1)直线232y x =过点(2,)A a 和点(,3)B b −, 3232a ∴=⨯=,332b =−, 2b ∴=−. 双曲线1k y x=过点(2,3)A , 236k ∴=⨯=,∴双曲线1k y x =的表达式为16y x=;(2)观察图象,可得当2x <−或02x <<时,反比例函数值大于一次函数值,即使得12y y >的x 的取值范围是2x <−或02x <<;(3)(2,3)A ,(2,3)B −−,12ABC AOC BOC S S S ∆∆∆=+=, ∴11331222OC OC ⨯+⨯=, 4OC ∴=,∴此时C 点的坐标为(4,0).【点评】此题考查了待定系数法求反比例函数解析式,一次函数与反比例函数的交点问题,函数图象上点的坐标特征,三角形的面积,利用了数形结合的思想,正确求出反比例函数解析式是解本题的关键.2.(2023•苏州)如图,一次函数2y x =的图象与反比例函数(0)k y x x=>的图象交于点(4,)A n .将点A 沿x 轴正方向平移m 个单位长度得到点B ,D 为x 轴正半轴上的点,点B 的横坐标大于点D 的横坐标,连接BD ,BD 的中点C 在反比例函数(0)k y x x=>的图象上. (1)求n ,k 的值;(2)当m 为何值时,AB OD ⋅的值最大?最大值是多少?【分析】(1)首先将点(4,)A n 代入2y x =可求出n ,再将点A 的坐标代入/y k x =即可求出k ;(2)过点C 作直线EF x ⊥轴于F AB 于E ,先证ECB ∆和FCD ∆全等,得BE DF =,4CE CF ==,进而可求出点(8,4)C ,根据平移的性质得点(4,8)B m +,则4BE DF m ==−,12OD m =−,据此可得出(12)AB DD m m ⋅=−,最后求出这个二次函数的最大值即可.【解答】解:(1)将点(4,)A n 代入2y x =,得:8n =,∴点A 的坐标为(4,8),将点(4,8)A 代入k y x=,得:32k =. (2)点B 的横坐标大于点D 的横坐标,∴点B 在点D 的右侧.过点C 作直线EF x ⊥轴于F ,交AB 于E ,由平移的性质得://AB x 轴,AB m =,B CDF ∴∠=∠,点C 为BD 的中点,BC DC ∴=,在ECB ∆和FCD ∆中,B CDF BC DC BCE DCF ∠=∠⎧⎪=⎨⎪∠=∠⎩,()ECB FCD ASA ∴∆≅∆,BE DF ∴=,CE CF =.//AB x 轴,点A 的坐标为(4,8),8EF ∴=,4CE CF ∴==,∴点C 的纵坐标为4,由(1)知:反比例函数的解析式为:32y x=, ∴当4y =时,8x =,∴点C 的坐标为(8,4), ∴点E 的坐标为(8,8),点F 的坐标为(8,0),点(4,8)A ,AB m =,//AB x 轴,∴点B 的坐标为(4,8)m +,484BE m m ∴=+−=−,4DF BE m ∴==−,8(4)12OD m m ∴=−−=−2(12)(6)36AB OD m m m ⋅=−=−−+∴当6m =时,AB OD ⋅取得最大值,最大值为36.【点评】此题主要考查了反比例函数的图象、二次函数的图象和性质,点的坐标平移等,解答此题的关键是熟练掌握待定系数法求函数的解析式,理解点的坐标的平移,难点是在解答(2)时,构造二次函数求最值.3.(2024•常州模拟)如图,反比例函数1k y x =的图象与一次函数2y k x b =+的图象交于点(1,2)A −,1(4,)2B −. (1)求函数1k y x=和2y k x b =+的表达式; (2)若在x 轴上有一动点C ,当2ABC AOB S S ∆∆=时,求点C 的坐标.【分析】(1)将点(1,2)A −,1(4,)2B −分别代入反比例函数1k y x =和一次函数2y k x b =+的解析式,求解即可;(2)设AB 与y 轴交于点D 作//CE y 轴交AB 于点E ,利用三角形的面积公式,列出方程,求解即可.【解答】解:(1)将点(1,2)A −,1(4,)2B −分别代入反比例函数1k y x =和一次函数2y k x b =+的解析式, 1122k ∴=−⨯=−,222142k b k b −+=⎧⎪⎨+=−⎪⎩, 12k ∴=,21232k b ⎧=−⎪⎪⎨⎪=⎪⎩. ∴反比例函数的解析式为:2y x =,一次函数的解析式为:1322y x =−+. (2)如图,设AB 与y 轴交于点D ,过点C 作//CE y 轴交AB 于点E ,设(,0)C m ,13(,)22E m m ∴−+.13||22CE m ∴=−+.令0x =,则32y =, 3(0,)2D ∴, 32OD ∴=, 11315()[4(1)]2224AOB B A S OD x x ∆∴=⋅−=⨯⨯−−=. 1522ABC AOB S S ∆∆∴==. ∴115()22B A CE x x ⋅−=,即11315||52222m ⋅−+⋅=. 解得3m =−或9m =,∴点C 的坐标为(3,0)−或(9,0).【点评】本题考查了反比例函数与一次函数的交点问题,求三角形的面积,求函数的解析式,正确掌握反比例函数的性质是解题的关键.4.(2024•常州模拟)如图,一次函数1(0)y kx b k =+≠与函数为2(0)m y x x =>的图象交于1(4,1),(,)2A B a 两点.(1)求这两个函数的解析式;(2)根据图象,直接写出满足120y y −>时x 的取值范围;(3)点P 在线段AB 上,过点P 作x 轴的垂线,垂足为M ,交函数2y 的图象于点Q ,若POQ ∆的面积为3,求点P 的坐标.【分析】(1)将A 点坐标代入即可得出反比例函数2(0)m y x x=>,求得函数的解析式,进而求得B 的坐标,再将A 、B 两点坐标分别代入1y kx b =+,可用待定系数法确定一次函数的解析式;(2)由题意即求12y y >的x 的取值范围,由函数的图象即可得出反比例函数的值小于一次函数值的x 的取值范围;(3)由题意,设(,29)P p p −+且142p ……,则4(,)Q p p ,求得429PQ p p=−+−,根据三角形面积公式得到14(29)32POQ S p p p∆=−+−⋅=,解得即可. 【解答】解:(1)反比例函数2(0)m y x x=>的图象经过点(4,1)A , 14m ∴=. 4m ∴=.∴反比例函数解析式为24(0)y x x=>. 把1(2B ,)a 代入24(0)y x x=>,得8a =. ∴点B 坐标为1(2,8), 一次函数解析式1y kx b =+图象经过(4,1)A ,1(2B ,8), ∴41182k b k b +=⎧⎪⎨+=⎪⎩.解得29k b =−⎧⎨=⎩. 故一次函数解析式为:129y x =−+.(2)由120y y −>,12y y ∴>,即反比例函数值小于一次函数值. 由图象可得,142x <<.(3)由题意,设(,29)P p p −+且142p ……, 4(,)Q p p∴. 429PQ p p∴=−+−. 14(29)32POQ S p p p∆∴=−+−⋅=. 解得152p =,22p =. 5(2P ∴,4)或(2,5). 【点评】本题主要考查一次函数与反比例函数交点问题,熟练掌握待定系数法求函数解析式是解题的关键.5.(2024•沭阳县模拟)如图,反比例函数k y x=的图象与一次函数y mx n =+的图象相交于(,1)A a −,(1,3)B −两点.(1)求反比例函数和一次函数的解析式;(2)设直线AB 交y 轴于点C ,点(,0)N t 是x 轴正半轴上的一个动点,过点N 作NM x ⊥轴交反比例函数k y x =的图象于点M ,连接CN ,OM .若3COMN S >四边形,求t 的取值范围.【分析】(1)将点B ,点A 坐标代入反比例函数的解析式,可求a 和k 的值,利用待定系数法可求一次函数解析式;(2)先求出点C 坐标,由面积关系可求解.【解答】解:(1)反比例函数k y x=的图象与一次函数y mx n =+的图象相交于(,1)A a −,(1,3)B −两点, 13(1)k a ∴=−⨯=⨯−,3k ∴=−,3a =,∴点(3,1)A −,反比例函数的解析式为3y x−=,由题意可得:313m n m n =−+⎧⎨−=+⎩,解得:12m n =−⎧⎨=⎩, ∴一次函数解析式为2y x =−+;(2)直线AB 交y 轴于点C ,∴点(0,2)C ,31222OMN OCN COMN S S S t ∆∆∴=+=+⨯⨯四边形, 3COMN S >四边形, ∴312322t +⨯⨯>, 32t ∴>. 【点评】本题考查了反比例函数与一次函数的交点问题,考查了利用待定系数法求解析式,反比例函数的性质等知识,求出两个解析式是解题的关键.6.(2024•宿迁二模)已知函数1y x=的图象与函数(0)y kx k =≠的图象交于点(,)P m n (1)若2m n =,求k 的值和点P 的坐标.(2)当||||m n …时,结合函数图象,直接写出实数k 的取值范围.【分析】(1)由(0)y kx k =≠得n k m =,然后由2m n =可得到k 的值,设(2,)P n n ,将点P 的坐标代入反比例函数解析式可求得n 的值;(2)由(0)y kx k =≠得n k m =,然后结合条件||||m n …可得k 的取值范围. 【解答】解:(1)(0)y kx k =≠, 122y n n k x m n ∴====.2m n =,(2,)P n n ∴,21n n ∴=,解得:2n =±.m ∴=P ∴或(.(2)y kx =, y n k x m ∴==,||||m n …,1k ∴….【点评】本题主要考查的是反比例函数和一次函数的交点问题,掌握待定系数法求函数解析式的方法是解题的关键.7.(2024•泉山区校级模拟)如图,在平面直角坐标系xOy 中,一次函数152y x =+和2y x =−的图象相交于点A ,反比例函数k y x =的图象经过点A . (1)求反比例函数的表达式;(2)设一次函数152y x =+的图象与反比例函数k y x=的图象的另一个交点为B ,连接OB ,求ABO ∆的面积.【分析】(1)联立方程求得A 的坐标,然后根据待定系数法即可求得;(2)联立方程求得交点B 的坐标,进而求得直线与x 轴的交点,然后利用三角形面积公式求得即可.【解答】解:(1)由1522y x y x ⎧=+⎪⎨⎪=−⎩得24x y =−⎧⎨=⎩,(2,4)A ∴−, 反比例函数ky x =的图象经过点A ,248k ∴=−⨯=−,∴反比例函数的表达式是8y x =−; (2)解8152y x y x ⎧=−⎪⎪⎨⎪=+⎪⎩得24x y =−⎧⎨=⎩或81x y =−⎧⎨=⎩,(8,1)B ∴−,由直线AB 的解析式为152y x =+得到直线与x 轴的交点为(10,0)−,111041011522AOB S ∆∴=⨯⨯−⨯⨯=. 【点评】本题考查了一次函数和反比例函数的交点问题,通过方程组求得交点坐标是解题的关键.8.(2023•常州)在平面直角坐标系中,一次函数y kx b =+的图象与反比例函数m y x=的图象相交于点(2,4)A 、(4,)B n .C 是y 轴上的一点,连接CA 、CB .(1)求一次函数、反比例函数的表达式;(2)若ABC ∆的面积是6,求点C 的坐标.【分析】(1)利用待定系数法求得即可;(2)先求得(0,6)D ,再根据ABC BCDACD S S S ∆∆∆=−得1(42)62CD ⨯⋅−=,进而得出6CD =,据此可得点C 的坐标.【解答】解:(1)点(2,4)A 在反比例函数m y x =的图象上, 248m ∴=⨯=,∴反比例函数解析式为8y x =; 又点(4,)B n 在8y x =上,2n ∴=, ∴点B 的坐标为(4,2),把(2,4)A 和(4,2)B 两点的坐标代入一次函数y kx b =+得2442k b k b +=⎧⎨+=⎩,解得16k b =−⎧⎨=⎩,∴一次函数的解析为6y x =−+.(2)对于一次函数6y x =−+,令0x =,则6y =,即(0,6)D , 根据题意得:1(42)62ABC BCD ACD S S S CD ∆∆∆=−=⨯⋅−=, 解得:6CD =,0OC ∴=或12,(0,0)C ∴或(0,12).【点评】本题主要考查了一次函数与反比例函数交点问题,解题时注意:一次函数与反比例函数交点坐标同时满足一次函数与反比例函数解析式.9.(2024•姜堰区一模)如图,一次函数12y x a =−+的图象与反比例函数2(0)k y k x=>的图象在第一象限相交于点(,)A m n ,(2,3)B m n −.(1)求a 、k 的值;(2)当120y y >>时,直接写出x 的取值范围.【分析】(1)根据反比例函数图象上点的坐标特征,得到3m =,代入A 、B 点的坐标再代入一次函数解析式组成方程组求出n 和a ,最后求出k 值即可;(2)根据函数图象直接写出当120y y >>时自变量取值范围即可.【解答】解:(1)点(,)A m n ,(2,3)B m n −都在反比例函数图象上,3(2)mn n m ∴=⨯−,整理得:2(3)0n m −=,0m ≠,0n ≠,30m ∴−=,解得3m =.(3,)A n ,(1,3)B n 在直线12y x a =−+的图象上,∴623a n a n −+=⎧⎨−+=⎩,解得28n a =⎧⎨=⎩,(3,2)A ∴,(3,2)A 在反比例函数图象上,6k ∴=.8a ∴=,6k =.(2)由(1)可知:(3,2)A ,(1,6)B ,根据函数图象可知,120y y >>时,x 的取值范围为:13x <<.【点评】本题考查了一次函数与反比例函数的交点问题,交点坐标满足两个函数解析式是关键.10.(2024•昆山市模拟)如图,一次函数11(0)y k x b k =+≠的图象与反比例函数22(0)k y k x=≠的图象相交于A ,B 两点,其中点A 的坐标为(2,1)−,点B 的坐标为(1,)n .(1)求这两个函数的表达式;(2)根据图象,直接写出满足21k k x b x+>的取值范围; (3)求ABO ∆的面积.【分析】(1)待定系数法求出两个函数解析式即可;(2)根据图像直接写出不等式的解集即可;(3)根据AOB AOC BOC S S S ∆∆∆=+代入数据计算即可.【解答】解:(1)(2,1)A −,(1,)B n 在反比例函数图象上,221k n ∴=−⨯=,22k n ∴==−,∴反比例函数解析式为:2y x =−, (2,1)A −,(1,2)B −在一次函数图象上,∴11212k b k b +−=⎧⎨+=−⎩,解得111k b =−⎧⎨=−⎩,∴一次函数解析式为:1y x =−−.(2)根据两个函数图象及交点坐标,不等式21k k x b x +>的解集为:2x <−或01x <<. (3)设直线AB 与y 轴的交点为C ,则(0,1)C −即1OC =,1131211222AOB AOC BOC S S S ∆∆∆∴=+=⨯⨯+⨯⨯=.【点评】本题考查了一次函数与反比例函数的交点问题,交点坐标满足两个函数解析式.11.(2024•兴化市一模)已知函数1(k y k x =是常数,0)k ≠,函数2392y x =−+. (1)若函数1y 和函数2y 的图象交于点(2,6)A ,点(4,2)B n −.①求k ,n 的值.②当12y y >时,直接写出x 的取值范围.(2)若点(8,)C m 在函数1y 的图象上,点C 先向下平移1个单位,再向左平移3个单位,得点D ,点D 恰好落在函数1y 的图象上,求m 的值.【分析】(1)①根据反比例函数图象上点的坐标特征进行解答即可;②根据图形分布和解答横坐标直接写出不等式解集即可;(2)先根据平移条件得到(5,1)D m −,再根据反比例函数图象上点的坐标特征求出m 值即可.【解答】解:(1)①函数1y 和函数2y 的图象交于点(2,6)A ,点(4,2)B n −,264(2)k n ∴=⨯=⨯−,解得:12k =,5n =. ②由①可知,反比例函数解析式为12y x =,图象分布在第一、三象限,(2,6)A ,(4,3)B 12y y ∴>时,x 的取值范围为:02x <<或4x >.(2)点(8,)C m 在函数1y 的图象上,点C 先向下平移1个单位,再向左平移3个单位,得点D , (5,1)D m ∴−, D 恰好落在函数1ky x =图象上, 5(1)8m m ∴−=,解得53m =−. 【点评】本题考查了反比例函数与一次函数的交点问题,交点坐标满足两个函数解析式是关键.12.(2024•南通模拟)如图,直线AB 交双曲线k y x=于A 、B 两点,交x 轴于点C ,且B 恰为线段AC 的中点,连接OA .若6OAC S ∆=.求k 的值.【分析】设出点B 的坐标,进而可以表示出点A 和点C 的坐标,再根据OAC ∆的面积即可解决问题.【解答】解:设点B 坐标为(,)k a a ,点B 为线段AC 的中点, ∴22A B ky y a ==, 则点A 的坐标为2(,)2a k a , ∴2A C x x a +=, ∴32C x a =,则点C 坐标为3(,0)2a .又AOC ∆的面积为6, ∴132622k a a ⋅⋅=,解得4k =,故k 的值为4.【点评】本题考查反比例函数与一次函数的交点问题,熟知反比例函数及一次函数的图象和性质是解题的关键.13.(2024•亭湖区模拟)如图,等腰三角形OAB 中,AO AB =,点B 坐标为(4,0)顶点A 在反比例函数k y x=的图象上,且OAB ∆的面积为12.(1)k = .(2)过B 点直线对应的解析式为y x b =+与双曲线k y x =在第一,三象限交点分别为点M ,N . ①求点M ,N 的坐标.②直接写出不等式0k x b x −−…的解集.【分析】(1)过点A 作AC OB ⊥于点C ,利用三角形面积求得AC 即可求得点A 的坐标是(2,6),将点A 的坐标代入反比例函数表达式,即可求解;(2)①求得一次函数的解析式,与反比例函数解析式联立,解方程组即可求解;②根据图象即可求得.【解答】解:(1)过点A 作AC OB ⊥于点C ,等腰三角形OAB 中,AO AB =,点B 坐标为(4,0),4OB ∴=,OAB ∆的面积为12, ∴1122OB AC ⋅=,6AC ∴=,(2,6)A ∴,顶点A 在反比例函数k y x =的图象上,解得:2612k =⨯=,故答案为:12;(2)①把B 点的坐标代入y x b =+得:40b +=,4b ∴=−,∴过B 点直线解析式为4y x =−, 联立412y x y x =−⎧⎪⎨=⎪⎩,解得62x y =⎧⎨=⎩或26x y =−⎧⎨=−⎩,(6,2)M ∴,(2,6)N −−; ②观察图象,不等式0k x b x −−…的解集是06x <…或2x −….【点评】本题是反比例函数与一次函数的交点问题,考查了等腰三角形的性质,三角形的面积,待定系数法求反比例函数的解析式,一次函数与反比例函数的交点的求法,函数与不等式的关系,求得A 点的坐标以及数形结合是解题的关键.14.(2024•常熟市模拟)如图,一次函数112y x =−的图象与y 轴相交于B 点,与反比例函数(0,0)k y k x x =≠>图象相交于点(,2)A m .(1)求反比例函数的表达式;(2)点C 在点A 的左侧,过点C 作y 轴平行线,交反比例函数的图象于点D ,连接BD .设点C 的横坐标为a ,求当a 为何值时,BCD ∆的面积最大,这个最大值是多少?【分析】(1)根据待定系数法求出反比例函数解析式即可;(2)根据三角形面积公式列出关于a 的代数式,利用二次函数的最值求法求出最大面积即可.【解答】解:(1)点(,2)A m 在一次函数112y x =−的图象上, ∴1122m −=,解得6m =, (6,2)A ∴,点(6,2)A 在反比例函数图象上,6212k ∴=⨯=,∴反比例函数解析式为:12y x =;(2)在一次函数112y x =−中,令0x =,则1y =−,(0,1)B ∴−,点C 的横坐标为a ,点C 的纵坐标为112a −,12(,)D a a ∴,12112CD a a ∴=−+, 1121(1)22BCD S a a a ∆=⨯−+⨯211642a a =−++2125(1)44a =−−+, 104−<,BCD S ∆∴有最大值,当1a =时,最大值254BCD S ∆=.【点评】本题考查了反比例函数与一次函数的交点问题,熟练掌握交点坐标满足两个函数关系式是关键.15.(2024•东海县一模)一次函数5y x =−+与反比例函数k y x=的图象在第一象限交于A ,B 两点,其中(1,)A a .(1)求反比例函数表达式;(2)结合图象,直接写出5x−+…时,x 的取值范围; (3)若把一次函数5y x =−+的图象向下平移b 个单位,使之与反比例函数k y x =的图象只有一个交点,请直接写出b 的值.【分析】(1)待定系数法求出k 值即可;(2)根据图像和两个函数的交点坐标,直线写出不等式的解集即可;(3)把一次函数5y x =−+的图象向下平移b 个单位得到新的解析式为:5y x b =−+−,联立方程组得到2(5)40x b x −−+=,利用判别式等于0,解出b 值即可.【解答】解:(1)(1,)A a 在一次函数图象上,154a ∴=−+=,即(1,4)A ,(1,4)A 在反比例函数图象上,144k ∴=⨯=,∴反比例函数解析式为:4y x =; (2)联立方程组45y x y x ⎧=⎪⎨⎪=−+⎩,解得14x y =⎧⎨=⎩或41x y =⎧⎨=⎩,(1,4)A ∴,(4,1)B , 根据两个函数图象可知:不等式5kx x −+…的解集为:01x <…或4x …; (3)把一次函数5y x =−+的图象向下平移b 个单位得到新的解析式为:5y x b =−+−, 联立方程组54y x b y x =−+−⎧⎪⎨=⎪⎩,消掉得:45x b x −+−=, 整理得:2(5)40x b x −−+=,△2(5)160b =−−=, 54b ∴−=±,9b ∴=或1.【点评】本题考查了一次函数与反比例函数的交点问题,交点坐标满足两个函数解析式.16.(2024•钟楼区校级模拟)如图,已知反比例函数k y x=的图象与一次函数y ax b =+的图象相交于点(2,3)A 和点(,2)B n −.(1)求反比例函数与一次函数的解析式;(2)直接写出不等式k ax b x >+的解集;(3)若点P 是x 轴上一点,且满足PAB ∆的面积是10,请求出点P 的坐标.【分析】(1)将点A 坐标代入反比例函数解析式求出k ,从而求出点B 坐标,再通过待定系数法求一次函数解析式;(2)通过观察图象交点求解;(3)设点P 坐标为(,0)m ,通过三角形PAB 的面积为10及三角形面积公式求解.【解答】解:(1)将(2,3)代入k y x =得32k=,解得6k =,∴反比例函数解析式为6y x =.26n ∴−=,解得3n =−,所以点B 坐标为(3,2)−−,把(3,2)−−,(2,3)代入y ax b =+得:2332a b a b −=−+⎧⎨=+⎩,解得11a b =⎧⎨=⎩,∴一次函数解析式为1y x =+;(2)由图象可得当3x <−或02x <<时式kax b x >+;(3)设点P 坐标为(,0)m ,一次函数与x 轴交点为E ,把0y =代入1y x =+得01x =+,解得1x =−,∴点E 坐标为(1,0)−.11532222PAB PAE PBE S S S PE PE PE ∆∆∆∴=+=⨯+⨯=, ∴5102PE =,即5|1|102m +=,解得3m =或5m =−.∴点P 坐标为(3,0)或(5,0)−.【点评】本题考查一次函数与反比例函数的结合,解题关键是掌握待定系数法求函数解析式,掌握函数与不等式的关系.17.(2024•姑苏区校级模拟)如图,以x 轴上长为1的线段AB 为宽作矩形ABCD ,矩形长AD 、BC 交直线3y x =−+于点F 、E ,反比例函数(0)k y x x=>的图象正好经过点F 、E . (1)线段EF 长为 ;(2)求k 值.【分析】(1)表示出E 、F 的坐标,然后利用勾股定理即可求得EF 的长度;(2)根据反比例函数图象上点的坐标特征得到(3)(1)(2)k m m m m =−+=+−+,解得即可.【解答】解:(1)点F 、E 在直线3y x =−+图象上,∴设(,3)F m m −+,则(1E m +,(1)3)m −++,即(1,2)m m +−+EF ∴.故答案为:(2)反比例函数(0)k y x x=>的图象正好经过点F 、E , (3)(1)(2)k m m m m ∴=−+=+−+,解得1m =,(3)122k m m ∴=−+=⨯=.【点评】本题是反比例函数与一次函数的交点问题,考查了一次函数图象上点的坐标特征,待定系数法求反比例函数的解析式,求线段的长度,正确表示出点的坐标是解题的关键.18.(2024•昆山市一模)如图,在平面直角坐标系xOy 中,一次函数11(y k x b k =+,b 为常数,且10)k ≠与反比例函数22(k y k x=为常数,且20)k ≠的图象交于点(,6)A m ,(4,3)B −. (1)求反比例函数和一次函数的表达式;(2)当210k k x b x>+>时,直接写出自变量x 的取值范围; (3)已知一次函数1y k x b =+的图象与x 轴交于点C ,点P 在x 轴上,若PAC ∆的面积为9;求点P 的坐标.【分析】(1(2)根据函数图象,写出反比例函数图象在一次函数上方时且在x 轴上方时,自变量的取值范围,即可求解;(3)先求得点C 的坐标,进而根据三角形的面积公式,即可求解.【解答】解:(1)将(4,3)B −代入2k y x=, 解得:212k =−,∴反比例函数表达式为12y x =−, 将(,6)A m 代入12y x=−, 解得:2m =−, (2,6)A ∴−,将(2,6)A −,(4,3)B −代入1y k x b =+,得112643k b k b −+=⎧⎨+=−⎩,解得:1323k b ⎧=−⎪⎨⎪=⎩, ∴一次函数的表达式为:332y x =−+; (2)(2,6)A −,(4,3)B −, 根据函数图象可得:当210k k x b x >+>时,20x −<<; (3)332y x =−+,令0y =, 解得:2x =,(2,0)C ∴,设(,0)P p ,则|2|PC p =−,PAC ∆的面积为9, ∴1|2|692p ⨯−⨯=, 解得:5p =或1−,(5,0)P ∴或(1,0)P −.【点评】本题是反比例函数与一次函数的交点问题,考查了待定系数法求反比例函数的解析式,一次函数19.(2024•盐城模拟)如图,已知一次函数11y k x b =+的图象与反比例函数22k y x=,分别交于点A 和点B ,且A 、B 两点的坐标分别是(1,2)A −−和(2B .)m ,连接OA 、OB .(1)求一次函数11y k x b =+与反比例函数22k y x =的函数表达式; (2)求AOB ∆的面积.【分析】(1)用待定系数法求出反比例函数解析式,用AB 两点坐标求出直线解析式即可;(2)求出直线AB 与x 轴的交点M 的坐标,利用AOB BMO AMO S S S ∆∆∆=+代入数据计算即可.【解答】解:(1)点(1,2)A −−在反比例函数图象上,2k ∴=,反比例函数解析式为:2y x=; (2B .)m 在反比例函数图象上,1m ∴=,即(2,1)B ,点AB 在一次函数11y k x b =+的图象上,∴11221k b k b −+=−⎧⎨+=⎩,解得:111k b =⎧⎨=−⎩, 一次函数解析式为:1y x =−,(2)设直线AB 交x 轴于点M ,当0y =,1x =,(1,0)M ,1OM =. 所以1131112222AOB BMO AMO S S S ∆∆∆=+=⨯⨯+⨯⨯=.小的分界点.20.(2024•天宁区校级模拟)如图,在平面直角坐标系xOy 中,一次函数2y x b =+的图象与x 轴交于点(1,0)A −,与y 轴交于点B ,与反比例函数(0)k y x x=>的图象交于点C ,且AB BC =.点D 是x 轴正半轴上一点,连接CD ,45ODC ∠=︒.(1)求b 和k 的值;(2)求ACD ∆的面积.【分析】(1)将点A 坐标代入一次函数解析式,求出b 的值,再利用平行线分线段成比例的性质得出1OH OA ==,24CH OB ==,求出C 点坐标,即可求出k 的值;(2)根据45ODC ∠=︒得到DCH ∆是等腰直角三角形,求出AD ,再求ACD ∆的面积即可.【解答】解:(1)将点(1,0)A −代入一次函数2y x b =+,得20b −+=,解得2b =,(0,2)B ∴,2OB ∴=,在22y x =+中,令0y =,则1x =−,(1,0)A ∴−,1OA ∴=,过点C 作CH x ⊥轴于点H ,则//OB , ∴OA OB AB AH CH AC==, AB BC =, ∴1212AH CH ==, 2AH ∴=,4CH =,1OH OA ∴==,(1,4)C ∴, 反比例函数(0)k y x x=>的图象过点C , 144k ∴=⨯=; (2)45ODC ∠=︒,CH x ⊥轴于点H ,45DCH ∴∠=︒,DCH ∴∆是等腰直角三角形,4DH CH ∴==,1146AD ∴=++=,ACD ∴∆的面积为:11641222AD CH ⋅=⨯⨯=.【点评】本题是反比例函数与一次函数的交点问题,考查了待定系数法求函数的解析式,平行线分线段成比例定理,等腰直角三角形的性质,求出点C 坐标是解决本题的关键.21.(2024•姑苏区校级一模)如图,一次函数1y kx b =+的图象与反比例函数2(0)m y x x=>的图象交于点(4,1)A 和点(2,)B n .(1)求一次函数和反比例函数解析式;(2)过点B 作BC y ⊥轴于点C ,连接OA ,求四边形OABC 的面积;(3)根据图象直接写出使kx b+<x 的取值范围.【分析】(1)采用待定系数法求函数解析式.先将点A 的坐标代入反比例函数解析式,求出m 值,再将点B 代入反比例函数解析式求出nn 值,然后将A 、B 点坐标代入一次函数解析数即可.(2)四边形OABC 的面积可由一次函数与坐标轴围成的三角形减去两个小三角形的面积得到,求出一次函数与坐标轴的交点即可求出面积.(3)结合图象确定x 的取值范围即可.【解答】解:(1)将点(4,1)A 代入2(0)m y x x =>中, 得14m =,解得4m =, 故24y x =; 将点(2,)B n 代入24y x =,可得422n ==,将(4,1)A ,(2,2)B 代入1y kx b =+,得1422k b k b =+⎧⎨=+⎩,解得123k b ⎧=−⎪⎨⎪=⎩, 故1132y x =−+;(2)如图所示,对于一次函数1132y x =−+,令0x =,则13y =,即(0,3)E令10y =,则6x =,即(6,0)D ,6OD ∴=,3OE =,(2,2)B ,BC y ⊥轴,2BC ∴=,321CE =−=,设AOD ∆的高为h ,由(4,1)A 可知1h =,DOE BOE AODOABC S S S S ∆∆∆=−−四边形 111222OD OE BC CE OD h =⨯⨯−⨯⨯−⨯⨯111632161222=⨯⨯−⨯⨯−⨯⨯5=;(3)结合图象可知,当mkx b x +<时, x 的取值范围为02x <<或4x >.【点评】本题主要考查反比例函数和一次函数的图象性质、待定系数法等综合知识,解决本题的关键是求得正确的点的坐标,将四边形OABC 放在大三角形中求解面积.22.(2024•新北区一模)如图,反比例函数(0)k y x x=>与一次函数2y x m =+的图象交于点(1,4)A ,BC y ⊥轴于点D ,分别交反比例函数与一次函数的图象于点B 、C .(1)求反比例函数和一次函数的表达式;(2)连接AB ,若1OD =,求ABC ∆的面积.【分析】(1)将点A 坐标分别代入两个解析式得到k 、m 值即可;(2)将1y =分别代入两个解析式求出点B 、C 坐标,根据三角形面积公式计算即可.【解答】解:(1)点(1,4)A 在反比例函数图象上,144k ∴=⨯=,∴反比例函数解析式为:4y x=, 2y x m =+的图象过点(1,4)A ,421m ∴=⨯+.解得2m =,∴一次函数解析式为:22y x =+.(2)将1y =代入4y x=得4x =, (4,1)B ∴,将1y =代入22y x =+得12x =−,1(2C ∴−,1), 194()22BC ∴=−−=, 1927(41)224ABC S ∆∴=⨯⨯−=. 【点评】本题考查了一次函数与反比例函数的交点问题,交点坐标满足两个函数解析式.23.(2024•武进区校级模拟)如图,直线3y x =−+与y 轴交于点A ,与x 轴交于点D ,与反比例函数(0)k y k x=≠的图象交于点C ,过点C 作CB x ⊥轴于点B ,3AD AC =. (1)求点A 的坐标及反比例函数的解析式;(2)若点E 是直线3y x =−+与反比例函数(0)k y k x=≠图象的另一个交点,求COE ∆的面积.【分析】(1)求出点A 、点D 的坐标,然后表示出AO 、DO 的长度,再根据//CB y 轴得出DA DO AC OB =,由3AD AC =得出3OD BO =,求出点的横坐标,代入直线解析式求出纵坐标,用待定系数法求出反比例函数解析式;(2)联立两个函数解析式求出点E 坐标,再根据三角形的面积公式求面积即可.【解答】解:(1)直线3y x =−+与y 轴交于点A ,与x 轴交于点D ,(0,3)A ∴,(3,0)D ,即3OA =,3OD =,CB x ⊥轴,//CB y ∴轴, ∴DA DO AC OB=, 3AD AC =,3OD OB ∴=,1OB ∴=,∴点C 的横坐标为1−,点C 在直线3y x =−+上, ∴点(1,4)C −,144k ∴=−⨯=−,∴反比例函数的解析式为4y x=−; (2)联立方程组34y x y x =−+⎧⎪⎨=−⎪⎩,解得14x y =−⎧⎨=⎩或41x y =⎧⎨=−⎩, ∴直线与反比例函数图象的另一个交点E 的坐标为(4,1)−,111115||||313422222COE AOC AOD C D S S S OA x OA x ∆∆∆∴=+=⋅+⋅=⨯⨯+⨯⨯=. 【点评】本题考查了一次函数与坐标轴的交点,一次函数与反比例函数的交点,待定系数法求函数解析式,求出反比例函数解析式是解答本题的关键.24.(2024•东海县一模)如图1,在平面直角坐标系中,一次函数y x b =+的图象经过点(2,0)A −,与反比例函数ky x=的图象交于(,4)B a ,C 两点. (1)求一次函数和反比例函数的表达式;(2)点M 是反比例函数图象在第一象限上的点,且4MAB S ∆=,请求出点M 的坐标;(3)反比例函数具有对称性,适当平移就可发现许多神奇的现象.将该双曲线在第一象限的一支沿射线BC 方向平移,使其经过点C ,再将双曲线在第三象限的一支沿射线CB 方向平移,使其经过点B ,平移后的两条曲线相交于P ,Q 两点,如图2,此时平移后的两条曲线围成了一只美丽的“眸”, PQ 为这只“眸”的“眸径”,请求出“眸径” PQ 的长.【分析】(1)用待定系数法分别求一次函数和反比例函数的表达式;(2)由4MAB S ∆=,得点M 满足在与2y x =+M 在y x =或4y x =+上,列方程组求出交点,即可求出点M ;(3)将反比例函数平移后组成方程组求出交点,再求出PQ 长即可. 【解答】解:(1)把(2,0)A −代入y x b =+,得02b =−+, 2b ∴=,2y x ∴=+,把(,4)B a 代入2y x =+,得42a =+, 2a ∴=, 248k ∴=⨯=, 8y x∴=, ∴一次函数和反比例函数的表达式分别为:2y x =+,8y x=; (2)令2y x =+中0y =,得2x =−, ∴点(2,0)A −,AB ∴=142MAB S h ∆==⨯,h ∴=M 满足在与2y x =+∴点M 在y x =或4y x =+上,由8y x y x =⎧⎪⎨=⎪⎩,得11x y ⎧=⎪⎨=⎪⎩22x y ⎧=−⎪⎨=−⎪⎩点M 在第一象限, ∴点M坐标为,由48y x y x =+⎧⎪⎨=⎪⎩,得1122x y ⎧=−+⎪⎨=+⎪⎩2222x y ⎧=−−⎪⎨=−⎪⎩ 点M 在第一象限,∴点M坐标为(2−+2+,综上点M坐标为或(2−+2+; (3)平移之后的曲线为:866y x =−+和866y x =+−, 由866866y x y x ⎧=+⎪⎪−⎨⎪=−⎪+⎩,得11x y ⎧=⎪⎨=−⎪⎩22x y ⎧=−⎪⎨=⎪⎩,∴点(P −点Q,−,PQ ∴=【点评】本题考查了一次函数及反比例函数的性质的应用,待定系数法的应用及交点的求法是解题关键. 25.(2024•泗阳县校级二模)如图,已知(4,)A n −,(2,4)B −是一次函数y kx b =+的图象和反比例函数my x=的图象的两个交点.(1)求反比例函数和一次函数的解析式;(2)求直线AB 与x 轴的交点C 的坐标及AOB ∆的面积; (3)直接写出一次函数的值小于反比例函数值的x 的取值范围.【分析】(1)先把B 点坐标代入代入my x =,求出m 得到反比例函数解析式,再利用反比例函数解析式确定A 点坐标,然后利用待定系数法求一次函数解析式;。
中考数学压轴题专项训练反比例函数含解析

2021年中考数学压轴题专项训练《反比例函数》1.如图,反比例函数y1=和一次函数y2=mx+n相交于点A(1,3),B(﹣3,a),(1)求一次函数和反比例函数解析式;(2)连接OA,试问在x轴上是否存在点P,使得△OAP为以OA为腰的等腰三角形,若存在,直接写出满足题意的点P的坐标;若不存在,说明理由.解:(1)∵点A(1,3)在反比例函数y1=的图象上,∴k=1×3=3,∴反比例函数的解析式为y1=,∵点B(﹣3,a)在反比例函数y1=的图象上,∴﹣3a=3,∴a=﹣1,∴B(﹣3,﹣1),∵点A(1,3),B(﹣3,﹣1)在一次函数y2=mx+n的图象上,∴,∴,∴一次函数的解析式为y2=x+2;(2)如图,∵△OAP为以OA为腰的等腰三角形,∴①当OA=OP时,∵A(1,3),∴OA=,∵OP=,∵点P在x轴上,∴P(﹣,0)或(,0),②当OA=AP时,则点A是线段OP的垂直平分线上,∵A(1,3),∴P(2,0),即:在x轴上存在点P,使得△OAP为以OA为腰的等腰三角形,此时,点P的坐标为(﹣,0)或(2,0)或(,0).2.在平面直角坐标系xOy中,函数y=(x>0)的图象G经过点A(3,2),直线l:y=kx﹣1(k≠0)与y轴交于点B,与图象G交于点C.(1)求m的值;(2)横、纵坐标都是整数的点叫做整点.记图象G在点A,C 之间的部分与线段BA,BC围成的区域(不含边界)为W.①当直线l过点(2,0)时,直接写出区域W内的整点个数;②若区域W内的整点不少于4个,结合函数图象,求k的取值范围.解:(1)把A(3,2)代入y=得m=3×2=6,(2)①当直线l过点(2,0)时,直线解析式为y=x﹣1,解方程=x﹣1得x1=1﹣(舍去),x2=1+,则C(1+,),而B(0,﹣1),如图1所示,区域W内的整点有(3,1)一个;②如图2,直线l在AB的下方时,直线l:y=kx﹣1过(6,1)时,1=6k﹣1,解得k=,当直线在OA的上方时,直线经过(1,4)时,4=k﹣1,解得k=5,观察图象可知:当k≤或k≥5时,区域W内的整点不少于4个.3.如图,在平面直角坐标系中,四边形OABC的顶点坐标分别为O(0,0),A(6,0),B(4,3),C(0,3).动点P从点O 出发,以每秒个单位长度的速度沿边OA向终点A运动;动点Q从点B同时出发,以每秒1个单位长度的速度沿边BC 向终点C运动,设运动的时间为t秒,PQ2=y.(1)直接写出y关于t的函数解析式及t的取值范围:;(2)当PQ=时,求t的值;(3)连接OB交PQ于点D,若双曲线y=经过点D,问k 的值是否变化?若不变化,请求出k的值;若变化,请说明理由.解:(1)过点P作PE⊥BC于点E,如图1所示.当运动时间为t秒时(0≤t≤4)时,点P的坐标为(t,0),点Q的坐标为(4﹣t,3),∴PE=3,EQ=|4﹣t﹣t|=|4﹣t|,∴PQ2=PE2+EQ2=32+|4﹣t|2=t2﹣20t+25,∴y关于t的函数解析式及t的取值范围:;故答案为:.(2)当时,整理,得5t2﹣16t+12=0,解得:t1=2,.(3)经过点D的双曲线的k值不变.连接OB,交PQ于点D,过点D作DF⊥OA于点F,如图2所示.∵OC=3,BC=4,∴.∵BQ∥OP,∴△BDQ∽△ODP,∴,∴OD=3.∵CB∥OA,∴∠DOF=∠OBC.在Rt△OBC中,,,∴,,∴点D的坐标为,∴经过点D的双曲线的k值为.4.如图,一次函数y=kx+b的图象与反比例函数y=的图象交于点A(﹣3,m+8),B(n,﹣6)两点.(1)求一次函数与反比例函数的解析式;(2)求△AOB的面积;(3)若P(x1,y1),Q(x2,y2)是该反比例函数图象上的两点,且当x1<x2时,y1>y2,指出点P、Q各位于哪个象限?解:(1)将A(﹣3,m+8)代入反比例函数y=得﹣3(m+8)=m,解得m=﹣6,∴点A的坐标为(﹣3,2),反比例函数解析式为y=﹣,将点B(n,﹣6)代入y=﹣得﹣6n=﹣6,解得n=1,∴点B的坐标为(1,﹣6),将点A(﹣3,2),B(1,﹣6)代入y=kx+b得,解得,∴一次函数解析式为y=﹣2x﹣4;(2)设AB与x轴相交于点C,如图,当﹣2x﹣4=0,解得x=﹣2,则点C的坐标为(﹣2,0),∴S△AOB=S△AOC+S△BOC,=×2×2+×2×6,=2+6,=8;(3)∵当x1<x2时,y1>y2,∴点P和点Q不在同一象限,∴P在第二象限,Q在第四象限.5.如图,平面直角坐标系中,一次函数y=x﹣1的图象与x轴,y轴分别交于点A,B,与反比例函数y=的图象交于点C,D,CE⊥x轴于点E,=.(1)求反比例函数的表达式与点D的坐标;(2)以CE为边作▱ECMN,点M在一次函数y=x﹣1的图象上,设点M的横坐标为a,当边MN与反比例函数y=的图象有公共点时,求a的取值范围.解:(1)由题意A(1,0),B(0,﹣1),∴OA=OB=1,∴∠OAB=∠CAE=45°∵AE=3OA,∴AE=3,∵EC⊥x轴,∴∠AEC=90°,∴∠EAC=∠ACE=45°,∴EC=AE=3,∴C(4,3),∵反比例函数y=经过点C(4,3),∴k=12,由,解得或,∴D(﹣3,﹣4).(2)如图,设M(a,a﹣1).当点N在反比例函数的图象上时,N(a,),∵四边形ECMN是平行四边形,∴MN=EC=3,∴|a﹣1﹣|=3,解得a=6或﹣2或﹣1±(舍弃),∴M(6,5)或(﹣2,﹣3),观察图象可知:当边MN与反比例函数y=的图象有公共点时4<a≤6或﹣3≤a≤﹣2.6.如图,一次函数y=kx+2的图象与y轴交于点A,正方形ABCD 的顶点B在x轴上,点D在直线y=kx+2上,且AO=OB,反比例函数y=(x>0)经过点C.(1)求一次函数和反比例函数的解析式;(2)点P是x轴上一动点,当△PCD的周长最小时,求出P 点的坐标;(3)在(2)的条件下,以点C、D、P为顶点作平行四边形,直接写出第四个顶点M的坐标.解:(1)设一次函数y=kx+2的图象与x轴交于点E,连接BD,如图1所示.当x=0时,y=kx+2=2,∴OA=2.∵四边形ABCD为正方形,OA=OB,∴∠BAE=90°,∠OAB=∠OBA=45°,∴∠OAE=∠OEA=45°,∴OE=2,点E的坐标为(﹣2,0).将E(﹣2,0)代入y=kx+2,得:﹣2k+2=0,解得:k=1,∴一次函数的解析式为y=x+2.∵∠OBD=∠ABD+∠OBA=90°,∴BD∥OA.∵OE=OB=2,∴BD=2OA=4,∴点D的坐标为(2,4).∵四边形ABCD为正方形,∴点C的坐标为(2+2﹣0,0+4﹣2),即(4,2).∵反比例函数y=(x>0)经过点C,∴n=4×2=8,∴反比例函数解析式为y=.(2)作点D关于x轴的对称点D′,连接CD′交x轴于点P,此时△PCD的周长取最小值,如图2所示.∵点D的坐标为(2,4),∴点D′的坐标为(2,﹣4).设直线CD′的解析式为y=ax+b(a≠0),将C(4,2),D′(2,﹣4)代入y=ax+b,得:,解得:,∴直线CD′的解析式为y=3x﹣10.当y=0时,3x﹣10=0,解得:x=,∴当△PCD的周长最小时,P点的坐标为(,0).(3)设点M的坐标为(x,y),分三种情况考虑,如图3所示.①当DP为对角线时,,解得:,∴点M1的坐标为(,2);②当CD为对角线时,,解得:,∴点M2的坐标为(,6);③当CP为对角线时,,解得:,∴点M3的坐标为(,﹣2).综上所述:以点C、D、P为顶点作平行四边形,第四个顶点M的坐标为(,2),(,6)或(,﹣2).7.如图在平面直角坐标系中,一次函数y=﹣2x﹣4的图象与反比例函数y=的图象交于点A(1,n),B(m,2)(1)求反比例函数关系式及m的值;(2)若x轴正半轴上有一点M满足△MAB的面积为16,求点M 的坐标;(3)根据函数图象直接写出关于x的不等式在<﹣2x﹣4的解集解:(1)∵一次函数y=﹣2x﹣4的图象过点A(1,n),B(m,2)∴n=﹣2﹣4,2=﹣2m﹣4∴n=﹣6,m=﹣3,∴A(1,﹣6)把A(1,﹣6)代入y=得,k=﹣6,∴反比例函数关系式为y=﹣;(2)设直线AB与x轴交于N点,则N(﹣2,0),设M(m,0),m>0,∵S△MAB=S△BMN+S△AMN,△MAB的面积为16,∴|m+2|×(2+6)=16,解得m=2或﹣6(不合题意舍去),∴M(2,0);(3)由图象可知:不等式在<﹣2x﹣4的解集是x<﹣3或0<x<1.8.如图,在平面直角坐标系中,点A(3,5)与点C关于原点O 对称,分别过点A、C作y轴的平行线,与反比例函数的图象交于点B、D,连结AD、BC,AD与x轴交于点E(﹣2,0).(1)求直线AD对应的函数关系式;(2)求k的值;(3)直接写出阴影部分图形的面积之和.解:(1)设直线AD对应的函数关系式为y=ax+b.∵直线AD过点A(3,5),E(﹣2,0),∴解得∴直线AD的解析式为y=x+2.(2)∵点A(3,5)关于原点O的对称点为点C,∴点C的坐标为(﹣3,﹣5),∵CD∥y轴,∴设点D的坐标为(﹣3,a),∴a=﹣3+2=﹣1,∴点D的坐标为(﹣3,﹣1),∵反比例函数y=的图象经过点D,∴k=﹣3×(﹣1)=3;(3)如图:∵点A和点C关于原点对称,∴阴影部分的面积等于平行四边形CDGF的面积,∴S阴影=4×3=12.9.如图,一次函数y=kx+b的图象分别与反比例函数y=的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.(1)求函数y=kx+b和y=的表达式;(2)已知点C(0,8),试在该一次函数图象上确定一点M,使得MB=MC,求此时点M的坐标.解:(1)把点A(4,3)代入函数得:a=3×4=12,∴y=,OA=5,∵OA=OB,∴OB=5,∴点B的坐标为(0,﹣5),把B(0,﹣5),A(4,3)代入y=kx+b得:∴y=2x﹣5;(2)作MD⊥y轴.∵点M在一次函数y=2x﹣5上,∴设点M的坐标为(x,2x﹣5).∵MB=MC,∴CD=BD,∴x2+(8﹣2x+5)2=x2+(﹣5﹣2x+5)2∴8﹣(2x﹣5)=2x﹣5+5解得:x=∴2x﹣5=,∴点M的坐标为(,).10.如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点B在反比例函数y=(k≠0)的第一象限内的图象上,OA =3,OC=5,动点P在x轴的上方,且满足S△PAO=S矩形OABC.(1)若点P在这个反比例函数的图象上,求点P的坐标;(2)连接PO、PA,求PO+PA的最小值;(3)若点Q是平面内一点,使得以A、B、P、Q为顶点的四边形是菱形,则请你直接写出满足条件的所有点Q的坐标.解:(1)由题意,可知:点B的坐标为(3,5).∵点B在反比例函数y=(k≠0)的第一象限内的图象上,∴k=3×5=15,∴反比例函数的解析式为y=.∵S△PAO=S矩形OABC,∴×3×y P=×3×5,∴y P=3.当y=3时,=3,解得:x=5,∴当点P在这个反比例函数的图象上时,点P的坐标为(5,3).(2)由(1)可知:点P在直线y=3上,作点O关于直线y =3的对称点O′,连接AO′交直线y=3于点P,此时PO+PA 取得最小值,如图1所示.∵点O的坐标为(0,0),∴点O′的坐标为(0,6).∵点A的坐标为(3,0),∴AO′==3,∴PO+PA的最小值为3.(3)∵AB∥y轴,AB=5,点P的纵坐标为3,∴AB不能为对角线,只能为边.设点P的坐标为(m,3),分两种情况考虑,如图2所示:①当点Q在点P的上方时,AP=AB=5,即(m﹣3)2+(3﹣0)2=25,解得:m1=﹣1,m2=7,∴点P1的坐标为(﹣1,3),点P2的坐标为(7,3).又∵PQ=5,且PQ∥AB∥y轴,∴点Q1的坐标为(﹣1,8),点Q2的坐标为(7,8);②当点Q在点P的下方时,BP=AB=5,即(m﹣3)2+(3﹣5)2=25,解得:m3=3﹣,m4=3+,同理,可得出:点Q3的坐标为(3﹣,﹣2),点Q4的坐标为(3+,﹣2).综上所述:当以A、B、P、Q为顶点的四边形是菱形时,点Q 的坐标为(﹣1,8),(7,8),(3﹣,﹣2)或(3+,﹣2).11.如图,已知C,D是反比例函数y=图象在第一象限内的分支上的两点,直线CD分别交x轴、y轴于A,B两点,设C,D的坐标分别是(x1,y1)、(x2,y2),且x1<x2,连接OC、OD.(1)若x1+y1=x2+y2,求证:OC=OD;(2)tan∠BOC=,OC=,求点C的坐标;(3)在(2)的条件下,若∠BOC=∠AOD,求直线CD的解析式.(1)证明:∵C,D是反比例函数y=图象在第一象限内的分支上的两点,∴y1=,y2=.∵x1+y1=x2+y2,即x1+=x2+,∴x1﹣x2=.又∵x1<x2,∴=1,∴=x2=y1,=x1=y2.∴OC==,OD==,∴OC=OD.(2)解:∵tan∠BOC=,∴=.又∵OC=,∴+=10,∴x1=1,y1=3或x1=﹣1,y1=﹣3.∵点C在第一象限,∴点C的坐标为(1,3).(3)解:∵∠BOC=∠AOD,∴tan∠AOD=,∴=.∵点C(1,3)在反比例函数y=的图象上,∴m=1×3=3,∴x2•y2=3,∴x2=3,y2=1或x2=﹣3,y2=﹣1.∵点D在第一象限,∴点D的坐标为(3,1).设直线CD的解析式为y=kx+b(k≠0),将C(1,3),D(3,1)代入y=kx+b,得:,解得:,∴直线CD的解析式为y=﹣x+4.12.如图,在平面直角坐标系中,矩形OABC的两边分别在x 轴、y轴上,D是对角线的交点,若反比例函数y=的图象经过点D,且与矩形OABC的两边AB,BC分别交于点E,F.(1)若D的坐标为(4,2)①则OA的长是8,AB的长是4;②请判断EF是否与AC平行,井说明理由;③在x轴上是否存在一点P.使PD+PE的值最小,若存在,请求出点P的坐标及此时PD+PE的长;若不存在.请说明理由.(2)若点D的坐标为(m,n),且m>0,n>0,求的值.解:(1)①∵点D的坐标为(4,2),∴点B的坐标为(8,4),∴OA=8,AB=4.故答案为:8;4.②EF∥AC,理由如下:∵反比例函数y=的图象经过点D(4,2),∴k=4×2=8.∵点B的坐标为(8,4),BC∥x轴,AB∥y轴,∴点F的坐标为(2,4),点E的坐标为(8,1),∴BF=6,BE=3,∴=,=,∴=.∵∠ABC=∠EBF,∴△ABC∽△EBF,∴∠BCA=∠BFE,∴EF∥AC.③作点E关于x轴对称的点E′,连接DE′交x轴于点P,此时PD+PE的值最小,如图所示.∵点E的坐标为(8,1),∴点E′的坐标为(8,﹣1),∴DE′==5.设直线DE′的解析式为y=ax+b(a≠0),将D(4,2),E′(8,﹣1)代入y=ax+b,得:,解得:,∴直线DE′的解析式为y=﹣x+5.当y=0时,﹣x+5=0,解得:x=,∴当点P的坐标为(,0)时,PD+PE的值最小,最小值为5.(2)∵点D的坐标为(m,n),∴点B的坐标为(2m,2n).∵反比例函数y=的图象经过点D(m,n),∴k=mn,∴点F的坐标为(m,2n),点E的坐标为(2m,n),∴BF=m,BE=n,∴=,=,∴=.又∵∠ABC=∠EBF,∴△ABC∽△EBF,∴==.13.如图,一次函数y=kx+b(k≠0)的图象与反比例函数y=(m ≠0)的图象交于A(﹣3,1),B(1,n)两点.(1)求反比例函数和一次函数解析式;(2)结合图象直接写出不等式﹣kx﹣b>0的解.解:(1)∵点A(﹣3,1)在反比例函数y=(m≠0)的图象上,∴m=(﹣3)×1=﹣3,∴反比例函数的表达式为y=﹣,∵点B(1,n)也在反比例函数y=﹣的图象上,∴n=﹣=﹣3,即B(1,﹣3),把点A(﹣3,1),点B(1,﹣3)代入一次函数y=kx+b中,得,解得,∴一次函数的表达式为y=﹣x﹣2;(2)如图所示,当>kx+b时,x的取值范围是﹣3<x<0或x >1,所以不等式﹣kx﹣b>0的解是:﹣3<x<0或x>1.14.如图,在平面直角坐标系xOy内,函数y=的图象与反比例函数y=(k≠0)图象有公共点A,点A的坐标为(8,a),AB⊥x轴,垂足为点B.(1)求反比例函数的解析式;(2)点P在线段OB上,若AP=BP+2,求线段OP的长;(3)点D为射线OA上一点,在(2)的条件下,若S△ODP=S△ABO,求点D的坐标.解:(1)∵函数y=的图象过点A(8,a),∴a=×8=4,∴点A的坐标为(8,4),∵反比例函数y=(k≠0)图象过点A(8,4),∴4=,得k=32,∴反比例函数的解析式为y=;(2)设BP=b,则AP=b+2,∵点A(8,4),AB⊥x轴于点B,∴AB=4,∠ABP=90°,∴b2+42=(b+2)2,解得,b=3,∴OP=8﹣3=5,即线段OP的长是5;(3)设点D的坐标为(d,d),∵点A(8,4),点B(8,0),点P(5,0),S△ODP=S△ABO,∴,解得,d=,∴d=,∴点D的坐标为(,).15.阅读理解:如图(1),在平面直角坐标系xOy中,已知点A的坐标是(1,2),点B的坐标是(3,4),过点A、点B作平行于x轴、y轴的直线相交于点C,得到Rt△ABC,由勾股定理可得,线段AB==.得出结论:(1)若A点的坐标为(x1,y1),B点的坐标为(x2,y2)请你直接用A、B两点的坐标表示A、B两点间的距离;应用结论:(2)若点P在y轴上运动,试求当PA=PB时,点P的坐标.(3)如图(2)若双曲线L1:y=(x>0)经过A(1,2)点,将线段OA绕点O旋转,使点A恰好落在双曲线L2:y=﹣(x>0)上的点D处,试求A、D两点间的距离.解:(1)∵A点的坐标为(x1,y1),B点的坐标为(x2,y2),∴根据两点间的距离公式得,AB=;(2)设点P(0,a),∵A的坐标是(1,2),点B的坐标是(3,4),∵PA=,PB=,∵PA=PB,∴=,∴a=5,∴P(0,5);(3)∵双曲线L1:y=(x>0)经过A(1,2)点,∴OA=,k=1×2=2,∴双曲线L1:y=(x>0),双曲线L2:y=﹣(x>0),设点D坐标为(m,﹣)(m>0),∴OD=,由旋转知,OA=OD,∴=,∴m=±1或m=±2,∵m>0,∴m=1或m=2,∴D(1,﹣2)或(2,﹣1).∵A(1,2),∴AD=4或.。
中考数学压轴题之反比例函数(中考题型整理,突破提升)及详细答案

则
,
解得
.
故直线 AP 的函数关系式为 y=x+3,
则点 C 的坐标(0,3),OC=3,
∴ S△ AOP=S△ AOC+S△ POC
= OC•AR+ OC•PS
又∵ 点 F 在反比例函数
(k>0)的图象上,∴ k=12,
∴ 该函数的解析式为 y= (x>0)
(2)解:由题意知 E,F 两点坐标分别为 E( ,4),F(6,
∴ 当 k=12 时,S 有最大值.S 最大=3
【解析】【分析】)当 F 为 AB 的中点时,点 F 的坐标为(3,1),由此代入求得函数解
C 与 D 横纵坐标乘积相等,求出 b 的值确定出 B 坐标,进而求出 k 的值,确定出双曲线解 析式;(3)抓住两个关键点,将 A 坐标代入双曲线解析式求出 b 的值;将 C 坐标代入双 曲线解析式求出 b 的值,即可确定出平行四边形与双曲线总有公共点时 b 的范围.
5.如图,正比例函数和反比例函数的图象都经过点 A(3,3),把直线 OA 向下平移后, 与反比例函数的图象交于点 B(6,m),与 x 轴、y 轴分别交于 C、D 两点.
(1)求 m 的值; (2)求过 A、B、D 三点的抛物线的解析式; (3)若点 E 是抛物线上的一个动点,是否存在点 E,使四边形 OECD 的面积 S1
, 是四边
形 OACD 面积 S 的 ?若存在,求点 E 的坐标;若不存在,请说明理由. 【答案】(1)解:∵ 反比例函数的图象都经过点 A(3,3),
中考数学反比例函数-经典压轴题附答案解析
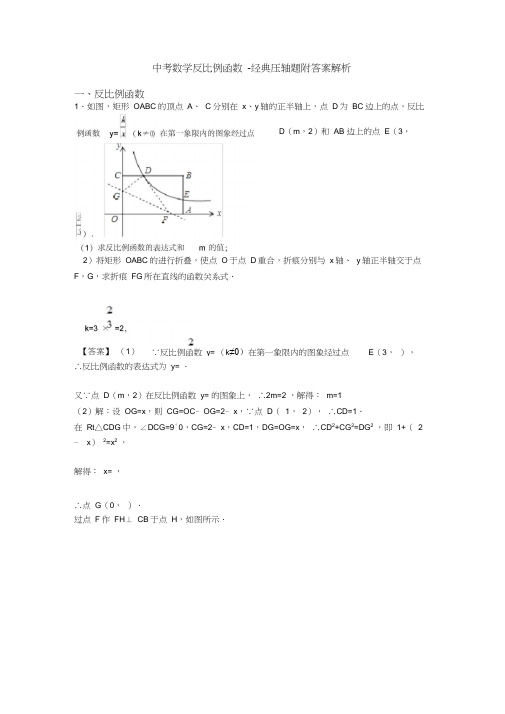
中考数学反比例函数 -经典压轴题附答案解析一、反比例函数1.如图,矩形 OABC 的顶点 A 、 C 分别在 x 、y 轴的正半轴上,点 D 为 BC 边上的点,反比2)将矩形 OABC 的进行折叠,使点 O 于点 D 重合,折痕分别与 x 轴、 y 轴正半轴交于点 F ,G ,求折痕 FG 所在直线的函数关系式. 【答案】 (1)∵反比例函数 y= (k ≠0)在第一象限内的图象经过点E (3, ), ∴反比例函数的表达式为 y= .又∵点 D (m ,2)在反比例函数 y= 的图象上, ∴2m=2 ,解得: m=1(2)解:设 OG=x ,则 CG=OC ﹣OG=2﹣x ,∵点 D ( 1, 2), ∴CD=1.在 Rt △CDG 中,∠DCG=9°0,CG=2﹣x ,CD=1,DG=OG=x , ∴CD 2+CG 2=DG 2 ,即 1+( 2﹣ x ) 2=x 2 ,解得: x= ,∴点 G (0, ).过点 F 作 FH ⊥ CB 于点 H ,如图所示.D (m ,2)和 AB 边上的点E (3,由折叠的特性可知: ∠GDF=∠GOF=9°0 ,OG=DG ,OF=DF . ∵∠ CGD+∠CDG=90 ,°∠CDG+∠ HDF=90 ,° ∴∠ CGD=∠HDF ,∵∠ DCG=∠ FHD=90 ,°∴△ GCD ∽△DHF ,∴ =2 ,∴DF=2GD= ,∴点 F 的坐标为( ,0).设折痕 FG 所在直线的函数关系式为 y=ax+b ,∴折痕 FG 所在直线的函数关系式为 y=﹣ x+【解析】 【分析】( 1)由点 E 的坐标利用反比例函数图象上点的坐标特征即可求出 k 值, 再由点 B 在反比例函数图象上,代入即可求出 m 值;( 2)设 OG=x ,利用勾股定理即可得 出关于 x 的一元二次方程,解方程即可求出 x 值,从而得出点 G 的坐标.再过点 F 作 FH ⊥CB 于点 H ,由此可得出 △GCD ∽△DHF ,根据相似三角形的性质即可求出线段 DF 的长 度,从而得出点 F 的坐标,结合点 G 、 F 的坐标利用待定系数法即可求出结论.∴有 ,解得:2.如图,一次函数y=kx+b 的图象交反比例函数y= (x> 0)的图象于A(4,-8)、 B (m,-2)两点,交x 轴于点C.(1)求反比例函数与一次函数的关系式;(2)根据图象回答:当x 为何值时,一次函数的值大于反比例函数的值?(3)以O、A、B、P为顶点作平行四边形,请直接写出点P 的坐标.【答案】(1)解:∵反比例函数y= (x>0)的图象于A(4,-8),∴k=4 ×(-8)=-32.∵双曲线y= 过点B(m,-2),∴m=16 .由直线y=kx+b 过点 A , B 得:,解得,反比例函数关系式为,一次函数关系式为(2)解:观察图象可知,当0<x<4或x>16时,一次函数的值大于反比例函数的值(3)解:∵ O(0,0),A(4,-8)、B(16,-2),分三种情况:① 若OB∥AP,OA∥ BP,∵O(0,0),A(4,-8),∴由平移规律,点B(16,-2)向右平移 4 个单位,向下平移8 个单位得到P 点坐标为(20,-10);② 若OP∥ AB,OA∥ BP,∵A(4,-8),B(16,-2),∴由平移规律,点O(0,0)向右平移12 个单位,向上平移 6 个单位得到P 点坐标为(12,6);③ 若OB∥ AP,OP∥AB,∵B(16,-2),A(4,-8),∴由平移规律,点O(0,0)向左平移12 个单位,向下平移 6 个单位得到P 点坐标为(- 12,-6);∴以O,A,B,P为顶点作平行四边形,第四个顶点P的坐标为(12,6)或(-12,-6)或(20,-10)【解析】【分析】(1)将点A(4,-8),B(m ,-2)代入反比例函数y= (x> 0)中,可求k、a;再将点A(4,-8),B(m,-2)代入y=kx+b 中,列方程组求k、b 即可;(2)根据两函数图象的交点,图象的位置可确定一次函数的值大于反比例函数的值时x 的范围;(3)根据平行四边形的性质,即可直接写出.3.如图,已知A(3,m),B(﹣2,﹣3)是直线AB 和某反比例函数的图象的两个交点.(1)求直线AB 和反比例函数的解析式;(2)观察图象,直接写出当x 满足什么范围时,直线AB 在双曲线的下方;(3)反比例函数的图象上是否存在点C,使得△OBC 的面积等于△OAB 的面积?如果不存在,说明理由;如果存在,求出满足条件的所有点 C 的坐标.【答案】(1)解:设反比例函数解析式为y= ,把B(﹣2,﹣3)代入,可得k=﹣2×(﹣ 3 )=6,∴反比例函数解析式为y= ;把A(3,m)代入y= ,可得3m=6,即m=2 ,∴A(3,2),设直线AB 的解析式为y=ax+b,把A(3,2),B(﹣2,﹣3)代入,可得解得,∴直线AB 的解析式为y=x﹣1(2)解:由题可得,当x满足:x<﹣2或0<x<3时,直线AB在双曲线的下方(3)解:存在点C.如图所示,延长AO 交双曲线于点C1 ,∵点 A 与点C1 关于原点对称,∴AO=C1O,∴△ OBC1的面积等于△ OAB的面积,此时,点C1的坐标为(﹣3,﹣2);如图,过点C1作BO的平行线,交双曲线于点C2 ,则△OBC2的面积等于△ OBC1的面积,∴△ OBC2的面积等于△ OAB的面积,由B(﹣2,﹣3)可得OB 的解析式为y= x ,可设直线C1C2 的解析式为y= x+b',把C1(﹣3,﹣2)代入,可得﹣2= ×(﹣3)+b',解得b'= ,∴直线C1C2 的解析式为y= x+ ,解方程组,可得C2();如图,过 A 作OB的平行线,交双曲线于点C3 ,则△OBC3 的面积等于△ OBA的面积,设直线AC3 的解析式为y= x+ ,把A(3,2)代入,可得2= ×3+ ,解得=﹣,∴直线AC3 的解析式为y= x﹣,解方程组,可得C3();综上所述,点C的坐标为(﹣3,﹣2),(()).【解析】【分析】(1)用待定系数法求出反比例函数解析式,一次函数解析式,将已知的点A,B 的坐标代入设的函数解析式列出关于待定系数的方程(组)求出系数,再回代到解析式(2)结合图像判断直线AB 在双曲线的交点坐标为A,B,X 取值范围为双曲线所在象限交点的横坐标,第一象限为为小于横坐标大于零,第三象限为小于横坐标(3)结合已知条件根据同底等高、等底同高作出与原三角形面积相等的三角形,再结合已知条件用待定系数法求出与双曲线有交点的直线的解析式,得出点的坐标,注意要考虑满足条件的所有点 C 的坐标。
2020-2021中考数学反比例函数提高练习题压轴题训练及答案

2020-2021中考数学反比例函数提高练习题压轴题训练及答案一、反比例函数1.如图直角坐标系中,矩形ABCD的边BC在x轴上,点B,D的坐标分别为B(1,0),D(3,3).(1)点C的坐标________;(2)若反比例函数y= (k≠0)的图象经过直线AC上的点E,且点E的坐标为(2,m),求m的值及反比例函数的解析式;(3)若(2)中的反比例函数的图象与CD相交于点F,连接EF,在直线AB上找一点P,使得S△PEF= S△CEF,求点P的坐标.【答案】(1)(3,0)(2)解:∵AB=CD=3,OB=1,∴A的坐标为(1,3),又C(3,0),设直线AC的解析式为y=ax+b,则,解得:,∴直线AC的解析式为y=﹣ x+ .∵点E(2,m)在直线AC上,∴m=﹣ ×2+ = ,∴点E(2,).∵反比例函数y= 的图象经过点E,∴k=2× =3,∴反比例函数的解析式为y=(3)解:延长FC至M,使CM= CF,连接EM,则S△EFM= S△EFC, M(3,﹣0.5).在y= 中,当x=3时,y=1,∴F(3,1).过点M作直线MP∥EF交直线AB于P,则S△PEF=S△MEF.设直线EF的解析式为y=a'x+b',∴,解得,∴y=﹣ x+ .设直线PM的解析式为y=﹣ x+c,代入M(3,﹣0.5),得:c=1,∴y=﹣ x+1.当x=1时,y=0.5,∴点P(1,0.5).同理可得点P(1,3.5).∴点P坐标为(1,0.5)或(1,3.5).【解析】【解答】解:(1)∵D(3,3),∴OC=3,∴C(3,0).故答案为(3,0);【分析】(1)由D的横坐标为3,得到线段OC=3,即可确定出C的坐标;(2)由矩形的对边相等,得到AB=CD,由D的纵坐标确定出CD的长,即为AB的长,再由B的坐标确定出OB的长,再由A为第一象限角,确定出A的坐标,由A与C的坐标确定出直线AC的解析式,将E坐标代入直线AC解析式中,求出m的值,确定出E的坐标,代入反比例解析式中求出k的值,即可确定出反比例解析式;(3)延长FC至M,使CM=CF,连接EM,则S△EFM=S△EFC, M(3,﹣0.5).求出F(3,1),过点M作直线MP∥EF交直线AB于P,利用平行线间的距离处处相等得到高相等,再利用同底等高得到S△PEF=S△MEF.此时直线EF与直线PM的斜率相同,由F的横坐标与C横坐标相同求出F 的横坐标,代入反比例解析式中,确定出F坐标,由E与F坐标确定出直线EF斜率,即为直线PM的斜率,再由M坐标,确定出直线PM解析式,由P横坐标与B横坐标相同,将B横坐标代入直线PM解析式中求出y的值,即为P的纵坐标,进而确定出此时P的坐标.2.如图,在平面直角坐标系中,直线AB与x轴交于点B,与y轴交于点A,与反比例函数y= 的图象在第二象限交于点C,CE⊥x轴,垂足为点E,tan∠ABO= ,OB=4,OE=2.(1)求反比例函数的解析式;(2)若点D是反比例函数图象在第四象限上的点,过点D作DF⊥y轴,垂足为点F,连接OD、BF.如果S△BAF=4S△DFO,求点D的坐标.【答案】(1)解:∵OB=4,OE=2,∴BE=OB+OE=6.∵CE⊥x轴,∴∠CEB=90°.在Rt△BEC中,∠CEB=90°,BE=6,tan∠ABO= ,∴CE=BE•tan∠ABO=6× =3,结合函数图象可知点C的坐标为(﹣2,3).∵点C在反比例函数y= 的图象上,∴m=﹣2×3=﹣6,∴反比例函数的解析式为y=﹣(2)解:∵点D在反比例函数y=﹣第四象限的图象上,∴设点D的坐标为(n,﹣)(n>0).在Rt△AOB中,∠AOB=90°,OB=4,tan∠ABO= ,∴OA=OB•tan∠ABO=4× =2.∵S△BAF= AF•OB= (OA+OF)•OB= (2+ )×4=4+ .∵点D在反比例函数y=﹣第四象限的图象上,∴S△DFO= ×|﹣6|=3.∵S△BAF=4S△DFO,∴4+ =4×3,解得:n= ,经验证,n= 是分式方程4+ =4×3的解,∴点D的坐标为(,﹣4).【解析】【分析】(1)由边的关系可得出BE=6,通过解直角三角形可得出CE=3,结合函数图象即可得出点C的坐标,再根据点C的坐标利用反比例函数图象上点的坐标特征,即可求出反比例函数系数m,由此即可得出结论;(2)由点D在反比例函数在第四象限的图象上,设出点D的坐标为(n,﹣)(n>0).通过解直角三角形求出线段OA的长度,再利用三角形的面积公式利用含n的代数式表示出S△BAF,根据点D在反比例函数图形上利用反比例函数系数k的几何意义即可得出S△DFO的值,结合题意给出的两三角形的面积间的关系即可得出关于n的分式方程,解方程,即可得出n值,从而得出点D的坐标.3.如图,过原点O的直线与双曲线交于上A(m,n)、B,过点A的直线交x轴正半轴于点D,交y轴负半轴于点E,交双曲线于点P.(1)当m=2时,求n的值;(2)当OD:OE=1:2,且m=3时,求点P的坐标;(3)若AD=DE,连接BE,BP,求△PBE的面积.【答案】(1)解:∵点A(m,n)在双曲线y=上,∴mn=6,∵m=2,∴n=3;(2)解:由(1)知,mn=6,∵m=3,∴n=2,∴A(3,2),∵OD:OE=1:2,设OD=a,则OE=2a,∵点D在x轴坐标轴上,点E在y轴负半轴上,∴D(a,0),E(0,﹣2a),∴直线DE的解析式为y=2x﹣2a,∵点A(3,2)在直线y=2x﹣2a上,∴6﹣2a=2,∴a=2,∴直线DE的解析式为y=2x﹣4①,∵双曲线的解析式为y=②,联立①②解得,(点A的横纵坐标,所以舍去)或,∴P(﹣2,﹣3);(3)解:∵AD=DE,点D在x轴坐标轴上,点E在y轴负半轴上,A(m,n),∴E(0,﹣n),D( m,0),∴直线DE的解析式为y= x﹣n,∵mn=6,∴m=,∴y= x﹣n③,∵双曲线的解析式为y=④,联立③④解得,∴(点A的横纵坐标,所以舍去)或,∴P(﹣2m,﹣2n),∵A(m,n),∴直线AB的解析式为y=x⑤.联立④⑤解得,(点A的横纵坐标,所以舍去)或∴B(﹣m,﹣n),∵E(0,﹣n),∴BE∥x轴,∴S△PBE= BE×|y E﹣y P|= ×m×|﹣n﹣(﹣2n)|= mn=3.【解析】【分析】(1)把A(2,n)代入解析式即可求出n;(2)先求出A点坐标,设OD=a,则OE=2a,得D(a,0),E(0,﹣2a),直线DE的解析式为y=2x﹣2a,把点A(3,2)代入求出a,再联立两函数即可求出交点P;(3)由AD=DE,点D在x轴坐标轴上,点E在y轴负半轴上,故A(m,n),E(0,﹣n),D( m,0),求得直线DE 的解析式为y= x﹣n,又mn=6,得y= x﹣n,与y=联立得,即为P点坐标,由直线AB的解析式为y= x与双曲线联立解得B (﹣m,﹣n),再根据S△PBE= BE×|y E﹣y P|= ×m×|﹣n﹣(﹣2n)|求出等于3.4.如图,直线y=2x+6与反比例函数y= (k>0)的图象交于点A(1,m),与x轴交于点B,平行于x轴的直线y=n(0<n<6)交反比例函数的图象于点M,交AB于点N,连接BM.(1)求m的值和反比例函数的表达式;(2)观察图象,直接写出当x>0时不等式2x+6﹣<0的解集;(3)直线y=n沿y轴方向平移,当n为何值时,△BMN的面积最大?最大值是多少?【答案】(1)解:∵直线y=2x+6经过点A(1,m),∴m=2×1+6=8,∴A(1,8),∵反比例函数经过点A(1,8),∴k=8,∴反比例函数的解析式为y= .(2)解:不等式2x+6﹣<0的解集为0<x<1.(3)解:由题意,点M,N的坐标为M(,n),N(,n),∵0<n<6,∴<0,∴﹣>0∴S△BMN= |MN|×|y M|= ×(﹣)×n=﹣(n﹣3)2+ ,∴n=3时,△BMN的面积最大,最大值为.【解析】【分析】(1)求出点A的坐标,利用待定系数法即可解决问题;(2)由图象直接求得;(3)构建二次函数,利用二次函数的最值即可解决问题.5.如图1,已知(x>0)图象上一点P,PA⊥x轴于点A(a,0),点B坐标为(0,b)(b>0),动点M是y轴正半轴上B点上方的点,动点N在射线AP上,过点B 作AB的垂线,交射线AP于点D,交直线MN于点Q,连结AQ,取AQ的中点为C.(1)如图2,连结BP,求△PAB的面积;(2)当点Q在线段BD上时,若四边形BQNC是菱形,面积为,求此时P点的坐标;(3)当点Q在射线BD上时,且a=3,b=1,若以点B,C,N,Q为顶点的四边形是平行四边形,求这个平行四边形的周长.【答案】(1)解:连接OP,(2)解:如图1,∵四边形BQNC是菱形,∴BQ=BC=NQ,∠BQC=∠NQC。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、反比例函数真题与模拟题分类汇编(难题易错题)1.如图,反比例函数y= 的图象与一次函数y= x的图象交于点A、B,点B的横坐标是4.点P是第一象限内反比例函数图象上的动点,且在直线AB的上方.(1)若点P的坐标是(1,4),直接写出k的值和△PAB的面积;(2)设直线PA、PB与x轴分别交于点M、N,求证:△PMN是等腰三角形;(3)设点Q是反比例函数图象上位于P、B之间的动点(与点P、B不重合),连接AQ、BQ,比较∠PAQ与∠PBQ的大小,并说明理由.【答案】(1)解:k=4,S△PAB=15.提示:过点A作AR⊥y轴于R,过点P作PS⊥y轴于S,连接PO,设AP与y轴交于点C,如图1,把x=4代入y= x,得到点B的坐标为(4,1),把点B(4,1)代入y= ,得k=4.解方程组,得到点A的坐标为(﹣4,﹣1),则点A与点B关于原点对称,∴OA=OB,∴S△AOP=S△BOP,∴S△PAB=2S△AOP.设直线AP的解析式为y=mx+n,把点A(﹣4,﹣1)、P(1,4)代入y=mx+n,求得直线AP的解析式为y=x+3,则点C的坐标(0,3),OC=3,∴S△AOP=S△AOC+S△POC= OC•AR+ OC•PS= ×3×4+ ×3×1= ,∴S△PAB=2S△AOP=15;(2)解:过点P作PH⊥x轴于H,如图2.B(4,1),则反比例函数解析式为y= ,设P(m,),直线PA的方程为y=ax+b,直线PB的方程为y=px+q,联立,解得直线PA的方程为y= x+ ﹣1,联立,解得直线PB的方程为y=﹣ x+ +1,∴M(m﹣4,0),N(m+4,0),∴H(m,0),∴MH=m﹣(m﹣4)=4,NH=m+4﹣m=4,∴MH=NH,∴PH垂直平分MN,∴PM=PN,∴△PMN是等腰三角形;(3)解:∠PAQ=∠PBQ.理由如下:过点Q作QT⊥x轴于T,设AQ交x轴于D,QB的延长线交x轴于E,如图3.可设点Q为(c,),直线AQ的解析式为y=px+q,则有,解得:,∴直线AQ的解析式为y= x+ ﹣1.当y=0时, x+ ﹣1=0,解得:x=c﹣4,∴D(c﹣4,0).同理可得E(c+4,0),∴DT=c﹣(c﹣4)=4,ET=c+4﹣c=4,∴DT=ET,∴QT垂直平分DE,∴QD=QE,∴∠QDE=∠QED.∵∠MDA=∠QDE,∴∠MDA=∠QED.∵PM=PN,∴∠PMN=∠PNM.∵∠PAQ=∠PMN﹣∠MDA,∠PBQ=∠NBE=∠PNM﹣∠QED,∴∠PAQ=∠PBQ.【解析】【分析】(1)过点A作AR⊥y轴于R,过点P作PS⊥y轴于S,连接PO,设AP 与y轴交于点C,如图1,可根据条件先求出点B的坐标,然后把点B的坐标代入反比例函数的解析式,即可求出k,然后求出直线AB与反比例函数的交点A的坐标,从而得到OA=OB,由此可得S△PAB=2S△AOP,要求△PAB的面积,只需求△PAO的面积,只需用割补法就可解决问题;(2)过点P作PH⊥x轴于H,如图2.可用待定系数法求出直线PB的解析式,从而得到点N的坐标,同理可得到点M的坐标,进而得到MH=NH,根据垂直平分线的性质可得PM=PN,即△PMN是等腰三角形;(3)过点Q作QT⊥x轴于T,设AQ交x轴于D,QB的延长线交x轴于E,如图3.可设点Q为(c,),运用待定系数法求出直线AQ的解析式,即可得到点D的坐标为(c﹣4,0),同理可得E(c+4,0),从而得到DT=ET,根据垂直平分线的性质可得QD=QE,则有∠QDE=∠QED.然后根据对顶角相等及三角形外角的性质,就可得到∠PAQ=∠PBQ.2.如图,已知直线y=ax+b与双曲线y= (x>0)交于A(x1, y1),B(x2, y2)两点(A与B不重合),直线AB与x轴交于P(x0,0),与y轴交于点C.(1)若A,B两点坐标分别为(1,3),(3,y2),求点P的坐标.(2)若b=y1+1,点P的坐标为(6,0),且AB=BP,求A,B两点的坐标.(3)结合(1),(2)中的结果,猜想并用等式表示x1,x2,x0之间的关系(不要求证明).【答案】(1)解:∵直线y=ax+b与双曲线y= (x>0)交于A(1,3),∴k=1×3=3,∴y= ,∵B(3,y2)在反比例函数的图象上,∴y2= =1,∴B(3,1),∵直线y=ax+b经过A、B两点,∴解得,∴直线为y=﹣x+4,令y=0,则x=4,∴P(4,O)(2)解:如图,作AD⊥y轴于D,AE⊥x轴于E,BF⊥x轴于F,BG⊥y轴于G,AE、BG 交于H,则AD∥BG∥x轴,AE∥BF∥y轴,∴= ,= = ,∵b=y1+1,AB=BP,∴= ,= = ,∴B(,y1)∵A,B两点都是反比例函数图象上的点,∴x1•y1= • y1,解得x1=2,代入= ,解得y1=2,∴A(2,2),B(4,1)(3)解:根据(1),(2)中的结果,猜想:x1, x2, x0之间的关系为x1+x2=x0【解析】【分析】(1)先把A(1,3)),B(3,y2)代入y= 求得反比例函数的解析式,进而求得B的坐标,然后把A、B代入y=ax+b利用待定系数法即可求得直线的解析式,继而即可求得P的坐标;(2)作AD⊥y轴于D,AE⊥x轴于E,BF⊥x轴于F,BG⊥y轴于G,AE、BG交于H,则AD∥BG∥x轴,AE∥BF∥y轴,得出 = , = = ,根据题意得出 = , = = ,从而求得B(, y1),然后根据k=xy得出x1•y1= • y1,求得x1=2,代入 = ,解得y1=2,即可求得A、B的坐标;(3)合(1),(2)中的结果,猜想x1+x2=x0.3.如图,在平面直角坐标系中,一次函数y1=ax+b(a≠0)的图象与y轴相交于点A,与反比例函数y2= (c≠0)的图象相交于点B(3,2)、C(﹣1,n).(1)求一次函数和反比例函数的解析式;(2)根据图象,直接写出y1>y2时x的取值范围;(3)在y轴上是否存在点P,使△PAB为直角三角形?如果存在,请求点P的坐标;若不存在,请说明理由.【答案】(1)解:把B(3,2)代入得:k=6∴反比例函数解析式为:把C(﹣1,n)代入,得:n=﹣6∴C(﹣1,﹣6)把B(3,2)、C(﹣1,﹣6)分别代入y1=ax+b,得:,解得:所以一次函数解析式为y1=2x﹣4(2)解:由图可知,当写出y1>y2时x的取值范围是﹣1<x<0或者x>3.(3)解:y轴上存在点P,使△PAB为直角三角形如图,过B作BP1⊥y轴于P1,∠B P1 A=0,△P1AB为直角三角形此时,P1(0,2)过B作BP2⊥AB交y轴于P2∠P2BA=90,△P2AB为直角三角形在Rt△P1AB中,在Rt△P1 AB和Rt△P2 AB∴∴P2(0,)综上所述,P1(0,2)、P2(0,).【解析】【分析】(1)利用待定系数法求出反比例函数解析式,进而求出点C坐标,最后用再用待定系数法求出一次函数解析式;(2)利用图象直接得出结论;(3)分三种情况,利用勾股定理或锐角三角函数的定义建立方程求解即可得出结论.4.如图1,已知一次函数y=ax+2与x轴、y轴分别交于点A,B,反比例函数y= 经过点M.(1)若M是线段AB上的一个动点(不与点A、B重合).当a=﹣3时,设点M的横坐标为m,求k与m之间的函数关系式.(2)当一次函数y=ax+2的图象与反比例函数y= 的图象有唯一公共点M,且OM= ,求a的值.(3)当a=﹣2时,将Rt△AOB在第一象限内沿直线y=x平移个单位长度得到Rt△A′O′B′,如图2,M是Rt△A′O′B′斜边上的一个动点,求k的取值范围.【答案】(1)解:当a=﹣3时,y=﹣3x+2,当y=0时,﹣3x+2=0,x= ,∵点M的横坐标为m,且M是线段AB上的一个动点(不与点A、B重合),∴0<m<,,DANG则,﹣3x+2= ,当x=m时,﹣3m+2= ,∴k=﹣3m2+2m(0<m<)(2)解:由题意得:,ax+2= ,ax2+2x﹣k=0,∵直线y=ax+2(a≠0)与双曲线y= 有唯一公共点M时,∴△=4+4ak=0,ak=﹣1,∴k=﹣,则,解得:,∵OM= ,∴12+(﹣)2=()2,a=±(3)解:当a=﹣2时,y=﹣2x+2,∴点A的坐标为(1,0),点B的坐标为(0,2),∵将Rt△AOB在第一象限内沿直线y=x平移个单位得到Rt△A′O′B′,∴A′(2,1),B′(1,3),点M是Rt△A′O′B′斜边上一动点,当点M′与A′重合时,k=2,当点M′与B′重合时,k=3,∴k的取值范围是2≤k≤3【解析】【分析】(1)当a=﹣3时,直线解析式为y=﹣3x+2,求出A点的横坐标,由于点M的横坐标为m,且M是线段AB上的一个动点(不与点A、B重合)从而得到m的取值范围,由﹣3x+2= ,由X=m得k=﹣3m2+2m(0<m<);(2)由ax+2= 得ax2+2x﹣k=0,直线y=ax+2(a≠0)与双曲线y= 有唯一公共点M时,△=4+4ak=0,ak=﹣1,由勾股定理即可;(3)当a=﹣2时,y=﹣2x+2,从而求出A、B两点的坐标,由平移的知识知A′,B′点的坐标,从而得到k的取值范围。
5.平面直角坐标系xOy中,点A、B分别在函数y1= (x>0)与y2=﹣(x<0)的图象上,A、B的横坐标分别为a、b.(1)若AB∥x轴,求△OAB的面积;(2)若△OAB是以AB为底边的等腰三角形,且a+b≠0,求ab的值;(3)作边长为2的正方形ACDE,使AC∥x轴,点D在点A的左上方,那么,对大于或等于3的任意实数a,CD边与函数y1= (x>0)的图象都有交点,请说明理由.【答案】(1)解:由题意知,点A(a,),B(b,﹣),∵AB∥x轴,∴,∴a=﹣b;∴AB=a﹣b=2a,∴S△OAB= •2a• =3(2)解:由(1)知,点A(a,),B(b,﹣),∴OA2=a2+()2, OB2=b2+(﹣)2,∵△OAB是以AB为底边的等腰三角形,∴OA=OB,∴OA2=OB2,∴a2+()2=b2+(﹣)2,∴a2﹣b2=()2﹣()2,∴(a+b)(a﹣b)=( + )(﹣)= ,∵a>0,b<0,∴ab<0,a﹣b≠0,∵a+b≠0,∴1= ,∴ab=3(舍)或ab=﹣3,即:ab的值为﹣3;(3)解:对大于或等于3的任意实数a,CD边与函数y1= (x>0)的图象都有交点.理由:如图,∵a≥3,AC=2,∴直线CD在y轴右侧且平行于y轴,∴直线CD一定与函数y1= (x>0)的图象有交点,∵四边形ACDE是边长为2的正方形,且点D在点A(a,)的左上方,∴C(a﹣2,),∴D(a﹣2, +2),设直线CD与函数y1= (x>0)相交于点F,∴F(a﹣2,),∴FC= ﹣ = ,∴2﹣FC=2﹣ = ,∵a≥3,∴a﹣2>0,a﹣3≥0,∴≥0,∴2﹣FC≥0,∴FC≤2,∴点F在线段CD上,即:对大于或等于3的任意实数a,CD边与函数y1= (x>0)的图象都有交点.【解析】【分析】(1)先判断出a=﹣b,即可得出AB=2a,再利用三角形的面积公式即可得出结论;(2)利用等腰三角形的两腰相等建立方程求解即可得出结论;(3)先判断出直线CD和函数y1= (x>0)必有交点,根据点A的坐标确定出点C,F的坐标,进而得出FC,再判断FC与2的大小即可.6.你吃过拉面吗?实际上在做拉面的过程中就渗透着数学知识:一定体积的面团做成拉面,面条的总长度y(m)是面条的粗细(横截面积)s(mm2)的反比例函数,其图象如图.(1)写出y与s的函数关系式;(2)求当面条粗3.2mm2时,面条的总长度是多少m?【答案】(1)解:设y与x的函数关系式为y= ,将x=4,y=32代入上式,解得:k=4×32=128,故y= .答:y与x的函数关系式y=(2)解:当x=3.2时,y= =40.答:当面条粗3.2mm2时,面条的总长度是40米【解析】【分析】(1)根据图象可设出关系式,再把一个点的坐标代入可求出关系式;(2)把x=3.2代入关系式可求出y的值,即得答案.7.如图1,已知直线y=x+3与x轴交于点A,与y轴交于点B,将直线在x轴下方的部分沿x轴翻折,得到一个新函数的图象(图中的“V形折现”)(1)类比研究函数图象的方法,请列举新函数的两条性质,并求新函数的解析式;(2)如图2,双曲线y= 与新函数的图象交于点C(1,a),点D是线段AC上一动点(不包括端点),过点D作x轴的平行线,与新函数图象交于另一点E,与双曲线交于点P.①试求△PAD的面积的最大值;②探索:在点D运动的过程中,四边形PAEC能否为平行四边形?若能,求出此时点D的坐标;若不能,请说明理由.【答案】(1)解:如图1,新函数的性质:1.函数的最小值为0;2.函数图象的对称轴为直线x=3.由题意得,点A的坐标为(-3,0),分两种情况:①当x-3时,y=x+3;②当x<-3时,设函数解析式为y=kx+b,在直线y=x+3中,当x=-4时,y=-1,则点(-4,-1)关于x轴的对称点为(-4,1),把点(-4,1),(-3,0),代入y=kx+b中,得:,解得:,∴y=-x-3.综上,新函数的解析式为y=.(2)解:如图2,①∵点C(1,a)在直线y=x+3上,∴a=4,∵点C(1,4)在反比例函数y=上,∴k=4,∴反比例函数的解析式为y=.∵点D是线段AC上一动点,∴设点D的坐标为(m,m+3),且-3<m<1,∵DP∥x轴,且点P在双曲线上,∴点P的坐标为(,m+3),∴PD=-m,∴S△PAD=(-m)(m+3)=m2-m+2=(m+)2+,∵a=<0,∴当m=时,S有最大值,最大值为,又∵-3<<1,∴△PAD的面积的最大值为.②在点D的运动的过程中,四边形PAEC不能为平行四边形,理由如下:当点D为AC的中点时,其坐标为(-1,2),此时点P的坐标为(2,2),点E的坐标为(-5,2),∵DP=3,DE=4,∴EP与AC不能互相平分,∴四边形PAEC不能为平行四边形.【解析】【分析】(1)根据一次函数的性质,结合函数图象写出新函数的两条性质;利用待定系数法求新函数解析式,注意分两种情况讨论;(2)①先求出点C的坐标,再利用待定系数法求出反比例函数解析式,设出点D的坐标,进而得到点P的坐标,再根据三角形的面积公式得出函数解析式,利用二次函数的性质求解即可;②先求出A的中点D的坐标,再计算DP、DE的长度,如果对角线互相平分,则能成为平行四边形,如若对角线不互相平分,则不能成为平行四边形.8.如图,在矩形OABC中,OA=6,OC=4,F是AB上的一个动点(F不与A,B重合),过点F的反比例函数的图象与BC边交于点E.(1)当F为AB的中点时,求该函数的解析式;(2)当k为何值时,△EFA的面积最大,最大面积是多少?【答案】(1)解:∵在矩形OABC中,OA=6,OC=4,∴B(6,4),∵F为AB的中点,∴F(6,2),又∵点F在反比例函数(k>0)的图象上,∴k=12,∴该函数的解析式为y= (x>0)(2)解:由题意知E,F两点坐标分别为E(,4),F(6,),∴,==== ,∴当k=12时,S有最大值.S最大=3【解析】【分析】)当F为AB的中点时,点F的坐标为(3,1),由此代入求得函数解析式即可;根据图中的点的坐标表示出三角形的面积,得到关于k的二次函数,利用二次函数求出最值即可.9.【阅读理解】我们知道,当a>0且b>0时,(﹣)2≥0,所以a﹣2 +≥0,从而a+b≥2 (当a=b时取等号),【获得结论】设函数y=x+ (a>0,x>0),由上述结论可知:当x= 即x= 时,函数y有最小值为2(1)【直接应用】若y1=x(x>0)与y2= (x>0),则当x=________时,y1+y2取得最小值为________.(2)【变形应用】若y1=x+1(x>﹣1)与y2=(x+1)2+4(x>﹣1),则的最小值是________(3)【探索应用】在平面直角坐标系中,点A(﹣3,0),点B(0,﹣2),点P是函数y= 在第一象限内图象上的一个动点,过P点作PC⊥x轴于点C,PD⊥y轴于点D,设点P的横坐标为x,四边形ABCD的面积为S①求S与x之间的函数关系式;②求S的最小值,判断取得最小值时的四边形ABCD的形状,并说明理由.【答案】(1)1;2(2)4(3)解:①设P(x,),则C(x,0),D(0,),∴AC=x+3,BD= +2,∴S= AC•BD= (x+3)( +2)=6+x+ ;②∵x>0,∴x+ ≥2 =6,∴当x= 时,即x=3时,x+ 有最小值6,∴此时S=6+x+ 有最小值12,∵x=3,∴P(3,2),C(3,0),D(0,2),∴A、C关于x轴对称,D、B关于y轴对称,即四边形ABCD的对角线互相垂直平分,∴四边形ABCD为菱形.【解析】【解答】解:(1)∵x>0,∴y1+y2=x+ ≥2 =2,∴当x= 时,即x=1时,y1+y2有最小值2,故答案为:1;2;(2)∵x>﹣1,∴x+1>0,∴ = =(x+1)+ ≥2 =4,∴当x+1= 时,即x=1时,有最小值4,故答案为:4;【分析】(1)直接由结论可求得其取得最小值,及其对应的x的值;(2)可把x+1看成一个整体,再利用结论可求得答案;(3)①可设P(x,),则可表示出C、D的坐标,从而可表示出AC和BD,再利用面积公式可表示出四边形ABCD的面积,从而可得到S 与x的函数关系式;②再利用结论可求得其最得最小值时对应的x的值,则可得到P、C、D的坐标,可判断A、C关于x轴对称,B、D关于y轴对称,可判断四边形ABCD为菱形.10.如图,在平面直角坐标系xOy中,直线y=kx+b(k≠0)与双曲线y= 相交于点A(m,3),B(﹣6,n),与x轴交于点C.(1)求直线y=kx+b(k≠0)的解析式;(2)若点P在x轴上,且S△ACP= S△BOC,求点P的坐标(直接写出结果).【答案】(1)解:)∵点A(m,3),B(﹣6,n)在双曲线y= 上,∴m=2,n=﹣1,∴A(2,3),B(﹣6,﹣1).将(2,3),B(﹣6,﹣1)带入y=kx+b,得:,解得.∴直线的解析式为y= x+2(2)解:当y= x+2=0时,x=﹣4,∴点C(﹣4,0).设点P的坐标为(x,0),∵S△ACP= S△BOC, A(2,3),B(﹣6,﹣1),∴×3|x﹣(﹣4)|= × ×|0﹣(﹣4)|×|﹣1|,即|x+4|=2,解得:x1=﹣6,x2=﹣2.∴点P的坐标为(﹣6,0)或(﹣2,0).【解析】【分析】(1)利用反比例函数图象上点的坐标特征可求出点A、B的坐标,再利用待定系数法即可求出直线AB的解析式;(2)利用一次函数图象上点的坐标特征可求出点C的坐标,设点P的坐标为(x,0),根据三角形的面积公式结合S△ACP= S△BOC,即可得出|x+4|=2,解之即可得出结论.11.如图,在平面直角坐标系中,OA⊥OB,AB⊥x轴于点C,点A(,1)在反比例函数y= 的图象上.(1)求反比例函数y= 的表达式;(2)在x轴的负半轴上存在一点P,使得S△AOP= S△AOB,求点P的坐标;(3)若将△BOA绕点B按逆时针方向旋转60°得到△BDE.直接写出点E的坐标,并判断点E是否在该反比例函数的图象上.【答案】(1)解:∵点A(,1)在反比例函数y= 的图象上,∴k= ×1= ,∴反比例函数表达式为y= .(2)解:∵A(,1),AB⊥x轴于点C,∴OC= ,AC=1,∵OA⊥OB,OC⊥AB,∴∠A=∠COB,∴tan∠A= =tan∠COB= ,∴OC2=AC•BC,即BC=3,∴AB=4,∴S△AOB= × ×4=2 ,∴S△AOP= S△AOB= ,设点P的坐标为(m,0),∴ ×|m|×1= ,解得|m|=2 ,∵P是x轴的负半轴上的点,∴m=﹣2 ,∴点P的坐标为(﹣2 ,0)(3)解:由(2)可知tan∠COB= = = ,∴∠COB=60°,∴∠ABO=30°,∵将△BOA绕点B按逆时针方向旋转60°得到△BDE,∴∠OBD=60°,∴∠ABD=90°,∴BD∥x轴,在Rt△AOB中,AB=4,∠ABO=30°,∴AO=DE=2,OB=DB=2 ,且BC=3,OC= ,∴OD=DB﹣OC= ,BC﹣DE=1,∴E(﹣,﹣1),∵﹣ ×(﹣1)= ,∴点E在该反比例函数图象上【解析】【分析】(1)由点A的坐标,利用待定系数法可求得反比例函数表达式;(2)由条件可求得∠A=∠COB,利用三角函数的定义可得到OC2=AC•BC,可求得BC的长,可求得△AOB的面积,设P点坐标为(m,0),由题意可得到关于m的方程,可求得m的值;(3)由条件可求得∠ABD=90°,则BD∥x轴,由BD、DE的长,可求得E点坐标,代入反比例函数解析式进行判断即可.12.如图,在菱形ABCD中,, ,点E是边BC的中点,连接DE,AE.(1)求DE的长;(2)点F为边CD上的一点,连接AF,交DE于点G,连接EF,若 ,①求证:△△;②求DF的长.【答案】(1)解:连结BD(2)解:①②【解析】【分析】(1)连结BD ,根据菱形的性质及等边三角形的判定方法首先判定出△CDB是等边三角形,根据等边三角形的性质得出DE⊥BC,CE=2,然后利用勾股定理算出DE的长;(2)①首先判断出△AGD∽△EGF,根据相似三角形对应边成比例得出,又∠AGE=∠DGF,故△AGE∽△DGF;②根据相似三角形的性质及含30°直角三角形的边之间的关系及勾股定理得出EF的长,然后过点E作EH⊥DC于点H,在Rt△ECH中,利用勾股定理算出FH的长,从而根据线段的和差即可算出答案.13.已知抛物线的顶点坐标为,经过点 .(1)求抛物线的解析式;(2)如图1,直线交抛物线于,两点,若,求的值;(3)如图2,将抛物线向下平移个单位长度得到抛物线,抛物线的顶点为,交轴的负半轴于点,点在抛物线上.①求点的坐标(用含的式子表示);②若,求,的值.【答案】(1)解:已知抛物线的顶点坐标为,∴设抛物线的解析式为,把代入得:6=16a-2,解得:,∴抛物线的解析式为(2)解:设直线交轴点,则点的坐标,∴ .∵,∴ .∴ .由得,∴,,∴,∴,∵,∴ .(3)解:①依题意得抛物线的解析式为 . 点在抛物线上,∴,∴顶点的坐标为,令,即 .∴,(舍去),∴点的坐标为 .②作轴于点,∵E(2-a,0),F(a,2a-2),∴,∴,又,∴,∵FH//y轴,∴∠FPO=∠PFH=22.5°,∴∠FPO=∠EFP,∴PD=FD,设交轴于点,过D作DG⊥FH于G,则DG=OH,∵∠EFH=45°,∴,∵∠FEH=45°,a>2,∴OD=OE=a-2,∴PD=a-2- = ,∵HO=a,∴,∴,(舍去),∴ .【解析】【分析】(1)观察函数图像可知抛物线关于y轴对称,可得到点A时抛物线的顶点坐标,因此设函数解析式为y=ax2-2,再将点B的坐标代入求出a的值,即可得到抛物线C的解析式。
