分区大小计算方法
最精确的硬盘整数G分区方法(附带基本原理、计算方法及10-1.

最精确的硬盘整数G分区方法各位同学,大家再也不用为硬盘分区无法得到整数G而烦恼了,本文将讲述硬盘容量计算的基本原理,计算方法,并在文后的表格当中提供10-1000GB硬盘分区对应的M数。
一、硬盘容量计算的基本原理硬盘一般有255磁头,63扇区,故每柱面大小为:512byte×255 x 63=8225280bytes(字节)我们知道,1024byte=1KB,1024KB=1MB,那么8225280 bytes换算成MB应当是:8225280÷1024÷1024=7.84423828125 MB;上述计算出来的数,是准确数。
下面我们讲讲如何进行整数分区,举例说明,如果我们要分40GB,我们知道,1024MB=1GB,那么40G换算成MB实际数为:40×1024MB=40960MB;那么,40960MB容量所需要占用硬盘柱面数为:40960÷7.84423828125=5221.66;注意,柱面是不能有小数的,因此,上述数字无条件进位取整,得到5222,也就是说,40GB的容量,需要占用到的柱面数为5222个,而5222个柱面的实际容量换算成MB应当是:5222×7.84423828125=40962.6123046875MB;同样对上述数字无条件进位取整取整,即40963MB,那么这个数40963MB就是操作系统认可的40.00GB的容量了。
这个方法NTFS和FAT32都是通用。
二、利用EXCEL自带的函数表格对整数G进行计算如上图所示,在A1单元格中输入我们需要分出的整数G分区的数值,在B1单元格中输入下列公式:=ROUNDUP(ROUNDUP(A1*1024/7.84423828125,0*7.84423828125,0按回车后,即可得到整数G分区对应的MB数值。
上述公式用到了一个函数:ROUNDUP(a,b,ROUNDUP就是无条件进位,a代表需要进行进位的那个数,b代表返回结果所保留的小数位数,我们需要无条件进位取整的话,就是不保留小数,所以b赋值为0。
硬盘分区整数G计算公式及计算器
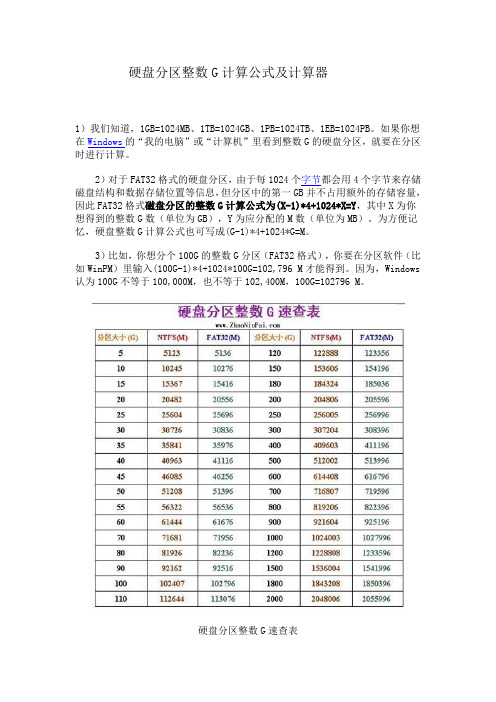
硬盘分区整数G计算公式及计算器1)我们知道,1GB=1024MB、1TB=1024GB、1PB=1024TB、1EB=1024PB。
如果你想在Windows的“我的电脑”或“计算机”里看到整数G的硬盘分区,就要在分区时进行计算。
2)对于FAT32格式的硬盘分区,由于每1024个字节都会用4个字节来存储磁盘结构和数据存储位置等信息,但分区中的第一GB并不占用额外的存储容量,因此FAT32格式磁盘分区的整数G计算公式为(X-1)*4+1024*X=Y,其中X为你想得到的整数G数(单位为GB),Y为应分配的M数(单位为MB)。
为方便记忆,硬盘整数G计算公式也可写成(G-1)*4+1024*G=M。
3)比如,你想分个100G的整数G分区(FAT32格式),你要在分区软件(比如WinPM)里输入(100G-1)*4+1024*100G=102,796 M才能得到。
因为,Windows 认为100G不等于100,000M,也不等于102,400M,100G=102796 M。
硬盘分区整数G速查表4)对于NTFS格式的硬盘分区,原理比较复杂。
NTFS分区的最小容量不能精确到1MB,而是柱面大小。
硬盘一般有255个磁头,63个扇区,故每个柱面的大小为:512bit*255*63=8,225,280bit=7.84423828125MB。
5)如果要分个10GB的NTFS分区,理应为10*1024MB=10240MB,实际需要的柱面数为10240÷7.84423828125=1305.4。
因柱面只能算整数,即1306个柱面,这样实际分配的M数为1306*7.84423828125=10244.575MB,不管小数点后面几位都进1,也就是10245MB,这样才会被Windows系统认成是10GB。
最准确分区数值

最准确分区数值分区大小=(分区大小-1)×4+1024×分区大小如果按照硬盘分区整数G计算公式X-1)*4+1024*X=Y 其中X就是你想要得到的整数分区的数值,单位是G,Y是你分区时应该输入的数字,单位是M,比如40GB=(40-1)×4+1024×40=41116MB 按照这样的计算方法:5G=5136MB10G=10276MB15G=15416MB20G=20556MB30G=30836MB40G=41116MB30G以内,输入上面的数据,如10G你输入10276,在Windows资源管理器里面显示的刚好10.00GB,而在管理工具-磁盘管理界面显示就是10.04GB,如果是40G你输入41116,那么在Windows资源管理器里面显示的刚好40.01GB。
因此上面的计算公式还不是很准确。
最精确硬盘分区的算法如下(来自网络搜索):硬盘一般有255磁头,63扇区,故每柱面大小为:512byte x 255 x 63=8225280bytes =7.84423828125 MB如果要分40GB,那么要40x1024MB=40960MB需要柱面数为40960÷7.84423828125=5221.66取整数既为5222个柱面应分M数为5222x7.84423828125=40962.6123046875MB不管小数点后面几位都进1,也就是40963MB,windows就认为是40GB了。
这个方法NTFS和FAT32通用。
下面附10GB到200GB整10GB递增的精确计算结果:10GB = 10245MB20GB = 20482MB30GB = 30726MB40GB = 40963MB50GB = 51208MB60GB = 61444MB70GB = 71681MB80GB = 81926MB90GB = 92162MB100GB = 102407MB110GB = 112644MB120GB = 122888MB130GB = 133125MB140GB = 143362MB150GB = 153606MB160GB = 163843MB170GB = 174088MB180GB = 184324MB190GB = 194561MB此精确分区结果,在管理工具-磁盘管理界面,和Windows资源管理器里面显示的是整数,10G就是10.00GB,20G就是20.00GB,40G就是40.00GB。
最精确的硬盘整数G分区方法(附带基本原理、计算方法及10-1000GB容量对应MB数值的表格)

最精确的硬盘整数G分区方法各位同学,大家再也不用为硬盘分区无法得到整数G而烦恼了,本文将讲述硬盘容量计算的基本原理,计算方法,并在文后的表格当中提供10-1000GB硬盘分区对应的M数。
一、硬盘容量计算的基本原理硬盘一般有255磁头,63扇区,故每柱面大小为:512byte×255 x 63=8225280bytes(字节)我们知道,1024byte=1KB,1024KB=1MB,那么8225280 bytes 换算成MB应当是:8225280÷1024÷1024=7.84423828125 MB;上述计算出来的数,是准确数。
下面我们讲讲如何进行整数分区,举例说明,如果我们要分40GB,我们知道,1024MB=1GB,那么40G换算成MB实际数为:40×1024MB=40960MB;那么,40960MB容量所需要占用硬盘柱面数为:40960÷7.84423828125=5221.66;注意,柱面是不能有小数的,因此,上述数字无条件进位取整,得到5222,也就是说,40GB的容量,需要占用到的柱面数为5222个,而5222个柱面的实际容量换算成MB应当是:5222×7.84423828125=40962.6123046875MB;同样对上述数字无条件进位取整取整,即40963MB,那么这个数40963MB就是操作系统认可的40.00GB的容量了。
这个方法NTFS和FAT32都是通用。
二、利用EXCEL自带的函数表格对整数G进行计算如上图所示,在A1单元格中输入我们需要分出的整数G分区的数值,在B1单元格中输入下列公式:=ROUNDUP(ROUNDUP(A1*1024/7.84423828125,0)*7.844238 28125,0)按回车后,即可得到整数G分区对应的MB数值。
上述公式用到了一个函数:ROUNDUP(a,b),ROUNDUP就是无条件进位,a代表需要进行进位的那个数,b代表返回结果所保留的小数位数,我们需要无条件进位取整的话,就是不保留小数,所以b赋值为0。
硬盘的实际容量和硬盘分区容量的最精确算法

硬盘的实际容量和硬盘分区容量的最精确算法(附:10-200G分区精确计算结果)一、硬盘的实际容量的最精确算法很多朋友买来硬盘以后发现硬盘实际容量不够,少则差几G,多则差几十G,这是怎么回事呢?原来硬盘厂商的换算法与系统的换算法不同,硬盘厂商是按照1000Byte=1KB,1000KB=1MB,1000MB=1GB;而系统的换算法则为1024Byte=1KB,1024KB=1MB,1024MB=1GB。
所以硬盘标称的容量会与实际容量有差距,那么该怎么算出硬盘的实际容量呢?我在这里给大家列一个公式:1000*1000*1000/1024/1024/1024=0.93132257461547815625结果得出一个数值——0.93132257461547815625,我们就把它看成0.9313吧,如果换算硬盘实际容量,只需要将硬盘标称的容量乘以0.9313就可以了例如:80G*0.9313=74.504G160G*0.9313=149.008G250G*0.9313=232.825G320G*0.9313=298.016G500G*0.9313=465.65G1T=1000G*0.9313=931.3G二、硬盘分区容量的最精确算法硬盘一般有255磁头,63扇区,故每柱面大小为:512byte x 255 x 63=8225280bytes =7.84423828125 MB如果要分40GB,那么要40x1024MB=40960MB需要柱面数为40960÷7.84423828125=5221.66取整数既为5222个柱面应分M数为5222x7.84423828125=40962.6123046875MB不管小数点后面几位都进1,也就是40963MB,windows就认为是40GB了。
这个方法NTFS和FAT32通用。
下面附10GB到200GB整10GB递增的精确计算结果:10GB = 10245MB20GB = 20482MB 30GB = 30726MB 40GB = 40963MB 50GB = 51208MB 60GB = 61444MB 70GB = 71681MB 80GB = 81926MB 90GB = 92162MB 100GB = 102407MB 110GB = 112644MB 120GB = 122888MB 130GB = 133125MB 140GB = 143362MB 150GB = 153606MB 160GB = 163843MB 170GB = 174088MB 180GB = 184324MB 190GB = 194561MB 190GB = 194561MB 200GB = 204806MB。
如何对硬盘进行整数分区的计算方法.

装系统或重装系统时,总是为硬盘容量不是整数发愁,原来是自己的计算方法不对,那么,如何通过正确计算对硬盘进行整数分区呢?下面的文章对您一定有所帮助硬盘整数分区计算方法一般算法:分区大小=(分区大小-1×4+1024×分区大小如果按照硬盘分区整数G计算公式:(X-1*4+1024*X=Y 其中X就是你想要得到的整数分区的数值,单位是G,Y是你分区时应该输入的数字,单位是M,比如40GB=(40-1×4+1024×40=41116MB 按照这样的计算方法:5G=5136MB10G=10276MB15G=15416MB20G=20556MB30G=30836MB40G=41116MB30G以内,输入上面的数据,如10G你输入10276,在Windows资源管理器里面显示的刚好10.00GB,而在管理工具-磁盘管理界面显示就是10.04GB,如果是40G你输入41116,那么在Windows资源管理器里面显示的刚好40.01GB。
因此上面的计算公式还不是很准确。
最精确硬盘分区的算法如下(来自网络搜索:硬盘一般有255磁头,63扇区,故每柱面大小为:512byte x 255 x 63=8225280bytes =7.84423828125 MB如果要分40GB,那么要40x1024MB=40960MB需要柱面数为40960÷7.84423828125=5221.66取整数既为5222个柱面应分M数为5222x7.84423828125=40962.6123046875MB不管小数点后面几位都进1,也就是40963MB,windows就认为是40GB了。
这个方法NTFS和FAT32通用。
下面附10GB到200GB整10GB递增的精确计算结果:10GB = 10245MB20GB = 20482MB30GB = 30726MB40GB = 40963MB50GB = 51208MB60GB = 61444MB70GB = 71681MB80GB = 81926MB90GB = 92162MB100GB = 102407MB110GB = 112644MB120GB = 122888MB130GB = 133125MB140GB = 143362MB150GB = 153606MB160GB = 163843MB170GB = 174088MB180GB = 184324MB190GB = 194561MB此精确分区结果,在管理工具-磁盘管理界面,和Windows资源管理器里面显示的是整数,10G就是10.00GB,20G就是20.00GB,40G就是40.00GB。
dma分区计算
dma分区计算
摘要:
1.DMA 分区的概念和作用
2.DMA 分区的计算方法
3.DMA 分区计算的实际应用
4.DMA 分区计算的注意事项
正文:
DMA 分区,全称为Direct Memory Access,即直接内存访问,是一种计算机硬件技术,它允许外部设备直接访问系统内存,从而减少了CPU 的负担,提高了数据传输的效率。
DMA 分区的计算,主要是根据设备的需要和系统的配置,确定DMA 传输的数据长度和缓冲区的大小。
一般来说,DMA 分区的计算需要考虑以下几个因素:
(1)设备的数据传输速率。
设备的数据传输速率决定了DMA 传输的速度,因此,在计算DMA 分区时,需要根据设备的数据传输速率,确定DMA 传输的数据长度。
(2)系统的内存配置。
系统的内存配置决定了DMA 分区的大小,因此,在计算DMA 分区时,需要根据系统的内存配置,确定DMA 分区的大小。
(3)设备的数据传输方向。
设备的数据传输方向决定了DMA 传输的方向,因此,在计算DMA 分区时,需要根据设备的数据传输方向,确定DMA
传输的方向。
在实际应用中,DMA 分区计算的主要目的是为了提高系统的性能。
例如,在视频处理中,通过DMA 分区计算,可以将视频数据直接传输到显存中,从而减少了CPU 的负担,提高了视频处理的效率。
在计算DMA 分区时,需要注意以下几点:
(1)DMA 分区的大小必须符合系统的内存配置。
(2)DMA 分区的计算必须考虑设备的数据传输速率和方向。
(3)DMA 分区的计算必须符合系统的硬件规范。
硬盘分区大小换算
分区大小(G)设置大小(MB)1 G 1024 MB2 G 2052 MB3 G 3080 MB4 G 4108 MB5 G 5136 MB6 G 6164 MB7 G 7192 MB8 G 8220 MB9 G 9248 MB10 G 10276 MB11 G 11304 MB12 G 12332 MB13 G 13360 MB14 G 14388 MB15 G 15416 MB16 G 16444 MB17 G 17472 MB18 G 18500 MB19 G 19528 MB20 G 20556 MB21 G 21584 MB22 G 22612 MB23 G 23640 MB24 G 24668 MB25 G 25696 MB26 G 26724 MB27 G 27752 MB28 G 28780 MB29 G 29808 MB30 G 30836 MB31 G 31864 MB32 G 32892 MB33 G 33920 MB34 G 34948 MB35 G 35976 MB36 G 37004 MB37 G 38032 MB38 G 39060 MB39 G 40088 MB40 G 41116 MB41 G 42144 MB42 G 43172 MB43 G 44200 MB44 G 45228 MB45 G 46256 MB46 G 47284 MB47 G 48312 MB48 G 49340 MB 49 G 50368 MB50 G 51396 MB51 G 52424 MB52 G 53452 MB53 G 54480 MB54 G 55508 MB55 G 56536 MB56 G 57564 MB57 G 58592 MB58 G 59620 MB59 G 60648 MB60 G 61676 MB61 G 62704 MB62 G 63732 MB63 G 64760 MB64 G 65788 MB65 G 66816 MB66 G 67844 MB67 G 68872 MB68 G 69900 MB69 G 70928 MB70 G 71956 MB71 G 72984 MB72 G 74012 MB73 G 75040 MB74 G 76068 MB75 G 77096 MB76 G 78124 MB77 G 79152 MB78 G 80180 MB79 G 81208 MB80 G 82236 MB81 G 83264 MB82 G 84292 MB83 G 85320 MB84 G 86348 MB85 G 87376 MB86 G 88404 MB87 G 89432 MB88 G 90460 MB89 G 91488 MB90 G 92516 MB91 G 93544 MB92 G 94572 MB93 G 95600 MB94 G 96628 MB95 G 97656 MB96 G 98684 MB97 G 99712 MB98 G 100740 MB99 G 101768 MB100 G 102796 MB无论是使用FDISK还是其他分区软件进行分区,都需要输入准备分配的分区容量,这个数值是以MB为单位,不过如果你输入2000MB的话并不会得到2GB的整数容量,而是1.9GB;众所周知,1GB并非等于1000MB,而是1024MB,但笔者在实际分区中却发现,即使输入2048MB也不会得到整数的2GB,而是仍然得到1.9GB,这其中大约有5%左右的误差。
硬盘整数分区计算方法
10G=10276MB
15G=15416MB
20G=20556MB
30G=30836MB
40G=41116MB
30G以内,输入上面的数据,如10G你输入10276,在Windows资源管理器里面显示的刚好10.00GB,而在管理工具-磁盘管理界面显示就是10.04GB,如果是40G你输入41116,那么在Windows资源管理器里面显示的刚好40.01GB。
80GB = 81926MB
90GB = 92162MB
100GB = 102407MB
110GB = 112644MB
120GB = 122888MB
130GB = 133125MB
140GB = 143362MB
150GB = 153606MB
160GB = 163843MB
硬盘整数分区计算方法
一般算法
(来自按照硬盘分区整数G计算公式X-1)*4+1024*X=Y 其中X就是你想要得到的整数分区的数值,单位是G,Y是你分区时应该输入的数字,单位是M,
比如40GB=(40-1)×4+1024×40=41116MB 按照这样的计算方法:
需要柱面数为40960÷7.84423828125=5221.66
取整数既为5222个柱面
应分M数为5222x7.84423828125=40962.6123046875MB
不管小数点后面几位都进1,也就是40963MB,windows就认为是40GB了。
这个方法NTFS和FAT32通用。
170GB = 174088MB
180GB = 184324MB
190GB = 194561MB
整数分区_精品文档
整数分区什么是整数分区整数分区是将一个正整数拆分成一些正整数的和的不同方式。
例如,将整数4拆分成1+1+1+1、1+1+2、1+3、2+2、4等等。
整数分区是组合数学中的一个经典问题,也是动态规划算法的一个常见应用。
分区数给定一个正整数n,我们希望计算出将n分区的不同方式数。
用P(n)表示将n分区的方式数。
递推公式分区数有一个递推公式可以计算。
假设我们已经求得了P(k)(1 ≤ k < n)的值,那么P(n)的值可以通过如下递推公式计算:P(n) = P(n-1) + P(n-2) - P(n-5) + P(n-7) - P(n-12) + P(n-15) - ...其中,符号的规律是依次交替出现的。
动态规划算法基于以上递推公式,我们可以使用动态规划算法来计算分区数。
我们创建一个长度为n+1的数组dp,并初始化dp[0]为1,其余元素为0。
然后,通过循环从1到n,依次计算dp[i]的值。
最终,dp[n]的值就是所求的P(n)。
下面是计算整数分区的动态规划算法的伪代码:Initialize dp[0] = 1for i from 1 to n dofor j from 1 to i dodp[i] = dp[i] + dp[i-j] * (-1)^(j+1)示例接下来,我们以n=5为例,演示如何计算整数分区的不同方式数。
首先,我们初始化dp数组,得到dp = [1, 0, 0, 0, 0, 0]。
接着,我们按照上述算法,依次循环计算dp[i]的值。
最终得到dp = [1, 1, 2, 3, 5, 7]。
因此,将整数5分区的不同方式数为7种。
应用整数分区问题在实际中有多种应用。
以下是一些常见的应用场景:1.划分问题:将一个集合分成若干不相交的子集,可以使用整数分区的思想来解决该问题。
每个子集的大小就对应着一个整数的分区方式。
2.组合数问题:整数分区的不同方式数对应着组合数问题中的解决方案数。
例如,将n个相同物品分成若干组,每组至少有一个物品,将组与组之间的顺序考虑在内,可以使用整数分区来计算解决方案的个数。
