2018-2019学年安徽省铜陵市第一中学高二上学期开学考试数学试题 Word版
安徽省铜陵市第一中学2018-2019学年高二上学期期中考试数学试题(pdf版)
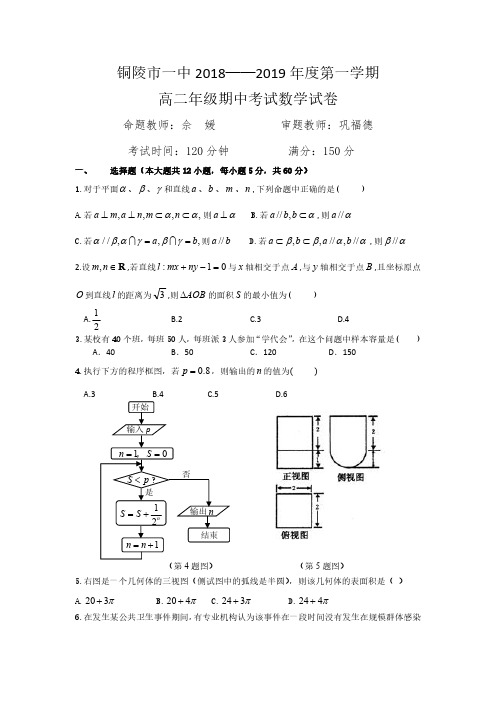
铜陵市一中2018——2019年度第一学期高二年级期中考试数学试卷命题教师:佘媛审题教师:巩福德考试时间:120分钟满分:150分一、选择题(本大题共12小题,每小题5分,共60分)1.对于平面α、β、γ和直线a 、b 、m 、n ,下列命题中正确的是()A.若,,,,a m a n m n αα⊥⊥⊂⊂则a α⊥B.若//,a b b α⊂,则//a αC.若//,,,a b αβαγβγ== 则//a bD.若,,//,//a b a b ββαα⊂⊂,则//βα2.设R ∈n m ,,若直线01:=-+ny mx l 与x 轴相交于点A ,与y 轴相交于点B ,且坐标原点O 到直线l 的距离为3,则AOB ∆的面积S 的最小值为()A.21 B.2 C.3D.43.某校有40个班,每班50人,每班派3人参加“学代会”,在这个问题中样本容量是()A .40B .50C .120D .1504.执行下方的程序框图,若0.8p =,则输出的n 的值为()A.3D.6(第4题图)(第5题图)5.右图是一个几何体的三视图(侧试图中的弧线是半圆),则该几何体的表面积是()A.π320+ B.π420+ C.π324+ D.π424+6.在发生某公共卫生事件期间,有专业机构认为该事件在一段时间没有发生在规模群体感染0.30.14.34.4 4.5 4.6 4.7 4.8 4.95.0 5.15.2视力频率组距的标志为“连续10天,每天新增疑似病例不超过7人”。
根据过去10天甲、乙、丙、丁四地新增疑似病例数据,一定符合该标志是(D)(A)甲地:总体均值为3,中位数为4(B)乙地:总体均值为1,总体方差大于0(C)丙地:中位数为2,众数为3(D)丁地:总体均值为2,总体方差为37.为了解某校高三学生的视力情况,随机地抽查了该校200名高三学生的视力情况,得到频率分布直方图,如右,由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频数成等差数列,设最多一组学生数为a ,视力在4.6到5.0之间的频率为b ,则a ,b 的值分别为(B )A .0.27,78B .54,0.78C .27,0.78D .54,788.如图所示,在长方体ABCD —A 1B 1C 1D 1中,AB =BC =2,AA 1=1,则BC 1与平面BB 1D 1D 所成角的正弦值为()A .63B .255C .155D .1059.已知平面//α平面β,直线α⊂m ,直线β⊂n ,点m A ∈,点n B ∈,记点A、B 之间的距离为a ,点A 到直线n 的距离为b ,直线m 和n 的距离为c ,则()A.c b a≤≤B.c a b≤≤C.a c b≤≤D.b c a≤≤10.已知三棱锥S ABC -的所有顶点都在球O 的球面上,SC 为球O 的直径,且SC OA ⊥,SC OB ⊥,OAB ∆为等边三角形,三棱锥S ABC -的体积为433,则球O 的半径为()A.3B.1C.2D.411.已知点),(y x P 是直线)0(04>=++k y kx 上一动点,PA 、PB 是圆02:22=-+y y x C 的两条切线,A 、B 是切点,若四边形PACB 的最小面积是2,则k 的值为()A.2B.221C.22 D.312.如图,点)4,3(P 为圆2522=+y x 上的一点,点E ,F 为y 轴上的两点,PEF △是以点P 为顶点的等腰三角形,直线PE ,PF 交圆于D ,C 两点,直线CD 交y 轴于点A ,则DAO ∠cos 的值为()A.54 B.53 C.52 D.43二、填空题(本大题共4小题,每小题5分,共20分)13.已知样本9,10,11,,x y 的平均数是10,标准差是2,则xy =.14.经过两条直线053=-+y x 与032=+-y x 的交点,且在两坐标轴上的截距相等的直线方程为________.15、如图,在直四棱柱1111ABCD A B C D -中,点,E F 分别在11,AA CC 上,且134AE AA =,113CF CC =,点,A C 到BD 的距离之比为3:2,F则三棱锥E BCD -和F ABD -的体积比E BCD F ABDVV --=.16.已知正四面体ABCD 的棱长为9,点P 是三角形ABC 内(含边界)的一个动点满足P 到面DAB 、面DBC 、面DCA 的距离成等差数列,则点P 到面DCA 的距离最大值为______.三、解答题(本大题共6小题,共70分,其中17题10分,其它题目每题12分)17.已知两直线042:1=+-y x l 和02:2=-+y x l 的交点为P .(1)直线l 过点P 且与直线0635=-+y x 垂直,求直线l 的方程;(2)圆C 过点)1,3(且与1l 相切于点P ,求圆C 的方程..18..如图,在梯形ABCD 中,CD AB ∥,E ,F 是线段AB 上的两点,且AB DE ⊥,AB CF ⊥,12=AB ,5=AD ,24=BC ,4=DE .现将ADE △,CFB △分别沿DE ,CF 折起,使A ,B 两点重合于点G ,得到多面体CDEFG .(1)求证:平面⊥DEG 平面CFG ;(2)求多面体CDEFG 的体积.19.下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据.x 3456y 2.534 4.5(1)请画出上表数据的散点图;(2)请根据上表提供的数据,用最小二乘法求出y关于x 的回归直线方程y ^=b ^x+a ^;(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(2)求出回归直线方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?(参考数值:3×2.5+4×3+5×4+6×4.5=66.5)(参考公式:∑∑==⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-=n i i ni i i x x y y x x b 12_1__^,__x b y a -=)20.已知过原点的动直线l 与圆056:221=+-+x y x C 相交于不同的两点A ,B .(1)求圆1C 的圆心坐标及动直线l 的斜率k 的取值范围;(2)求线段AB 的中点M 的轨迹C 的方程;(3)是否存在实数m ,使得直线)4(:-=x m y L 与曲线C 只有一个交点?若存在,求出m 的取值范围;若不存在,说明理由.21.如图,在四棱锥ABCD P -中,底面ABCD 是平行四边形,平面⊥PBD 平面ABCD ,2=AD ,52=PD ,4==PB AB , 60=∠BAD .(1)求证:PB AD ⊥;(2)E 是侧棱PC 上一点,记λ=PCPE,当⊥PB 平面ADE 时,求实数λ的值.22.在平面直角坐标系xOy 中,已知圆C 经过)2,0(A ,)0,0(O ,)0)(0,(>t t D 三点,M 是线段AD 上的动点,1l ,2l 是过点)0,1(B 且互相垂直的两条直线,其中1l 交y 轴于点E ,2l 交圆C 于P 、Q 两点.(1)若6==PQ t ,求直线2l 的方程;(2)(文)若4=t ,求三角形EPQ 的面积的最小值.(理)若t 是使BM AM 2≤恒成立的最小正整数,求三角形EPQ 的面积的最小值.。
安徽省铜陵市第一中学2018-2019学年高二数学上学期开学考试试卷【word版】.doc

安徽省铜陵市第一中学2018-2019学年高二数学上学期开学考试试题一、选择题(12题共60分)1.一个几何体的三视图如图所示,则该几何体的直观图可以是()2.某几何体的三视图如图所示,则该几何体的体积为()A.16+8π B.8+8πC.16+16π D.8+16π3.如图所示,在底面为正方形,侧棱垂直于底面的四棱柱ABCD-A1B1C1D1中,AA 1=2AB ,则异面直线A 1B 与AD 1所成角的余弦值为( )A.15B.25C.35D.454.直线x cos140°+y sin40°+1=0的倾斜角是( ) A .40° B .50° C .130°D .140°5.在等腰三角形AOB 中,AO =AB ,点O (0,0),A (1,3),点B 在x 轴的正半轴上,则直线AB 的方程为( )A .y -1=3(x -3)B .y -1=-3(x -3)C .y -3=3(x -1)D .y -3=-3(x -1)6.直线2x +(m +1)y +4=0与直线mx +3y -2=0平行,则m =( ) A .2 B .-3 C .2或-3D .-2或-37.经过两条直线2x +3y +1=0和x -3y +4=0的交点,并且垂直于直线3x +4y -7=0的直线方程为( )A .4x -3y +9=0B .4x +3y +9=0C .3x -4y +9=0D .3x +4y +9=08.在正方体ABCD -A 1B 1C 1D 1中,棱长为a ,M ,N 分别为A 1B 和AC 上的点,若A 1M =AN =2a3,则MN 与平面BB 1C 1C 的位置关系是( )A .相交B .平行C .垂直D .不能确定9.圆x 2+y 2+2x -6y +1=0关于直线ax -by +3=0(a >0,b >0)对称,则1a +3b 的最小值是( )A .2 3 B.203 C .4D.16310.在三棱锥S -ABC 中,△ABC 是边长为6的正三角形,SA =SB =SC =15,平面DEFH 分别与AB ,BC ,SC ,SA 交于D ,E ,F ,H .D ,E 分别是AB ,BC 的中点,如果直线SB ∥平面DEFH ,那么四边形DEFH 的面积为( )A.452B. 4532C .45D .45 311.已知在圆M :x 2+y 2-4x +2y =0内,过点E (1,0)的最长弦和最短弦分别是AC 和BD ,则四边形ABCD 的面积为( )A .3 5B .6 5C .415D .215 12.已知点P (x ,y )在圆C :x 2+y 2-6x -6y +14=0上,则x +y 的最大值与最小值是( )A .6+22,6-2 2B .6+2,6- 2C .4+22,4-2 2D .4+2,4- 2二、填空题(4题共20分)13.已知a ∈R ,若方程a 2x 2+(a +2)y 2+4x +8y +5a =0表示圆,则此圆心坐标是________.14.已知点A (-3,-4),B (6,3)到直线l :ax +y +1=0的距离相等,则实数a 的值为________.15.如图,四棱锥P -ABCD 中,PA ⊥底面ABCD ,底面ABCD 为正方形,则下列结论:①AD ∥平面PBC ; ②平面PAC ⊥平面PBD ; ③平面PAB ⊥平面PAC ; ④平面PAD ⊥平面PDC .其中正确的结论序号是________.16.在平面直角坐标系xOy 中,A (-12,0),B (0,6),点P 在圆O :x 2+y 2=50上.若PA →·PB →≤20,则点P 的横坐标的取值范围是________.三、解答题(6题。
安徽省铜陵市第一中学2018_2019学年高二数学1月月考试题201901090128

18.已知在平面直角坐标系 ������������������中的一个椭圆,它的中心在原点,左焦点为 ������( ― 3,0),右顶点为 ������(2,0), (1)求该椭圆的标准方程; (2) (文)若������是椭圆上的动点,过 P 作垂直于 x 轴的垂线,垂足为 M,延长 MP 至 N,使得 P 恰好为 MN 中点,求点 N 的轨迹方程; (理)若已知点������(1,2),������是椭圆上的动点,求线段������������中点������的轨迹方程;
A. 2
B.
4 3
C.
6 5
D. 1 2
二、填空题(本大题共 4 小题,每小题 5 分,共 20 分) 13.某同学同时掷两颗均匀正方形骰子,得到的点数分别为 a, b ,则椭圆 的概率是__________.
3 x2 y2 14.椭圆 2 2 1( a b 0) 的左、右焦点分别为������1,������2,顶点������(0,������)到������2的距离为 4,直线������ = 2������ a b
2
B. (1, 1 5 ) 2
C.
(
1 5 ,) 2
D. ( 3 5 ,)
2
2 5.若命题“ x0 R, x0 2mx0 m 2 0 ”为假命题,则������的取值范围是(
) D. ( ― 1,2)
1
A. ( ― ∞, ― 1] ∪ [2, + ∞)
B. ( ― ∞, ― 1) ∪ (2, + ∞)
i 1 i n i 1 i
n
i
y)
,������ = ������ ― ������������)
2
安徽省铜陵市第一中学2018-2019学年高二1月月考数学试题(解析版)

数学试卷一、单选题(本大题共12小题,每小题5分,共60分)1.下列判断中正确的是()A. “若,则有实数根”的逆否命题是假命题B. “”是“直线与直线平行”的充要条件C. 命题“”是真命题D. 命题“”在时是假命题【答案】D【解析】【分析】分别对四个选项进行判断:A原命题与逆否命题同真同假,只需要判断原命题真假或者写出逆否命题判断真假;B 根据两直线平行的条件可解得的值,然后判断是直线平行的什么条件;C先用三角函数辅助角公式化解,再对全称命题判断真假;D利用二次函数判别式小于0判断t的范围,然后判断其真假.【详解】A:原命题“若,则有实数根”的逆否命题为“若没有实数根,则”.∵方程无实数根,∴,因此“若没有实数根,则”为真.B:若,则两条直线分别是和,显然平行. 因此“”是“直线与直线平行”的充分条件.反之,若“直线与直线平行”,则由=≠,得但当时,两直线分别是也平行, 满足题意. 因此“”是“直线与直线平行”的不必要条件.综上可知,“”是“直线与直线平行”的充分不必要条件.C:因为,所以命题“”是假命题. D:当即是假命题.故选D.【点睛】本题考查了四种命题、两直线平行的条件、充分条件必要条件、全称命题、特称命题的真假判断,涉及的知识点较多,综合性较强,属于中档题,是高考热点题型之一,解题中需要对各个知识点熟练掌握,准确应用. 2.如图,等腰直角三角形的斜边长为,分别以三个顶点为圆心,1为半径在三角形内作圆弧,三段圆弧与斜边围成区域(图中阴影部分),若在此三角形内随机取一点,则此点取自区域的概率为A. B. C. D.【答案】D【解析】试验发生包含的所有事件是直角三角形的面积,因为三角形内角和为,所以三个扇形的面积和为,可得阴影部分的面积,点落在区域内的概率为,故选B.【方法点睛】本题題主要考查“面积型”的几何概型,属于中档题. 解决几何概型问题常见类型有:长度型、角度型、面积型、体积型,求与面积有关的几何概型问题关鍵是计算问题的总面积以及事件的面积;几何概型问题还有以下几点容易造成失分,在备考时要高度关注:(1)不能正确判断事件是古典概型还是几何概型导致错误;(2)基本裏件对应的区域测度把握不准导致错误;(3)利用几何概型的概率公式时, 忽视验证事件是否等可能性导致错误.3.已知统计某校1000名学生的某次数学水平测试成绩得到样本频率分布直方图如图所示,则直方图中实数a的值是A. B. C. D.【答案】A【解析】【分析】由频率分布直方图的性质列方程,能求出a.【详解】由频率分布直方图的性质得:,解得.故选:A.【点睛】本题考查实数值的求法,考查频率分布直方图的性质等基础知识,考查运算求解能力,考查函数与方程思想,是基础题.4.双曲线C的中心在坐标原点O,右顶点,虚轴的上端点,虚轴下端点,左右焦点分别为、,直线与直线交于P点,若为锐角,则双曲线C的离心率的取值范围为A. B. C. D.【答案】B【解析】【分析】设双曲线的方程为,求出点P的坐标,再根据是钝角,则,得到,继而得到,解得即可.【详解】设双曲线的方程为,由题意可得,,,,故直线的方程为,直线的方程为,联立方程组,解得,,即,,,是钝角,,,,即,,又,,故选:B.【点睛】本题考查双曲线的几何性质及其应用,解题时根据对称性和题设条件判断出双曲线的渐近线斜率的范围,列出不等式并转化为关于离心率的不等式是解答的关键,对于双曲线的离心率是双曲线最重要的几何性质,求双曲线的离心率(或离心率的取值范围),常见有两种方法:①求出,代入公式;②只需要根据一个条件得到关于的齐次式,结合转化为的齐次式,然后等式(不等式)两边分别除以或转化为关于的方程(不等式),解方程(不等式)即可得(的取值范围).5.若命题“”为假命题,则的取值范围是()A. B. C. D.【答案】C【解析】【分析】根据题干的到命题等价于恒成立,故只需要判别式小于等于0即可.【详解】若命题“,”为假命题,则命题等价于恒成立,故只需要故答案为:C.【点睛】这个题目考查了由命题的真假求参数的范围问题,是基础题.6.P是双曲线左支上的一点,F1、F2分别是左、右焦点,且焦距为2c,则的内切圆的圆心的横坐标为()A. -aB. -bC. -CD. a+b-c【答案】A【解析】【分析】将内切圆的圆心坐标进行转化成圆与横轴切点Q的横坐标,PF2﹣PF1=F2N﹣F I M=F2Q﹣F1Q=2a,F1Q+F2Q=F1F2解出OQ.【详解】如图设切点分别为M,N,Q,则△PF1F2的内切圆的圆心的横坐标与Q横坐标相同.由双曲线的定义,PF2﹣PF1=2a.由圆的切线性质PF2﹣PF1=F2N﹣F I M=F2Q﹣F1Q=2a,∵F1Q+F2Q=F1F2=2c,∴F2Q=c+a,OQ=a,Q横坐标为-a.故选:A.【点睛】本题巧妙地借助于圆的切线的性质,考查了双曲线的定义,属于中档题.7.已知分别为椭圆的左右焦点,点在椭圆上,当时,则点横坐标的取值范围是()A. B. C. D.【答案】C【解析】如上图,假设时,三角形的面积等于因为点P在椭圆上,故代入椭圆方程得到x=,当点P向上运动时,越靠近上顶点角越大,又因为椭圆的对称性,得到P点的活动范围应是。
安徽省某知名中学2018-2019学年高二数学上学期开学考试试题 理_2

屯溪一中高二年级开学考试数学试卷(理科)一、选择题(本大题共12小题,共60.0分)1.已知是奇函数,当时,当时,等于A. B. C. D.2.已知偶函数在区间单调递增,则满足的x取值范围是A. B. C. D.3.已知,,,则A. B. C. D.4.若向量,满足,,,则与的夹角为A. B. C. D.5.已知函数是上的偶函数,若对于,都有,且当时,,则的值为A. B. C. 2 D. 16.已知等比数列中,,,则A. 3B. 15C. 48D. 637.已知是锐角,,且,则为A. B. C. 或 D. 或8.的图象为A. B.C. D.9.已知函数,若在区间上取一个随机数,则的概率是A. B. C. D.10.若,,且,则的最小值是A. 2B.C.D.11.设x,y满足约束条件则的取值范围是A. B. C. D.12.已知函数满足:,且当时,,那么方程的解的个数为A. 1个B. 8个C. 9个D. 10个二、填空题(本大题共4小题,共20.0分)13.已知集合,若集合A中只有一个元素,则实数a的取值为______ .14.已知向量,,则在方向上的投影等于______.15.设的内角A,B,C的对边分别为a,b,若,,,则 ______ .16.数列1,的前n项和为,则正整数n的值为______ .三、解答题(本大题共6小题,共70分)17.已知等差数列的前n项和为,,.求;设数列的前n项和为,证明:.18.已知函数.求的最小正周期;求图象的对称轴方程和对称中心的坐标.19.20名学生某次数学考试成绩单位:分的频率分布直方图如图:Ⅰ求频率分布直方图中a的值;Ⅱ分别求出成绩落在与中的学生人数;Ⅲ从成绩在的学生任选2人,求此2人的成绩都在中的概率.20.已知a,b,c分别是内角A,B,C的对边,且满足.求角A的大小;若,,求的面积.21.已知函数,且时,总有成立.求a的值;判断并证明函数的单调性;求在上的值域.22.设函数,其中.若,求函数在区间上的取值范围;若,且对任意的,都有,求实数a的取值范围.若对任意的,,都有,求t的取值范围.一、选择题(本大题共12小题,共60.0分)23.已知是奇函数,当时,当时,等于A. B. C. D.解:当时,,则.又是R上的奇函数,所以当时.故选项A正确.24.已知偶函数在区间单调递增,则满足的x取值范围是A. B. C. D.解:是偶函数,,不等式等价为,在区间单调递增,,解得.故选:A.25.已知,,,则A. B. C. D.解:,,,综上可得:,故选:A.26.若向量,满足,,,则与的夹角为A. B. C. D.解:设与的夹角为,,,,,,,,故选:C.27.已知函数是上的偶函数,若对于,都有,且当时,,则的值为A. B. C. 2 D. 1解:数是上的偶函数,且对于,都有,又当时,,,故选D.28.已知等比数列中,,,则A. 3B. 15C. 48D. 63解:,,,,.故选C.29.已知是锐角,,且,则为A. B. C. 或 D. 或解:根据题意,,若,则有,即有,又由是锐角,则有,即或,则或,故选C.30.的图象为A. B.C. D.可知函数的定义域为:或,函数的图象关于对称.由函数的图象,可知,A、B、D不满足题意.故选:C.31.已知函数,若在区间上取一个随机数,则的概率是A. B. C. D.令,可得或,则,或,时,.所求概率为.故选C.32.若,,且,则的最小值是A. 2B.C.D.解:当且仅当时,等号成立故选D33.设x,y满足约束条件则的取值范围是A. B. C. D.解:x,y满足约束条件的可行域如图:目标函数,经过可行域的A,B时,目标函数取得最值,由解得,由解得,目标函数的最大值为:2,最小值为:,目标函数的取值范围:.故选:B.34.已知函数满足:,且当时,,那么方程的解的个数为A. 1个B. 8个C. 9个D. 10个解:函数满足:,是周期为2的周期函数,当时,,作出和两个函数的图象,如下图:结合图象,得:方程的解的个数为10个.故选:D.二、填空题(本大题共4小题,共20.0分)35.已知集合,若集合A中只有一个元素,则实数a的取值为______ .解:因为集合有且只有一个元素,当时,只有一个解,当时,一元二次方程只有一个元素则方程有重根,即即.所以实数或.36.已知向量,,则在方向上的投影等于______.解:根据投影的定义可得:在方向上的投影为,.故答案为:37.设的内角A,B,C的对边分别为a,b,若,,,则 ______ .解:,或当时,,,,由正弦定理可得,则当时,,与三角形的内角和为矛盾故答案为:138.数列1,的前n项和为,则正整数n的值为______ .解:由题意可知,数列的通项故答案为9三、解答题(本大题共6小题,共72.0分)39.已知等差数列的前n项和为,,.求;设数列的前n项和为,证明:.解:设等差数列的公差为d,,,,,;证明:,则.40.已知函数.求的最小正周期;求图象的对称轴方程和对称中心的坐标.解:函数,的最小正周期为;函数,令,,解得,,图象的对称轴方程为:,;再令,,解得,,图象的对称中心的坐标为,.41.20名学生某次数学考试成绩单位:分的频率分布直方图如图:Ⅰ求频率分布直方图中a的值;Ⅱ分别求出成绩落在与中的学生人数;Ⅲ从成绩在的学生任选2人,求此2人的成绩都在中的概率.解:Ⅰ根据直方图知组距,由,解得.Ⅱ成绩落在中的学生人数为,成绩落在中的学生人数为.Ⅲ记成绩落在中的2人为A,B,成绩落在中的3人为C,D,E,则成绩在的学生任选2人的基本事件有AB,AC,AD,AE,BC,BD,BE,CD,CE,DE共10个,其中2人的成绩都在中的基本事件有CD,CE,DE共3个,故所求概率为.42.已知a,b,c分别是内角A,B,C的对边,且满足.求角A的大小;若,,求的面积.解:,可得:,由余弦定理可得:,又,由及正弦定理可得:,,,由余弦定理可得:,解得:,,43.已知函数,且时,总有成立.求a的值;判断并证明函数的单调性;求在上的值域.解:,,即,,.函数为R上的减函数,的定义域为R,任取,,且,,.即函数为R上的减函数.由知,函数在上的为减函数,,即,即函数的值域为44.设函数,其中.若,求函数在区间上的取值范围;若,且对任意的,都有,求实数a的取值范围.若对任意的,,都有,求t的取值范围.解:因为,所以在区间上单调减,在区间上单调增,且对任意的,都有,若,则.当时单调减,从而最大值,最小值.所以的取值范围为;当时单调增,从而最大值,最小值.所以的取值范围为;所以在区间上的取值范围为分“对任意的,都有”等价于“在区间上,”.若,则,所以在区间上单调减,在区间上单调增.当,即时,由,得,从而.当,即时,由,得,从而.综上,a的取值范围为区间分设函数在区间上的最大值为M,最小值为m,所以“对任意的,,都有”等价于“”.当时,,.由,得.从而.当时,,.由,得.从而.当时,,.由,得.从而.当时,,.由,得.从而.综上,t的取值范围为区间。
铜陵市一中2018-2019学年高二上学期第二次月考试卷数学

铜陵市一中2018-2019学年高二上学期第二次月考试卷数学 班级__________ 姓名__________ 分数__________一、选择题1. 已知函数f (x )是R 上的奇函数,且当x >0时,f (x )=x 3﹣2x 2,则x <0时,函数f (x )的表达式为f (x )=( ) A .x 3+2x 2B .x 3﹣2x 2C .﹣x 3+2x 2D .﹣x 3﹣2x 22. 设集合3|01x A x x -⎧⎫=<⎨⎬+⎩⎭,集合(){}2|220B x x a x a =+++>,若 A B ⊆,则的取值范围 ( )A .1a ≥B .12a ≤≤ C.a 2≥ D .12a ≤< 3. 定义某种运算S=a ⊗b ,运算原理如图所示,则式子+的值为( )A .4B .8C .10D .134. A={x|x <1},B={x|x <﹣2或x >0},则A ∩B=( )A .(0,1)B .(﹣∞,﹣2)C .(﹣2,0)D .(﹣∞,﹣2)∪(0,1)5. 在△ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c ,已知a=3,,A=60°,则满足条件的三角形个数为( ) A .0B .1C .2D .以上都不对6. 已知集合{}{}421,2,3,,4,7,,3A k B a a a ==+,且*,,a N x A y B ∈∈∈使B 中元素31y x =+和A 中的元素x 对应,则,a k 的值分别为( ) A .2,3 B .3,4 C .3,5 D .2,57. P是双曲线=1(a >0,b >0)右支上一点,F 1、F 2分别是左、右焦点,且焦距为2c ,则△PF 1F 2的内切圆圆心的横坐标为( )A .aB .bC .cD .a+b ﹣c8. 已知M={(x ,y )|y=2x },N={(x ,y )|y=a},若M ∩N=∅,则实数a 的取值范围为( ) A .(﹣∞,1) B .(﹣∞,1] C .(﹣∞,0) D .(﹣∞,0]9. 函数y=(x 2﹣5x+6)的单调减区间为( )A.(,+∞) B .(3,+∞)C .(﹣∞,) D .(﹣∞,2)10.已知集合 M={x||x|≤2,x ∈R},N={﹣1,0,2,3},则M ∩N=( )A .{﹣1,0,2}B .{﹣1,0,1,2}C .{﹣1,0,2,3}D .{0,1,2,3}11.定义在R 上的偶函数()f x 满足(3)()f x f x -=-,对12,[0,3]x x ∀∈且12x x ≠,都有1212()()0f x f x x x ->-,则有( )A .(49)(64)(81)f f f <<B .(49)(81)(64)f f f << C. (64)(49)(81)f f f << D .(64)(81)(49)f f f << 12.已知集合A={0,1,2},则集合B={x ﹣y|x ∈A ,y ∈A}中元素的个数是( ) A .1B .3C .5D .9二、填空题13.在4次独立重复试验中,随机事件A 恰好发生1次的概率不大于其恰好发生两次的概率,则事件A 在一次试验中发生的概率P 的取值范围是 .14.若正数m 、n 满足mn ﹣m ﹣n=3,则点(m ,0)到直线x ﹣y+n=0的距离最小值是 .15.一个圆柱和一个圆锥的母线相等,底面半径也相等,则侧面积之比是 .16.已知函数322()7f x x ax bx a a =++--在1x =处取得极小值10,则ba的值为 ▲ .17.设集合 {}{}22|27150,|0A x x x B x x ax b =+-<=++≤,满足AB =∅,{}|52A B x x =-<≤,求实数a =__________.18.直线ax+by=1与圆x 2+y 2=1相交于A ,B 两点(其中a ,b 是实数),且△AOB 是直角三角形(O 是坐标原点),则点P (a ,b )与点(1,0)之间距离的最小值为 .三、解答题19.已知函数f (x )=2x 2﹣4x+a ,g (x )=log a x (a >0且a ≠1).(1)若函数f(x)在[﹣1,3m]上不具有单调性,求实数m的取值范围;(2)若f(1)=g(1)①求实数a的值;②设t1=f(x),t2=g(x),t3=2x,当x∈(0,1)时,试比较t1,t2,t3的大小.20.已知椭圆C:+=1(a>b>0)的左,右焦点分别为F1,F2,该椭圆的离心率为,以原点为圆心,椭圆的短半轴长为半径的圆与直线y=x+相切.(Ⅰ)求椭圆C的方程;(Ⅱ)如图,若斜率为k(k≠0)的直线l与x轴,椭圆C顺次交于P,Q,R(P点在椭圆左顶点的左侧)且∠RF1F2=∠PF1Q,求证:直线l过定点,并求出斜率k的取值范围.21.某游乐场有A、B两种闯关游戏,甲、乙、丙、丁四人参加,其中甲乙两人各自独立进行游戏A,丙丁两人各自独立进行游戏B.已知甲、乙两人各自闯关成功的概率均为,丙、丁两人各自闯关成功的概率均为.(1)求游戏A被闯关成功的人数多于游戏B被闯关成功的人数的概率;(2)记游戏A、B被闯关总人数为ξ,求ξ的分布列和期望.22.设椭圆C:+=1(a>b>0)过点(0,4),离心率为.(1)求椭圆C的方程;(2)求过点(3,0)且斜率为的直线被椭圆所截得线段的中点坐标.23.已知函数f(x)=在(,f())处的切线方程为8x﹣9y+t=0(m∈N,t∈R)(1)求m和t的值;(2)若关于x的不等式f(x)≤ax+在[,+∞)恒成立,求实数a的取值范围.24.如图,已知五面体ABCDE,其中△ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,且DC⊥平面ABC.(Ⅰ)证明:AD⊥BC(Ⅱ)若AB=4,BC=2,且二面角A﹣BD﹣C所成角θ的正切值是2,试求该几何体ABCDE的体积.铜陵市一中2018-2019学年高二上学期第二次月考试卷数学(参考答案)一、选择题1.【答案】A【解析】解:设x<0时,则﹣x>0,因为当x>0时,f(x)=x3﹣2x2所以f(﹣x)=(﹣x)3﹣2(﹣x)2=﹣x3﹣2x2,又因为f(x)是定义在R上的奇函数,所以f(﹣x)=﹣f(x),所以当x<0时,函数f(x)的表达式为f(x)=x3+2x2,故选A.2.【答案】A【解析】考点:集合的包含关系的判断与应用.【方法点晴】本题主要考查了集合的包含关系的判定与应用,其中解答中涉及到分式不等式的求解,一元二次不等式的解法,集合的子集的相关的运算等知识点的综合考查,着重考查了转化与化归思想、分类讨论思想的应用,以及学生的推理与运算能力,属于中档试题,本题的解答中正确求解每个不等式的解集是解答的关键. 3.【答案】C【解析】解:模拟执行程序,可得,当a≥b时,则输出a(b+1),反之,则输出b(a+1),∵2tan=2,lg=﹣1,∴(2tan)⊗lg=(2tan)×(lg+1)=2×(﹣1+1)=0,∵lne=1,()﹣1=5,∴lne⊗()﹣1=()﹣1×(lne+1)=5×(1+1)=10,∴+=0+10=10.故选:C.4. 【答案】D【解析】解:∵A=(﹣∞,1),B=(﹣∞,﹣2)∪(0,+∞),∴A ∩B=(﹣∞,﹣2)∪(0,1),故选:D .【点评】此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.5. 【答案】B 【解析】解:∵a=3,,A=60°,∴由正弦定理可得:sinB===1,∴B=90°,即满足条件的三角形个数为1个. 故选:B .【点评】本题主要考查三角形个数的判断,利用正弦定理是解决本题的关键,考查学生的计算能力,属于基础题.6. 【答案】D 【解析】试题分析:分析题意可知:对应法则为31y x =+,则应有42331331a a a k ⎧=⨯+⎪⎨+=⋅+⎪⎩(1)或42313331a k a a ⎧=⋅+⎪⎨+=⨯+⎪⎩(2),由于*a N ∈,所以(1)式无解,解(2)式得:25a k =⎧⎨=⎩。
2018-2019学年安徽省铜陵市第一中学高二上学期期中考试数学试题答案
GD 2 DE 2 3 , GC 2 CF 2 4 ,所以 EF 5 ,
由 GC 4 2 , CF 4 ,得 BF FG
在 △EFG 中 ,有 EF 2 GE 2 FG 2 ,所以 EG GF , 又因为 CF EF , CF FG ,得 CF 平面 EFG ,
19、 (12 分) 解:(1)散点图如下: 3+4+5+6 2.5+3+4+4.5 (2) x = =4.5, y = =3.5, 4 4
4
∑xiyi=3×2.5+4×3+5×4+6×4.5=66.5,
i=1 4 i=1
2 2 2 2 ∑x2 i=3 +4 +5 +6 =86,
^
∑xiyi-4 x
1 1 1 x 1 ,点 E 0, 所以 BE 1 2 k k k 4k 2 2k 4 2 1 k 2
2
k 1 又圆心 C 到 l2 的距离为 ,所以 PQ 2 5 2 1 k 2 1 k
故 S DEPQ
4 ,当 k 0 时,直线 l1 与 y 轴无交点,不合题意,舍去. 3
4 时直线 l2 的方程为 4 x 3 y 4 0 .(6 分) 3 x y 1 ,即 2 x ty 2t 0 . t 2
(2)设 M ( x, y ) ,由点 M 在线段 AD 上,得
2 2 由 AM 2 BM ,得 ( x ) ( y )
由余弦定理可得 BD 2 3 . AD 2 BD 2 AB 2 , AD BD . 平面 PBD 平面 ABCD ,交线为 BD , AD 平面 PBD , AD PB . (6 分)
(2)解:作 EF ∥ BC ,交 PB 于点 F ,连接 AF , 由 EF ∥ BC ∥ AD 可知 A , D , E , F 四点共面, 连接 DF ,所以由(1)的结论可知, PB 平面 ADE ,当且仅当 PB DF . 在 △PBD 中,由 PB 4 , BD 2 3 , PD 2 5 , 余弦定理求得 cos BPD
安徽省铜陵市第一中学2018-2019学年高二10月月考数学试题 Word版
3 2 333 2 33铜陵一中高二年级 10 月份月考数学试卷考试时间:120 分钟满分:150 分一、选择题(本大题共 12 小题,每小题 5 分,共 60 分) 1、直线3x + 4 y - 2 = 0 和直线6x + 8 y + 1 = 0 的距离是(). 3 1 A.B.523 1 C.D.1052、下列命题正确的是().A. 两两相交的三条直线可确定唯一一个平面B. 两个平面与第三个平面所成的角都相等,则这两个平面一定平行C. 过平面外一点的直线与这个平面只能相交或平行D. 和两条异面直线都相交的两条直线一定是异面直线3、如图所示是水平放置的∆ABC 按“斜二测画法”得到的直观图,B 'O ' =C 'O ' = 1, A 'O ' =3 ,则原∆ABC 中∠ABC 的大小是().2A. 30ºB. 45ºC. 60ºD. 90º4、执行下面的程序框图,如果输入的 x i m ,y i h ,n i h ,则输出的 x 、y 的值满足().A. y = 2xB. y = 3xC. y = 4xD. y = 5x5、已知某几何体的三视图如右上图所示,则该几何体的体积是().A. 2 +πB. 2 + 2πC.+π D.+ 2π13 23 3 3317 17 2 6、若点A 是点 B (1,2,3) 关于x 轴的对称点,点C 是点 D (2,-2,5) 关于y 轴对称的点,则 AC =().A. 5B. C. 10 D.7、已知直线l 1:2x - y + 1 = 0 ,直线l 2 过点(1,1) ,且倾斜角为直线l 1 的倾斜角的两倍,则直线l 2 的方程为().A. 4x + 3y - 7 = 0B. 4x + 3y + 1 = 0C. 4x - y - 3 = 0D. 4x - y + 5 = 08、点 P (4,-2) 与圆 x 2 + y 2 = 4 上任意一点连线的中点轨迹方程是().A. ( x - 2)2 + ( y - 1)2 = 1B. ( x + 2)2 + ( y - 1)2 = 1C. ( x - 2)2 + ( y + 1)2 = 1D. ( x - 1)2 + ( y + 2)2 = 19、古希腊数学家阿波罗尼斯(约公元前 262-190 年)证明过这样一个命题:平面内到两定点距离之比为常数 k (k > 0且k ≠ 1) 的点的轨迹是圆,人们称之为阿氏圆。
铜陵市第一高级中学2018-2019学年上学期高二数学12月月考试题含答案
铜陵市第一高级中学2018-2019学年上学期高二数学12月月考试题含答案班级__________ 座号_____ 姓名__________ 分数__________一、选择题1.是z的共轭复数,若z+=2,(z﹣)i=2(i为虚数单位),则z=()A.1+i B.﹣1﹣i C.﹣1+i D.1﹣i2.过点(2,﹣2)且与双曲线﹣y2=1有公共渐近线的双曲线方程是()A.﹣=1 B.﹣=1 C.﹣=1 D.﹣=13.四棱锥的八条棱代表8种不同的化工产品,由公共点的两条棱代表的化工产品放在同一仓库是危险的,没有公共点的两条棱代表的化工产品放在同一仓库是安全的,现打算用编号为①、②、③、④的4个仓库存放这8种化工产品,那么安全存放的不同方法种数为()A.96 B.48 C.24 D.04.在《张邱建算经》中有一道题:“今有女子不善织布,逐日所织的布比同数递减,初日织五尺,末一日织一尺,计织三十日”,由此推断,该女子到第10日时,大约已经完成三十日织布总量的()A.33% B.49% C.62% D.88%5.函数y=的图象大致是()A.B.C.D.6.已知函数f(x)=2x﹣+cosx,设x1,x2∈(0,π)(x1≠x2),且f(x1)=f(x2),若x1,x0,x2成等差数列,f′(x)是f(x)的导函数,则()A.f′(x0)<0 B.f′(x0)=0C.f′(x0)>0 D.f′(x0)的符号无法确定7.下列结论正确的是()A .若直线l ∥平面α,直线l ∥平面β,则α∥β.B .若直线l ⊥平面α,直线l ⊥平面β,则α∥β.C .若直线l 1,l 2与平面α所成的角相等,则l 1∥l 2D .若直线l 上两个不同的点A ,B 到平面α的距离相等,则l ∥α8. 数列﹣1,4,﹣7,10,…,(﹣1)n (3n ﹣2)的前n 项和为S n ,则S 11+S 20=( )A .﹣16B .14C .28D .309. 将函数y=cosx 的图象上各点的横坐标伸长到原来的2倍(纵坐标不变),再向右平移个单位,所得函数图象的一条对称轴方程是( )A .x=πB .C .D .10.过抛物线22(0)y px p =>焦点F 的直线与双曲线2218-=y x 的一条渐近线平行,并交其抛物线于A 、 B 两点,若>AF BF ,且||3AF =,则抛物线方程为( )A .2y x =B .22y x =C .24y x =D .23y x =【命题意图】本题考查抛物线方程、抛物线定义、双曲线标准方程和简单几何性质等基础知识,意在考查方程思想和运算能力.11.已知函数f (x )=3cos (2x ﹣),则下列结论正确的是( )A .导函数为B .函数f (x )的图象关于直线对称C .函数f (x )在区间(﹣,)上是增函数D .函数f (x )的图象可由函数y=3co s2x 的图象向右平移个单位长度得到12.执行如图所示的程序框图,则输出结果S=( )A .15B .25C .50D .100二、填空题13.设,x y 满足条件,1,x y a x y +≥⎧⎨-≤-⎩,若z ax y =-有最小值,则a 的取值范围为 .14.命题:“∀x ∈R ,都有x 3≥1”的否定形式为 .15.若直线y ﹣kx ﹣1=0(k ∈R )与椭圆恒有公共点,则m 的取值范围是 .16.81()x x-的展开式中,常数项为___________.(用数字作答)【命题意图】本题考查用二项式定理求指定项,基础题.17.已知实数x ,y 满足约束条,则z=的最小值为 .18.在空间直角坐标系中,设)1,3(,m A ,)1,1,1(-B ,且22||=AB ,则=m . 三、解答题19.(本小题满分12分)如图,四棱锥P ABCD -中,底面ABCD 为矩形,PA ⊥平面ABCD ,E 是PD 的中点. (1)证明://PB 平面AEC ;(2)设1AP =,AD =P ABD -的体积4V =,求A 到平面PBC 的距离.111]20.【常熟中学2018届高三10月阶段性抽测(一)】已知函数()()2ln R f x x ax x a =-+-∈.(1)若函数()f x 是单调递减函数,求实数a 的取值范围; (2)若函数()f x 在区间()0,3上既有极大值又有极小值,求实数a 的取值范围.21.解关于x 的不等式12x 2﹣ax >a 2(a ∈R ).22.请你设计一个包装盒,如图所示,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得A,B,C,D四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E、F在AB上,是被切去的等腰直角三角形斜边的两个端点,设AE=FB=x(cm).(1)若广告商要求包装盒侧面积S(cm2)最大,试问x应取何值?(2)若广告商要求包装盒容积V(cm3)最大,试问x应取何值?并求出此时包装盒的高与底面边长的比值.23.巳知二次函数f(x)=ax2+bx+c和g(x)=ax2+bx+c•lnx(abc≠0).(Ⅰ)证明:当a<0时,无论b为何值,函数g(x)在定义域内不可能总为增函数;(Ⅱ)在同一函数图象上取任意两个不同的点A(x1,y1),B(x2,y2),线段AB的中点C(x0,y0),记直线AB的斜率为k若f(x)满足k=f′(x0),则称其为“K函数”.判断函数f(x)=ax2+bx+c与g(x)=ax2+bx+c•lnx 是否为“K函数”?并证明你的结论.24.从正方形四个顶点及其中心这5个点中,任取2个点,则这2个点的距离不小于该正方形边长的概率为()ABCD铜陵市第一高级中学2018-2019学年上学期高二数学12月月考试题含答案(参考答案)一、选择题1.【答案】D【解析】解:由于,(z﹣)i=2,可得z﹣=﹣2i ①又z+=2 ②由①②解得z=1﹣i故选D.2.【答案】A【解析】解:设所求双曲线方程为﹣y2=λ,把(2,﹣2)代入方程﹣y2=λ,解得λ=﹣2.由此可求得所求双曲线的方程为.故选A.【点评】本题考查双曲线的渐近线方程,解题时要注意公式的灵活运用.3.【答案】B【解析】排列、组合的实际应用;空间中直线与直线之间的位置关系.【专题】计算题;压轴题.【分析】首先分析题目已知由公共点的两条棱代表的化工产品放在同一仓库是危险的,没有公共点的两条棱代表的化工产品放在同一仓库是安全的,现打算用编号为①、②、③、④的4个仓库存放这8种化工产品,求安全存放的不同方法的种数.首先需要把四棱锥个顶点设出来,然后分析到四棱锥没有公共点的8条棱分4组,只有2种情况.然后求出即可得到答案.【解答】解:8种化工产品分4组,设四棱锥的顶点是P,底面四边形的个顶点为A、B、C、D.分析得到四棱锥没有公共点的8条棱分4组,只有2种情况,(PA、DC;PB、AD;PC、AB;PD、BC)或(PA、BC;PD、AB;PC、AD;PB、DC)那么安全存放的不同方法种数为2A44=48.故选B.【点评】此题主要考查排列组合在实际中的应用,其中涉及到空间直线与直线之间的位置关系的判断,把空间几何与概率问题联系在一起有一定的综合性且非常新颖.4.【答案】B【解析】5.【答案】C【解析】解:∵f(﹣x)==﹣f(x),∴函数y=的图象关于原点对称,故排除B,当x→+∞时,y→0,且为正值,故排除A、D,故选C.【点评】本题考查了函数的图象的判断,常利用排除法.6.【答案】A【解析】解:∵函数f(x)=2x﹣+cosx,设x1,x2∈(0,π)(x1≠x2),且f(x1)=f(x2),∴,∴存在x1<a<x2,f'(a)=0,∴,∴,解得a=,假设x1,x2在a的邻域内,即x2﹣x1≈0.∵,∴,∴f(x)的图象在a的邻域内的斜率不断减少小,斜率的导数为正,∴x0>a,又∵x>x0,又∵x>x0时,f''(x)递减,∴.故选:A.【点评】本题考查导数的性质的应用,是难题,解题时要认真审题,注意二阶导数和三阶导数的性质的合理运用.7.【答案】B【解析】解:A选项中,两个平面可以相交,l与交线平行即可,故不正确;B选项中,垂直于同一平面的两个平面平行,正确;C选项中,直线与直线相交、平行、异面都有可能,故不正确;D中选项也可能相交.故选:B.【点评】本题考查平面与平面,直线与直线,直线与平面的位置关系,考查学生分析解决问题的能力,比较基础.8.【答案】B【解析】解:∵a n=(﹣1)n(3n﹣2),∴S11=()+(a2+a4+a6+a8+a10)=﹣(1+7+13+19+25+31)+(4+10+16+22+28)=﹣16,S20=(a1+a3+…+a19)+(a2+a4+…+a20)=﹣(1+7+...+55)+(4+10+ (58)=﹣+=30,∴S11+S20=﹣16+30=14.故选:B.【点评】本题考查数列求和,是中档题,解题时要认真审题,注意分组求和法和等差数列的性质的合理运用.9.【答案】B【解析】解:将函数y=cosx的图象上各点的横坐标伸长到原来的2倍(纵坐标不变),得到y=cos x,再向右平移个单位得到y=cos[(x)],由(x)=kπ,得x=2kπ,即+2kπ,k∈Z,当k=0时,,即函数的一条对称轴为,故选:B【点评】本题主要考查三角函数的对称轴的求解,利用三角函数的图象关系求出函数的解析式是解决本题的关键.10.【答案】C【解析】由已知得双曲线的一条渐近线方程为=y ,设00(,)A x y ,则02>p x,所以0002002322ì=ïï-ïïïï+=íïï=ïïïïîy p x p x y px ,解得2=p 或4=p ,因为322->p p,故03p <<,故2=p ,所以抛物线方程为24y x . 11.【答案】B【解析】解:对于A ,函数f ′(x )=﹣3sin (2x ﹣)•2=﹣6sin (2x ﹣),A 错误;对于B ,当x=时,f ()=3cos (2×﹣)=﹣3取得最小值,所以函数f (x )的图象关于直线对称,B 正确;对于C ,当x ∈(﹣,)时,2x ﹣∈(﹣,),函数f (x )=3cos (2x ﹣)不是单调函数,C 错误;对于D ,函数y=3co s2x 的图象向右平移个单位长度,得到函数y=3co s2(x ﹣)=3co s (2x ﹣)的图象,这不是函数f (x )的图象,D 错误. 故选:B .【点评】本题考查了余弦函数的图象与性质的应用问题,是基础题目.12.【答案】C【解析】解:根据程序框图,S=(﹣1+3)+(﹣5+7)+…+(﹣97+99)=50,输出的S 为50. 故选:C .【点评】本题主要考查了循环结构的程序框图,模拟执行程序框图,正确得到程序框图的功能是解题的关键,属于基础题.二、填空题13.【答案】[1,)+∞【解析】解析:不等式,1,x y a x y +≥⎧⎨-≤-⎩表示的平面区域如图所示,由z ax y =-得y ax z =-,当01a ≤<时,平移直线1l 可知,z 既没有最大值,也没有最小值;当1a ≥时,平移直线2l 可知,在点A 处z 取得最小值;当10a -<<时,平移直线3l 可知,z 既没有最大值,也没有最小值;当1a ≤-时,平移直线4l 可知,在点A 处z 取得最大值,综上所述,1a ≥.14.【答案】 ∃x 0∈R ,都有x 03<1 .【解析】解:因为全称命题的否定是特称命题.所以,命题:“∀x ∈R ,都有x 3≥1”的否定形式为:命题:“∃x 0∈R ,都有x 03<1”.故答案为:∃x 0∈R ,都有x 03<1.【点评】本题考查全称命题与特称命题的否定关系,基本知识的考查.15.【答案】 [1,5)∪(5,+∞) .【解析】解:整理直线方程得y ﹣1=kx ,∴直线恒过(0,1)点,因此只需要让点(0.1)在椭圆内或者椭圆上即可,由于该点在y 轴上,而该椭圆关于原点对称,故只需要令x=0有5y 2=5m得到y 2=m要让点(0.1)在椭圆内或者椭圆上,则y ≥1即是y 2≥1得到m ≥1∵椭圆方程中,m ≠5m 的范围是[1,5)∪(5,+∞) 故答案为[1,5)∪(5,+∞)【点评】本题主要考查了直线与圆锥曲线的综合问题.本题采用了数形结合的方法,解决问题较为直观.16.【答案】70【解析】81()x x -的展开式通项为8821881()(1)r r r r r rr T C x C x x--+=-=-,所以当4r =时,常数项为448(1)70C -=.17.【答案】.【解析】解:作出不等式组对应的平面区域如图:(阴影部分).由z==32x+y ,设t=2x+y , 则y=﹣2x+t , 平移直线y=﹣2x+t ,由图象可知当直线y=﹣2x+t 经过点B 时,直线y=﹣2x+t 的截距最小, 此时t 最小.由,解得,即B (﹣3,3),代入t=2x+y 得t=2×(﹣3)+3=﹣3.∴t 最小为﹣3,z 有最小值为z==3﹣3=.故答案为:.【点评】本题主要考查线性规划的应用,利用目标函数的几何意义,结合数形结合的数学思想是解决此类问题的基本方法.18.【答案】1 【解析】 试题分析:()()()()2213111222=-+--+-=m AB ,解得:1=m ,故填:1.考点:空间向量的坐标运算三、解答题19.【答案】(1)证明见解析;(2. 【解析】试题解析:(1)设BD 和AC 交于点O ,连接EO ,因为ABCD 为矩形,所以O 为BD 的中点,又E 为PD 的中点,所以//EO PB ,EO ⊂且平面AEC ,PB ⊄平面AEC ,所以//PB 平面AEC .(2)1366V PA AB AD AB ==,由4V =,可得32AB =,作A H P B ⊥交PB 于H .由题设知BC ⊥平面PAB ,所以BC AH ⊥,故AH ⊥平面PBC ,又31313PA AB AH PB ==,所以A 到平面PBC 的距离为.1 考点:1、棱锥的体积公式;2、直线与平面平行的判定定理. 20.【答案】(1)a ≤2)193a <<. 【解析】试题分析:(1)原问题等价于()0f x '≤对()0,+∞恒成立,即12a x x≤+对()0,+∞恒成立,结合均值不等式的结论可得a ≤(2)由题意可知()2210x ax f x x-+-'==在()0,3上有两个相异实根,结合二次函数根的分布可得实数a 的取值范围是193a <<.试题解析:(2)∵函数()f x 在()0,3上既有极大值又有极小值,∴()2210x ax f x x-+-'==在()0,3上有两个相异实根, 即2210x ax -+=在()0,3上有两个相异实根,记()221g x x ax =-+,则()()003{ 40030ag g ∆><<>>,得{012 193a a a a -<<<,即193a <<.21.【答案】【解析】解:由12x2﹣ax﹣a2>0⇔(4x+a)(3x﹣a)>0⇔(x+)(x﹣)>0,①a>0时,﹣<,解集为{x|x<﹣或x>};②a=0时,x2>0,解集为{x|x∈R且x≠0};③a<0时,﹣>,解集为{x|x<或x>﹣}.综上,当a>0时,﹣<,解集为{x|x<﹣或x>};当a=0时,x2>0,解集为{x|x∈R且x≠0};当a<0时,﹣>,解集为{x|x<或x>﹣}.22.【答案】【解析】解:设包装盒的高为h(cm),底面边长为a(cm),则a=x,h=(30﹣x),0<x<30.(1)S=4ah=8x(30﹣x)=﹣8(x﹣15)2+1800,∴当x=15时,S取最大值.(2)V=a2h=2(﹣x3+30x2),V′=6x(20﹣x),由V′=0得x=20,当x∈(0,20)时,V′>0;当x∈(20,30)时,V′<0;∴当x=20时,包装盒容积V(cm3)最大,此时,.即此时包装盒的高与底面边长的比值是.23.【答案】【解析】解:(Ⅰ)证明:如果g(x)是定义域(0,+∞)上的增函数,则有g′(x)=2ax+b+=>0;从而有2ax2+bx+c>0对任意x∈(0,+∞)恒成立;又∵a<0,则结合二次函数的图象可得,2ax2+bx+c>0对任意x∈(0,+∞)恒成立不可能,故当a<0时,无论b为何值,函数g(x)在定义域内不可能总为增函数;(Ⅱ)函数f(x)=ax2+bx+c是“K函数”,g(x)=ax2+bx+c•lnx不是“K函数”,事实上,对于二次函数f(x)=ax2+bx+c,k==a(x1+x2)+b=2ax0+b;又f′(x0)=2ax0+b,故k=f′(x0);故函数f(x)=ax2+bx+c是“K函数”;对于函数g(x)=ax2+bx+c•lnx,不妨设0<x1<x2,则k==2ax0+b+;而g′(x0)=2ax0+b+;故=,化简可得,=;设t=,则0<t<1,lnt=;设s(t)=lnt﹣;则s′(t)=>0;则s(t)=lnt﹣是(0,1)上的增函数,故s(t)<s(1)=0;则lnt≠;故g(x)=ax2+bx+c•lnx不是“K函数”.【点评】本题考查了导数的综合应用及学生对新定义的接受能力,属于中档题.24.【答案】C【解析】。
铜陵市高中2018-2019学年高二上学期第一次月考试卷数学
铜陵市高中2018-2019学年高二上学期第一次月考试卷数学 班级__________ 姓名__________ 分数__________一、选择题1. 已知集合A={4,5,6,8},B={3,5,7,8},则集合A ∪B=( ) A .{5,8}B .{4,5,6,7,8}C .{3,4,5,6,7,8}D .{4,5,6,7,8}2. 已知直线l的参数方程为1cos sin x t y t αα=+⎧⎪⎨=⎪⎩(t 为参数,α为直线l 的倾斜角),以原点O 为极点,x 轴正半轴为极轴建立极坐标系,圆C 的极坐标方程为4sin()3πρθ=+,直线l 与圆C 的两个交点为,A B ,当||AB 最小时,α的值为( )A .4πα=B .3πα=C .34πα=D .23πα=3. 已知向量,,其中.则“”是“”成立的( )A .充分而不必要条件B .必要而不充分条件C .充要条件D .既不充分又不必要条件 4. 设函数()y f x =对一切实数x 都满足(3)(3)f x f x +=-,且方程()0f x =恰有6个不同的实根,则这6个实根的和为( )A.18B.12C.9D.0【命题意图】本题考查抽象函数的对称性与函数和方程等基础知识,意在考查运算求解能力.5. “x ≠0”是“x >0”是的( )A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件6. 执行如图所示的程序框图,如果输入的t =10,则输出的i =( )A .4B .5C .6D .77. 由小到大排列的一组数据x 1,x 2,x 3,x 4,x 5,其中每个数据都小于﹣1,则样本1,x 1,﹣x 2,x 3,﹣x 4,x 5的中位数为( )A .B .C .D .8. 若f (x )为定义在区间G 上的任意两点x 1,x 2和任意实数λ(0,1),总有f (λx 1+(1﹣λ)x 2)≤λf (x 1)+(1﹣λ)f (x 2),则称这个函数为“上进”函数,下列函数是“上进”函数的个数是( )①f (x )=,②f (x )=,③f (x )=,④f (x )=.A .4B .3C .2D .19. 下列满足“∀x ∈R ,f (x )+f (﹣x )=0且f ′(x )≤0”的函数是( ) A .f (x )=﹣xe |x| B .f (x )=x+sinxC .f (x )=D .f (x )=x 2|x|10.已知实数x ,y 满足a x <a y (0<a <1),则下列关系式恒成立的是( )A .B .ln (x 2+1)>ln (y 2+1)C .x 3>y 3D .sinx >siny11.已知函数⎩⎨⎧≤>=)0(||)0(log )(2x x x x x f ,函数)(x g 满足以下三点条件:①定义域为R ;②对任意R x ∈,有1()(2)2g x g x =+;③当]1,1[-∈x 时,()g x 则函数)()(x g x f y -=在区间]4,4[-上零点的个数为( )A .7B .6C .5D .4【命题意图】本题考查利用函数图象来解决零点问题,突出了对分段函数的转化及数形结合思想的考查,本题综合性强,难度大.12.在区域内任意取一点P (x ,y ),则x 2+y 2<1的概率是( )A .0B .C .D .二、填空题13.由曲线y=2x 2,直线y=﹣4x ﹣2,直线x=1围成的封闭图形的面积为 .14.若6()mx y +展开式中33x y 的系数为160-,则m =__________.【命题意图】本题考查二项式定理的应用,意在考查逆向思维能力、方程思想.15.设复数z 满足z (2﹣3i )=6+4i (i 为虚数单位),则z 的模为 . 16.17.已知函数f (x )是定义在R 上的奇函数,且它的图象关于直线x=1对称.17.的展开式中的系数为 (用数字作答).18.已知直线l :ax ﹣by ﹣1=0(a >0,b >0)过点(1,﹣1),则ab 的最大值是 .三、解答题19.(本题满分12分)在长方体1111D C B A ABCD -中,a AD AA ==1,E 是棱CD 上的一点,P 是棱1AA 上的一点.(1)求证:⊥1AD 平面D B A 11; (2)求证:11AD E B ⊥;(3)若E 是棱CD 的中点,P 是棱1AA 的中点,求证://DP 平面AE B 1.20f x =sin ωx+φω00φ2π(1)求f(x)的解析式;(2)求函数g(x)=f(x)+sin2x的单调递增区间.21.如图,边长为2的正方形ABCD绕AB边所在直线旋转一定的角度(小于180°)到ABEF的位置.(Ⅰ)求证:CE∥平面ADF;(Ⅱ)若K为线段BE上异于B,E的点,CE=2.设直线AK与平面BDF所成角为φ,当30°≤φ≤45°时,求BK的取值范围.22.为了解学生身高情况,某校以10%的比例对全校700名学生按性别进行抽样检查,测得身高情况的统计图如下:(Ⅰ)估计该校男生的人数;(Ⅱ)估计该校学生身高在170~185cm之间的概率;(Ⅲ)从样本中身高在180~190cm之间的男生中任选2人,求至少有1人身高在185~190cm之间的概率.23.已知函数f(x)=log a(1﹣x)+log a(x+3),其中0<a<1.(1)求函数f(x)的定义域;(2)若函数f(x)的最小值为﹣4,求a的值.24.已知函数f(x)=lnx﹣ax+(a∈R).(Ⅰ)当a=1时,求曲线y=f(x)在点(1,f(1))处的切线方程;(Ⅱ)若函数y=f(x)在定义域内存在两个极值点,求a的取值范围.铜陵市高中2018-2019学年高二上学期第一次月考试卷数学(参考答案)一、选择题1. 【答案】C【解析】解:∵A={4,5,6,8},B={3,5,7,8}, ∴A ∪B={3,4,5,6,7,8}. 故选C2. 【答案】A【解析】解析:本题考查直线的参数方程、圆的极坐标方程及其直线与圆的位置关系.在直角坐标系中,圆C的方程为22((1)4x y +-=,直线l 的普通方程为tan (1)y x α=-,直线l 过定点M ,∵||2MC <,∴点M 在圆C 的内部.当||AB 最小时,直线l ⊥直线MC ,1MC k =-,∴直线l 的斜率为1,∴4πα=,选A .3. 【答案】A【解析】【知识点】平面向量坐标运算【试题解析】若,则成立;反过来,若,则或所以“”是“”成立的充分而不必要条件。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2018-2019学年安徽省铜陵市第一中学高二上学期开学考试数学试题
一、选择题(12题共60分)
1.一个几何体的三视图如图所示,则该几何体的直观图可以是( )
2.某几何体的三视图如图所示,则该几何体的体积为( )
A.16+8πB.8+8π
C.16+16πD.8+16π
3.如图所示,在底面为正方形,侧棱垂直于底面的四棱柱ABCD-A1B1C1D1中,AA1=2AB,则异面直线A1B与AD1所成角的余弦值为( )
A.15
B.25
C.35
D.45
4.直线x cos140°+y sin40°+1=0的倾斜角是( ) A .40° B .50° C .130°
D .140°
5.在等腰三角形AOB 中,AO =AB ,点O (0,0),A (1,3),点B 在x 轴的正半轴上,则直线
AB 的方程为( )
A .y -1=3(x -3)
B .y -1=-3(x -3)
C .y -3=3(x -1)
D .y -3=-3(x -1)
6.直线2x +(m +1)y +4=0与直线mx +3y -2=0平行,则m =( ) A .2 B .-3 C .2或-3
D .-2或-3
7.经过两条直线2x +3y +1=0和x -3y +4=0的交点,并且垂直于直线3x +4y -7=0的直线方程为( )
A .4x -3y +9=0
B .4x +3y +9=0
C .3x -4y +9=0
D .3x +4y +9=0
8.在正方体ABCD -A 1B 1C 1D 1中,棱长为a ,M ,N 分别为A 1B 和AC 上的点,若A 1M =AN =2a
3,
则MN 与平面BB 1C 1C 的位置关系是( )
A .相交
B .平行
C .垂直
D .不能确定
9.圆x 2+y 2
+2x -6y +1=0关于直线ax -by +3=0(a >0,b >0)对称,则1a +3b
的最小值是
( )
A .2 3 B.203 C .4
D.163
10.在三棱锥S -ABC 中,△ABC 是边长为6的正三角形,SA =SB =SC =15,平面DEFH 分别与AB ,BC ,SC ,SA 交于D ,E ,F ,H .D ,E 分别是AB ,BC 的中点,如果直线SB ∥平面DEFH ,那么四边形DEFH 的面积为( )
A.452
B. 4532
C .45
D .45 3
11.已知在圆M :x 2+y 2
-4x +2y =0内,过点E (1,0)的最长弦和最短弦分别是AC 和BD ,则四边形ABCD 的面积为( )
A .3 5
B .6 5
C .415
D .215
12.已知点P (x ,y )在圆C :x 2
+y 2
-6x -6y +14=0上,则x +y 的最大值与最小值是( ) A .6+22,6-2 2 B .6+2,6- 2 C .4+22,4-2 2 D .4+2,4- 2
二、填空题(4题共20分)
13.已知a ∈R ,若方程a 2x 2
+(a +2)y 2
+4x +8y +5a =0表示圆,则此圆心坐标是________.
14.已知点A (-3,-4),B (6,3)到直线l :ax +y +1=0的距离相等,则实数a 的值为________.
15.如图,四棱锥P -ABCD 中,PA ⊥底面ABCD ,底面ABCD 为正方形,则下列结论:
①AD ∥平面PBC ; ②平面PAC ⊥平面PBD ; ③平面PAB ⊥平面PAC ; ④平面PAD ⊥平面PDC .
其中正确的结论序号是________.
16.在平面直角坐标系xOy 中,A (-12,0),B (0,6),点P 在圆O :x 2+y 2=50上.若PA →·PB →
≤20,则点P 的横坐标的取值范围是________.
三、解答题(6题。
17题10分,其余各题12分,共70分)
17.如图,ABCD 是正方形,O 是正方形的中心,PO
底面ABCD , E 是PC 的中点。
BDE
PAC平面BDE
18.已知直线l:x-2y+8=0和两点A(2,0),B(-2,-4).
(1)在直线l上求一点P,使|PA|+|PB|最小;
(2)在直线l上求一点P,使||PB|-|PA||最大.
19.已知直线l经过直线2x+y-5=0与x-2y=0的交点P.
(1)点A(5,0)到l的距离为3,求l的方程;
(2)求点A(5,0)到l的距离的最大值.
20.在三棱锥P-ABC中,△PAB是等边三角形,PA⊥AC,PB⊥BC.
(1)证明:AB⊥PC;
(2)若PC=2,且平面PAC⊥平面PBC,求三棱锥P-ABC的体积.
21.已知圆C经过P(4,-2),Q(-1,3)两点,且y轴被圆截得的弦长为43,半径小于5.
(1)求直线PQ与圆C的方程;
(2)若直线l∥PQ,且l与圆C交于点A,B且以线段AB为直径的圆经过坐标原点,求直线l的方程.
22.已知过原点的动直线l与圆C1:x2+y2-6x+5=0相交于不同的两点A,B.
(1)求圆C1的圆心坐标;
(2)求线段AB的中点M的轨迹C的方程;
(3)是否存在实数k,使得直线L: y=k(x-4)与曲线C只有一个交点?若存在,求出k 的取值范围;若不存在,说明理由.
1-12 DADBD CABDA DA 13. (-2,-4) 14.-13或-79
15.①②④ 16.[-52,1]
17.略 18.(1)(-2,3) (2)(12,10) 19.(1)x =2或4x -3y -5=0.(2)10. 20.(1)略(2)13
.
21.(1)PQ 的方程为x +y -2=0.圆C 的方程为(x -1)2
+y 2
=13 (2)x +y -4=0或x +y +3=0.
22.(1)(3,0).(2)⎝ ⎛⎭⎪⎫x -322+y 2=94⎝ ⎛⎭
⎪⎫53<x ≤3.
(3)-257≤k ≤257或k =±3
4。
