跨声速压气机非定常流动及损失的数值研究
高负荷跨音速轴流压气机的叶型优化设计

能。
压气机的全三维数值优化技 术集三维 流场求解 、 优化 技
术 为 一 体 , 过 对 原 型 机 进 行 参 数 化 而 扰 动 几 何 构 型 , 从 通 以
中寻优。 目前较常用 的方法是结合神 经网络 ( 响应面模 型的
一
种) 与遗传算法 的优 化方法。众多国外学者 已在该领域 进
第2 卷 第7 9 期
文 章 编 号 :06 94 (0 2 0 - 0 5 0 1 0 - 3 8 2 1 )7 07 - 5
计
算
机
仿
真
21年7 02 月
荷 跨 音 速 轴 流压 气 机 的 叶型 优 化 设 计
李相 君 , 武利 , 皓光 , 楚 张 米 攀
( 西北工业大学 动力与 能源学 院, 陕西 西安 7 07 102)
定 范 围 内扰 动 , 可 以 得 到 一 系 列 新 的 叶 型 , 就 以此 构 建 叶 型
面处则使用 周向平 均法进 行数 值传 递。计算 区域 包括进 口
导 叶、 转子及静子 排 。另外 为提 高计 算效 率 , 采用 了多重 网
格 法 、 部 时 间 步 长 和 隐 式 残 差 光 顺 三 种 措 施 加 速 计 算 收 局
一
7 — 5
表 1 计 算 网格 数 量分 布
压气机跨音速叶栅叶型的数值模拟

求解器采用耦合求解器隐式方案 , 根据湍流模型
收 稿 日期 :0 8— 6—0 20 0 3 作 者 简介 : 张广 (9 3一 , , 龙 江 哈 尔滨 人 , 读 硕 士 , 18 )男 黑 在 主要 研
对弯度. 最大相对厚度 e不变的基础上 , 厂 _ 、 将最大 弯度 位置 、 最大 厚度 位 置 向后 缘移 动 , 过 这 通
摘
要: 以抑制叶型吸力面激波强度 、 附面层分离 , 降低叶型损失为 目标 , 对某型 压气机跨 音速 叶
栅 叶型进行气 动优化 。运用数值模拟 的方法对 比研究优化后 的叶栅 同原型叶栅在相 同工况下 的 气动性能 , 概述了气动性能产生变化 的机 理。与优化 前对 比发现 , 优化后 的叶 型具 有低损 失 , T
采用 迎风 格式 的有 限体积 法对 二维 定 常 Ⅳ 一 s方程 进行 数 值 求 解 , 维 流 场 计 算 区域 采 用 H 二
型 网格 , 网格 数 为 9 ( 距 方 向 ) ×3 0 流 动 方 0栅 8(
2 气 动 优 化 思 路
借 鉴高 亚音 速叶栅 以及 超音 速 叶栅 叶型特点 对 该跨 音速 叶 型进 行 优 化设 计 , 索 验 证 叶 型最 探
马赫数 。叶栅 前后 延伸 部分 均采用 周期 性边 界条 件 。叶盆和 叶背均 采用 绝热 的无 滑移壁 面条 件 。
研究 方 向。本 文通 过 求 解 可 压缩 雷 诺 平 均 N—s
方程 , 数值 模拟 了压 气机 叶栅跨 音速 流 动情况 。
1 计 算方 法 与边 界 条 件
作 范 围大 的特 点 。
关键 词 : 跨音速压气机 ; 叶型 ; 气动优化 ; 数值计算
跨声速轴流压气机非设计点特性计算

t u ba nn t e p n w s a rd n mi p r mee s n c a a t r t u v s t d s n n o - e i p i t. T e h s o ti i g h s a — ie eo y a c a a tr a d h rc ei i c re a e i a d f d sg sc g n o ns h c mp r o i e tr s l n iae h tt e l s n e it n a g e mo e s efc ie fr t e c mp e s r p roma c o ai n w t t s e u t i d c ts t a h o s a d d va i n l d li f t o h o r so e fr n e s h s o e v
Nu ei a i l to fa c ran t p fta s nc a ilfo c mpr so sc rid o tu i te mlne c r aur t d, m rc lsmu ai n o et i y e o r n o i x a— w o l e s r i a re u sng sra i u v t e meho
摘要 : 基于公开发表 的研究成果 , 发展了一种适用于跨声速轴流压气机 的损失和落后 角模型 , 采用流线 曲率法对某
单级跨声速轴流压气机进行了数值模拟 , 到了展 向参数分 布和 全工况下 的性能 曲线 。通 过与实验值 的 比较 , 得 验 证 了该方法和模型在跨声速轴流压气机非设计点性能预测 中的有效性 。
prdito e c in. Ke r y wo ds:t e m ln ur at e;t a on c;de i to a sr a i e c v ur r ns i v a i n ngl ls e; o s
跨声速轴流压气机转子Rotor37周向槽机匣处理的数值研究

跨声速轴流压气机转子Rotor37周向槽机匣处理的数值研究何文博;史磊【摘要】以跨声速压气机转子Rotor37为研究对象,采用商业软件NUMECA数值研究了单槽处理机匣的轴向位置对于压气机性能及内部流场的影响.周向槽处理机匣的宽度为3 mm,深度为10倍叶尖间隙,即3.56 mm,起始位置分别位于轮缘机匣尖部型面的10%、20%、30%、40%、50%相对弦长处.数值计算结果表明:原始光壁压气机转子的失速原因为叶尖泄漏流动引发的低速区对于尖部叶片通道的堵塞,其稳定工作裕度为14.74%.采取的周向槽机匣处理能够改变转子叶尖流动堵塞状况.当机匣处理起始位置位于30%相对弦长时,压气机转子稳定工作裕度的提升量最大,相比原始压气机转子的稳定裕度提高了1.86%.【期刊名称】《科学技术与工程》【年(卷),期】2018(018)028【总页数】6页(P164-169)【关键词】跨声速压气机;周向槽机匣处理;叶尖泄漏流动;稳定工作裕度【作者】何文博;史磊【作者单位】中国民航大学天津市民用航空器适航与维修重点实验室,天津300300;中国民航大学天津市民用航空器适航与维修重点实验室,天津300300【正文语种】中文【中图分类】V231.3近些年来,航空发动机的推重比在升高,压气机的轴向尺寸在不断缩短,级数在逐渐减少,平均级负荷水平一直在提高。
然而负荷水平的提高使得压气机的稳定工作范围减小,因此有必要拓宽压气机的稳定工作边界;其中机匣处理即作为一种有效的扩稳技术手段。
人们对机匣处理的扩稳认识始于20世纪60年代初,此后美国NASA、法国国家、航空航天研究院、英国剑桥大学、日本东京大学等纷纷开展了对机匣处理技术的研究[1]。
进入70年代,大量的实验研究工作侧重于槽类和缝类机匣处理的设计方法、扩稳效果及结构尺寸的优化,Lewis研究中心针对机匣处理就做了大量的工作,得出了机匣处理可以使压气机裕度改进,但同时又使压气机效率降低的结论[2,3]。
吸附式跨声速压气机参数化设计研究

1 设 计 和 分 析 方 法
1 I数 值 方 法 .
罗建枫 一朱俊 强 卢新 根 , , ,
( .中国科 学院工程 热物 理研 究所 ; . 国科 学院研 究 生院 北京 10 8 ) 1 2 中 0 0 0
摘 要 : 文 借 助 S/ 2两 类 流 面 迭 代 和 s 流 面 正反 问 题 混 合 计 算 方 法 , 叶 片 吸 力 面 边 界 层 吸 气 为手 段 , 本 1¥ l 以
详 细研 究 了边界 层抽 吸 的吸气 量 和吸气 位置 对跨声 速压 气机 叶栅 气 动 性 能 的影 响 , 果 表 明 叶 栅来 流 结
Ma 和方 向一定 时 , 吸气 位 置和 吸气 量是相 互 关联 的 关键 参数 , 想的 吸 气 位 置应 该 是 在 靠 近 激 波后 边 理
迭代 计算 , 中无 粘 计 算 部分 使 用 牛顿 法 求 解 欧 拉 其 方程组 , 粘性 影响 由边界层 积分方 程计算 得 出的边 界
中 图分 类 号 : K 7 . T 44 8 1
提高转 子 的转速 或增 加 叶片 的气动 负荷 是提 高 轴 流压气 机级 压 比的 有 效途 径 , 而转 子 转 速 的 提 然 高 除受 到叶 片所 能 承受 最 大 应 力 的 限 制外 , 使 激 还 波本 身 以及激 波 所 诱 发 的 一 系列 损 失 增 加 。因 此 ,
讨 , 文将 从 以上两 方面 展开பைடு நூலகம்详细 研究 。 本
压气机失速信号分析
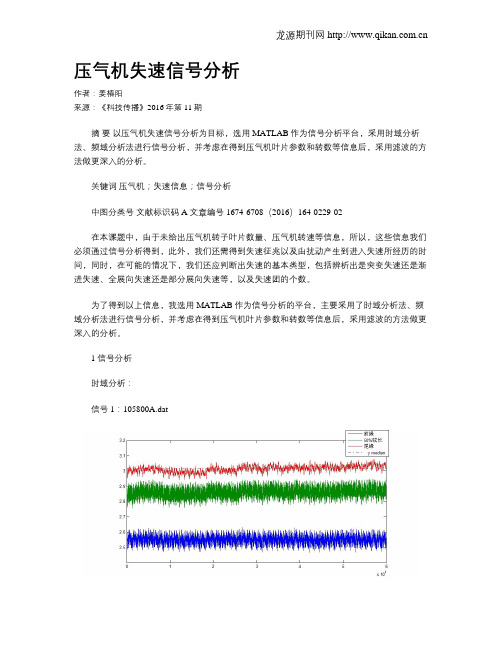
压气机失速信号分析作者:姜椿阳来源:《科技传播》2016年第11期摘要以压气机失速信号分析为目标,选用MATLAB作为信号分析平台,采用时域分析法、频域分析法进行信号分析,并考虑在得到压气机叶片参数和转数等信息后,采用滤波的方法做更深入的分析。
关键词压气机;失速信息;信号分析中图分类号文献标识码 A 文章编号 1674-6708(2016)164-0229-02在本课题中,由于未给出压气机转子叶片数量、压气机转速等信息,所以,这些信息我们必须通过信号分析得到,此外,我们还需得到失速征兆以及由扰动产生到进入失速所经历的时间,同时,在可能的情况下,我们还应判断出失速的基本类型,包括辨析出是突变失速还是渐进失速、全展向失速还是部分展向失速等,以及失速团的个数。
为了得到以上信息,我选用MATLAB作为信号分析的平台,主要采用了时域分析法、频域分析法进行信号分析,并考虑在得到压气机叶片参数和转数等信息后,采用滤波的方法做更深入的分析。
1 信号分析时域分析:信号1:105800A.dat如图1所示,即为近设计点工况时域图,横坐标按采集点个数均分,由于采样频率恒定为12K,采样时间为5s,所以采集点个数也就表征了时间。
由上图可以看出,近工况状态下,前缘、50%弦长和尾缘的压强信号基本保持稳定,只是在小范围内有脉动,将测得参数按按时间平均,并设前缘静压平均量为P1,50%弦长处P2,尾缘P3,则有P1=2.544,P3=3.013,于是得近设计点工况增压比n1=P1/P3=1.184。
如图2所示,压气机的近失速点实际即为压气机叶片气流分离点位于50%弦长处时,此时,微小扰动即可导致压气机进入失速状态。
按上一数据的处理方法,我们得到近失速点压比为n2=1.156,较近设计点工况略小,这是由于流动的分离导致压气机效率降低造成的/但是当进入失速状态时(近失速状态),我们可以定性的分析出尾缘处静压与前缘处静压在数值上呈现近似的负相关关系,这是由失速团的性质决定的,并且,节流阀开启后,压气机增压绝对值突然上升又剧烈下降,最后,成周期性变化,由此可以初步判定该失速类型为突变型失速。
基于CFD

第8卷㊀第6期2023年11月气体物理PHYSICSOFGASESVol.8㊀No.6Nov.2023㊀㊀DOI:10.19527/j.cnki.2096 ̄1642.1088基于CFD/CSD耦合的火箭跨声速气动阻尼特性分析李泳德ꎬ㊀郭㊀力ꎬ㊀季㊀辰(中国航天空气动力技术研究院ꎬ北京100074)CharacterizationofTransonicAerodynamicDampingofRocketsBasedonCFD/CSDCouplingLIYong ̄deꎬ㊀GUOLiꎬ㊀JIChen(ChinaAcademyofAerospaceAerodynamicsꎬBeijing100074ꎬChina)摘㊀要:随着新型大推力火箭的发展ꎬ弯曲模态频率的不断降低ꎬ以及流动分离和跨声速飞行时产生的激波震荡等因素ꎬ其在跨声速飞行过程中更容易出现非定常振动发散ꎮ文章以某带助推的运载火箭模型为研究对象ꎬ通过数值计算获取火箭强迫振动时的气动阻尼ꎬ并对影响火箭气动阻尼的因素进行了分析ꎮ包括结构节点位置㊁振动振幅大小㊁脉动压力等ꎮ研究表明:助推主要起到增大气动阻尼的作用ꎻ前节点主要影响收缩段的气动阻尼ꎻ振动振幅大小和脉动压力对气动阻尼的影响可忽略不计ꎮ关键词:气动阻尼ꎻ数值计算ꎻ跨声速ꎻ气动弹性ꎻ运载火箭㊀㊀㊀收稿日期:2023 ̄09 ̄25ꎻ修回日期:2023 ̄10 ̄23第一作者简介:李泳德(1995 ̄)㊀男ꎬ工学硕士ꎬ助理工程师ꎬ主要研究方向为气动弹性分析ꎮE ̄mail:562064169@qq.com通信作者简介:季辰(1982 ̄)㊀男ꎬ工学博士ꎬ研究员ꎬ主要研究方向为气动弹性力学ꎮE ̄mail:jichen167@hotmail.com中图分类号:V475.1㊀㊀文献标志码:AAbstract:Withthedevelopmentofnewhigh ̄thrustrocketsꎬthedecreasingfrequencyofthebendingmodesoftherocketꎬaswellasthefactorssuchasflowseparationandshockoscillationsgeneratedduringtransonicflightmakeitmorepronetonon ̄constantvibration.Inthispaperꎬalaunchvehiclemodelwithboostwastakenastheresearchobjectꎬandtheaerody ̄namicdampingoftherocketduringforcedvibrationwasobtainedthroughnumericalcalculation.Thefactorsaffectingtheaerodynamicdampingoftherocketwereanalyzedꎬincludingthepositionofstructuralnodesꎬthemagnitudeofvibrationam ̄plitudeꎬpulsatingpressureandsoon.Thestudyshowsthattheboostmainlyplaystheroleofincreasingaerodynamicdamp ̄ingandthefrontnodemainlyaffectstheaerodynamicdampingofthecontractionsection.Thevibrationamplitudesizeandthepulsatingpressurehaveanegligibleeffectontheaerodynamicdamping.Keywords:aerodynamicdampingꎻnumericalcalculationꎻtransonicꎻaeroelasticityꎻlaunchvehicle引㊀言通常情况下人们认为气动力对火箭的振动起到阻尼作用ꎬ即气动阻尼为正值ꎮ然而随着大推力火箭发展ꎬ火箭的长细比逐渐加大ꎬ导致弯曲刚度越来越小ꎬ同时为了满足有效载荷的外形要求ꎬ火箭头部整流罩尺寸不断加大ꎬ后续箱体的直径却保持不变ꎬ形成了典型的锤头体外形ꎮ国内外大量的火箭研制经验表明[1 ̄9]ꎬ对于此类锤头体外形火箭的气动设计ꎬ必须要进行动态气动载荷与动态气弹稳定性分析ꎬ否则设计的疏忽可能会导致火箭结构出现毁灭性的破坏进而导致发射失败ꎮ目前常用的衡量气弹稳定性的方法是通过风洞试验来获取气动阻尼系数ꎮ早在1963年ꎬ美国国家航空航天局Ames研究中心(NASAAmesRe ̄searchCenter)采用半刚性模型开展试验研究[10]ꎬ获取火箭头部的气动阻尼来评估其稳定性ꎬ但这只能用来模拟火箭弯曲振型前节点之前部分的结构动力学特性ꎮ直到兰利研究中心(NASALangleyResearchCenter)开发了全弹性模型气动阻尼试验气体物理2023年㊀第8卷技术ꎬ其可以模拟整体的结构动力学特性以及气动外形ꎬ并应用于多款运载火箭研制[11 ̄15]ꎮ国内ꎬ中国航天空气动力技术研究院对气动阻尼问题开展过较多的研究[16 ̄20]ꎬ从模型设计方法㊁模型制作工艺㊁试验机构设计和数据处理等诸多方面ꎬ逐步改进实现了从半刚性模型到全弹性模型的过渡ꎬ并在多个型号上得到验证ꎮ然而通过风洞试验研究气动弹性问题ꎬ技术难度大ꎬ试验成本高ꎬ同时几乎不可能开展全尺寸试验ꎮ因此通过数值计算的方法开展相关研究是另一种重要的手段ꎮ刘子强等[21]实现了通过数值计算确定气动阻尼系数的技术和方法ꎬ并与试验结果进行对比ꎬ证实了该方法的可靠性ꎮ冉景洪等[22]通过模态数据结合准定常理论的方法分析了减阻杆加后体这一弹性结构的气动阻尼ꎬ结果表明减阻杆造成的分离流会对后体的气动阻尼系数产生影响ꎮ朱剑等[23]针对新一代捆绑式运载火箭发展了非结构网格下的气动阻尼计算方法ꎬ并分析了攻角㊁Mach数等参数对气动阻尼的影响ꎮ本文在之前的计算方法[23]的基础上采用IDDES模型ꎬ考虑脉动压力的影响ꎬ通过强迫振动的方式ꎬ针对捆绑式运载火箭的某一特定模态进行数值计算仿真ꎬ研究前节点位置ꎬ振动振幅ꎬ脉动压力等参数对气动阻尼的影响规律ꎮ1㊀计算方法图1为本文所用的捆绑式运载火箭的计算模型ꎬ是典型的锤头体结构ꎮ在跨声速阶段ꎬ其头部会产生激波造成激波边界层干扰ꎬ而在锤头体外形的过渡段会出现气流分离ꎮ为探究各部分气动阻尼的变化ꎬ将整个箭体分为头部㊁过渡段㊁弹身3个部分ꎮ图1㊀表面网格及区域划分Fig.1㊀Surfacegridandregiondivision1.1㊀流场仿真模型本文分别用Reynolds平均法(Reynolds ̄averagedNavier ̄StokesꎬRANS)和改进的延迟分离涡模拟(improveddelayeddetached ̄eddysimulationꎬID ̄DES)[24 ̄25]进行计算ꎬ在RANS方程中ꎬ将变量分为平均值和波动值两部分ꎬ对于速度分量有ui=ui+uᶄi其中ꎬi=1ꎬ2ꎬ3ꎬui和uᶄi分别代表平均量和波动量ꎬ对于压强和其他标量也采用类似的形式ꎬ将这种形式代入连续性方程和动量方程中ꎬ并写成张量形式∂ρ∂t+∂∂xi(ρui)=0(1)∂∂t(ρui)+∂∂xj(ρuiuj)=∂p∂xi+∂∂xjμ∂ui∂xj+∂uj∂xi-23δij∂uk∂xkæèçöø÷éëêêùûúú+∂∂xj(-ρuᶄiuᶄj)(2)其中ꎬiꎬjꎬk可分别取1ꎬ2ꎬ3ꎻρ是密度ꎻt是时间ꎻ当i=j时δij取0ꎬ否则取1ꎮ式(1)㊁(2)是RANS方程ꎬ由方程可知RANS方法将湍流脉动对平均流动的作用模化为Reynolds应力项即-ρuᶄiuᶄjꎬ之后采用湍流模型进行封闭ꎬ本文采用的湍流模型为SSTk ̄ω模型ꎬ其输运方程为∂∂t(ρk)+∂∂xi(ρkui)=∂∂xjΓk∂k∂xjæèçöø÷+Gk-Yk∂∂t(ρω)+∂∂xi(ρωui)=∂∂xjΓω∂ω∂xjæèçöø÷+Gω-Yω其中ꎬk和ω分别代表湍流动能和湍流耗散率ꎬΓk和Γω分别代表k和ω的有效扩散系数ꎬGk和Gω分别代表k和ω的生成率ꎬYk和Yω分别代表k和ω的耗散率ꎮ因此RANS方法只能计算大尺度的平均流动ꎬ本文采用IDDES方法计算脉动压力对气动阻尼的影响ꎮIDDES方法是由分离涡模拟(detached ̄eddysimulationꎬDES)方法改进而来ꎬ其本质思想与DES方法相同ꎬ是想以网格尺度和模型中的特征尺度隐式划分RANS和大涡模拟(large ̄eddysimulationꎬLES)区域ꎬ使其既能处理RANS方法无法得到的脉动场ꎬ也能降低LES方法在模拟高Reynolds数流动时所需的计算资源ꎮ区别在于当边界层较厚或者分离区域较窄时ꎬDES方法会出现如模型应力损耗(modeledstressdepletionꎬMSD)ꎬ网格诱导分离(grid ̄inducedseparationꎬGIS)以及对数层不匹配(logarithmic ̄layermismatchꎬLLM)问题[24]ꎬ而IDDES模型通过改良计算区域划分ꎬ结合延迟分离涡模拟(delayeddetached ̄eddysimulationꎬDDES)和03第6期李泳德ꎬ等:基于CFD/CSD耦合的火箭跨声速气动阻尼特性分析壁面模型大涡模拟(wall ̄modeledlarge ̄eddysimula ̄tionꎬWMLES)ꎬ定义新的长度尺度解决了这些问题ꎬ具体公式详见文献[25]ꎮ流场网格如图2㊁图3所示ꎬ边界层采用棱柱层结构ꎬ并调整第1层网格高度使得y+小于1ꎬ远场部分采用六面体结构网格ꎬ与边界层的过渡层采用非结构网格ꎮ整体网格单元数量为4.2ˑ106ꎮ图2㊀y方向截面网格示意图Fig.2㊀Schematicdiagramofcross ̄sectionalgridinthey ̄direction图3㊀x方向截面网格示意图Fig.3㊀Schematicdiagramofcross ̄sectionalgridinthex ̄direction物面边界条件为无滑移壁面条件ꎬ远场采用压力远场边界条件ꎬ湍流模型采用SSTk ̄ω模型ꎬ采用密度基求解ꎬ气体黏性采用Sutherland定律ꎬ空间离散采用2阶迎风格式ꎬ对流通量采用Roe格式ꎮ1.2 结构分析模型结构与流场耦合分析过程中ꎬ结构部分可以采用模态方法描述ꎮ结构模态可以通过有限元方法与结构模态试验方法获得ꎮ本文采用有限元分析结果获得的模态ꎬ图4所示为结构的前3阶模态ꎬ本文只分析计算结果中气动阻尼最小的第2阶模态ꎮ(a)f=1.200Hz(b)f=2.460Hz(c)f=2.957Hz图4㊀结构的前3阶模态Fig.4㊀Firstthreemodesofthestructure由于火箭结构外形简单ꎬ一般不考虑其扭转影响ꎬ因此可以将其简化为简单的梁模型ꎬ这样就可以给出其模态振动方程q㊆i+2biωiq˙i+ω2iqi=fi(3)式中ꎬqi为第i阶模态的广义位移ꎬbi为第i阶模态的结构阻尼系数ꎬωi为第i阶模态的固有频率ꎬ13气体物理2023年㊀第8卷fi为第i阶模态下质量归一化的广义气动力ꎮ若将fi按照Taylor展开并略去高阶项ꎬ可以将其转化为气动阻尼项与气动刚度项的形式ꎬ则式(3)可写为q㊆i+2(bi+Bi)ωiq˙i+(Ki+1)ω2iqi=0(4)式中ꎬBi为气动阻尼系数ꎬKi为气动刚度系数ꎬ研究表明[26]ꎬ气动刚度相对于结构刚度为小量可以忽略不计ꎬ而在计算中结构阻尼往往设置为0ꎬ因此气动阻尼可以直接反映其气弹稳定性ꎮ1.3㊀气动阻尼分析原理气动阻尼的分析可以采用强迫振动或者自由振动的方式进行ꎬ这两种方法获得的时域数据不同ꎬ提取气动阻尼的方式也不同ꎮ强迫振动方法初始演化过程较短ꎬ因此计算量较小ꎬ同时能够分析某一种振动形式的气动阻尼ꎬ明确该振动形式是收敛还是发散ꎮ分析过程中能够获得不同部位与部件的气动阻尼ꎮ但是对于多模态相互作用引起的发散(例如颤振)较难预测ꎮ自由振动方法需要一定的自由演化时间才能够对时域数据进行分析ꎬ不过自由振动方法能够获得最能够吸收能量的模态及其振动频率ꎮ对于本研究所关注的问题ꎬ气动载荷对结构振动的过程中气动阻尼的影响较大ꎬ而对气动刚度与气动质量影响较小ꎬ即结构的固有振动频率受到来流的影响较小ꎬ其稳定性问题主要由气动阻尼的正㊁负引起ꎬ所以采用强迫振动方法分析ꎮ强迫振动下结构做简谐模态振动qi(t)=Asin(ωit)式中ꎬA表示振动的振幅ꎬ将其代入计算气动力的公式中[21]并做正交积分可得Bi=ʏl0Bx(x)dx=-1MiAω2iTʏl0ʏt0+Tt0G(xꎬt)cos(ωit)dtdx(5)式中ꎬMi为第i阶模态的模态质量ꎬT为整数倍周期ꎬG为广义气动力ꎮ根据式(5)便可以得到局部或分区域的气动阻尼ꎮ1.4㊀耦合计算流程首先进行模态分析ꎬ以确定结构的模态频率与振型ꎬ用以设计强迫振动的频率和振幅ꎮ非定常流场计算前先进行定常流场计算ꎬ来加快非定常计算的演化速度并增强收敛性ꎬ结构节点位移通过径向基函数(RBF)插值方法[27]映射到气动网格节点上ꎬ来进行网格的变形ꎬ这里径向基函数选用WendlandC2ꎬ如下所示φ(x)=(1-x)4(4x+1)最后将计算出来的广义力提取出来ꎬ截取演化完毕的整数倍周期ꎬ进行气动阻尼计算ꎮ耦合计算流程图如图5所示ꎮ图5㊀耦合计算流程图Fig.5㊀Flowchartofcoupledcalculation2㊀结果分析与讨论2.1㊀流场分析结果计算的来流Mach数范围为0.7~1.2ꎮ其中中截面的压力分布如图6所示ꎮ可以看出在头部出现了膨胀波以及跨声速激波ꎬ在过渡段存在流动分离ꎬ随着Mach数的增大ꎬ头部低压区域逐渐扩张ꎬ并且能明显看到ꎬ在流动再附的位置产生了再附激波ꎮ(a)Ma=0.7023第6期李泳德ꎬ等:基于CFD/CSD耦合的火箭跨声速气动阻尼特性分析(b)Ma=0.75(c)Ma=0.80(d)Ma=0.85(e)Ma=0.88(f)Ma=0.90(g)Ma=0.92(h)Ma=0.96(i)Ma=0.9833气体物理2023年㊀第8卷(j)Ma=1.00(k)Ma=1.05(l)Ma=1.10图6㊀不同Mach数下的中截面压力分布Fig.6㊀PressuredistributioninthemiddlesectionatdifferentMachnumbers2.2 气动阻尼分布通过上述流场分析ꎬ可以看出火箭不同部位流动结构并不相同ꎬ在头部与箭身上ꎬ流动主要为附着流动ꎬ而在过渡段会出现较为复杂的波系结构以及流动分离ꎮ针对不同的流动结构随流向站位x的变化ꎬ设该位置上广义力与广义位移的相位差为φ(x)ꎬ并且简谐振动没有引入其他模态的广义力ꎬ则广义力的表达式为G(xꎬt)=Fgen sin[ωt+φ(x)]+F0(6)其中ꎬFgen为广义力的振动幅度ꎬF0为广义力的常数偏移量ꎮ将式(6)代入到式(5)中得到B(x)=-FgenMAω2Tʏt0+Tt0sin[ωt+φ(x)]cos(ωt)dt其中ꎬ广义力的常数偏移量F0的积分为0ꎬ因此省略ꎮ通过将等式中的正弦函数部分进行和差化积得到B(x)=-FgenMAω2Tʏt0+Tt0sin(ωt)cos[φ(x)]cos(ωt)dt+[ʏt0+Tt0sin[φ(x)]cos(ωt)cos(ωt)dt](7)式(7)中第1部分在整个周期中的积分为0ꎬ只有第2部分保留ꎬ因此得到B(x)=-Fgensin[φ(x)]MAω2Tʏt0+Tt0cos2(ωt)dt(8)式(8)中积分部分恒为正值ꎬ决定整个气动阻尼的部分只有相位角φ(x)的正弦值sin[φ(x)]ꎬ为了能够更加直观地获得相位角与气动阻尼B之间的关系ꎬ须将符号转化为对应的正弦函数转角ꎬ根据正弦关系ꎬ此转角为πꎬ因此得到B(x)=-Fgen(x)sin[φ(x)+π]MAω2Tʏt0+Tt0cos2(ωt)dt(9)图7为气动阻尼变化曲线ꎬ可以看出随着Mach数的增大ꎬ整体气动阻尼先增大后减少ꎬ在Mach数为0.98时达到最大值ꎬ过渡段与箭体的气动阻尼变化趋势与整体基本相同ꎬ而头部区域则不同ꎬ是随着Mach数的增大一直增大ꎬ只是增长速率变缓ꎮ图7㊀有助推时气动阻尼变化曲线Fig.7㊀Aerodynamicdampingchangecurvewithboost根据式(9)ꎬ得到相位角与气动阻尼B之间的关系为:当φ(x)ɪ(-πꎬ0)时ꎬ相位角滞后ꎬ气动阻尼B为负值ꎻ当φ(x)ɪ(0ꎬπ)ꎬ相位角提前ꎬ43第6期李泳德ꎬ等:基于CFD/CSD耦合的火箭跨声速气动阻尼特性分析气动阻尼B为正值ꎻ为当φ(x)=0时ꎬ无相位角差别ꎬ气动阻尼B为0ꎮ在过渡段上ꎬ复杂的波系结构以及流动分离ꎬ使得气动力与结构位移之间会出现较为明显的迟滞现象ꎬ从而导致相位角φ(x)ɪ(-πꎬ0)ꎬ由此在过渡段上产生了负的气动阻尼ꎮ计算过程中的广义力与广义位移随时间变化曲线如图8所示ꎬ可以看出所有工况计算结果都表现良好ꎬ需要注意的是在非定常计算初期ꎬ演化的不完全导致广义力存在一些突变异常的结果ꎬ计算气动阻尼时须剔除ꎬ选择后面演化完全的周期ꎮ本文计算了9个周期ꎬ剔除了第1个周期出现的错误结果ꎬ采用后8个周期进行气动阻尼分析ꎮ强迫运动振幅为芯级直径的0.5%ꎮ(a)Ma=0.70㊀㊀㊀(b)Ma=0.75(c)Ma=0.80㊀㊀㊀(d)Ma=0.85(e)Ma=0.88㊀㊀㊀(f)Ma=0.9053气体物理2023年㊀第8卷(g)Ma=0.92㊀㊀㊀(h)Ma=0.96(i)Ma=0.98㊀㊀㊀(j)Ma=1.00(k)Ma=1.05㊀㊀㊀(l)Ma=1.10图8㊀不同工况下的广义力与广义位移随时间变化曲线Fig.8㊀Timedependentcurvesofgeneralizedforceandgeneralizeddisplacementunderdifferentoperatingconditions2.3㊀气动阻尼影响因素2.3.1㊀有无助推对气动阻尼的影响捆绑式运载火箭相比于传统的运载火箭ꎬ最大的区别就是在尾部四周捆绑了助推器ꎬ使得其流场特性变得复杂ꎬ因此须分析其对气动阻尼的影响ꎮ图7㊁图9分别为有无助推时气动阻尼变化曲线ꎬ可以看出随着Mach数的增大整体气动阻尼先增大后减少ꎬ在Mach数为0.98时达到最大值ꎬ过63第6期李泳德ꎬ等:基于CFD/CSD耦合的火箭跨声速气动阻尼特性分析渡段与箭体的气动阻尼变化趋势与整体基本相同ꎬ而头部区域则不同ꎬ是随着Mach数的增大一直增大ꎬ只是增长速率变缓ꎮ对比两个图可知ꎬ助推主要起增大气动阻尼的作用ꎮ还可以看出有无助推情况下头部的气动阻尼变化很小ꎬ意味着在箭体尾部施加控制很难影响到头部的气动阻尼ꎬ特别是在超声速流场中ꎮ图9㊀无助推时气动阻尼变化曲线Fig.9㊀Aerodynamicdampingchangecurvewithoutboost2.3.2㊀前节点位置影响为了考察前节点位置变化对气动阻尼的影响ꎬ在保持振动频率不变㊁头部最大振型位置与振幅不变的条件下移动前节点ꎬ变化后的振型如图10所示ꎮ(a)Frontnodeafterthetransitionregion(b)Frontnodeinthetransitionregion(c)Frontnodebeforethetransitionregion图10㊀前节点变化后的振型Fig.10㊀Vibrationmodeafterthechangeofformernode根据对计算结果的分析分别获得了不同前节点位置的整体气动阻尼对比与过渡段气动阻尼对比ꎬ如图11㊁图12所示ꎬ可以看出前节点位置的改变并没有影响整体气动阻尼随Mach数增大而增大的趋势ꎬ且前节点在过渡段上与过渡段前的整体气动阻尼相差不大ꎬ而前节点在过渡段后的整体气动阻尼要高于另两种情况ꎬ因此过渡段与头部放在同一侧有助于提高气动阻尼ꎮ过渡段的气动阻尼会随着前节点的变化发生剧烈改变ꎬ前节点在过渡段前后随Mach数增大的变化规律相反ꎬ节点前后的振动相位变化导致不同节点位置过渡段的振动相位不同ꎬ进而导致气动阻尼发生变化ꎮ图11㊀不同节点位置的整体气动阻尼Fig.11㊀Overallaerodynamicdampingatdifferentnodepositions图12㊀不同节点位置的过渡段气动阻尼Fig.12㊀Aerodynamicdampingofthetransitionregionatdifferentnodepositions2.3.3㊀强迫振动振幅大小对气动阻尼的影响为了考察强迫振动振幅大小对气动阻尼的影响ꎬ在保证流场结构不发生改变的前提下ꎬ振动振幅分别为原来的一半和两倍ꎬ根据工程经验ꎬ如果振幅超过芯级直径的5%ꎬ则须考虑流场结构改变所造成的影响ꎮ图13㊁图14分别为不同振幅下的整体与头部气动阻尼ꎮ73气体物理2023年㊀第8卷图13㊀不同振幅下整体气动阻尼Fig.13㊀Overallaerodynamicdampingatdifferentamplitudes图14㊀不同振幅下头部气动阻尼Fig.14㊀Aerodynamicdampingoftheheadregionatdifferentamplitudes可以发现改变振幅无论是对整体气动阻尼还是头部气动阻尼来说变化都很小ꎬ这意味着气动阻尼的大小主要取决于气动力与结构振动的相位差ꎬ不依赖于振动幅度的大小ꎮ2.3.4㊀脉动压力对气动阻尼的影响为了模拟出脉动压力的影响ꎬ采用IDDES方法对火箭气动阻尼进行计算ꎬ计算来流Mach数为0.92ꎬ计算过程中的广义力与广义位移如图15所示ꎬ相较于图8可以看出广义力随时间变化曲线并不光滑ꎬ脉动压力的存在导致广义力由多个频率叠加而成ꎮ由于第2阶模态的频率为2.46Hzꎬ而由分离流㊁激波振荡等引起的脉动压力频率往往远大于此频率ꎬ因此这里选择3.5Hz为分界ꎬ将高于3.5Hz的部分视为由抖振脉动压力引起的广义力ꎬ低于3.5Hz的部分视为强迫振动引起的广义力ꎬ通过低通滤波把高于3.5Hz的广义力滤掉ꎬ可以获得由强迫振动引起的广义力与广义位移变化曲线ꎬ如图16所示ꎬ通过此广义力计算的气动阻尼为2.08ɢꎮ同样地ꎬ进行高通滤波将低于3.5Hz的广义力滤掉ꎬ可以获得由抖振脉动压力引起的气动阻尼为(2.94ˑ10-3)ɢꎬ由此得到脉动压力引起的气动阻尼变化为0.14%ꎬ可以忽略不计ꎮ同时使用RANS方法计算的气动阻尼为2.07ɢꎬ与IDDES的计算结果相比误差约为(2.94ˑ10-3+2.08-2.07)/2.07ʈ0.48%ꎬ这说明针对气动阻尼的模拟ꎬ抖振引起的脉动压力对气动阻尼的计算结果影响很小ꎬ起主要作用的还是广义力的变化ꎬ该变化由强迫振动引起的结构边界变化所导致ꎮ图15㊀基于IDDES的广义力与广义位移变化曲线Fig.15㊀VariationcuresofgeneralizedforceandgeneralizeddisplacementbasedonIDDES图16㊀滤波后的广义力与广义位移变化曲线Fig.16㊀Variationcuresofgeneralizedforceandgeneralizeddisplacementvariationcurveafterfiltering3㊀结论本文通过数值计算方法研究了火箭的气动阻尼特性ꎮ根据流动特征分析与理论推导ꎬ发现火箭过渡段几何外形的收缩导致该区域出现复杂的分离与激波结构ꎬ从而造成了气动力相对于结构振动83第6期李泳德ꎬ等:基于CFD/CSD耦合的火箭跨声速气动阻尼特性分析相位的滞后ꎬ导致了该区域为气动负阻尼ꎬ即气动不稳定性的主要来源ꎮ在此机理的基础上ꎬ分析了前节点位置㊁振动振幅㊁脉动压力等因素对气动阻尼的影响规律ꎮ可以得出以下结论:1)助推增加了正阻尼区域的面积ꎬ从而相对于没有助推的构型起到了增加气动阻尼的作用ꎮ2)前节点位置的改变对过渡段气动阻尼影响很大ꎬ节点前后的振动方向相反ꎬ导致节点在过渡段前后的气动阻尼变化规律也截然相反ꎬ将过渡段与头部区域放在节点的同一侧有助于增加气动阻尼ꎮ3)在不改变流场结构的前提下ꎬ改变振动的振幅ꎬ气动力也会产生相应幅度的变化ꎬ因此结构振幅对气动阻尼的影响可忽略不计ꎮ4)高频部分的广义力对气动阻尼的贡献很小ꎬ即结构振动引起的广义力变化对气动阻尼起主要作用ꎬ而脉动压力对计算气动阻尼影响不大ꎬ可忽略不计ꎮ参考文献(References)[1]㊀CoeCF.Steadyandfluctuatingpressuresattransonicspeedsontwospace ̄vehiclepayloadshape[R].NASATMX ̄503ꎬ1961.[2]ColeSRJrꎬHenningTLꎬRaineyAG.NASAspaceve ̄hicledesigncriteria[R].NASASP ̄8001(REV)ꎬ1964. [3]EricssonLEꎬRedingJP.Analysisofflowseparationeffectsonthedynamicsofalargespacebooster[J].Jour ̄nalofSpacecraftandRocketsꎬ1965ꎬ2(4):481 ̄490. [4]RedingJPꎬEricssonLE.Effectofaeroelasticconsidera ̄tionsonseasat ̄Apayloadshrouddesign[J].JournalofSpacecraftandRocketsꎬ1981ꎬ18(3):241 ̄247. [5]程镇煌.宇航飞行器跨音速气动弹性问题探讨[J].上海航天ꎬ1997(6):16 ̄21.ChengZH.Discussionontransonicpneumaticelasticityofspacecraft[J].AerospaceShanghaiꎬ1997(6):16 ̄21(inChinese).[6]倪嘉敏.我国运载火箭气动设计回顾[C].近代空气动力学研讨会论文集ꎬ2005.NiJM.ReviewofaerodynamicdesignofChinaᶄslaunchvehicle[C].Proceedingsofthemodernaerodynamicssymposiumꎬ2005(inChinese).[7]臧涛成ꎬ胡焕性.大长细比弹箭弹性效应研究综述[J].弹道学报ꎬ1999ꎬ11(3):89 ̄93ꎬ96.ZangTCꎬHuHX.Areviewofgreatslendernessratioprojectileelasticeffectresearch[J].JournalofBallisticsꎬ1999ꎬ11(3):89 ̄93ꎬ96(inChinese). [8]吴志刚ꎬ杨超.细长体弹箭的气动弹性问题与研究方法[C].第九届(2005年)全国空气弹性学术交流会论文ꎬ2005.WuZGꎬYangC.Aeroelasticityproblemsandresearchmethodsofslenderbodymissiles[C].9thNationalSym ̄posiumonAeroelasticityꎬ2005(inChinese). [9]张贺ꎬ黄晓鹏.弹性细长旋转弹箭运动稳定性问题的研究进展[C].第九届(2005年)全国空气弹性学术交流会论文ꎬ2005.ZhangHꎬHuangXP.Researchprogressonthestabilityofelasticslenderrotatingprojectiles[C].9thNationalSymposiumonAeroelasticityꎬ2005(inChinese). [10]ColeHAJr.Dynamicresponseofhammerheadlaunchvehiclestotransonicbuffeting[R].NASATND ̄1982ꎬ1963.[11]BartelsREꎬWiesemanCDꎬMineckRE.ComputationalaeroelasticanalysisoftheAreslaunchvehicleduringas ̄cent[R].AIAA2010 ̄4374ꎬ2010.[12]AzevedoJLF.Aeroelasticanalysisoflaunchvehiclesintransonicflight[J].JournalofSpacecraftandRocketsꎬ1989ꎬ26(1):14 ̄23.[13]SinclairAꎬFlowersG.Low ̄orderaeroelasticmodeloflaunch ̄vehicledynamics[R].AIAA2010 ̄7725ꎬ2010. [14]DotsonKW.Transientcouplingoflaunchvehiclebendingresponseswithaerodynamicflowstatevariations[J].JournalofSpacecraftandRocketsꎬ2001ꎬ38(1):97 ̄104.[15]ColeSRꎬHenningTL.Buffetresponseofahammerheadlaunchvehiclewind ̄tunnelmodel[J].JournalofSpacecraftandRocketsꎬ1992ꎬ29(3):379 ̄385.[16]崔尔杰.流固耦合力学研究与应用进展[C].钱学森科学贡献暨学术思想研讨会论文集ꎬ2001.CuiEJ.Researchandapplicationprogressoffluid ̄struc ̄tureinteractionmechanics[C].ProceedingsofSeminarofQianXuesenScientificContributionsandAcademicThoughtsꎬ2001(inChinese).[17]冯明溪ꎬ王志安.火箭跨音速动导数和抖振实验[J].宇航学报ꎬ1987(1):55 ̄63.FengMXꎬWangZA.Experimentsoftransonicderiva ̄tivesandbuffetingofrocket[J].JournalofAstronauticsꎬ1987(1):55 ̄63(inChinese).[18]白葵ꎬ冯明溪.弹性模型实验技术[J].流体力学实验与测量ꎬ1999ꎬ13(1):38 ̄42.BaiKꎬFengMX.Aeroelasticmodelandthebuffetex ̄perimentaltechnique[J].ExperimentsandMeasurementsinFluidMechanicsꎬ1999ꎬ13(1):38 ̄42(inChinese). [19]JiCꎬRanJHꎬLiFꎬetal.Theaerodynamicdamping93气体物理2023年㊀第8卷testofelasticlaunchvehiclemodelintransonicflow[C].Proceedingsofthe64thInternationalAstronauticalCon ̄gressꎬ2013.[20]季辰ꎬ吴彦森ꎬ何岗ꎬ等.运载火箭气动阻尼风洞试验研究[C].第十二届全国空气弹性学术交流会论文集ꎬ2011.JiCꎬWuYSꎬHeGꎬetal.Experimentalstudyonaero ̄dynamicdampingwindtunneloflaunchvehicle[C].Pro ̄ceedingsofthe12thNationalAeroelasticityConferenceꎬ2011(inChinese).[21]刘子强ꎬ白葵ꎬ毛国良ꎬ等.锤头体弹性振动跨音速气动阻尼系数的确定[J].宇航学报ꎬ2002ꎬ23(6):1 ̄7.LiuZQꎬBaiKꎬMaoGLꎬetal.Thedeterminationofaerodynamicdampingonhammerheadlaunchvehiclesattransonicspeeds[J].JournalofAstronauticsꎬ2002ꎬ23(6):1 ̄7(inChinese).[22]冉景洪ꎬ刘子强ꎬ胡静ꎬ等.减阻杆气动阻尼研究[J].力学学报ꎬ2014ꎬ46(4):636 ̄641.RanJHꎬLiuZQꎬHuJꎬetal.Researchofaero ̄dampingforbluntwithspike[J].ChineseJournalofThe ̄oreticalandAppliedMechanicsꎬ2014ꎬ46(4):636 ̄641(inChinese).[23]朱剑ꎬ冉景洪ꎬ吴彦森ꎬ等.捆绑式运载火箭的气动阻尼数值计算方法[C].第十三届全国空气弹性学术交流会论文集.哈尔滨:中国力学学会ꎬ中国空气动力学会ꎬ2013.ZhuJꎬRanJHꎬWuYSꎬetal.Numericalcalculationmethodforaerodynamicdampingofbundlelaunchvehicles[C].Proceedingsofthe13thNationalAeroelasticityCon ̄ference.Harbin:ChineseSocietyofTheoreticalandAp ̄pliedMechanicsꎬChinaAeromechanicsSocietyꎬ2013(inChinese).[24]SpalartPR.Detached ̄eddysimulation[J].AnnualReviewofFluidMechanicsꎬ2009ꎬ41:181 ̄202. [25]GritskevichMSꎬGarbarukAVꎬSchützeJꎬetal.Devel ̄opmentofDDESandIDDESformulationsforthek ̄ωshearstresstransportmodel[J].FlowꎬTurbulenceandCombustionꎬ2012ꎬ88(3):431 ̄449.[26]季辰ꎬ吴彦森ꎬ侯英昱ꎬ等.捆绑式运载火箭跨声速气动阻尼特性试验研究[J].实验流体力学ꎬ2020ꎬ34(6):24 ̄31.JiCꎬWuYSꎬHouYYꎬetal.Experimentalstudyofaerodynamicdampingcharacteristicsofalaunchvehiclewithboostersintransonicflow[J].JournalofExperimentsinFluidMechanicsꎬ2020ꎬ34(6):24 ̄31(inChinese). [27]AllenCꎬRendallTCS.UnifiedapproachtoCFD ̄CSDinterpolationandmeshmotionusingradialbasisfunctions[R].AIAA2007 ̄3804ꎬ2007.04。
2023 年湍流与噪声和 CFD 方法暑期高级讲习班 会议手册说明书

2023年湍流与噪声和CFD方法暑期高级讲习班2023 Advanced Summer Program on Turbulence,Noise and CFD Methods会议手册时间:2023年7月28至8月5日地点:香港科技大学主办单位:中国空气动力学会承办单位:香港科技大学(HKUST)上海大学南方科技大学复旦大学中国空气动力学会CFD专委会中国空气动力学会低跨超专委会上海市应用数学和力学研究所上海市力学信息学前沿科学基地上海市能源工程力学重点实验室粤港澳数据驱动下的流体力学与工程应用联合实验室中国航空学会航空声学分会协办单位:《空气动力学学报》《实验流体力学》《Advances in Aerodynamics》二零二三年七月二十六日2023年湍流与噪声和CFD方法暑期高级讲习班为了促进流体力学与空气动力学的发展、推动学术交流与合作、培育培养优秀人才,助力解决流体力学与空气动力学等相关领域“卡脖子”技术,经中国空气动力学会批准,2023年湍流与噪声和CFD 方法暑期高级讲习班将于2023年7月28日至8月5日在香港科技大学(HKUST)举行。
会议邀请内地与香港地区在湍流、噪声和CFD方法等方面的专家学者、青年学者为讲习班授课。
现诚邀内地与港澳台地区研究生、工程师、相关领域专家学者以及高年级本科生参会。
本次讲习班由中国空气动力学会主办,香港科技大学(HKUST)、上海大学、南方科技大学、复旦大学、中国空气动力学会CFD专委会、中国空气动力学会低跨超专委会、上海市应用数学和力学研究所、上海市力学信息学前沿科学基地、上海市能源工程力学重点实验室、粤港澳数据驱动下的流体力学与工程应用联合实验室等单位承办。
本次讲习班采用线上线下同时进行的方式,其中线上使用腾讯会议App进行直播,会议号码:964-8147-9182,也可直接扫描下面的二维码参会:2023年湍流与噪声和CFD方法暑期高级讲习班专家报告日程安排报告安排以专家自选日程排列,不分先后次序,后续如有变动以最终表格为准。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
跨声速压气机非定常流动及损失的数值研究压气机性能的进一步的提高很大程度上依赖于我们对其内部非定常流动机理及相应损失机制的认识。
数值模拟的方法在这方面发挥着日益重要的作用,但是还面临很多问题。
本文将在计算压气机内部复杂非定常流动的数值方法和合理衡量压气机的损失等方面开展工作,并基于这些工作,对跨声速压气机级Rotor35/Stator37内的损失进行分析。
在数值方法方面,构造了以下三个不同程度上反应多维效应的数值格式,(1)将精度和稳健性都已得到广泛认可的二维旋转迎风格式推广为三维。
(2)通过在计算数值通量时近似求解完整的流体力学方程来体现多维效应的影响,本文构造了多维输运格式。
对于粘性流动,该格式无粘通量的计算能够考虑粘性通量的影响。
(3)基于线化多维欧拉方程的次特征线理论构造了考虑无限多方向影响的局部演化迦辽金格式。
这三种方法的共同特点是相对于已有的考虑多维效应的格式更加简单、高效,且可以直接推广到非结构网格的计算。
本文将三维旋转迎风格式格式应用到自行开发的多级叶轮机械模拟程序中。
数值验证表明多维格式在模拟跨声速压气机内复杂流动方面有一定优势。
在衡量压气机内损失方面,本文基于热力学定律,在有用功分析的框架提出了一种相比现有损失评估方法更适于非定常流场局部损失分析的损失评估参数-损失功,其强度量-损失功强度便于用来将流场结构与损失联系起来。
这两个参数物理意义明确,能够被用来方便的、定量的研究局部区域内由于不可逆过程导致的熵产引起的损失。
相比于先前同类方法,这两个参数能够考虑具体流动结构对于局部熵增的影响,从而能够更准确的衡量局部自身熵产的大小。
这两个参数为压气机的设计、优化和改型提供了一个有效工具。
