第三讲 材料的热膨胀
材料热膨胀系数
材料热膨胀系数
材料的热膨胀系数是指在温度变化时，单位温度变化引起的单位长度变化。
材料的热膨胀系数是一个重要的物理量，它与材料的性质有关，对于工程设计和材料选择具有重要的影响。
材料的热膨胀系数通常用线膨胀系数和体膨胀系数来表示。
线膨胀系数是指材料在长度方向上的膨胀量与初始长度之比，通常用α表示，单位是1/℃。
体膨胀系数是指材料在体积方向上的膨胀量与初始体积之比，通常用β表示，单位是1/℃。
不同材料的热膨胀系数通常是不同的。
一般来说，固体的热膨胀系数比液体和气体要小。
金属是一类常用材料，其热膨胀系数较大。
例如，铝的线膨胀系数约为23×10^-6/℃，铜的线膨胀系数约为16×10^-6/℃。
相比之下，水在0-30℃的温度范围内的线膨胀系数约为207×10^-6/℃。
这就意味着在相同温度范围内，相同长度的铝和水在温度变化时，铝的长度变化相对较小。
材料的热膨胀系数对于工程设计和材料选择具有重要的意义。
例如，在建筑设计中，需要考虑材料的热膨胀系数来确定结构的稳定性。
如果不同部分的材料热膨胀系数相差太大，就可能导致结构的变形，从而影响其使用寿命和安全性。
此外，在高温设备中，材料的热膨胀系数也需要考虑，以避免由于温度变化引起的热应力和破裂。
综上所述，材料的热膨胀系数是一个重要的物理量，它与材料的性质有关，对工程设计和材料选择具有重要的影响。
不同材
料的热膨胀系数不同，需要根据具体应用考虑选择合适的材料，以确保结构的稳定性和安全性。
第三节材料热膨胀
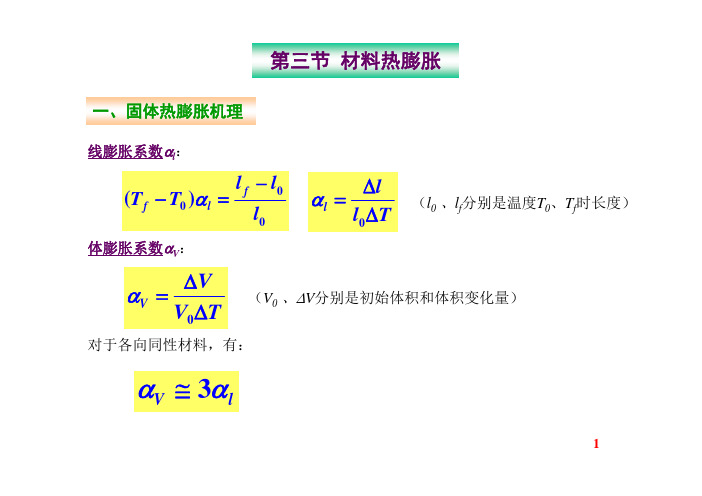
第三节材料热膨胀一、固体热膨胀机理线膨胀系数αl ：体膨胀系数αV ：对于各向同性材料，有：00()f f l l l T T l α−−=0l l l TαΔ=Δ（l 0、l f 0V V V TαΔ=Δ（V 0、ΔV 分别是初始体积和体积变化量）3V lαα≅热膨胀本质：从原子的观点看，热膨胀是点阵结构中的质点间平均距离随温度升高而增大现象的宏观反映质点的振动可分为简谐振动和非简谐振动材料热膨胀的物理本质是质点振动的非简谐效应简谐效应：质点围绕其平衡位置作简谐振动，质点之间相互作用势能对平衡位置是对称的，温度升高只能增大振幅，并不改变平衡位置。
质点间平均距离不会因温度升高而改变，即不改变晶体的大小和形状，晶体受热不膨胀非简谐效应：原子之间斥力项（玻恩斥力B/r n，n和原子的电子层有关，电子层越多，n越大，nHe =5，nNe=7，nAr=9）随原子间距的变化比引力项（库仑力A/r2）的变化更快。
热振动不是左右对称的线性振动，而是非线性振动23在质点平衡位置r 0的两侧，合力曲线的斜率是不相等的。
当r <r 0时，曲线的斜率较大；r >r 0时，斜率较小。
r <r 0时斥力随位移变化很快；r >r 0时引力随位移的变化要慢一些在这样的受力情况下，质点振动时的平均位置就不在r 0处，而要向右移。
因此相邻质点间平均距离增加温度越高，振幅越大，质点在r 0两侧受力不对称情况越显著，平衡位置向右移动越多，相邻质点间平均距离就增加得越多，以致晶胞参数增大，晶体膨胀从点阵能曲线的非对称性同样可以得到具体解释非对称势能曲线对称势能曲线T 1T 2T 3T 4T 5对于给定的点阵能曲线，r，β，β’均为常数，似乎α也为常数。
但如再考虑δ4，δ5，…时，则可得α随温度而变化的规律除了质点的非对称振动外，作为次要因素，晶体中的各种热缺陷的形成也将造成局部点阵的畸变和膨胀且随着温度升高，缺陷浓度按指数关系增加。
材料的热膨胀与热稳定性分析
材料的热膨胀与热稳定性分析随着现代科技的发展，材料科学在工程领域扮演着重要角色。
其中，材料的热膨胀与热稳定性是研究材料行为的重要方面。
本文将探讨材料的热膨胀与热稳定性的关系，并分析其在实际应用中的影响。
热膨胀是指材料在受热或冷却过程中发生的体积变化现象。
材料的热膨胀系数是衡量材料热膨胀程度的重要参数。
不同材料具有不同的热膨胀系数，这与材料的结构和成分有关。
一般来说，固体材料的热膨胀系数比液体和气体要小。
这是因为在固态下，材料的分子更加紧密排列，其相互作用力更强，因而对温度的变化更加敏感。
热膨胀不仅仅是一个理论概念，它在实际应用中具有重要的意义。
例如，在建筑工程中，选择合适的材料对于房屋的结构稳定性至关重要。
如果材料的热膨胀系数与环境中的温度变化不匹配，就会导致材料的变形或破裂。
因此，对于建筑材料的选择，需要考虑到其热膨胀性能，以确保建筑物在温度变化下的稳定性。
不仅在建筑工程中，热膨胀也对其他领域的工程设计产生着影响。
例如，在航空航天领域，航天器的材料需要能够承受极端的温度变化。
如果材料的热膨胀系数不稳定，就可能导致失控的热膨胀，进而损坏航天器的结构。
因此，在航天器的设计中，材料的热稳定性是一个重要的考虑因素。
然而，材料的热稳定性并不仅仅受到其热膨胀系数的影响。
材料的结构、热处理过程以及外部环境条件也都会对其热稳定性产生影响。
例如，金属材料的晶格结构可以通过热处理进行调控，以改善其热稳定性。
此外，外部环境的温度和湿度等条件的变化也会对材料的稳定性产生不可忽视的影响。
为了提高材料的热稳定性，科学家们通过研究材料的微观结构和热力学特性，不断探索新的材料制备方法。
例如，纳米材料由于其特殊的结构和界面效应，其热膨胀性能通常更稳定。
因此，纳米材料在高温环境下具有广泛的应用前景。
此外，复合材料也被用于提高材料的热稳定性。
通过将不同材料的优点融合在一起，可以制备出具有优异热膨胀性能的复合材料。
总之，材料的热膨胀与热稳定性是材料科学研究中的重要方面。
材料物理性能课件-1.3材料的热膨胀
V0[1(a
b
c)T]
V
a
b
c
由于膨胀系数是随温度变化的，所以上述各值都是指
定温度范围内的平均值，因此与平均热容一样，应用
时要注意适用的温度范围。膨胀系数的精确表达为：
dl
l lT dT
dV
V VT dT
continue
热膨胀的物理本质
在晶格振动中，曾近似地认为质点的热振动是 简谐振动。对于简谐振动，升高温度只能增大 振幅，并不会改变平衡位置。因此质点间平均 距离不会因温度升高而改变。热量变化不能改 变晶体的大小和形状，也就不会有热膨胀。这 样的结论显然是不正确的。
熔点越低，则热膨胀系数越大。由于单质的熔点与周 期表存在一定的规律性，所以热膨胀系数与周期表也 存在相应关系。
continue
格律乃森给出的金属热膨胀极限方程
V Tm C
对于大多数立方和六方结构的金属，C值在0.06~0.076
线膨胀系数与德拜温度的关系
l
A V 2/3M
1 2D
continue
5、X射线衍射法 是一种微观的检测方法。借助晶体对x射线的衍射， 测量晶格常数(原子间距)随温度的变化。
continue
热膨胀在工程中的意义
热膨胀系数是材料的一项重要热学性能指标，在实
际工程应用中具有重要意义。
1) 是决定材料抗热震性的主要因素。
2) 陶瓷坯上釉，二者α应匹配。釉α适当小于坯，烧结
谐振动，晶格振动中相邻质点间的作用力实际上是非 线性的，位能曲线也是非对称的。
导致热膨胀的次要因素
晶体中各种热缺陷的形成将造成局部点阵的畸变和 膨胀。随温度的升高，热缺陷浓度指数增加，所以 高温时，这方面的影响对某些晶体也就变得重要了。
材料的热膨胀.ppt
U r
U r0
dU dr
r0
x
1 2!
d 2U dr 2
对于六角和三角晶系，膨胀系数由二个方向的热膨胀系数决定， 即平行和垂直六角（三角）柱体晶轴：
11 22 ,33 //
六角、三角、四角晶系的平均热膨胀系数：
1 3
//
斜方晶系的热膨胀三个垂直方向的热膨胀系数：
3 1 2 3
2.3.4 铁磁性转变
线膨胀系数： l
l0T
体积膨胀系数： V
V0T
相应的真膨胀系数为：
T
dl l0dT
dV
V0dT
t
对于立方晶系：
3
t1
t2
t
2.3 影响热膨胀的因素
2.3.1 合金成分与相变
如果合金形成均一的单相固溶体，则合金的膨胀系数一般是介于组 元的膨胀系数之间，符合相加律的规律。
2 材料的热膨胀与导热性
热胀冷缩是自然规律，但为什么热胀冷缩呢？就一定会热 胀冷缩吗？什么情况下会出现热缩冷胀?
2.1 热膨胀来自原子的非简谐振动
固体材料热膨胀本质归结为点陈结构中的质点间平均距离随温度 升高而增大。 简谐近似：当原子离开其平衡位置发生位移时，它受到的相邻 原子作用力与该原子的位移成正比。
2.3.2 晶体缺陷
由空位引起的晶体变化可写成：
材料热膨胀系数
材料热膨胀系数材料的热膨胀系数是指在单位温度变化下，材料长度、面积或体积的变化量与原长度、面积或体积的比值。
热膨胀系数是描述材料在温度变化下的物理性质的重要参数，对于工程设计和材料选择具有重要意义。
热膨胀系数的定义。
材料在温度变化下会发生长度、面积或体积的变化，这种变化与温度变化的比例关系可以用热膨胀系数来描述。
一般来说，热膨胀系数可以分为线膨胀系数、面膨胀系数和体膨胀系数。
线膨胀系数是指材料在单位温度变化下长度的变化与原长度的比值；面膨胀系数是指材料在单位温度变化下面积的变化与原面积的比值；体膨胀系数是指材料在单位温度变化下体积的变化与原体积的比值。
热膨胀系数的影响因素。
材料的热膨胀系数受多种因素的影响，包括材料的组成、结构、晶体结构等。
一般来说，金属的热膨胀系数较大，而非金属材料的热膨胀系数较小。
此外，晶体结构的不同也会导致材料的热膨胀系数不同，例如单晶材料的热膨胀系数通常比多晶材料小。
此外，材料的温度范围也会对热膨胀系数产生影响，一般来说，在高温下，材料的热膨胀系数会增大。
热膨胀系数的应用。
热膨胀系数在工程设计和材料选择中具有重要的应用价值。
在工程设计中，了解材料的热膨胀系数有助于预测材料在温度变化下的变形情况，从而避免因温度变化引起的尺寸不稳定问题。
在材料选择中，热膨胀系数也是一个重要的考量因素，特别是在高温环境下，需要选择热膨胀系数较小的材料，以保证设备的稳定性和可靠性。
热膨胀系数的测量。
热膨胀系数的测量通常采用膨胀仪或差示扫描热量计等仪器进行。
通过在不同温度下测量材料的长度、面积或体积的变化量，可以得到材料的热膨胀系数。
在实际测量中，需要注意控制温度的均匀性和稳定性，以确保测量结果的准确性。
总结。
热膨胀系数是描述材料在温度变化下物理性质的重要参数，对工程设计和材料选择具有重要意义。
了解材料的热膨胀系数有助于预测材料在温度变化下的变形情况，避免尺寸不稳定问题。
在材料选择中，热膨胀系数也是一个重要的考量因素，特别是在高温环境下。
第三讲-材料热膨胀
相变的影响
一级相变：体积突变，有相变潜热。
直接用热膨胀实验分析
二级相变：无体积突变和相变潜热； 但膨胀系数和比热容有突变。
用热膨胀实验可以研究二级相变 Nhomakorabea二级相变
同素异构体转变
Fe：α相 β相
有序—无序转变
Cu-Au合金
温度变化时发生的晶型转变
化学成分的影响
αl Cu – Au合金 膨胀系数
0 20 40 60 80 100
Si Al2O3 SiC Si3N4 石英玻璃
αl /10-6 K-1 24.9 9.2 10.60 16.7 17.1 17.18 5.19 0~2 10.5 ~ 12 18.5 ~ 21 6.95 8.8 4.7 2.7 0.5
温度范围
303 ~ 573
153 ~ 1133
523 ~ 753
303 ~ 1123
693 ~ 1263
373 1573 293 ~ 373 273 ~ 473 293 ~
无机材料的线膨胀系数 一般都不大
某些无机材料的热膨胀系数与 温度之间的关系
物理本质（作用力曲线解释）
0 K时，原子处在平衡位置。 温度升高，原子振动激烈。 原子向右移动的幅度更大一些，
导致振动中心右移。
温度升高时发生的晶型转变，也会引起膨胀系 数的改变。
ZrO2陶瓷的热膨胀曲线
1000℃时 单斜晶型
四方晶型
发生体积收缩 4 %
4. 与相变的关系
一级
二级
第二节 材料的热膨胀
热膨胀的本质 与其他物理性能的关系 影响因素 热膨胀测量方法 热膨胀的工程应用
3. 影响热膨胀性能的因素
相变的影响 成分和组织的影响 各向异性的影响
第一章 材料的热学性能(热膨胀)
线膨胀系数和金属熔Байду номын сангаас的关系式
三、影响固体材料热膨胀系数的一些因素
3．晶体缺陷
格尔茨利坎、荻梅斯费尔德等人研究了空位对固体热膨胀的影响。 格尔茨利坎、荻梅斯费尔德等人研究了空位对固体热膨胀的影响。
空位引起的晶体附加体积变化
辐射空位引起热膨胀系数变化
三、影响固体材料热膨胀系数的一些因素
4．结构
结构紧密的晶体膨胀系数大， 结构紧密的晶体膨胀系数大，结构空敞的晶体膨 胀系数小。 胀系数小。这是由于开放结构能吸收振动能及调整 键角来吸收振动能所导致的。 键角来吸收振动能所导致的。
格律爱森（ 定律指出： 格律爱森（Grueisen)定律指出：体膨胀 定律指出 与定容热容成正比， 与定容热容成正比，它们有相似的温度依 赖关系， 赖关系，在低温下随温度升高急剧增大 德拜T 定律），而到高温则趋于平缓。 ），而到高温则趋于平缓 （德拜 3定律），而到高温则趋于平缓。
金属材料
三、影响固体材料热膨胀系数的一些因素
简谐振动是指质点间的作用力与距离成正比，即微观弹性模量β 为常数。（平衡位置不变，只适用于热容分析。） 非简谐振动是指作用力并不简单地与位移成正比，热振动不是 左右对称的线性振动而是非线性振动。 固体材料热膨胀的本质是 源于材料内部的质点(分子或原子)之 间相互作用力关于质点平衡位置的不对称性。
晶格质点振动受力分析
晶格质点振动能量分析
双原子势能曲线： 双原子势能曲线：与合力变化相 对应， 对应，两原子相互势能成一个不 对称曲线变化。温度上升， 对称曲线变化。温度上升，势能 增高，不对称性越明显， 增高，不对称性越明显，导致振 动中心右移，原子间距增大。 动中心右移，原子间距增大。宏 观上表现为热膨胀。 观上表现为热膨胀。
材料的热膨胀
4.晶体各向异性对热膨胀的影响
由于晶体结构的不对称性, 在不同的晶轴上产生 不相等的热膨胀, 所以晶体的热膨胀量也需要用六 个独立的参数来表征。 固体中热膨胀的各向异性可以定性地从原子间结 合力的强弱来说明。在非立方晶系中, 特别是在具 有一次轴对称的晶系中，平行于轴向和垂直于轴向 的原子间结合力差别甚大。若在某一个方向上结合 力较其它方向为小，则晶体首先在该方向上受到热 激发，因此在该方向上的热膨胀迅速增加，与此同 时往往伴随着垂直于该方向上的收缩，因此出现膨 胀系数的负值。αl源自Cu-Au合金膨胀系数
rE / %
2.相变对热膨胀的影响
当金属和合金发生一级或二级相变时, 其膨胀 量和膨胀系数都会发生变化。 一级相变：金属与合金中的大多数相变都属于 一级相变, 一级相变的特征是能量、体积和晶 体结构的不连续变化, 即是转变将伴随比容的 突变, 相应的膨胀系数将有不连续的变化, 其转 变点处a 将为无限大。 二级相变：相变时两相的化学势相等, 相变时 虽然没有体积的不连续变化, 但仍存在膨胀系 数的不连续变化。属于二级相变的磁性转变和 有序无序转变,在其相变处膨胀系数温度曲线上 有折点。
Thank You!
定义：在等压(p一定)下，单位 温度变化所导致的体积变化， 即热膨胀系数。
线膨胀系数α：α=ΔL/(L*ΔT) 面膨胀系数β：β=ΔS/(S*ΔT)
体膨胀系数γ：γ=ΔV/(V*ΔT)
式中ΔL为所给长度变化ΔT下物体温度的改变，L为初始长度；ΔS 为所给面积变化ΔT下物体温度的改变，S为初始面积；ΔV为所给 体积变化ΔT下物体温度的改变，V为初始体积。
材料的热膨胀
一、 热膨胀的本质
定义：通常是指外压强不变的 情况下，大多数物质在温度升 高时，其体积增大，温度降低 时体积缩小的现象。
材料热膨胀系数PPT课件
玻璃的热历史对 其膨胀系数有重要的 影响。
退火玻璃曲线发 生曲折是由于温度超 过 Tg 以 后 ， 伴 随 玻 璃转变发生结构变化， 膨胀更加剧烈。
至于急冷玻璃， 是由于试样存在热应 变，在某温度以上开 始出现弛豫的结果。
材料热膨胀系数
加热速度对玻璃线膨胀系数的影响
• 加热速度是个极重要的因素。玻 璃快速加热时，性质来不及反映 该温度的最终值。
ΔL / L0 = al Δt 试样规格为直径3-8mm，长度10-20mm的圆棒。
材料热膨胀系数
立式膨胀仪是将试样 安放在一端封闭的石英管 底部，使其保持良好的接 触，试样的另一端通过一 个石英顶杆将膨胀引起的 位移传递到千分表上，即 可读出不同温度下的膨胀 量。
材料热膨胀系数
自制立式膨胀仪
材料热膨胀系数
十九世纪到现在，人们创造了许多测定方法。上世纪60年代出现了 激光法，出现了用计算机控制或记录处理测定数据的测量仪器。
测定无机非金属材料热膨胀系数常用：千分表法、热机 械法（光学法、电磁感应法）、体积法 等。
它们的共同点都是试样在加热炉中受热膨胀，通过顶杆 将膨胀传递到检测系统。不同之处在于检测系统。
自制立式膨胀仪（智能型）
材料热膨胀系数
卧式膨胀仪
材料热膨胀系数
四．示差法的测定原理（石英膨胀仪）
图43-3 示差法测定材料膨胀系数的装置 １— 测温热电偶；２—膨胀仪电炉；３—电热丝；４—电流表；５—调压器；
６—电炉铁壳；７—铜柱电炉芯；８—待测试棒；９—石英玻璃棒； １０—石英玻璃管；１１—遮热板；１２—铁制支承架；１３—千分表；
材料热膨胀系数
千分表法是用千分表直接测量试样的伸长量。
光学热机械法是通过顶杆的伸长量来推动光学系统内的反 射镜转动经光学放大系统而使光点在影屏上移动来测定试样的 伸长量。
材料热膨胀系数课件
利用热膨胀仪测量
热膨胀仪是一种专门用于测量材料热 膨胀系数的仪器，通过测量材料在不 同温度下的长度变化来计算热膨胀系 数。
02
材料热膨胀系数的应 用
在材料科学中的应用
材料性能研究
热膨胀系数是材料的重要性能参 数之一，对于材料性能研究具有 重要意义。通过研究材料的热膨 胀系数，可以了解材料的热稳定
重点
本课件重点介绍了材料热膨胀系数的定义、测量方法和影响因素，以及在不同材料中的应用和表现。 通过对这些内容的深入学习和理解，可以更好地掌握材料热膨胀系数的相关知识和技能，为实际应用 提供指导。
结语
难点
本课件的难点主要在于如何理解和掌握 不同材料的热膨胀系数及其影响因素， 以及如何将所学知识应用到实际工程实 践中。为了更好地掌握这些难点，需要 结合实际案例和实践经验进行学习和理 解。
03
影响材料热膨胀系数 的因素
材料成分
不同材料具有不同的热膨胀系数，这 是由于材料成分的差异。例如，金属 的热膨胀系数通常比非金属高。
化学键的强度和类型也会影响材料的 热膨胀系数。例如，离子键和共价键 材料的热膨胀系数通常较低，而金属 键材料的热膨胀系数则较高。
微观结构
01
材料的微观结构对其热膨胀系数 有很大的影响。例如，晶格结构 、晶体取向和晶粒尺寸等都会影 响材料的热膨胀系数。
03
新材料研发：随着新材料技术的不断 发展，未来将会有越来越多的新型材 料被研发和应用到生产实践中。这些 新型材料可能具有一些特殊的物理和 化学性质，例如高热膨胀系数、低热 导率、强吸波性能等，这些性质将为 材料的应用和设计带来新的机遇和挑 战。因此，对于新材料研发来说，需 要深入研究和掌握材料的热膨胀系数 等物理和化学性质，以更好地发挥其 优势和应用潜力。
材料的热膨胀与工程应用
材料的热膨胀与工程应用在我们的日常生活中，材料的热膨胀是一个非常常见而且重要的现象。
它不仅影响着我们使用的物品，还决定了许多工程设计的成败。
材料的热膨胀现象是由于温度的变化引起的，随着温度的升高，材料会膨胀，而温度的降低则会导致材料收缩。
材料的热膨胀现象是由材料中的分子或原子振动引起的。
当物质受热时，分子或原子的振动会增加，造成材料体积的扩大。
这是因为高温下，原子或分子振动的幅度将增大，以至于它们相互间的间距也会增大，导致材料整体呈现膨胀的状态。
而在低温下，原子或分子的振动幅度变小，它们相互间的间距缩小，从而使材料收缩。
了解材料的热膨胀性质对于工程应用至关重要。
例如，在建筑设计中，工程师必须考虑到建筑材料的热膨胀系数，以确保在不同温度条件下建筑结构的稳定性。
如果没有正确考虑热膨胀，建筑物在温度变化时可能会发生形变甚至倒塌的风险。
此外，在机械设计中，工程师必须考虑到材料的热膨胀对机械零件的影响。
例如，在汽车制造中，引擎零件可能会因为温度的变化而发生膨胀或收缩，这可能会导致配合间隙的变化，使得零件之间无法正常运动。
因此，工程师需要根据材料的热膨胀系数选择合适的材料，并合理设计零件的结构，以避免产生不必要的摩擦和磨损。
除了建筑和机械设计之外，材料的热膨胀还在其他工程领域发挥着重要作用。
在电子设备制造中，电路板的热膨胀特性必须与其他组件相匹配，以避免由于温度变化而产生的破坏性应力。
在航空航天工程中，航天器和卫星的设计必须考虑到在极端温度条件下的材料热膨胀，以保证其结构的完整性和性能。
为了更好地利用材料的热膨胀性质，科学家和工程师也在进行相关研究和创新。
例如，有些材料具有负热膨胀系数，即在受热时会收缩而不是膨胀。
这些材料被广泛应用于精密仪器和光学系统中，可以帮助提高仪器的精确度和稳定性。
此外，材料科学家也研究和开发一些具有可调节热膨胀性质的材料。
这些材料能够根据需要调整其膨胀或收缩的程度，从而实现更灵活的工程设计。
材料的热膨胀性与热循环稳定性
材料的热膨胀性与热循环稳定性热膨胀性和热循环稳定性是材料工程中非常重要的概念。
热膨胀性指的是材料在温度变化下的尺寸变化程度，而热循环稳定性则是指材料在多次热循环中的稳定性能。
这两个因素对于材料的使用寿命和性能至关重要。
首先，热膨胀性是任何材料都必须面对的问题。
当材料受热时，分子内部的能量增加，使原子或分子间的相对距离增大，从而导致材料的尺寸膨胀。
热膨胀性对于许多工程设计都是一个重要的考虑因素，特别是在高温应用中。
例如，在航空航天和能源领域，材料的热膨胀性能直接影响到发动机、液体燃料槽等部件的性能和可靠性。
如果材料的热膨胀系数过高，就会导致在温度变化过程中产生尺寸不稳定，从而引起各种问题，如应力集中和裂纹形成。
因此，热膨胀性需要被精确地评估，并在工程设计过程中进行合理的控制。
其次，热循环稳定性是指材料在多次热循环中的稳定性能。
在许多工业应用中，材料需要经受不断的温度循环，如锅炉和汽车发动机中的高温循环，以及雨林地区到寒带地区的航空器循环。
在这些环境下，材料将不断经历热胀冷缩的过程，而这对于材料的性能和寿命应有一定的抗循环疲劳能力。
如果材料的热循环稳定性较差，就会导致材料快速疲劳和劣化，甚至可能引发严重的结构失效。
因此，对于材料的热循环稳定性进行评估和测试也是非常重要的。
然而，材料的热膨胀性与热循环稳定性之间并不总是简单的线性关系。
有些材料在低温下表现出较低的热膨胀系数，而在高温下则呈现较高的系数。
这种非线性关系使得材料的设计和选择更具挑战性。
因此，为了解决这个问题，研究人员发展了一些合金材料，通过调节不同元素的含量和晶体结构来改善材料的热膨胀性和热循环稳定性。
例如，金属基复合材料在高温情况下表现出良好的热膨胀性和热循环稳定性，这是因为复合材料的结构可以抵消不同材料的热膨胀系数差异，并提供更好的热循环性能。
此外，材料的热膨胀性和热循环稳定性还受到其他因素的影响，如晶体结构、缺陷和杂质。
例如，晶体结构的不对称性会导致材料的热膨胀系数随温度变化而变化。
材料物理 第三节 热膨胀
V a b c
对于各向同性的材料，
聊城大学材料科学与工程学院
V 3 L
第三节 热膨胀
注意： ①固体的热膨胀系数不是一个常数，通常随温度升高而增大； ②无机材料热膨胀系数较小，约为10-5-10-6K-1；各种金属和合 金约为10-5-10-6K-1；钢的热膨胀系数(10-20)×10-6K-1； ③材料线膨胀系数一般用平均线膨胀系数表征。 二、热膨胀机理 在晶格振动理论中，将势能函数在平衡位置展成级数：
2、热膨胀应用 陶瓷和釉的膨胀系数要
适应。
釉的膨胀系数要小于陶 瓷的膨胀系数，但不能
小太多。
精密仪表零件、电子封 装器件等需要防止膨胀 ，
以提高仪器精度。
聊城大学材料科学与工程学院
第三节 热膨胀
研究相变温度 相变时，组织转变会附加体积效应，从而使膨胀曲线产生拐折。
热膨胀法确定钢相变的临界点
聊城大学材料科学与工程学院
1
C 3
V
( )l ( )v d
注意：因为晶格热振动非简谐效应的存在，格波间有一定的耦 合作用，声子间会产生碰撞，导致声子的平均自由程减小。格
波间相互作用愈大，声子间碰撞几率愈大，相应的平均自由程
愈小，热导率也就愈低，因此这种声子间碰撞引起的散射是晶 体中热阻的主要来源。
聊城大学材料科学与工程学院
V
V 2 V1 1 T 2 T1 V 1
L
V 2 V 1 (1 V T )
L 1 T L1
对于各向异性的材料，设各方向线膨胀系数为 a , b , c
V T L aT L bT L cT L a 0 L b 0 L c 0 (1 a T )( 1 b T )( 1 c T ) V 0 [1 ( a b c ) T ]
材料的热膨胀.
无机材料的线膨胀 系数一般都不大
某些无机材料的热膨胀系数与温度之间的关系
三、 影响热膨胀的因素
1. 合金成分对热膨胀的影响
组成合金的溶质元素及含量对合金的热膨胀 的影响极为明显。固溶体中加人膨胀系数大 的溶质元素时, 膨胀系数增大; 反之, 加人溶质元素的膨胀系数 较小时, 固溶体的膨胀系数减小。
4.晶体各向异性对热膨胀的影响
由于晶体结构的不对称性, 在不同的晶轴上产生 不相等的热膨胀, 所以晶体的热膨胀量也需要用六 个独立的参数来表征。 固体中热膨胀的各向异性可以定性地从原子间结 合力的强弱来说明。在非立方晶系中, 特别是在具 有一次轴对称的晶系中，平行于轴向和垂直于轴向 的原子间结合力差别甚大。若在某一个方向上结合 力较其它方向为小，则晶体首先在该方向上受到热 激发，因此在该方向上的热膨胀迅速增加，与此同 时往往伴随着垂直于该方向上的收缩，因此出现膨 胀系数的负值。
3.晶体缺陷对热膨胀的影响
实际晶体中总是含有某些缺陷, 它们在室温处于 “ 冻结” 状态, 但它们可明显地影响晶体的物 理性能。 Timmesfeld等人研究了空位对固体热膨胀的影响 。由空位引起的晶体附加体积变化为:
△ V = BV0exp[-Q/kT]
式中，Q 是空位形成能，B 是常数， V0是晶体0k 时的体积，k 是玻耳兹曼常数，T 是温度( K )。 这里的空位可以由辐射或高温淬火产生。
定义：在等压(p一定)下，单位 温度变化所导致的体积变化， 即热膨胀系数。
线膨胀系数α：α=ΔL/(L*ΔT) 面膨胀系数β：β=ΔS/(S*ΔT)
体膨胀系数γ：γ=ΔV/(V*ΔT)
式中ΔL为所给长度变化ΔT下物体温度的改变，L为初始长度；ΔS 为所给面积变化ΔT下物体温度的改变，S为初始面积；ΔV为所给 体积变化ΔT下物体温度的改变，V为初始体积。
材料热膨胀系数概述.
一．目的意义
录
二．材料的热膨胀系数 三．材料热膨胀系数的检测方法
四．示差法的测定原理
五．实验过程 六．主要影响因素讨论 七．实验数据处理
一．目的意义
• 热膨胀 物体的体积或长度随温度的升高而增大的现象称为热膨胀。热膨 胀系数是材料的主要物理性质之一，它是衡量材料的热稳定性好坏的 一个重要指标。 • 提高材料的热稳定性
例：夹层玻璃
目的意义
• 焊接或熔接
当两种不同的材料彼此焊接或熔接时，都要求二种材料具备相近 的膨胀系数。
如两种不同金属的焊接，玻璃仪器的焊接加工，在电真空工业和 仪器制造工业中广泛地将非金属材料（玻璃、陶瓷）与各种金属焊接， 也要求两者有相适应的热膨胀系数。
如果选择材料的膨胀系数相差比较大，焊接时由于膨胀的速度不
三．材料热膨胀系数的检测方法
人类很早（十八世纪）就测定固体的热膨胀。当时的测定装置很原 始：水平放置约 15厘米长的试样，下面点燃几支蜡烛加热，通过齿轮机 构放大来确定试样长度的变化。 十九世纪到现在，人们创造了许多测定方法。上世纪 60 年代出现了 激光法，出现了用计算机控制或记录处理测定数据的测量仪器。
测定无机非金属材料热膨胀系数常用：千分表法、热机 械法（光学法、电磁感应法）、体积法 等。 它们的共同点都是试样在加热炉中受热膨胀，通过顶杆 将膨胀传递到检测系统。不同之处在于检测系统。
千分表法是用千分表直接测量试样的伸长量。
光学热机械法是通过顶杆的伸长量来推动光学系统内的反 射镜转动经光学放大系统而使光点在影屏上移动来测定试样的 伸长量。
相当于温度升高1时物体体积的相对增 大值。 由于总有内能存在，物质的每个粒子 都在振动。
当物质受热时，由于温度升高，每个粒子 的热能增大，导致振幅也随之增大，由（非简谐） 力相互结合的两个原子之间的距离也随之增大， 物质就发生膨胀。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
4. 与相变的关系
一级
二级
.
第二节 材料的热膨胀
热膨胀的本质 与其他物理性能的关系 影响因素 热膨胀测量方法 热膨胀的工程应用
.
3. 影响热膨胀性能的因素
相变的影响 成分和组织的影响 各向异性的影响
.
相变的影响
一级相变：体积突变，有相变潜热。
直接用热膨胀实验分析
二级相变：无体积突变和相变潜热； 但膨胀系数和比热容有突变。
千分表式膨胀仪 杠杆式膨胀仪
标准试样 待测试样
光 底片
光杠杆式膨胀仪原理图
.
热膨胀测试仪（德国耐驰公司）
测试原理：
将样品放入炉体内，施一定 温度程序，此时样品长度的变化 通过推杆传递到左侧的检测单元， 并由位移传感器测量得到结果。
材料学院A306室 .
德国耐驰 DIL402C热膨胀仪
一、技术参数： 1. 升降温速率：0-50 K/min 2. 测量范围：500／5000 μm 3. 样品长度：最大 50 mm 样品直径：最大 12 mm 4. ΔL 分辨率：0.125 nm / 1.25 nm 5. 样品支架：石英支架（< 1100℃），氧化铝支架（< 1700℃），
内应力抑制了热膨胀
两相材料热膨胀系数计算值的比较 多相合金体的膨胀系数主要取决于组成相的性质和数量
.
第二节 材料的热膨胀
热膨胀的本质 与其他物理性能的关系 影响因素 热膨胀测量方法 热膨胀的工程应用
.
4. 热膨胀的测量
光学膨胀仪
光杠杆膨胀仪 光干涉法
电测试膨胀仪
电感式膨胀仪 电容式膨胀仪
机械式膨胀仪
1、与热容的关系
V
rC V K 0V
V
rC V K 0V
格律乃森定律
l
T/K
体膨胀与定容热容成正比，并且它们有相似依赖关系。
.
Al2O3的热容和膨胀系数随温度的变化
.
2、与结合能、熔点的关系
金属的结合能越大）
TmV
VTm V0 V0
C0.06
l
1 l0
l t
t1
微分线膨胀系数
t
1 lt
dl dt
t t
t2
体膨胀系数
V
1
Vt
dV dt
V 3l
Vab . c
各向同性 各向异性
部分材料的线性膨胀系数
材料名称
Al Ti Cr Fe Ni Cu W Invar合金6Ni-Fe 铸铁 黄铜
Si Al2O3 SiC Si3N4 石英玻璃
αl /10-6 K-1 24.9 9.2 10.60 16.7 17.1 17.18 5.19 0~2 10.5 ~ 12 18.5 ~ 21 6.95 8.8 4.7 2.7 0.5
中心右移。
势能曲线是不对称 的！
.
材料热膨胀的本质: 在于晶格点阵实际上在作非 简谐振动，晶格振动中相邻质点间的作用力实际 上是非线性的，点阵能曲线也是非对称的。
理想状态
实际状态
.
第二节 材料的热膨胀
热膨胀的本质 与其他物理性能的关系 影响因素 热膨胀测量方法 热膨胀的工程应用
.
2. 与其他物理性能的关系
石墨支架（2000℃） 二、主要特点： 1. DIL提供多种类型的样品支架与炉体配置。 2. 提供各种配件使测试更灵活方便。 3. 提供速率控制烧结软件（RCS）。 4. 提供 c-DTA 功能，可通过图谱分析计算得到差热DTA曲线。 三、 应用领域：
可测量固体、熔融金属、粉末、涂料等各类样品，广泛应用于无机 陶瓷、金属材料、塑胶聚合物、建筑材料、涂层材料、耐火材料、 复合材料等领域。
8
Tml 0.022
对所有的纯金属
.
几种材料的线膨胀系数、结合能与熔点
.
3、与结构的关系 对结构紧密的晶体，膨胀系数较大。 而对无定形的玻璃，膨胀系数较小。 温度升高时发生的晶型转变，也会引起膨胀系 数的改变。
.
ZrO2陶瓷的热膨胀曲线
1000℃时 单斜晶型
四方晶型
发生体积收缩 4 %
.
.
材料的种类（依据热膨胀系数）
.
温度范围
303 ~ 573 153 ~ 1133 523 ~ 753 303 ~ 1123 693 ~ 1263
373 1573 293 ~ 373 273 ~ 473 293 ~ 573 273 ~ 373 273 ~1273 273 ~1273 273 ~1273 273 ~1273
无机材料的线膨胀系数 一般都不大
第一章 材料的热学性能
顾修全
.
本章内容
热容 热膨胀 热传导 热稳定性
.
第二节 材料的热膨胀
热膨胀的本质 与其他物理性能的关系 影响因素 热膨胀测量方法 热膨胀的工程应用
.
1. 热膨胀的物理本质
什么是热膨胀？ 热膨胀系数 热膨胀的物理本质
.
热膨胀系数
温度每平均升高1个单位，长度的相对变化量。
平均线膨胀系数
.
热膨胀仪典型图谱
.
第二节 材料的热膨胀
热膨胀的本质 与其他物理性能的关系 影响因素 热膨胀测量方法 热膨胀的工程应用
.
5. 热膨胀的工程应用
1、热膨胀的工程意义
陶瓷工业
施釉 要求釉层的膨胀系数比坯体要小
烤瓷牙
为什么？
微机械（MENS）领域
结合后面涉及到的热应力知识 进行解释。
金属的表面改性
薄膜生长
航天器的设计
.
热膨胀在工程中的意义
热膨胀系数是材料的一项重要热学性能指标，在实 际工程应用中具有重要意义。 1) 是决定材料抗热震性的主要因素。 2) 陶瓷坯上釉， 二者α应匹配。釉α适当小于坯，烧 结冷却过程中，釉层收缩小，使釉层中存在压应力， 提高釉层强度，防止裂纹产生。小的太多也不行，会 使釉层脱落。 3) 集成电路、电子管、特种灯生产中。 4) 复合材料制备。 5) 精密仪器仪表。
用热膨胀实验可以研究二级相变
.
二级相变
同素异构体转变
Fe：α相 β相
有序—无序转变
Cu-Au合金
温度变化时发生的晶型转变
.
化学成分的影响
αl Cu – Au合金 膨胀系数
0 20 40 60 80 100
rE / %
Cu – Au合金固溶体的膨胀系数
固溶体的热膨胀系数略低于按直线规律计算的值。
.
某些无机材料的热膨胀系数与 温度之间的关系
.
物理本质（作用力曲线解释）
➢ 0 K时，原子处在平衡位置。 ➢ 温度升高，原子振动激烈。 ➢ 原子向右移动的幅度更大一些，
导致振动中心右移。
原子热振动是非线性 的！
.
物理本质（势能曲线解释）
➢ 0 K时，原子的势能最低。 ➢ 温度升高，原子的势能增加。 ➢ 势能曲线的不对称，使振动