2003电子科技大学博士研究生入学考试初试随机过程试题全解全析
最新电子科技大学研究生模式识别试题-.04-(附答案)
精品文档电子科技大学研究生试卷(考试时间: 至 ,共 2 小时)课程名称 模式识别 教师 学时 40 学分 2 教学方式 课堂教学 考核日期 年 月 日 成绩 考核方式: (学生填写)1、(5分)简述有监督学习和无监督学习的异同。
答:(1)有监督学习必须要有训练集和测试样本,而非监督学习没有训练集; (2)有监督学习的目的就是识别事物,识别结果表现在给待识别数据加上了标号,因此训练样本集必须由带标号的样本组成,而非监督学习方法只有要分析的数据集本身,预先没有什么标号。
(3)非监督学习方法在寻找数据集中的规律性,这种规律性并不一定要达到分数据集的目的,也就是说不一定要“分类”。
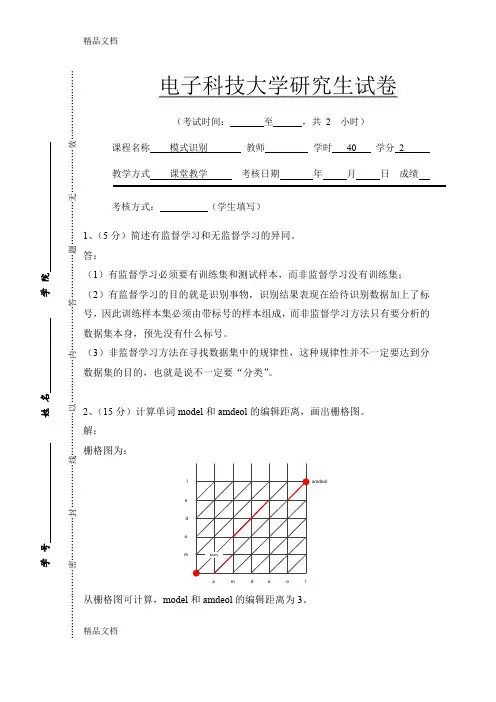
2、(15分)计算单词model 和amdeol 的编辑距离,画出栅格图。
解: 栅格图为:a m d e o lmo d e lamdeolbcaty从栅格图可计算,model 和amdeol 的编辑距离为3。
学 号 姓 名 学 院……………………密……………封……………线……………以……………内……………答……………题……………无……………效……………………精品文档3、(15分)已知A 类样本为:123[0,1];[2,2];[2,3]a a a ===,B 类样本为:123[3,1];[4,3];[1,5]b b b ===,计算最小二乘分类面的方程(取值为-1和+1),并写出LMS 算法的流程。
解:(1)计算最小二乘分类面为[]0.4,0.26,1.45Tω=--。
(2)LMS 算法流程:步骤1. 初始化训练样本、权向量;步骤2. 选择一个训练样本,利用下列公式更新权向量:()[][1][1]2()k k T k iiy μ--=--w w x xw 训练样本数目步骤3. 重复所有样本。
4、(15分)在目标识别中,有1ω和2ω两种目标类型,它们的先验概率分别为0.8和0.2,在一次试验中,获得样本的类概率密度分别为()10.2p x ω=,()20.4p x ω=,并且已知110λ=,126λ=,211λ=,220λ=。
山东大学2003博士入学高量试题(A)

1山 东 大 学二OO 三年招收博士学位研究生入学考试试题报考专业 物理类各专业 考试科目 高等量子力学1)全试题共五大题,满分100分; 试题后有数学公式备查。
【一】质量为m 做一维运动粒子的哈密顿算符是mP 22=H ,在0=t 时坐标表象中的波函数是⎪⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛=2e xp )0,(21x x απαψ。
⑴求空间发生平移l 时,该粒子在动量表象中的波函数; ⑵计算空间平移后的态中坐标算符的不确定值22xx x -=∆。
【二】对于全同玻色子系统,用m j m j a a ,,,+表示单粒子角动量算符z J J ,2本征态m j ,(量子数为m j ,)的单粒子产生、消灭算符。
⑴求证全同粒子系统的总角动量算符z J J ,±表示为∑+±±±-+=mj m j m j a a m m j j ,,1,)1()1( J ∑+=mj jm jm Z a a m , J 。
⑵证明角动量算符代数成立,如证明[]±±±=J J J ,Z ,其他关系也可以类似方法得到。
【三】设一原子系统总角动量为J ,相应的磁矩为 /J B g μ-=μ,这里g 是朗德因子,B μ是玻尔磁子。
设0=t 时原子处于轨道角动量本征态m j ,,在0>t 后置于恒定外磁场n B B t =)(中,系统的哈米顿算符是B H ⋅=μ-。
磁场的方向n 位于xy 平面内,与坐标轴x 夹角为ϕ。
⑴计算角动量算符)(t J ,⑵计算系统t 时刻系统的状态)(t ψ,进而给出态矢)(t ψ含有角动量算符J n n ⋅=J 本征值为 m 的几率。
【四】谐振子相干态等价的表示如下∑+--==+nnn z zaz a n z z 0)ˆ(!e 0e e 222121∑-=nn z n n z !e 221⑴求相干态在动量表象中的波函数。
⑵求动量表象相中干态t 时刻的波函数。
杭州电子科技大学数字电路2003--2016年考研真题

输入序列X1:010101101
输出序列X2:000101001
最近这几年杭电的数字电路每年的题型都不一样,所以不要指望会碰到以前的原题。参考往年的试题你要知道要考哪些东西这时最重要的,存储器、数模转换,可编程逻辑等等,全考。这几年的数电题都不是太难。2011年的数电有130分的题都算是简单的,两个小时就能搞定。最后一个15分的大题特难,看不懂。
5、写出图所示电路的驱动方程、输出方程和状态方程、画出状态转换图,判断电路逻辑功能,最后检查电路能否自启动。
4、设计题
1、用或非门设计一个1位全加器电路。
2、用8选1的MUX实现下列函数:
要求A2A1A0=WXY
3、用4位二进制计数器74LS161接成48进制计数器,标出输入、输出端。可以附加必要的门电路。
A
B
C
L
0
0
0
0
0
0
1
0
0
1
0
0
0
1
1
1
1
0
0
1
1
0
1
1
1
1
0
X
1
1
1
X
4.设 ,则反函数为 =______________对偶函数为 =____________
5.某或非门低电平输入电流为1mA,高电平输入电流为10μA,最大灌电流为12mA,最大拉电流为450μA,则其扇出系数为______________
2007年杭州电子科技大学数字电路考研试题
1、填空题
1.(36)10=()2=()8421BCD
成都电子科技大学电磁场与电磁波2003-2016年考研初试真题+答案

电子科技大学2016年攻读硕士学位研究生入学考试试题考试科目:813 电磁场与电磁波注:所有答案必须写在答题纸上,做在试卷或草稿纸上无效。
一、填空题(每空1分,共20分)1. 在磁导率为μ的均匀介质中,已知恒定(稳恒)磁场的磁感应强度为B ,则介质中的电流体密度J 可以表示成 ,磁化电流体密度M J 可以表示成 。
2. 电荷的定向运动形成电流,当电荷密度ρ满足0=∂∂tρ时,电流密度J 应满足 ,此时电流线的形状应为 。
3. 某线极化波由空气中斜入射到与理想介质(03εε=、0μμ=、0σ=)的分界平面上。
如要使反射波振幅为零,则入射波的极化方式是 、入射角i θ= 。
4. 麦克斯韦通过数学的方法引入 ,从而建立了完整的麦克斯韦方程组。
5. 时变电磁场可以用矢量位A 和标量位ϕ来描述,但是位函数一般是不唯一的,如要得到唯一确定的位函数,可以规定 。
6. 均匀平面波在某一均匀媒质中传播,其电磁波的电场强度E 与磁场强度H 不同相位,则这种媒质是 。
7. 若两个同频率、同方向传播、极化方向互相垂直的线极化波的合成波为圆极化波,则它们的振幅___________、相位差为 ______________;如果两个波的合成波为纯驻波,则它们的传播方向 、且极化方向 。
8. 在理想导体表面上, 矢量总是平行于导体表面, 矢量总是垂直于导体表面。
9. 均匀平面电磁波由空气中垂直入射到与无损耗介质(02.25εε=、0μμ=、0σ=)的分界平面上时,反射系数Γ= ,折射(透射)系数 τ= 。
10.自由空间中位于r '处的源(ρ或J )在t 时刻发生变化,此变化将在 时刻影响到r 处的位函数(ϕ或A )。
11.横截面尺寸为25mm 20mm a b ⨯=⨯的矩形波导中填充介质为空气,能传输的电磁波的最低频率为 Hz ;若要实现单模传输,则电磁波的最高工作频率为 Hz 。
二、判断题,正确的划“√”,错误的划“×”(每题1分,共10分)1. 方程ρ=⋅∇D 表明,电位移矢量D 只与自由电荷有关,而与极化电荷无关,即D 与电介质无关。
电子科技大学2003年攻读硕士学位研究生入学试题当代世界政治经济概论及答案详解

电子科技大学2003年攻读硕士学位研究生入学试题当代世界政治经济概论及答案详解(311)一、简述以下几个基本概念的涵义(每小题6分,共30分)1.世界政治2.世界经济格局3.时代主题4.世界政治经济秩序5.南南合作二、辨析题(回答正确与否,并说明理由。
每小题8分,共40分)1.在国际政治领域,阶级斗争的观点和阶级分析的方法已经过时。
2.当今世界的主要矛盾是“东西矛盾”。
3.国家利益原则,是国际关系中的最高原则。
4.人权高于主权。
5.促进共同发展是当今世界的核心问题。
三、简述题(每小题l0分,共50分)1.简述世界经济与世界政治的关系。
2.请用“合力论”的观点,分析苏联解体的原因。
3.简述当代世界经济大发展的主要原因。
4.简述战后世界社会主义大发展的历史意义。
5.简述当今世界朝着多极化方向发展的主要原因。
四、论述题(每题重5分,共30分)1.试论经济全球化趋势对当代世界政治经济的影响。
2.试述邓小平国际战略理论的基本内容和重大意义。
电子科技大学2003年攻读硕士学位研究生当代世界政治经济概论入学试题答案要点(311)一、简述以下几个基本概念的涵义(每小题6分,共30分)1.世界政治世界政治,是指国际关系行为主体在政治领域的总和,包括世界范围内战争、和平、强权、民主等政治现象。
2.世界经济格局世界经济格局,是指活跃于世界经济舞台充当主角的国家和国际组织之间在一定历史时期内,相互作用形成的一种经济结构与态势。
3.时代主题时代主题,是指时代所面临的全球性、战略性问题。
它构成时代最根本的特征,是体现时代个性以区别其他时代的主要标志,又是同时代面临的诸多问题巾最具有共同性的问题。
4.世界政治经济秩序世界政治经济秩序,又称国际秩序,是指国际社会中行为主体之间发牛关系的行为准则.规范.相互作用的运行机制及其状态。
5.南南合作发展十国家之间的合作与团结,简称“南南合作”。
这是发展中国家共同发展.联合抗争的多渠道、多方式、多方位的合作,是一种建立在互相尊重主权。
2003数一数三考研数学真题及解析

2003年全国硕士研究生入学统一考试数学一试题一、填空题(本题共6小题,每小题4分,满分24分.)(1))1ln(12)(cos lim x x x +→= .(2)曲面22y x z+=与平面042=-+z y x 平行的切平面的方程是.(3)设)(cos 02ππ≤≤-=∑∞=x nx ax n n,则2a =.(4)从2R 的基⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛=11,0121αα到基⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛=21,1121ββ的过渡矩阵为 .(5)设二维随机变量(,)X Y 的概率密度为,y x x y x f 其他,10,0,6),(≤≤≤⎩⎨⎧= 则=≤+}1{Y X P.(6)已知一批零件的长度X (单位:cm )服从正态分布)1,(μN ,从中随机地抽取16个零件,得到长度的平均值为40(cm ),则μ的置信度为0.95的置信区间是.(注:标准正态分布函数值(1.96)0.975,(1.645)0.95.ΦΦ==)二、选择题(本题共6小题,每小题4分,满分24分.每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内.)(1)设函数()f x 在),(+∞-∞内连续,其导函数的图形如图所示,则()f x 有(A ) 一个极小值点和两个极大值点. (B ) 两个极小值点和一个极大值点. (C ) 两个极小值点和两个极大值点. (D ) 三个极小值点和一个极大值点.(2)设}{},{},{n n n c b a 均为非负数列,且0lim =∞→n n a ,1lim =∞→n n b ,∞=∞→n n c lim ,则必有(A ) n n b a <对任意n 成立.(B ) n n c b <对任意n 成立.(C ) 极限n n n c a ∞→lim 不存在.(D ) 极限n n n c b ∞→lim 不存在.(3)已知函数(,)f x y 在点(0,0)的某个邻域内连续,且22200(,)lim1()x y f x y xyx y →→-=+,则 (A ) 点(0,0)不是(,)f x y 的极值点. (B ) 点(0,0)是(,)f x y 的极大值点. (C ) 点(0,0)是(,)f x y 的极小值点.(D ) 根据所给条件无法判断点(0,0)是否为(,)f x y 的极值点.(4)设向量组I:r ααα,,,21 可由向量组II:s βββ,,,21 线性表示,则 (A ) 当s r <时,向量组II 必线性相关.(B ) 当s r>时,向量组II 必线性相关.(C ) 当s r <时,向量组I 必线性相关.(D ) 当s r >时,向量组I 必线性相关.(5)设有齐次线性方程组0Ax =和0Bx =,其中,A B 均为n m ⨯矩阵,现有4个命题: ①若0Ax =的解均是0Bx =的解,则秩(A )≥秩(B ); ②若秩(A )≥秩(B ),则0Ax =的解均是0Bx =的解; ③若0Ax =与0Bx =同解,则秩(A )=秩(B ); ④若秩(A )=秩(B ),则0Ax =与0Bx =同解. 以上命题中正确的是(A ) ①②.(B ) ①③.(C ) ②④.(D ) ③④.(6)设随机变量21),1)((~X Y n n t X =>,则 (A ) )(~2n Yχ.(B ) )1(~2-n Yχ.(C ) )1,(~n F Y .(D ) ),1(~n F Y .过坐标原点作曲线ln y x =的切线,该切线与曲线ln y x =及x 轴围成平面图形D . (1)求D 的面积A ;(2)求D 绕直线x e =旋转一周所得旋转体的体积V .四、(本题满分12分)将函数x xx f 2121arctan )(+-=展开成x 的幂级数,并求级数∑∞=+-012)1(n n n 的和.五、(本题满分10分) 已知平面区域}0,0),{(ππ≤≤≤≤=y x y x D ,L 为D 的正向边界.试证:(1)dx ye dy xe dx ye dy xe xLy x Ly sin sin sin sin -=-⎰⎰--; (2).22sin sin π≥--⎰dx ye dy xex Ly六、(本题满分10分)某建筑工程打地基时,需用汽锤将桩打进土层.汽锤每次击打,都将克服土层对桩的阻力而作功.设土层对桩的阻力的大小与桩被打进地下的深度成正比(比例系数为,0k k >).汽锤第一次击打将桩打进地下a (m ).根据设计方案,要求汽锤每次击打桩时所作的功与前一次击打时所作的功之比为常数(01)r r <<.问(1)汽锤击打桩3次后,可将桩打进地下多深? (2)若击打次数不限,汽锤至多能将桩打进地下多深? (注:m 表示长度单位米.)七、(本题满分12分)设函数()y y x =在),(+∞-∞内具有二阶导数,且)(,0y x x y =≠'是()y y x =的反函数.(1)试将()x x y =所满足的微分方程0))(sin (322=++dy dx x y dyx d 变换为()y y x =满足的微分方程;(2)求变换后的微分方程满足初始条件23)0(,0)0(='=y y 的解.设函数()f x 连续且恒大于零,222()22()()()()t D t f xy z dVF t f x y d σΩ++=+⎰⎰⎰⎰⎰,22()2()()()D t tt f x y d G t f x dxσ-+=⎰⎰⎰,其中}),,{()(2222t z y x z y x t ≤++=Ω,}.),{()(222t y x y x t D ≤+=(1)讨论()F t 在区间),0(+∞内的单调性. (2)证明当0t >时,).(2)(t G t F π>九、(本题满分10分)设矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=322232223A ,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=100101010P ,P A P B *1-=,求2B E +的特征值与特征向量,其中*A 为A 的伴随矩阵,E 为3阶单位矩阵.十、(本题满分8分)已知平面上三条不同直线的方程分别为:1l 032=++c by ax ,:2l 032=++a cy bx , :3l 032=++b ay cx .试证这三条直线交于一点的充分必要条件为.0=++c b a十一、(本题满分10分)已知甲、乙两箱中装有同种产品,其中甲箱中装有3件合格品和3件次品,乙箱中仅装有3件合格品.从甲箱中任取3件产品放入乙箱后,求:(1)乙箱中次品件数X 的数学期望; (2)从乙箱中任取一件产品是次品的概率.十二、(本题满分8分)设总体X 的概率密度为⎩⎨⎧≤>=--,,,0,2)()(2θθθx x e x f x其中0>θ是未知参数.从总体X 中抽取简单随机样本n X X X ,,,21 ,记12ˆmin(,,,X X θ=L )n X .(1)求总体X 的分布函数()F x ; (2)求统计量θˆ的分布函数)(ˆx F θ;(3)如果用θˆ作为θ的估计量,讨论它是否具有无偏性.2003年考研数学一试题答案与解析一、填空题(1)【分析】 属1∞型. 原式=1cos 1cos 1ln(1)lim[1(cos 1)].x x x x x -⋅-+→+-利用等价无穷小因子替换易求得2121lim)1ln(1)1(cos lim 22020-=-=+⋅-→→x xx x x x , 故原式=12.e -(2)【分析】 曲面在任意点(,,)P x y z 处的法向量{2,2,1}x y =-n ,n 与平面042=-+z y x 的法向量{2,4,1}=-0n 平行,λλ⇔=0n n 为某常数,即22,24,1.x y λλλ==-=- 从而1, 2.x y ==,又点P 在曲面上22(1,2)()5z x y P ⇒=+=⇒点处的{2,4,1}=-n .因此所求切面方程是0)5()2(4)1(2=---+-z y x ,即245x y z +-=.(3)【分析】 这是求傅氏系数的问题. 已知)()(2ππ≤≤-=x x x f 是以2π为周期的偶函数,按傅氏系数计算公式得2220002211cos 2sin 22sin 22a x xdx x d x x xdx ππππππ===-⎰⎰⎰=00111cos 2cos 2cos 2 1.xd x x x xdx ππππππ=-=⎰⎰(4)【分析】 设由基12,αα到基12,ββ的过渡矩阵为C ,则1212(,)(,)C ββαα=,即11212(,)(,).C ααββ-=那么,由111110231023011201120112⎡⎤⎡⎤⎡⎤→→⎢⎥⎢⎥⎢⎥----⎣⎦⎣⎦⎣⎦ 可知应填:23.12⎡⎤⎢⎥--⎣⎦当然也可先求出11111,0101-⎡⎤⎡⎤=⎢⎥⎢⎥--⎣⎦⎣⎦再作矩阵乘法而得到过渡矩阵.(5)【分析】 =≤+}1{Y X P 1(,)x y f x y dxdy +≤⎰⎰11206xxdx xdy -=⎰⎰12016(12).4x x dx =-=⎰(6)【分析】 这是一个正态总体方差已知求期望值μ的置信区间问题,该类型置信区间公式为(,),I x x =+其中λ由{}0.95P U λ<=确定(~(0,1))U N 即 1.96λ=.将40,1,16, 1.96x n σλ====代入上面估计公式,得到μ的置信度为0.95的置信区间是(39.51,40.49).二、选择题(1)【分析】 由图,()f x 有三个驻点和一个不可导点0.x ='()f x 在三个驻点处,一个由正变负,两个由负变正,因而这三个驻点中一个是极大值点,两个是极小值点;而点0x =(()f x 的连续点)的左侧'()0f x >,0x =的右侧'()0f x <,0x =是()f x 由增变减的交界点,因而是极大值点.应选(C ).(2)【分析】 (A ),(B )显然不对,因为由数列极限的不等式性质只能得出数列“当n 充分大时”的情况,不可能得出“对任意n 成立”的性质.(C )也明显不对,因为“无穷小⋅无穷大”是未定型,极限可能存在也可能不存在. 故应选(D ).(3)【分析】 由条件000lim[(,)]0lim (,)(0,0)0.x x y y f x y xy f x y f →→→→⇒-=⇒==由极限与无穷小的关系⇒222(,)1(1)()f x y xyo x y -=++ (0).ρ=→⇒2222222(,)()(())()(0).f x y xy x y o x y xy o ρρ=++++=+→ 当y x =时,2(,)(0,0)[1(1)]0f x y f x o -=+>(0ρδ<<时), 当y x =-时,2(,)(0,0)[1(1)]0f x y f x o -=-+<(0ρδ<<时),其中δ是充分小的正数,因此,(0,0)不是(,)f x y 的极值点.应选(A ).(4)【分析】 根据定理“若12,,,s αααL可由12,,,t βββL 线性表出,且s t >,则12,,,s αααL 必线性相关”,即若多数向量可以由少数向量线性表出,则这多数向量必线性相关,故应选(D ).(5)【分析】 显然命题④错误,因此排除(C ),(D ).对于(A )与(B )其中必有一个正确,因此命题①必正确,那么②与③哪一个命题正确呢?由命题①,“若0Ax =的解均是0Bx =的解,则秩(A )≥秩(B )”正确,知“若0Bx =的解均是0Ax =的解,则秩(A )≥秩(B )”正确,可见“若0Ax =与0Bx =同解,则秩(A )=秩(B )”正确.即命题③正确,所以应当选(B ).(6)【分析】 根据t 分布的性质,2~(1,)X F n ,再根据F 分布的性质21~(,1),F n X因此21~(,1)Y F n X=.故应选择(C ).三、【解】(1)曲线ln y x =在点0000(,)(ln )x y y x =处的切线方程为0001();y y x x x -=- 由切线过原点(0,0),得000,y x e ==,所以该切线方程为x y e=.从而,图形的D 面积为(如图)1() 1.2y eA e ey dy =-=-⎰ (2)切线y x e x =、轴与直线x e =所围三角形绕x e =旋转所得圆锥体的体积为211,3V e π=而曲线ln y x x =、轴与直线x e =所围曲边三角形绕x e =的旋转体体积为1222011()(2),22y V e e dy e e ππ=-=-+-⎰或者221112()ln (2).22e V e x xdx e e ππ=-=-+-⎰因此所求旋转体的体积为 212(5123).6V V V e e π=-=-+四、【分析与求解】 (1)因为'()f x 简单,先求'()f x 的展开式,然后逐项积分得()f x 的展开式.因2220112211()()'2(1)4,(,),121214221()12n n nn x f x x x x x x x∞=--'==-=--∈--++++∑ 又(0)4f π=,两边积分得221000(1)411()2(1)42,(,).442122n n x n n nn n n f x t dt x x n ππ∞∞+==-=--=-∈-+∑∑⎰因为()f x 在21=x 连续,21102(1)41(1)21221n n nn x n n xn n ∞∞+===--=++∑∑收敛,所以210(1)411()2,(,].42122n n n n f x x x n π∞+=-=-∈-+∑(2)令21=x ,得21001(1)41(1)()2.24212421n n n n n n f n n ππ∞∞+==--=-⋅=-++∑∑又0)21(=f ,因此0(1).214n n n π∞=-=+∑五、【分析与证明】用格林公式把第二类曲线积分转化为二重积分.(1)由格林公式,有左边曲线积分=sin sin sin sin [()()](),y x y x DDxe ye dxdy e e dxdy x y --∂∂--=+∂∂⎰⎰⎰⎰ 右边曲线积分=sin sin ().y x De e dxdy -+⎰⎰ 因为区域D 关于y x =对称⇒⎰⎰-+Dx y dxdy e e )(sin sin =⎰⎰+-Dxy dxdy e e )(sin sin (x 与y 互换). 因此dx ye dy xe dx ye dy xex Ly x Lysin sin sin sin -=---.①(2)由(1)的结论,有sin sin sin sin sin sin ()()y x y x y yLDDxe dy ye dx e e dxdy e e dxdy ----=+=+⎰⎰⎰⎰⎰Ñ2222.DDdxdy π≥==⎰⎰⎰⎰六、【分析】 设第n 次打击后,桩被打进地下n x ,第n 次打击时,气锤所作的功为),3,2,1( =n W n . 由题设,已知当桩被打进地下的深度为x 时,土层对桩的阻力的大小为kx ,1n n W rW -=要求的是(n x n 3)=及lim .n n x →+∞【解】 通过求1nii W =∑直接求出nx .按功的计算公式:12211011,22x W kxdx kx ka ===⎰2312123,,,.nn x x x n x x x W kxdx W kxdx W kxdx -===⎰⎰⎰L相加得 21201.2nx n n W W W kxdx kx +++==⎰L又 21121n n n n W rW r W r W ---====L ,代入上式得21221111(1),.22n n r r r W kx W ka -++++==L 于是().n x a m ==因此3().x m ==lim ).n n x m →+∞=七、【证明】 (1)实质上是求反函数的一、二阶导数的问题.由反函数求导公式知y dy dx '=1,2211()'()'()'''y y x d x dx dx dy dy y y dy===⋅33''().y dxy y dy ''=-=-' 代入原微分方程,便得常系数的二阶线性微分方程.sin x y y =-''(*)(2)特征方程210r -=的两个根为1,21;r =±由于非齐次项()sin f x x =sin x e x αβ=,0,α=1β=,i i αβ±=±不是特征根,则设(*)的特解*cos sin y a x b x =+,代入(*)求得,10,2a b ==-,故x y sin 21*-=,于是(*)的通解为121()sin .2x x y x C e C e x -=+- 又由初始条件得1,121-==C C ,所求初值问题的解为.sin 21x e e y x x --=-八、【分析与证明】(1)分别作球坐标变换:sin cos ,sin sin ,cos x y z ρϕθϕθρϕ===与极坐标变换:cos ,sin .x r y r θθ==将()F t 中的分子与分母表成定积分,于是222220222()sin 2()().()()ttttd d f drf drF t d f r rdrf r rdrπππθϕρρϕρρθ==⎰⎰⎰⎰⎰⎰⎰下面求'()F t ,由它的符号讨论()F t 的单调性.由变限积分求导法得2222222022()()()()()2(())tttt f t f r rdr t f t f r r drF t f r rdr -'=⎰⎰⎰220220()()()20,[()]tttf t f r r t r drf r rdr -=>⎰⎰(0,)t ∈+∞.因此()F t 在),0(+∞单调增加.(2)如同题(1),先将()G t 表成定积分:22200022()()().2()()ttttd f r rdrf r rdrG t f r rdrf r drπθπ==⎰⎰⎰⎰⎰要证0t >时,2()(),F t G t π>即证2220022()(),()()t t ttf r r dr f r rdr f r rdrf r dr>⎰⎰⎰⎰即证222220()()[()]0.ttt f r dr f r r dr f r rdr ->⎰⎰⎰(*)我们将利用单调性证明这个不等式. 令222220()()()[()],tttt f r dr f r r dr f r rdr Φ=-⎰⎰⎰⇒2222222200'()()()()()2[()]()tttt f t f r r dr f t tf r dr f r rdr f t t Φ=+-⋅⎰⎰⎰2220()()()0t f t f r t r dr =->⎰,(0,)t ∈+∞又()t Φ在0t =处连续⇒()t Φ在[0,)+∞单调增加0t ⇒>时,()(0)0.t ΦΦ>=因此0t >时,).(2)(t G t F π>九、【解】由于322777232232223011E A λλλλλλλλλλ-------=---=--------2111(7)(1)232(1)(7),011λλλλλ=-----=---故A 的特征值为.7,1321===λλλ因为7,i A λ==∏若,A αλα=则.AA ααλ*=所以,A *的特征值为:7,7,1.由于1B P A P -*=,即A *与B 相似,故B 的特征值为7,7,1.从而2B E +的特征值为9,9,3.因为11111()()(),AB P P A P P P A P ααααλ--*--*-===按定义可知矩阵B 属于特征值Aλ的特征向量是1Pα-.因此2B E +属于特征值2+λA的特征向量是1Pα-.由于,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=-1000011101P ,而当1λ=时,由222111()0,222000,222000E A x ---⎡⎤⎡⎤⎢⎥⎢⎥-=---→⎢⎥⎢⎥⎢⎥⎢⎥---⎣⎦⎣⎦得到属于1λ=的线性无关的特征向量为111,0α-⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦210.1α-⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦ 当7λ=时,由422121(7)0,242011,224000E A x ---⎡⎤⎡⎤⎢⎥⎢⎥-=--→-⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦ 得到属于7λ=的特征向量为311.1α⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦那么1111,0P α-⎡⎤⎢⎥=-⎢⎥⎢⎥⎣⎦1211,1P α--⎡⎤⎢⎥=-⎢⎥⎢⎥⎣⎦1301.1P α-⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦故2B E +属于特征值9λ=的全部特征向量为121111,01k k -⎡⎤⎡⎤⎢⎥⎢⎥-+-⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦12,k k 是不全为零的任意常数. 而2B E +属于特征值3λ=的全部特征向量为301,1k ⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦,其中3k 为非零的任意常数.十、【解】必要性:若三条直线交于一点,则线性方程组23,23,23ax by c bx cy a cx ay b +=-⎧⎪+=-⎨⎪+=-⎩(*)有唯一解,故()()2r A r A ==.于是0.A =由于23111236()23a bc A b c a a b c b c a c a b c a b--=-=++---2226()()a b c ab c ab ac bc =++++---2223()[()()()],a b c a b b c c a =++-+-+-(* *)由321,,l l l 是三条不同直线,知a b c ==不成立,那么0)()()(222≠-+-+-a c c b b a .故必有.0=++c b a充分性:若0,a b c ++=由(**)知0=A ,故秩() 3.r A <由22222132()2[()]2[()]0,224a b ac b a a b b a b b b c =-=-++=-++≠(否则0a b c ===.)知秩() 2.r A =于是()() 2.r A r A ==因此,方程组(*)有唯一解,即三条直线321,,l l l 交于一点.十一、【解】 (1)易见,X 服从超几何分布,其分布参数为123,3n N N ===,根据超几何分布的期望公式,可直接得到1123.2N EX nN N ==+(2)设A 表示事件“从乙箱中任意取出的一件产品是次品”,由于{0},{1},{2}X X X ===和{3}X =构成完备事件组,因此根据全概率公式,有3300(){}{}{}6k k kP A P X k P A X k P X k =======⋅∑∑3011131{}.66624k kP X k EX =====⋅=∑十二、【解】 (1)2(),1,()().0,x xx e F x f t dt x θθθ---∞≥⎧-==⎨<⎩⎰(2)}),,,{min(}ˆ{)(21ˆx X X X P x P x F n≤=≤=θθ 12121{min(,,,)}1{,,,}n n P X X X x P X x X x X x =->=->>>L L 121{}{}{}n P X x P X x P X x =->>>L1[1()]nF x =--=2(),1,.0,n x x e x θθθ--≥⎧-⎨<⎩(3)ˆθ的概率密度为 2()ˆˆ,2,()'().0,n x x ne f x F x x θθθθθ-->⎧==⎨≤⎩因为2()ˆ1ˆ()2,2n x E xf x dx nxe dx nθθθθθθ+∞+∞---∞===+≠⎰⎰ 所以ˆθ作为θ的矩估计量不具有无偏性.。
2003考研数学一真题及答案解析
2003年全国硕士研究生入学统一考试数学(一)试卷答案解析一、填空题(本题共6小题,每小题4分,满分24分.把答案填在题中横线上)(1))1ln(12)(cos lim x x x +→=e1.【分析】∞1型未定式,化为指数函数或利用公式)()(lim x g x f )1(∞=)()1)(lim(x g x f e -进行计算求极限均可.【详解1】)1ln(12)(cos lim x x x +→=xx x ecos ln )1ln(1lim20+→,而212cos sin lim cos ln lim )1ln(cos ln lim 02020-=-==+→→→x x xx x x x x x x ,故原式=.121ee =-【详解2】因为2121lim )1ln(1)1(cos lim 22020-=-=+⋅-→→xxx x x x ,所以原式=.121ee=-【评注】本题属常规题型(2)曲面22y x z +=与平面042=-+z y x 平行的切平面的方程是542=-+z y x .【分析】待求平面的法矢量为}1,4,2{-=n,因此只需确定切点坐标即可求出平面方程,而切点坐标可根据曲面22y x z +=切平面的法矢量与}1,4,2{-=n平行确定.【详解】令22),,(y x z z y x F --=,则x F x 2-=',y F y 2-=',1='z F .设切点坐标为),,(000z y x ,则切平面的法矢量为}1,2,2{00y x --,其与已知平面042=-+z y x 平行,因此有11422200-=-=-y x ,可解得2,100==y x ,相应地有.520200=+=y x z 故所求的切平面方程为0)5()2(4)1(2=---+-z y x ,即542=-+z y x .【评注】本题属基本题型。
(3)设)(cos 02ππ≤≤-=∑∞=x nx ax n n,则2a =1.【分析】将)()(2ππ≤≤-=x x x f 展开为余弦级数)(cos 02ππ≤≤-=∑∞=x nx ax n n,其系数计算公式为⎰=ππ0cos )(2nxdx x f a n .【详解】根据余弦级数的定义,有xd x xdx x a 2sin 12cos 22022⎰⎰=⋅=ππππ=⎰⋅-πππ2]22sin 2sin [1xdx x xx =⎰⎰-=πππππ]2cos 2cos [12cos 1xdx xx x xd =1.【评注】本题属基本题型,主要考查傅里叶级数的展开公式,本质上转化为定积分的计算.(4)从2R 的基⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛=11,0121αα到基⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛=21,1121ββ的过渡矩阵为⎪⎪⎭⎫ ⎝⎛--2132.【分析】n 维向量空间中,从基n ααα,,,21 到基n βββ,,,21 的过渡矩阵P 满足[n βββ,,,21 ]=[n ααα,,,21 ]P ,因此过渡矩阵P 为:P=[121],,,-n ααα [],,,21n βββ .【详解】根据定义,从2R 的基⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛=11,0121αα到基⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛=21,1121ββ的过渡矩阵为P=[121],-αα[⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡-=-21111011],121ββ.=.213221111011⎥⎦⎤⎢⎣⎡--=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡-【评注】本题属基本题型。
2003级北邮硕士生“概率论与随机过程”试题
六、(7分)设 n , n 1,2,是取值为0或1的独立随机变量序列,其分布为p1 1 n 和 七、( 10分)给定一个随机变量 t 和任意实数x,定义另一个随机过程: 1 t x t 0 t x 证明 t 的均值函数和自相关函数分别为 t 的一维和二维分布函数。
九、 (7 分)已知某平稳过程的相关函数 R e a cos( 0 ) ,其中 a>0 , 0 为常数. 求该随机过程的谱密度函数。 十、 (9 分) 连续掷一骰子,以 Xn 记前 n 次投掷中出现的最大点数,则 {Xn , n 1 } 为 Markov 链,试求其 n 步转移概率矩阵。 十一、 (10 分)设马氏链的状态空间 E ={1,2,3,4,5},转移概率矩阵为:
(1)求 X , Y 的边缘分布律; (2)判断 X 与 Y 是否相互独立; (3)求 X 2 时 Y 的条件分布律; (4)求 X 2 时 Y 的条件数学期望; (5)求 X 2 时 Y 的条件方差 四、 (12 分)设(X,Y)的联合密度函数为:
2 2 1 1 xy x y f ( x, y) 4 0
k q k p,0 p 1, q 1 p, k 0,1,2, ,则ξ的特征函数 2.设ξ服从分布: P
。 条件下,两个随机过程{X(t),t∈T},{Y(t),t∈ T}相互正交; 条件下,两个随机过程互不相关。
三、 (10 分)设随机变量 ( X , Y ) 的联合分布律为: 0 1/4 1/16 0 1 0 1/4 1/16 2 0 0 1/16 3 1/16 1/4 0
x1 x n 当 n 时是否几乎处处收敛于 p? n
1 八、 ( 8 分 ) 设 {Yn , n 1, 2, } 是 相 互 独 立 的 随 机 变 量 序 列 , 且 P (Yn 1) , n 1 P (Yn 0) 1 。证明: Yn 均方收敛到 0。 n
成都电子科技大学大学物理2003-2016年考研初试真题+答案
共6页第1页 电子科技大学2016年攻读硕士学位研究生入学考试试题考试科目:811 大学物理注:所有答案必须写在答题纸上,写在试卷或草稿纸上均无效。
一、选择题(本题共计42分,每题3分)1两个物体A 和B 的质量以及它们的速率都不相同,若物体A 的动量在数值上比物体B 的大,则A 的动能E KA 与B 的动能E KB 之间(A) E KB 一定大于E KA . (B) E KB 一定小于E KA .(C) E KB =E KA . (D) 不能判定谁大谁小. [ ] 2 如图所示,两个同心均匀带电球面,内球面半径为R 1、带有电荷Q 1,外球面半径为R 2、带有电荷Q 2,则在外球面外面、距离球心为r 处的P 点的场强大小E 为: (A) 20214rQ Q επ+. (B)()()2202210144R r Q R r Q -π+-πεε. (C) ()2120214R R Q Q -π+ε. (D) 2024r Q επ. [ ]3设某种气体的分子速率分布函数为f (v ),则速率在v 1─v 2区间内的分子的平均速率为(A) ()⎰21d v v v v v f . (B) ()⎰21d v v v v v v f . (C)()⎰21d v v v v v f /()⎰21d v v v v f . (D) ()⎰21d v v v v f /()⎰∞0d v v f . [ ]4电流I 由长直导线1沿平行bc 边方向经a 点流入由电阻均匀的导线构成的正三角形线框,再由b 点沿垂直ac 边方向流出,经长直导线2返回电源(如图).若载流直导线1、2和三角形框中的电流在框中心O 点产生的磁感强度分别用1B 、2B 和3B 表示,则O 点的磁感强度大小 (A) B = 0,因为B 1 = B 2 = B 3 = 0. (B) B = 0,因为虽然B 1≠ 0、B 2≠ 0,但021=+B B ,。
2003年研究生入学考试试题半导体物理与器件
一. 简单回答:(20分) 1. 在原子间距为 a 的一维单原子晶格中,波矢 q=1/4(2π/a),和 q=1/4(2π/a)+2π/a 的两种格波所描述的原子振动的情况有何 异同? 2. 含施主浓度为 Nd=210cm,受主浓度为 Na=210×cm 的硅样品,温度 为 300K 和温度为 500K 时该样品的载流子浓度各是多少?
的晶格振动的独立波矢数都为 4 ○ 有 ;其中有 8 ○ 5 ○ 类横波,有
;晶格振动的总的格波数都是 7 类纵波,有 ○ 支声学波,
支光学波。
2、某一维半导体晶体价带顶附近的电子能量,在国际单位制中可 表示为 E(k)=E0-10 ,现将其中一波矢 k=10 cm 的电子移走,则此 电子留下的空穴能量为 速度为 4 ○ 、准动量为 1 、有效质量为 ○ 5 。 ○ 2 ○ 、波矢为 3 ○ 、
在有一个受主浓度为 Na 的 P 型半导体:
1.
在表面空间电荷区为积累层、耗尽层、反型层三种情况 下,分别画出能带图(必须画出费米能级和本征费米能 级) :
2.
已知强反型层开始出现的条件是:表面触地少子浓度等 于体内的多子浓度。画出开始出现强反型层时的能带 图,证明开始出现强反型层时,表面势 Vs = 2 φ f 。这里
,试由
τ =τ p
n0 + n1 p + p1 +τ n 0 n0 + p0 n0 + p0 验证上述关系:并说明激活能
Ec − Ei kT
∆ E 的物理意义。 (式中 n1 = N c e
, p1 = N v e
Ei − Ec kT
)
四. ( 15 分)两种载流子同时起作用,半导体的霍尔系数为:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
dt
RC
dY (t) Y (t) X (t) dt
两边同时进行傅里叶变换
jwY (w) Y (w) X (w)
此时可以得到
H (w) jw
此时系统的脉冲响应函数可以得到,为:
h(t
)
F
1[
H
(w)]
et
0
t 0 t0
mY (t) mX h(t)dt 0 0
(3)中先求一部分 输出过程的功率谱密度函数为:
w
)
)。
(6)马氏链{X (n), n 0,1, 2...} 的转移概率为 Pij (m, k) ,称{X (n), n 0,1, 2...} 为齐次马
氏链,即( Pij (m, k) pij (k) (k 1, 2...) )。
二(14 分)
齐次马氏链的状态空间 E {0,1, 2...} 状态转移矩阵为:
(
sin(bu) bu
)。
(3)随机正弦波 X (t) cos(wt )( t ) ,其中 , 为常数, 是在[0, 2 ]
上的均匀分布。则 X (t) 的均值函数 m(t) (0),协方差函数 C(s,t) ( a2 cos (t s) )。 2
(4)平均过程
X
(t)
的相关函数
RX
13
13
五(14 分)
叙述平稳过程 {X (t), t } 具有均方遍历性(各态历经性)定义。讨论随机过程 X (t) Y ( t ) 的均方遍历性。(其中,Y 是随机变量,且 D(Y ) 0 ,D(Y ) ) 解:平稳过程{X (t), t }满足 P{X (t) mX } 1且 P{X (t)X (t ) RX ( )} 1 称{X (t), t }具有均方遍历性 又对于随机过程 X (t) Y ( t ) 而言
RX
( )
2e
,
0,
1 RC
,
试求:
(1)输出过程{Y (t), t }的均值 mY (t)
(2)自相关函数 RY ( )
(3)自谱密度函数 SY (w) 以及互谱密度函数 SXY (w)
解:此题解答顺序不一定按照提问的顺序 由电路性质,可知其 (1)由电路知识分析可知
RC dY (t) Y (t) X (t),令 1
E[ X (t)] E[Y ] 常数 , E[X (t)X (t )] E[Y 2] DY (EY )2 R( )
故{X (t), t }为平稳过程
但是 X (t) lim
1
T
Ydt Y , X (t)X (t ) lim
1
T
Y YdY Y 2
T 2T T
T 2T T
由于 D(Y ) 0 , P{Y EY} 1, P{E(Y 2 ) Y 2} 1,所以不成立
故{X (t), t }不具有均方遍历性
六(14 分)
(与 2002 年第六题重复)给定一 R-C 电路系统,具体如图(图参照 2002 年第六题给出):
如果输入平稳过程{X (t), t },均值 mX (t) 0 ,自相关函数
A
0
t
e uv dudv
0
2A
min(s,
t
)
A 2
[e s
et
e ts
1]
四(14 分)
一修理工人负责修理 2 台同类设备,设备从开始正常工作到出故障需要维修的时间服从平均
率为 1(台/周)的指数分布,维修时间服从参数为 4 (台/周)的指数分布,二者
相互独立,求系统运行指标。 解:此系统为 M/M/1 顾客为有限源等待制系统:
2003 电子科技大学博士研究生入学考试初 试随机过程试题全解全析
一、填空题(30 分,每小题 5 分)
(1)已知随机向量
(X
0
y
x
1上均匀分布,则
E[Y
|
X
]
(
X 2
0
X 0 ), X 0
E[ X
|
Y
]
(
Y
1 2
Y 0 )。
0 Y 0
(2)服从均匀分布的随机变量,
X
~ U (b,b) 的特征函数X (u)
m 2, 1, 4
(1)
0
系统空闲概率:
2
{
k 0
m! ( (m k)!
k
) }1
8 13
2
1 13
(2) (3) (4)
顾客在系统逗留平均数
Ls
6 13
,顾客在系统等待平均数
Lq
1 13
顾客在系统逗留的平均时间为Ws
3 10
,顾客在系统平均等待时间Wq
1 20
设备处于正常运行状态的台数为 K 20 ,设备利用率 10
A 与 为常数)
解:先求解均值函数
t
mY (t) X (s)ds 0,t 0 0
所得自相关函数为:
s
t
RY (s,t) E[Y (s)Y (t)] E[ X (u)du X (v)dv]
0
0
s 0
t 0
E[ X (u) X (v)]dudv
s
0
t 0
R(u, v)dudv
s
1 2n
,
f00
n1
f00 (n) 1
0
n f00 (n)
n1
n1 2n
n1
2 , p00 (1)
p00
1 0 2
故状态
0
为非周期、正常返、遍历状态。又因
p00
1 2
,i
E
{0,1, 2...} 与状态
0
互通。
故状态 i 与状态 0 有相同的状态性质,都是非周期、正常返、遍历状态。该马氏链为不可约
1
2
1 2
0
0
0
...
1 2
0
1 2
0
0
...
P
1
0
0
1
0
...
2
2
1
0
0
0
1
...
2
2
... ... ... ... ... ...
(1)画出状态转移图 (2)讨论状态性质并分类 解:(1)状态转移图如下:
(2)状态
0:
f00 (1)
1, 2
f00 (2)
1 22
,以此类推,
f00 (n)
遍历的齐次马氏链。
三(14 分)
设 随 机 过 程 {X (t ) ,t 0的} 均 值 mX (t ) 0, 自 相 关 函 数 RX (s ,t ) Ae ts , 若
t
Y (t) X (s)ds,t 0 ,求随机过程{Y (t),t 0} 的均值 mY (t) 与自相关函数 RY (s,t)(其中 0
SY (w)
H (w) 2 SX (w)
(
)
e 2
,则其导过程 Y
(t)
dX (t) dt
和Y (t)
d
2 X (t) dt 2
的互相关函数 Ryy ( ) ( 4 (2 3)e 2 )。
(5)设{X (t),t T} 是随机电报信号,其相关函数 R( ) 1 e2 , ( t ) ,则谱密 4
度函数
S (w)
(
2 42
w2
(
