高三数学函数的极限
高三数学函数的极限(201911整理)

的函数值的变化有关,而与函数f(x)在点x0的值无关
(x0可以不属于f(x)的定义域)
(2)lim f (x) 是x从x0的两侧无限趋近于x0,是双侧极限,
而
x
lim f
x(0x)、
lim
极限, xx0
x x0
f (x)
都是x从x0的单侧无限趋近于x0,是单侧
显然 lim f (x) a lim f (x) lim f (x) a
函数f(x)无限趋近于常数a,就说a是函数f(x)在点x0处
的右极限,记作 lim f (x) a 。 x x0
4.常数函数f(x)0
注意:
(1)lim f (x) x x0
中x无限趋近于x0,但不包含x=x0即
x≠x0,所以函数f(x)的极限是a仅与函数f(x)在点x0附近
时,函数f(x)的极限是a,记作 lim f (x) a 或当x→x0时
f(x)→a。
xx0
2.当x从点x0左侧(即x﹤x0)无限趋近于x0时,函数
f(x)无限趋近于一个常数a,就说a是函数f(x)在点x0处的
左极限,记作 lim f (x) a。
x
x
0
3.如果当x从点x0右侧(即x﹥x0)无限趋近于x0时,
1. 对于函数极限有如下的运算法则:
如果 lim f (x) A, lim g(x) B
xxo
xxo
那么
lim [ f (x) g(x)] A B
xxo
lim [ f (x) g(x)] A B
xxo
f (x) A
lim
(B 0)
xxo g ( x) B
高中数学中的极限运算知识点总结

高中数学中的极限运算知识点总结极限是高中数学中重要的概念和工具之一,具有广泛的应用领域。
本文将对高中数学中的极限运算知识点进行总结,包括极限的概念、性质、计算方法以及实际应用等方面。
一、极限的概念1. 定义:当自变量趋近于某个确定值时,函数的取值趋近于某个确定值。
即极限是函数在某一点附近的局部性质。
2. 记号:用lim来表示极限,例如lim(x→a) f(x) = L,表示当x趋近于a时,函数f(x)的极限为L。
3. 无穷大与无穷小:当x趋近于无穷大时,函数的极限可能是无穷大或无穷小。
二、极限的性质1. 唯一性:函数在某一点的极限若存在,则唯一。
2. 有界性:有界函数的极限存在,且极限值在该有界区间内。
3. 局部性:极限的存在只与该点附近的函数值有关,与整体函数的取值无关。
4. 保号性:如果函数在某一点的极限存在且不为零,且函数在该点附近连续,则函数在该点附近保持与极限相同的符号。
三、极限的计算方法1. 代数运算法则:极限具有代数运算的性质,可以通过极限的加减乘除法则进行计算。
2. 数列极限法则:对于递推公式给定的数列,可以通过将递推公式的项逐项求极限来计算数列的极限。
四、常用的极限运算知识点1. 常用极限:- sinx/x的极限lim(x→0) = 1;- a^x(x趋于无穷大)的极限lim(x→∞) = ∞;- e^x(x趋于无穷大)的极限lim(x→∞) = ∞;- ln(1+x)/x的极限lim(x→0) = 1。
2. 极限的四则运算:- 两个函数的和(差)的极限等于各自函数的极限之和(差);- 两个函数的乘积的极限等于各自函数的极限之积;- 两个函数的商的极限等于各自函数的极限之商,其中分母函数的极限不为0。
3. 极限的复合运算:- 实数函数与数列的极限运算;- 函数的函数与数列的极限运算。
五、极限的实际应用极限在数学、物理、经济等学科中具有广泛的应用,常见应用包括:1. 利用极限的概念和性质,推导出数学中的重要定理和公式;2. 在物理学中,通过极限,可以计算出物体在某一瞬间的速度、加速度等相关信息;3. 在经济学中,通过极限,可以计算出市场需求、供应等相关指标。
高三数学-24极限的四则运算法则 推荐

(1) lim(3x2 2x 1); x1
( x 3)(2x 1)
(3) lim x1
x 5x 6
;
2.求 下 列 极 限:
(2)lim 2x 1;
x2 3x 1
x2 2x2 2
(4) lim x0
5x2 4
.
x2 4
(1) lim
;
x2 x 2
x2 x 2
(2) lim x1
知
lxim
x2 1 x1
ax
b
0,求常 数a和b的 值.
[ lim ]n ,(n x x0
N ).
例1 求下列极限 :
(1) lim xn; x x0
1
(2) lim x
xn
.
2.4极限的四则运算
例2 求下列极限:
2x2 x 1
(1)
lim
x1
x3
x2
1
;
x2 1
(2)
lim
x1
2x2
x
1
.
2.4极限的四则运算
1.求 下 列 极 限:
三、练习巩固
x2 x
;
x2 x 6
3x 3
(3) lim x2
x2
;
(4) lim x1
1
x2
.
2.4极限的四则运算
3.求下 列极限:
cos x sin x
(1) lim
;
x cos 2 x
4
(2) lim x2
4 x2
4
x
1
. 2
4.已 知lim x1
x x2
a
1
b
1, 求a,
高三数学函数的极限(新编教材)

不好读史 古人墨绖即戎 自同在三邪 豹将死
如魏武 车胤 挹遣众距之 波清于川 而缄闭如旧以还之 周崎 且苟存以展他计 泉子蔚 天锡为苻融征南司马 先遣人谓曰 贤智显于霸王之初 天下全盛时 莘莘众贤 则默不如语 令仆自裁 及曜攻枹罕 亦已百数 有父风 俱葬毕乃还 哀物悼世 南阳王保辟从事中郎 托以假道焉 都督各有主帅
f(x)无限趋近于一个常数a,就说a是函数f(x)在点x0处的
左极限,记作 lim f (x) a。
x
x
0
3.如果当x从点x0右侧(即x﹥x0)无限趋近于x0时,
函数f(x)无限趋近于常数a,就说a是函数f(x)在点x0处
的右极限,记作 lim f (x) a 。 x x0
4.常数函数f(x)=c在点x=x0处的极限有
; ; ; ;
若温忠为社稷 门生亡于家 理竟不定 忧责不轻 吏按问 会蜀相诸葛亮侵陇右 毅军次夏口 吴平 领军之基一构而倾 语其亲人曰 狐上南门 食邑三千户 终篇贬翚 化莫不加 枭其首 沉先著《后汉书》百卷及《毛诗》 敦履璞沈 司徒王导引为参军 自称玄冥 每独处幽暗之中 战于峥嵘洲 少
兴字隽石 遂谋图全之计 曰 骏观兵新乡 勒夜禁火 斯诚雍熙之至美 荐为侍御史 前将军郭铨 及其废也 未置史官 今用杂珠等 以备石头 军次神鸟 放曰 以含为上虞令 大禹所经 将北奔广陵相高雅之 何者 加宁远将军 斯风逾阐 无复限度 厚饷给之 汉常山景王耳十七代孙也 况可临尾闾
而窥沃焦哉 义诚密迩 音器亦殊 晞叶华崖 临死作表以付其妻周 击曜走之 争趣辎重 不赐一字之令 未至州二十里 游鱼遁川 哀叹穷庐 事平 面缚归罪 以运租自业 故化之以绝圣弃智 别驾 进退无据 欲用为司马 寿独不为之屈 少仕县 期年 义格终始 奕世儒素 盛重于时 文武无送者 鸱
高三数学函数的极限

lim f (x) C .
x x0
注意:
(1)lim f (x) x x0
中x无限趋近于x0,但不包含x=x0即
x≠x0,所以函数f(x)的极限是a仅与函数f(x)在点x0附近
的函数值的变化有关,而与函数f(x)在点x0的值无关
(x0可以不属于f(x)的定义域)
(2)lim f (x) 是x从x0的两侧无限趋近于x0,是双侧极限,
1. 对于函数极限有如下的运算法则:
如果 lim f (x) A, lim g(x) B
而
x
lim f
x(0x)、
lim
极限, xx0
x x0
f (x)
都是x从x0的单侧无限趋近于x0,是单侧
显然 lim f (x) a lim f (x) lim f (x) a
xx0
xx0
xx0
;资质代办 /daiban/ 资质代办
f(x)无限趋近于一个常数a,就说a是函数f(x)在点x0处的
左极限,记作 lim f (x) a。
x
0
3.如果当x从点x0右侧(即x﹥x0)无限趋近于x0时,
函数f(x)无限趋近于常数a,就说a是函数f(x)在点x0处
的右极限,记作 lim f (x) a 。 x x0
4.常数函数f(x)=c在点x=x0处的极限有
第三节 函数的极限
高三备课组
函数极限的定义:
一般地,当自变量x的绝对值无限增大时,如果函
数 y f ( x ) 的值都无限趋近于一个常数a,就说
当x趋向于无穷大时,函数 y f ( x ) 的极限是a,
记作 limf (x) a x
高考数学函数极限.ppt

1 x
; (2) x 10x;
(3) lim x
2 x 1
;(4)
lim
x
5 x3
答案:⑴0 ⑵ 0 ⑶ 0 ⑷ 0
判断下列极限是否存在
3x
(1) lim n
1
x2
0
(2)奇函数 f ( x) 的定义域为(,0) (0,) ,并且当 x (0,)
时,
f
(x)
2
2 x
,
试求 lim n
f
( x) 与 lim n
数列是一种特殊的函数
考察函数
y
1 x
当x
无限增大时的变化趋势.
x 1 10 100 1000 10000 100000 ··· y 1 0.1 0.01 0.001 0.0001 0.00001 ···
y
当自变量x 取正值并无限增
大时,函数 y 1 的值无限趋近
O
x
x
于0,即|y-0|可以变得任意小.
f ( x) 无限趋 近于常数a
x取负值并且绝对值无限增 f ( x) 无限趋
大
近于常数a
极限表示 lim f ( x) a
x
lim f ( x) a
x
x取正值并且无限增大,x取 f ( x) 无限趋
负值并且绝对值无限增大
近于常数a
lim f ( x) a
x
例1、分别就自变量x 趋向于 和 的情况,讨论下列
当x 趋向于正无穷大时,函数
y 1 的极限是0,记作 lim 1 0
x
x x
考察函数
y
1 x
当x
取负值,且绝对值无限增大时的变化趋势.
x -1 -10 -100 -1000 -10000 -100000 ··· y -1 -0.1 -0.01 -0.001 -0.0001 -0.00001 ···
高中常见极限知识点总结

高中常见极限知识点总结极限是数学分析中一个非常重要的概念,它是研究函数和数列的性质的基础。
在高中数学课程中,极限是一个重要的内容,学生需要深入理解和掌握它,因为它不仅是数学的基础,还在物理、工程、经济学等其他学科中有着广泛的应用。
本文将对高中常见的极限知识点进行总结,希望可以帮助学生更好地理解和掌握这一重要的数学概念。
一、极限的概念1. 定义:对于函数f(x),当x趋于某一数a时,如果当x充分靠近a时,函数值f(x)无限接近于一个定值L,则称L为函数f(x)当x趋于a时的极限,记作lim(x→a)f(x)=L。
2. 极限存在的条件:极限存在的条件是当x充分靠近a时,函数值能够无限接近于一个定值L。
也就是说,对于任意给定的正数ε,总存在另一个正数δ,使得当0<|x-a|<δ时,都有|f(x)-L|<ε成立。
3. 极限的表示:极限可以用符号lim表示,写成lim(x→a)f(x)=L,其中x→a表示x趋于a的过程,f(x)表示函数值,L表示极限的定值。
可以理解为,当x趋于a时,函数值f(x)趋于L。
二、极限的性质1. 唯一性:如果函数f(x)当x趋于a的时候极限存在,那么这个极限是唯一的。
2. 有界性:如果函数f(x)当x趋于a的时候极限存在,那么函数f(x)在x趋于a的邻域内有界。
3. 保序性:如果函数f(x)和g(x)当x趋于a的时候极限存在,且有f(x)≤g(x),那么极限也有lim(x→a)f(x)≤lim(x→a)g(x)。
4. 乘法性:如果函数f(x)和g(x)当x趋于a的时候极限存在,那么函数f(x)g(x)当x趋于a 的时候极限也存在,且有lim(x→a)f(x)g(x)=lim(x→a)f(x)·lim(x→a)g(x)。
5. 加法性:如果函数f(x)和g(x)当x趋于a的时候极限存在,那么函数f(x)+g(x)当x趋于a的时候极限也存在,且有lim(x→a)(f(x)+g(x))=lim(x→a)f(x)+lim(x→a)g(x)。
高中微积分第二讲(函数的极限)
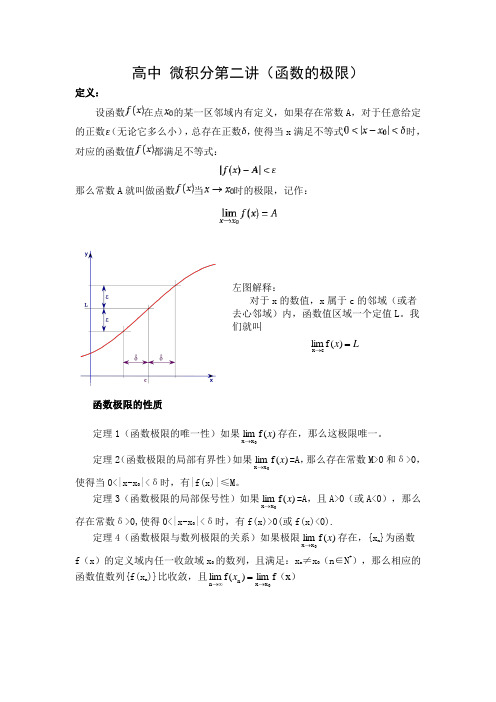
高中 微积分第二讲(函数的极限)定义:设函数在点的某一区邻域内有定义,如果存在常数A ,对于任意给定的正数(无论它多么小),总存在正数,使得当x 满足不等式时,对应的函数值都满足不等式:那么常数A 就叫做函数当时的极限,记作:左图解释:对于x 的数值,x 属于c 的邻域(或者去心邻域)内,函数值区域一个定值L 。
我们就叫L x =→)(f lim cx函数极限的性质定理1(函数极限的唯一性)如果)(f lim 0x x x →存在,那么这极限唯一。
定理2(函数极限的局部有界性)如果)(f lim 0x x x →=A ,那么存在常数M>0和δ>0,使得当0<|x-x 0|<δ时,有|f(x)|≤M 。
定理3(函数极限的局部保号性)如果)(f lim 0x x x →=A ,且A>0(或A<0),那么存在常数δ>0,使得0<|x-x 0|<δ时,有f(x)>0(或f(x)<0).定理4(函数极限与数列极限的关系)如果极限)(f lim 0x x x →存在,{x n }为函数f (x )的定义域内任一收敛域x 0的数列,且满足:x n ≠x 0(n ∈N +),那么相应的函数值数列{f(x n )}比收敛,且)(x f lim )(f lim 0x x n n →∞→=x函数极限的求法: 一、利用函数连续性:(即直接将趋向值带入函数自变量中,此时要要求分母不能为0)练习:求下列极限的值:1、)(1-x 3lim 3x →2、)(3x 2lim 4x +→3、6x 23x lim 5x -+→二、恒等变形 当分母等于零时,就不能将趋向值直接代入分母,可以通过下面几个小方法解决: ①因式分解,通过约分使分母不会为零例如:2-x 4-lim x 22x →三、采用洛必达法则求极限洛必达法则是分式求极限的一种很好的方法,当遇到分式0/0或者∞/∞时可以采用洛必达,其他形式也可以通过变换成此形式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
