5-1反比例函数
反比例函数知识点及举例

反比例函数知识梳理知识点l. 反比例函数的概念重点:掌握反比例函数的概念 难点:理解反比例函数的概念一般地,如果两个变量x 、y 之间的关系可以表示成xk y =或y=kx -1(k 为常数,0k ≠)的形式,那么称y 是x 的反比例函数。
反比例函数的概念需注意以下几点:(1)k 是常数,且k 不为零;(2)x k中分母x 的指数为1,如22y x=不是反比例函数。
(3)自变量x 的取值范围是0x ≠一切实数.(4)自变量y 的取值范围是0y ≠一切实数。
知识点2. 反比例函数的图象及性质重点:掌握反比例函数的图象及性质 难点:反比例函数的图象及性质的运用反比例函数xky =的图象是双曲线,它有两个分支,这两个分支分别位于第一、三象限或第二、四象限。
它们关于原点对称、反比例函数的图象与x 轴、y 轴都没有交点,即双曲线的两个分支无限接近坐标轴,但永远不与坐标轴相交。
画反比例函数的图象时要注意的问题: (1)画反比例函数图象的方法是描点法;(2)画反比例函数图象要注意自变量的取值范围是0x ≠,因此不能把两个分支连接起来。
(3)由于在反比例函数中,x 和y 的值都不能为0,所以画出的双曲线的两个分支要分别体现出无限的接近坐标轴,但永远不能达到x 轴和y 轴的变化趋势。
反比例函数的性质xky =)0k (≠的变形形式为k xy =(常数)所以: (1)其图象的位置是:当0k >时,x 、y 同号,图象在第一、三象限; 当0k <时,x 、y 异号,图象在第二、四象限。
(2)若点(m,n)在反比例函数xky =的图象上,则点(-m,-n )也在此图象上,故反比例函数的图象关于原点对称。
(3)当0k >时,在每个象限内,y 随x 的增大而减小; 当0k <时,在每个象限内,y 随x 的增大而增大; 知识点3. 反比例函数解析式的确定。
重点:掌握反比例函数解析式的确定 难点:由条件来确定反比例函数解析式(1)反比例函数关系式的确定方法:待定系数法,由于在反比例函数关系式xky =中,只有一个待定系数k ,确定了k 的值,也就确定了反比例函数,因此只需给出一组x 、y 的对应值或图象上点的坐标,代入xky =中即可求出k 的值,从而确定反比例函数的关系式。
九年级数学-反比例函数

第19讲 反比例函数知识导航1.反比例函数的定义和解析式;2.反比例函数的图象和性质;3.反比例面数与方程及不等式;4.反比例函教与神奇的几何性质;5.反比例函数与直线y =a 或x =a ;6.反比例函数与全等相似;7.反比例函数与图形变换;8.反比例函数与定值及最值。
【板块一】反比例函数的定义和解析式 方法技巧 根据定义解题1.定义:一般地,形如ky x=(k 为常数,k ≠0)的函数,叫做反比例函数,其中x 是自变量,y 是函数.自变量x 的取值范围是不等于0的一切实数.2.解析式:ky x=(k ≠0)或xy =k (k ≠0)或1y kx -= (k ≠0). 题型一根据定义判断反比例函数【例1】下列函数:①2x y =;@2y x =;③y =12y x =;⑤12y x =+;⑥12y x =- ;⑦2xy =; ⑧12y x -=;⑨22y x = .其中y 是x 的反比例函数的有 (填序号).【解析】②③④⑦⑧.题型二根据定义确定k 值或解析式 【例2】(1)反比例函数32y x =- ,化为ky x=的形式,相应的k = ; (2)函数ky x =中,当x =2时,y =3,则函数的解析式为 【解析】(1)32- ;(2)6y x=.题型三根据定义确定待定系数的值【例3】(1)如果函数2+1m y x = 是关于x 的反比例函数,则m 的值为 (2)若函数()252m y m x -=+ (m 为常数)是关于x 的反比例函数,求m 的值及函数的解析式。
【解析】(1)-1;(2)m =2,y =4x .针对练习11.下列函数中,为反比例函数的是(B )A . 3x y =B . 13y x =C . 13y x =-D .21y x=答案:B2.反比例函数y =一化为ky x=的形式后,相应的k =答案: 3.若关于x 的函数()2274mm y m x --=- 是反比例函数,求m 的值答案:3.【板块二】反比例函数的图象和性质 式抓住反比例函数的性质并结合图象解题 一般地,对于反比例函数()0ky k x=≠,由函数图象,并结合解析式,我们可以发现: 1.图象分布当k >0时,x ,y (同号或异号),函数图象为第 象限的两支曲线;当k <0时,x ,y (同号或异号),函数图象为第 象限的两支曲线。
北师大版九年级数学上册第六章《反比例函数》

探究一:初步了解反比例函数的形式,探究反比例函数
1.游泳池体积150(立方米),那么底面积s(平方米)和 高h(米)之间的关系式为:h=___1_5__0_____.
s
2.京沪高速铁路全长约为1318km,列车沿京沪高速铁路 从上海驶往北京,列车行完全程所需的时间t(h)与行驶
说一说
你能举出生活中反比例函 数的例子吗?
基础练习
1.下列函数表达式中,x表示自变量,哪些是反 比例函数?若是,请指出相应的k值。
(1)y = 0.4(2) y =5-x (3) y = 3x1
x
(4)xy = - 2(5)y =
x 2
(6) y =
1 6x
2. y是x的反比例函数,下图给出了x与 y的一些值:
x -5 -2 -1
y
2
5
12
① 求出这个反比例函Hale Waihona Puke 的表达式;2 77
② 根据函数表达式完成上表。
解: 1设y k k 0
x
当x -1, y -2时,k -1 2 -2
y 2 x
互动课堂
问题1:
若
y n6 x
是反比例函数,则n应
满足的条件是n 6.
问题2: 已知y是x的反比例函数,当x=2 时,y=5求:当x=1时,y的值.
北师大版九年级数学上册
第六章 反比例函数 6.1 反比例函数
函数的定义
一般地.在某个变化过程中,有两个变量x和y, 如果给定一个x的值,相应地y就有唯一确定的 值和它相对应,那么我们称y是x的函数,其中x 叫自变量,y叫因变量.
回顾与思考
如果y=kx+b(k、b为常数,k≠0),那么y 是x的一次函数.
05-(五)反比例函数九年级上册数学冀教版

2.一题多解[2023广西中考]如图,过的图像上点,分别作轴、 轴的平行线交的图像于, 两点,以,为邻边的矩形 被坐标轴分割成四个小矩形,面积分别记为,,, . 若,则 的值为( )
C
A.4 B.3 C.2 ቤተ መጻሕፍቲ ባይዱ.1
【解析】 解法一设.在中,令,得;令 ,得.,,,, ,.,, .解法二根据反比例函数中 的几何意义,得,.,, .
【解析】 矩形的顶点,,的坐标分别为, ,,, 可设平移后点,的对应点, 的坐标分别为,.当点落在函数 的图像上时,可得,解得;当点落在函数 的图像上时,可得,解得 若平移后的矩形与函数 的图像有公共点,则的取值范围是 .
6.[2023石家庄四十二中一模]如图,平面直角坐标系中,反比例函数 与一次函数的图像交于 , 两点.
第3题图
3.跨学科·物理[2023温州中考]在温度不变的条件下,通过一次又一次地对汽缸顶部的活塞加压,加压后气体对汽缸壁所产生的压强 与汽缸内气体的体积成反比例,关于 的函数图像如图所示.若压强由加压到 ,则气体体积压缩了____ .
20
【解析】 设关于的函数表达式为. 当时, ,,.当时, ;当时,, 气体体积压缩了 .
(1)求反比例函数与一次函数的表达式;
解:把代入,得 , 反比例函数的表达式为 .把代入,得 .把,分别代入 ,得解得 一次函数的表达式为 .
(2)直接写出 的解集;
解:由题图可知的解集为或 .
(3)已知直线与轴交于点,点是轴上一动点,作 轴交反比例函数图像于点,当以,,, 为顶点的四边形的面积等于2时,求 的值.
4.新趋势·结论开放[2023日照中考]已知反比例函数 且的图像与一次函数 的图像共有两个交点,且两交点横坐标的乘积,请写出一个满足条件的 值:_____________________________________________.
反比例函数知识点总结,比例系数k的几何意义和七大常考模型
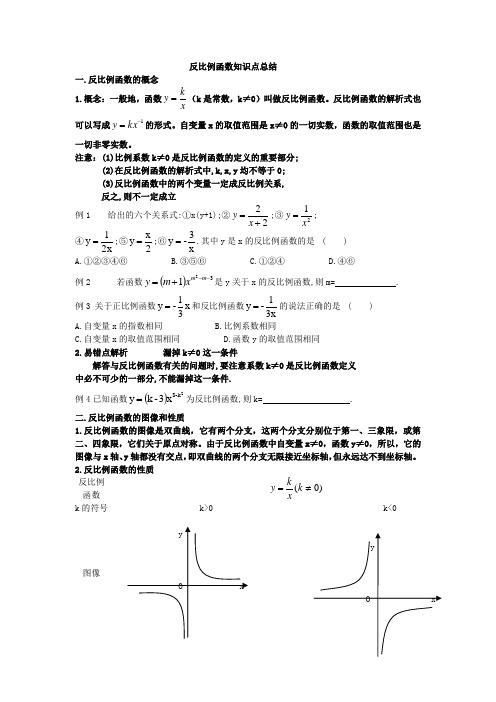
反比例函数知识点总结一.反比例函数的概念1.概念:一般地,函数x k y =(k 是常数,k ≠0)叫做反比例函数。
反比例函数的解析式也可以写成1-=kx y 的形式。
自变量x 的取值范围是x ≠0的一切实数,函数的取值范围也是一切非零实数。
注意:(1)比例系数k ≠0是反比例函数的定义的重要部分;(2)在反比例函数的解析式中,k,x,y 均不等于0;(3)反比例函数中的两个变量一定成反比例关系,反之,则不一定成立例1 给出的六个关系式:①x(y+1);②22+=x y ;③21x y =; ④x 21y =;⑤2x y =;⑥x3-y =.其中y 是x 的反比例函数的是 ( ) A.①②③④⑥ B.③⑤⑥ C.①②④ D.④⑥ 例2 若函数()321--+=m m x m y 是y 关于x 的反比例函数,则m= .例3 关于正比例函数x 31-y =和反比例函数x31-y =的说法正确的是 ( ) A.自变量x 的指数相同 B.比例系数相同C.自变量x 的取值范围相同D.函数y 的取值范围相同2.易错点解析 漏掉k ≠0这一条件解答与反比例函数有关的问题时,要注意系数k ≠0是反比例函数定义中必不可少的一部分,不能漏掉这一条件.例4已知函数()2k -8x 3-k y =为反比例函数,则k= .二.反比例函数的图像和性质1.反比例函数的图像是双曲线,它有两个分支,这两个分支分别位于第一、三象限,或第二、四象限,它们关于原点对称。
由于反比例函数中自变量x ≠0,函数y ≠0,所以,它的图像与x 轴、y 轴都没有交点,即双曲线的两个分支无限接近坐标轴,但永远达不到坐标轴。
2.反比例函数的性质反比例函数 )0(≠=k xk y k 的符号 k>0 k<0图像性质 ①x 的取值范围是x ≠0, y 的取值范围是y ≠0; ②当k>0时,函数图像的两个分支分别 在第一、三象限。
在每个象限内,y 随x 的增大而减小。
反比例函数的图像和性质ppt课件

7、若点(-2,y1)、(-1,y2)、(2,y3)在
反比例函数 y = - 1 0 0 的图象上,则(
xቤተ መጻሕፍቲ ባይዱ
B
)
A、y1>y2>y3 C、y3>y1>y2
B、y2>y1>y3 D、y3>y2>y1
资金是运动的价值,资金的价值是随 时间变 化而变 化的, 是时间 的函数 ,随时 间的推 移而增 值,其 增值的 这部分 资金就 是原有 资金的 时间价 值
已知点A(2,y1), B(5,y2)C是(反-3比,y例3)函是数y 象上的两点.请比较y1,y2的,y大3的小大.小.
4 x
图
y
⑴代入求值
y1 A B
-3 y2 O2 5
C y3
⑵利用增减性
⑶根据图象判断
x
资金是运动的价值,资金的价值是随 时间变 化而变 化的, 是时间 的函数 ,随时 间的推 移而增 值,其 增值的 这部分 资金就 是原有 资金的 时间价 值
1、反比例函数y= - 5 的图象大致是( D )
y
x
y
A:
o
x
B:
o
x
y
C:
o
x
D:
y
o x
资金是运动的价值,资金的价值是随 时间变 化而变 化的, 是时间 的函数 ,随时 间的推 移而增 值,其 增值的 这部分 资金就 是原有 资金的 时间价 值
2、我校食堂有5吨煤,用y表示可以用的天数
,用x表示每天的烧煤量,则y关于x的函数的
10
1、这几个函数图象有 8 什么共同点?
2、函数图象分别位于 6 哪几个象限?
4
3、y随的x变化有怎
反比例函数小结
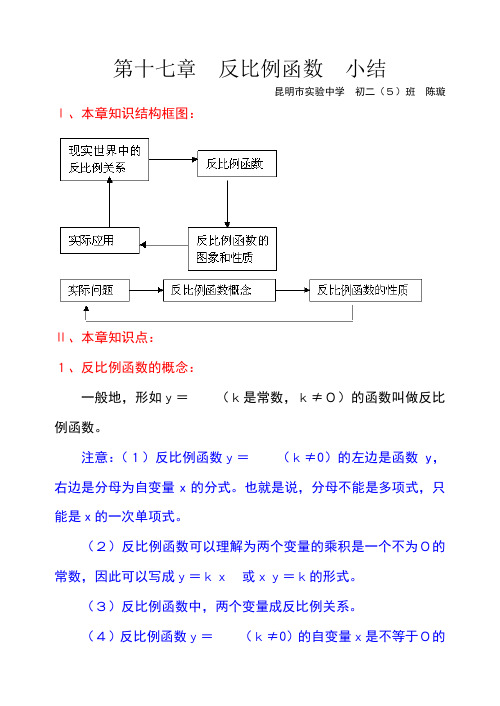
第十七章反比例函数小结昆明市实验中学初二(5)班陈璇Ⅰ、本章知识结构框图:Ⅱ、本章知识点:1、反比例函数的概念:一般地,形如y=(k是常数,k≠0)的函数叫做反比例函数。
注意:(1)反比例函数y=(k≠0)的左边是函数y,右边是分母为自变量x的分式。
也就是说,分母不能是多项式,只能是x的一次单项式。
(2)反比例函数可以理解为两个变量的乘积是一个不为0的常数,因此可以写成y=kx或xy=k的形式。
(3)反比例函数中,两个变量成反比例关系。
(4)反比例函数y=(k≠0)的自变量x是不等于0的任意实数。
2、反比例函数的图象:反比例函数y=(k≠0)的图象是双曲线。
注意:(1)反比例函数的图象是双曲线,它有两个分支,它的两个分支时断开的。
(2)当k>0时,两个分支位于第一、三象限;当k<0时,两个分支位于第二、四象限。
(3)反比例函数y=(k≠0)的图象的两个分支关于原点对称。
(4)反比例函数的图象与x轴、y轴都没有交点,即双曲线的两个分支无限接近坐标轴,但永远不与坐标轴相交,这是因为x≠0,y≠0。
3、反比例函数解析式的确定:因为反比例函数的解析式y=(k≠0)中,只有一个系数k,确定了k的值,也就确定了反比例函数,因此只需给出一组x、y的对应值或图象上一点的坐标,利用待定系数法,即可确定反比例函数的解析式。
4、反比例函数的性质:反比例函数的性质与k的符号有关,反比例函数的性质如下表所示:注意:(1)反比例函数图象的位置和函数的增减性,都是由比例系数k的符号决定的。
反过来,有双曲线所在的位置或函数的增减性,也可以判断出k的符号。
(2)反比例函数的增减性,只能在每个象限内讨论;当k>0时,在每一象限(第一、三象限)y随x的增大而减小,但不能笼统地说:当k>0时,y随x的增大而减小,同样,当k<0时,在每一象限(第二、四象限)y随x的增大而增大,也不能笼统地说:当k<0时,y随x的增大而增大。
5、反比例函数y=(k≠0)中比例系数k的几何意义:反比例函数中比例系数k的几何意义:如图所示,过双曲线上任意一点P作x轴、y轴的垂涎PN、PM,所得矩形PMON的面积S=PM·PN=︱x︱·︱y︱=︱xy︱=︱k︱。
反比例函数图象及性质

2x
2x
4x
800x
3、下列反比例函数图像的一个分支,在第三象限的是( B )
3
21k3(A) y (B)y (C) y (D) y
x
x
x
x
4、函数 y 1 a2 的图象在第 二、四 象限.
x
例题讲解
2 例1:在反比例函数 y x 的图象上有两点(x1,y1)、
(x2,y2),若x1>x2 ,则y1>y2吗?
x 当k>0时,双曲线的两支分别位于第一、第三象限, 在每个 象限内y值随x值的增大而减小.
当k<0时,双曲线的两支分别位于第二、第四象限, 在每个 象限内y值随x值的增大而增大.
y
6
y=
6 x
5 4
3
2
1
-6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 x
-1
-2 -3
-4 -5
-6
观察y 6 和y 6 的图象
x
x
发现函数值y怎样随着自变量x的变化而变化?
1、在每一个象限内 2、在整个自变量的取值范围内
如图xB< xA 但yB< yA
y
6
6
5
y x
4
· 3
A
y
· C 6
6
5
y
x
4
3
2
2
xB
1
x -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 x
-1
A
· -2
B
-3
-4 -5
1
-6 -5 -4 -3 -2 -1 0 1 2
3
-1
-2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
k y=— x
y kx
( k是不等于零的常数). ( k是不等于零的常数).
1
形式4: x y= k (k≠0)
形式5: ቤተ መጻሕፍቲ ባይዱ量 y 与 x 成反比例,比例系数为k(k≠0)
课外练习
( ( ( ( ( (
判断下列说法是否正确(对”√”, 错”×”)
)(1)一矩形的面积为 cm2 , 相邻的两条边长分别为 (cm)和y (cm), 20 x 则变量y是变量x的反比例函数 . )(2)圆的面积公式s r 2中,s与r成正比例 . )(3)矩形的长为a,宽为b,周长为C,当C为常量时, a是b的反比例函数 . )(4)一个正四棱柱的底面正 方形的边长为x,高为y, 当其体积V为常量时,y是x的反比例函数 . )(6)当被除数(不为零)一 定时,商和除数成反比 . 例 )(8)计划修建铁路 1200km, 则铺轨天数y (d )是每日铺轨量 x(km / d )的反比例函数 .
k y ( k为常数, k 0) x
练 习 1
1 、在下列函数中,y是x的反比例函数的是( C ) 2 8 (A)y = (B)y = 2 + 7 x X+5 (C)x y = 5
3 (D)y = x
练 习 2
2.已知函数 y = xm-7 是正比例函数,
8 则 m = ___
;
1 x x
函
数
一般地.在某个变化过程中,有两个变量x和
y,对于变量x的每一个值,变量y都有唯一确
定的值和它对应,那么我们就把x叫自变量,
y叫因变量,称y是x的函数.
如:y=3x 函数的实质是两个变量之间的关系
ztbwxczhaofeng
观察与思考:
因为改变电阻就能控制电流的变化,电阻大则 舞台灯光可以在短时间内明暗交替变化, 瞬间就能 产生白天与黑夜的舞台效果,难道幕后调光师有“魔 电流小,灯光就较暗;反之,电阻小则电流大, 手”?其实他们的做法挺简单,就是通过改变电阻来 灯光就较亮。从而达到瞬间控制灯光明暗的效 达到想要的明暗效果。你能来解释其做法道理吗? 果。
课 外 练 习
在下列函数表达式中,x均为自变量,那么哪些是反 比例函数?每一个反比例函数相应的k的值是多少?
1 () y 1 x
1 (2) y - x
2 (4) y 3x
3 (5) y 2x
x (3) y 2
1 (6) y 2 x
0 .4 (7 ) y x
2 (8) y 5x
y的值都等于 ,求y与x之间的函数关系。 10
归纳总结
反比例函数的定义:一般地,如果变量x、y有关系
k y = — ( k是不等于零的常数),那么称变量x、y x k 成反比例,函数 y = — 叫做反比例函数。 x
反比例函数的五种不同的表现形式:
形式1: y 是 x 反比例函数。 形式2: 形式3:
x (2)y= 4
×
√
(4)- x y=3√ (6)y= 5x -1√
(5)3+xy2=0√
例2,已知:函数Y=(m+2)X 是反比例函数,求:m值
m²-2m-9
例题 3 已知变量y与x成反比例,且当x=2时,y=9.
(1)写出y与x之间的函数解析 k 解:因为 y与x成反比例,所以y= x (k≠o) 把x=2,y=9代入, 得k=2×9=18 , (2)当x=3.5时,求y的值. 18 36 1 解:当x=3.5时, y = = =5 3.5 7 7 (3)当y=5时,求x的值. 3 18 18 =3- 解:当y=5时,5= , X= X 5 5
是反比例函
数,则m = ___ . 0
②若函数
y (m 2) x
m 5
2
-2 是反比例函数,则m=_____.
作 业 1
已知变量y与x-5成反比例,且当x=2时,y=9. (1)写出y与x之间的函数解析式. (2)当x=8时,求y的值. (3)当y=5时,求x的值.
巩固与提高 2
已知y y1 y2,y1与x成正比例, y2与x成反比例,并且 2与x 3时, x
100 P ( S 0) S
例6.你吃过拉面吗?一体积面团做成拉面,面 条总 长度Y(m)是面条横截面积S (m㎡)的 反比例函数,若当面条横截面积S =4 m㎡时, 面条总长度Y=32m (1)你能求出Y与S的关系式吗?(2)当横截 面积S为1.6 m㎡时,你能求面条总长度吗?
反比例函数 与正比例函数 y kx(k为常数,k 0)
,这样的 做一做 已知一个矩形的面积是10cm²
矩形你能做出来吗? 1 长 x(cm) 10 宽 y(cm)
2.5 4
5 2
10cm² 10cm² 10cm²
问: 长 ( X )与宽( y )之 间存在怎样的关系?
设矩形的一边长为x cm,另一边长为y cm。
xy 10( 定值 ), 10 y ( x 0). x
1 (9) s 2 x
1 (10) z x
(13) y 5 x
(11) y 3x
1 (12 ) xy 3
2a (14) y (a为常数, a 0) x
同 学 们 再 见 !
18 ∴ y与x之间的函数关系式是 y= X
想一想:
如果变量z与y成正比例,y与x成反比例, 那么z与x成正比例还是反比例?为什么?
解:∵ z与y成正比例, y与x成反比例
k2 ∴可设z=k1y, y= x ,(其中k1、k2为常数) k2 k1k2 ∴z=k1· x = x
例4.已知:Y=Y1+Y2 ,Y1与X-1 成正比例,Y2与X反比例,且当 X=1时,Y=2:当X=2时,Y=4, 求:Y与X 之间函数关系式
它们有何共同特点?
反比例函数的定义:
k 一般地,形如 y x (k是常数,k 0 )
的函数叫做反比例函数.
其中k叫反比例系数.
(也可以用y = kx-1或者XY=K表示)
例题 1 判断下列函数表达式中,表示反比例函
数的是哪几个?如果是,反比例系数k是多少?
1 (1)y= 2x √
3 (3)y= 4x
60 m (0 n 7的整数) n
观察思考 10 变量y与x之间的关系: y= x :
5 变量t与v之间的关系: t (v 0) v 2 变量a与b之间的关系: a (b 0) b 60 变量m与n之间的关系: m (0 n 7的整数) n
220 变量I与R之间的关系: I R
. 例题 5 写出下列函数的解析式,并判断它们是不
是反比例函数,如果是,写出自变量的取值范围.
⑴一个圆柱形钢材的体积是800cm3,写出它的 底面积和高的函数关系. 800 S ( h 0) h ⑵压强大小是由单位面积所受到的压力决定的, 那么当物体受到的垂直压力为100牛时,写出压 强与受力面积的函数关系.
生活中的数学
1.小红家到学校的路程有5km,她上学所用的时间t(h)与 速度v(km/h)的函数; 5
t
v
( v 0)
2.有一个矩形面积是2m2,它的长a(m)是宽b(m)的函数; 2 a (b 0) b 3.十一放七天假,老师布置要记忆60个单词。设小明 完成的天数为n,每天的单词量为m,写出m与n的函数 关系式.
我们知道,电流I、电阻R、电压U之间满 足关系式 U=IR 当电压U=220V时 220 . (1)你能用含R的代数式表示I吗? I= (2)利用写出的关系式完成下表:
R/Ώ 20 40 60 80 100
R
I/A
11
1 5 2
2 3 3
3 2 4
1 2 5
(3)当R越来越大时,I怎样变化?当R越来越小呢? (4) 变量I是R的函数吗?
1
3.已知函数 y = 3x m-7是反比例函数,
6 则 m = ___ .
练 习 3
2x+1 ①已知y与x成反比例, 并且当x=3时,y=7, 21 y= x 求y与x的函数关系式. ②已知y与x2成反比例,并且当x=3时,y=4, 求x=1.5时,y的值. y=16
巩固与提高1 ①若函数
m2-1 y=2x
