耐克函数创作说明
高三一轮复习资料-Nike函数的图象和性质

专题:Nike 函数的图象和性质【复习要求】1、掌握耐克函数的图像与性质;2、会用耐克函数处理函数最值等问题;3、会解含参数的耐克函数的最值问题【知识板块】函数xx y 1+=你还记得吗?我们都研究了这个函数的哪些性质? (1) 定义域是____________ (2) 值域是____________ (3) 奇偶性是___________ (4) 单调性是___________ (5) 最值是_____________函数()0>+=a xax y 你还记得吗?我们都研究了这个函数的哪些性质?请画出图像再回答: (6) 定义域是___________(7) 值域是___________ (8) 奇偶性是___________ (9) 单调性是___________ (10) 最值是_____________ 思考:()0<+=a xax y 时,函数的以上性质有哪些变化?Oxyxy =xx y =+a【例题板块】【例题】求函数xx y 32+=的单调区间,并用函数单调性定义证明之。
● 函数xx y 94+=,]5,3[∈x 的最大、最小值?【例题】)21(12224)(2->+++=x x x x x f 的值域.● 已知0t >,求函数241t t y t-+=的最小值为.● 求)1(21)(2>++-=x x x x x f 的值域。
● 求函数4522++=x x y 的值域【例题】若,,3,x y R xy y +∈+=求x y +的最小值是;● 若,,2x y R x y xy +∈++=求x y +的最小值是;【例题】已知函数()2af x x x=+的定义域为(]0,2(a 为常数). (1)证明:当8a ≥时,函数()y f x =在定义域上是减函数;(2)求函数()y f x =在定义域上的最大值及最小值,并求出函数取最值时x 的值.● 已知]2,1[,3)(∈-+=x xbx x f (1) 2=b 时,求)(x f 的值域;(2) 2≥b 时,)(x f 的最大值为M ,最小值为m ,且满足:4≥-m M ,求b 的取值范围.● 已知函数xax y +=有如下性质:如果常数0>a ,那么该函数在],0(a 上是减函数,在),[+∞a 上是增函数.(1)如果函数)0(,3>+=x xx y m的值域是),6[+∞,求实数m 的值; (2)求函数)(x f =2x +2x a(0>a ) 在]2,1[∈x 上的最小值)(a g 的表达式.● 已知函数xax y +=有如下性质:如果常数a >0,那么该函数在(0,a ]上是减函数,在[a ,+∞)上是增函数.(1)如果函数y =x +x b2(x >0)的值域为[6,+∞),求b 的值;(2)研究函数y =2x +2x c (常数c >0)在定义域内的单调性,并说明理由;(3)对函数y =x +x a 和y =2x +2xa (常数a >0)作出推广,使它们都是你所推广的函数的特例.研究推广后的函数的单调性(只须写出结论,不必证明),并求函数)(x F =n x x )1(2++nx x)1(2+(n是正整数)在区间[21,2]上的最大值和最小值(可利用你的研究结论).● (10奉贤一模)设()x m x x h +=,⎥⎦⎤⎢⎣⎡∈5,41x , 其中m 是不等于零的常数, (1)写出()x h 4的定义域; (2)求()x h 的单调递增区间;(3)已知函数()f x ([,])x a b ∈,定义:1()min{()|}f x f t a t x =≤≤([,])x a b ∈,2()max{()|}f x f t a t x =≤≤([,])x a b ∈.其中,min{()|}f x x D ∈表示函数()f x 在D 上的最小值,max{()|}f x x D ∈表示函数()f x 在D 上的最大值.例如:()cos f x x =,[0,]x π∈,则1()c o s ,[0,]f x xx π=∈ ,2()1,[0,]f x x π=∈ ,当1=m 时,设()()()()()2424x h x h x h x h x M -++=,不等式()()n x M x M t ≤-≤21【例题】若方程0122=+-ax x 在),3[+∞有解,求实数a 的取值范围.● 已知函数1()2x f x +=定义在R 上.(1)若存在x ,使得()()f x f x a +-=成立,求实数a 的取值范围;(2)若()f x 可以表示为一个偶函数()g x 与一个奇函数()h x 之和,设()h x t =,2()(2)2()1()p t g x mh x m m m =++--∈R ,求出()p t 的解析式;(3)若对任意[1,2]x ∈都有2()1p t m m ≥--成立,求实数m 的取值范围.【例题】某学校要建造一个面积为10000平方米的运动场。
耐克函数的研究成果(对号函数)

课题研究——对于“耐克函数”的研究经过小组研究,现发现形如xb ax y +=(a>0,b>0) 的函数有如下的特点:即x=1时最小值为2.当给出的定义域区间不包括耐克函数的顶点时,求最值应该利用耐克函数的单调性来解。
如下面这个例子 例.求函数324222++++=x x x x y 的最小值。
解:令322++=x x t ,则22)1(2≥++=x ttt tt y 112+=+=根据对号函数tt y 1+=在(1,+∞)上是增函数及t 的取值范围,当2=t 时y有最小值223。
此时x=-1.此题是一道求最值的问题,由于t ≥2,所以不能用均值不等式t+t1≥2来解,所以用耐克函数的单调性来解比较简易。
例 已知函数],1[,2)(2+∞∈++=x xax x x f 。
(1) 当21=a 时,求函数)(x f 的最小值:Oxyxy =221解:(1)2)(21++=xx x f设xx x g 21)(+= [)+∞∈,1x ,其图象如图所示, 在[)+∞,1上是增函数,当1=x 时,23)(m in =x g27)(m in =x f面对这个函数 f(x)=ax+b/x , 我们应该想得更多,需要我们深入探究:(1)它的单调性与奇偶性有何应用?而值域问题恰好与单调性密切相关,所以命题者首先想到的问题应该与值域有关;(2)函数与方程之间有密切的联系,所以命题者自然也会想到函数与方程思想的运用;(3)众所周知,双曲线中存在很多定值问题,所以很容易就想到定值的存在性问题。
因此就由特殊引出了一般结论;继续拓展下去,用所猜想、探索的结果来解决较为复杂的函数最值问题。
对勾函数

对勾函数是一种类似于反比例函数的一般双曲函数,是形如f(x)=ax+b/x(a>0)的函数。
中文名对勾函数别称耐克函数、双勾函数、对号函数、双飞燕函数表达式f(x)=ax+b/x (a>0)1定义定义所谓的对勾函数(双曲函数),是形如(a>0)的函数。
名称由图像得名,又被称为“双勾函数”、“勾函数”、"对号函数"、“双飞燕函数”等。
也被形象称为“耐克函数”或“耐克曲线”。
2性质图像对勾函数是数学中一种常见而又特殊的函数,见图示,在作图时最好画出渐近线最值当x>0时,有最小值(这里为了研究方便,规定a>0,b>0),也就是当时,f(x)取最小值。
奇偶性、单调性奇偶性双勾函数是奇函数。
单调性令k=,那么:增区间:{x|x≤-k}和{x|x≥k};减区间:{x|-k≤x<0}和{x|0<x≤k}变化趋势:在y轴左边先增后减,在y轴右边先减后增,是两个勾。
渐近线对勾函数的图像是分别以y轴和y=ax为渐近线的两支曲线,且图像上任意一对勾函数点到两条渐近线的距离之积恰为渐近线夹角(0-180°)的正弦值与|b|的乘积。
3对勾函数最小值与均值不等式对勾函数性质的研究离不开均值不等式。
说到均值不等式,其实也是根据二次函数得来的。
我们都知道展开,得,即两边同时加上2ab,整理得,两边开平方,就得到了均值定理的公式:将中看做a,看做b代入上式,得这里有个规定:当且仅当ax=b/x时取到最小值,解出x=sqrt(b/a),对应的f(x)=2sqrt(ab)。
我们再来看看均值不等式,它也可以写成这样:(a+b)/2≥sqrt(ab),前式大家都知道,是求平均数的公式。
那么后面的式子呢?也是平均数的公式,但不同的是,前面的称为算术平均数,而后面的则称为几何平均数,总结一下就是算术平均数绝对不会小于几何平均数。
4导数求解其实用导数也可以研究对勾函数的性质。
“耐 克” 函数及其性质

x
x
x
f (x) 2 综上知,函数 f (x) 的值域为(-∞,-2]∪[2,+∞).
(5)单调性:由于奇函数在对称区间上的单调性相同,故只研究当 x﹥0 时的单调性:
1
1)定义法:任取 x1, x2 0, 且 x1 x2 则令
A
f
(x2 )
f
x1
x2
1 x2
x1
20 当 0 x1 x2 1 时, x2 x1 1,此时 A 0 .
由上可知,函数在 (0,1)上单调递减,在[1,+∞)上单调递增.又由函数在对称区间上单调性相同知,f(x) 在(-∞,-1]上单调递增,在(-1,0)上单调递减.
2)导数法: f (x) x 1 x
f
' ( x)
1
1 x2
2) 当
n为 奇 数 时 , 当
x0时 ,
axn
0,
b xn
0,
则
利
用
均
值
不
等
式
,
3
f (x) axn b 2 axn b 2 ab 当且仅当 axn b 即 x 2n b 时等号成立,
xn
xn
xn
a
故 f (x) 2 ab 又当 n 为奇数时 f (x) 为奇函数,而奇函数在对称区间上的值域相反,所以当 x 0
则当
x
,
1
1,
时,
f
' ( x)
1
1 x2
0
当
x 1, 0 0,1 时,
f
' ( x)
1
1 x2
0 ,故函数在(-∞,-1)和[1,+∞)上
耐克函数
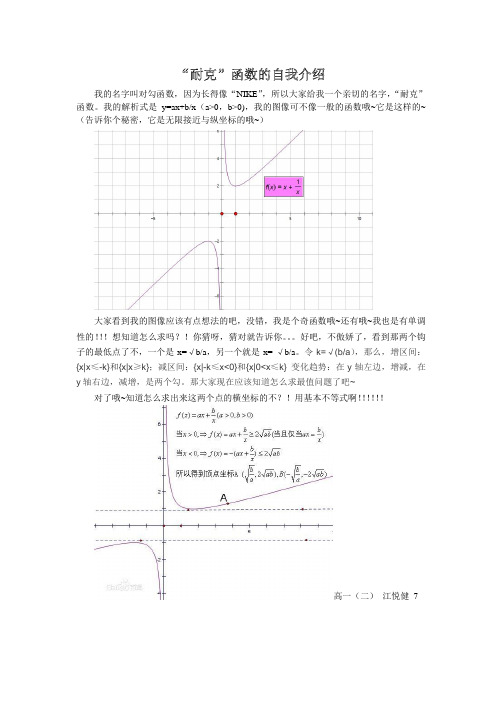
我的名字叫对勾函数,因为长得像“NIKE”,所以大家给我一个亲切的名字,“耐克”函数。
我的解析式是y=ax+b/x(a>0,b>0),我的图像可不像一般的函数哦~它是这样的~(告诉你个秘密,它是无限接近与纵坐标的哦~)
大家看到我的图像应该有点想法的吧,没错,我是个奇函数哦~还有哦~我也是有单调性的!!!想知道怎么求吗?!你猜呀,猜对就告诉你。
好吧,不傲娇了,看到那两个钩子的最低点了不,一个是x=√b/a,另一个就是x=-√b/a。
令k=√(b/a),那么,增区间:{x|x≤-k}和{x|x≥k};减区间:{x|-k≤x<0}和{x|0<x≤k} 变化趋势:在y轴左边,增减,在y轴右边,减增,是两个勾。
那大家现在应该知道怎么求最值问题了吧~ 对了哦~知道怎么求出来这两个点的横坐标的不?!用基本不等式啊!!!!!!
高一(二)江悦健7。
揭开“耐克”的面纱

22
4
旋转变换的公式为
X = xcosθ ysinθ= 2 x 2 y, 22
Y = xcosθ+ ysinθ= 2 x + 2 y. 22
由 XY = 1 得 x2 y2 = 1 . 22
下面我们回到“耐克”函数中来.
构造“双勾”函数 y = 3( x + 2 ) ( x ≠0) ,显然图 3x
象对称中心为 (0,0) ,
2 3)2
(x+2)2 +(
32 x+
3 +2
3)2
3x
3x
38
福建中学数学
2008 年第 12 期
=
2
23
( 3x +
2 3)2
3
x
2 (
2 3x +
3 +2
3) 2
3
x
= 2 3x + 2 3 2 3 2 3x + 2 3 + 2 3 = 4 3 ,
3
x
3
x
即 P ( x, 3 3
x+
2 3)到 x
构比较复杂,因而没有结出一般的旋转变换公式.
从上面的分析中,不难得出结论:函数 y = k x
( k ≠0、x ≠0) 和函数 y = ax + b (a b ≠0、x ≠0) 图象 x
本质上都是双曲线. 至此,我们揭开了“耐克”函数的本来面目.问题
的解决还进 一步启示我们 ,对于许多 熟悉的问题 , 加强思考和 反思,仍会有 许多收获. 只有养成思 考 的习惯,学 习的能力和思 维的本质才 会有本质的 突 破,正如华 罗庚先生所言 :不断积累 ,飞跃必来 , 突破随之.
双勾函数

则),就先用平移公式或我总结出的平移规律还原以后再研究,这个能力非常重
要,一定要多练,争取做到特别熟练的地步。
事实上,利用将对勾函数进行选择可以得到
标准的双曲线方程。也就是说,对勾
2006年高考上海数学试卷(理工农医类)已知函数 y=x+a/x 有如下性质:如果
常数a>0,那么该函数在 (0,√a] 上是减函数,在 ,[√a,+∞)上是增函数.
⑴如果函数 y=x+(2^b)/x (x>0)的值域为 [6,+∞),求b 的值;
⑵研究函数 y=x^2+c/x^2 (常数c >0)在定义域内的单调性,并说明理由;
当x<0,-x>0
f(x)=-(-x-1/x)
<=-2
当-x=-1/x取等。
x=-1,有最大值,没有最小值。
值域是:(负无穷,-2)并(2,正无穷)
--------------
证明函数f(x)=ax+b/x,(a>0,b>0)在x>0上的单调性
设x1,x2∈(0,+∝)且x1>x2
∴f(x1)-f(x2)<0,即x∈(0,√(b/a))时,f(x)=ax+b/x单调递减
∴ 当x∈(√(b/a),+∞)时,x1x2>b/a, 则ax1x2-b>b-b=0
∴f(x1)-f(x2)>0,即x∈(√(b/a),+∞)时,f(x)=ax+b/x单调递增。
高考数学第一轮复习 第16讲 耐克函数

第16讲耐克函数[基础篇]一、函数b y ax x =+(ab≠0)是奇函数:当a>0,b>0时,它的递减区间是(和)⎡⎣,递增区间是(),-∞⋃+∞当a>0,b<0时,它没有递减区间,递增区间是(),0-∞和()0,+∞二、求某些分式函数的最大(小)值:一般思路是先将其变形、换元成形如b y ax x=+(ab≠0)的函数,求其最值问题时,要注意均值不等式成立的3个条件;特别注意等号成立的条件,当等号不成立(即给定的区间内不存在使等号成立的自变量x)时,用函数单调性的方法解决。
三、如果函数解析式或给定区间的端点含有字母,注意是否需要分类讨论:四、换元后,注意求出新变量的取值范围:[技能篇]例题1、函数13y x x =+,1,24x ⎡⎤∈⎢⎥⎣⎦的值域为例题2、函数2y =的值域为例题3、函数1212log log x y x =+,(]1,3x ∈的值域为例题4、已知函数22()x x a f x x++=(x>0)(1)设12a =,分别求(]0,1x ∈,[]12,1x ∈,[)1,x ∈+∞时,函数()f x 的值域(2)设12a =,[),x m ∈+∞时,求函数()f x 的值域(3)对a R ∈,求[)1,x ∈+∞时,函数()f x 的值域[竞技篇]一、填空题:1、函数11y x x =+-(x>1)的值域为2、函数234x y x =+的值域为3、函数2225x y x x -=-+的值域为4、函数22331x x y x x ++=++,[]1,1x ∈-的值域为5、函数22122y x x =++的最小值为6、函数25122x x y x -+=-,[]4,8x ∈的值域为7、函数2y =(a>0)的最小值为。
8、已知2()f x x ax b =++,()()f x g x x=,若()g x 在(]0,2上是减函数,则b 的取值范围为二、解答题:9、已知函数()a f x x x =+的定义域为()0,+∞,且(2)22f =+,设点P 是函数图像上的任意一点,过点P 分别作直线y=x 和y 轴的垂线,垂足分别为M、N(1)求a 的值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《耐克函数》创作说明
函数是高中数学中的重要内容,函数的观点和方法贯穿整个高中数学的全过程。
对勾函数是数学中一种常见而又特殊的函数,近几年高考试题中,对勾函数部分占有相当大比重。
学生对对勾函数的掌握有一定的困难,这节课通过对勾函数性质的整体分析,结合图像,运用数形结合来研究对勾函数的性质。
这节课的设计主要考虑到以下几点:
1、文化性:
耐克NIKE这个名字,英文原意指希腊胜利女神。
在西方人的眼光里很是吉利,而且易读易记,能叫得很响。
耐克商标,图案是个小钩子,象征着希腊胜利女神翅膀的羽毛,代表着速度,同时也代表着动感和轻柔。
造型简洁有力,急如闪电,一看就让人想到速度和爆发力。
耐克函数由图像得名,又被称为“对勾函数”、“双勾函数”、“勾函数”、“对号函数”、“双飞燕函数”等。
因函数图像和耐克商标相似,也被形象称为“耐克函数”或“耐克曲线”,是形如f(x)=ax+b/x(a,b ≠0)的函数。
2、知识性:对勾函数与基本不等式的相关知识。
3、思想和方法:数形结合、转化思想、几何画板的应用
4、内容的独立性、完整性:把基本不等式和对勾函数的关键点巧妙结合。
