对勾函数最小值的公式
对勾函数绝对经典
对勾函数是一种类似于反比例函数的一般函数,形如f(x)=ax+ (接下来写作对勾函数f(x)二ax+二的图象与性质X繁华分享对勾函数是数学中一种常见而又特殊的函数。
它在高中教材上不出现,但考试总喜欢考的函数,所以也要注意它和了解它。
(一) 对勾函数的图像f(x)=ax+b/x )。
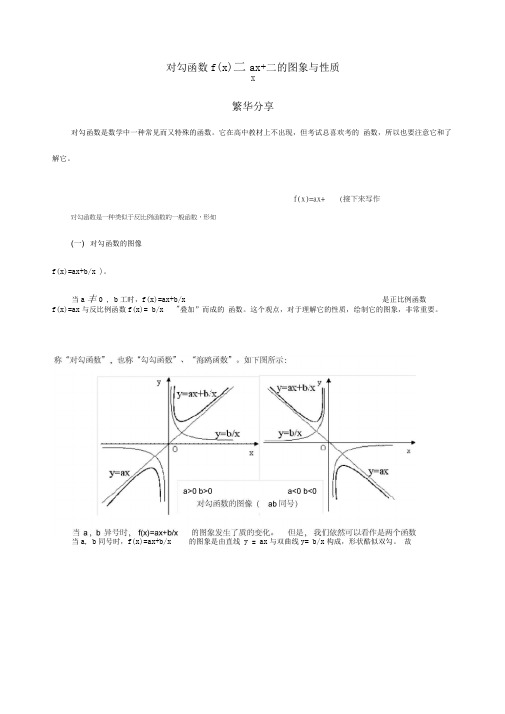
当a丰0 , b工时,f(x)=ax+b/x 是正比例函数f(x)=ax与反比例函数f(x)= b/x "叠加”而成的函数。
这个观点,对于理解它的性质,绘制它的图象,非常重要。
当a, b同号时,f(x)=ax+b/x 的图象是由直线y = ax与双曲线y= b/x构成,形状酷似双勾。
故加”而成。
(请自己在图上完成:他是如何叠加而成的。
ab异号)般地,我们认为对勾函数是反比例函数的一个延伸,即对勾函数也是双曲线的一种,只不过它的焦点和渐进线的位置有所改变罢了。
接下来,为了研究方便,我们规定a>0,b>0。
之后当a<0,b<0时,根据对称就很容易得出结论了。
(二)对勾函数的顶点对勾函数性质的研究离不开均值不等式。
利用均值不等式可以得到:当x>0时,g = 是2耐当且黯心扌时取等号),此时卞=卡。
当x<0时,f(£ = 3龙十g玉一2耳旺律且尽当= £时IR等号卜此时耳=-皆。
即对勾函数的定点坐标:ulr2,-2 vabA;(三)对勾函数的定义域、值域由(二)得到了对勾函数的顶点坐标,从而我们也就确定了对勾函数的定义域、值域等性质。
定义域:図£ = 0% 值域;{y|y >厶飯或v< -2VaS)(四)对勾函数的单调性对于函数f(x)= ax-1-单调增区间’fl U 卡卄);单调减2>(五)对勾函数的渐进线由图像我们不难得到:对于函它的渐进线有两離"Xiy = is;F =0;X(六)对勾函数的奇偶性对勾函数在定义域内是奇函数,利用对号函数以上性质,在解某些数学题时很简便,下面举例说明:1、求函数yx2 2x 4 .x22x 的最小值。
对勾函数讲解与例题解析
对勾函数对勾函数:数学中一种常见而又特殊的函数。
如图一、对勾函数f(x)=ax+错误!未找到引用源。
的图象与性质对勾函数是数学中一种常见而又特殊的函数。
它在高中教材上不出现,但考试总喜欢考的函数,所以也要注意它和了解它。
(一) 对勾函数的图像对勾函数是一种类似于反比例函数的一般函数,形如f(x)=ax+错误!未找到引用源。
(接下来写作f(x)=ax+b/x )。
当a≠0,b≠0时,f(x)=ax+b/x 是正比例函数f(x)=ax 与反比例函数f(x)= b/x “叠加”而成的函数。
这个观点,对于理解它的性质,绘制它的图象,非常重要。
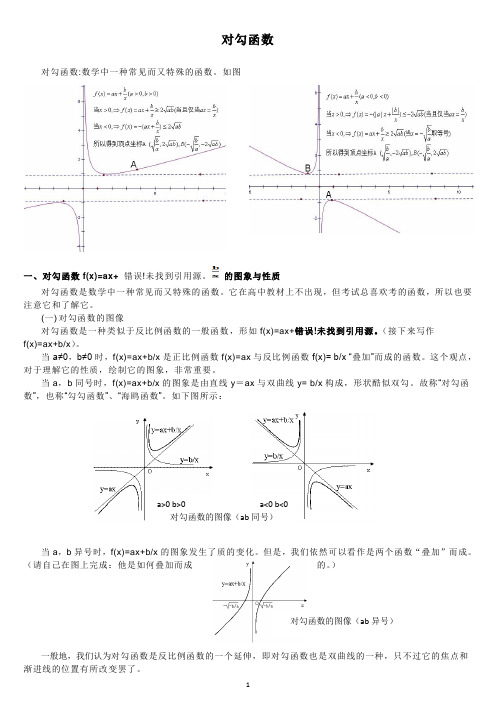
当a ,b 同号时,f(x)=ax+b/x 的图象是由直线y =ax 与双曲线y= b/x 构成,形状酷似双勾。
故称“对勾函数”,也称“勾勾函数”、“海鸥函数”。
如下图所示:当a ,b 异号时,f(x)=ax+b/x 的图象发生了质的变化。
但是,我们依然可以看作是两个函数“叠加”而成。
(请自己在图上完成:他是如何叠加而成的。
)一般地,我们认为对勾函数是反比例函数的一个延伸,即对勾函数也是双曲线的一种,只不过它的焦点和渐进线的位置有所改变罢了。
a>0 b>0 a<0 b<0 对勾函数的图像(ab 同号)对勾函数的图像(ab 异号)接下来,为了研究方便,我们规定a>0,b>0。
之后当a<0,b<0时,根据对称就很容易得出结论了。
(二) 对勾函数的顶点对勾函数性质的研究离不开均值不等式。
利用均值不等式可以得到:当x>0时,错误!未找到引用源。
当x<0时,错误!未找到引用源。
即对勾函数的定点坐标:(三) 对勾函数的定义域、值域由(二)得到了对勾函数的顶点坐标,从而我们也就确定了对勾函数的定义域、值域等性质。
(四) 对勾函数的单调性(五) 对勾函数的渐进线 由图像我们不难得到: (六)对勾函数的奇偶性 :对勾函数在定义域内是奇函数, 二、均值不等式(基本不等式) 对勾函数性质的研究离不开均值不等式。
对勾函数

对勾函数对勾函数,又称为符号函数,是一种常见的数学函数,其定义如下:$$f(x) = \begin{cases}1, & x>0 \\0, & x= 0 \\-1, & x<0 \\\end{cases}$$对勾函数是一个以0为界限,将实数轴分为三个区间的函数。
当$x>0$时,对勾函数的输出为1;当$x=0$时,对勾函数的输出为0;当$x<0$时,对勾函数的输出为-1。
对勾函数在数学和应用领域都有广泛的应用。
在数学上,它常被用来描述分段函数的行为或定义符号。
在实际应用中,对勾函数可以用来表示正负号、描述一些变化的特征等。
首先,让我们来看一下对勾函数的一些基本性质。
对勾函数是一个分段函数,其图像可以用一条竖直的线段来表示。
当$x>0$时,对勾函数的取值为1,表示正号;当$x=0$时,对勾函数的取值为0;当$x<0$时,对勾函数的取值为-1,表示负号。
这一特性使得对勾函数在描述正负关系时非常方便,例如在表示数轴上的正负数时,我们可以使用对勾函数。
其次,对勾函数还可以用来描述一些变化的特征。
在某些数学问题中,我们需要考虑某个变量的增减性或者是一个函数在不同区间的取值情况。
对勾函数可以帮助我们简洁地描述这些特征。
以$x$为自变量的函数$f(x)$为例,如果我们想要描述$f(x)$在不同区间的增减性,我们可以将$x$的取值范围分为多个区间,并在每个区间里使用对勾函数来表示该区间内$f(x)$的增减性。
这样一来,我们可以更加清晰地描述函数的特性。
此外,对勾函数在数学问题的解法中也有一定的应用。
在某些问题中,我们需要考虑多个条件的约束,而对勾函数可以帮助我们将这些条件转化为可计算的形式。
例如,在一些最优化问题中,我们希望找到一个变量的取值范围,在这个范围内函数取得最大或最小值。
这时,我们可以将这个范围用对勾函数表示出来,然后通过对这个函数进行求导、分析等数学方法来求解问题。
对勾函数

对勾函数图象性质对勾函数:数学中一种常见而又特殊的函数。
如图一、对勾函数f(x)=ax+的图象与性质对勾函数是数学中一种常见而又特殊的函数。
它在高中教材上不出现,但考试总喜欢考的函数,所以也要注意它和了解它。
(一) 对勾函数的图像对勾函数是一种类似于反比例函数的一般函数,形如f(x)=ax+(接下来写作f(x)=ax+b/x )。
当a≠0,b≠0时,f(x)=ax+b/x 是正比例函数f(x)=ax 与反比例函数f(x)= b/x “叠加”而成的函数。
这个观点,对于理解它的性质,绘制它的图象,非常重要。
当a ,b 同号时,f(x)=ax+b/x 的图象是由直线y =ax 与双曲线y= b/x 构成,形状酷似双勾。
故称“对勾函数”,也称“勾勾函数”、“海鸥函数”。
如下图所示:当a ,b 异号时,f(x)=ax+b/x 的图象发生了质的变化。
但是,我们依然可以看作是两个函数“叠加”而成。
(请自己在图上完成:他是如何叠加而成的。
)一般地,我们认为对勾函数是反比例函数的一个延伸,即对勾函数也是双曲线的一种,只不过它的焦点和渐进线的位置有所改变罢了。
接下来,为了研究方便,我们规定a>0,b>0。
之后当a<0,b<0时,根据对称就很容易得出结论了。
a>0 b>0 a<0 b<0 对勾函数的图像(ab 同号) 对勾函数的图像(ab 异号)(二) 对勾函数的顶点对勾函数性质的研究离不开均值不等式。
利用均值不等式可以得到: 当x>0时,。
当x<0时,。
即对勾函数的定点坐标:(三) 对勾函数的定义域、值域由(二)得到了对勾函数的顶点坐标,从而我们也就确定了对勾函数的定义域、值域等性质。
(四) 对勾函数的单调性(五) 对勾函数的渐进线由图像我们不难得到:(六) 对勾函数的奇偶性 :对勾函数在定义域内是奇函数, 二、类耐克函数性质探讨 函数xbax y +=,在时或00==b a 为简单的单调函数,不予讨论。
数学 对勾函数
性质二
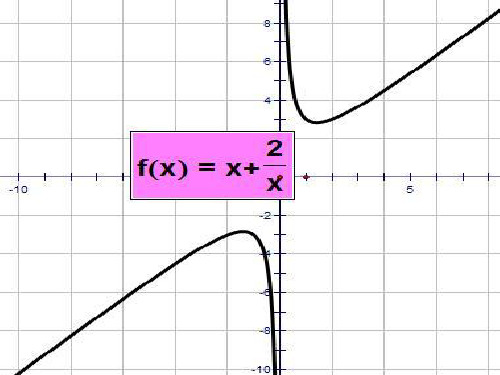
⑸极 值: 当x﹥0时,当x= 根号b/a时, y最小=2根号ab 当x﹤0时,当x=根号b/a时,y最大=-2 根号ab ⑹对称性:图像关于原点对称 ⑺顶点坐标:(根号b/a ,2根号ab )、 (-根号b/a ,-2根号ab ) ⑻渐近 线:y轴和y=ax Ⅱ当a、b均小于 零时
图像一
性质一
函数y=ax+b/x的性质 Ⅰ当a、b均大于零时,性质 ⑴定义域:x≠0 ⑵值
:
域:(-∞,-2 根号ab)∪(2根号ab , +∞) ⑶奇偶性:奇函根号b/a 时,y为增函 数 当x﹤0时,当- 根号b/a﹤x﹤0时,y 为减函数 当x﹤根号b/a- 时,y为增函 数
简介
对勾函数:图像,性质,单调性 对勾函数是数学中一种常见而又特殊的函数,见 图示。 对勾函数是一种类似于反比例函数的一般函 数,又被称为“双勾函数”、"勾函数"等。也被 形象称为“耐克函数” 所谓的对勾函数(双曲线函数),是形如 f(x)=ax+b/x的函数。由图像得名。 当x>0时,f(x)=ax+b/x有最小值(这里为了研 究方便,规定a>0,b>0),也就是当x=sqrt(b/a) 的时候(sqrt表示求二次方根)
性质简介
1.对号函数是双曲线旋转得到的,所以也有渐近线、 焦点、顶点等等 2.对号函数永远是奇函数,关于原点呈中心对称 3.对号函数的两条渐进线永远是y轴和y=ax 4.当a、b>0时,图像分布在第一、三象限两条渐近 线的锐角之间部分,由于其对称性,只讨论第一象 限中的情形。利用平均值不等式(a>0,b>0且ab 的值为定值时,a+b≥2√ab)可知最小值是2倍根号 ab,在x=根号下b/a的时候取得,所以在(0,负根 号下b/a)上单调递减,在(根号下b/a,正无穷) 上单调递增
对勾函数知识点总结

对勾函数知识点总结对勾函数是一种常见的数学函数,也被称为Kronecker delta函数。
它在数学、物理、工程等领域中都有广泛的应用。
本文将对对勾函数的定义、性质和应用进行总结。
一、对勾函数的定义对勾函数是一个二元函数,通常用符号δ(i,j)表示。
它的定义如下:当i=j时,δ(i,j)=1;当i≠j时,δ(i,j)=0。
简单来说,对勾函数在i=j时取值为1,在i≠j时取值为0。
这个函数的定义看起来很简单,但它在实际应用中有着重要的作用。
二、对勾函数的性质1. 对勾函数是对称的,即δ(i,j)=δ(j,i)。
2. 对勾函数满足线性性质,即对于任意的实数a和b,有δ(i,j)=aδ(i,j)+bδ(i,j)。
3. 对勾函数在矩阵运算中有着重要的作用。
例如,对于一个n阶方阵A,可以定义一个n阶单位矩阵I,其中I(i,j)=δ(i,j)。
这样,矩阵A和I的乘积就等于A本身。
三、对勾函数的应用1. 矩阵运算对勾函数在矩阵运算中有着广泛的应用。
例如,在线性代数中,可以使用对勾函数来定义矩阵的转置、逆矩阵等运算。
2. 离散信号处理对勾函数在离散信号处理中也有着重要的应用。
例如,在数字信号处理中,可以使用对勾函数来表示离散时间信号的采样。
3. 物理学对勾函数在物理学中也有着广泛的应用。
例如,在量子力学中,可以使用对勾函数来表示量子态之间的内积。
对勾函数是一种非常重要的数学函数,它在数学、物理、工程等领域中都有着广泛的应用。
对勾函数的定义、性质和应用都需要我们深入学习和掌握。
对勾函数

对号函数的图像是分别以y轴和y=ax为渐近线的两支双曲线。编辑本段均值不等式 对勾函数性质的研究离不开均值不等式。说到均值不等式,其实也是根据二次函数得来的。我们都知道,(a-b)^2≥0,展开就是a^2-2ab+b^2≥0,有a^2+b^2≥2ab,两边同时加上2ab,整理得到(a+b)^2≥4ab,同时开根号,就得到了平均值定理的公式:a+b≥2sqrt(ab)。现在把ax+b/x套用这个公式,得到ax+b/x≥2sqrt(axb/x)=2sqrt(ab),这里有个规定:当且仅当ax=b/x时取到最小值,解出x=sqrt(b/a),对应的f(x)=2sqrt(ab)。我们再来看看均值不等式,它也可以写成这样:(a+b)/2≥sqrt(ab),前式大家都知道,是求平均数的公式。那么后面的式子呢?也是平均数的公式,但不同的是,前面的称为算术平均数,而后面的则称为几何平均数,总结一下就是算术平均数绝对不会小于几何平均数。这些知识点也是非常重幂的换算,这也很简单,但要熟练掌握。举几个例子:1/x=x^-1,4/x^2=4x^-2。明白了吧,x为分母的时候可以转化成负指数幂。那么就有f(x)=ax+b/x=ax+bx^-1,求导方法一样,求得的导函数为a+(-b)x^-2,令f'(x)=0,计算得到b=ax2,结果仍然是x=sqrt(b/a),如果需要的话算出f(x)就行了。平时做题的时候用导数还是均值定理,就看你喜欢用那个了。不过注意均值定理最后的讨论,有时ax≠b/x,就不能用均值定理了。 上述研究都是建立在x>0的基础上的,不过对勾函数是奇函数,所以研究出正半轴图像的性质后,自然能补出对称的图像。如果出现平移了的问题(图像不再规则),就先用平移公式或我总结出的平移规律还原以后再研究,这个能力非常重要,一定要多练,争取做到特别熟练的地步。 事实上,利用将对勾函数进行选择可以得到标准的双曲线方程。也就是说,对勾函数是双曲线,这个利用二阶矩阵的变幻也是可以得到的。 另外对于二次曲线,他只可能是以下几种情况:圆,椭圆,双曲线,抛物线,或者是两条直线。 由对勾函数的图像看出来,非双曲线莫属了。编辑本段其它解法 面对这个函数 f(x)=ax+b/x,我们应该想得更多,需要我们深入探究:⑴它的单调性与奇偶性有何应用?而值域问题恰好与单调性密切相关,所以命题者首先想到的问题应该与值域有关;⑵函数与方程之间有密切的联系,所以命题者自然也会想到函数与方程思想的运用;⑶众所周知,双曲线中存在很多定值问题,所以很容易就想到定值的存在性问题。因此就由特殊引出了一般结论;继续拓展下去,用所猜想、探索的结果来解决较为复杂的函数最值问题。
对勾函数

面对这个函数 f(x)=ax+b/x, 我们应该想得更多,需要我们深入探究:(1)它的单调性与奇偶性有何应用?而值域问题恰好与单调性密切相关,所以命题者首先想到的问题应该与值域有关;(2)函数与方程之间有密切的联系,所以命题者自然也会想到函数与方程思想的运用;(3)众所周知,双曲线中存在很多定值问题,所以很容易就想到定值的存在性问题。因此就由特殊引出了一般结论;继续拓展下去,用所猜想、探索的结果解
其实用导数也可以研究对勾函数的性质。不过首先要会负指数幂的换算,这也很简单,但要熟练掌握。举几个例子:1/x=x^-1,4/x^2=4x^-2。明白了吧,x为分母的时候可以转化成负指数幂。那么就有f(x)=ax+b/x=ax+bx-1,求导方法一样,求的的导函数为a+(-b)x^-2,令f'(x)=0,计算得到b=ax2,结果仍然是x=sqrt(b/a),如果需要的话算出f(x)就行了。平时做题的时候用导数还是均值定理,就看你喜欢用那个了。不过注意均值定理最后的讨论,有时ax≠b/x,就不能用均值定理了。 上述研究都是建立在x>0的基础上的,不过对勾函数是奇函数,所以研究出正半轴图像的性质后,自然能补出对称的图像。如果出现平移了的问题(图像不再规则),就先用平移公式或我总结出的平移规律还原以后再研究,这个能力非常重要,一定要多练,争取做到特别熟练的地步。 对勾函数实际是反比例函数的一个延伸,至于它是不是双曲线还众说不一
极值不等式
对勾函数性质的研究离不开均值不等式。
说到均值不等式,其实也是根据二次函数得来的。
我们都知道,(a-b)^2≥0,展开就是a^2-2ab+b^2≥0,
有a^2+b^2≥2ab,两边同时加上2ab,整理得到(a+b)^2≥4ab,同时开根号,
