黄金分割__习题精选

合集下载

黄金分割__习题精选

黄金分割习题精选一、请你填一填（1）如图，若点P 是AB 的黄金分割点，则线段A P 、PB 、AB 满足关系式________，即AP 是________与________的比例中项.（2）黄金矩形的宽与长的比大约为________（精确到0.001）.（3）如果线段d 是线段a 、b 、c 的第四比例项，其中a =2 cm,b =4 cm,c =5 cm,则d =_____________cm.（4）已知O 点是正方形ABCD 的两条对角线的交点，则AO ∶AB ∶AC =________.（5）若d c b a ==3（b +d ≠0），则db c a ++=________. 二、认真选一选（1）已知yx 23=,那么下列式子成立的是（） A.3x =2yB.xy =6C.32=y xD.32=x y （2）把ab =21cd 写成比例式，不正确的写法是（） A.b d c a2= B.b d c a =2 C.b d c a =2 D.d a b c 2=（3）已知线段x ,y 满足（x +y ）∶（x －y ）=3∶1,那么x ∶y 等于（）A.3∶1B.2∶3C.2∶1D.3∶2（4）有以下命题:①如果线段d 是线段a ,b ,c 的第四比例项，则有dc b a= ②如果点C 是线段AB 的中点，那么AC 是AB 、BC 的比例中项③如果点C 是线段AB 的黄金分割点，且AC >BC ，那么AC 是AB 与BC 的比例中项④如果点C 是线段AB 的黄金分割点，AC >BC ，且AB =2，则AC =5－1其中正确的判断有（）A.1个B.2 个C.3个D.4个5、已知P 为线段AB 的黄金分割点，且AP ＜PB ，则（）A 、PB AB AP ⋅=2； B 、PB AP AB ⋅=2；C 、AB AP PB ⋅=2；D 、222AB BP AP =+4、已知P 、Q 是线段AB 的两个黄金分割点，且AB ＝10cm ，则PQ 长为（）A 、)15(5-B 、)15(5+C 、)25(10-D 、)53(5-三、细心算一算已知实数a ,b ,c 满足c b a b a c a c b +=+=+,求a c b +的值.五、已知743c b a ==，且0≠⋅⋅c b a ，求cb ac b a 432234-+-+的值。

黄金分割(基础篇)(专项练习)-2022-2023学年九年级数学下册基础知识专项讲练(人教版)

专题27.13 黄金分割（基础篇）（专项练习）一、单选题1．大自然巧夺天工，一片树叶也蕴含着“黄金分割”．如图，P为AB的黄金分割点（AP>PB），如果AB的长度为8cm，那么BP的长度是（）A．125-C．454D．54 -B．9452．已知点C是线段AB的黄金分割点，且2<，则AC长是（）AB=，AC BCA51-B51C．35D3523．把2米的线段进行黄金分割，则分成的较短的线段长为（）A．35B51C．15D．354．已知2AB=，点P是线段AB上的黄金分割点，且AP BP>，则AP的长为（）A51B51-C35D．3525．下列说法正确的是（）A．每条线段有且仅有一个黄金分割点B．黄金分割点分一条线段为两条线段，其中较长的线段约是这条线段的0.618倍C．若点C把线段AB黄金分割，则AC2＝AB•BCD．以上说法都不对6．下列说法正确的是（）A．每一条线段有且只有一个黄金分割点B．黄金分割点分一条线段为两段，其中较短的一段是这条线段的0.618倍C．若点C把线段AB黄金分割，则AC是AB和BC的比例中项D．黄金分割点分一条线段为两段，其中较短的一段与较长的一段的比值约为0.6187．下列命题正确的是（）A．任意两个等腰三角形一定相似B．任意两个正方形一定相似C ．如果C 点是线段AB 的黄金分割点，那么51AC AB -=D ．相似图形就是位似图形8．如图，线段1AB =，点1P 是线段AB 的黄金分割点(且11AP BP <)，点2P 是线段1AP 的黄金分割点（212AP PP <），点3P 是线段3AP 的黄金分割点()323,,AP P P <依此类推，则线段2020AP 的长度是（）A ．202051-⎝⎭B ．202151-⎝⎭C ．202035-⎝⎭D ．202135-⎝⎭9．已知点C 把线段AB 分成两条线段AC 、BC ，且AC BC >，下列说法错误的是（） A ．如果AC BCAB AC=，那么线段AB 被点C 黄金分割 B ．如果2AC AB BC =⋅，那么线段AB 被点C 黄金分割C ．如果线段AB 被点C 黄金分割，那么BC 与AB 的比叫做黄金比D ．0.618是黄金比的近似值10．等腰△ABC 中，AB=AC ，△A=36°，D 是AC 上的一点，AD=BD ，则以下结论中正确的有（）△△BCD 是等腰三角形；△点D 是线段AC 的黄金分割点；△△BCD△△ABC ；△BD 平分△ABC ． A ．1个B ．2个C ．3个D ．4个11．在△ABC 中，△A=36°，AB=AC ，BD 是△ABC 的角平分线，下列结论： △△ABD ，△BCD 都是等腰三角形； △AD=BD=BC ； △BC 2=CD•CA ； △D 是AC 的黄金分割点其中正确的是（）A ．1个B ．2个C ．3个D ．4个二、填空题12．在线段AB 上，点C 把线AB 分成两条线段AC 和BC ，若AC BCAB AC=，则点C 叫做线段AB 的黄金分割点．若点P 是线段MN 的黄金分割点（PM PN >），当1MN =时，PM 的长是__________．13．勾股定理与黄金分割是几何中的双宝，前者好比黄金，后者堪称珠玉，生活中到处可见黄金分割的美．如图是一种贝壳的俯视图，点C 分线段AB 近似于黄金分割，已知AB =10 cm ，AC ＞BC ，那么AC 的长约为____________cm （结果精确到0.1 cm ）． 14．把2米长的线段进行黄金分割，则分成的较长的线段长为__________.15．古希腊时期，51-（称为黄金分割比例），著名的“断臂维纳斯”5 2.236≈，则黄金分割比例约为______________．（精确到0.01）16．已知AB=2,点C 是线段AB 的黄金分割点（AC>BC ），则AC= . 17．把长度为4cm 的线段进行黄金分割，则较长线段的长是__________cm ．18．已知线段4AB =，点P 是线段AB 的黄金分割点（AP BP >），那么线段AP =______.（结果保留根号）19．已知线段AB 长为2cm ，P 是AB 的黄金分割点，则较长线段PA ＝ ___；PB ＝______． 20510.61803398-=…，将这个分割比保留4个有效数字的近似数是．21．若点C 为线段AB 的黄金分割点，且AC ＜BC ，若AB ＝10，则BC ＝_____． 22．若点P 是线段AB 的黄金分割点，AB=10cm ，则较长线段AP 的长是_____cm ．三、解答题23．已知C 、D 是线段AB 上的点，CD ＝(√5﹣2)AB ，AC ＝BD ，则C 、D 是黄金分割点吗？为什么？24．已知线段MN = 1，在MN 上有一点A ，如果AN =，求证：点A 是MN 的黄金分割点.25．（1）对于实数a 、b ，定义运算“⊕”如下：2a b a b ⊕=-．若(1)(2)8x x +⊕-=，求: 2(2)(23)x x x -⊕-的值；（2）已知点C 是线段AB 的黄金分割点（AC ＜BC ），若AB ＝4，求AC 的长．26．（1）我们知道，将一条线段AB 分割成大小两条线段AP 、PB ，使AP ＞PB ，点P 把线段AB 分成两条线段AP 和BP ，且=AP BP AB AP ，点P 就是线段AB 的黄金分割点，此时PAAB的值为（填一个实数）：（2）如图，Rt△ABC 中，△B=90°，AB=2BC ，现以C 为圆心、CB 长为半径画弧交边AC 于D ，再以A 为圆心、AD 长为半径画弧交边AB 于E ．求证：点E 是线段AB 的黄金分割点．27．某校要设计一座2m 高的雕像(如图)，使雕像的点C (肚脐)为线段AB (全身)的黄金分割点，上部AC (肚脐以上)与下部BC (肚脐以下)的高度比为黄金比．则雕像下部设计的高度应该为______(结果精确到0.001)米． 5 2. 236=，结果精确到0.001)．28．在等边三角形ABC中，点D，E分别在BC，AC上，且DC=AE，AD与BE交于点P，连接PC．(1)证明：ΔABE△ΔCAD．(2)若CE=CP，求证△CPD=△PBD．(3)在(2)的条件下，证明：点D是BC的黄金分割点.参考答案1．A【分析】根据黄金分割的定义得到AP 51-AB ，然后把AP 的长度代入可求出AB 的长．【详解】解：△P 为AB 的黄金分割点（AP ＞PB ）， △AP 51-AB ， △AB 的长度为8cm ， △AP 51-×8=454（cm ）， △BP =AB -AP =8-（454）=125- 故选：A ．【点拨】本题考查了黄金分割：把线段AB 分成两条线段AC 和BC （AC ＞BC ），且使AC 是AB 和BC 的比例中项（即AB ：AC =AC ：BC ），叫做把线段AB 黄金分割，点C 叫做线段AB 的黄金分割点，其中AC 51-AB ． 2．C 【分析】利用黄金分割比的定义即可求解. 【详解】由黄金分割比的定义可知 5151251BC AB --=== △2(51)35AC AB BC =-=-= 故选C【点拨】本题主要考查黄金分割比，掌握黄金分割比是解题的关键. 3．A 【分析】根据黄金分割的定义列式进行计算即可得解. 【详解】解: 较短的线段长=2⨯ (15-1=255 故选A.【点拨】本题考查了黄金分割的概念, 熟记黄金分割的比值5-1是解题的关键.4．A 【分析】根据黄金分割点的定义和AP BP>得出51AP AB-=，代入数据即可得出AP的长度．【详解】解：由于P为线段AB＝2的黄金分割点，且AP BP>，则5151251ABAP--===．故选：A．352，51-．5．B【分析】根据黄金分割的定义分别进行解答即可．【详解】A．每条线段有两个黄金分割点，故本选项错误；B．黄金分割点分一条线段为两条线段，其中较长的线段约是这条线段的0.618倍，正确；C．若点C把线段AB黄金分割，则AC2＝AB•BC，不正确，有可能BC2＝AB•AC．故选B．【点拨】本题考查了黄金分割，熟练掌握黄金分割的定义是解题的关键．6．D【分析】根据比例中项和黄金分割的概念分析各个说法.【详解】解：A、每一条线段有两个黄金分割点，错误；B、黄金分割点分一条线段为两段，其中较长的一段是这条线段的0.618倍，错误；C、若点C把线段AB黄金分割，则AC是AB和BC的比例中项，错误；D、黄金分割点分一条线段为两段，其中较长的一段与这条线段的比值约为0.618，正确；故选D．【点拨】此题考查黄金分割问题，理解比例中项、黄金分割的概念，是解题的关键． 7．B 【分析】根据相似多边形的概念、黄金分割点及位似可直接进行排除选项．【详解】解：A 、任意两个等腰三角形的底角或顶角相等，则这两个等腰三角形相似，故原命题错误； B 、任意两个正方形一定相似，故原命题正确；C 、如果C 点是线段AB 的黄金分割点（AC ＞BC ），那么51AC AB -=D 、相似图形不一定是位似图形，故原命题错误；故选B ．【点拨】本题主要考查相似多边形的概念、黄金分割点及位似，熟练掌握相似多边形的概念、黄金分割点及位似是解题的关键． 8．C 【分析】根据把一条线段分成两部分，使其中较长的线段为全线段与较短线段的比例中项，这样的线51-叫做黄金比进行解答即可．【详解】解：根据黄金比的比值，151BP -= 则151351AP --==23233535,,AP AP --==⎝⎭⎝⎭…依此类推，则线段2020202035AP -=⎝⎭，故选C ．【点拨】本题考查的是黄金分割的知识，理解黄金分割的概念，找出黄金分割中成比例的对应线段是解决问题的关键． 9．C 【解析】【分析】根据黄金分割的定义判断即可.【详解】根据黄金分割的定义可知A、B、D正确;C.如果线段AB被点C黄金分割（AC>BC）,那么AC与AB的比叫做黄金比,所以C错误.所以C选项是正确的.【点拨】本题考查了黄金分割的概念:把线段AB分成两条线段AC和BC（AC>BC）,且使AC是AB和BC的比例中项(即AB:AC=AC:BC),叫做把线段AB黄金分割,点C叫做线段AB 的黄金分割点.注意线段AB的黄金分割点有两个.10．D【详解】△AB=AC，△△ABC=△C=12（180°-△A）=12（180°-36°）=72°，△AD=BD，△△DBA=△A=36°，△△BDC=2△A=72°，△△BDC=△C，△△BCD为等腰三角形，所以△正确；△△DBC=△ABC-△ABD=36°，△△ABD=△DBC，△BD平分△ABC，所以△正确；△△DBC=△A，△BCD=△ACB，△△BCD△△ABC，所以△正确；△BD：AC=CD：BD，而AD=BD，△AD：AC=CD：AD，△点D是线段AC的黄金分割点，所以△正确．故选D.11．D【解析】试题分析：在△ABC，AB=AC，△A=36°，BD平分△ABC交AC于点D，可推出△BCD，△ABD 为等腰三角形，可得AD=BD=BC，利用三角形相似解题．解：如图，△AB=AC，△A=36°，△△ABC=△C=72°，△BD平分△ABC交AC于点D，△△ABD=△CBD=△ABC=36°=△A，△AD=BD，△BDC=△ABD+△A=72°=△C ， △BC=BD ，△△ABD ，△BCD 都是等腰三角形，故△正确； △BC=BD=AD ，故△正确； △△A=△CBD ，△C=△C ， △△BCD△△ACB ， △，即BC 2=CD•AC ，故△正确； △AD=BD=BC ，△AD 2=AC•CD=（AD+CD ）•CD ， △AD=CD ，△D 是AC 的黄金分割点．故△正确，故选D ．考点：相似三角形的判定与性质；黄金分割． 1251- 【分析】根据若点P 是线段MN 的黄金分割点（PM PN >），则PM MN 51-计算即可．【详解】当PM ＞PN 时，51-51-， 51-． 51-是解题的关键． 13．6.2 【分析】黄金分割又称黄金率，是指事物各部分间一定的数学比例关系，即将整体一分为二，较大部分与较小部分之比等于整体与较大部分之比，其比值为1：0.618或1.618：1，即长段为全段的0.618，0.618被公认为最具有审美意义的比例数字．上述比例是最能引起人的美感的比例，因此被称为黄金分割．【详解】由题意知AC :AB =BC :AC ，△AC :AB ≈0.618，△AC =0.618×10cm ≈6.2(结果精确到0.1cm )故答案为6.2.【点拨】本题考查黄金分割，解题关键是掌握黄金分割定理.14．51-米【解析】【分析】把一条线段分成两部分，使其中较长的线段为全线段与较短线段的比例中项，这样的线段分51-叫做黄金比．【详解】解：△将长度为2米的线段进行黄金分割，△较长的线段=2⨯51-51- 51-米.51-是解的关键． 15．0.62【分析】把黄金分割比例按要求进行计算即可．【详解】解：51-5 2.236≈， 51-≈2.23612-≈0.62，故答案为：0.62．【点拨】本题考查了求一个数的近似值，有理数的除法，正确计算是解题的关键． 1651 【解析】51251AC -==17．()252cm ．【解析】根据黄金分割的定义得到较长线段的长=×4，然后进行二次根式的运算即可．解：较长线段的长=×4=（2）cm ．故答案为（2）cm ． 18．52 【分析】51-计算即可. 【详解】解：△点P 是线段AB 的黄金分割点（AP>BP ） △51AP 252AB -== 故答案为：252.【点拨】本题考查的知识点是黄金分割，熟记黄金分割点的比值是解题的关键.19．)51cm (35cm 【分析】根据黄金分割的概念得到较长线段51-AB ，则PB=AB -352AB ，然后把AB=2cm 代入计算即可．【详解】解：△P 是AB 的黄金分割点， △较长线段51-AB ， △PB=AB -352AB ，而AB=2cm ， △PA=)51cm ，PB=(35cm ．故答案为：)51cm ；(35cm ．【点拨】本题考查了黄金分割的概念：一个点把一条线段分成两段，其中较长线段是较短线段与整个线段的比例中项，那么就说这条线段被这点黄金分割，这个点叫这条线段的黄金分51-倍． 20．0.6180【解析】根据有效数字的定义，运用四舍五入法保留4个有效数字，需观察第五位有效数字，由于第五位有效数字是，不需往前面进一位．所以0.61803398…≈0.618021．555【分析】根据黄金分割点的定义，知BC 为较长线段；则BC 51-AB ，代入数据即可得出AC 的值．【详解】解：由于C 为线段AB ＝10的黄金分割点，且AC ＜BC ，BC 为较长线段；则BC ＝51-＝55．故答案为：555．【点拨】本题考查黄金分割：把线段AB 分成两条线段AC 和BC （AC ＞BC ），且使AC 是AB 和BC 的比例中项（即AB ：AC=AC ：BC ），叫做把线段AB 黄金分割，点C 叫做线段AB 的黄金分割点．其中51-AB≈0.618AB ，并且线段AB 的黄金分割点有两个． 22．555【解析】△P 是线段AB 的黄金分割点，AP ＞BP ，51-AB ， △AB=10cm ， △AP=5110555-=. 故答案为555．点睛：若点P 是线段AB 的黄金分割点，且AP>BP ，则AP 2=BP·AB ，即51-AB. 23．C 、D 是黄金分割点.【解析】【分析】根据题意求出AC 与AB 的关系，计算出AD 与AB 的关系，根据黄金比值进行判断即可．【详解】解：C 、D 是黄金分割点，△AC+CD+BD ＝AB ，CD ＝(√5﹣2)AB ，AC ＝BD ，△AC ＝3−√52AB ， AD ＝AC+CD ＝3−√52AB+(√5﹣2)AB ＝√5−12AB ， △D 是AB 的黄金分割点，同理C 也是AB 的黄金分割点．【点拨】本题考查黄金分割，关键是掌握黄金分割的概念和黄金比.24．见解析【解析】试题分析：先求得AM=√5−12，即可得到AM MN =AN AM =√5−12，结论得证。

《黄金分割》随堂练习

§ 6.2黄金分割姓名班级学号【基础知识】1．一条线段的黄金分割点有（）A．1个B．2个C．3个D．无数个2．黄金分割比的准确值是是（）3．小明同学发现自己一本书的宽与长之比是黄金比约为0.618．已知这本书的长为20cm，则它的宽约为（）A．12.36cm B．13.6cm C．32.386cm D．7.64cm3．已知P为线段AB的黄金分割点，且AP＞PB，则（）A．AP2+BP2＝AB2 B．BP2＝AP•AB C．AP2＝AB•BP D．AB2＝AP•PB4．如图，若点P是线段AB的黄金分割点，AP＞BP，AB＝2，则AP的长度是（）A．B．C．D．5．如图，电视节目主持人在主持节目时，站在舞台的黄金分割点处最自然得体，若舞台AB长为20m，试计算主持人应走到离A点至少．．多少米处是比较得体的位置？（结果精确到0.1m）【能力达标】6．如图，乐器上的一根弦AB＝80cm，两个端点A，B固定在乐器板面上，支撑点C是靠近点B的黄金分割点，支撑点D是靠近点A的黄金分割点，则C，D之间的距离为（）A．（405﹣40）cm B．（805﹣40）cmC．（120﹣405）cm D．（805﹣160）cm7．我们把宽与长的比值等于黄金比例512的矩形称为黄金矩形．如图，在黄金矩形()ABCD AB BC的边AB上取一点E，使得BE BC，连接DE，则AEAD等于()A．22B．512C．352D．5128．如图，已知点C是线段AB的黄金分割点，且BC＞AC．若S1表示以BC为边的正方形面积，S2表示长为AB、宽为AC的矩形面积，则S1与S2的大小关系为（）A．S1＞S2B．S1＝S2C．S1＜S2D．不能确定9．在人体躯和身高的比例上，肚脐是理想的黄金分割点，即（下半身长m与身高l）比例越接近0.618越给人以美感，某女士身高165cm，下半身长（脚底到肚脐的高度）与身高的比值是0.60，为尽可能达到匀称的效果，求她应该选择的高跟鞋得高度．（结果保留整数）【拓展提升】10．如图，以长为2的线段AB为边作正方形ABCD，取AB的中点P，连接PD，在BA的延长线上取点F，使PF＝PD，以AF为边作正方形AMEF，点M在AD上．(1)求AM，DM的长．(2)点M是线段AD的黄金分割点吗？请说明理由．。

4.2黄金分割练习题

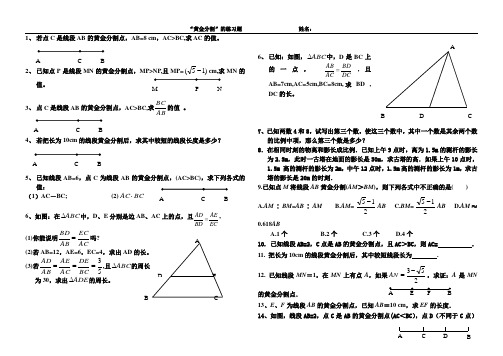
D EB CA1、若点C 是线段AB 的黄金分割点，AB=8 cm ，AC>BC,求AC 的值。

2、已知点P 是线段MN 的黄金分割点，MP>NP,且MP=)15(-cm,求MN 的值。

3、点C 是线段AB 的黄金分割点，AC>BC,求ABBC 的值。

4、若把长为10cm 的线段黄金分割后，求其中较短的线段长度是多少？5、已知线段AB=6，点C 为线段AB 的黄金分割点，(AC>BC)，求下列各式的值：（1）AC －BC; (2)BC AC ⋅6、如图：在ABC ∆中，D 、E 分别是边AB 、AC 上的点，且ECAE BDAD =,(1)你能说明AC EC AB BD =吗?(2)若AB=12，AE=6，EC=4，求出AD 的长。

(3)若53===BCDE ACAE ABAD ,且ABC ∆的周长为30，求出ADE ∆的周长。

6、已知：如图，ABC ∆中，D 是BC 上的一点，DCBD ACAB =,且AB=7cm,AC=5cm,BC=8cm,求BD , DC 的长。

7、已知两数4和8，试写出第三个数，使这三个数中，其中一个数是其余两个数的比例中项，那么第三个数是多少？8．在相同时刻的物高和影长成比例．已知上午9点时，高为1.5m 的测杆的影长为2.5m ，此时一古塔在地面的影长是50m ，求古塔的高．如果上午10点时，1.5m•高的测杆的影长为2m ，中午12点时，1.5m 高的测杆的影长为1m ，求古塔的影长是20m 的时刻．9.已知点M 将线段AB 黄金分割(AM ＞BM )，则下列各式中不正确的是( ) A.AM ∶BM =AB ∶AM B.AM =215-AB C.BM =215-AB D.AM ≈0.618ABA.1个B.2个C.3个D.4个10. 已知线段AB=2，C 点是AB 的黄金分割点，且AC ＞BC ，则AC= . 11. 把长为10cm 的线段黄金分割后，其中较短线段长为 .12. 已知线段MN ＝1，在MN 上有点A ，如果253-=AN ，求证：A 是MN 的黄金分割点．13、E 、F 为线段AB 的黄金分割点，已知AB ＝10 cm ，求EF 的长度． 14、如图，线段AB=2，点C 是AB 的黄金分割点(AC ＜BC ），点D （不同于C 点）A CB M P N AC BA CB AC BAB D CAEFBACDB在AB 上，且AB BD AD ⋅=2，求：ACCD 的值。

4.2 黄金分割(含答案)-

C BA CBAC BA4.2 黄金分割一、选择题:1.如图,点C 把线段AB 分成两条线段AC 和BC,如果AC BCAB AC=,那么下列说法错误的是( ) A.线段AB 被点C 黄金分割; B.点C 叫做线段AB 的黄金分割点C.AB 与AC 的比叫做黄金比;D.AC 与AB 的比叫做黄金比2.如图的五角星中,AC AB 与BCAC 的关系是( ) A.相等; B.AC AB >BC AC ; C.AC AB <BCAC; D.不能确定3.一条线段的黄金分割点有( )A.1个B.2个C.3个D.无数个4.黄金分割比是( ) A.12 B.12 C.12D.0.618 5.如图,点C 是AB 的黄金分割点,那么AC AB 与ACBC的值分别是( ) A.12,12 B.12,12; C.12,12; D.12,126.如图,若点C 是AB 的黄金分割点,AB=2,则AC= ( ) A.12 B.1211 二、填空题:1.点C 把线段AB 分成两条线段AC 和BC,如果_________,那么称线段AB 被点C•黄金分割,点C 叫做线段AB 的________,AC 与AB 的比叫做_________.2.如图,若点C 是AB 的黄金分割点,AB=1,则AC=_______,BC=______.3.已知点C 是AB 的黄金分割点,即AC AB ,那么ACCB=________.4.如图,点C 是AB 的黄金分割点,AB=4,则AC 2=________.5.宽与长的比等于________的矩形叫做黄金矩形.6.已知黄金矩形的长等于6,则这个黄金矩形的宽等于_________. 三、计算题:1.已知线段AB 长6厘米,点P 是AB 的黄金分割点,且AP>BP,求AP 和BP 的长.CBA2.仿照课本上“做一做”的方法,画出线段AB的黄金分割点.AB3.请你在实际生活中搜集一个与黄金分割有关的资料,并与同伴相互交流.四、已知一个等腰三角形如果腰与底边的比是黄金比,•那么这样的等腰三角形称为黄金三角形.请你设法作出一个黄金三角形.五、已知线段AB=1,C为AB的黄金分割点,且AC>BC,求AC-BC的值.六、如图的五角星中,AD=BC,且C、D两点都是AB的黄金分割点,AB=1,求CD的长.AD C B七、已知C、D是线段AB上的两点,且不难证明当AB=1时,C、D是线段AB的黄金分割点,试探究当AB任意长时,C、D是否是线段AB的黄金分割点?为什么?答案:一、1.C 2.A 3.B 4.B 5.B 6.C二、1.AC BCAB AC=;黄金分割点;黄金比 2. 12;32-3.12黄金比三、1.因为点P 是AB 的黄金分割点,且AP>BP,所以AP PB AB AP==12,AP=12×AB=12×2.(1)过点B 作BD ⊥AB 且BD=12AB,连接AD (2)以D 为圆心BD 为半径作圆弧交AD 于E(3)以A 为圆心AE 为半径作圆弧交AB 于C,则C 为AB 的黄金分割点 3.查阅资料四、先做出线段AB,及其黄金分割点C(AC>BC)分别以A 、B 为圆心,AC 为半径作圆弧,交点为P,则△PAB 就是黄金三角形五、根据C 为AB 的黄金分割点,AC>BC 得AC AB=12,因为AB=1,所以AC=12BC=AB-AC=1-12= 32-,•所以AC-BC=12-32-六、根据C 、D 都是AB 的黄金分割点得ACAB ,BD AB因为AB=1,所以,所以AD=AB-BD=1-12=32,因此七、C 、D 是线段AB 的黄金分割点.。

黄金分割专项练习30题

黄金分割专项练习21定义：如图1，点C 在线段AB 上，若满足AC =BC?AB ，则称点C 为线段AB 的黄金分割点.如图 2, △ ABC 中，AB=AC=1 , / A=36 ° BD 平分/ ABC 交 AC 于点 D .(1) 求证：点D 是线段AC 的黄金分割点;2 .如图，用长为 40cm 的细铁丝围成一个矩形 ABCD (AB > AD ).99cm 2,求 AB 的长度；101cm 2吗？若能，求出 AB 的长度，若不能，说明理由;AD 与AB 之比等于黄金比逅二丄)，求该矩形的面积.9.在数学上称长与宽之比为黄金分割比的矩形为黄金矩形，如在矩形ABCD 中，当-'_ J 时，称矩形ABCD为黄金矩形ABCD .请你证明黄金矩形是由一个正方形和一个更小的黄金矩形构成.40cw(1) 若这个矩形的面积等于 (2) 这个矩形的面积可能等于 (3) 若这个矩形为黄金矩形((结果保留根号)(2)求出线段AD 的长.10.如图，设AB是已知线段，在AB上作正方形ABCD ;取AD的中点E，连接EB;延长DA至F,使EF=EB ; 以线段AF为边作正方形AFGH .则点H是AB的黄金分割点.为什么说上述的方法作出的点H是这条线段的黄金分割点，你能说出其中的道理吗？请试一试，说一说.12 .已知AB=2，点C是AB的黄金分割线，点D在AB上，且AD2=BD?AB，求「的值.AC14.五角星是我们常见的图形，如图所示，其中，点C, D分别是线段AB的黄金分割点，AB=20cm，求EC+CD15•人的肚脐是人的身高的黄金分割点，一般来讲，当肚脐到脚底的长度与身高的比为0.618时，是比较好看的黄金身段.一个身高1.70m的人，他的肚脐到脚底的长度为多少时才是黄金身段（保留两位小数）？17.如图，点P 是线段AB 的黄金分割点，且 AP >BP ,设以AP 为边长的正方形面积为 S 1,以PB 为宽和以AB 为长的矩形面积为S 2，试比较S 1与S 2的大小.20.(如图1),点P 将线段AB 分成一条较小线段 AP 和一条较大线段詈罟k ，则k就是黄金比，并且k战618.(1) 以图1中的AP 为底，BP 为腰得到等腰△ APB (如图2),等腰△ APB 即为黄金三角形，黄金三角形的定义为: 满足寺石一耳亍0.618的等腰三角形是黄金三角形；类似地，请你给出黄金矩形的定义：(2) 如图1,设AB=1，请你说明为什么 (3) 由线段的黄金分割点联想到图形的3),点P 是线段AB 的黄金分割点，那么直线 CP 是厶ABC 的黄金分割线吗？请说明理由;18.如图，在平行四边形 ABCD 中，E 为边AD 延长线上的一点，且r -] D 为AE 的黄金分割点，即仙——AE ，k 约为 0.618;黄金分割线”，类似地给出黄金分割线”的定义：直线I 将一个面积为S 的图形分成面积为 S 1和面积为S 2的两部分(设 I 为该图形的黄金分割线. (如图BP ,如果那么称点P 为线段AB 的黄金分割点，设S 1V S 2),如果那么称直线(4)图3中的△ ABC的黄金分割线有几条？21 •在人体躯干（脚底到肚脐的长度）与身高的比例上，肚脐是理想的黄金分割点，即比例越接近0.618，越给人以美感•张女士原来脚底到肚脐的长度与身高的比为0.60，她的身高为1.60m，她应该选择多高的高跟鞋穿上看起来更美？（精确到十分位）23.如图，用纸折出黄金分割点：裁一张正方的纸片ABCD，先折出BC的中点E,再折出线段AE，然后通过折叠使EB落到线段EA 上，折出点B的新位置B',因而EB'=EB .类似地，在AB上折出点B〃使AB 〃=AB 这时B〃就是AB的黄金分割点.请你证明这个结论.25.如图，在△ ABC 中，点D 在边AB 上，且DB=DC=AC，已知 / ACE=108 ° BC=2 .（1）求/ B的度数；（2）我们把有一个内角等于36 °勺等腰三角形称为黄金三角形.它的腰长与底边长的比（或者底边长与腰长的比）等于黄金比—L2①写出图中所有的黄金三角形，选一个说明理由；②求AD的长；③在直线AB或BC上是否存在点P （点A、B除外），使△ PDC是黄金三角形？若存在，在备用图中画出点P,简要说明画出点P的方法（不要求证明）；若不存在，说明理由.28 •折纸与证明——用纸折出黄金分割点：第一步：如图(1),先将一张正方形纸片ABCD对折，得到折痕EF;再折出矩形BCFE的对角线BF • 第二步：如图(2),将AB 边折到BF上，得到折痕BG,试说明点G为线段AD的黄金分割点(AG > GD )P A D29.三角形中，顶角等于36 °勺等腰三角形称为黄金三角形，如图1，在△ ABC中，已知：AB=AC，且/ A=36 °(1)在图1中，用尺规作AB的垂直平分线交AC于D，并连接BD (保留作图痕迹，不写作法)；(2)△ BCD是不是黄金三角形？如果是，请给出证明；如果不是，请说明理由；(3)设，试求k的值；AC(4)如图2,在厶A1B1C1中，已知A1B1=A1C1, / A仁108°且A1B仁AB，请直接写出"巴的值.黄金分割线”类似地给出黄金分割线”的定义：直线I 将一个面积为S 的图形S i , S 2,如果—-_2,那么称直线I 为该图形的黄金分割线.S 3](1) 研究小组猜想：在 △ ABC 中，若点D 为AB 边上的黄金分割点(如图 2),则直线CD 是厶ABC 的黄金分割线.你认为对吗？为什么？(2) 请你说明：三角形的中线是否也是该三角形的黄金分割线？ (3)研究小组在进一步探究中发现：过点C 任作一条直线交 AB 于点E ,再过点D 作直线DF// CE ，交AC 于点F , 连接EF (如图3),则直线EF 也是△ ABC 的黄金分割线.请你说明理由.(4) 如图4,点E 是平行四边形 ABCD 的边AB 的黄金分割点，过点 E 作EF / AD ，交DC 于点F ，显然直线EFABCD 的黄金分割线，使它不经过平行四边形 ABCD课题学习时，由黄金分割点联想到分成两部分，这两部分的面积分别为是平行四边形ABCD 的黄金分割线•请你画一条平行四边形各边黄金分割点.黄金分割专项练习30题参考答案:1.(1)证明：•/ AB=AC=1 ,••• / ABC= / C== (180°- / A )=丄(180 °- 36 ° =72 °2 3••• BD平分/ ABC交AC于点D,•/ ABD= / CBD=2/ ABC=36 °2•/ BDC=180 ° - 36°- 72°72 °•DA=DB , BD=BC,•AD=BD=BC ,易得△ BDC ABC ,2•BC : AC=CD : BC，即BC2=CD?AC ,2•AD =CD ?AC,•点D是线段AC的黄金分割点；(2)设AD=x，贝U CD=AC - AD=1 - x,2•/ AD 2=CD ?AC ,•x2=1 - x，解得x1= --- , x2= _ ',即AD的长为―一-22.解：(1)设AB=xcm，贝U AD= (20 - x) cm,根据题意得x (20 - x) =99 ,整理得x2- 20x+99=0 ,解得X1=9, x2=11,当x=9 时，20 - x=11 ;当x=11 时，20- 1仁9,而AB > AD,所以x=11，即AB的长为11cm;(2)不能.理由如下：设AB=xcm，贝V AD= (20 - x) cm,根据题意得x (20 - x) =101 ,整理得x2- 20x+101=0 ,因为△ =202 - 4X101=- 4V 0,所以方程没有实数解，所以这个矩形的面积可能等于101cm2;(3)设AB=xcm，则AD= (20 - x) cm,丫斥"1根据题意得20 - x= ——x,2解得x=10 ( . 口- 1),贝U 20 - x=10 ( 3-肛),所以矩形的面积=10 ( - 1) ?10 (3-「,)= (400 !.- 800) cm2.3.解：(1) •/ / A=36 ° AB=AC ,•/ ABC= / ACB=72 °•/ BD 平分 / ABC ,•/ CBD= / ABD=36 ° / BDC=72 °•AD=BD , BC=BD,•△ ABC BDC ,•上丄:一 I"即—AB = BC ，AC rAD ，2• AD =AC?CD .•••点D 是线段AC 的黄金分割点. (2) •••点D 是线段AC 的黄金分割点， • AD=——AC ,2•/ AC=2 , • AD= . ■- 14. 解：(1)腰与底之比为黄金比为黄金比如图,(2) 作法：①画线段AB 作为三角形底边；② 取AB 的一半作 AB 的垂线 AC ,连接BC ,在BC 上取CD=CA . ③ 分别以A 点和B 点为圆心、以BD 为半径划弧，交点为 E ; ④ 分别连接EA 、EB ,则厶ABE 即是所求的三角形.(3) 证明：设 AB=2，贝U AC=1 , BC= 口，AE=BE=BD=BC - CD=「- 1, AE 出-1|■:.6 .解：(1)设 AC=x ，贝U BC=AB - AC=12•/ AC 2=BC ?AB ,2• x =1 X ( 1 - x), 整理得x 2+x -仁0,解得 X 1=U^, X 2=: 一(舍去)，所以线段AC 的长度为「一5 .解：(1)由于P 为线段AB=2的黄金分割点, 「=>1 ,则 AP=2 2或 AP=2 -(「- 1) =3 -(2)设线段AD的长度为x, AC=I ,2••• AD =CD ?AC ,2••• X =| X ( I - x),••• X1=—^, X2= l「(舍去)，2 2•线段AD的长度——AC ;|2(3)同理得到线段AE的长度：l - \D ;2上面各题的结果反映：若线段AB分成两条线段AC和BC (AC > BC),且使AC是AB和BC的比例中项(即AB : AC=AC : BC),则C点为AB的黄金分割点7.解：D是AC的黄金分割点.理由如下：•••在△ ABC 中，AB=AC , / A=36 °•••/ ABC= / ACB= _ 厂=72 °2•/ / 1 = / 2,•/ 1 = / 2=丄/ ABC=36 °2•在厶BDC 中，/ BDC=180。

黄金分割练习题

黄金分割练习题1、若点C 是线段AB 的黄金分割点，AB=8 cm ，AC>BC,求AC 的值。

2、已知点P 是线段MN 的黄金分割点，MP>NP ,且MP=)15(-cm,求MN 的值。

3、点C 是线段AB 的黄金分割点，AC>BC,求ABBC 的值。

4、若把长为10cm 的线段黄金分割后，求其中较短的线段长度是多少？5、已知线段AB=6，点C 为线段AB 的黄金分割点，(AC>BC)，求下列各式的值：（1）AC －BC; (2)BC AC ⋅6、已知线段AB ，请利用尺规作图画出线段的黄金分割点。

（只画出一个即可）A CBA B7、如图：在ABC ∆中，D 、E 分别是边AB 、AC 上的点，且EC AE BD AD =, (1)你能说明ACEC AB BD =吗? (2)若AB=12，AE=6，EC=4，求出AD 的长。

(3)若3===DE AE AD ,且ABC ∆的周长为30，求出ADE ∆的周长。

7、已知：如图，ABC ∆中，D 是BC 上的一点，DC BD AC AB =,且AB=7cm,AC=5cm,BC=8cm, 求BD , DC 的长。

5、（2007山东青岛）某饮料厂开发了A 、B 两种新型饮料，主要原料均为甲和乙，每瓶饮料中甲、乙的含量如下表所示．现用甲原料和乙原料各2800克进行试生产，计划生产A 、B 两种饮料共100瓶．设生产A 种饮料x 瓶，解答下列问题：（1）有几种符合题意的生产方案？写出解答过程；（2）如果A 种饮料每瓶的成本为2.60元，B 种饮料每瓶的成本为2.80元，这两种饮料成本总额为y 元，请写出y 与x 之间的关系式，并说明x 取何值会使成本总额最低？B D C。

比例线段黄金分割习题

⽐例线段黄⾦分割习题例1．下列各组中的四条线段成⽐例的是( )A.a =2，b =3，c =2，d =3B.a =4，b =6，c =5，d =10C.a =2，b =5，c =23，d =15D.a =2，b =3，c =4，d =1例2. 已知线段a 、b 、c 、d 满⾜ab =cd ，把它改写成⽐例式，错误的是( )A.a ∶d =c ∶bB.a ∶b =c ∶dC.d ∶a =b ∶cD.a ∶c =d ∶b 例3. 若a =2,b =3,c =33,则a 、b 、c 的第四⽐例项d 为________例4. 若ac =bd ，则下列各式⼀定成⽴的是( )A.dc b a =B.ccb d d a +=+ C.c d b a =22 D.dacd ab = 例5. 已知dcb a =,则下列式⼦中正确的是（） A. a ∶b =c 2∶d 2B. a ∶d =c ∶bC. a ∶b =（a +c ）∶（b +d ）D. a ∶b =（a －d ）∶（b －d ）例6．已知5:4:2::=c b a ，且632=+-a b a ，求c b a 23-+的值。

例7.在⽐例尺为1∶500000的地图上，A 、B 两地的距离是64 cm ，则这两地间的实际距离是______ 例8.在⼀张地图上，甲、⼄两地的图上距离是3 cm,⽽两地的实际距离为1500 m ，那么这张地图的⽐例尺为________.例9．（1）已知ba ab b a x +=+=+=222，求x 的值（2）已知524232xz z y y x -=-=-，求y x z y x -++2的值例10.已知点M 将线段AB 黄⾦分割(AM ＞BM )，则下列各式中不正确的是( ) A ．AM ∶BM =AB ∶AM B.AM =215-AB C.BM =215-AB D.AM ≈0.618AB 例11．如图，线段AB=2，点C 是AB 的黄⾦分割点(AC ＜BC ），点D （不同于C 点）在AB 上，且AB BD AD ?=2，A CDB求：ACCD的值【经典练习】1．如果bc ad =，那么下列⽐例中错误的是（）A 、d b c a =B 、b a d c =C 、b d c a =D 、cd a b =2．若5:6:=y x ，则下列等式中，不正确的是（）A 、511=+y y x B 、51=-y y x C 、6=-yx x D 、5=-x y y3．若2:1:::===d c c b b a ，则=d a :（）A 、1:2B 、1:4C 、1:6D 、1:8 4．若3:2:1::=c b a ，则cb a cb a +---的值为（）A 、-2B 、2C 、3D 、-35．已知875cb a ==，且20=++c b a ，则=-+c b a 2（） A 、11 B 、12 C 、314D 、96．若4:3:2::=c b a ，且5=-+c b a ，则b a -的值是（）A 、5B 、-5C 、20D 、-20 7．若43xx =，则x 等于（） A 、12 B 、32 C 、-32 D 、32± 8．已知AB=1，)15(2 1-=AC ，且BC AB AC ?=2，则BC 的长为（） A 、215- B 、215+ C 、)53(21- D 、)53(21+ 9．已知P 是线段AB 的黄⾦分割点，且15-=AP ，则AB 的长为（）A 、2B 、15+C 、2或15+D 、以上都不对 10．已知572zy x ==，设x z y x C y z x B z y x y A -+=+=++=,,，那么A 、B 、C 的⼤⼩顺序为（） A 、A>B>C B 、AA>B D 、A35=y x ，则=-+)(:)(y x y x 12．如果32=b a ，且3,2≠≠b a ，那么=-++-51b a b a 13．已知a b a 3)(7=-，则=ba14．如果2===c z b y a x ，那么=+-+-cb a z y x 3232 15．已知：2,2,1三个数，请你再填⼀个数，可写成⼀个⽐例式，这个数是 16．把长为5的线段进⾏黄⾦分割，则较短的线段长是17．若65432+==+c b a ,且2a －b +3c =21.试求a ∶b ∶c . 19. 若54,23,43===d c c b b a ，则22db ac+等于多少？20. 已知xbc a x a c b x c b a =+=+=+,,，求x 的值1.如果线段a=3，b=12，那么线段a 、b 的⽐例中项x=___________。

10.2 黄金分割(练习)

C B A C B A 10．2 黄金分割概念：点C 把线段AB 分成两条线段AC 和BC ，如果ACBC AB AC =，那么称线段被点C 黄金分割（golden section ），点C 叫做线段AB 的黄金分割点，AC 与AB 的比叫做黄金比，AC ∶AB=215-∶1≈0．618。

注意：（1）如图，AC 是较长线段，则AC ∶AB=215-∶ 1 （2）如图，AC 是较短线段，则BC ∶AB=215-：1 练习：一、选择题：1、如图,点C 把线段AB 分成两条线段AC 和BC,如果AC BC AB AC =,那么下列说法错误的是 ( ) A 、线段AB 被点C 黄金分割 B 、点C 叫做线段AB 的黄金分割点C 、AB 与AC 的比叫做黄金比D 、AC 与AB 的比叫做黄金比2、如果点C 是线段AB 的黄金分割点（AC ＞BC ），则下列比例式正确的是（）A 、BC AC AC AB = B 、AC BC BC AB = C 、AB BC BC AC = D 、BCAB AB AC = 3、如图,点C 是AB 的黄金分割点,那么AC AB 与AC BC的值分别是( ) AB,C , 4、如图的五角星中,AC AB 与BC AC的关系是 ( ) A 、相等 B 、AC AB >BC AC C 、AC AB <BC AC D 、不能确定 5、若P 为线段AB 的黄金分割点且AP>PB,则下列各式成立的是( )A. AB 2=AP·BPB. BP 2=AP· ABC. PA 2=2BA·BPD. AP 2=AB·BP6、点C 为线段AB 的黄金分割点,AC 为较长线段,若AC=1,则AB 等于( ) 253.253.215.215.+-+-D C B A 7、已知点C 是AB 的黄金分割点(AC >BC)，若AB=4cm ，则AC 的长为（）(A)(2 5 –2)cm(B)(6-2 5 )cm(C)( 5–1)cm (D)(3- 5 )cm8、把长为8cm 的线段进行黄金分割,则较长的线段的长为 ( ) A (4.4).8).4)cm B cm C cm D cm -D C BA 1)2)二、填空题：1、一条线段的黄金分割点有个。

黄金分割中考题精选

黄金分割中考题精选
黄金分割在中考中是一个常见的考点，以下是一些相关题目：
1. 设点 P 是线段 MN 上一点，NP > MP，若 NP^2 = MP MN，则称点P 是线段 MN 的黄金分割点。

在直角三角形 ABC 中，∠ACB = 90°，CD 是斜边 AB 上的高，BD > AD，若点 D 是线段 AB 的黄金分割点，给出下列说法：①AC = BD；②S△CBD = S△ADC S△ABC；③sinB = 5 - 12；
④tanA = 2。

其中正确的有（）
A. ①④
B. ②③
C. ①②③
D. ①②③④
2. 舞台主持人的位置是舞台的黄金分割点，此时观众看起来最舒服。

若舞台长为20米，则主持人从舞台一侧进入，至少走多少米时，才能恰好站在舞台的黄金分割点上？
以上题目主要考查了黄金分割点的定义和性质，以及如何根据实际情况应用这些性质来解决问题。

这些题目都是一些典型的例题，可以帮助你理解和学习黄金分割的相关知识。

黄金分割专项练习题有答案

黄金分割专项练习30题（有答案）1．定义：如图1，点C在线段AB上，若满足AC2=BC?AB，则称点C为线段AB的黄金分割点．如图2，△ABC 中，AB=AC=1，∠A=36°，BD平分∠ABC交AC于点D．（1）求证：点D是线段AC的黄金分割点；（2）求出线段AD的长．2．如图，用长为40cm的细铁丝围成一个矩形ABCD（AB＞AD）．（1）若这个矩形的面积等于99cm2，求AB的长度；（2）这个矩形的面积可能等于101cm2吗？若能，求出AB的长度，若不能，说明理由；（3）若这个矩形为黄金矩形（AD与AB之比等于黄金比），求该矩形的面积．（结果保留根号）3．定义：如图1，点C在线段AB上，若满足AC2=BC?AB，则称点C为线段AB的黄金分割点．如图2，△ABC中，AB=AC=2，∠A=36°，BD平分∠ABC交AC于点D．（1）求证：点D是线段AC的黄金分割点；（2）求出线段AD的长．4．作一个等腰三角形，使得腰与底之比为黄金比．（1）尺规作图并保留作图痕迹；（2）写出你的作法；（3）证明：腰与底之比为黄金比．5．（1）已知线段AB的长为2，P是AB的黄金分割点，求AP的长；（2）求作线段AB的黄金分割点P，要求尺规作图，且使AP＞PB．6．如图，线段AB的长度为1．（1）线段AB上的点C满足系式AC2=BC?AB，求线段AC的长度；（选做）（2）线段AC上的点D满足关系式AD2=CD?AC，求线段AD的长度；（选做）（3）线段AD上的点E满足关系式AE2=DE?AD，求线段AE的长度；上面各题的结果反映了什么规律？（提示：在每一小题中设x和l）7．如图，在△ABC中，AB=AC，∠A=36°，∠1=∠2，请问点D是不是线段AC的黄金分割点．请说明理由．8．在△ABC中，AB=AC=2，BC=﹣1，∠A=36°，BD平分∠ABC，交于AC于D．试说明点D是线段AC的黄金分割点．9．在数学上称长与宽之比为黄金分割比的矩形为黄金矩形，如在矩形ABCD中，当时，称矩形ABCD为黄金矩形ABCD．请你证明黄金矩形是由一个正方形和一个更小的黄金矩形构成．10．如图，设AB是已知线段，在AB上作正方形ABCD；取AD的中点E，连接EB；延长DA至F，使EF=EB；以线段AF为边作正方形AFGH．则点H是AB的黄金分割点．为什么说上述的方法作出的点H是这条线段的黄金分割点，你能说出其中的道理吗？请试一试，说一说．11．如图，已知△ABC中，D是AC边上一点，∠A=36°，∠C=72°，∠ADB=108°．求证：（1）AD=BD=BC；（2）点D是线段AC的黄金分割点．12．已知AB=2，点C是AB的黄金分割线，点D在AB上，且AD2=BD?AB，求的值．13．如果一个矩形ABCD（AB＜BC）中，≈0.618，那么这个矩形称为黄金矩形，黄金矩形给人以美感．在黄金矩形ABCD内作正方形CDEF，得到一个小矩形ABFE（如图），请问矩形ABFE是否是黄金矩形？请说明你的结论的正确性．14．五角星是我们常见的图形，如图所示，其中，点C，D分别是线段AB的黄金分割点，AB=20cm，求EC+CD的长．15．人的肚脐是人的身高的黄金分割点，一般来讲，当肚脐到脚底的长度与身高的比为0.618时，是比较好看的黄金身段．一个身高1.70m的人，他的肚脐到脚底的长度为多少时才是黄金身段（保留两位小数）？16．如图所示，以长为2的定线段AB为边作正方形ABCD，取AB的中点P，连接PD，在BA的延长线上取点F，使PF=PD，以AF为边作正方形AMEF，点M在AD上．（1）求AM，DM的长；（2）点M是AD的黄金分割点吗？为什么？17．如图，点P是线段AB的黄金分割点，且AP＞BP，设以AP为边长的正方形面积为S1，以PB为宽和以AB为长的矩形面积为S2，试比较S1与S2的大小．18．如图，在平行四边形ABCD中，E为边AD延长线上的一点，且D为AE的黄金分割点，即，BE交DC于点F，已知，求CF的长．19．图1是一张宽与长之比为的矩形纸片，我们称这样的矩形为黄金矩形．同学们都知道按图2所示的折叠方法进行折叠，折叠后再展开，可以得到一个正方形ABEF和一个矩形EFDC，那么EFDC这个矩形还是黄金矩形吗？若是，请根据图2证明你的结论；若不是，请说明理由．20．（如图1），点P将线段AB分成一条较小线段AP和一条较大线段BP，如果，那么称点P为线段AB的黄金分割点，设=k，则k就是黄金比，并且k≈0.618．（1）以图1中的AP为底，BP为腰得到等腰△APB（如图2），等腰△APB即为黄金三角形，黄金三角形的定义为：满足≈0.618的等腰三角形是黄金三角形；类似地，请你给出黄金矩形的定义：；（2）如图1，设AB=1，请你说明为什么k约为0.618；（3）由线段的黄金分割点联想到图形的“黄金分割线”，类似地给出“黄金分割线”的定义：直线l将一个面积为S的图形分成面积为S1和面积为S2的两部分（设S1＜S2），如果，那么称直线l为该图形的黄金分割线．（如图3），点P是线段AB的黄金分割点，那么直线CP是△ABC的黄金分割线吗？请说明理由；（4）图3中的△ABC的黄金分割线有几条？21．在人体躯干（脚底到肚脐的长度）与身高的比例上，肚脐是理想的黄金分割点，即比例越接近0.618，越给人以美感．张女士原来脚底到肚脐的长度与身高的比为0.60，她的身高为1.60m，她应该选择多高的高跟鞋穿上看起来更美？（精确到十分位）22．已知线段AB，按照如下的方法作图：以AB为边作正方形ABCD，取AD的中点E，连接EB，延长DA到F，使EF=EB，以线段AF为边，作正方形AFGH，那么点H是线段AB的黄金分割点吗？请说明理由．23．如图，用纸折出黄金分割点：裁一张正方的纸片ABCD，先折出BC的中点E，再折出线段AE，然后通过折叠使EB落到线段EA上，折出点B的新位置B′，因而EB′=EB．类似地，在AB上折出点B″使AB″=AB′．这时B″就是AB的黄金分割点．请你证明这个结论．24．如图，用纸折出黄金分割点：裁一张边长为2的正方形纸片ABCD，先折出BC的中点E，再折出线段AE，然后通过折叠使EB落在线段EA上，折出点B的新位置F，因而EF=EB．类似的，在AB上折出点M使AM=AF．则M是AB的黄金分割点吗？若是请你证明，若不是请说明理由．25．如图，在△ABC中，点D在边AB上，且DB=DC=AC，已知∠ACE=108°，BC=2．（1）求∠B的度数；（2）我们把有一个内角等于36°的等腰三角形称为黄金三角形．它的腰长与底边长的比（或者底边长与腰长的比）等于黄金比．①写出图中所有的黄金三角形，选一个说明理由；②求AD的长；③在直线AB或BC上是否存在点P（点A、B除外），使△PDC是黄金三角形？若存在，在备用图中画出点P，简要说明画出点P的方法（不要求证明）；若不存在，说明理由．26．宽与长的比是的矩形叫黄金矩形．心理测试表明：黄金矩形令人赏心悦目，它给我们以协调，匀称的美感．现将小波同学在数学活动课中，折叠黄金矩形的方法归纳如下（如图所示）：第一步：作一个正方形ABCD；第二步：分别取AD，BC的中点M，N，连接MN；第三步：以N为圆心，ND长为半径画弧，交BC的延长线于E；第四步：过E作EF⊥AD，交AD的延长线于F．请你根据以上作法，证明矩形DCEF为黄金矩形．27．在△ABC中，AB=AC，∠A=36°，把像这样的三角形叫做黄金三角形．（1）请你设计三种不同的分法，将黄金三角形ABC分割成三个等腰三角形，使得分割成的三角形中含有两个黄金三角形（画图工具不限，要求画出分割线段；标出能够说明不同分法所得三角形的内角度数，不要求写画法，不要求证明．分别画在图1，图2，图3中）注：两种分法只要有一条分割线段位置不同，就认为是两种不同的分法．（2）如图4中，BF平分∠ABC交AC于F，取AB的中点E，连接EF并延长交BC的延长线于M．试判断CM 与AB之间的数量关系？只需说明结果，不用证明．答：CM与AB之间的数量关系是．28．折纸与证明﹣﹣﹣用纸折出黄金分割点：第一步：如图（1），先将一张正方形纸片ABCD对折，得到折痕EF；再折出矩形BCFE的对角线BF．第二步：如图（2），将AB边折到BF上，得到折痕BG，试说明点G为线段AD的黄金分割点（AG＞GD）29．三角形中，顶角等于36°的等腰三角形称为黄金三角形，如图1，在△ABC中，已知：AB=AC，且∠A=36°．（1）在图1中，用尺规作AB的垂直平分线交AC于D，并连接BD（保留作图痕迹，不写作法）；（2）△BCD是不是黄金三角形？如果是，请给出证明；如果不是，请说明理由；（3）设，试求k的值；（4）如图2，在△A1B1C1中，已知A1B1=A1C1，∠A1=108°，且A1B1=AB，请直接写出的值．30．如图1，点C将线段AB分成两部分，如果，那么称点C为线段AB的黄金分割点．某研究小组在进行课题学习时，由黄金分割点联想到“黄金分割线”，类似地给出“黄金分割线”的定义：直线l将一个面积为S的图形分成两部分，这两部分的面积分别为S1，S2，如果，那么称直线l为该图形的黄金分割线．（1）研究小组猜想：在△ABC中，若点D为AB边上的黄金分割点（如图2），则直线CD是△ABC的黄金分割线．你认为对吗？为什么？（2）请你说明：三角形的中线是否也是该三角形的黄金分割线？（3）研究小组在进一步探究中发现：过点C任作一条直线交AB于点E，再过点D作直线DF∥CE，交AC于点F，连接EF（如图3），则直线EF也是△ABC的黄金分割线．请你说明理由．（4）如图4，点E是平行四边形ABCD的边AB的黄金分割点，过点E作EF∥AD，交DC于点F，显然直线EF是平行四边形ABCD的黄金分割线．请你画一条平行四边形ABCD的黄金分割线，使它不经过平行四边形ABCD各边黄金分割点．黄金分割专项练习30题参考答案: 1．（1）证明：∵AB=AC=1，∴∠ABC=∠C=（180°﹣∠A）=（180°﹣36°）=72°，∵BD平分∠ABC交AC于点D，∴∠ABD=∠CBD=∠ABC=36°，∴∠BDC=180°﹣36°﹣72°=72°，∴DA=DB，BD=BC，∴AD=BD=BC，易得△BDC∽△ABC，∴BC：AC=CD：BC，即BC2=CD?AC，∴AD2=CD?AC，∴点D是线段AC的黄金分割点；（2）设AD=x，则CD=AC﹣AD=1﹣x，∵AD2=CD?AC，∴x2=1﹣x，解得x1=，x2=，即AD的长为2．解：（1）设AB=xcm，则AD=（20﹣x）cm，根据题意得x（20﹣x）=99，整理得x2﹣20x+99=0，解得x1=9，x2=11，当x=9时，20﹣x=11；当x=11时，20﹣11=9，而AB＞AD，所以x=11，即AB的长为11cm；（2）不能．理由如下：设AB=xcm，则AD=（20﹣x）cm，根据题意得x（20﹣x）=101，整理得x2﹣20x+101=0，因为△=202﹣4×101=﹣4＜0，所以方程没有实数解，所以这个矩形的面积可能等于101cm2；（3）设AB=xcm，则AD=（20﹣x）cm，根据题意得20﹣x=x，解得x=10（﹣1），则20﹣x=10（3﹣），所以矩形的面积=10（﹣1）?10（3﹣）=（400﹣800）cm2．3．解：（1）∵∠A=36°，AB=AC，∴∠ABC=∠ACB=72°，∵BD平分∠ABC，∴∠CBD=∠ABD=36°，∠BDC=72°，∴AD=BD，BC=BD，∴△ABC∽△BDC，∴=，即=， ∴AD 2=AC?CD ．∴点D 是线段AC 的黄金分割点．（2）∵点D 是线段AC 的黄金分割点，∴AD=AC ，∵AC=2，∴AD=﹣14．解：（1）腰与底之比为黄金比为黄金比如图，（2）作法：①画线段AB 作为三角形底边；②取AB 的一半作AB 的垂线AC ，连接BC ，在BC 上取CD=CA ．③分别以A 点和B 点为圆心、以BD 为半径划弧，交点为E ；④分别连接EA 、EB ，则△ABE 即是所求的三角形．（3）证明：设AB=2，则AC=1，BC=，AE=BE=BD=BC ﹣CD=﹣1，=． 5．解：（1）由于P 为线段AB=2的黄金分割点，则AP=2×=﹣1，或AP=2﹣（﹣1）=3﹣；（2）如图，点P 是线段AB 的一个黄金分割点．6．解：（1）设AC=x ，则BC=AB ﹣AC=1﹣x ，∵AC 2=BC?AB ，∴x 2=1×（1﹣x ），整理得x 2+x ﹣1=0，解得x 1=，x 2=（舍去），所以线段AC 的长度为；（2）设线段AD 的长度为x ，AC=l ，∵AD 2=CD?AC ，∴x 2=l×（l ﹣x ），∴x 1=，x 2=（舍去），∴线段AD 的长度AC ；（3）同理得到线段AE 的长度AD ；上面各题的结果反映：若线段AB 分成两条线段AC 和BC （AC ＞BC ），且使AC 是AB 和BC 的比例中项（即AB ：AC=AC ：BC ），则C 点为AB 的黄金分割点7．解：D 是AC 的黄金分割点．理由如下：∵在△ABC 中，AB=AC ，∠A=36°，∴∠ABC=∠ACB==72°．∵∠1=∠2，∴∠1=∠2=∠ABC=36°．∴在△BDC中，∠BDC=180°﹣∠2﹣∠C=72°，∴∠C=∠BDC，∴BC=BD．∵∠A=∠1，∴AD=BC．∵△ABC和△BDC中，∠2=∠A，∠C=∠C，∴△ABC∽△BDC，∴，又∵AB=AC，AD=BC=BD，∴，∴AD2=AC?CD，即D是AC的黄金分割点8．证明：∵AB=AC，∠A=36°，∴∠ABC=（180°﹣36°）=72°，∵BD平分∠ABC，交于AC于D，∴∠DBC=×∠ABC=×72°=36°，∴∠A=∠DBC，又∵∠C=∠C，∴△BCD∽△ABC，∴∵AB=AC，∴=，∵AB=AC=2，BC=﹣1，∴（﹣1）2=2×（2﹣AD），解得AD=，AD：AC=（）：2．∴点D是线段AC的黄金分割点．9．证明：在AB上截取AE=BC，DF=BC，连接EF．∵AE=BC，DF=BC，∴AE=DF=BC=AD，又∵∠ADF=90°，∴四边形AEFD是正方形．BE=，∴，∴矩形BCFE的宽与长的比是黄金分割比，矩形BCFE是黄金矩形．∴黄金矩形是由一个正方形和一个更小的黄金矩形构成．10．解：设正方形ABCD的边长为2，在Rt△AEB中，依题意，得AE=1，AB=2，由勾股定理知EB===，∴AH=AF=EF﹣AE=EB﹣AE=﹣1，HB=AB﹣AH=3﹣；∴AH2=（）2=6﹣2，AB?HB=2×（3﹣）=6﹣2，∴AH2=AB?HB，所以点H是线段AB的黄金分割点．11．证明：（1）∵∠A=36°，∠C=72°，∴∠ABC=180°﹣36°﹣72°=72°，∵∠ADB=108°，∴∠ABD=180°﹣36°﹣108°=36°，∴△ADB是等腰三角形，∵∠BDC=180°﹣∠ADC=180°﹣108°=72°，∴△BDC是等腰三角形，∴AD=BD=BC．（2）∵∠DBC=∠A=36°，∠C=∠C，∴△ABC∽△BDC，∴BC：AC=CD：BC，∴BC2=AC?DC，∵BC=AD，∴AD2=AC?DC，∴点D是线段AC的黄金分割点．12．解：∵D在AB上，且AD2=BD?AB，∴点D是AB的黄金分割点而点C是AB的黄金分割点，∴AC=AB=﹣1，AD=AB﹣AB=AB=3﹣或AD=﹣1，AC=3﹣，∴CD=﹣1﹣（3﹣）=2﹣4，∴==或==．13．解：矩形ABFE是黄金矩形．∵AD=BC，DE=AB，∴==﹣1==．∴矩形ABFE是黄金矩形．14．解：∵D为AB的黄金分割点（AD＞BD），∴AD=AB=10﹣10，∵EC+CD=AC+CD=AD，∴EC+CD=（10﹣10）cm．15．解：设他的肚脐到脚底的长度为xm时才是黄金身段，根据题意得x：1.70=0.618，即x=1.70×0.618≈1.1（m）．答：他的肚脐到脚底的长度为1.1m时才是黄金身段．16．解：（1）在Rt△APD中，AP=1，AD=2，由勾股定理知PD===，∴AM=AF=PF﹣AP=PD﹣AP=﹣1，DM=AD﹣AM=3﹣．故AM的长为﹣1，DM的长为3﹣；（2）点M是AD的黄金分割点．由于=，∴点M是AD的黄金分割点．17．解：∵点P是线段AB的黄金分割点，且AP＞BP，∴AP2=BP×AB，又∵S1=AP2，S2=PB×AB，∴S1=S2．18．解：∵四边形ABCD为平行四边形，∴∠CBF=∠AEB，∠BCF=∠BAE，∴△BCF∽△EAB，∴，即，把AD=，AB=+1代入得，=，解得：CF=2．故答案为：2．19．解：矩形EFDC是黄金矩形，证明：∵四边形ABEF是正方形，∴AB=DC=AF，又∵，∴，即点F是线段AD的黄金分割点．∴，∴，∴矩形CDFE是黄金矩形．20．解：（1）满足≈0.618的矩形是黄金矩形；（2）由=k得，BP=1×k=k，从而AP=1﹣k，由得，BP2=AP×AB，即k2=（1﹣k）×1，解得k=，∵k＞0，∴k=≈0.618；（3）因为点P是线段AB的黄金分割点，所以，设△ABC的AB上的高为h，则，∴∴直线CP是△ABC的黄金分割线．（4）由（2）知，在BC边上也存在这样的黄金分割点Q，则AQ也是黄金分割线，设AQ与CP交于点W，则过点W的直线均是△ABC的黄金分割线，故黄金分割线有无数条．21．解：根据已知条件得下半身长是160×0.6=96cm，设选择的高跟鞋的高度是xcm，则根据黄金分割的定义得：=0.618，解得：x≈7.5cm．故她应该选择7.5cm左右的高跟鞋穿上看起来更美．22．解：设正方形ABCD的边长为2a，在Rt△AEB中，依题意，得AE=a，AB=2a，由勾股定理知EB==a，∴AH=AF=EF﹣AE=EB﹣AE=（﹣1）a，HB=AB﹣AH=（3﹣）a；∴AH2=（6﹣2）a2，AB?HB=2a×（3﹣）a=（6﹣2）a2，∴AH2=AB?HB，所以点H是线段AB的黄金分割点．23．证明：设正方形ABCD的边长为2，E为BC的中点，∴BE=1∴AE==，又∵B′E=BE=1，∴AB′=AE﹣B′E=﹣1，∴AB″∴点B″是线段AB的黄金分割点．24．证明：∵正方形ABCD的边长为2，E为BC的中点，∴BE=1∴AE==，∵EF=BE=1，∴AF=AE﹣EF=﹣1，∴AM=AF=﹣1，∴AM：AB=（﹣1）：2，∴点M是线段AB的黄金分割点．25．解：（1）∵BD=DC=AC．则∠B=∠DCB，∠CDA=∠A．设∠B=x，则∠DCB=x，∠CDA=∠A=2x．又∠BOC=108°，∴∠B+∠A=108°．∴x+2x=108，x=36°．∴∠B=36°；（2）①有三个：△BDC，△ADC，△BAC．∵DB=DC，∠B=36°，∴△DBC是黄金三角形，（或∵CD=CA，∠ACD=180°﹣∠CDA﹣∠A=36°．∴△CDA是黄金三角形．或∵∠ACE=108°，∴∠ACB=72°．又∠A=2x=72°，∴∠A=∠ACB．∴BA=BC．∴△BAC是黄金三角形．②△BAC是黄金三角形，∴，∵BC=2，∴AC=﹣1．∵BA=BC=2，BD=AC=﹣1，∴AD=BA﹣BD=2﹣（﹣1）=3﹣，③存在，有三个符合条件的点P1、P2、P3．ⅰ）以CD为底边的黄金三角形：作CD的垂直平分线分别交直线AB、BC得到点P1、P2．ⅱ）以CD为腰的黄金三角形：以点C为圆心，CD为半径作弧与BC的交点为点P3．26．证明：在正方形ABCD中，取AB=2a，∵N为BC的中点，∴NC=BC=a．在Rt△DNC中，．又∵NE=ND，∴CE=NE﹣NC=（﹣1）a．∴．故矩形DCEF为黄金矩形．27．解：（1）（2）CM=AB（4分）28．证明：如图，连接GF，设正方形ABCD的边长为1，则DF=．在Rt△BCF中，BF==，则A′F=BF﹣BA′=﹣1．设AG=A′G=x，则GD=1﹣x，在Rt△A′GF和Rt△DGF中，有A'F2+A'G2=DF2+DG2，即，解得x=，即点G是AD的黄金分割点（AG＞GD）．29．解：（1）如图所示；（2）△BCD是黄金三角形．证明如下：∵点D在AB的垂直平分线上，∴AD=BD，∴∠ABD=∠A．∵∠A=36°，AB=AC，∴∠ABC=∠C=72°，∴∠ABD=∠DBC=36°．又∵∠BDC=∠A+∠ABD=72°，∴∠BDC=∠C，∴BD=BC，∴△BCD是黄金三角形．（3）设BC=x，AC=y，由（2）知，AD=BD=BC=x．∵∠DBC=∠A，∠C=∠C，∴△BDC∽△ABC，∴，即，整理，得x2+xy﹣y2=0，解得．因为x、y均为正数，所以．（4）．理由：延长BC到E，使CE=AC，连接AE．∵∠A=36°，AB=AC，∴∠ACB=∠B=72°，∴∠ACE=180°﹣72°=108°，∴∠ACE=∠B1A1C1．∵A1B1=AB，∴AC=CE=A1B1=A1C1，∴△ACE≌△B1A1C1，∴AE=B1C1．由（3）知，∴，，∴．30．解：（1）直线CD是△ABC的黄金分割线．理由如下：设△ABC的边AB上的高为h．则，，，∴，．又∵点D为边AB的黄金分割点，∴，∴．故直线CD是△ABC的黄金分割线．（2）∵三角形的中线将三角形分成面积相等的两部分，∴，即，故三角形的中线不可能是该三角形的黄金分割线．（3）∵DF∥CE，∴△DFC和△DFE的公共边DF上的高也相等，∴S△DFC=S△DFE，∴S△ADC=S△ADF+S△DFC=S△ADF+S△DFE=S△AEF，S△BDC=S四边形BEFC．又∵，∴．因此，直线EF也是△ABC的黄金分割线．（7分）（4）画法不惟一，现提供两种画法；画法一：如答图1，取EF的中点G，再过点G作一条直线分别交AB，DC于M，N点，则直线MN就是平行四边形ABCD的黄金分割线．画法二：如答图2，在DF上取一点N，连接EN，再过点F作FM∥NE交AB于点M，连接MN，则直线MN 就是平行四边形ABCD的黄金分割线．（9分）。

有关黄金分割比的试题(精改)

“黄金分割比”专题练习1•下列各组中的四条线段成比例的是（）A.a= . 2， b=3，c=2， d= . 3B.a=4， b=6， c=5， d=10C.a=2， b= . 5， c=2 . 3，d= .152. 已知线段a 、b 、c 、d 满足ab =cd ，把它改写成比例式，错误的是（）A.a : d=c : bB.a : b=c : dC.d : a=b : cD.a : c=d : b3. 已知点M 将线段AB 黄金分割（AM> BM ，则下列各式中不正确的是（）D.AM 〜0.618AB4. 现有三个数1 , .、2 , 2，请你再添上一个数写出一个比例式，这样的比例式唯一吗?5、宽与长的比等于黄金比的矩形也称为黄金矩形，若一黄金矩形的长为 _______________ cm .6、黄金比的近似值为 __________________ ，准确值为 _______________________ .7、（2005?嘉兴）顶角为 36°的等腰三角形称为黄金三角形.如图，△ABC 、△ BDC 、△ DEC 都是黄金三角形，已知AB=1 ,则DE= _____________________ . & （ 2004?安徽）如图，扇子的圆心角为 x 。

，余下的扇形的圆心角为 y °, x 与y 的比通常按黄金比为设计，这样的扇子外形较美观，若取黄金比为 0.6,则c（"黄金线段组”.黄 b 2金线段组中的三条线段（）A .必构成锐角三角形B •必构成直角三角形C .必构成钝角三角形D .不能构成三角形A.AM : BM=AB : AMB.AM =、5 12ABx 为（）A . 216B . 135C . 120D . 108 9、（湖北省十堰市）如图1，已知线段 AB ，点C 在AB 上，且有 AC 匹，则AC 的数值为AB AC AB ______ ;若AB 的长度与中央电视台演播厅舞台的宽度一样长，那么节目主持人应站在 _______ 位置最好.i A▽' CR上1D.a=2， b=3，c=4， d=12 cm ，则其宽为C.BM =10、如果三条线段的长 a 、b 、c 满足-a5 i11、(扬州市)若一个矩形的短边与长边的比值为(黄金分割数)，我们把这样的矩2形叫做黄金矩形.(1)操作：请你在如图2所示的黄金矩形ABCD(AB AD)中，以短边AD为一边作正方形AEFD ;(2)探究：在(1)中的四边形EBCF是不是黄金矩形？若是，请予以证明；若不是, 请说明理由；(3)归纳：通过上述操作及探究，请概括出具有一般性的结论(不需要证明) .黄金矩形给人以美感•在黄金矩形ABCD内作正方形CDEF，得到一个小矩形ABFE(如图1), 请问矩形ABFE是否是黄金矩形？请说明你的结论的正确性*12.如果一个矩形ABCD(AB V BC)中,ABBC-0.618,那么这个矩形称为黄金矩形,5 113、（2009?枣庄）宽与长的比是的矩形叫黄金矩形•心理测试表明：黄金矩形令人2赏心悦目，它给我们以协调，匀称的美感•现将小波同学在数学活动课中，折叠黄金矩形的方法归纳如下（如图所示）：第一步：作一个正方形 ABCD ;AM __DF第二步：分别取 AD , BC 的中点M , N ，连接MN ;、第三步：以N 为圆心，ND 长为半径画弧，交 BC 的延长线\于E ;:第四步：过E 作EF 丄AD ，父AD 的延长线于F . 3N C请你根据以上作法，证明矩形 DCEF 为黄金矩形.形，黄金三角形的定义为：底腰满足腰=底腰^°618的等腰三角形是黄金三角形；类似地,请你给出黄金矩形的定义： ________________________________________________________ ; （2）如图1,设AB=1，请你说明为什么 k 约为0.618;（3）由线段的黄金分割点联想到图形的 “黄金分割线”，类似地给出“黄金分割线”的定义: 直线l 将一个面积为 S 的图形分成面积为S 1和面积为S 2的两部分（设 S 1V S 2）,如果鱼,那么称直线l 为该图形的黄金分割线.（如图3）,点P 是线段AB 的黄金分割点,S 2S14、（如图1），点P 将线段AB 分成一条较小线段 AP 那么称点P 为线段AB 的黄金分割点，设 APBP（1）以图1中的AP 为底，BP 为腰得到等腰△ AP 和一条较大线段 APBP，如果茨BP ABBP =k ，贝U k 就是黄金比，并且 k 疋0.618.AB那么直线CP 是厶ABC 的黄金分割线吗？请说明理由;为线段AB 的黄金分割点•某研究小组在进行课题学习时，由黄金分割点联想到“黄金分割线”类似地给出“黄金分割线”的定义：直线 I 将一个面积为 S 的图形分成两部分，这两（1）研究小组猜想：在△ ABC 中，若点D 为AB 边上的黄金分割点（如图 2），则直线CD 是厶ABC 的黄金分割线.你认为对吗？为什么？（2）请你说明：三角形的中线是否也是该三角形的黄金分割线？（3）研究小组在进一步探究中发现：过点 C 任作一条直线交 AB 于点E ,再过点D 作直线 DF // CE ,交AC 于点F ，连接EF （如图3）,则直线EF 也是△ ABC 的黄金分割线.请你说明理由. （4）如图4,点E 是平行四边形 ABCD 的边AB 的黄金分割点，过点E 作EF / AD ，交DC 于点F ，显然直线EF 是平行四边形 ABCD 的黄金分割线.请你画一条平行四边形 ABCD 的黄金分割线，使它不经过平行四边形 ABCD 各边黄金分割点..4 C &图1遐415、（2007?连云港）如图J 点C 将线段AB 分成两部分，如果ABAC BCAC ，那么称点部分的面积分别为 S i ， S 2，如果S邑，那么称直线I 为该图形的黄金分割线.。

黄金分割测试题(含答案)

黄金分割测试题(含答案)4．2黄金分割一、目标导航 1．黄金分割定义:点C把线段AB分成两条线段AC和BC，如果AC:AB=BC:AC，那么称线段AB被点C黄金分割．点C叫做线段AB的黄金分割点，AC与AB的比叫做黄金比． 2．．二、基础过关 1．若点P是AB的黄金分割点，则线段AP、PB、AB满足关系式． 2．黄金矩形的宽与长的比大约为________（精确到0．001）． 3．电视节目主持人在主持节目时，站在舞台的黄金分割点处最自然得体，若舞台AB长为20m，试计算主持人应走到离A点至少 m处？，如果他向B点再走 m，也处在比较得体的位置．（结果精确到0．1m）三、能力提升 4．有以下命题：①如果线段d是线段a，b，c的第四比例项，则有；②如果点C是线段AB的中点，那么AC是AB、BC的比例中项；③如果点C是线段AB的黄金分割点，且AC>BC，那么AC是AB与BC的比例中项；④如果点C是线段AB的黄金分割点，AC>BC，且AB=2，则AC= －1．其中正确的判断有（） A．1个 B．2个 C．3个 D．4个 5．已知点M将线段AB黄金分割(AM＞BM)，则下列各式中不正确的是( ) A．AM∶BM=AB∶AM B．AM= AB C．BM= ABD．AM≈0．618AB 6．已知C是线段AB的黄金分割点(AC＞BC），则AC∶BC = ( ) A． ( －1)∶2 B．（ +1）∶2 C．（3－）∶2 D．（3+ ）∶2 7．在长度为１的线段上找到两个黄金分割点Ｐ，Ｑ．则ＰＱ＝（）A ． B ． C． D ． 8．已知线段MN = 1，在MN上有一点A，如果AN = ．求证：点A是MN的黄金分割点．四、聚沙成塔 9．如图，以长为2的线段AB为边作正方形ABCD，取AB的中点P，连结PD，在BA的延长线上取点F，使PF=PD，以AF为边作正方形AMEF，点M在AD上．（1）求AM、DM的长．（2）求证：AM2=AD•DM．（3）根据（2）的结论你能找出图中的黄金分割点吗？ 10．如果一个矩形ABCD(AB＜BC)中，≈0．618，那么这个矩形称为黄金矩形，黄金矩形给人以美感．在黄金矩形ABCD内作正方形CDEF，得到一个小矩形ABFE(如图)，请问矩形ABFE是否是黄金矩形？请说明你的结论的正确性． 4．2黄金分割 1．AP =BP•AB或PB =AP•AB；2．0.618；3．7.6，4.8；4．C；5．C；6．B；7．C；8证得AM =AN•MN即可；9．⑴AM= －1；DM=3－；⑵略；⑶点M是线段AD的黄金分割点；10．通过计算可得，所以矩形ABFE是黄金矩形．。

分割黄金智力测试题(3篇)

第1篇一、选择题1. 下列关于黄金分割的描述，正确的是：A. 黄金分割是指将一条线段分为两部分，其中较大部分与整体的比例等于较小部分与较大部分的比例。

B. 黄金分割是指将一条线段分为两部分，其中较大部分与整体的比例等于较小部分与较大部分的比例，且比例为1：1。

C. 黄金分割是指将一条线段分为两部分，其中较大部分与整体的比例等于较小部分与较大部分的比例，且比例为2：1。

D. 黄金分割是指将一条线段分为两部分，其中较大部分与整体的比例等于较小部分与较大部分的比例，且比例为3：2。

2. 黄金分割的比值约为：A. 1.618B. 2.618C. 0.618D. 1.4143. 黄金分割在以下哪个领域有广泛的应用？A. 数学B. 物理C. 建筑D. 以上都是4. 下列哪个不是黄金分割的应用实例？A. 斐波那契数列B. 古希腊建筑C. 印度教神像D. 荷兰风车5. 黄金分割在音乐中的运用体现在：A. 旋律B. 和弦C. 节奏D. 以上都是6. 黄金分割在艺术创作中的运用体现在：A. 形状B. 色彩C. 线条D. 以上都是7. 下列哪个不是黄金分割的特点？A. 比例关系B. 美学价值C. 经济效益D. 生物学意义8. 黄金分割在建筑设计中的运用体现在：A. 室内布局B. 外观造型C. 结构设计D. 以上都是9. 黄金分割在植物生长中的运用体现在：A. 叶片排列B. 花朵形态C. 果实分布D. 以上都是10. 下列哪个不是黄金分割的应用领域？A. 设计B. 科学研究C. 农业种植D. 医学治疗二、填空题1. 黄金分割的比值是__________。

2. 黄金分割在数学中被称为__________。

3. 黄金分割在自然界中普遍存在，如__________、__________等。

4. 黄金分割在艺术创作中的应用实例有__________、__________等。

5. 黄金分割在建筑设计中的应用实例有__________、__________等。

黄金分割：习题精选

习题精选
一
1．若点C是线段AB的黄金分割点（），则．
2．根据你的生活体验，你认为舞台上主持人报幕时站在舞台的何处，会显得更加自然大方？
3．量一量你家中电视机屏幕的长和宽，计算一下它的长与宽的比．
4．若是线段AB上的两个黄金分割点，且，则．参考答案
1．．
2．答案不惟一．有人认为主持人站在舞台前沿的黄金分割点处会显得自然大方．
3．略．
4．．
二
1．如图，等腰三角形ABC中，顶角，底角平分线BD交AC于D，得D是线段AC的黄金分割点，若 cm，则．
2．若点C是线段AB的黄金分割点（），则AB与AC的比值是__________，BC与AC的比值是_________．
参考答案
1．6.18cm 2．1：0.618；0.372：0.618
三
同学们，你们一定对“黄金分割”很感兴趣吧！其实，在我们的生活中许多地方都体现了黄金分割．如：建筑师们常常把黄金比作为门窗的比例；主持人在报幕时往往不会站在舞台正中，而是站在舞台的黄金分割点上等等．现在就请同学们到生活中去找一找，看看哪些地方还用到了黄金分割．
参考答案
略。

黄金分割专项练习题有答案

黄金分割专项练习30题（有答案）1．定义：如图1，点C在线段AB上，若满足AC2=BC•AB，则称点C为线段AB的黄金分割点．如图2，△ABC 中，AB=AC=1，∠A=36°，BD平分∠ABC交AC于点D．（1）求证：点D是线段AC的黄金分割点；（2）求出线段AD的长．2．如图，用长为40cm的细铁丝围成一个矩形ABCD（AB＞AD）．（1）若这个矩形的面积等于99cm2，求AB的长度；（2）这个矩形的面积可能等于101cm2吗？若能，求出AB的长度，若不能，说明理由；（3）若这个矩形为黄金矩形（AD与AB之比等于黄金比），求该矩形的面积．（结果保留根号）3．定义：如图1，点C在线段AB上，若满足AC2=BC•AB，则称点C为线段AB的黄金分割点．如图2，△ABC中，AB=AC=2，∠A=36°，BD平分∠ABC交AC于点D．（1）求证：点D是线段AC的黄金分割点；（2）求出线段AD的长．4．作一个等腰三角形，使得腰与底之比为黄金比．（1）尺规作图并保留作图痕迹；（2）写出你的作法；（3）证明：腰与底之比为黄金比．5．（1）已知线段AB的长为2，P是AB的黄金分割点，求AP的长；（2）求作线段AB的黄金分割点P，要求尺规作图，且使AP＞PB．6．如图，线段AB的长度为1．（1）线段AB上的点C满足系式AC2=BC•AB，求线段AC的长度；（选做）（2）线段AC上的点D满足关系式AD2=CD•AC，求线段AD的长度；（选做）（3）线段AD上的点E满足关系式AE2=DE•AD，求线段AE的长度；上面各题的结果反映了什么规律？（提示：在每一小题中设x和l）7．如图，在△ABC中，AB=AC，∠A=36°，∠1=∠2，请问点D是不是线段AC的黄金分割点．请说明理由．8．在△ABC中，AB=AC=2，BC=﹣1，∠A=36°，BD平分∠ABC，交于AC于D．试说明点D是线段AC的黄金分割点．9．在数学上称长与宽之比为黄金分割比的矩形为黄金矩形，如在矩形ABCD中，当时，称矩形ABCD 为黄金矩形ABCD．请你证明黄金矩形是由一个正方形和一个更小的黄金矩形构成．10．如图，设AB是已知线段，在AB上作正方形ABCD；取AD的中点E，连接EB；延长DA至F，使EF=EB；以线段AF为边作正方形AFGH．则点H是AB的黄金分割点．为什么说上述的方法作出的点H是这条线段的黄金分割点，你能说出其中的道理吗？请试一试，说一说．11．如图，已知△ABC中，D是AC边上一点，∠A=36°，∠C=72°，∠ADB=108°．求证：（1）AD=BD=BC；（2）点D是线段AC的黄金分割点．12．已知AB=2，点C是AB的黄金分割线，点D在AB上，且AD2=BD•AB，求的值．13．如果一个矩形ABCD（AB＜BC）中，≈0.618，那么这个矩形称为黄金矩形，黄金矩形给人以美感．在黄金矩形ABCD内作正方形CDEF，得到一个小矩形ABFE（如图），请问矩形ABFE是否是黄金矩形？请说明你的结论的正确性．14．五角星是我们常见的图形，如图所示，其中，点C，D分别是线段AB的黄金分割点，AB=20cm，求EC+CD 的长．15．人的肚脐是人的身高的黄金分割点，一般来讲，当肚脐到脚底的长度与身高的比为0.618时，是比较好看的黄金身段．一个身高1.70m的人，他的肚脐到脚底的长度为多少时才是黄金身段（保留两位小数）？16．如图所示，以长为2的定线段AB为边作正方形ABCD，取AB的中点P，连接PD，在BA的延长线上取点F，使PF=PD，以AF为边作正方形AMEF，点M在AD上．（1）求AM，DM的长；（2）点M是AD的黄金分割点吗？为什么？17．如图，点P是线段AB的黄金分割点，且AP＞BP，设以AP为边长的正方形面积为S1，以PB为宽和以AB为长的矩形面积为S2，试比较S1与S2的大小．18．如图，在平行四边形ABCD中，E为边AD延长线上的一点，且D为AE的黄金分割点，即，BE交DC于点F，已知，求CF的长．19．图1是一张宽与长之比为的矩形纸片，我们称这样的矩形为黄金矩形．同学们都知道按图2所示的折叠方法进行折叠，折叠后再展开，可以得到一个正方形ABEF和一个矩形EFDC，那么EFDC这个矩形还是黄金矩形吗？若是，请根据图2证明你的结论；若不是，请说明理由．20．（如图1），点P将线段AB分成一条较小线段AP和一条较大线段BP，如果，那么称点P为线段AB的黄金分割点，设=k，则k就是黄金比，并且k≈0.618．（1）以图1中的AP为底，BP为腰得到等腰△APB（如图2），等腰△APB即为黄金三角形，黄金三角形的定义为：满足≈0.618的等腰三角形是黄金三角形；类似地，请你给出黄金矩形的定义：；（2）如图1，设AB=1，请你说明为什么k约为0.618；（3）由线段的黄金分割点联想到图形的“黄金分割线”，类似地给出“黄金分割线”的定义：直线l将一个面积为S的图形分成面积为S1和面积为S2的两部分（设S1＜S2），如果，那么称直线l为该图形的黄金分割线．（如图3），点P是线段AB的黄金分割点，那么直线CP是△AB C的黄金分割线吗？请说明理由；（4）图3中的△ABC的黄金分割线有几条？21．在人体躯干（脚底到肚脐的长度）与身高的比例上，肚脐是理想的黄金分割点，即比例越接近0.618，越给人以美感．张女士原来脚底到肚脐的长度与身高的比为0.60，她的身高为1.60m，她应该选择多高的高跟鞋穿上看起来更美？（精确到十分位）22．已知线段AB，按照如下的方法作图：以AB为边作正方形ABCD，取AD的中点E，连接EB，延长DA到F，使EF=EB，以线段AF为边，作正方形AFGH，那么点H是线段AB的黄金分割点吗？请说明理由．23．如图，用纸折出黄金分割点：裁一张正方的纸片ABCD，先折出BC的中点E，再折出线段AE，然后通过折叠使EB落到线段EA上，折出点B的新位置B′，因而EB′=EB．类似地，在AB上折出点B″使AB″=AB′．这时B″就是AB的黄金分割点．请你证明这个结论．24．如图，用纸折出黄金分割点：裁一张边长为2的正方形纸片ABCD，先折出BC的中点E，再折出线段AE，然后通过折叠使EB落在线段EA上，折出点B的新位置F，因而EF=EB．类似的，在AB上折出点M使AM=AF．则M是AB的黄金分割点吗？若是请你证明，若不是请说明理由．25．如图，在△ABC中，点D在边AB上，且DB=DC=AC，已知∠ACE=108°，BC=2．（1）求∠B的度数；（2）我们把有一个内角等于36°的等腰三角形称为黄金三角形．它的腰长与底边长的比（或者底边长与腰长的比）等于黄金比．①写出图中所有的黄金三角形，选一个说明理由；②求AD的长；③在直线AB或BC上是否存在点P（点A、B除外），使△PDC是黄金三角形？若存在，在备用图中画出点P，简要说明画出点P的方法（不要求证明）；若不存在，说明理由．26．宽与长的比是的矩形叫黄金矩形．心理测试表明：黄金矩形令人赏心悦目，它给我们以协调，匀称的美感．现将小波同学在数学活动课中，折叠黄金矩形的方法归纳如下（如图所示）：第一步：作一个正方形ABCD；第二步：分别取AD，BC的中点M，N，连接MN；第三步：以N为圆心，ND长为半径画弧，交BC的延长线于E；第四步：过E作EF⊥AD，交AD的延长线于F．请你根据以上作法，证明矩形DCEF为黄金矩形．27．在△ABC中，AB=AC，∠A=36°，把像这样的三角形叫做黄金三角形．（1）请你设计三种不同的分法，将黄金三角形ABC分割成三个等腰三角形，使得分割成的三角形中含有两个黄金三角形（画图工具不限，要求画出分割线段；标出能够说明不同分法所得三角形的内角度数，不要求写画法，不要求证明．分别画在图1，图2，图3中）（2）如图4中，BF平分∠ABC交AC于F，取AB的中点E，连接EF并延长交BC的延长线于M．试判断CM 与AB之间的数量关系？只需说明结果，不用证明．答：CM与AB之间的数量关系是．28．折纸与证明﹣﹣﹣用纸折出黄金分割点：第一步：如图（1），先将一张正方形纸片ABCD对折，得到折痕EF；再折出矩形BCFE的对角线BF．第二步：如图（2），将AB边折到BF上，得到折痕BG，试说明点G为线段AD的黄金分割点（AG＞GD）29．三角形中，顶角等于36°的等腰三角形称为黄金三角形，如图1，在△ABC中，已知：AB=AC，且∠A=36°．（1）在图1中，用尺规作AB的垂直平分线交AC于D，并连接BD（保留作图痕迹，不写作法）；（2）△BCD是不是黄金三角形？如果是，请给出证明；如果不是，请说明理由；（3）设，试求k的值；（4）如图2，在△A1B1C1中，已知A1B1=A1C1，∠A1=108°，且A1B1=AB，请直接写出的值．30．如图1，点C将线段AB分成两部分，如果，那么称点C为线段AB的黄金分割点．某研究小组在进行课题学习时，由黄金分割点联想到“黄金分割线”，类似地给出“黄金分割线”的定义：直线l将一个面积为S的图形分成两部分，这两部分的面积分别为S1，S2，如果，那么称直线l为该图形的黄金分割线．（1）研究小组猜想：在△ABC中，若点D为AB边上的黄金分割点（如图2），则直线CD是△ABC的黄金分割线．你认为对吗？为什么？（2）请你说明：三角形的中线是否也是该三角形的黄金分割线？（3）研究小组在进一步探究中发现：过点C任作一条直线交AB于点E，再过点D作直线DF∥CE，交AC于点F，连接EF（如图3），则直线EF也是△ABC的黄金分割线．请你说明理由．（4）如图4，点E是平行四边形ABCD的边AB的黄金分割点，过点E作EF∥AD，交DC于点F，显然直线EF 是平行四边形ABCD的黄金分割线．请你画一条平行四边形ABCD的黄金分割线，使它不经过平行四边形ABCD 各边黄金分割点．黄金分割专项练习30题参考答案:1．（1）证明：∵AB=AC=1，∴∠ABC=∠C=（180°﹣∠A）=（180°﹣36°）=72°，∵BD平分∠ABC交AC于点D，∴∠ABD=∠CBD=∠ABC=36°，∴∠BDC=180°﹣36°﹣72°=72°，∴DA=DB，BD=BC，∴AD=BD=BC，易得△BDC∽△ABC，∴BC：AC=CD：BC，即BC2=CD•AC，∴AD2=CD•AC，∴点D是线段AC的黄金分割点；（2）设AD=x，则CD=AC﹣AD=1﹣x，∵AD2=CD•AC，∴x2=1﹣x，解得x1=，x2=，即AD的长为2．解：（1）设AB=xcm，则AD=（20﹣x）cm，根据题意得x（20﹣x）=99，整理得x2﹣20x+99=0，解得x1=9，x2=11，当x=9时，20﹣x=11；当x=11时，20﹣11=9，而AB＞AD，所以x=11，即AB的长为11cm；（2）不能．理由如下：设AB=xcm，则AD=（20﹣x）cm，根据题意得x（20﹣x）=101，整理得x2﹣20x+101=0，因为△=202﹣4×101=﹣4＜0，所以方程没有实数解，所以这个矩形的面积可能等于101cm2；（3）设AB=xcm，则AD=（20﹣x）cm，根据题意得20﹣x=x，解得x=10（﹣1），则20﹣x=10（3﹣），所以矩形的面积=10（﹣1）•10（3﹣）=（400﹣800）cm2．∵BD平分∠ABC，∴∠CBD=∠ABD=36°，∠BDC=72°，∴AD=BD，BC=BD，∴△ABC∽△BDC，∴=，即=，∴AD2=AC•CD．∴点D是线段AC的黄金分割点．（2）∵点D是线段AC的黄金分割点，∴AD=AC，∵AC=2，∴AD=﹣14．解：（1）腰与底之比为黄金比为黄金比如图，（2）作法：①画线段AB作为三角形底边；②取AB的一半作AB的垂线AC，连接BC，在BC上取CD=CA．③分别以A点和B点为圆心、以BD为半径划弧，交点为E；④分别连接EA、EB，则△ABE即是所求的三角形．（3）证明：设AB=2，则AC=1，BC=，AE=BE=BD=BC﹣CD=﹣1，=．5．解：（1）由于P为线段AB=2的黄金分割点，则AP=2×=﹣1，或AP=2﹣（﹣1）=3﹣；（2）如图，点P是线段AB的一个黄金分割点．6．解：（1）设AC=x，则BC=AB﹣AC=1﹣x，∵AC2=BC•AB，∴x2=1×（1﹣x），整理得x2+x﹣1=0，解得x1=，x2=（舍去），所以线段AC的长度为；（2）设线段AD的长度为x，AC=l，∵AD2=CD•AC，∴x2=l×（l﹣x），∴x1=，x2=（舍去），∴线段AD的长度AC；（3）同理得到线段AE的长度AD；上面各题的结果反映：若线段AB分成两条线段AC和BC（AC＞BC），且使AC是AB和BC的比例中项（即AB：AC=AC：BC），则C点为AB的黄金分割点7．解：D是AC的黄金分割点．理由如下：∵在△ABC中，AB=AC，∠A=36°，∴∠ABC=∠ACB==72°．∵∠1=∠2，∴∠1=∠2=∠ABC=36°．∴在△BDC中，∠BDC=180°﹣∠2﹣∠C=72°，∴∠C=∠BDC，∴BC=BD．∵∠A=∠1，∴AD=BC．∵△ABC和△BDC中，∠2=∠A，∠C=∠C，∴△ABC∽△BDC，∴，又∵AB=AC，AD=BC=BD，∴，∴AD2=AC•CD，即D是AC的黄金分割点8．证明：∵AB=AC，∠A=36°，∴∠ABC=（180°﹣36°）=72°，∵BD平分∠ABC，交于AC于D，∴∠DBC=×∠ABC=×72°=36°，∴∠A=∠DBC，又∵∠C=∠C，∴△BCD∽△ABC，∴∵AB=AC，∴=，∵AB=AC=2，BC=﹣1，∴（﹣1）2=2×（2﹣AD），解得AD=，AD：AC=（）：2．∴点D是线段AC的黄金分割点．9．证明：在AB上截取AE=BC，DF=BC，连接EF．∵AE=BC，DF=BC，∴AE=DF=BC=AD，又∵∠ADF=90°，∴四边形AEFD是正方形．BE=，∴，∴矩形BCFE的宽与长的比是黄金分割比，矩形BCFE是黄金矩形．∴黄金矩形是由一个正方形和一个更小的黄金矩形构成．10．解：设正方形ABCD的边长为2，在Rt△AEB中，依题意，得AE=1，AB=2，由勾股定理知EB===，∴AH=AF=EF﹣AE=EB﹣AE=﹣1，HB=AB﹣AH=3﹣；∴AH2=（）2=6﹣2，AB•HB=2×（3﹣）=6﹣2，∴AH2=AB•HB，所以点H是线段AB的黄金分割点．11．证明：（1）∵∠A=36°，∠C=72°，∴∠ABC=180°﹣36°﹣72°=72°，∵∠ADB=108°，∴∠ABD=180°﹣36°﹣108°=36°，∴△ADB是等腰三角形，∵∠BDC=180°﹣∠ADC=180°﹣108°=72°，∴△BDC是等腰三角形，∴AD=BD=BC．（2）∵∠DBC=∠A=36°，∠C=∠C，∴△ABC∽△BDC，∴BC：AC=CD：BC，∴BC2=AC•DC，∵BC=AD，∴AD2=AC•DC，∴点D是线段AC的黄金分割点．12．解：∵D在AB上，且AD2=BD•AB，∴点D是AB的黄金分割点而点C是AB的黄金分割点，∴AC=AB=﹣1，AD=AB﹣AB=AB=3﹣或AD=﹣1，AC=3﹣，∴CD=﹣1﹣（3﹣）=2﹣4，∴==或==．13．解：矩形ABFE是黄金矩形．∵AD=BC，DE=AB，∴==﹣1==．∴矩形ABFE是黄金矩形．14．解：∵D为AB的黄金分割点（AD＞BD），∴AD=AB=10﹣10，∵EC+CD=AC+CD=AD，∴EC+CD=（10﹣10）cm．15．解：设他的肚脐到脚底的长度为xm时才是黄金身段，根据题意得x：1.70=0.618，即x=1.70×0.618≈1.1（m）．答：他的肚脐到脚底的长度为1.1m时才是黄金身段．16．解：（1）在Rt△APD中，AP=1，AD=2，由勾股定理知PD===，∴AM=AF=PF﹣AP=PD﹣AP=﹣1，DM=AD﹣AM=3﹣．故AM的长为﹣1，DM的长为3﹣；（2）点M是AD的黄金分割点．由于=，∴点M是AD的黄金分割点．17．解：∵点P是线段AB的黄金分割点，且AP＞BP，∴AP2=BP×AB，又∵S1=AP2，S2=PB×AB，∴S1=S2．18．解：∵四边形ABCD为平行四边形，∴∠CBF=∠AEB，∠BCF=∠BAE，∴△BCF∽△EAB，∴，即，把AD=，AB=+1代入得，=，解得：CF=2．故答案为：2．19．解：矩形EFDC是黄金矩形，证明：∵四边形ABEF是正方形，∴AB=DC=AF，又∵，∴，即点F是线段AD的黄金分割点．∴，∴，∴矩形CDFE是黄金矩形．20．解：（1）满足≈0.618的矩形是黄金矩形；（2）由=k得，BP=1×k=k，从而AP=1﹣k，由得，BP2=AP×AB，即k2=（1﹣k）×1，解得k=，∵k＞0，∴k=≈0.618；（3）因为点P是线段AB的黄金分割点，所以，设△ABC的AB上的高为h，则，∴∴直线CP是△ABC的黄金分割线．（4）由（2）知，在BC边上也存在这样的黄金分割点Q，则AQ也是黄金分割线，设AQ与CP交于点W，则过点W的直线均是△ABC的黄金分割线，故黄金分割线有无数条．21．解：根据已知条件得下半身长是160×0.6=96cm，设选择的高跟鞋的高度是xcm，则根据黄金分割的定义得：=0.618，解得：x≈7.5cm．故她应该选择7.5cm左右的高跟鞋穿上看起来更美．22．解：设正方形ABCD的边长为2a，在Rt△AEB中，依题意，得AE=a，AB=2a，由勾股定理知EB==a，∴AH=AF=EF﹣AE=EB﹣AE=（﹣1）a，HB=AB﹣AH=（3﹣）a；∴AH2=（6﹣2）a2，AB•HB=2a×（3﹣）a=（6﹣2）a2，∴AH2=AB•HB，所以点H是线段AB的黄金分割点．23．证明：设正方形ABCD的边长为2，E为BC的中点，∴BE=1∴AE==，又∵B′E=BE=1，∴AB′=AE﹣B′E=﹣1，∴AB″∴点B″是线段AB的黄金分割点．24．证明：∵正方形ABCD的边长为2，E为BC的中点，∴BE=1∴AE==，∵EF=BE=1，∴AF=AE﹣EF=﹣1，∴AM=AF=﹣1，∴AM：AB=（﹣1）：2，∴点M是线段AB的黄金分割点．25．解：（1）∵BD=DC=AC．则∠B=∠DCB，∠CDA=∠A．设∠B=x，则∠DCB=x，∠CDA=∠A=2x．又∠BOC=108°，∴∠B+∠A=108°．∴x+2x=108，x=36°．∴∠B=36°；（2）①有三个：△BDC，△ADC，△BAC．∵DB=DC，∠B=36°，∴△DBC是黄金三角形，（或∵CD=CA，∠ACD=180°﹣∠CDA﹣∠A=36°．∴△CDA是黄金三角形．或∵∠ACE=108°，∴∠ACB=72°．又∠A=2x=72°，∴∠A=∠ACB．∴BA=BC．∴△BAC是黄金三角形．②△BAC是黄金三角形，∴，∵BC=2，∴AC=﹣1．∵BA=BC=2，BD=AC=﹣1，∴AD=BA﹣BD=2﹣（﹣1）=3﹣，③存在，有三个符合条件的点P1、P2、P3．ⅰ）以CD为底边的黄金三角形：作CD的垂直平分线分别交直线AB、BC得到点P1、P2．ⅱ）以CD为腰的黄金三角形：以点C为圆心，CD为半径作弧与BC的交点为点P3．26．证明：在正方形ABCD中，取AB=2a，∵N为BC的中点，∴NC=BC=a．在Rt△DNC中，．又∵NE=ND，∴CE=NE﹣NC=（﹣1）a．∴．故矩形DCEF为黄金矩形．27．解：（1）（2）CM=AB（4分）28．证明：如图，连接GF，设正方形ABCD的边长为1，则DF=．在R t△BCF中，BF==，则A′F=BF﹣BA′=﹣1．设AG=A′G=x，则GD=1﹣x，在Rt△A′GF和Rt△DGF中，有A'F2+A'G2=DF2+DG2，即，解得x=，即点G是AD的黄金分割点（AG＞GD）．29．解：（1）如图所示；（2）△BCD是黄金三角形．证明如下：∵点D在AB的垂直平分线上，∴AD=BD，∴∠ABD=∠A．∵∠A=36°，AB=AC，∴∠ABC=∠C=72°，∴∠ABD=∠DBC=36°．又∵∠BDC=∠A+∠ABD=72°，∴∠BDC=∠C，∴BD=BC，∴△BCD是黄金三角形．（3）设BC=x，AC=y，由（2）知，AD=BD=BC=x．∵∠DBC=∠A，∠C=∠C，∴△BDC∽△ABC，∴，即，整理，得x2+xy﹣y2=0，解得．因为x、y均为正数，所以．（4）．理由：延长BC到E，使CE=AC，连接AE．∵∠A=36°，AB=AC，∴∠ACB=∠B=72°，∴∠ACE=180°﹣72°=108°，∴∠ACE=∠B1A1C1．∵A1B1=AB，∴AC=CE=A1B1=A1C1，∴△ACE≌△B1A1C1，∴AE=B1C1．由（3）知，∴，，∴．30．解：（1）直线CD是△ABC的黄金分割线．理由如下：设△ABC的边AB上的高为h．则，，，∴，．又∵点D为边AB的黄金分割点，∴，∴．故直线CD是△ABC的黄金分割线．（2）∵三角形的中线将三角形分成面积相等的两部分，∴，即，故三角形的中线不可能是该三角形的黄金分割线．（3）∵DF∥CE，∴△DFC和△DFE的公共边DF上的高也相等，∴S△DFC=S△DFE，∴S△ADC=S△ADF+S△DFC=S△ADF+S△DFE=S△AEF，S△BDC=S四边形BEFC．又∵，∴．因此，直线EF也是△ABC的黄金分割线．（7分）（4）画法不惟一，现提供两种画法；画法一：如答图1，取EF的中点G，再过点G作一条直线分别交AB，DC于M，N点，则直线MN就是平行四边形ABCD的黄金分割线．画法二：如答图2，在DF上取一点N，连接EN，再过点F作FM∥NE交AB于点M，连接MN，则直线MN就是平行四边形ABCD的黄金分割线．（9分）。

黄金分割练习题

黄金分割一、目标导航1．黄金分割定义:点C 把线段AB 分成两条线段AC 和BC ，如果AC :AB =BC :AC ，那么称线段AB 被点C 黄金分割．点C 叫做线段AB 的黄金分割点，AC 与AB 的比叫做黄金比．2．．二、基础过关1．若点P 是AB 的黄金分割点，则线段AP 、PB 、AB 满足关系式．2.如果线段AB=10cm ，点C 是AB 上的黄金分割点，且AC>BC ，则AC=变式：点C 是线段AB 的黄金分割点，且AB=2，则AC=3．电视节目主持人在主持节目时，站在舞台的黄金分割点处最自然得体，若舞台AB 长为20m ，试计算主持人应走到离A 点至少 m 处？，如果他向B 点再走 m ，也处在比较得体的位置．（结果精确到0.1m ）三、能力提升4．有以下命题：①如果线段d 是线段a ， b ，c 的第四比例项，则有；②如果点C 是线段AB 的中点，那么AC 是AB 、BC 的比例中项；③如果点C 是线段AB 的黄金分割点，且AC >BC ，那么AC 是AB 与BC 的比例中项；④如果点C 是线段AB 的黄金分割点，AC >BC ，且AB =2，则AC =－1．其中正确的判断有( )A ． 1个B ．2个C ．3个D ．4个 5．已知点M 将线段AB 黄金分割(AM ＞BM )，则下列各式中不正确的是( )A ．AM ∶BM =AB ∶AM B ．AM =AB C ．BM =AB D ．AM ≈0．618AB 6．已知C 是线段AB 的黄金分割点(AC ＞BC ），则AC ∶BC = ( )A ．(－1)∶2B ．（ +1）∶2C ．（3－）∶2D ．（3+）∶27．在长度为1的线段上找到两个黄金分割点P ，Q ．则PQ ＝( )618.0215≈-=AB AC dc b a =5215-215-5555A ．B ．C ．D ． 8．已知线段MN = 1，在MN 上有一点A ，如果AN =．求证：点A 是MN 的黄金分割点．四、聚沙成塔9.如图，已知等腰三角形ABC 中，顶角∠A=36。

黄金分割例题

黄金分割例题
例题1：求一个线段分割成两部分时，使得两部分的比例符合黄金分割。

解题思路：
设线段的长度为x，根据黄金分割的定义，分割后较长部分和整个线段的比例等于较短部分和较长部分的比例，即：
x / (x - y) = (x - y) / y
解方程得：
y^2 - (x - y)y - x^2 = 0
根据求根公式，得：
y = (x - √(5x^2))/2 或y = (x + √(5x^2))/2
注意：由于线段必须分割成两部分，因此y必须大于0。

我们可以观察到，当y = (x + √(5x^2))/2 时，y大于0，因此我们选择这个解。

例题2：一个长方形的长和宽分别为x和y，求一个正方形的边长，使得这个正方形和长方形的比例符合黄金分割。

解题思路：
根据黄金分割的定义，长方形的长和宽的比例等于正方形的边长和长方形的宽的比例，即：
x / y = y / a
解方程得：
a = (√(5) + 1) * y / 2x
因此，正方形的边长为(√(5) + 1) * y / 2x。