解读投入产出表
投入产出表设计的主要内容
投入产出表设计的主要内容投入产出表是一种用于分析经济系统中各个部门之间相互依赖关系的工具。
它可以帮助我们了解一个经济体系中各个部门之间的资源流动情况，以及资源的利用效率和经济增长潜力。
投入产出表设计的主要内容包括以下几个方面：1. 经济部门划分：投入产出表将整个经济系统划分为不同的部门，每个部门代表着一个特定的产业或行业。
常见的部门划分包括农业、工业、建筑业、交通运输业、金融业等。
2. 生产活动：每个部门在投入产出表中都有相应的生产活动。
生产活动是指一个部门所进行的生产过程，包括原材料采购、加工制造、产品销售等环节。
这些生产活动通过物质和货币流动来实现。
3. 投入要素：每个部门进行生产活动时需要消耗一定数量的投入要素，如劳动力、原材料、资本等。
这些投入要素在投入产出表中以物质或货币形式列示。
4. 产品输出：每个部门在完成生产活动后会生成一定数量的产品输出，即产出。
这些产品输出可以是最终产品，也可以是中间产品，用于供给其他部门的生产活动。
5. 交易关系：投入产出表中记录了各个部门之间的交易关系。
这包括部门之间的物质流动和货币流动。
物质流动指的是各个部门之间通过原材料、半成品等物质的交换来实现生产活动；货币流动则指的是各个部门之间通过购买和销售产品来实现经济交换。
6. 中间需求和最终需求：投入产出表中还记录了各个部门的中间需求和最终需求。
中间需求指的是一个部门对其他部门生产的中间产品的需求；最终需求则指消费者对最终产品的需求。
通过分析中间需求和最终需求，可以评估不同行业对经济增长的贡献程度。
7. 产业关联系数：投入产出表还包括各个部门之间的产业关联系数。
这些系数反映了不同行业之间相互依赖程度，即一个行业对其他行业生产和就业的影响力。
通过分析这些关联系数，可以评估经济体系中不同行业之间存在的复杂关系。
8. 经济效益分析：投入产出表可以用于评估经济系统的效益。
通过对投入产出表进行综合分析，可以计算出各个部门的生产效率、就业弹性、资源利用效率等指标，从而评估经济体系的整体效益和潜力。
投入产出分析投入产出表
§1.2 投入产出表投入产出分析的基础是投入产出表。
在任何一个层次上、为了任何一个目的应用投入产出分析，首先的也是最重要的工作就是编制投入产出表。
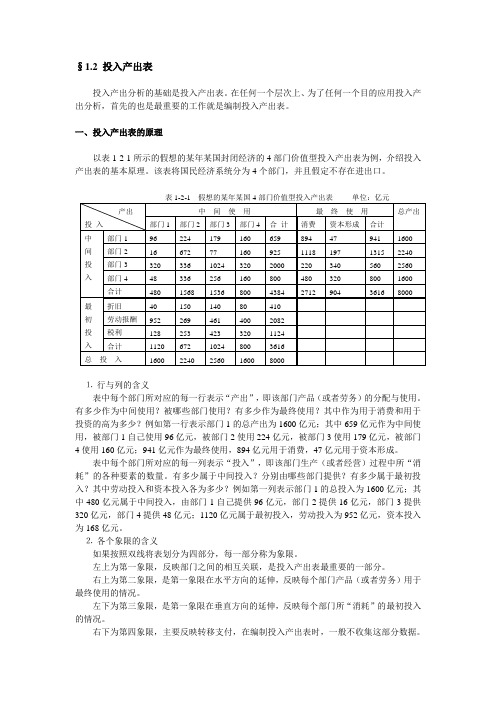
一、投入产出表的原理以表1-2-1所示的假想的某年某国封闭经济的4部门价值型投入产出表为例，介绍投入产出表的基本原理。
该表将国民经济系统分为4个部门，并且假定不存在进出口。
⒈行与列的含义表中每个部门所对应的每一行表示“产出”，即该部门产品（或者劳务）的分配与使用。
有多少作为中间使用？被哪些部门使用？有多少作为最终使用？其中作为用于消费和用于投资的高为多少？例如第一行表示部门1的总产出为1600亿元；其中659亿元作为中间使用，被部门1自己使用96亿元，被部门2使用224亿元，被部门3使用179亿元，被部门4使用160亿元；941亿元作为最终使用，894亿元用于消费，47亿元用于资本形成。
表中每个部门所对应的每一列表示“投入”，即该部门生产（或者经营）过程中所“消耗”的各种要素的数量。
有多少属于中间投入？分别由哪些部门提供？有多少属于最初投入？其中劳动投入和资本投入各为多少？例如第一列表示部门1的总投入为1600亿元；其中480亿元属于中间投入，由部门1自己提供96亿元，部门2提供16亿元，部门3提供320亿元，部门4提供48亿元；1120亿元属于最初投入，劳动投入为952亿元，资本投入为168亿元。
⒉各个象限的含义如果按照双线将表划分为四部分，每一部分称为象限。
左上为第一象限，反映部门之间的相互关联，是投入产出表最重要的一部分。
右上为第二象限，是第一象限在水平方向的延伸，反映每个部门产品（或者劳务）用于最终使用的情况。
左下为第三象限，是第一象限在垂直方向的延伸，反映每个部门所“消耗”的最初投入的情况。
右下为第四象限，主要反映转移支付，在编制投入产出表时，一般不收集这部分数据。
⒊ 几个平衡关系将表1-2-1中的数字用符号表示，并将部门数量扩充到n ，见表1-2-2。
投入产出核算(第一节)2017.10
第Ⅱ象限 (最终产品或最终使用 ) ： 反映各部门提供
最终产品的数量和构成情况（细分为消费、投资和
净出口）。
第Ⅲ象限 ( 最初投入或增加值 ) ： 反映各部门的最初
投入数量及其构成（细分为劳动报酬、生产税净额、 盈余和折旧）。
第Ⅳ象限：空白（可在国民核算矩阵中适当开发）。
13
二、准确理解投入产出表中数据的含义
采用 产品部门×产业部门 表式 行 表示：各种产品的使用去向的 列 表示：各产业部门都消耗了那些产品 此表又称投入表，或U表
第一产业行第二产业列的数据（24917）的含义：
24917个单位的农产品提供给用于第二产业生 产活动用 或第二产业部门所消耗的农产品的数量24917
29
不同国家公布的投入产出表的类型不同
11
第Ⅰ象限(中间产品或中间消耗)：核心。反映各部门之间相 互提供、相互消耗产品的技术经济联系。 特点： 1、横行标题和纵栏标题是名称、排序相同的产品部门， 具有严整的棋盘式结构；
2、横行：提供中间产品的部门(产出部门)； 纵栏：消耗中间产品的部门(投入部门)； 表中每项数据都具有“产出”与“消耗”的双重涵义。
如某年，产业部门口径的石油和天然气开采业
总产值为1989.37亿元，而产品部门口径的该部门 总产值为1631.39亿元。
产业部门和产品部门举例
假设一个经济体只有两家企业，
企业 A B 主要生产 次要生产 总产值 活动产出 活动产出 按产业部门统计 按产品部门统计 22 23 发电20万 炼焦2万 33 32 炼焦30万 发电3万
为获得这些成果，要进行中间投入和最初投入
8
中间投入共计20234亿元，包括： 消耗了6877亿元的本部门产品、10260亿元的 第二产业产品和3097亿元的第三产业产品。
投入产出表的结构及中国投入产出表ppt课件
一、中国式投入产出表的基本表式
中国1997年投入产出表（按当年生产者价格计算）
中间使用
最终使用
产出
物质生产部门（共101个部门）
非物质街道部门 （共23个部门）
第一产业 第二产业
第三产业
投入
（共5个部门） （共85个部门）
（共34个部门）
物质生
中 产部门
间
（101个 部门）
投
入 非物质生
产部门 （23个部
表的左下角称为第Ⅲ象限，其宾栏项目与第Ⅰ象限宾 栏项目相同，其主栏项目有固定资产折旧、劳动者 报酬、生产税净额、营业盈余等。固定资产折旧单 独作为一行列出，根据需要可归并到第Ⅰ象限或第 Ⅲ象限。第Ⅲ象限如果包括固定资产折旧，则反映 各部门增加值的构成。
• 表的右下角称为第Ⅳ象限。从理论上讲该象限是反 映最终产品的再分配的情况，实际上再分配是很复 杂的经济问题。因此，目前该象限的应用还在研究 之中。
表的右上角称为第Ⅱ象限，其主栏项目与第Ⅰ象限 主栏项目相同，其宾栏项目有最终消费、资本形成、 进出口等。在实际编表时上述这些项目还可以细分。 该象限反映不参加本期生产的最终产品的使用情况；
资金是运动的价值，资金的价值是随 时间变 化而变 化的， 是时间 的函数 ，随时 间的推 移而增 值，其 增值的 这部分 资金就 是原有 资金的 时间价 值
资金是运动的价值，资金的价值是随 时间变 化而变 化的， 是时间 的函数 ，随时 间的推 移而增 值，其 增值的 这部分 资金就 是原有 资金的 时间价 值
（五）确定部门规模的一般原则
既要坚持纯部门划分的规定，又不要使部门划分过细。
在全面衡量需要与可能后确定一个适度的规模。 所谓“需要”，是指编制投入产出表的目的：如果用于
解读投入产出表
• 投入产出表在二十世 纪三十年代产生于美 国，它是由美国经济 学家、哈佛大学教授 瓦西里· 列昂惕夫 （W.Leontief）在前人 关于经济活动相互依 存性的研究基础上首 先提出并研究和编制 的。
• 投入产出表，也被称为里昂惕夫表或产业联系表， 它以矩阵形式，描述国民经济各部门在一定时期 （通常为一年）生产中的投入来源和产出使用去 向，揭示国民经济各部门间相互依存、相互制约 的数量关系，使用它可以从生产消耗和分配使用 两方面分析产品在产业之间的运动过程。 • 根据计量标准的不同，分为实物型投入产出表和 价值型投入产出表。
实物投入产出表的（行）平衡关系式为： (1) 中间产品 + 最终产品 = 总产品
qij+Yi=Qi
(2) 劳动力总量= 各产品生产所需劳动力数量之和
L=
Lj
实物投入产出模型只有行模型没有列模型。
这是因为列向各类产品的计量单位不一致，故不能进行运 算
价值型投入产出表是实物型投入产出表的扩充，以货币为
Xij
外生部分
Xj
•
•
左上为中间产品部分，反映部门之间的经济技术联系(相 互提供产品与消耗产品)，是投入产出表最重要的一部分
xij 表示 j产品部门生产过程中消耗的i产品价值量
• •
右上为最终产品部分，反映每个部门产品（或劳务）用 于最终使用的情况，包括消费、投资和净出口三部分。 左下为毛附加值部分，反映每个部门的折旧和新创造的 价值。
平衡关系
1、行平衡关系 中间产品+最终产品=总产出
i 1 , 2 , n x Y X ij i i
j 1
n
对全社会有：
xij yi X i
投入产出表相关知识介绍
投入产出表相关知识介绍（一）投入产出表的由来投入产出表是运用投入产出技术，将国民经济各部门生产中投入的各种费用的来源与产出的各种产品和服务的使用去向，组成纵横交错的棋盘式平衡表，全面而系统地反映国民经济各部门在生产过程中互相依存、互相制约的经济技术联系。
投入产出表的投入是指各部门在生产货物和服务时的各种投入，包括中间投入的最初投入。
产出是指各部门的产出及其使用去向，包括中间使用和最终使用。
投入产出表于二十世纪三十年代产生于美国，它是由美国经济学家、哈费大学教授瓦西里·列昂惕夫（W.Leontief）在前人关于经济活动相互依存性的研究基础上首先提出并研究和编制的。
列昂惕夫从1931年开始研究投入产出技术，编制投入产出表，目的是研究当时美国的经济结构。
为此，他利用美国国情普查资料编制了1919年和1929年美国投入产出表，并分析美国的经济结构和经济均衡问题。
1936年他在美国《经济学和统计学评论》（1936年8月）上发表了投入产出法的第一篇论文“美国经济制度中投入产出数量关系”，标志着投入产出分析的诞生。
1941年他出版了《美国经济结构1919—1929》一书，他在该书中详细阐述了投入产出技术的主要内容。
1951年该书在增加了1939年投入产出表和一些论文后再版。
1953年，列昂惕夫与他人合作，出版了《美国经济结构研究》一书。
通过这些论著，列昂惕夫提出了投入产出表的概念及其编制方法，阐述了投入产出技术的基础原理，创立了投入产出技术这一科学理论。
正是在投入产出技术方面的卓越贡献，列昂惕夫于1973年获得了第五届诺贝尔经济学奖。
投入产了方法在西方产生也不是偶然的，是有一定历史背景的，主要是为了适应当时资本主义经济发展的需要。
1929年爆发的震撼资本主义世界的经济危机是资本主义国家历史上最严重、持续时间最长的一次经济危机，传统的西方经济理论已无法解释这个问题，这一冲击在资本主义社会产生了极大的反响。
投入产出表与模型投入产出分析知识介绍
数据来源
数据主要来源于统计调查、财务报告、行业协会等渠道。
数据质量审核
对收集到的数据进行质量审核，确保数据的准确性和完整性。
数据处理和分析
对数据进行处理和分析，包括数据的筛选、整理、计算等。
编制结果展示
表格形式展示
将编制结果以表格形式展示，包 括投入产出表、直接消耗系数表、 完全消耗系数表、最终使用表和 初次投入表等。
收集各部门之间的投入产出数据，编制直接消耗系数表，反映各部门 生产过程中的直接消耗关系。
编制完全消耗系数表
根据直接消耗系数表，推算出完全消耗系数表，反映各部门之间的间 接消耗关系。
编制最终使用表和初次投入表
根据完全消耗系数表，编制最终使用表和初次投入表，反映最终使用 和初次投入情况。
数据收集与策制定提供科学依据，帮 助政府和企业制定更加合理和有效的经济政策。
决策支持
投入产出表与模型可以为决策者提供全面的经济分析 和预测，帮助决策者做出更加明智和前瞻性的决策。
THANKS
感谢观看
智能化
借助人工智能和机器学习技术，投入产出表 与模型将实现智能化分析，自动识别数据规 律和趋势，为决策提供更精准的依据。
跨行业与跨区域的应用
跨行业
随着产业融合和跨界合作的发展，投入产出表与模型将应用于更多行业，帮助不同行业 之间实现资源共享和协同发展。
跨区域
随着全球化和区域一体化的发展，投入产出表与模型将应用于更广泛的区域，促进地区 间的经济交流和合作。
通过投入产出模型分析，可以预测经 济发展趋势，为制定经济发展规划提 供支持。
环境影响评价
通过投入产出模型分析，可以评估经 济发展对环境的影响，为环境保护提 供依据。
03
oecd投入产出表中文对照
oecd投入产出表中文对照摘要：一、OECD 投入产出表简介1.OECD 的背景介绍2.投入产出表的概念和作用二、OECD 投入产出表中文对照1.表格的列名及含义2.行名及含义3.数据的具体解读三、OECD 投入产出表的应用价值1.对经济发展的分析2.对政策制定的参考作用3.对学术研究的支持四、我国与OECD 投入产出表的对比1.我国投入产出表的编制情况2.与OECD 投入产出表的差异3.启示与借鉴正文：一、OECD 投入产出表简介OECD，全称经济合作与发展组织，是一个国际性的经济组织。
它致力于研究全球经济发展趋势，为成员国提供政策建议。
投入产出表是一种描述国民经济各部门之间生产、消费和投资活动的关系的矩阵表。
通过投入产出表，我们可以了解各部门之间的相互依赖关系，进而分析经济结构和政策效果。
二、OECD 投入产出表中文对照OECD 投入产出表包含了各个成员国在一定时期内的生产、消费和投资数据。
表格的主要列名包括：部门名称、总产出、中间消费、投资、政府消费、净出口等。
行名则包括各种生产要素和最终用途。
通过中文对照，我们可以更直观地理解表格中的数据含义。
三、OECD 投入产出表的应用价值OECD 投入产出表为政策制定者、经济学家和学者提供了丰富的信息，有助于分析经济发展趋势、研究政策效果和支撑学术研究。
例如，通过分析各部门的产出和投入，我们可以了解哪些部门对经济增长的贡献较大，进而制定有利于经济发展的政策。
四、我国与OECD 投入产出表的对比我国也编制了自己的投入产出表。
与OECD 投入产出表相比，我国的表格在部门划分、数据质量和编制方法上存在一定差异。
通过对比，我们可以发现我国在投入产出表编制方面还有待改进。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
外生部分
外生部分 Xj
• 左上为中间产品部分，反映部门之间的经济技术联系(相
互提供产品与消耗产品)，是投入产出表最重要的一部分
x •
ij 表示 j产品部门生产过程中消耗的i产品价值量
• 右上为最终产品部分，反映每个部门产品（或劳务）用 于最终使用的情况，包括消费、投资和净出口三部分。
• 左下为毛附加值部分，反映每个部门的折旧和新创造的 价值。
实物投入产出表的（行）平衡关系式为： (1) 中间产品 + 最终产品 = 总产品
qij+Yi=Qi
(2) 劳动力总量= 各产品生产所需劳动力数量之和
L= Lj
实物投入产出模型只有行模型没有列模型。
这是因为列向各类产品的计量单位不一致，故不能进行运 算
价值型投入产出表是实物型投入产出表的扩充，以货币为
• 根据计量标准的不同，分为实物型投入产出表和 价值型投入产出表。
实物型投入产出表
j i
总产品
qij
Yi
Qi
第j种产品生产时所消耗的第i种产品的数量
L1 L2
Lj
Ln
L
实物型投入产出表以产品的标准单位作为计量单位 ，比如吨、 千克等单位
• qij是指第j种产品生产时所消耗的第i种产品的数量
• Yi是指第i种产品用作最终产品的数量 • Qi是指第i种产品的生产总量 • Lj是指第j种产品的劳动力需求数量 • L是指各种产品所需劳动力之和
解读投入产出表
• 投入产出表在二十世 纪三十年代产生于美 国，它是由美国经济 学家、哈佛大学教授 瓦西里·列昂惕夫 （W.Leontief）在前人 关于经济活动相互依 存性的研究基础上首 先提出并研究和编制 的。
• 投入产出表，也被称为里昂惕夫表或产业联系表， 它以矩阵形式，描述国民经济各部门在一定时期 （通常为一年）生产中的投入来源和产出使用去 向，揭示国民经济各部门间相互依存、相互制约 的数量关系，使用它可以从生产消耗和分配使用 两方面分析产品在产业之间的运动过程。
计量单位记录了全部的中间产品价值、最终产品价值、毛 附加值价值以及总产值，目前是使用最广泛的投入产出表。 特点： 1.既综合又具体地反映经济关系 2.既可以从使用价值形态又可以从价值形态反映社会产 品的运动 3.既可以用表格形式又可以用数学模型描述经济问题
价值型投入产出表
净 合 计
Xij
内生部分
Yi Xi
nn
n
nn
n
xij yi xij n j
i1 j1
i 1
j1 i1
j
可得
在数量上：
n
n
各产业最终产出=折旧+新价值
yi n j
i1
j
这里需要注意的是： 在数量上，同一部门的最终产品价值不等于其增 加值，即
yi n j 当i j
表 1-2-1 假想的某年某国 4 部门价值型投入产出表 单位：亿元
47 941 1600 197 1315 2240 340 560 2560 320 800 1600 904 3616 8000
最 折旧
40 150 140 80 410
初 劳动报酬 952 269 461 400 2082
投 税利
128 253 423 320 1124
入 合计
1120 672 1024 800 3616
产出
中间使用
最 终 使 用 总产
投入
部门 部门 部门 部门 合 消费 资 本 合计 出
1 2 3 4计
形成
中 部门 1 间 部门 2 投 部门 3 入 部门 4
合计
96 224 179 16 672 77 320 336 1024 48 336 256 480 1568 1536
160 659 894 160 925 1118 320 2000 220 160 800 480 800 4384 2712
总投入
1600 2240 2560 1600 8000
The end,thank you!
平衡关系
1、行平衡关系 中间产品+最终产品=总产出
n
xij Yi X i i 1,2,n
j 1
对全社会有：
nn
n
n
xij yi X i
i1 j1
i 1
i 1
2、列平衡关系 中间投入+毛附加值=总投入
n
xij nNjj X j j 1,2,n
i 1
对全社会有：
Nj=Dj+Vj+Tj+Mj
nn
n
n
xij N j X i
j 1 i1
j 1
j 1
3、同一个部门的平衡关系 n
xij yi
xij n j
j 1
i 1
4、全社会的平衡关系
总投入=总产出