t检验与单因素方差分析
T检验 F检验 单因素分析
《》配对t检验的目的是检验两个样本均数所代表的未知总体均数是否有差别1,T检验和F检验的由来一般而言，为了确定从样本(sample)统计结果推论至总体时所犯错的概率，我们会利用统计学家所开发的一些统计方法，进行统计检定。
通过把所得到的统计检定值，与统计学家建立了一些随机变量的概率分布(probability distribution)进行比较，我们可以知道在多少%的机会下会得到目前的结果。
倘若经比较后发现，出现这结果的机率很少，亦即是说，是在机会很少、很罕有的情况下才出现；那我们便可以有信心的说，这不是巧合，是具有统计学上的意义的(用统计学的话讲，就是能够拒绝虚无假设null hypothesis,Ho)。
相反，若比较后发现，出现的机率很高，并不罕见；那我们便不能很有信心的直指这不是巧合，也许是巧合，也许不是，但我们没能确定。
F值和t值就是这些统计检定值，与它们相对应的概率分布，就是F分布和t分布。
统计显著性（sig）就是出现目前样本这结果的机率。
2，统计学意义（P值或sig值）结果的统计学意义是结果真实程度（能够代表总体）的一种估计方法。
专业上，p值为结果可信程度的一个递减指标，p值越大，我们越不能认为样本中变量的关联是总体中各变量关联的可靠指标。
p值是将观察结果认为有效即具有总体代表性的犯错概率。
如p=0.05提示样本中变量关联有5%的可能是由于偶然性造成的。
即假设总体中任意变量间均无关联，我们重复类似实验，会发现约20个实验中有一个实验，我们所研究的变量关联将等于或强于我们的实验结果。
（这并不是说如果变量间存在关联，我们可得到5%或95%次数的相同结果，当总体中的变量存在关联，重复研究和发现关联的可能性与设计的统计学效力有关。
）在许多研究领域，0.05的p值通常被认为是可接受错误的边界水平。
3，T检验和F检验至於具体要检定的内容，须看你是在做哪一个统计程序。
举一个例子，比如，你要检验两独立样本均数差异是否能推论至总体，而行的t检验。
t检验与方差分析
第六章数值变量资料的统计分析数值变量资料又称计量资料，通常是指每个观察单位某项指标量的大小，一般具有计量单位。
这类资料按分析的内容一般可分为两种：一种是比较几种处理之间的效应，简单地讲就是比较各处理组观察值均数、方差的大小；另一种是寻找指标间的关系，即某个（或某些）指标的取值是否受其它指标的影响。
本章主要介绍不同设计类型的数值变量资料的比较。
§样本均数与总体均数比较的t 检验t检验亦称student's t 检验，主要用于下列三种情况：(1)样本均数与总体均数比较；(2)配对数值变量资料的比较；(3)两样本均数的比较。
Stata用于样本均数与总体均数比较的t 检验的命令是：ttest 变量名= #val这里，＃val 表示总体均数。
命令中可以选用if 语句和in 语句对要分析的内容加一些条件限制。
对已知样本含量、均数和标准差的资料，欲将其与某总体均数进行比较，Stata 还提供了更为简洁的命令是：】ttesti #obs #mean #sd #val这里，#obs 表示样本含量，#mean 表示样本均数，#sd 表示样本标准差， #val 表示总体均数。
§两样本均数比较的t检验一、配对设计ｔ检验医学研究中常将受试对象配成对子，对每对中的两个受试对象分别给予两种不同的处理，观察两种处理的结果是否一致，称为配对(设计)研究。
有时以同一个受试对象先后给予两种不同的处理，观察两种处理的结果是否相同，这种配对称为自身配对。
配对设计的优点是能消除或部分消除个体间的差异，使比较的结果更能真实地反映处理的效应。
配对t检验首先计算每对结果之差值，再将差值均数与0作比较。
如两种处理的效应相同，则差值与0没有显著性差异。
检验假设H0为：两种处理的效应是相同，或总体差值均数为0。
stata用于配对样本t检验的命令是：\Ttest 变量1 = 变量2这里，这里“变量1”和“变量2”是成对输入的配对样本。
t检验和方差分析的前提条件及应用误区
t检验和方差分析的前提条件及应用误区集团标准化工作小组 #Q8QGGQT-GX8G08Q8-GNQGJ8-MHHGN#t检验和方差分析的前提条件及应用误区用于比较均值的t检验可以分成三类，第一类是针对单组设计定量资料的；第二类是针对配对设计定量资料的；第三类则是针对成组设计定量资料的。
后两种设计类型的区别在于事先是否将两组研究对象按照某一个或几个方面的特征相似配成对子。
无论哪种类型的t检验，都必须在满足特定的前提条件下应用才是合理的。
若是单组设计，必须给出一个标准值或总体均值，同时，提供一组定量的观测结果，应用t检验的前提条件就是该组资料必须服从正态分布；若是配对设计，每对数据的差值必须服从正态分布；若是成组设计，个体之间相互独立，两组资料均取自正态分布的总体，并满足方差齐性。
之所以需要这些前提条件，是因为必须在这样的前提下所计算出的t统计量才服从t分布，而t检验正是以t分布作为其理论依据的检验方法。
值得注意的是，方差分析与成组设计t检验的前提条件是相同的，即正态性和方差齐性。
t检验是目前医学研究中使用频率最高，医学论文中最常见到的处理定量资料的假设检验方法。
t检验得到如此广泛的应用，究其原因，不外乎以下几点：现有的医学期刊多在统计学方面作出了要求，研究结论需要统计学支持；传统的医学统计教学都把t检验作为假设检验的入门方法进行介绍，使之成为广大医学研究人员最熟悉的方法；t检验方法简单，其结果便于解释。
简单、熟悉加上外界的要求，促成了t检验的流行。
但是，由于某些人对该方法理解得不全面，导致在应用过程中出现不少问题，有些甚至是非常严重的错误，直接影响到结论的可靠性。
将这些问题归类，可大致概括为以下两种情况：不考虑t检验的应用前提，对两组的比较一律用t检验；将各种实验设计类型一律视为多个单因素两水平设计，多次用t检验进行均值之间的两两比较。
以上两种情况，均不同程度地增加了得出错误结论的风险。
而且，在实验因素的个数大于等于2时，无法研究实验因素之间的交互作用的大小。
统计学0715单因素方差分析
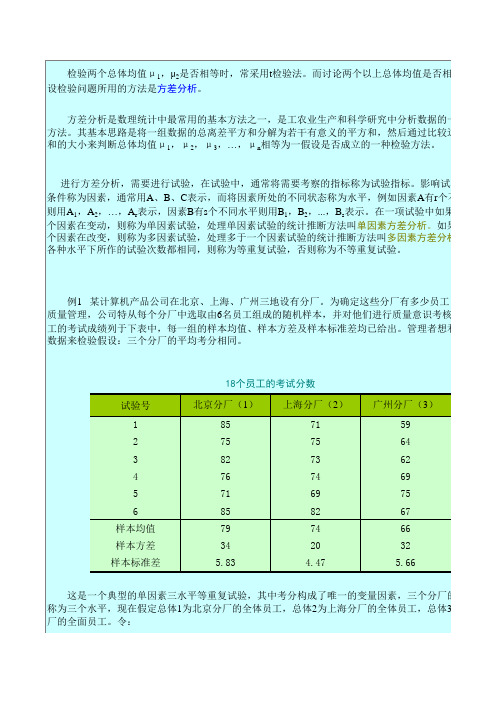
18名员
μ1=总体1的平均考分
μ2=总体2的平均考分
μ3=总体3的平均考分
尽管并不知道μ1、μ2、μ3的实际值，但仍可通过样本资料来检验如下假设：
H0：μ1=μ2=μ3
H1：μ1，μ2，μ3不全相等
如果检验结果发现三个样本均值的差异足够大，这时就有理由拒绝原假设，接受备择假设，即认为三个分厂的平均考分不相同，也就是说三个分厂的全面质量管理效果不一样。
从例1中可以看出，进行方差分析需要满足以下三个假定：
1、对每个总体而言，各变量因素服从正态分布。
具体到此例题，要求三个分厂的考试分数服从正态分布。
2、要求各变量因素的方差对所有总体都相同。
3、观察值是独立的。
如此例，意味着每个员工的考分都与其他员工的考分独立。
均值是否相等时的假
分析数据的一种重要后通过比较这些平方验方法。
标。
影响试验指标的因素A有r个不同水平试验中如果只有一差分析。
如果多于一因素方差分析。
若在。
有多少员工了解全面量意识考核。
18名员。
管理者想利用这些
，三个分厂的位置就员工，总体3为广州分
厂的考试分数服从正立。
：
接受备择假设，即认。
t检验与方差分析
移动靶与固定靶）实验设计
• 注意
– 变量的定义（define） – 交互作用不显著只报告主效应的结果就可以
• 本来应该显著，但是没有显著
–β过大 –Observed power (1- β),0.8
• 五类地区教师工资收入差距，省会地区教 师的工资比非省会地区的教师工资高，但 是差异不显著。县城地区教师的工资高于 乡镇的，乡镇与村庄没有差别。同时省会 和非省会地区的工资高于县城、乡镇和村 庄三地区的，且差异显著。
几种方差分析的区别
• 组间，被试间
– ANOVA
• 单因素方差分析，如只有两个水平也可以做t检验
-Univariate
• 单因素或多因素方差分析 • 如交互作用显著，做简单效应比较
• 组内（被试内）混合实验设计
– Repeated measures
Post hoc
• 当某个因素的水平多于2个时，做事后多重 比较
内设计
• 方差齐性检验
– 方差即离散程度 – Levene's Test for Equality of Variances
独立样本单因素和多因素方差分析
• ANOVA和Univariate • 方差分析也称F检验 • 适用条件
– 正态 – 独立性（可加性） – 变异同质（方差齐性）Homogeneity tests
• 运动多少有没有性别差异？
– 组间方差分析，独立样本t检验
• 阴天时的心情和晴天时的心情会不同吗？
– 重复测量方差分析，相关样本t检验
• 漂亮的人朋友越多吗？
– 组间方差分析，如果漂亮是连续变量可以做相关
t检验和方差
炼的中学生心脏功能是否与一般的中学生相同，现收集了某地区中学常年
参加体育锻炼的16名男生的心率资料，问能否认为常年参加体育锻炼的男 生心率次数低于一般男生？（xinlv.sav）
29
综合练习
4.18名黑热病兼贫血患者被随机分成两组各9名，分别用葡萄糖锑钠（A） 和复方葡萄糖锑钠（B）治疗，观察治疗前后血色素（%）的变化，测定 结果如下。试评价①这两种药是否都有效。②A,B两药的疗效是否有差
分变量
分组变量
19
三、两独立样本t检验 Independent-Samples T Test 过程
结果解释
结果分为两部分，第一部分为Levene’s方差齐性检验结果，用于判断两总体方差是否 齐。本例， F=0.440 ， P=0.514 ，方差齐；第二部分则分别给出两组所在总体方差齐和不齐
时的t检验结果：第一行代表方差齐的结果，第二行代表方差不齐时的t’检验结果。
病人
健康人
2.90 5.41 5.48 4.60 4.03 5.10 4.97 4.24 4.36 2.72 2.37 2.09 7.10 5.92
5.18
8.79
3.14
6.46
3.72
6.64
5.60
4.57
7.71
4.99
4.01
18
三、两独立样本t检验 Independent-Samples T Test 过程
36
一、单因素方差分析 One-Way ANOVA
1、Statistics复选框： Descriptive：输出常用统计描述指标
Homogeneity of variance test：方差齐性检验
2、Means plot：用各组均数作均数图
T检验及单因素方差分析
T检验及单因素方差分析T检验是一种用于比较两个样本均值是否具有统计学意义的方法，而单因素方差分析则是一种用于比较三个或更多个样本均值是否具有统计学意义的方法。
本文将详细介绍T检验和单因素方差分析的基本原理、假设条件、计算公式以及实际应用。
一、T检验的基本原理T检验是由英国统计学家威廉·塞吉威德·高斯特及学生威廉·赖斯·格斯特发展而来的。
T检验基于样本均值与总体均值的比较，通过计算差异的标准误差来判断这种差异是否具有统计学意义。
T检验的基本原理是假设样本的均值服从正态分布，通过计算样本均值与总体均值之间的标准差来估计差异的大小。
二、T检验的假设条件T检验的假设条件包括正态分布假设、独立性假设和方差齐性假设。
1.正态分布假设：样本来自正态分布总体或样本容量足够大时，可以近似看作来自正态分布总体。
2.独立性假设：样本之间是相互独立的，即一个样本的观察值与另一个样本的观察值之间没有关联。
3.方差齐性假设：不同样本的方差相等，即总体的方差是相同的。
三、T检验的计算公式T检验的计算公式包括两种情况：独立样本T检验和配对样本T检验。
1.独立样本T检验：适用于两个独立的样本均值比较。
计算公式为：t = (X1 - X2) / se其中，X1和X2分别为两个样本的均值，se为标准误差，t为检验统计量。
2.配对样本T检验：适用于两个相关的样本均值比较。
计算公式为：t=(X1-X2)/(s/√n)其中，X1和X2分别为两个样本的均值，s为差异的标准差，n为样本容量，t为检验统计量。
四、单因素方差分析的基本原理单因素方差分析是用于比较三个或更多个样本均值是否具有统计学意义的方法。
它基于样本之间的差异和样本内的差异，通过计算组间方差和组内方差的比值来判断这种差异是否显著。
单因素方差分析的基本原理是假设总体均值相等，通过计算组间方差和组内方差的比值来检验这一假设。
五、单因素方差分析的假设条件单因素方差分析的假设条件包括正态分布假设、独立性假设和方差齐性假设。
STATA第四章t检验和单因素方差分析命令输出结果说明
第四章 t检验和单因素方差分析命令与输出结果说明·单因素方差分析单因素方差分析又称为Oneway ANOVA,用于比较多组样本的均数是否相同，并假定：每组的数据服从正态分布,具有相同的方差，且相互独立，则无效假设。
原假设：H0:各组总体均数相同。
在STATA中可用命令：oneway 观察变量分组变量[, means bonferroni]其中子命令bonferroni是用于多组样本均数的两两比较检验。
例：测定健康男子各年龄组的淋巴细胞转化率(%)，结果见表，问:各组的淋巴细胞转化率的均数之间的差别有无显著性？健康男子各年龄组淋巴细胞转化率(%)的测定结果:11-20 岁组：58 61 61 62 63 68 70 70 74 7841-50 岁组：54 57 57 58 60 60 63 64 6661-75 岁组：43 52 55 56 60用变量x 表示这些淋巴细胞转化率以及用分组变量group=1，2，3分别表示11-20岁组，41-50岁组和61-75岁组,即：数据表示为：x 58 61 61 62 63 68 70 70 74 78 54 57 group 1 1 1 1 1 1 1 1 1 1 2 2x 57 58 60 60 63 64 66 43 52 55 56 60 group 2 2 2 2 2 2 2 3 3 3 3 3则用 STATA 命令：oneway x group, mean bonferroni| Summary of xgroup | Mean ①-------------+------------1 | 66.52 | 59.8888893 | 53.2------+------------Total | 61.25 ②Analysis of VarianceSource SS df MS F Prob > F-------------------------------------------------------------------------------Between groups 616.311111③ 2 ④ 308.155556⑤ 9.77⑥ 0.0010⑦Within groups 662.188889⑧ 21⑨ 31.5328042⑴-------------------------------------------------------------------------------Total 1278.50 23 55.586956（2）Bartlett's test for equal variances:chi2(2) = 2.1977 （3）Prob>chi2=0.333Comparison of x by group(Bonferroni)Row Mean- |Col Mean | 1 2-------------- --|--------------------------------------2 | -6.61111 （4）| 0.054 （5）|3 | -13.3 （6） -6.68889（8）| 0.001 （7） 0.134 （9）①对应三个年龄组的淋巴细胞转化率的均数；②三组合并在一起的总的样本均数；③组间离均差平方和；④组间离均差平方和的自由度；⑤组间均方和(即：⑤=③/④)；⑧组内离均差平方和；⑨组内离均差平方和的自由度；（1）组内均方和(即：（1）=⑧/⑨)；⑥为F 统计值(即为⑤/（1）)；⑦为相应的p值；（2）为方差齐性的Bartlett检验；（3）方差齐性检验相应的p值；（4）第二组的淋巴细胞转化率样本均数—第一组的淋巴细胞转化率的样本均数的差；（5）第二和第一组均数差的显著性检验所对应p 值；（6）第三组的淋巴细胞转化率样本均数—第一组的淋巴细胞转化率的样本均数的差；（7）第三和第一组均数差的显著性检验所对应的 p 值；（8）第三组的淋巴细胞转化率样本均数—第二组的淋巴细胞转化率的样本均数的差；（9）第三和第二组均数差的显著性检验所对应的p 值。
单因素试验的方差分析
>weight=c(51,40,43,48,23,25,26,23,28) >A=factor(c(rep(1,4),rep(2,3),rep(3,2))) >result=aov(weight~A) >summary(result)
方差分析表
方差来源 平方和 自由度 均方和 F 值
F 值临介值
组间
1）组间差别：因素效应
灯泡的使用寿命——试验指标
灯丝的配料方案——试验因素（唯一的一个） 四种配料方案（甲乙丙丁）——四个水平
因此，本例是一个四水平的单因素试验。
用X1，X2，X3，X4分别表示四种灯泡的使用寿命，即为 四个总体。假设X1，X2，X3，X4相互独立，且服从方差 相同的正态分布，即Xi~N（i，2）（i=1，2，3，4）
单因素试验方差分析表
方差来源 平方和 自由度 均方和
F值
组间 组内
SS A
df A
MS A
SS A df A
F MSA MSE
SSE
df E
MSE
SSE df E
总和 SST dfT
r ni
2
SST
Xij X
i1 j1
dfT n 1
r ni
2
SSA
Xi X
i1 j1
dfA r 1
引言
在工农业生产和科研活动中，我们经常遇到这样 的问题：影响产品产量、质量的因素很多，例如影 响农作物的单位面积产量有品种、施肥种类、施肥 量等许多因素。我们要了解这些因素中哪些因素对 产量有显著影响，就要先做试验，然后对测试结果 进行分析，作出判断。方差分析就是分析测试结果 的一种方法。
Hale Waihona Puke 基本概念本例问题归结为检验假设 H0：1= 2= 3= 4 是否成立
STATA第四章t检验和单因素方差分析命令输出结果说明
第四章 t检验和单因素方差分析命令与输出结果说明·单因素方差分析单因素方差分析又称为Oneway ANOVA,用于比较多组样本的均数是否相同，并假定：每组的数据服从正态分布,具有相同的方差，且相互独立，则无效假设。
原假设：H0:各组总体均数相同。
在STATA中可用命令：oneway 观察变量分组变量[, means bonferroni]其中子命令bonferroni是用于多组样本均数的两两比较检验。
例：测定健康男子各年龄组的淋巴细胞转化率(%)，结果见表，问:各组的淋巴细胞转化率的均数之间的差别有无显著性？健康男子各年龄组淋巴细胞转化率(%)的测定结果:11-20 岁组：58 61 61 62 63 68 70 70 74 7841-50 岁组：54 57 57 58 60 60 63 64 6661-75 岁组：43 52 55 56 60用变量x 表示这些淋巴细胞转化率以及用分组变量group=1，2，3分别表示11-20岁组，41-50岁组和61-75岁组,即：数据表示为：x 58 61 61 62 63 68 70 70 74 78 54 57 group 1 1 1 1 1 1 1 1 1 1 2 2x 57 58 60 60 63 64 66 43 52 55 56 60 group 2 2 2 2 2 2 2 3 3 3 3 3则用 STATA 命令：oneway x group, mean bonferroni| Summary of xgroup | Mean ①-------------+------------1 | 66.52 | 59.8888893 | 53.2------+------------Total | 61.25 ②Analysis of VarianceSource SS df MS F Prob > F-------------------------------------------------------------------------------Between groups 616.311111③ 2 ④ 308.155556⑤ 9.77⑥ 0.0010⑦Within groups 662.188889⑧ 21⑨ 31.5328042⑴-------------------------------------------------------------------------------Total 1278.50 23 55.586956（2）Bartlett's test for equal variances:chi2(2) = 2.1977 （3）Prob>chi2=0.333Comparison of x by group(Bonferroni)Row Mean- |Col Mean | 1 2-------------- --|--------------------------------------2 | -6.61111 （4）| 0.054 （5）|3 | -13.3 （6） -6.68889（8）| 0.001 （7） 0.134 （9）①对应三个年龄组的淋巴细胞转化率的均数；②三组合并在一起的总的样本均数；③组间离均差平方和；④组间离均差平方和的自由度；⑤组间均方和(即：⑤=③/④)；⑧组内离均差平方和；⑨组内离均差平方和的自由度；（1）组内均方和(即：（1）=⑧/⑨)；⑥为F 统计值(即为⑤/（1）)；⑦为相应的p值；（2）为方差齐性的Bartlett检验；（3）方差齐性检验相应的p值；（4）第二组的淋巴细胞转化率样本均数—第一组的淋巴细胞转化率的样本均数的差；（5）第二和第一组均数差的显著性检验所对应p 值；（6）第三组的淋巴细胞转化率样本均数—第一组的淋巴细胞转化率的样本均数的差；（7）第三和第一组均数差的显著性检验所对应的 p 值；（8）第三组的淋巴细胞转化率样本均数—第二组的淋巴细胞转化率的样本均数的差；（9）第三和第二组均数差的显著性检验所对应的p 值。
3-SPSSt检验与单因素方差分析
5.18
8.79
3.14
6.46
3.72
6.64
5.60
4.57
7.71
4.99
4.01
2013-8-15
Page17
SPSS统计软件操作
Independent-Sample t test 过程
Group Statistics
分 组 支管人 气病 健人 康
N 14 11 Mean 4.3 779 5.5 282 Std . Deviation 1.4 498 9 1.7 354 0 Std . Error Mean .38 750 .52 324
• 是指采用统计图、统计表、统计指标等形式来对资 料的数量特征和分布规律作出测定和描述的一种方
法。
statistical inference统计推断 • 统计推断包括研究如何抽样，如何由样本信息来推 断总体特征。
2013-8-15
Page3
SPSS统计软件操作
理论回顾
假设检验 Hypothesis test
Page19
SPSS统计软件操作
Paired-sample t test
操作提示：Analyze →Compare Means →Paired-Sample T Test …
待选变量 配对变量
2013-8-15
Page20
SPSS统计软件操作
Paired-sample t test
【例4】
10例患者治疗前后的血红蛋白见数据“血红蛋白.sav”。问
差相等
优点： 不受比较组数的限制，可比较多组均数 可同时分析多个因素的作用 可分析因素间的交互作用
2013-8-15
Page24SPSS统计软件操作One-way ANOVA
t检验与单方差分析PPT资料
事实上，小概率事件在随机抽样中还是可能发生的，
如果该P值太小，成为了我们所定义的小概率事件（小于等于α水准），则我们怀疑所做的假设不成立，从而拒绝H0。
察在假设条件下随机样本的特征信息是否属小概率事
• 二是与H0相对立的备择假设 (alternative hypothesis),记为H1。
统计方法应当注意其适用条件
近，不存在差别）考试后的成绩是否存在差异？
均数为正，因此可推断出是使得病人血压下
三、计算检验统计量和P值
三、完全随机的两样本t检验
完全随机的两样本t检验
目的：
推断两个样本是否来自相同的总体，更具体地说，
是要检验两样本所代表的总体均数是否相等。
检验假设
无效假设H0：μ1＝μ2
检验结果
多个子集，利用studentized
range分布来进行
件，若为小概率事件，则怀疑假设成立有悖于该样本
基本思想：先建立一个关于样本所属总体的假设，考
D=X- u0
所提供特征信息，因此拒绝假设
•因此，认为两者的差别无统计学意义，但是这并不意味着可以接受H0
• 二是与H0相对立的备择假设 (alternative hypothesis),记为H1。
检验假设H0本来是成立的，而根据样本信息拒
绝H0的可能性大小的度量，换言之，α是拒绝
了实际上成立的H0的概率。
常用的检验水准为α = 0.05，其意义是：在所设
H0的总体中随机抽得一个样本，其均数比手头
样本均数更偏离总体均数的概率不超过5％
假设检验的基本步骤
三、计算检验统计量和P值
检验统计量的特点：
基本思想：先建立一个关于样本所属总体的假设，考
统计学常用检验方法
统计学常用检验方法
一、t-检验
t-检验是用来检验两个样本或分组数据是否有显著性差异的常用统计
学方法。
t-检验分为单样本t检验、双样本t检验、单因素方差分析t检验、多元t检验和配对t检验等几种。
t检验不需要数据符合正态分布，
但是样本量较少（一般大于30）时，其检验结果更可靠。
二、x2检验
x2检验是统计学常用的检验方法之一，它用来检验实验结果是否符
合假设的要求。
x2检验有单因素x2检验、双因素x2检验、多因素x2检
验等几种。
x2检验的原理是根据频率相对差异计算x2统计量，根据x2
分布表查出检验的显著水平。
以科学的方法检验观察到的数据和期望得到
的数据是否一致。
x2检验可以用来检测比例分布的符合程度，也可以用
来检测总体参数的有无变化的符合程度。
三、F检验
F检验是统计学中用来检验两个母体均方差是否相等的一种检验方法，它通常用来检验两个样本的数据是否具有显著差异或者一个样本下受试者
分布于不同实验条件下是否具有显著性差异。
F检验又分为单因素方差分
析F检验和双因素方差分析F检验等几种。
F检验的原理是根据数据的不
同情况计算F检验的统计量，再根据F分布表查出检验的显著水平。
t检验、u检验、卡方检验、F检验、方差分析
配对 t 检验：是采用配对设计方法观察以下几种情形，1，两个同质受试对象分别接受两种不同的 处理；2,同一受试对象接受两种不同的处理；3，同一受试对象处理前后。 u 检验：t 检验和就是统计量为 t,u 的假设检验，两者均是常见的假设检验方法。当样本含量 n 较 大时，样本均数符合正态分布，故可用 u 检验进行分析。当样本含量 n 小时，若观察值 x 符合正 态分布，则用 t 检验（因此时样本均数符合 t 分布），当 x 为未知分布时应采用秩和检验。
检验中如果是比较大于小于之类的就用单侧检验等于之类的问题就用双侧检卡方检验是对两个或两个以上率构成比进行比较的统计方法在临床和医学实验中应用十分广泛特别是临床科研中许多资料是记数资料就需要用到卡方检验
精心整理
统计中经常会用到各种检验，如何知道何时用什么检验呢，根据结合自己的工作来说一说：
t 检验有单样本 t 检验，配对 t 检验和两样本 t 检验。
F 检验又叫方差齐性检验。在两样本 t 检验中要用到 F 检验。
从两研究总体中随机抽取样本，要对这两个样本进行比较的时候，首先要判断两总体方差是否相同， 即方差齐性。若两总体方差相等，则直接用 t 检验，若不等，可采用 t'检验或变量变换或秩和检验 等方法。 其中要判断两总体方差是否相等，就可以用 F 检验。 简单的说就是检验两个样本的方差是否有显着性差异这是选择何种 T 检验（等方差双样本检验， 异方差双样本检验）的前提条件。 在 t 检验中，如果是比较大于小于之类的就用单侧检验，等于之类的问题就用双侧检验。 卡方检验 是对两个或两个以上率（构成比）进行比较的统计方法，在临床和医学实验中应用十分广泛，特别 是临床科研中许多资料是记数资料，就需要用到卡方检验。 方差分析 用方差分析比较多个样本均数,可有效地控制第一类错误。方差分析(analysisofvariance,ANOVA)由 英国统计学家首先提出，以 F 命名其统计量，故方差分析又称 F 检验。 其目的是推断两组或多组资料的总体均数是否相同，检验两个或多个样本均数的差异是否有统计学 意义。我们要学习的主要内容包括 单因素方差分析即完全随机设计或成组设计的方差分析（one-wayANOVA）： 用途：用于完全随机设计的多个样本均数间的比较，其统计推断是推断各样本所代表的各总体均数 是否相等。完全随机设计（completelyrandomdesign）不考虑个体差异的影响，仅涉及一个处理因 素，但可以有两个或多个水平，所以亦称单因素实验设计。在实验研究中按随机化原则将受试对象 随机分配到一个处理因素的多个水平中去，然后观察各组的试验效应；在观察研究（调查）中按某 个研究因素的不同水平分组，比较该因素的效应。 两因素方差分析即配伍组设计的方差分析（two-wayANOVA）： 用途：用于随机区组设计的多个样本均数比较，其统计推断是推断各样本所代表的各总体均数是否 相等。随机区组设计考虑了个体差异的影响，可分析处理因素和个体差异对实验效应的影响，所以 又称两因素实验设计，比完全随机设计的检验效率高。该设计是将受试对象先按配比条件配成配伍 组（如动物实验时，可按同窝别、同性别、体重相近进行配伍），每个配伍组有三个或三个以上受 试对象，再按随机化原则分别将各配伍组中的受试对象分配到各个处理组。值得注意的是，同一受 试对象不同时间（或部位）重复多次测量所得到的资料称为重复测量数据
SPSS基础学习方差分析—单因素分析
SPSS基础学习⽅差分析—单因素分析为什么要进⾏⽅差分析？单样本、两样本t检验其最终⽬的都是分析两组数据间是否存在显著性差异，但如果要分析多组数据间是否存在显著性差异就很困难，因此⽤⽅差分析解决这个问题；举例：t检验可以分析⼀个班男⼥的⼊学成绩差异；⽽⽅差分析可以分析⼀个班来⾃各省市地区同学的⼊学成绩。
在⽅差分析中，涉及到控制变量和随机变量以及观测变量；举例：施肥量是否会给农作物产量带来显著影响；这⾥，控制变量：施肥量，观测变量：农作物产量，随机变量：天⽓、温度……单因素分析⽬的：分析单⼀控制因素影响下的多组样本的均值是否存在显著性差异。
适⽤条件：正态性，每个⽔平下的因变量应服从正态分布；同⽅差性，各组之间的具有相同的⽅差；独⽴性，各组之间是相互独⽴的。
案例分析：案例描述：在某⼀公司下，分析⼴告形式对销售额的影响。
（数据来源：《统计分析与SPSS的应⽤》（第五版）薛薇第六章）题⽬分析：在题⽬中，⼴告形式不⾄两种，没办法⽤两独⽴样本t检验分析形式和销售额之间的显著性差异，同时，只有⼀个控制因素，所以采⽤⽅差分析中的单因素分析。
提出原假设：⼴告形式和销售额之间不存在显著性差异。
界⾯操作步骤：分析—⽐较均值—单因素ANOVA关键步骤截图：分清楚因变量列表和因⼦；因⼦：控制变量，因变量列表：观测变量结果分析：单因素⽅差分析销售额平⽅和df均⽅F显著性组间5866.08331955.36113.483.000组内20303.222140145.023总数26169.306143分析：平⽅和：组间离差平⽅和（SSA）是由控制变量的不同⽔平造成的变差，组内离差平⽅和（SSE）是由随机变量的不同⽔平造成的变差；df：组间⾃由度，在本题中根据⼴告形式的不同分为四组，所以⾃由度为k-1=4-1=3;组内⾃由度n-k=144-k=140;均⽅：即为⽅差；F=SSA/(k-1)÷（SSE/(n-k)）=组间⽅差/组内⽅差，F值显著性⼤于1，说明控制变量对观测变量的影响⽐随机变量⼤，反之有效；P-值=0.00<0.05，所以拒绝原假设，认为不同的⼴告形式和地区对销售额的平均值产⽣了显著影响，不同的⼴告形式、地区对销售额的影响效应不全为0。
统计分析方法(t检验、单因素方差分析和多因素方差分析)
两组独立样本的比较：独立样本t检验 在变量视图中填入变量：这里的X为需分析数据，G代表分组
在数据视图中录入数据： G下方的数据1、2为分组 X下方的数据为相应的分组 对应的需要分析的数据
在工具栏里选择分析——描述统计——探索
将X选入因变量列表，G选入因子列表， 然后单击绘制
勾选带检验的正态图，其余的 可按照默认值 单击继续
在输出页面中找到上述表格，如果sig即P值，大于0.05，说明该 组数据属于正态性数据，可以继续进行独立样本的t检验；如果 有任何一组P值小于0.05，则需改用非参数检验
数据符合正态时，在工具栏中选 择分析，在下拉菜单中选择比较 均值，再选择独立样本T检验
将X选入检验变量，G选入分组变 量，然后点击定义组，组1后填 入1，组2后填入2，继续——确定
在输出页面中找到上述表格，如果sig即P值，大于0.05，说明两组数据方差齐，则 看第一行数据，如果小于0.05，说明两组数据方差不齐，则看第二行数据；sig的 值即为最终所需P值。
单因素方差分析
数据录入后，进行正态性检验，方法 见4、5、6页PPT。检验结果需要全部 正态才能进行单因素方差分析，否则 需要用非参数检验，但非参数检验没 有两两比较。
分析——比较均值——单因素ANOVA 将X选入因变量列表，G选入因子列表 中，单击两两比较，选择LSD，继续， 单击选项，选择方差同质性检验，继 续——确定
方差齐性检验结果显著性大于0.05， 说明方差齐，可以进行单因素方差分 析，如果显著性小于0.05，则说明方 差不齐，则不能进行单因素方差分析
该表为总体的显著性
该表为两两比较的结果 1 2 为1组与2组比较
T检验及其与方差分析的区别
T检验及其与方差分析的区别假设检验是通过两组或多组的样本统计量的差别或样本统计量与总体参数的差异来推断他们相应的总体参数是否相同。
t 检验：1.单因素设计的小样本（n＜50）计量资料2.样本来自正态分布总体3.总体标准差未知4.两样本均数比较时，要求两样本相应的总体方差相等•根据研究设计t检验可由三种形式：–单个样本的t检验–配对样本均数t检验(非独立两样本均数t检验)–两个独立样本均数t检验（1）单个样本t检验•又称单样本均数t检验(one sample t test),适用于样本均数与已知总体均数μ0的比较,其比较目的是检验样本均数所代表的总体均数μ是否与已知总体均数μ0有差别。
•已知总体均数μ0一般为标准值、理论值或经大量观察得到的较稳定的指标值。
•单样t检验的应用条件是总体标准s未知的小样本资料( 如n<50),且服从正态分布。
（2）配对样本均数t检验•配对样本均数t检验简称配对t检验(paired t test),又称非独立两样本均数t检验,适用于配对设计计量资料均数的比较,其比较目的是检验两相关样本均数所代表的未知总体均数是否有差别。
•配对设计(paired design)是将受试对象按某些重要特征相近的原则配成对子，每对中的两个个体随机地给予两种处理。
•应用配对设计可以减少实验的误差和控制非处理因素，提高统计处理的效率。
•配对设计处理分配方式主要有三种情况：①两个同质受试对象分别接受两种处理，如把同窝、同性别和体重相近的动物配成一对，或把同性别和年龄相近的相同病情病人配成一对；②同一受试对象或同一标本的两个部分，随机分配接受两种不同处理，如例5.2资料；③自身对比(self-contrast)。
即将同一受试对象处理（实验或治疗）前后的结果进行比较，如对高血压患者治疗前后、运动员体育运动前后的某一生理指标进行比较。
（3）两独立样本t检验两独立样本t 检验(two independent samples t-test)，又称成组t 检验。
t检验和单因素方差分析
参数估计
参数估计
参数：统计学中总体的指标称为参数
如总体均数 μ、总体标准差 σ、总体率 π
统计量：样本的指标称为统计量
如样本均数x、样本标准差 S、样本率 p
参数估计：是指由样本统计量估计总体参数。包括点估计（point
estimation）和区间估计(interval estimation)。
2.用肝素封管留置针的平均使用时间是3.1天，用生理盐水封管平均使用时间是2.9天
问：肝素封管相对生理盐水封管是否可以延长留置针留置时长？
3.采用坐位测量100人的血压得平均收缩压为120±20mmHg，再采用卧位测量这100人得
平均收缩压为118±21mmHg
问：坐位测得的血压要比卧位测得的血压高吗？
4.调查某医院住院100名男患者和100名女患者，男患者的平均焦虑得分是8±2.5，女患者
的平均焦虑得分是7.9±2.4分
问：男患者是否比女患者更容易产生住院焦虑情绪？
t检验
单样本 t 检验 已知样本均数与已知总体均数的比较
• 两受试对象分别接受两种不同的处理后的数据
配对样本 t 检验
• 同一样品用两种不同的方法检验出的结果
选择检验方法，计算检验统计量
根据资料类型、研究设计方案和统计推断的目的，选择适当的检验方法和计算公式。
T检验、z检验、F检验、 2 检验、
根据P 值做出统计推断
P≤α，按照α检验水准则拒绝H0，接受H1
P＞α，则不能拒绝H0
结论：
①P≤0.05，拒绝H0 ，差异有统计学意义，认为联合组和对照组对心脏收缩功能的影响不同。
差异关系
使用新药和未使用新药的两组患者
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
ｔ检验(t test)是以t分布为理论
基础，对一个或两个样本的数值变 量资料进行假设检验常用的方法， 属于参数检验。
正态分布的公式
总体均数
f ( X ) 1 e , ( X -)2 / 2 2 ∞ X ∞
2
总体标准差
μ和σ是正态分布的两个参数，μ和σ决定了x 的概率分布；习惯上用 N (μ, σ2)表示均数为μ，标 准差为σ的正态分布。
季聪华 2012.10.18
假设检验步骤
• 1.建立假设、确定检验水准
(1)零假设或无效假设： H0：μ=μ0，即两 总体均数相同。
➢(2)备择假设或有统计学意义假设H1：
μ≠μ0，即两总体均数不同。根据专业知
识及数据特征，备择假设H1 也有单侧形式：
μ<μ0 ，μ>μ0 。
➢选择双侧检验，还是单侧检验需依据数据 特征和专业知识进行确定。
• 2.选择检验方法、计算统计量
假设检验的方法应针对不同研究目的、设 计及资料的类型选定，并计算相应的检验 统计量。
如在总体方差已知的情况下，进行两均数 的比较用z检验或u检验；在总体方差未知 情况下，进行两均数的比较用 t 检验等。
• 3.确定P值、作出推论
根据计算的检验统计量，确定P值，P值是 在H0成立的情况下随机抽样，获得大于及 等于或(和)小于及等于现有样本资料求得的 检验统计量的概率。
• t检验（n较小时）的计算公式：
• U检验（n较大时）的计算公式：
【例1】已知一般无肝肾疾患的健康人群血尿素氮 均值为 4.882 (mmol/L)，10名脂肪肝患者的血尿素 氮 (mmol/L)测定值为 6.24，4.26，5.36，8.13， 6.96，11.8，5.74，4.37，5.18，8.68。 问：脂肪肝患者血尿素氮含量是否不同于健康人?
应的总体方差相等（方差齐性） u 检验：1.大样本
2.样本小，但总体标准差已知
t检验 • 样本均数与总体均数比较的t检验 • 配对设计资料比较的t检验 • 两独立样本均数比较的t检验 方差分析 • 完全随机设计的单因素方差分析 • 多个样本均数间的多重比较
样本均数与总体均数的比较的t检验，亦 称单样本t检验(one sample t test) 。
• 第二步：将10个数据依次 录入SPSS，形成10行1列的 数据集。
• 第三步：选择分析→比较均值→单样本T检验
• 第四步：在单样本T检验对话框中，检验变 量处移入血尿素氮，检验值处填上4.882。
• 第五步：点确定后产生结果，结果解读。
• 结果解读1
• N：总的样本例数=10 • 均值：算术平均数=6.6720 • 标准差：标准差=2.32515 • 均值的标准误：标准误=0.73528
1. 位置参数：μ
当σ固定不变时，μ越大，曲线沿横轴 越向右移动；反之， μ越小，则曲线沿横轴越向左移 动，所以μ叫正态曲线N（μ, σ2）的位置参数， 。
正态分布位置随参数μ变换示意图
2. 形状参数：σ
当μ固定不变时，σ越大，曲线越平阔； σ越小，曲线越尖峭，σ 叫正态曲线N（μ, σ2）的形 状参数。
单因素方差分析，理论上若不满足方差齐性及正态分布（哪怕有一 条不符合也算），则用秩和检验。
正态分布的检验，首先先将资料进行分组处理 ，然后-非参数检验-旧对话框-1-样本 （看最后
出来的p>0.05则为正态分布） 但一般来说，多直接只看方差齐性，不用看是
否满足正态分布
医学统计学（04） ——t检验与单因素方差分析
f(X)
0.9
0.8
σ=1
0.7
0.6
0.5
0.4
0.3
σ=1.5
0.2
0.1 0
σ=2
-6 -5 -4 -3 -2 -1 0 1 2 3 4 5 8 1.96
t 检验和 u 检验
应用条件： t 检验：1.单因素设计的小样本（n＜50）计
量资料 2.样本来自正态(近似正态)分布总体 3.总体标准差未知 4.两样本均数比较时，要求两样本相
假设检验的分类
➢根据是否正态分布：分参数检验和非参数 检验
➢根据处理因素：分单因素分析和多因素分 析
➢根据比较类型：分优效性、等效性和非劣 效性。
常用假设检验方法的选择（1）
两均数 比较
多组均 数比较
样本与总体比较
两样本 比较
配对 资料
非配对 资料
完全随机设计资 料
配伍组设计资料
拉丁方设计资料 正交设计
用于从正态总体中获得含量为n的样本， 算得均数和标准差，判断其总体均数μ 是否与某个已知总体均数μ0相同。
➢已知的总体均数一般为公认的理论数值、 经验数值、期望数值或经过大量观察所得 的稳定值，如人的正常生理指标(红细胞数、 身高、血压等)。
➢样本均数与总体均数比较的 t 检验，其应用 条件是资料服从正态分布或近似正态分布。
t检验 • 样本均数与总体均数比较的t检验 • 配对设计资料比较的t检验 • 两独立样本均数比较的t检验 方差分析 • 完全随机设计的单因素方差分析 • 多个样本均数间的多重比较
t检验 • 样本均数与总体均数比较的t检验 • 配对设计资料比较的t检验 • 两独立样本均数比较的t检验 方差分析 • 完全随机设计的单因素方差分析 • 多个样本均数间的多重比较
查表，t与自由度为9（10-1）时的t界值进行 比较，得到0.01<p<0.05。
• P=2*[1-CDF.T(2.434,9)]
CDF.T(quant, df)。数值。返回 t 分布（指定自由度为 df）中的 值将小于 quant 的累积概率。
SPSS软件操作
• 第一步：以“血尿素氮” 为变量名，建立变量
• 结果解读2
• t：统计量t=2.434 • Sig（双侧）：p值=0.038 • 均值差值：两个均数的差值=1.79 • 差值的95%CI：0.1267~3.4533
样本均数与总体均数比较的t检验 配对t检验
符号秩和检验 两独立样本比较的t检验
两组资料的秩和检验 中位数检验
单因素方差分析 H检验，多个样本两两比较的秩和检验
两因素方差分析 M检验
三向方差分析 多向方差分析
《中华医学杂志》对来稿统计学处理的有关要求
《中华医学杂志》对来稿统计学处理的有关要求
单因素均数比较