最新5-轴力杆件
轴向受力杆件

在一般情形下,杆件横截面积 A(x)可以
是 x 的函数,沿杆的轴线也可以有轴向分布
载荷 f(x)(图 5-6)。假定此时平面截面假
设仍然成立,由此可以推断同一截面上的应 F1 力仍为均匀分布,但不同截面上的应力是变
化的,即σ x (x) 是 x 的函数。公式(2-9) 已给出轴力的平衡微分关系
dFN dx
f
在微伸长 dδ上做功 fdδ 。如果最终力达
图 5-3
δ Δl
到 F 时的伸长为 Δl ,那么力 F 做的功为
∫ ∫ W =
Δl fdδ =
0
Δl kδ dδ
0
=
kΔl 2
Δl
=
1 2
FΔl
(5-3)
外力做功等于图 5-3 的 f (δ ) 曲线下的面积。这部分功全部转换为杆的应变能,即
U
=W
=
1 2
力集中(stress concentration)。
应力集中的程度用截面上的局部最大应力σmax与名义应力(nominal stress)σ0之比来 表示:
K = σ max σ0
(5-8)
式中σ 0
=
F A0
,A0为开孔处截面的净面积。K称为应力集中系数(stress
concentration
factor)。
F
⋅ Δl
=
1 2
F 2l EA
(5-4)
三、圣维南原理
一般情况下外力将通过夹具、销钉、铆钉、焊接等方式从端部传递给杆件。式(5-1) 对于外力 F 作用点附近的区域并不适用。在 F 力的作用点附近应力分布并不均匀。然而, 只要作用于杆端的分布力的合力的作用线与杆的轴线重合,则可近似地用轴力杆的模型对 杆件做力学分析。法国力学家圣维南(Saint-Venant)指出,作用在弹性体某一局部区域内 的外力系可以用等效力系来代替,这种代替仅仅对原力系作用区域附近的应力有影响。这 就是圣维南原理(Saint-Venant’s principle)。对轴力杆来说,外力作用于杆端的方式的不同, 只会使与杆端距离不大于杆的横向尺寸的范围内的应力分布受到影响,在较远距离处应力 分布不受影响。
工程力学05-杆件的内力图

Bengbu college . The Department of Mechanical and Electronical Engineering .w.p_chen
构件内力图概念、画法
杆件基本变形时内力图的表示
内力图沿杆轴线的分布规律 最大内力与危险截面的确定
《工程力学》
Bengbu college . The Department of Mechanical and Electronical Engineering .w.p_chen
5.2 轴力图与扭矩图
5.2.2 扭矩图 1)扭转内力分量与扭矩
作用在杆件上的外力偶矩可以向杆轴线简化, 简化的结果若力偶作用面在横截面上,该力偶矩分 量——扭矩 扭矩可以是外力简化,也可以由传递的功率计 算得到 2)功率P、转速n和外力偶矩T P (5-1) T=9549 n (N.m) 式中: P:功率(kW) n:转速(r/min)
d
D MD D
确定控制截面
《工程力学》
Bengbu college . The Department of Mechanical and Electronical Engineering .w.p_chen
5.2 轴力图与扭矩图
5.2.2 扭矩图 MA=1146N.m,MB=MC=350N.m,MD=446N.m。 MB MC MA 求各截面扭矩 BC段 SMx= 0 B C A
C
l l MO =2FPl
FP D B
MC C
l
FP
D B
FQC
S M C= 0
解得:
– MC + MO – FP×l =0
FQC=FP MC = MO – FP×l = 2FPl– FPl = FPl
杆件轴力计算

杆件轴力计算摘要:一、杆件轴力计算的基本概念1.杆件轴力的定义2.杆件轴力的作用二、杆件轴力的计算方法1.直接计算法2.间接计算法3.数值计算法三、影响杆件轴力的因素1.杆件的材料性能2.杆件的几何尺寸3.杆件的边界条件四、杆件轴力计算的应用1.工程结构设计2.结构强度分析3.工程事故分析与处理正文:一、杆件轴力计算的基本概念1.杆件轴力的定义杆件轴力是指作用在杆件上的沿轴线方向的力。
在工程结构中,杆件轴力通常是由于外力作用或其他因素引起的。
杆件轴力对杆件的力学性能和稳定性产生重要影响。
2.杆件轴力的作用杆件轴力的作用主要体现在以下几个方面:(1)使杆件产生拉伸或压缩变形;(2)引起杆件的弯曲变形;(3)导致杆件的剪切变形;(4)影响杆件的稳定性。
二、杆件轴力的计算方法1.直接计算法直接计算法是根据杆件所受的外力和边界条件,直接求解杆件轴力。
这种方法适用于简单杆件和受力清晰的结构。
计算公式为:F = F1 + F2 + ...+ Fn其中,F1、F2、...、Fn分别为杆件所受的外力。
2.间接计算法间接计算法是通过求解杆件的弯矩、剪力等内力分布,进而计算杆件轴力。
这种方法适用于复杂杆件和受力复杂的结构。
计算公式为:F = Mx / I其中,Mx为杆件某一点的弯矩,I为杆件截面的惯性矩。
3.数值计算法数值计算法是利用数值分析方法(如有限元法)对杆件轴力进行计算。
这种方法适用于大型结构和高精度要求的计算。
计算公式为:F = ∫Fdσ其中,F为杆件所受的单元力,σ为单元面积。
三、影响杆件轴力的因素1.杆件的材料性能杆件的材料性能直接影响其抗拉、抗压、抗弯等性能。
不同材料具有不同的强度和刚度,从而影响杆件轴力的计算结果。
2.杆件的几何尺寸杆件的几何尺寸(如长度、截面形状和尺寸)对其轴力计算有重要影响。
较大的杆件尺寸会导致较大的轴力,而较小的杆件尺寸会增加其稳定性。
3.杆件的边界条件杆件的边界条件对其轴力计算有很大影响。
《工程力学》第五章 杆件的变形与刚度计算

根据杆所受外力,作出其轴力图如 图 b所示。
(2)计算杆的轴向变形 因轴力FN和横截面面积A沿杆轴线变
化,杆的变形应分段计算,各段变形的 代数和即为杆的轴向变形。
l
FNili FN1l1 FN 2l2 FN 2l3
EAi
EA1
EA1
EA2
1 200 103
( 20 103 100 500
10 103 100 500
10 103 100 )mm 200
0.015mm
例5-2 钢制阶梯杆如图,已知
轴向外力F1=50kN,F2=20kN,
各段杆长为l1=150mm,
l2=l3=120mm,横截面面积为:
1
A1=A2=600mm2,A3=300mm2,
钢的弹性模量E=200GPa。求各
x
l 3
,ym
ax
9
Ml2 3E
I
xMl2 16EI
A
M 6EIl
(l 2
3b2 )
B
M 6EIl
(l 2
3a2 )
三、叠加法计算梁的变形
➢叠加法前提条件:弹性、小变形。 ➢叠加原理:梁在几个载荷共同作用下任一截面的挠度或转角, 等于各个载荷单独作用下该截面挠度或转角的代数和。
F1=2kN,齿轮传动力F2=1kN。主轴的许可变形为:卡盘 C处的挠度不超过两轴承间距的 1/104 ;轴承B处的转角
不超过 1/103 rad。试校核轴的刚度。
解(1)计算截面对中 性轴的惯性矩
Iz
D4
64
(1 4 )
804 (1 0.54 )mm4
64
188104 mm4
(2)计算梁的变形
杆件的内力与内力图轴向拉压杆的内力轴力图轴向拉压杆的内力轴
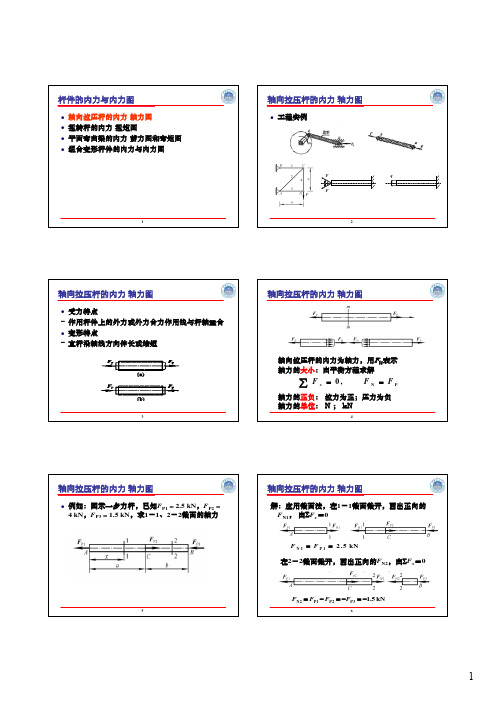
Fθθ34轴向拉压杆的内力轴向拉压杆的内力为轴力,用F N 表示轴力的大小:由平衡方程求解PN ,0F F F x ==∑轴力的正负:拉力为正;压力为负轴力的单位:N ;kN6轴向拉压杆的内力轴力图解:应用截面法,在F N1,由∑F x =0kN5.21P 1N ==F F kN5.13P 2P 1P 2N -=-=-=F F F F 在2-2截面截开,画出正向的F N2,由∑F x =089= 6 kN = -4 kN轴力图画在受力图正下方;10轴向拉压杆的内力轴力图例2 图示一砖柱,柱高3.5m ,截面尺寸370×370mm 2,柱顶承受轴向力F P =60 kN ,砖砌体容重ρ.g =18 kN/m 3。
试绘柱的轴力图。
11轴力图应用截面法,由平衡方程求得:kN46.260P y y A g F --=⋅⋅⋅-ρ,kN 6.68)5.3(,kN 60)0N -=-=F ㈠F N /kNy68.66012轴向拉压杆的内力轴力图等截面直杆在上端A 处固定,其受力如图试绘制杆件的轴力图。
kN,10kN,5P2=F l(a)Cl(b)机械传动轴杆件各相邻横截面产生绕杆轴的相对转动ϕ1720扭矩沿轴线的变化规律e21221. 外力偶矩的计算m N ⋅=1146AmN ⋅=3509549n PB m N ⋅=446n D23扭矩的计算m N 350e ⋅-=-=B M m N 700e e ⋅-=--B C M M mN 446e ⋅=D M 扭矩图问题:如将轮A 与轮C 互换,扭矩图如何?哪种布置受力更合理?mN 700max ⋅=轴力图剪力图和弯矩图组合变形杆件的内力与内力图25梁的外力和内力均可仅由静力平衡方程求解27纵向对称面内时,梁的轴线由位于纵向对称面内的直28单跨静定梁的三种基本形式由静力平衡方程无法全部确定梁所有外力和内力29平面弯曲梁的内力剪力图和弯矩图:剪力F S 和弯矩M 求内力的方法:截面法A F R =M MaF A R =30平面弯曲梁的内力剪力图和弯矩图单位;kNN ·m ;kN ·m31截面,并取右段研究221qa -33平面弯曲梁的内力剪力图和弯矩图剪力方程剪力沿梁轴线的变化规律,即F S =F S (x )弯矩方程弯矩沿梁轴线的变化规律,即M=M (x )按比例绘出F S (x )的图线按比例绘出M (x )的图线剪力图和弯矩图受力分析,画受力图,由平衡方程求支座约束力分段列出剪力方程和弯矩方程,标出变量x 的取值根据剪力方程,求各控制面的剪力值,按比例绘剪力图。
05工程力学(静力学和材料力学)第2版课后习题答案_范钦珊主编_第5章_轴向拉伸与压缩

eBook工程力学(静力学与材料力学)习题详细解答(教师用书)(第5章)范钦珊 唐静静2006-12-18第5章轴向拉伸与压缩5-1试用截面法计算图示杆件各段的轴力,并画轴力图。
解:(a)题(b)题(c)题(d)题习题5-1图F NxF N(kN)x-3F Nx A5-2 图示之等截面直杆由钢杆ABC 与铜杆CD 在C 处粘接而成。
直杆各部分的直径均为d =36 mm ,受力如图所示。
若不考虑杆的自重,试求AC 段和AD 段杆的轴向变形量AC l Δ和AD l Δ解:()()N N 22ssππ44BCAB BC AB ACF l F l l d dE E Δ=+33321501020001001030004294720010π36.××+××=×=××mm ()3N 232c100102500429475286mm π10510π364..CDCD AD AC F l l l d E ΔΔ×××=+=+=×××5-3 长度l =1.2 m 、横截面面积为1.10×l0-3 m 2的铝制圆筒放置在固定的刚性块上;-10F N x习题5-2图刚性板固定刚性板A E mkN习题5-4解图直径d =15.0mm 的钢杆BC 悬挂在铝筒顶端的刚性板上;铝制圆筒的轴线与钢杆的轴线重合。
若在钢杆的C 端施加轴向拉力F P ,且已知钢和铝的弹性模量分别为E s =200GPa ,E a =70GPa ;轴向载荷F P =60kN ,试求钢杆C 端向下移动的距离。
解: a a P A E l F u u ABB A −=−(其中u A = 0)∴ 935.0101010.11070102.1106063333=×××××××=−B u mm钢杆C 端的位移为33P 32s s601021100935450mm π20010154...BC C B F l u u E A ×××=+=+=×××5-4 螺旋压紧装置如图所示。
《工程力学》第5章 杆件的内力图

①扭矩变化规律; ②|T|max值及其截面位置,强度计算(危险截面)
27/65
5.2 轴力图与扭矩图----扭矩图
【例4】圆轴受有四个绕轴线转动的外加力偶,各 力偶的力偶矩的大小和方向均示于图中,其中力 偶矩的单位为N.m,尺寸单位为mm。试画出圆轴 的扭矩图。
【例3】 图示杆的A、B、C、D点分别作用着大小为5P 、8P、4P和 P 的力,试画出杆的轴力图。
OA
BC
D
PA
N1
A
PBPCBCPD D Nhomakorabeax
PA
PB
PC
PD
解: 求OA段内力N1:设置截面如图,列平衡方程
Fx 0 N1 PA PB PC PD 0
N1 PA PB PC PD 5P 8P 4P P 2P21/65
剪力方程和弯矩方程。
MO=2FPl
FP
B
A
C
l
l
39/65
5.3 剪力图与弯矩图--剪力方程与弯矩方程
解:1.确定控制面和分段
截面A、B、C均为控制面。需要分为AC和CB两段建
立剪力和弯矩方程。
2.建立Oxy坐标系
3.建立剪力方程和弯矩方程
y
MO=2FPl
O
A
C
F
P
x
B
l
l
40/65
5.3 剪力图与弯矩图--剪力方程与弯矩方程
41/65
5.3 剪力图与弯矩图--剪力方程与弯矩方程
y
MO=2FPl
O
A
C
l
FP
B l
x2
FP
最新钢结构轴力构件-附答案

钢结构练习四 轴心受力构件一、选择题(××不做要求)1.工字形轴心受压构件,翼缘的局部稳定条件为()yf t b 2351.0101λ+≤,其中λ的含义为( A )。
A )构件最大长细比,且不小于30、不大于100 B )构件最小长细比C )最大长细比与最小长细比的平均值D )30或1002.轴心压杆整体稳定公式f AN ≤ϕ的意义为( D )。
A )截面平均应力不超过材料的强度设计值B )截面最大应力不超过材料的强度设计值C )截面平均应力不超过构件的欧拉临界应力值D )构件轴心压力设计值不超过构件稳定极限承载力设计值3.用Q235钢和Q345钢分别制造一轴心受压柱,其截面和长细比相同,在弹性范围内屈曲时,前者的临界力( C )后者的临界力。
A )大于B )小于C )等于或接近D )无法比较4.为防止钢构件中的板件失稳采取加劲措施,这一做法是为了( A )。
A )改变板件的宽厚比B )增大截面面积C )改变截面上的应力分布状态D )增加截面的惯性矩5.为提高轴心压杆的整体稳定,在杆件截面面积不变的情况下,杆件截面的形式应使其面积分布( B )。
A )尽可能集中于截面的形心处B )尽可能远离形心C )任意分布,无影响D )尽可能集中于截面的剪切中心××6.轴心压杆采用冷弯薄壁型钢或普通型钢,其稳定性计算( B )。
A )完全相同B )仅稳定系数取值不同C )仅面积取值不同D )完全不同7.实腹式轴压杆绕x ,y 轴的长细比分别为λx ,λy ,对应的稳定系数分别为φx , φy ,若λx =λy ,则( D )。
A )φx >φyB )φx =φyC )φx <φyD )需要根据稳定性分类判别8.轴心受压杆的强度与稳定,应分别满足( B )。
A )f A N n ≤=σ,f A N n⋅≤=ϕσ B )f A N n ≤=σ,f AN ⋅≤=ϕσ C )f A N ≤=σ,f A N n ⋅≤=ϕσD )f A N ≤=σ,f AN ⋅≤=ϕσ 式中,A 为杆件毛截面面积;A n 为净截面面积。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
正确理解许用应力和安全系数的概念和意义;熟练应用拉、压
通
强度条件进行强度校核、截面尺寸设计和许用荷载确定。
大
灵活运用杆件的变形计算式求桁架结构节点的位移;
学
熟练用变形比较法解简单超静定问题;了解装配、热应力;
了解应力集中的概念,掌握应力集中系数的确定。
SJTU
材料力学 Mechanics of Materials
变截面拉压杆,例题
例题:涡轮机的叶片在涡轮旋转时受离心力作用。设叶片的截面积为
常数A,弹性模量为E,密度为,涡轮转动的角速度为。涡轮的变形
忽略不计。试计算叶片横截面上的正应力、叶片的位移和总伸长。
解:1,求正应力 在离涡轮轴心x处,取长度为
dx的一段叶片,其质量为,
上 海
dmAdx
x处截面受到离心轴力为
5-轴力杆件
材料力学 Mechanics of Materials
第五章 轴向受力杆件
本章目的
本章目的
推导拉、压杆横截面上正应力公式及杆的变形计算式; 建立拉、压强度条件; 介绍求解简单超静定问题的基本方法; 建立应力集中的概念。
上 基本要求
海
掌握应力推导的方法和步骤;理解平面假设和圣维南原理;
交
kN。l1=l3=300mm, l2=400 mm。直径d1=12mm,d2=16
l3
l2
l1
上 海
mm,d3=24mm。试作AD杆的 轴 力 图 , 求 最 大 正 应 力 max (绝对值),B截面轴向位移,
FN(kN)
交 通
以及AD杆的伸长lAD。
大 学
解: 1, AD杆的轴力分布如右图所示。
轴向伸长
L L F N ( x ) d x L ( y 2 /3 ) x d x L x d x L 2 0 E A ( x ) 0 E (y 2 ) 3 E 0 6 E
上式右边的量纲是长度,由此可以验证公式。
SJTU
材料力学 Mechanics of Materials
第五章 轴向受力杆件
上 海 交 通 大 学
SJTU
材料力学 Mechanics of Materials
上 海 交 通 大 学
SJTU
材料力学 Mechanics of Materials
上 海 交 通 大 学
SJTU
材料力学 Mechanics of Materials
上 海 交 通 大 学
SJTU
材料力学 Mechanics of Materials
d F * x2 d m 2A x d x
交
通 大 学
FN(x)
RodF*2ARo
x
x
xdx
22A(Ro2 x2)
f(x) dx
FN(x) Ro
x Ri
SJTU
材料力学 Mechanics of Materials
第五章 轴向受力杆件
变截面拉压杆,例题
解法一
F N(x)22 A(R o2x2)
海 交
l C D 4 F E N d 3 l 3 2 3 4 2 1 0 ( 5 1 0 0 0 9 0 0 2 ) 4 2 0 .3 1 0 6 0 .1 5 8 m m
通
u B l B C l C D ( 0 . 1 4 2 0 . 1 5 8 ) m m = 0 . 3 m m 向左位移
总伸长可从微段dx的伸长经积分求得
上
因为 d(Δl)FN(x)dx
海
EA
交 通 大
Δ l R R i o F N E ( A x ) d x 2 2 E R R i o ( R o 2 x 2 ) d x 6 2 E ( 2 R o 3 R i 3 3 R o 2 R i )
上 CD段:
海 交 通
C D F A N 3 3 4 F d N 3 2 3 4 ( 2 4 5 2 0 0 1 0 0 0 ) 6 1 1 0 .5 M P a
大 所以最大正应力发生在AB段,
学
m ax176.8M P a
SJTU
材料力学 Mechanics of Materials
上 海 交 通 大 学
SJTU
材料力学 Mechanics of Materials
上 海 交 通 大 学
SJTU
材料力学 Mechanics of Materials
第五章 轴向受力杆件
拉、压杆的变形
2 拉、压杆的变形
变截面圆钢杆ABCD,已知F1
=20kN, F2=35kN, F3=35
D
C F3 B F2
-15 -50
2, 求最大正应力
SJTU
A F1
20
x
材料力学 Mechanics of Materials
第五章 轴向受力杆件
拉、压杆的变形
2 拉、压杆的变形
AB段:
A B F A N 1 1 4 F d N 1 2 1 4 1 2 2 2 0 0 0 1 0 0 6 1 7 6 .8 M P a
第五章 轴向受力杆件 变截
面拉压杆,例题
例题:高度为Lr0 x
重力作用下圆锥体沿轴向的伸长。
解:在高度x处,截面半径为
x
y r0 x L
FN(x) L
上 截面内力等于截面以下圆锥体的重量:
W(x)
海 交
FN(x)1 3y2x
y
通 大 学
大 学
lA D lA B lB C lC D (0 .2 5 3 0 .1 4 2 0 .1 5 8 )m m = 0 .0 4 7 m m 缩短
SJTU
材料力学 Mechanics of Materials
第五章 轴向受力杆件 变截
面拉压杆
变渐变截截面面,杆受分布轴向力的拉压杆
第五章 轴向受力杆件
拉、压杆的变形
3,求uB, lAD
lA B 4 F E N d 1 l 1 2 1 2 4 1 0 2 1 0 0 0 9 0 0 1 2 0 2 .3 1 0 6 0 .2 5 3 m m
上
l B C 4 F E N d 2 l 2 2 2 4 2 1 0 ( 1 1 5 0 0 9 0 0 1 ) 6 2 0 .4 1 0 6 0 .1 4 2 m m
假定平面截面假 设仍成立
微段dx应变
( x) FN( x)
A( x)
(x) dL
dx
F1
A( x )
f(x)
x dx L
F2
L
上
胡克定律 E
海
FN ( x ) F N (x)dF N (x)
交
dLFN(x)dx
dL
通
EA(x)
大 学
L LFN(x)dx 0 EA(x)
20
SJTU
材料力学 Mechanics of Materials
