五年级奥数-组合图形的面积(二)
五年级奥数--图形的面积(二)
文档收集于互联网，已重新整理排版.word版本可编辑.欢迎下载支持.图形的面积（二）我们已经学习过三角形、正方形、长方形、平行四边形、梯形以及圆、扇形等基本图形的面积计算，在实际问题中，我们遇到的往往不是基本图形，而是由基本图形组合、拼凑成的组合图形，它们的面积不能直接用公式计算。
在本讲和后面的两讲中，我们将学习如何计算它们的面积。
例1、大小两个正方形组成下图所示的组合图形。
已知组合图形的周长是52厘米，DG=4厘米，求阴影部分的面积。
例2、如左下图所示，四边形ABCD与DEFG都是平行四边形，证明它们的面积相等。
例3、如左下图所示，一个腰长是20厘米的等腰三角形的面积是140平方厘米，在底边上任意取一点，这个点到两腰的垂线段的长分别是a厘米和b厘米。
求a+b的长。
在例2、例3中，通过添加辅助线，使图形间的关系更清晰，从而使问题得解。
下面再看一例。
例4、如左下图所示，三角形ABC的面积是10平方厘米，将AB，BC，CA分别延长一倍到D，E，F，两两连结D，E，F，得到一个新的三角形DEF。
求三角形DEF的面积。
例5、一个正方形，将它的一边截去15厘米，另一边截去10厘米，剩下的长方形比原来正方形的面积减少1725平方厘米，求剩下的长方形的面积。
练习：1、等腰直角三角形的面积是20平方厘米，在其中做一个最大的正方形，求这个正方形的面积。
2、如下图所示，平行四边形ABCD的周长是75厘米，以BC为底的高是14厘米，以CD为底的高是16厘米。
求平行四边形ABCD的面积。
3、如下图所示，在一个正方形水池的周围，环绕着一条宽2米的小路，小路的面积是80平方米，正方形水池的面积是多少平方米？4、如下图所示，一个长方形被一线段分成三角形和梯形两部分，它们的面积差是28平方厘米，梯形的上底长是多少厘米？5、如下图，在三角形ABC中，BD=DE=EC，BF=FA。
若三角形EDF的面积是1，则三角形ABC的面积是多少？6、一个长方形的周长是28厘米，如果它的长、宽都分别增加3厘米，那么得到的新长方形比原长方形的面积增加了多少平方厘米？7、如下图所示，四边形ABCD的面积是1，将BA，CB，DC，AD分别延长一倍到E，F，G，H，连结E，F，G，H。
五年级上册数学教案-第二单元 组合图形面积的计算-苏教版
五年级上册数学教案-第二单元组合图形面积的计算-苏教版一、教学目标1.掌握组合图形面积的计算方法。
2.能够根据所给条件计算组合图形的面积。
3.培养学生的空间想象力和计算能力。
二、教学重点1.理解组合图形的概念及构成。
2.掌握组合图形面积的计算方法。
三、教学难点1.解决组合图形的面积计算问题。
2.发现组合图形中的规律。
四、教学准备1.教师准备：教学教材、黑板笔、教学PPT。
2.学生准备：学习用书、笔记本、尺子、铅笔、橡皮。
五、教学过程1. 导入1.通过教学PPT展示几种组合图形（如长方形与半圆组成图形等）。
2.讲解组合图形的定义，并让学生进行回答互动。
2. 推导组合图形面积计算公式1.以长方形与半圆组成的图形为例，提问学生对它的面积计算方法。
2.对答案进行讲解后，用黑板进行图形的细化，让学生自行进行计算。
3.汇总结果，推导出组合图形面积计算公式。
3. 练习1.在黑板上展示几个组合图形，要求学生自行计算它们的面积。
2.让学生交流并互相检验答案，及时纠错。
4. 总结1.让学生得出本节课的知识点和难点，并通过PPT进行展示。
2.总结教学内容，强化学生的记忆。
六、作业1.完成课堂练习题。
2.课后作业：纸上练习，巩固相关知识点。
七、教学反思通过本节课的教学，我发现学生比较容易在理解组合图形的过程中犯错误，导致面积计算的答案出错。
针对这一问题，我增加了对组合图形的细化步骤，并在课堂练习中加强了学生的相互检验。
此外，我还结合实际情况，引入了一些有趣的案例，增强了学生的兴趣，提升了教学效果。
五年级奥数秋季教材
四年级秋季目录第1讲平均数 ------------------------（ 2）第2讲等差数列 ------------------------（ 7）第3讲长方形，正方形周长 ------------------------（ 13）第4讲长方形，正方形面积 ------------------------（20）第5讲分类数图形 ------------------------（26）第6讲尾数和余数 ------------------------（32）第7讲一般应用题（一） ----------------------- （37）第8讲一般应用题（二） ----------------------- （42）第9讲一般应用题（三）----------------------- （47）第10讲数阵----------------------- （51）第11讲最小公倍数和最大公因数----------------------- （59）第12讲周期问题----------------------- （66）第13讲盈亏问题----------------------- （72）第14讲组合图形面积（一）----------------------- （78）第15讲组合图形面积（二）---------------------- （85）第16讲数字趣题----------------------- （92）第1讲平均数(一)一、知识要点把几个不相等的数，在总数不变的条件下，通过移多补少，使它们完全相等，求得的相等的数就是平均数。
如何灵活运用平均数的数量关系解答一些稍复杂的问题呢？下面的数量关系必须牢记：平均数=总数量÷总份数总数量=平均数×总份数总份数=总数量×平均数二、精讲精练【例题1】有4箱水果，已知苹果、梨、橘子平均每箱42个，梨、橘子、桃平均每箱36个，苹果和桃平均每箱37个。
五年级奥数组合图形的面积
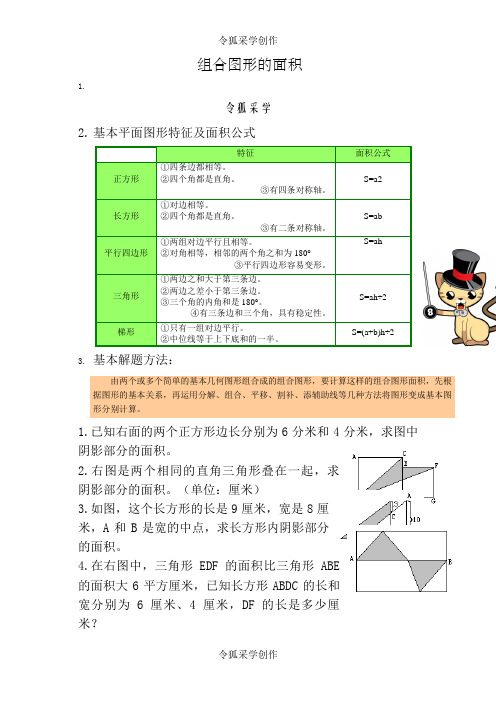
组合图形的面积1.令狐采学2.基本平面图形特征及面积公式特征面积公式正方形①四条边都相等。
②四个角都是直角。
③有四条对称轴。
S=a2长方形①对边相等。
②四个角都是直角。
③有二条对称轴。
S=ab平行四边形①两组对边平行且相等。
②对角相等，相邻的两个角之和为180°③平行四边形容易变形。
S=ah三角形①两边之和大于第三条边。
②两边之差小于第三条边。
③三个角的内角和是180°。
④有三条边和三个角，具有稳定性。
S=ah÷2梯形①只有一组对边平行。
②中位线等于上下底和的一半。
S=(a+b)h÷23.基本解题方法：由两个或多个简单的基本几何图形组合成的组合图形，要计算这样的组合图形面积，先根据图形的基本关系，再运用分解、组合、平移、割补、添辅助线等几种方法将图形变成基本图形分别计算。
1.已知右面的两个正方形边长分别为6分米和4分米，求图中阴影部分的面积。
2.右图是两个相同的直角三角形叠在一起，求阴影部分的面积。
（单位：厘米）3.如图，这个长方形的长是9厘米，宽是8厘米，A和B是宽的中点，求长方形内阴影部分的面积。
4.在右图中，三角形EDF的面积比三角形ABE的面积大6平方厘米，已知长方形ABDC的长和宽分别为6厘米、4厘米，DF的长是多少厘米？5.正方形ABCD的面积是100平方厘米，AE=8厘米，CF=6厘米，求阴影部分的面积。
6.右图是一块长方形公园绿地，绿地长24米，宽16米，中间有一条宽为2米的道路，求草地（阴影部分）的面积。
7.如图，三角形ABC的面积是24平方厘米，且DC=2AD，E、F 分别是AF、BC的中点，那么阴影部分的面积是多少？8.如下图，是一块长方形草地，长方形的长是16米，宽是10米，中间有两条宽2米的道路，一条是长方形，一条是平行四边形，那么有草部分（阴影部分）的面积有多大？9.如图，一个三角形的底长5米，如果底延长1米，那么面积就增加2平方米。
小学五年级奥数第19讲 组合图形的面积(二)(含答案分析)
第19讲组合图形的面积（二）一、知识要点在组合图形中，三角形的面积出现的机会很多，解题时我们还可以记住下面三点：1.两个三角形等底、等高，其面积相等；2.两个三角形底相等，高成倍数关系，面积也成倍数关系；3.两个三角形高相等，底成倍数关系，面积也成倍数关系。
二、精讲精练【例题1】如图，ABCD是直角梯形，求阴影部分的面积和。
（单位：厘米）练习1：1.求下图中阴影部分的面积。
2.求图中阴影部分的面积。
（单位：厘米）3.下图的长方形是一块草坪，中间有两条宽1米的走道，求植草的面积。
【例题2】下图中，边长为10和15的两个正方体并放在一起，求三角形ABC （阴影部分）的面积。
练习2：1.下图中，三角形ABC的面积是36平方厘米，三角形ABE与三角形AEC的面积相等，如果AB=9厘米，FB=FE，求三角形AFE的面积。
2.图中两个正方形的边长分别是10厘米和6厘米，求阴影部分的面积。
3.图中三角形ABC的面积是36平方厘米，AC长8厘米，DE长3厘米，求阴影部分的面积（ADFC不是正方形）。
【例题3】两条对角线把梯形ABCD分割成四个三角形。
已知两个三角形的面积（如图所示），求另两个三角形的面积各是多少？（单位：平方厘米）练习3：1.如下图，图中BO=2DO，阴影部分的面积是4平方厘米，求梯形ABCD的面积是多少平方厘米？2.下图的梯形ABCD中，下底是上底的2倍，E是AB的中点。
那么梯形ABCD的面积是三角形BDE面积的多少倍？3.下图梯形ABCD中，AD=7厘米，BC=12厘米，梯形高8厘米，求三角形BOC的面积比三角形AOD的面积大多少平方厘米？【例题4】在三角形ABC中，DC=2BD，CE=3AE，阴影部分的面积是20平方厘米，求三角形ABC的面积。
练习4：1.把下图三角形的底边BC四等分，在下面括号里填上“＞”、“＜”或“=”。
甲的面积（）乙的面积。
2.如图，在三角形ABC中，D是BC的中点，E、F是AC的三等分点。
五年级奥数-组合图形的面积(二)姜璐
分析 ：
1，因为三角形ABD与三角形ACD等底 等高，所以面积相等。因此，三角形 ABO的面积和三角形DOC的面积相等， 也是6平方厘米。 2，因为三角形BOC的面积是三角形 DOC面积的2倍，所以BO的长度是OD 的2倍，即三角形ABO的面积也是三角 形AOD的2倍。所以，三角形AOD的面 积是6÷2=3平方厘米。
练 习 三 2、下图的梯形ABCD中，下底是上底的2倍， E是AB的中点。那么梯形ABCD的面积是 三角形BDE面积的多少倍？
因为梯形和三角形等高 梯形ABCD的面积比三角形BDE面积为梯形上下底之和与三角 形底边长的比 即（1+2）：1=3：1 梯形ABCD的面积是三角形BDE面积的3倍
例4 、在三角形ABC中，DC=2BD，
△ADE的面积＝4×4÷2＝8（平方厘米） ∵F长是9厘米的正三角形的面积是
边长为3厘米的正三角形面积的多少倍？
分析： 题中的已知条件不能计算出两种三 角形的面积，我们可以用边长是3厘 米的正三角形拼一个边长是9厘米的 正三角形，从而看出它们之间的倍 数关系。从下图中可以看出：边长9 厘米的正三角形是边长3厘米的正三 角形面积的9倍。
练 习 二
1、下图中，三角形ABC的面积是36平方厘米，三角
形ABE与三角形AEC的面积相等，如果AB=9厘米， FB=FE，求三角形AFE的面积。
36÷2=18（平方厘米） 18×2÷9=4（厘米） 0.5×4×4=8（平方厘米） 18-8=10（平方厘米）
2、图中两个正方形的边长分别是
10厘米和6厘米，求阴影部分的面积。
2、求图中阴影部分的面积。 （单位：厘米） 28×20=560（平方厘米）
例2 、下图中，边长为10和15的两个正方体并
五年级奥数组合图形的面积
组合图形的面积我们已经学过长方形、正方形、三角形、平行四边形、梯形面积的计算方法，组合图形面积的计算，就要综合运用各种面积计算公式。
解组合图形常用的方法有分解法和割补法。
对于稍复杂的组合图形，有时还要用到运动变换法。
画出辅助线，更容易找到各部分之间的关系。
例1：如图所示，正方形的边长为6厘米，求阴影部分的面积是多少？1、如图所示，两个完全一样的直角三角形重叠在一起，求阴影部分的面积。
（单位：cm）2、把边长是10cm的正方形卡片按下图的方法重叠起来，3张这样的卡片重叠以后组成的图形的面积是多少？3、有一块长方形草地，长16m，宽12m，中间有一条宽2m的小路，求草地（阴影部分）的面积。
例2、如图所示，两个正方形，求图中阴影部分的面积。
（长度单位：厘米）1、下面大正方形边长为3厘米，小正方形边长为2厘米，求阴影部分的面积。
2、如图所示，长方形ABCD，三角形ABP的面积为20平方厘米，三角形CDQ的面积为35平方厘米，求阴影部分的面积。
3、如图所示，四边形ACEH是梯形，ACEG是平行四边形，ABGH是正方形，CDFG是长方形。
已知AC=8厘米，HE=13厘米，求三角形CDE和三角形GFE的面积之和。
例3：如图所示，三角形ABC被分成四个小三角形，其中三个三角形的面积分别为8平方厘米，6平方厘米，12平方厘米，求阴影部分的面积。
1、平行四边形ABCD中，AE=EF=FB，AG=2CG，三角形GEF的面积是6平方厘米，平行四边形的面积是多少平方厘米？2、下图中ABCD是直角梯形，两条对角线把梯形分成4个三角形（O是AC和BD的交点）。
已知其中两个三角形的面积为3平方厘米和6平方厘米，求直角梯形ABCD的面积。
自主练习：1、在腰长为10cm，面积为34cm²的等腰三角形的底边上任取一点，设这个点到两腰的垂线段分别长为a cm，b cm，那么a+b的长度是多少厘米？2、长方形ABCD的周长是16cm，在它的每条边上各画一个以该边为边长的正方形，已知这四个正方形的面积和是68 cm²，求长方形ABCD的面积。
五年级奥数组合图形的面积
组合图形的面积【2 】1.根本平面图形特点及面积公式特点面积公式正方形①四条边都相等.②四个角都是直角.③有四条对称轴.S=a2长方形①对边相等.②四个角都是直角.③有二条对称轴.S=ab平行四边形①两组对边平行且相等.②对角相等,相邻的两个角之和为180°③平行四边形轻易变形.S=ah三角形①双方之和大于第三条边.②双方之差小于第三条边.③三个角的内角和是180°.④有三条边和三个角,具有稳固性.S=ah÷2梯形①只有一组对边平行.②中位线等于高低底和的一半.S=(a+b)h÷22.根本解题办法：由两个或多个简略的根本几何图形组合成的组合图形,要盘算如许的组合图形面积,先依据图形的根本关系,再应用分化.组合.平移.割补.添帮助线等几种办法将图形变成根本图形分离盘算.1.已知右面的两个正方形边长分离为6分米和4分米,求图中暗影部分的面积.2.右图是两个雷同的直角三角形叠在一路,求暗影部分的面积.（单位：厘米）3.如图,这个长方形的长是9厘米,宽是8厘米,A和B是宽的中点,求长方形内暗影部分的面积.4.在右图中,三角形EDF的面积比三角形ABE的面积大6平方厘米,已知长方形ABDC的长和宽分离为6厘米.4厘米,DF的长是若干厘米？5.正方形ABCD的面积是100平方厘米,AE=8厘米,CF=6厘米,求暗影部分的面积.6.右图是一块长方形公园绿地,绿地长24米,宽16米,中央有一条宽为2米的道路,求草地（暗影部分）的面积.7.如图,三角形ABC的面积是24平方厘米,且DC=2AD,E.F分离是AF.BC的中点,那么暗影部分的面积是若干？8.如下图,是一块长方形草地,长方形的长是16米,宽是10米,中央有两条宽2米的道路,一条是长方形,一条是平行四边形,那么有草部分（暗影部分）的面积有多大？9.如图,一个三角形的底长5米,假如底延伸1米,那么面积就增长2平方米.问本来的三角形的面积是若干平方米?1米组合图形的面积功课1.在右图中,三角形EDF的面积比三角形ABE的面积大75平方厘米,已知正方形ABCD的边长为15厘米,DF的长是若干厘米？2.如图,ABCD是一个长12厘米,宽5厘米的长方形,求暗影部分三角形ACE的面积.3.已知正方形乙的边长是8厘米,正方形甲的面积是36平方厘米,那么图中暗影部分的面积是若干？4.如图,A.B两点是长方形长和宽的中点,那么暗影部分占长方形的面积是若干？5.如图,在平行四边形ABCD中,E.F分离是AC.BC的三等分点,且平行四边形的.面积为54平方厘米,求S△BEF6.盘算右边图形的面积.（至罕用3种办法）（单位：米）。
【奥数】五年级上6—2组合图形的面积
组合图形的面积组合图形的面积：例题：求下面组合图形的面积。
（单位：厘米）知识精讲：求组合图形的面积组合图形是由几个简单的图形组合而成，其面积既可以看作几个简单图形相加，也可以看作几个简单图形相减。
计算组合图形的面积，要根据已知条件对图形进行分解，转化成已学过的简单图形，先分别计算出它们的面积，再求和或差。
估算不规则图形的面积时，可以先通过数格子确定面积的范围，再将不满一格的都按半格计算，也可以根据图形的特点转化成已学过的图形来估算面积。
巩固练习：求阴影部分的面积：灵活运用推理法、转化法、画辅助线法、平移法、剔除法、分割法等方法，使计算简便。
（1）求下图中阴影部分的面积。
（单位：m）（2）求阴影部分的面积（3）平行四边形ABCD的底是30厘米，高是12厘米（如右图），求阴影部分的面积。
（4）如右图，AE=5 cm，AB=4 cm，BD=9 cm。
左边梯形和右边三角形的面积相等，求三角形的底是多少？（5）已知F、E分别是平行四边形ABCD左右两边的中点，连接ＡF、CE。
如果平行四边形ABCD 的面积是36 cm2，求平行四边形AECF的面积。
（6）如右图，E、F分别是平行四边形ABCD上下两边的中点，连接DE、BF。
如果阴影部分（平行四边形EBFD）的面积是28 cm2，求平行四边形ABCD的面积。
（7）在四边形ABCD中，M为AB的中点，N为CD的中点，如果四边形ABCD的面积是80 cm2，求阴影部分BNDM的面积。
（8）在四边形ABCD中，E为AB边上的中点，F为CD边上的中点，如果四边形AECF的面积是32cm2，求四边形ABCD的面积。
（9）已知三角形ABC的面积是32.4 cm2，是三角形EFB面积的3倍。
平行四边形EFCD的面积是多少？（10）三角形ABC的面积是36cm2，DC=3BD，阴影部分的面积是多少平方厘米？（11）三角形ABC和三角形EFD是两个完全相同的直角三角形，把它们的一部分叠放在一起，如下图所示。
小学五年级《组合图形的面积》奥数教案
五年级备课教员：第十二讲组合图形的面积一、教学目标： 1.结合生活实际认识组合图形，会把组合图形分解成学过的平面图形并计算出面积。
2.理解计算组合图形的多种方法，并能根据各种组合图形的条件，有效地选择计算方法,进行正确解答。
3.培养识图的能力和综合运用有关知识的能力，能合理的运用“割”、“补”等方法来计算组合图形的面积，在这一过程中感受转化的数学思想。
4.通过观察、思考、运用等过程，激发学生积极参与学习探究的热情，培养学生倾听、合作、交流的良好学习习惯。
二、教学重点：探索组合图形面积的计算方法：1.分割法：把一个复杂的组合图形分割成我们学过的几个简单的基本图形，通过求这几个简单的基本图形的面积来得到组合图形的面积。
2.添补法：充分利用已知的数据，恰当地使用辅助线，用添补的方法，把复杂的组合图形转化为简单的图形，从而计算出组合图形的面积。
3.挖空法：就是把多边形看成是一个完整的规则图形，计算它的面积以后，再减去空缺部分的面积。
三、教学难点：根据图形之间的联系，选择有效的方法求组合图形的面积，在学习中去探索掌握解决问题的思考策略及解决问题方法的最优化。
四、教学准备：课件、活页练习纸、展示图。
五、教学过程：第一课时（50分钟）一、导入（5分)师：同学们，让大家准备的七巧板，你们都准备了吗？生：准备了。
师：真棒，现在就请同学们拿出自己准备的七巧板，动动你们的小手，拼出自己最喜欢的图形给你的同桌看。
看看你和同桌谁拼的图形更好看。
生：（开始动手拼）师：（投影展示学生作品）同学们看，这位同学拼的图形像什么呀？生：小鱼。
师：能说说这条小鱼是怎么拼成的吗？生：由两个三角形拼成的。
师：同学们观察得真仔细。
师：老师现在再叫几位同学来分享，要说清楚你拼成的是什么，是怎么拼的。
生：我拼的是一只猫，是用七巧板的七个图形拼成的。
生：我拼的是一棵树，是用两个三角形和一个正方形拼成的。
生：……师：同学们有没有发现拼的图形都有一个共同的特征？是什么呢？生：拼成的图形都是由几个图形组合而成的。
【精品奥数】五年级上册数学思维训练讲义-第15讲 组合图形的面积(二) 人教版(含答案)
第十五讲 组合图形面积（二）第一部分：趣味数学梯形面积今有邪田，一头广三十步，一头广四十二步，正从六十四步。
问为田几何？赏析：邪田即直角梯形。
最早的文字记载见于《九章算术》“方田”章。
“邪田术曰：并两斜而半之，以乘正从若广”。
也就是说，直角梯形的面积等于两底和的一半与高的乘积。
刘徽注称：“并而半之者，以盈补虚也。
”同样根据“出入相补”原理、采用“以盈补虚”的方法可将直角梯形化为与之等积的长方形，再利用“方田术”计算其面积。
解答：根据梯形的面积=（上底+下底）×高÷2，得出（30+42）×64÷2=72×64÷2=2304（步）第二部分：奥数小练一、知识要点组合图形是由两个或两个以上的简单的几何图形组合而成的。
组合的形式分为两种：一是拼合组合，二是重叠组合。
由于组合图形具有条件相等的特点，往往使得问题的解决无从下手。
要正确解答组合图形的面积，应该注意以下几点：1.切实掌握有关简单图形的概念、公式，牢固建立空间观念；2.仔细观察，认真思考，看清所求图形是由哪几个基本图形组合而成的；3.适当采用增加辅助线等方法帮助解题；4，采用割、补、分解、代换等方法，可将复杂问题变得简单。
二、精讲精练【例题1】 一个等腰直角三角形，最长的边是12厘米，这个三角形的面积是多少平方厘米？【思路导航】由于此三角形中只知道最长的边是12厘米，所以，不能用三角形的面积公式来计算它的面积。
我们可以假设有4个这样的三角形，且拼成了下图正方形。
显然，这个正方形的面积是12×12.那么，一个三角形的面积就是12×12÷4=36平方厘米。
练习一：1.求图（1）四边形ABCD的面积。
（单位：厘米）2.已知图（2）正方形ABCD的边长是7厘米，求正方形EFGH的面积。
图（1）图（2）3.有一个梯形，它的上底是5厘米，下底7厘米。
如果只把上底增加3厘米，那么面积就增加4.5平方厘米。
小学五年级上学期数学培优奥数讲义(全国通用)-第25讲 组合图形的面积(含答案)
第25讲组合图形的面积知识装备平面组合图形是由两个或两个以上简单的几何图形组合而成，与平面组合图形相关的计算应看清所求图形是由哪几个基本图形组合而成，还要找出图中的隐蔽条件与已知条件和要求的问题间的关系。
在实际问题中，常采用数据推导、割补、平移、巧添辅助线、旋转、组合等方法，将复杂问题简单化。
初级挑战1如下图，空白部分是两个平行四边形，求图中阴影部分的面积。
思路引领：图中空白部分是两个（），可将它们转化成与之等底等高的（），再平移到图形的一侧，那么阴影部分的面积就变成了规则的（）。
答案：28×20＝560（平方米）能力探索1下图是一块长10米，宽8米的长方形草坪，中间有两条走道，求草地的面积。
答案：（10－1）×（8－1）＝63（平方米）初级挑战2求四边形ABCD的面积。
（单位：厘米）思路引领：如下图延长BA、CD交于E，△BEC中，S四边形ABCD ＝S△EBC－S△ADE。
根据∠C＝45°可知，BE＝BC＝7，因此S△BEC＝（）。
∠E＝（），那么△ADE中，DE＝AD＝3，S△ADE＝（）。
答案：S△BCE ：7×7÷2＝24.5（平方厘米）；S△ADE：3×3÷2＝4.5（平方厘米）；S四边形ABCD：24.5－4.5＝20（平方厘米）。
能力探索2计算下面图形的面积（单位：厘米）答案：将图形分割成一个三角形和长方形，再计算面积。
三角形面积：（12－8）×（10－5）÷2＝4×5÷2＝10（平方厘米）；长方形面积：8×10＝80（平方厘米）；图形面积：10＋80＝90（平方厘米）。
中级挑战1下面一个长方形被分成六个小长方形，其中四个长方形的面积如图所示（单位：平方厘米），求A和B的面积。
思路引领：长方形的面积＝（）×（）①两个长方形的长相等，它们面积的倍数等于对应宽的倍数②两个长方形的宽相等，它们面积的倍数等于对应长的倍数。
五年级上册数学培优奥数讲义-第13讲平面组合图形2
第13讲平面组合图形2知识与方法1、三角形的等积变换指的是使三角形面积相等的变换。
通过三角形的等积变换，可以解决许多与三角形相关的面积计算。
2、三角形的等积变形中常用的几个重要结论：（1）平行线间的距离处处相等。
（2）等底等高的两个三角形面积相等。
（3）底在同一条直线上并且相等，底所对的顶点是同一个，这样的两个三角形的面积相等。
如下图，△ABD与△ACD底在同一直线上，且BD＝DC，S△ABD ＝S△ADC。
（4）若两个三角形的高（或底）相等，其中一个三角形的底（或高）是另一个三角形的几倍，那么这个三角形的面积也是另一个三角形的面积的几倍。
如下图，△ABD与△ACD的高相等，DC＝2BD，S△ADC ＝2S△ABD。
（5）若几个三角形的底边相等，并在两条平行线中的同一条直线上，而且相等的底边所对的顶点在两条平行线中的另一条边上，则这几个三角形的面积相等。
如下图，三个三角形的底相等，那么S①＝S②＝S③。
把任意一个三角形分成四个面积相等的三角形，可以怎样分？思维点拨：根据“等底等高的两个三角形面积相等”，对三角形进行分割，即可保证分割的小三角形面积相等。
答案：提供几种分法如下（答案不唯一）。
……能力探索1在△ABC中，E、D、G分别是AB、BC、AD的中点，图中与△AGC面积相等的三角形有哪些？答案：共3个，分别是△CDG、△BDE、△ADE。
如图，ABCD是直角梯形，求阴影部分的面积和。
（单位：厘米）思路引领：比较阴影部分两个三角形，高相等，底在同一直线上。
根据“等底等高的两个三角形面积相等”，你能将阴影部分两个三角形转化在一起吗？答案：如下图，△ACE的面积等于原△CDE的面积，所求阴影部分的面积和就是△ABC的＝3×6÷2＝9（平方厘米）。
面积，S阴影能力探索2求下图中阴影部分的面积和。
答案：S阴影＝25×10÷2＝125（平方厘米）中级挑战1如图，长方形ABCD的面积为80平方厘米，E、F、G分别为AB、BC、CD的中点，H 为AD上的任意一点，求阴影部分的面积和。
五年级《组合图形的面积》奥数教案
星座站备课教员：第二讲组合图形的面积一、教学目标：1、认识组合图形，会把组合图形分解成已学过的平面图形；2、通过找一找、分一分、拼一拼，培养学生识图的能力和综合运用有关知识的能力，能合理地运用“割”“补”等方法来计算组合图形的面积；3、培养学生的观察能力和动手操作的技能，发展空间的观念，提高思维的灵活性。
二、教学重点：探索并掌握组合图形的面积计算方法。
三、教学难点：理解并掌握组合图形的组成及分解方法。
四、教学准备：PPT五、教学过程：第一课时（40分钟）一、外星游记（5分钟）师：同学们，老师想知道你们已经学会计算哪些平面图形的面积？生：(自主回答)师：大家学会的知识可真多。
（课件展示）你们都这么聪明那老师要奖励你们，接下来老师带你们去一个地方。
（课件展示）师：同学们观察得真仔细！除了这些外，老师也发现了一些漂亮的图形。
（课件展示）师：这些图形，我们把它们称为组合图形，那这些图形我们要怎么去计算它的面积呢？【出示课题：组合图形的面积】二、星海遨游（30分钟）（一）星海遨游1（10分钟）一个等腰直角三角形，最长的边是12厘米，这个三角形的面积是多少平方厘米？师：同学们！三角形面积是不是底乘高除以2啊？生：是。
师：可是题目没有告诉我们三角形的高啊，只知道最长的边是12厘米，那我们该怎么来计算呢？同学们想一想。
生：（自主回答）师：同学们的想法都很新颖，我们能不能试着这样来做呢，假设我们有四个一样大小的这样的三角形，同学们，能告诉我他们都能拼成什么图形吗？生：长方形、正方形、平行四边形……师：嗯，那么我们用这四个三角形组成的正方形是不是就能知道边长，（结合PPT）我们所要求的三角形的面积是不是等于这个正方形面积的四分之一啊？生：是的。
板书：12×12÷4=36（平方厘米）答：这个三角形的面积是36平方厘米。
（一）星海历练1（5分钟）已知正方形ABCD的边长是7厘米，求正方形EFGH的面积。
小学五年级奥数举一反三第19周 组合图形(二)
=10（平方厘米）
举一反三3
1.下图中每个长方形小格的面积都是1平方厘米，求阴影部 分的面积。 2.把等边三角形ABC的每条边6等分，组成如下图所示的三 角形网。如果图中每个小三角形的面积都是1平方厘米，求 图中三角形DEF的面积。 3.如图所示，在长方形ABCD中，AD=15厘米，AB=8厘米， 图中阴影部分的面积为68平方厘米，四边形EFGO的面积是 多少平方厘米？
王牌例题4： 在三角形ABC中，DC=2BD，CE=3AE，阴影部分的面积是 20平方厘米，求三角形ABC的面积。
【思路导航】（1）因为CE=3AE，所以，三 角形ADC的面积是三角形ADE面积的4倍，是 20×（1＋3）=80平方厘为； （2）又因为DC=2BD，所以，三角形ABD的面积是三角形 ADC面积的一半，是80÷2=40平方厘米。因此，三角形 ABC的面积是80＋40=120平方厘主。
王牌例题5： 边长是9厘米的正三角形的面积是边长为3厘米的正三角形 面积的多少倍？
【思路导航】题中的已知条件不能计算 出两种三角形的面积，我们可以用边长 是3厘米的正三角形拼一个边长是9厘米 的正三角形，从而看出它们之间的倍数关系。从下图中可 以看出：边长9厘米的正三角形是边长3厘米的正三角形面 积的9倍。
五邯郸市峰峰矿区 杨桂林
知识要点
在组合图形中，三角形的面积出现的机会很多，解题时 我们还可以记住下面三点： 1，两个三角形等底、等高，其面积相等； 2，两个三角形底相等，高成倍数关系，面积也成倍数 关系； 3，两个三角形高相等，底成倍数关系，面积也成倍数 关系。
举一反三 5
1.边长是8厘米的正三角形的面积是边长为2厘米的正三角形 面积的多少倍？ 2.一个梯形与一个三角形等高，梯形下底的长是上底的2倍， 梯形上底的长又是三角形底长的2倍。这个梯形的面积是三 角形面积的多少倍？ 3.如下图所示，有两种自然的放法将正方形内接于等腰直角 三角形。已知等腰直角三角形的面积是36平方厘米，两个正 方形的面积分别是多少？
2022-2023学年小学五年级奥数(全国通用)测评卷24《组合图形的面积》(解析版)
【五年级奥数举一反三—全国通用】测评卷24《组合图形的面积》试卷满分：100分考试时间：100分钟姓名：_________班级：_________得分：_________ 一．选择题（共8小题，满分16分，每小题2分）1．（2分）如图中长方形的面积相等，则图中阴影部分面积相比较，()A．甲的面积大B．乙的面积大C．甲和乙的面积相等D．无法确定【解答】解：甲的面积=长方形的长⨯长方形的宽2÷；乙的面积=长方形的长⨯长方形的宽2÷；即：甲乙的面积都是长方形面积的一半，它们的面积一样大．故选：C。
2．（2分）在图中，平行线间的三个图形，它们的面积()A．平行四边形最大B．三角形最大C．梯形最大D．一样大【解答】解：设他们的高为h，平行四边形的面积4h=三角形的面积184 2h h =⨯⨯=梯形面积(26)24h h=+⨯÷=所以它们的面积相比，都相等；故选：D。
3．（2分）甲长方形包含16个小正方形，乙长方形包含12个小正方形．甲长方形与乙长方形的面积相比，结果是什么？()A．甲的面积大B．乙的面积大C．无法确定【解答】解：因为不能确定甲、乙长方形包含的小正方形的面积是否相等，所以无法比较甲长方形与乙长方形面积的大小；故选：C．4．（2分）如图所示，把一个长方形分成一个梯形和一个三角形．已知梯形的面积比三角形的面积大18厘米2，那么梯形的上底长为()厘米．A．2 B．3 C．4 D．6【解答】解：设梯形的上底为a厘米，那么三角形的底为(12)a-厘米，根据题意可得：+⨯÷--⨯÷=(12)62(12)6218a a+⨯--⨯=a a(12)3(12)318+-+=a a33636318a=618a=3答：梯形的上底是3厘米．故选：B．5．（2分）如图，甲、乙两个平行四边形中阴影部分面积的大小为()A．甲>乙B．甲=乙C．甲<乙D．无法确定【解答】解：如图：甲+丙=乙+丙，丙是公共部分，所以甲=乙，答：甲的面积等于乙的面积．故选：B ．6．（2分）如图的长方形中有三个三角形，它们面积间的关系是( )A ．123S S S +=B ．13S S =C ．23S S =D ．321S S S =-【解答】解：由图可知：2S 的面积是长方形形面积的一半，3S 和1S 的面积和也是长方形面积的一半，由此可得：132S S S +=，即：321S S S =-．故选：D ．7．（2分）图中，直线//a b ，比较三角形ADC 和三角形ABD 面积的大小，结果是( )A ．三角形ADC 面积大B ．三角形ABD 面积大C ．它们的面积相等D ．无法比较【解答】解：由题意可知：三角形ADC 和三角形ABD 等底等高，所以角形ADC 和三角形ABD 面积相等． 故选：C ．8．（2分）如图ABCD 是长方形，已知4AB =厘米，6BC =厘米，三角形EFD 的面积比三角形ABF 的面积大6平方厘米，求(ED = )厘米．A ．9B ．7C ．8D ．6【解答】解：长方形ABCD 的面积：4624⨯=（平方厘米）；三角形EBC的面积：+=（平方厘米）；24630⨯÷=（厘米）；CE的长：302610DE的长：1046-=（厘米）．故选：D．二．填空题（共9小题，满分18分，每小题2分）9．（2分）如图，图中2=，阴影部分的面积是6平方厘米，求梯形ABCD的面积是27平方厘米．BO DO【解答】解：因为2=，BO DO所以三角形CDO的面积=三角形BCO面积的一半，即三角形CDO的面积3=平方厘米；三角形BCD与三角形ACD同底等高，所以三角形BCD与三角形ACD的面积相等，三角形AOD的面积=三角形BCO的面积，即三角形AOD的面积6=平方厘米；=，三角形ABO的面积是三角形AOD面积的2倍，BO DO2即三角形AOB的面积12=平方厘米；梯形ABCD的面积为：6361227+++=（平方厘米），答：梯形ABCD的面积为27平方厘米．故答案为：27．10．（2分）如图涂色部分的面积是322cm．【解答】解：8866⨯+⨯=+6436=（平方厘米）100(86)62882+⨯÷+⨯÷=+423274=（平方厘米）⨯-÷6(86)2=⨯÷6226=（平方厘米）-+100746=+266=（平方厘米）32答：涂色部分的面积是232cm．故答案为：32．11．（2分）如图，它是由两个正方形拼成的，小正方形的边长为2厘米，大正方形的边长为4厘米，阴影部分的面积为6平方厘米．【解答】解：(24)22+⨯÷=⨯÷622=（平方厘米）6答：阴影部分的面积是6平方厘米．故答案为：6．12．（2分）六个等腰三角形如图摆放，那么四个空白三角形的面积和是两个阴影三角形的面积和的6倍．【解答】解：如下图：把这六个等腰直角三角形从小到大分别编号为①②③④⑤⑥，设①号三角形的面积为1，则②号的面积为2，③号的面积为4，④号的面积为8，⑤号的面积为16，⑥号的面积为32，+++÷+(241632)(18)=÷5496=答：四个空白三角形的面积和是两个阴影三角形的面积和的6倍．故答案为：6．13．（2分）如图，梯形的面积是18．【解答】解：如图：已知45BAC∠=︒，90ABC∠=︒，所以180904545ACB∠=︒-︒-︒=︒，所以AB BC=；因为90ACE∠=︒，所以180904545ECD∠=︒-︒-︒=︒，则45DEC∠=︒，所以DE CD=，梯形的面积()62DE AB=+⨯÷()62BC CD=+⨯÷662=⨯÷18=．故答案为：18．14．（2分）如图：ABCD是一个面积为36平方厘米的长方形，E为BC中点，则阴影部分的面积是15平方厘米．【解答】解：据分析可知：三角形ABE的面积为13694⨯=（平方厘米）；三角形DHC的面积和三角形ADH的面积比是1:2，而三角形ADC的面积是36218÷=（平方厘米），所以三角形DHC 的面积为18(12)6÷+=（平方厘米），则三角形AHE 的面积也是6平方厘米．所以阴影部分的面积是9615+=（平方厘米）．答：阴影部分的面积是15平方厘米．故答案为：15．15．（2分）如图，ABCD 是直角梯形，5AD =厘米，3DC =厘米，三角形DOC 的面积是1.5平方厘米，则阴影部分的面积是 6 平方厘米．【解答】解：352 1.5⨯÷-，7.5 1.5=-，6=（平方厘米）； 答：阴影部分的面积是6平方厘米．故答案为：6．16．（2分）图中直角三角形里有3个正方形，已知25AD cm =，100BD cm =，阴影部分的面积是 10754 2cm ．【解答】解：100:25100254=÷=4BC AB =4(25100)=⨯+500=（厘米）设最小正方形的边长为x 厘米4()1005004x x x x ++++= 6.25100500x ++=6.25100100500100x +-=-6.25400x =6.25 6.25400 6.25x ÷=÷64x =中正方形的边长：4x x + 64644=+6416=+80=（厘米）500(25100)2(10010080806464)⨯+÷-⨯+⨯+⨯5001252(1000064004096)=⨯÷-++3125020496=-10754=（平方厘米）答：阴影部分的面积是10754平方厘米．故答案为：10754．17．（2分）如图，已知正方形ABCD 的周长是40厘米， 6.4DE =厘米，阴影部分的面积是 32 平方厘米．【解答】解：由分析可知阴影部分的面积为：6.4(404)2⨯÷÷6.4102=⨯÷642=÷32=（平方厘米）； 答：阴影部分的面积是32平方厘米．故答案为：32．三．计算题（共3小题，满分18分，每小题6分）18．（6分）求阴影部分面积．【解答】解：（1）222+=，空白三角形是一个直角三角形，304050空白三角形的面积：30402⨯÷=÷12002=（平方分米）600斜边上的高：⨯÷600250=÷120050=（分米）24+⨯÷(4050)242=⨯÷90242=（平方分米）1080-=（平方分米）1080600480答：阴影部分的面积是480平方分米．（2）40403030⨯+⨯=+1600900=（平方分米）2500⨯÷=（平方分米）40402800+⨯÷(4030)302=⨯÷70302=÷21002=（平方分米）1050--25008001050=-17001050=（平方分米）650答：阴影部分的面积是650平方分米．19．（6分）平行四边形ABCD的边BC长10厘米，直角三角形的直角边EC长8厘米．已知阴影部分的面积比三角形EGF的面积大9平方厘米．求CF的长．【解答】解：设EF长为x厘米，则CF就是8x-厘米，根据题干分析可得方程：x⨯-=⨯÷+10(8)10829-=801049xx=1031x=3.1-=（厘米）；8 3.1 4.9答：CF长为4.9厘米．20．（6分）求图中阴影部分的面积．【解答】解：6644662(64)42⨯+⨯-⨯÷-+⨯÷3616181042=+--⨯÷=+--36161820=（平方厘米）14答：阴影部分的面积是14平方厘米．四．应用题（共5小题，满分29分）21．（5分）如图是一幢楼房占地的平面图，算一算它的占地面积有多大？（单位：)m你能想出几种算法？【解答】解：方法一如图：⨯+-⨯-÷6048(6030)(7248)2=+⨯÷288030242=+28803603240=（平方米）方法二如图：⨯-+⨯-÷7260(6030)(7248)2432090242=-⨯÷=-43201080=（平方米）3240答：它的占地面积有3240平方米。
小学五年级奥数组合图形的面积
组合图形的面积十一右图正方形边长为12厘米，四边形EFGH面积是6平方厘米，那么阴影面积是多少平方厘米？分析：S阴影=S AFC+S BDF－2*S EFGH=FC*AB÷2+BF*AB÷2－2*S EFGH=（FC+ BF）*AB÷2－2*S EFGH =BC*AB÷2－2*S EFGH=12*12÷2－2*6=60平方厘米十二如图，正方形ABCD的边长是12厘米，CE=4厘米。
求阴影部分的面积。
分析：△CEF与△AFB相似；CE：AB=4：12=1：3 EF：BF=1：3S BCE=CE*BC÷2=4*12÷2=24平方厘米，EF：BF=1：3，所以S BCF=3S CFES CFE=6平方厘米S BCF=18平方厘米；S AFE=18平方厘米S阴影= S BCF + S AFE=36平方厘米十三在右图中，三角形EDF的面积比三角形ABE的面积大75平方厘米，已知正方形ABCD 的边长为15厘米，DF的长是多少厘米？分析：S ACF=（CD+DF）*AC÷2=（15+DF）*15÷2S ABCD=AB*AC=15*15=225平方厘米S ACF－S ABCD=（S ACDE+S EDF）－（S ACDE+S ABE）S ACF－S ABCD= S EDF－S ABE=75（15+DF）*15÷2－225=75DF=25厘米十四如图，ABCD是一个长12厘米，宽5厘米的长方形，求阴影部分三角形ACE的面积。
分析：过E点做S AEC的高，其值等于CD，为55厘米S AEC=AC*CD÷2=12*5÷2=30平方厘米十五已知正方形乙的边长是8厘米，正方形甲的面积是36平方厘米，那么图中阴影部分的面积是多少？分析：S阴影=（8*8+6*6 ）－{（6+8）*8÷2+6*6÷2+8*2÷2} =100－82=18平方厘米十六如图，A、B两点是长方形长和宽的中点，那么阴影部分占长方形的面积是多少？分析：长方形的长和宽为a,b；S阴影=a×b－（ a×b÷2+ a×b÷8）=3/8 a×b十七、在正方形ABCD中，AB是4厘米，三角形BCF比三角形DEF的面积多2平方厘米，求DE的长。
五年级奥数 第19讲 组合图形的面积(2)
五年级奥数第19讲组合图形面积（二）知识要点在组合图形中，三角形的面积出现的机会很多，解题时我们还需要记住下面三点：1、两个三角形等底、等高，其面积相等；2、两个三角形底相等，高成倍数关系，面积也成倍数关系；3、两个三角形高相等，底成倍数关系，面积也成倍数关系。
例1、如图所示，已知三角形ABC的面积是88平方厘米，是平行四边形DEFC的两倍，求阴影部分的面积。
练习：1、下图中，梯形的下底为12厘米，高为8厘米，求阴影部分的面积。
2、如图所示，四边形ABCD是直角梯形，AD＝9厘米，CD＝12厘米，求阴影部分的面积。
3、求图中阴影部分的面积。
(单位:厘米)例2、下图中，边长为10和15的两个正方形并放在一起，求三角形ABC(阴影部分)的面积。
练习：1、下图中，三角形ABC的面积是36平方厘米，三角形ABE与三角形AEC的面积相等，如果AB ＝9厘米，FB＝FE，求三角形AFE的面积。
2、图中两个正方形的边长分别是10厘米和6厘米，求阴影部分的面积。
3、图中三角形ABC的面积是36平方厘米，AC长8厘米，DE长3厘米。
求阴影部分的面积(ADFC是长方形)。
例3、下图中每个长方形小格的面积都是1平方厘米，求阴影部分的面积练习：1、下图中每个长方形小格的面积都是1平方厘米，求阴影部分的面积。
2、把等边三角形ABC的每条边6等分，组成如下图所示的三角形网。
如果图中每个小三角形的面积都是1平方厘米，求图中三角形DEF的面积。
3、如图所示，在长方形ABCD中，AD＝15厘米，AB＝8厘米图中阴影部分面积为68平方厘米，四边形EFGO的面积是多少平方厘米?例4、在三角形ABC中(如下图所示)，DC＝2BD，CE＝3AE，阴影部分的面积是20平方厘米。
求三角形ABC的面积。
练习：1、把下图三角形的底边BC四等分，在下面括号里填上“＞”“＜”或“＝”。
2、如图所示，在三角形ABC中，D是BC的中点，E、F是AC的三等分点。
五年级数学《组合图形的面积》试题及答案
五年级数奥数：《组合图形的面积》1、求图形的面积(单位：厘米)梯形面积：三角形面积：（8+12）×÷2 12×3÷2= 20×÷2 = 36÷2= 170÷2 = 18（cm2）= 85（cm2）图形面积= 梯形面积–三角形面积： 85-18=67（cm2）2、校园里有两块花圃(如图)，你能计算出它们的面积吗(单位：m)图形面积=长方形面积6×（5-2）+ 正方形面积（2×2）图形面积=长方形面积 - 梯形面积6×（5-2）+ 2×2 10×6 –[（3+6）×2÷2 ]= 6×3 + 4 = 60 -[ 9×2÷2 ]= 18 + 4 = 60 - 9= 22（m2） = 51（m2）3、下图直角梯形的面积是49平方分米，求阴影部分的面积。
直角梯形的高=直角三角形的高（阴影部分面积）直角梯形的高= 49÷（6+8）×2 直角三角形面积= 6×7÷2= 49÷14×2 = 42÷2= ×2 = 21（dm²）= 7（dm²）4、图中梯形中空白部分是直角三角形，它的面积是45平方厘米，求阴影部分面积。
直角梯形的高=直角三角形的高梯形面积=（5+12）×÷2= 45÷12×2 = 17×÷2= ×2 = ÷2= （cm2） = （cm2）阴影部分面积=梯形面积–空白部分面积： - 45 = （cm2）5、阴影部分面积是40平方米，求空白部分面积。
（单位：米）梯形的高=三角形的高（阴影部分三角形）梯形面积=（6+10）×8÷2= 40÷10×2 = 16×8÷2= 4×2 = 128÷2= 8（m2） = 64（m2）空白部分面积=梯形面积–阴影部分面积：64–40 = 24（m2）6、如图，平行四边形面积240平方厘米，求阴影部分面积。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
3，下图的长方形是一块草坪， 中间有两条宽1米的走道， 求植草的面积。
例2 、下图中，边长为10和15的
两个正方体并放在一起，求三角形 ABC（阴影部分）的面积。
分析 与解答： 三角形ADC的面积是：10×15÷2=75， 而三角形ABC的高是三角形BCD高的 15÷10=1.5倍， 它们都以BC为边为底，所以，三角形 ABC的面积是三角形BCD的1.5倍。 阴影部分的面积是： 7.5÷（1＋1.5）×1.5=45。
专题简析：
在组合图形中，三角形的面积出现的机 会很多，解题时我们还可以记住下面三 点：
1，两个三角形等底、等高，其面积相等；
2，两个三角形底相等，高成倍数关系， 面积也成倍数关系； 3，两个三角形高相等，底成倍数关系， 面积也成倍数关系。
例1 、如图，ABCD是直角梯形，
求阴影部分的面积和。 （单位：厘米）
例4 、在三角形ABC中，
DC=2BD，CE=3AE，阴影部分 的面积是20平方厘米，求三角形 ABC的面积。
分析 ：
（1）因为CE=3AE，所以，三角形 ADC的面积是三角形ADE面积的4倍， 是20×（1＋3）=80平方厘为； （2）又因为DC=2BD，所以，三角 形ABD的面积是三角形ADC面积的一 半，是80÷2=40平方厘米。因此， 三角形ABC的面积是80＋40=120平 方厘主。
分析与解答： 按照一般解法，首先要求出梯形的 面积，然后减去空白部分的面积即 得所求面积。其实，只要连接AC， 显然三角形AEC与三角形DEC同底 等高其面积相等，这样，我们把两 个阴影部分合成了一个三角形ABC。 面积是：6×3÷2=9平方厘米。
练 习 一
1，1，求下图中阴影部分的面积。 2，求图中阴影部分的面积。 （单位：厘米）
练 习 四
1，1，把下图三角形的底边BC四等分， 在下面括号里填上“＞”、“＜”或“=”。 甲的面积（ ）乙的面积。
2，如图，在三角形ABC中，D是BC的中点， E、F是AC的三等分点。已知三角形的面积 是108平方厘米，求三角形CDE的面积。
3，下图中，BD=2厘米，DE=4厘米， EC=2厘米，F是AE的中点， 三角形ABC的BC边上的高是4厘米， 阴影面积是多少平方厘米？
练 习 三
1，如下图，图中BO=2DO，阴影部分的 面积是4平方厘米，求梯形ABCD的面积 是多少平方厘米？
2，下图的梯形ABCD中，下底是上底的2倍， E是AB的中点。那么梯形ABCD的面积是 三角形BDE面积的多少倍？
3，下图梯形ABCD中，AD=7厘米， BC=12厘米，梯形高8厘米， 求三角形BOC的面积比三角形 AOD的面积大多少平方厘米？
练 习 二
1，下图中，三角形ABC的面积是36平方厘米，三角形ABE 与三角形AEC的面积相等，如果AB=9厘米， FB=FE，求三角形AFE的面积。
2，图中两个正方形的边长分别是 10厘米平方厘米， AC长8厘米，DE长3厘米，求阴影部分 的面积（ADFC不是正方形）。
练 习 五
1，边长是8厘米的正三角形的面积是边长为2厘米的 正三角形面积的多少倍？ 2，一个梯形与一个三角形等高，梯形下底的长是上 底的2倍，梯形上底的长又是三角形底长的2倍。这 个梯形的面积是三角形面积的多少倍？ 3，有两种自然的放法将正方形内接于等腰直角三角 形。已知等腰直角三角形的面积是36平方厘米，两 个正方形的面积分别是多少？
例5 、边长是9厘米的正 三角形的面积是边长为3 厘米的正三角形面积的 多少倍？
分析： 题中的已知条件不能计算出两种三 角形的面积，我们可以用边长是3厘 米的正三角形拼一个边长是9厘米的 正三角形，从而看出它们之间的倍 数关系。从下图中可以看出：边长9 厘米的正三角形是边长3厘米的正三 角形面积的9倍。
例3、两条对角线把梯形ABCD分割
成四个三角形。已知两个三角形的 面积（如图所示），求另两个三角 形的面积各是多少？（单位：平方 厘米）
分析 ：
1，因为三角形ABD与三角形ACD等底 等高，所以面积相等。因此，三角形 ABO的面积和三角形DOC的面积相等， 也是6平方厘米。 2，因为三角形BOC的面积是三角形 DOC面积的2倍，所以BO的长度是OD 的2倍，即三角形ABO的面积也是三角 形AOD的2倍。所以，三角形AOD的面 积是6÷2=3平方厘米。