梁内力组合计算表
盖梁计算
六、盖梁设计(一)荷载计算1.恒载计算上部结构恒载见表62.活载计算(1)活载横向分布系数计算活载横向分布系数计算时荷载对称布置及非对称布置均采用杠杆原理方法进行计算。
单列车对称布置时见图11单列车非对称布置时见图12双列车对称布置时见图13单列车非对称布置时见图141 2 300.12210.8750.437 2ηηη===⨯=1 2 310.560.27821(0.4340.315)0.375 210.6480.3242ηηη=⨯==⨯+==⨯=图110.8750.8750.566图120.6840.434 0.31512310.2860.143210.7010.350210.950.4752ηηη=⨯==⨯==⨯=12310.5560.27821(0.4340.315)0.37521(0.6480.355)0.5022ηηη=⨯==⨯+==⨯+=(2)按顺桥向活载移动情况，求支座活荷载反力的最大值 布载长度L 取15.96m a. 单孔荷载（见图15）0.556 0.7011 0.951 0.4340.3150.648 0.355图14 图130.286b.单列车时支座反力R 2=140×(1+0.913)+120×(0.474+0.386)×30×0.199=236.99KN 两列车时支座反力2×R 2=2×236.99=473.96 KN b.双孔荷载（见图16）单列车时支座反力R 1=140×(0.562+0.65)=169.68 KN R 2=120×(1+0.913)+30×0.725=251.31KN R=R 1 +R 2=169.68+251.31=420.99KN 双列车时支座反力2×（R 1 + R 2）=2×420.99=841.98KN (3)载横向分布后各梁支点反力计算见表9表9 主梁支点反力计算120 140 30140 120 图150.913 0.474 0.3860.199120 140 30140120 0.650.913 1.00 0.7250.562R 2图16(4)各梁恒载、活载反力组合各梁恒载、活载反力组合计算见表10，表中均取主梁最大值。
主梁内力计算
主梁的内力计算主梁的内力计算包括恒载内力计算和活载内力计算。
根据上述梁跨结构纵、横截面的布置，计算活载作用下的梁桥荷载横向分布系数，求出各主梁控制截面（取跨中、四分点、变化点截面及支点截面）的恒载和最大活载内力，然后再进行主梁内力组合。
一、恒载内力计算1、恒载集度⑴预制梁自重（第一期恒载）①．跨中截面段主梁自重（四分点截面至跨中截面，长7.25m ）(1)0.861625.07.25156.165g KN =⨯⨯=②．马蹄抬高与腹板变宽段梁的自重近似计算（长3.7m ） 主梁端部截面面积为A=1.176m 2()(2) 1.17600.8616 3.725.0/294.239g KN =+⨯⨯=③．支点段梁的自重（长3.55m ）(3) 1.1760 3.5525.0=104.37g KN =⨯⨯④．横隔梁的自重 中横隔梁体积为：()30.16 1.590.920.240.72/20.120.12/20.219072m ⨯⨯-⨯-⨯= 端横隔梁体积为：()30.25 1.840.80.20.6/20.353m ⨯⨯-⨯=故半跨内横隔梁重量()(4)20.21907210.3532519.7786g KN =⨯+⨯⨯=⑤．主梁永久作用集度()156.16594.239104.3719.7786/14.9825.00/g KN m KN m I =+++= （2）第二期恒载①翼缘板中间湿接缝集度()50.40.1625.0 1.6/g KN m =⨯⨯=②现浇部分横隔梁一片中横隔梁（现浇部分）体积：30.16 1.590.20.05088m ⨯⨯= 一片端横隔梁（现浇部分）体积：30.250.2 1.840.092m ⨯⨯= 故()()630.0508820.09225.0/29.960.2809/g KN m =⨯+⨯⨯=③桥面铺装层6cm 沥青混凝土铺装：0.0612.52317.25/KN m ⨯⨯=将桥面铺装重量均分给五片主梁，则()717.25/5 3.45/g KN m ==④防撞栏：两侧防撞栏均分给五片主梁，则()87.52/53/g KN m =⨯=⑤主梁二期永久作用集度II 1.60.2809 3.4538.3309/g KN m =+++=2、永久作用效用：下面进行永久作用效用计算（参照图1-4），设c 为计算截面至左侧支座的距离，并令/a c l =。
第三章 静定结构的内力计算
FAy
1 3a 4 FP a M q 3a 3a 2 5
第三章
静定结构的内力计算
M
B
0
3a 4 FAy 3a M q 3a FP a 0 2 5 1 3a 4 FAy FP a M q 3a 3a 2 5
第三章
无荷载 平行轴线
Q图
静定结构的内力计算
均布荷载
集中力 发生突变
P
集中力偶
无变化 发生突变
m
斜直线
M图
二次抛物线 凸向即q指向
出现尖点
两直线平行 备 注
Q=0区段M图 Q=0处，M 平行于轴线 达到极值
集中力作用截 集中力偶作用 面剪力无定义 面弯矩无定义
在自由端、铰支座、铰结点处，无集中力偶作用，截面弯矩 等于零，有集中力偶作用，截面弯矩等于集中力偶的值。
第三章 静定结构的内力计算
第三章
静定结构的内力计算
§3-1单跨静定梁
一、静定结构概述 1．概念：是没有多余约束的几何不变体系。 2．特点：在任意荷载作用下，所有约束反力和内力都 可由静力平衡方程唯一确定。 平衡方程数目 = 未知量数目 3．常见的静定结构 常见的静定结构有：单跨静定梁、多跨静定梁、静 定平面刚架、三铰拱、静定平面桁架、静定组合结构等 (如下图）。
0 FYA FYA 0 FYB FYB
A
x
C
L
斜梁的反力与相应简支 梁的反力相同。
第三章
（2）内力
静定结构的内力计算
求斜梁的任意截面C的内力，取隔离体AC： a FP1 A
FYA x Fp1 FYA
0
MC
内力组合及内力调整
7 内力组合及内力调整7.1内力组合各种荷载情况下的框架内力求得后，根据最不利又是可能的原则进行内力组合。
当考虑结构塑性内力重分布的有利影响时，应在内力组合之前对竖向荷载作用下的内力进行增幅。
分别考虑恒荷载和活荷载由可变荷载效应控制的组合和由永久荷载效应控制的组合，并比较两种组合的内力，取最不利者。
由于构件控制截面的内力值应取自支座边缘处，为此，进行组合前，应先计算各控制截面处的（支座边缘处的）内力值。
1）、在恒载和活载作用下，跨间max M 可以近似取跨中的M 代替，在重力荷载代表值和水平地震作用下，跨内最大弯矩max M 采用解析法计算：先确定跨内最大弯矩max M 的位置，再计算该位置处的max M 。
当传到梁上的荷载为均布线荷载或可近似等效为均布线荷载时，按公式7-1计算。
计算方式见图7-1、7-2括号内数值，字母C 、D 仅代表公式推导，不代表本设计实际节点标号字母。
2max182M M M ql +≈-右左 且满足2max 116M ql = （7-1） 式中：q ——作用在梁上的恒荷载或活荷载的均布线荷载标准值；M 左、M 右——恒载和活载作用下梁左、右端弯矩标准值；l ——梁的计算跨度。
2）、在重力荷载代表值和地震作用组合时，左震时取梁的隔离体受力图，见图7-1所示, 调幅前后剪力值变化,见图7-2。
图7-1 框架梁内力组合图图7-2 调幅前后剪力值变化图中：GC M 、GD M ——重力荷载作用下梁端的弯矩； EC M 、CD M ——水平地震作用下梁端的弯矩C R 、D R ——竖向荷载与地震荷载共同作用下梁端支座反力。
左端梁支座反力：()C 1=2GD GC EC ED ql R M M M M l--++；由0M ddx=，可求得跨间max M 的位置为:1C /X R q = ； 将1X 代入任一截面x 处的弯矩表达式,可得跨间最大弯矩为： 弯矩最大点位置距左端的距离为1X ，1=/E X R q ；()101X ≤≤； 最大组合弯矩值：2max 1/2GE EF M qX M M =-+；当10X <或11X >时，表示最大弯矩发生在支座处，取1=0X 或1=X l ，最大弯矩组合设计值的计算式为：2max C 11/2GE EF M R X qX M M =--+； 右震作用时，上式中的GE M 、EF M 应该反号。
混凝土简支桥梁计算书—计算表格
1.2549 1.2549 1.2549
表5-1 内力值 153.31 181.86 -54.11 -6.01 -21.32 -19.91 80.79 79.81 57.26
3411.97
2559.02 1.4 1.4 0.8 3216.64 2412.52 2993.40 2245.09 表4-10 弯矩效应①×②× (③×④+⑤×⑥) 94.67 87.28 87.98
：kN） la 19.68
lb 5.28
a
b
7.76
4.72
表4-12 剪力效应 170.43 147.04 174.27
kN·m）
表4-8 弯矩效应 ω0 ①×②× ③ ③ 75.03 115.47 56.27 75.03 56.27 75.03 56.27 86.60 74.62 55.96 67.53 50.65 表4-9
γ Qj
γ Q1
ψc
γ 0 (γ Gi S Qik +ψ c γ Qj S Qjk +γ Q1 S Q1k )
γ0
γ Gi
1（5）
M 1/2
1（5） 2（4） 3
M 1/4 M 1/2 M 1/4 M 1/2 M 1/4
1002.46 1391.38 1043.53 1391.38 1043.53
86.60 74.62 55.96 67.53 50.65
899.34 1045.30 784.00 891.51 668.66 1.0 1.2
主梁截面尺寸及参数 表4-1 平均板厚h 1 重心位置a x 惯性矩I x 截面尺寸/cm cm 翼板宽 翼板厚 端部 根部 160 8 14 160 18 11 53.8 11780672
梁内力组合表(有公式)
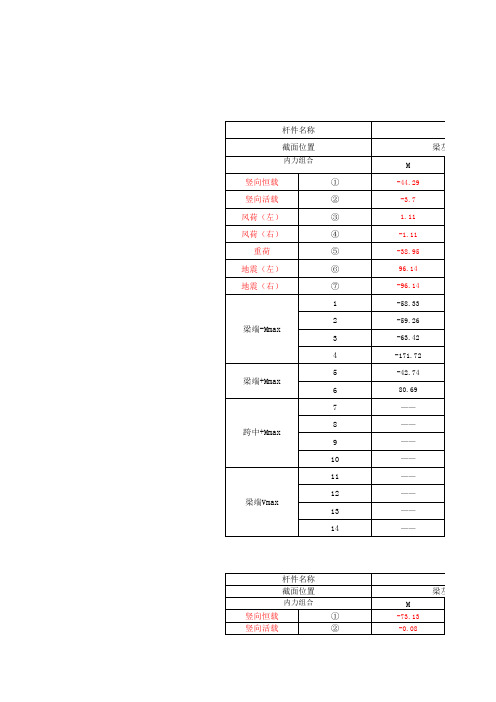
BC跨 梁左端 V
13.34 5.63 -2.75 2.75 16.16 -161.23 161.23 —— —— —— —— —— —— —— —— —— —— 25.38 26.20 23.53 228.99
跨中 M
3.73 1.76 0 0 4.61 0 0 —— —— —— —— —— —— 6.20 6.76 6.94 5.53 —— —— —— ——
竖向恒载 竖向活载 风荷（左） 风荷（右） 重荷 地震（左） 地震（右）
梁端-Mmax
梁端+Mmax
跨中+Mmax
梁端Vmax
杆件名称 截面位置
内力组合
梁左端 M ① ② ③ ④ ⑤ ⑥ ⑦ 1 2 3 4 5 6
-48.8 -15.68 4.62 -4.62 -56.64 239.89 -239.89 -80.39 -84.39 -81.25 -379.83 -42.33 263.06
梁右端 M
-49.89 -16.13 -2.8 2.8 -57.95 -164.86 164.86 -79.60 -84.80 -83.16 -283.86 -45.97 164.43 —— —— —— —— —— —— —— ——
V
-62.92 -23.47 -1 1 -74.66 -58.65 58.65 —— —— —— —— —— —— —— —— —— —— -99.90 -109.20 -107.94 -165.84
梁右端 M
-48.1 -15.54 -4.6 4.6 -55.87
V
-63.2 -23.57 -1.71 1.71 -74.99
-78.12 78.12 —— —— —— —— —— —— —— —— —— —— 99.60 108.37 106.52 189.97
门式刚架荷载计算及内力组合
（一）荷载分析及受力简图：1、永久荷载永久荷载包括结构构件的自重和悬挂在结构上的非结构构件的重力荷载，如屋面、檩条、支撑、吊顶、墙面构件和刚架自重等。
恒载标准值（对水平投影面）：板及保温层 0.30kN/㎡檩条 0.10kN/㎡悬挂设备 0.10kN/㎡0.50kN/㎡换算为线荷载：7.50.5 3.75 3.8/=⨯=≈q KN m2、可变荷载标准值门式刚架结构设计的主要依据为《钢结构设计规范》（GB50017-2003）和《冷弯薄壁型钢结构技术规范》（GB50018-2002）。
对于屋面结构，《钢结构设计规范》m，但构件的荷载面积大于602m的可乘折减系数0.6，门规定活荷载为0.5KN/2m。
由荷载规范查得，大连地区式刚架符合此条件，故活荷载标准值取0.3KN/2雪荷载标准值为0.40kN/㎡。
屋面活荷载取为 0.30kN/㎡雪荷载为 0.40kN/㎡取二者较大值 0.40kN/㎡换算为线荷载：7.50.43/q KN m =⨯=3、风荷载标准值 ：0k z s z ωβμμω=（1） 基本风压值 20kN/m 6825.065.005.1=⨯=ω（2） 高度Z 处的风振系数z β 取1.0（门式刚架高度没有超过30m ，高宽比不大于1.5，不考虑风振系数）（3） 风压高度变化系数z μ由地面粗糙度类别为B 类，查表得：h=10m ，z μ＝1.00；h=15m ，z μ＝1.14 内插：低跨刚架，h=10.5m ，z μ＝ 1.14 1.111.00(10.510)1510-+⨯--＝1.014；高跨刚架，h=15.7m ，z μ＝ 1.25 1.141.14(15.715)2015-+⨯--＝1.155。
（4） 风荷载体型系数s μ-0.5-0.6-0.4-0.4-0.5-0.5-0.2+0.8μsμs1其中，s μ＝0.2010.24.760.032301230arctg -⨯=⨯=+ 1s μ＝12 1.00.6(1)0.6(12)0.36915.710.5h h ⨯-=⨯-=+-各部分风荷载标准值计算：w 1k =0z s z βμμω＝7.5×1.0×0.8×1.014×0.6825=4.15 kN/m w 2k =0z s z βμμω＝7.5×1.0×0.032×1.014×0.6825=0.17kN/m w 3k =0z s z βμμω＝7.5×1.0×（-0.6）×1.014×0.6825=-3.11kN/m w 4k = 0z s z βμμω＝7.5×1.0×0.369×1.014×0.6825=1.91 kN/m w 5k = 0z s z βμμω＝7.5×1.0×（-0.2）×1.014×0.6825=-1.04 kN/mw 6k = w 7k ＝w 8k ＝0z s z βμμω＝7.5×1.0×（-0.5）×1.014×0.6825=-2.60 kN/m w 9k = w 10k ＝0z s z βμμω＝7.5×1.0×（-0.4）×1.014×0. 6825=-2.08 kN/m 用PKPM 计算门式刚架风荷载结果如下：其中，'1k ω＝4.2KN/m ≈1k ω=4.15 kN/m ；'2kω＝0.2KN/m ≈2k ω=0.17 kN/m ； '3k ω＝-3.1N/m ≈1k ω=-3.11 kN/m ；'4kω＝2.2KN/m ≈2k ω=1.91 kN/m ； '5k ω＝-1.2KN/m ≈1k ω=-1.04kN/m ；'6kω＝-3.0KN/m ≈6k ω=-2.60kN/m ； '7kω＝-3.0KN/m ≈7k ω=-2.60kN/m ；'8k ω＝-2.6KN/m ＝8k ω； '9k ω＝-2.1KN/m ≈9k ω=-2.08kN/m ；'10kω＝-2.1KN/m ≈10k ω=-2.08kN/m 。
弹性地基梁计算图表
1.00
0.000
0.112
0.239
-0.342 -0.500 0.500 0.342 0.191 0.045 0.095 0.236
1.25 1.50 1.75 2.00 2.25 2.50
0.000 0.000 0.000 0.000 0.000 0.000
0.056 0.009 -0.022 -0.052 -0.079 -0.105
表五
1.25 0.236 0.095
0.00 0.25
0.50
0.000
-0.310 -0.473 0.527 0.377
-0.157
-0.045
0.75
80 0.520 0.365 0.219 0.091 -0.030 -0.144 -0.257
-0.191
1.50 -0.209 -0.148 -0.084 -0.017 0.062 0.159 0.272 0.159 0.062 -0.017 -0.084 -0.148 -0.209
ηq 表
力所在位置 λ 0.00 0.25 0.00 （3.00） -1.000 0.000 0.25 （2.75） -0.559 -0.654 0.346 0.254 0.50
λ总=3.0
所要计算剪力的截面至梁左端的折算距离Φ 0.75 （2.75） -0.016 -0.174 1.00 （2.00） 0.123 -0.030 1.25 （1.75） 0.195 0.062
λ总=3.0
所要计算弯矩的截面至梁左端的折算距离Φ
表七
0.00（3.00） 0.25（2.75） 0.50（2.50） 0.75（2.75） 1.00（2.00） 1.25（1.75） 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 -0.192 0.045 0.032 0.022 0.013 0.007 0.002 -0.001 -0.003 -0.005 -0.006 -0.006 -0.007 -0.289 -0.084 0.124 0.087 0.056 0.032 0.013 0.000 -0.008 -0.015 -0.020 -0.022 -0.026 -0.319 -0.152 0.019 0.194 0.132 0.080 0.040 0.010 -0.011 -0.027 -0.039 -0.049 -0.060 -0.304 -0.176 -0.045 0.092 0.241 0.156 0.088 0.034 -0.005 -0.035 -0.060 -0.082 -0.102 -0.263 -0.172 -0.077 0.024 0.136 0.266 0.164 0.084 0.019 -0.033 -0.076 -0.117 -0.154
《主梁内力计算》PPT课件
2
4
24
4
(81.4)
(595.0)
x=1/2
00:16
Q=0 (0)
M 1 16.0619.52 763.4 8
(793.3)
1 活载内力计算方法
•活载内力计算方法
计算步骤 求横向分布系数m； 应用主梁内力影响线，将荷载乘m后，在纵向按 最不利位置布载，求得主梁最大活载内力。
计算方法
4 主梁内力计算例题
简支梁基频的简化计算公式：
f
EIc 2l 2 mc
mc G g
单根主梁：
A 0.3902m2 , Ic 0.066146m4 ,
G 0.3902 25 9.76N / m
G g 9.76 9.81 0.995103 NS 3 m2
C30混凝土
E 1010 N m2
3.4主梁内力计算
00:16
主梁内力计算
•计算截面的确定
小跨径简支梁：
计算跨中截面的
、支M点m截ax面和跨中截面的剪力；
剪力：支点、跨中按直线变化；
弯矩：支点、跨中按二次抛物线变化
Mx
4Mmax x(l x) l2
大跨径简支梁：
还应计算 截L面、截面变化处等的弯矩和剪力。 4
00:16
1 恒载内力计算
S 867.72
73.1
13.39 74.68
88.07
3.75
00:16
4 主梁内力计算例题
计算车道荷载、人群荷载的支点截面剪力
m变化区荷载重心处的内力影响线坐标为：
y 1(19.5 1 4.9) 19.5 0.916 3
车道荷载支点截面剪力：
S
(1
)
基于不同支承模型的连续梁内力分析
计 算 纵梁 内力时 ， 不考 虑面板 结 构 ， 按矩 形 截 面计 算 。 混 凝 土强 度 等 级 采 用 Ｃ ５ 弹性 模 量 Ｅ － ． ￣１７ Ｐ ， ３， Ｐ ３１ ０ｋ ａ ５ 桩 身截 面 面积 Ａ ：．３ｍ ， Ｐ ＩｉＩ２ 桩长 Ｌ ２ｍ 由此 计 算 的桩 的轴 向 ＝５ ， 刚性 系数 ＫＩ ２ Ｘ１６ Ｎｍ ＝． ５ ０ Ｋ ／ 。 ４
桩 端 嵌 入 中风 化 岩 面 以下 ３ 。 部 结 构 采 用 梁 板 式 装 配 整 ｍ 上 体 式 结 构 ， 向排 架 间距 为 ６ ， ６跨 ， 端 悬 臂 各 ｌ ｍ 横 ｍ共 两 ＿ 。 ５
“ 支承于横梁上 的装配整体式纵梁， 具有弹性支承性质 ， 对于 横梁 采用倒 “ ”型截面， Ｔ 总高 ３ ０ｍ ， ０ ０ ｍ 下横梁 高 １０ ｍ ， ４ ０ ｍ 宽 重要工程 宜按弹性支承连续梁计算 ， 一般 工程可简化 按刚性 ２ ０ｍ ， ０ ０ ｍ 上横梁高 １０ ｍ ， ７ ０ｍ 纵梁及轨道梁支承在下 ６０ ｍ 宽 ０ ｍ 。
１ 引 言 ．
对于梁板式高桩码头纵梁尤其是轨道梁， 荷载较大， 计算结果
对 结 构 安全 尤 为重 要 。 文 分别 按 刚性 支 承 、 本 弹性 点支 承 、 考
高 桩码 头 是一种 常见 的码 头结 构 型式 ， 要 结构等部分组成。 按上部结构型式分类 ， 高桩码头 虑 支 座 宽度 的弹 性 支承 对连 续梁 进 行 计 算 ， 对 计 算结 果 进 并
主要 有 承台式 、 粱 板 式、 无 梁板 式 、 架 式 、 架 式 等。 中梁 行比较。 桁 框 其 限于篇幅， 为了便于对计算结果进行 比较 ， 计算荷载仅
板式结构 由于各构件受力明确合理、 结构计算简便、 可承受较 考虑 结构 自重和 码头 面堆 货荷载 。
框架计算简图及梁柱线刚度
标准层8×0.2×（5.4-0.65）＝7.6 KN/m水泥粉刷墙面（5.4-0.65）×2×0.36＝3.42 KN/m合计：11.02 KN/m
底层8×0.2×（6-0.65）＝8.56 KN/m
2
水泥粉刷墙面（6-0.65）×2×0.36＝3.852 KN/m合计：12.412 KN/m
m第三跨：M左＝-210.47×0.8＝-168.38 KN·
mM右＝214.41×0.8＝171.53 KN·
m V左＝127.11KN V右＝-127.92 KN M中＝213.5 KN·
m右边跨：M左＝-228.69×0.8＝-182.95KN·
m M右＝173.03×0.8＝138.42 KN·
⑹、K轴柱纵向集中荷载的计算：
5顶层柱恒载＝7.8×4.465+3.9×2.76+2×7.8××6.14×1.95＝162.33 KN 8
5标准层柱恒载＝7.8×4.465+3.9×2.76+2×7.8××3.4×1.95＝110.23 KN 8
3、恒载作用下的梁端弯矩计算：
用叠加法计算梁的固端弯矩，计算结果见下表1：
50.3852 +0.3853）×3.9+2.76×3.9+2××6.14×1.95×3.9+2.768
5×3+2×1.5××6.14＝236.79 KN 8
5标准层柱恒载＝4.465×7.8+2×3.4×1.95××3.9×2+2×3.4×1.5×（1-28
5×0.3852 +0.3853）×3.9+2.76×（3.9+3）+2×1.5××3.4＝8
40m组合梁上部结构计算
一、概述一跨简支，标准跨径：40m，计算跨径38.5m，斜交角77°，主梁中心高1.8m，采用预弯钢-砼组合箱梁结构，钢箱梁中心高1.5m，采用Q345C钢材，现浇混凝土C50钢纤维混凝土，厚30cm。
桥型截面布置如下（单位：mm）：单幅桥主梁断面图 1二、主梁材料及参数1．主梁Q345C钢，工厂预制。
Q345C钢物理－力学性能如下：弹性模量: E s＝2.06x105 MPa剪切模量: G s＝0.79x105 MPa质量密度: r＝78.5 kN/m3线膨胀系数: a s＝1.2 x10-5/℃泊松比: m s＝0.3应力松弛: s＝1.5%局部次要钢结构采用Q235C钢屈服强度取σs＝324MPa，其相应的基本容许应力乘以折减系数324/343＝0.945，折减后见上表括号内数值。
2. C50混凝土抗压标准强度：f ck＝32.4MPa、抗压设计强度为f cd＝22.4MPa；抗拉标准强度：ft k＝2.65MPa、抗拉设计强度为f td＝1.83MPa；弹性模量Ec＝3.45x104MPa3．普通钢筋：R235钢筋的抗拉(抗压)设计强度：f sd=195MPa；HRB335钢筋的抗拉(抗压)设计强度：f sd=280MPa；三、荷载计算1、主梁自重边梁1＃、3＃梁宽5.1m、2＃梁宽4.8m一片钢箱梁自重（每延米）： q＝863.7*1.05/40＝22.67 kN/m现浇层自重（每延米）：1＃、3＃梁 q＝5.1*0.3*26＝39.78 kN/m2＃梁 q＝4.8*0.3*26＝37.44 kN/m2、二期恒载铺装自重（每延米）：1＃、3＃梁 q＝5.1*0.1*24＝12.24 kN/m2＃梁 q＝4.8*0.1*24＝11.52 kN/m地袱及盖板（每延米）： q＝16 kN/m栏杆（每延米）： q＝2 kN/m防撞墙（每延米）： q＝8 kN/mD500mm水管及支撑板： q＝2.9 kN/m（※钢箱梁、现浇层、附属构造具体尺寸详见施工图※）3、可变作用1）温度荷载简支梁整体温差按±30℃考虑，温度梯度按《公路桥涵设计通用规范》（JTG D60-2004）的规定计算。
组合梁桥截面特性计算表
2800 2800 2800 2800 2800 2800 2800 2800 2800 2800 2800 2800 2800 2800 2800
一期恒载作用时的截面特性 混凝土面 换算后 钢梁面 积 Ac 混凝土面积 积As （mm2） Ac'（mm2） （mm2） 15.29 15.29 15.29 15.29 15.29 15.29 15.29 15.29 15.29 15.29 15.29 15.29 15.29 15.29 15.29 1950000 1950000 1950000 1950000 1950000 1950000 1950000 1950000 1950000 1950000 1950000 1950000 1950000 1950000 1950000 127534.336 127534.336 127534.336 127534.336 127534.336 127534.336 127534.336 127534.336 127534.336 127534.336 127534.336 127534.336 127534.336 127534.336 127534.336 136960 169420 244640 330560 330560 244640 169420 136960 169420 244640 330560 330560 244640 169420 136960 换算后 截面面积 A0 264494.3 296954.3 372174.3 458094.3 458094.3 372174.3 296954.3 264494.3 296954.3 372174.3 458094.3 458094.3 372174.3 296954.3 264494.3
钢梁面
【土木毕设】横梁内力组合_内力组合最不利表
138.9 231.19 69.48 277.84
132.14 266.76 53.43 271.5
Nmax 78.46 287.68 45.99 340.17
69.16 268.95 40.72 321.44
69.16 268.95 40.72 321.44
1633.46 1633.46 1023.66
181.33 181.33 35.59
1680.12 1680.12 1521.48
258.49 1605.26 216.59 1651.92
31.69 1841.58 32.17 1894.06
205.66 1518.53 163.17 1565.18
内力种类
M N M N V M N M N V M N M N V M N M N V
内力种类
Mmax N
166.59 909.63 120.87 956.29
M Nmax 35.49 919.04 120.87 956.29
M Nmin 107.76 664.74 62.03 711.39
197.59 907.42 140.53 954.08
31.59 1402.98 136.8 1248.64
225.9 1254.58 189.63 1301.24
225.9 1254.58 31.64 1500.91
31.59 1402.97 136.8 1248.64
189.27 1261.06 160.2 1307.7
189.27 1261.06 160.2 1307.7
截面 上端 下端
上端 下端
上端 下端
上端 下端