相交圆的公共弦定理
平面几何中的圆及其相关定理

平面几何中的圆及其相关定理圆是平面上最基本的几何形状之一,它具有许多特殊的性质和定理。
本文将介绍圆的定义、圆心角定理、弧长定理以及切线定理等相关内容。
一、圆的定义圆是平面上所有到一个固定点距离相等的点的集合。
这个点被称为圆心,到圆心的距离称为半径。
圆的符号通常用字母"〇"来表示。
二、圆心角定理圆心角是以圆心为顶点的角。
圆心角定理指出,在同一个圆中,不论圆心角所对的弧长长短如何,其对应的圆心角大小都相等。
也就是说,对于同一圆上的两个弧所对应的圆心角相等。
三、弧长定理弧是由圆上的两个点所确定的一段弧线。
弧长是弧所对的圆心角的一部分,它等于整个圆的周长乘以圆心角所占的比例。
弧长定理可以表示为:弧长 = (圆的周长 / 360°) ×圆心角的度数。
四、切线定理在圆上,从切点引出的切线与半径垂直。
根据切线定理,切线与半径的垂直关系可以推导出许多重要的定理和性质。
切线定理的一个重要应用是圆的切线与半径之间的关系。
如果从圆的外部点引出两条切线,并连接切点和该点,那么连接两个切点所得的线段垂直于两个切线的连线,并且等于两个切线的长度之和。
五、圆的相交定理当两个圆相交时,有以下几种可能的情况:内切、外切、相交和包含。
内切是指两个圆的内部都有公共的一部分;外切是指两个圆的外部都有公共的一部分;相交是指两个圆的内部和外部都有公共的一部分;包含是指一个圆的内部包含了另一个圆。
根据圆的相交定理,当两个圆相交时,连接两个圆的圆心与两个切点,可以得到一条直线。
此直线称为两个圆的公共弦,对于内切和外切的情况,公共弦也是切线。
六、圆内接四边形定理圆内接四边形是指一个四边形的四个顶点都在同一个圆上。
根据圆内接四边形定理,一个四边形是圆内接四边形的充分必要条件是对角线互相垂直,即两对对角线的交点构成的四个角互为直角。
结论通过对平面几何中的圆及其相关定理的介绍,我们了解到圆与圆心角的关系、弧长定理、切线定理、圆的相交情况以及圆内接四边形的定理。
切割线定理割线定理相交弦定理等及几何题解
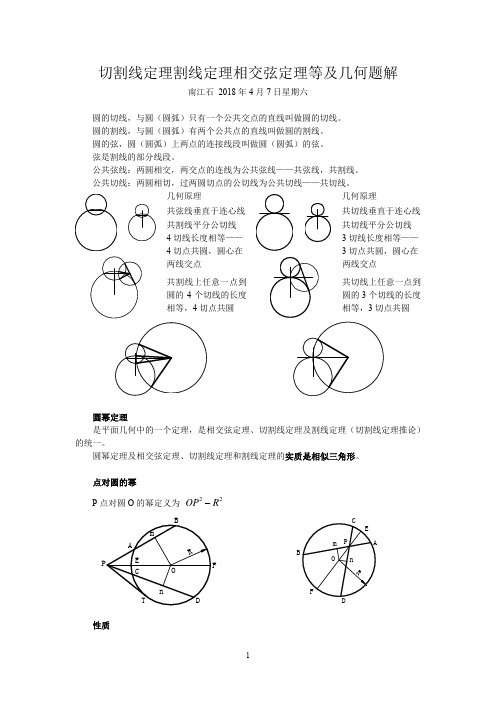
切割线定理割线定理相交弦定理等及几何题解南江石 2018年4月7日星期六圆的切线,与圆(圆弧)只有一个公共交点的直线叫做圆的切线。
圆的割线,与圆(圆弧)有两个公共点的直线叫做圆的割线。
圆的弦,圆(圆弧)上两点的连接线段叫做圆(圆弧)的弦。
弦是割线的部分线段。
公共弦线:两圆相交,两交点的连线为公共弦线——共弦线,共割线。
公共切线:两圆相切,过两圆切点的公切线为公共切线——共切线。
几何原理 几何原理共弦线垂直于连心线共切线垂直于连心线共割线平分公切线 共切线平分公切线4切线长度相等—— 4切点共圆,圆心在两线交点3切线长度相等——3切点共圆,圆心在两线交点共割线上任意一点到圆的4个切线的长度相等,4切点共圆共切线上任意一点到圆的3个切线的长度相等,3切点共圆圆幂定理是平面几何中的一个定理,是相交弦定理、切割线定理及割线定理(切割线定理推论)的统一。
圆幂定理及相交弦定理、切割线定理和割线定理的实质是相似三角形。
点对圆的幂P 点对圆O 的幂定义为22R OP FB性质点P 对圆O 的幂的值,和点P 与圆O 的位置关系有下述关系: 点P 在圆O 内→P 对圆O 的幂为负数; 点P 在圆O 外→P 对圆O 的幂为正数; 点P 在圆O 上→P 对圆O 的幂为0。
切割线定理从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项。
PBPTPT PA =PB PA PT ∙=2 222Am Pm PT -=割线定理(切割线定理的推论)从圆外一点引圆的两条割线,这一点到每条割线与圆交点的距离的积相等。
PD PC PB PA ∙=∙2222Cn Pn Am Pm -=-相交弦定理圆内的两条相交弦,被交点分成的两条线段长的积相等,或经过圆内一点引两条弦,各弦被这点所分成的两线段的积相等。
PD PC PB PA ∙=∙2222A Pn Cn Pm m -=-垂径定理(相交弦定理推论)如果弦与直径垂直相交,那么弦的一半是它所分直径所成的两条线段的比例中项。
“公共弦”的那些事儿

为1的直线l,使得以l被圆C截得的弦A B为直径的圆过原
点?若存在,求出直线l的方程;若不存在,请说明理由.
思路分析院这是一道存在性的探究题,首先,解题时
要注意答题格式的规范性,其次,如何理解并转化“使得
以l被圆C截得的弦A B为直径的圆过原点”这句话?一种
理解:将以A B为直径的圆的方程表示出来,并代入原点
-2 O 2 -2 C
B(4x2,y62)x
m,与圆C的两个交点分别为 A(x1,y1)-4
A(x1,y1),B(x2,y2),以A B为直 径的圆过 原点,如 图4所 示,
-6 图4
将直线l的 方 程 y=x+m 代入 圆 C的 方 程 中,整 理 得2x2+
(2m+2)x+m2+4m -4=0.因 为 直 线l与 圆 C相 交 ,所以 驻 =
圆的公共弦所在的直线方程.
嗓 解法2院
将两圆的方程联立得
x2+y2=1,
将
x2+y2-2x-2y+1=0,
两个方程相减,整理得x+y-1=0,所以圆C1与圆C2的公共 弦所在的直线方程为x+y-1=0.
点评院很明显袁在解法1中袁由于需要解二元二次方
程组袁其计算量不言而喻袁这也是大部分学生不希望遇
到的袁而解法2避开了解方程组袁大大弱化了计算量袁也 为我们提供了一种便捷的求公共弦所在直线方程的途 径袁即两圆方程相减袁消去二次项袁便可得到公共弦所在 的直线方程.
9-
9 5
=
6姨 5
5
.故公共弦长|A B|=2|A H |=
12 姨 5 . 5 点评院解法2与解法3侧重于图形中的几何运算袁也
圆公共弦定理证明

圆公共弦定理证明圆的十八个定理1、圆心角定理:在同圆或等圆中,相等的圆心角所对弧相等,所对的弦相等,所对的弦的弦心距相等。
推论:在同圆或等圆中,如果两个圆心角、两条弧、两条弦或两弦的弦心距中有一组量相等那么它们所对应的其余各组量都相等2、圆周角定理:一条弧所对的圆周角等于它所对的圆心角的一半。
推论1:同弧或等弧所对的圆周角相等;同圆或等圆中,相等的圆周角所对的弧也相等推论2:半圆(或直径)所对的圆周角是直角;90°的圆周角所推论3:如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形3、垂径定理:垂直弦的直径平分该弦,并且平分这条弦所对的两条弧。
推论1:①平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧②弦的垂直平分线经过圆心,并且平分弦所对的两条弧推论2:圆的两条平行弦所夹的弧相等4、切线之判定定理:经过半径的外端并且垂直于该半径的直线是圆的切线。
5、切线长定理:从圆外一点引圆的两条切线,他们的切线长相等,这一点与圆心的连线平分这两条切线的夹角。
6、公切线长定理:如果两圆有两条外公切线或两条内公切线,那么这两条外公切线长相等,两条内公切线长也相等。
如果他们相交,那么交点一定在两圆的连心线上。
7、相交弦定理:圆内两条弦相交,被交点分成的两条线段长的乘积相等。
8、切割线定理:从圆外一点向圆引一条切线和一条割线,则切线长是这点到割线与圆的两个交点的两条线段长的比例中项。
9、割线长定理:从圆外一点向圆引两条割线,这一点到每条割线与圆的交点的两条线段长的积相等。
10、切线的性质定理:圆的切线垂直于经过切点的半径推论1:经过圆心且垂直于切线的直线必经过切点推论2:经过切点且垂直于切线的直线必经过圆心11、弦切角定理:弦切角等于它所夹的弧对的圆周角推论:如果两个弦切角所夹的弧相等,那么这两个弦切角也相等12、定理:相交两圆的连心线垂直平分两圆的公共弦13、定理:把圆分成n(n≥3):(1)依次连结各分点所得的多边形是这个圆的内接正n边形2)经过各分点作圆的切线,以相邻切线的交点为顶点的多边形是这个圆的外切正n边形14、定理:任何正多边形都有一个外接圆和一个内切圆,这两个圆是同心圆15、定理:任何正多边形都有一个外接圆和一个内切圆,这两个圆是同心圆16、定理:正n边形的半径和边心距把正n边形分成2n个全等的直角三角形17、定理:圆的内接四边形的对角互补,并且任何一个外角都等于它的内对角。
求两圆公共弦长的方法

求两圆公共弦长的方法嘿,咱今儿就来唠唠求两圆公共弦长的那些事儿!你想啊,这两个圆就像是两个小伙伴,它们有时候会有一条共同的“线”牵连着,这就是公共弦啦!那怎么找到这条弦的长度呢?咱先说一个简单直接的办法,那就是把两个圆的方程相减!这一减,嘿,就得出了公共弦所在的直线方程。
然后呢,咱再在其中一个圆里,利用圆心到直线的距离公式,算出圆心到这条公共弦的距离。
就好比你要知道你和小伙伴之间的距离一样。
有了这个距离,再结合圆的半径,用勾股定理一捣鼓,不就能求出公共弦长的一半啦!然后再乘以 2,公共弦长不就出来了嘛。
还有啊,有时候咱可以通过图形来直观感受。
想象一下,那两个圆就像是两个大圆盘摆在那,公共弦就是它们之间的那根纽带。
咱仔细观察这个图形,利用一些几何关系,也能找到公共弦长呢。
再比如说,咱可以设出公共弦的端点坐标,然后把这些坐标代入到两个圆的方程里,这不就有了一堆等式嘛。
再通过解方程组,就能把端点坐标求出来,那公共弦长不也就知道了嘛。
哎呀,你说这求公共弦长的方法是不是挺有意思的?就像解谜题一样,一点点地去探索,去发现。
这可需要咱有点耐心和细心哦!可别嫌麻烦,等你真正掌握了这些方法,再遇到求两圆公共弦长的问题,那还不是手到擒来呀!你想想,要是以后有人问你怎么求两圆公共弦长,你就能胸有成竹地告诉他,用这个方法,用那个方法,多牛啊!而且这在数学里可重要啦,好多问题都可能涉及到呢。
总之呢,求两圆公共弦长的方法有好几种,咱得根据具体情况选择合适的方法。
就跟咱出门穿衣服一样,得看天气和场合嘛。
咱得把这些方法都掌握好了,才能在数学的世界里畅游无阻呀!所以呀,别小瞧了这些方法,它们可是咱探索数学奥秘的重要工具呢!好好学,好好用,你肯定能行的!。
两两相交的圆的三公弦共点

两两相交的圆的三公弦共点1.引言1.1 概述在几何学中,圆是一种基本的几何图形,它具有许多独特的性质和特点。
当两个圆相交时,我们可以发现一些有趣的几何特征。
其中之一就是两两相交的圆的三公弦共点的性质。
所谓两两相交的圆,指的是存在两个圆,它们的边界相交于两个不同的点。
这种情况在几何中非常常见,许多几何问题和现实世界中的场景都与两个相交的圆有关。
当我们构造这两个圆的公切线时,我们会发现一条有趣的线段——三公弦。
三公弦是指通过两个相交圆的公共切点,并且与圆相交的线段。
这条线段有一个特殊的性质,即两两相交的圆的三公弦共点。
也就是说,不论两个相交的圆的位置如何变化,它们的三公弦都会交于同一个点。
对于这个特殊的现象,我们需要进行一定的证明来确保其正确性。
通过几何证明,我们可以得出结论:两两相交的圆的三公弦确实共点。
这个结论在几何学中具有重要的意义。
首先,它可以帮助我们解决一些与圆有关的问题,例如圆的切线构造、圆的内切和外切等。
其次,它也能够拓展我们的几何思维,让我们对圆的性质有更深入的理解。
在接下来的正文中,我们将探讨两两相交的圆的基本性质以及三公弦的定义和性质。
并通过几何证明,确认两两相交的圆的三公弦确实共点。
最后,我们将探讨这个结论的应用和意义,展示它在几何学中的重要作用。
1.2文章结构文章结构部分的内容应包括本文的主要内容和各个部分的简要介绍。
下面是一个可能的内容编写示例:在本文中,将探讨"两两相交的圆的三公弦共点"的现象和相关性质。
文章结构如下:第一部分:引言1.1 概述1.2 文章结构1.3 目的第二部分:正文2.1 两两相交的圆的基本性质2.2 三公弦的定义和性质第三部分:结论3.1 两两相交的圆的三公弦共点的证明3.2 应用和意义在正文部分,我们将首先介绍两两相交的圆的基本性质,包括相交的位置关系和相交点的性质。
随后,我们将详细讨论三公弦的定义和性质,探究这种特殊的弦与圆的关系。
圆的性质和定理
【圆的平面几何性质和定理】[圆的基本性质与定理]1定理不在同一直线上的三点确定一个圆。
(圆的确定)2圆的对称性质:圆是轴对称图形,其对称轴是任意一条过圆心的直线。
圆也是中心对称图形,其对称中心是圆心。
3垂径定理垂直于弦的直径平分这条弦并且平分弦所对的两条弧推论1 ①平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧②弦的垂直平分线经过圆心,并且平分弦所对的两条弧③平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧推论2 圆的两条平行弦所夹的弧相等113、圆是以圆心为对称中心的中心对称图形[有关圆周角和圆心角的性质和定理]1定理在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对的弦的弦心距相等推论在同圆或等圆中,如果两个圆心角、两条弧、两条弦或两弦的弦心距中有一组量相等那么它们所对应的其余各组量都相等2圆周角定理一条弧所对的圆周角等于它所对的圆心角的一半3圆心角定理圆心角的度数等于他所对的弧的度数推论1 同弧或等弧所对的圆周角相等;同圆或等圆中,相等的圆周角所对的弧也相等推论2 半圆(或直径)所对的圆周角是直角;90°的圆周角所对的弦是直径推论3 如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形[园内接四边形的性质与定理]1定理圆的内接四边形的对角互补2定理并且任何一个外角都等于它的内对角3圆内接四边形判定定理如果一个四边形对角互补,那么这个四边形的四个顶点共圆推论如果一个四边形的一个外角等于它的内角的对角,那么这个四边形的四个顶点共圆[有关切线的性质和定理]1切线的判定定理经过半径的外端并且垂直于这条半径的直线是圆的切线2切线的性质定理圆的切线垂直于经过切点的半径推论1 经过圆心且垂直于切线的直线必经过切点推论2 经过切点且垂直于切线的直线必经过圆心[与圆有关的比例线段]1相交弦定理圆内的两条相交弦,被交点分成的两条线段长的积相等推论如果弦与直径垂直相交,那么弦的一半是它分直径所成的两条线段的比例中项2 割线定理从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线段长的积相等3切割线定理从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项4切线长定理从圆外一点引圆的两条切线,它们的切线长相等圆心和这一点的连线平分两条切线的夹角[圆的其他性质定理]1弦切角定理弦切角等于它所夹的弧对的圆周角推论如果两个弦切角所夹的弧相等,那么这两个弦切角也相等2①直线L和⊙O相交d<r②直线L和⊙O相切d=r③直线L和⊙O相离d>r3圆的外切四边形的两组对边的和相等[圆与圆]1如果两个圆相切,那么切点一定在连心线上2①两圆外离d>R+r②两圆外切d=R+r③两圆相交R-r<d<R+r(R>r)④两圆内切d=R-r(R>r)⑤两圆内含d<R-r(R>r)3定理相交两圆的连心线垂直平分两圆的公共弦4定理把圆分成n(n≥3): ⑴依次连结各分点所得的多边形是这个圆的内接正n边形⑵经过各分点作圆的切线,以相邻切线的交点为顶点的多边形是这个圆的外切正n边形(有关外接圆和内切圆的性质和定理)5定理任何正多边形都有一个外接圆和一个内切圆,这两个圆是同心圆6一个三角形有唯一确定的外接圆和内切圆。
已知两圆方程求公共弦方程
已知两圆方程求公共弦方程
已知两圆方程求公共弦方程如下:
1、首先,计算两个圆心的两个坐标;
2、然后根据两点之间的距离公式,计算计算出两个圆心的距离;
3、根据“连接两个中心的线垂直且平分相交弦”的相交弦定理,最终连接相交弦与任意圆的交点;
4、根据上面的定理,用勾股定理计算出一半的相交弦,然后就可以计算出相交弦长,即共弦的弦长。
扩展资料:
1、在圆心取一点,圆的半径为r,得到直线距离d,公弦长为s,(s/2)^2=r^2-d^2是直角三角形的弦长。
2、第一个圆方程减去第二个圆方程得到公共弦所在的直线,然后将方程组合。
3、连接两个圆的中心,找到中心之间的距离,然后将弦垂直平分。
与圆有关的定理
与圆有关的定理
圆的定理:1、垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的2条弧。
2、垂径定理:垂直弦的直径平分该弦,并且平分这条弦所对的两条弧。
3、切线定理:垂直
于过切点的半径;经过半径的外端点,并且垂直于这条半径的直线,是这个圆的切线。
1、公切线长定理:如果两圆有两条外公切线或两条内公切线,那么这两条外公切线
长相等,两条内公切线长也相等。
如果他们相交,那么交点一定在两圆的连心线上。
2、切线短定理:从铅直一点至圆的两条切线的长成正比,那点与圆心的连线平分切
线的夹角。
4、割线定理:从圆外一点引圆的两条割线,这一点到每条割线与圆交点的距离的积
相等。
5、垂径定理:旋转轴弦的直径平分这条弦,并且平分这条弦所对的两条弧。
6、弦切角定理:弦切角等于对应的圆周角。
(弦切角就是切线与弦所夹的角)。
7、圆心角定理:在同圆或等圆中,成正比的圆心角所对弧成正比,面元的弦成正比,面元的弦的弦心距成正比。
8、圆周角定理:一条弧所对的圆周角等于它所对的圆心角的一半。
9、平行弦定理:圆内两条弦平行,被交点分为的两条线段长的乘积成正比。
10、定理:任何正多边形都有一个外接圆和一个内切圆,这两个圆是同心圆。
11、定理:任何正多边形都存有一个外接圆和一个内切圆,这两个圆就是同心圆。
12、定理:相交两圆的连心线垂直平分两圆的公共弦。
13、定理:把圆分为n(n≥3):。
初三《圆》知识点及定理(1)
《圆》知识点及定理一、圆的概念集合形式的概念: 1、圆可以看作是到定点的距离等于定长的点的集合;2、圆的外部:可以看作是到定点的距离大于定长的点的集合;3、圆的内部:可以看作是到定点的距离小于定长的点的集合轨迹形式的概念:1、圆:到定点的距离等于定长的点的轨迹就是以定点为圆心,定长为半径的圆;(补充)2、垂直平分线:到线段两端距离相等的点的轨迹是这条线段的垂直平分线(也叫中垂线);3、角的平分线:到角两边距离相等的点的轨迹是这个角的平分线;4、到直线的距离相等的点的轨迹是:平行于这条直线且到这条直线的距离等于定长的两条直线;5、到两条平行线距离相等的点的轨迹是:平行于这两条平行线且到两条直线距离都相等的一条直线.二、点与圆的位置关系1、点在圆内⇒d r<⇒点C在圆内;2、点在圆上⇒d r=⇒点B在圆上;3、点在圆外⇒d r>⇒点A在圆外;三、直线与圆的位置关系1、直线与圆相离⇒d r>⇒无交点;2、直线与圆相切⇒d r=⇒有一个交点;3、直线与圆相交⇒d r<⇒有两个交点;四、圆与圆的位置关系外离(图1)⇒无交点⇒d R r>+;外切(图2)⇒有一个交点⇒d R r=+;相交(图3)⇒有两个交点⇒R r d R r-<<+;内切(图4)⇒有一个交点⇒d R r=-;内含(图5)⇒无交点⇒d R r<-;五、垂径定理垂径定理:垂直于弦的直径平分弦且平分弦所对的弧。
推论1:(1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;(2)弦的垂直平分线经过圆心,并且平分弦所对的两条弧;(3)平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧以上共4个定理,简称2推3定理:此定理中共5个结论中,只要知道其中2个即可推出其它3个结论,即:①AB是直径②AB CD⊥③CE DE=④弧BC=弧BD⑤弧AC=弧AD中任意2个条件推出其他3个结论。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
相交圆的公共弦定理
相交圆的公共弦定理是指:如果有两个相交的圆,那么它们的两条公共弦所夹的弧度是相等的。
具体来说,设有两个相交的圆,圆心分别为O1和O2,半径分别为r1和r2。
这两个圆相交于点A和点B。
连接点A和点B,得到一条弦AB。
再连接O1和O2,得到一条直线。
设这条直线与弦AB的交点分别为C和D(如下图所示)。
这时,相交圆的公共弦定理告诉我们:弧ACB的弧度等于弧ADB的弧度。
二、证明
相交圆的公共弦定理的证明可以通过几何推导来完成。
具体来说,可以采用如下的证明方法。
(1)连接O1A、O1B、O2A和O2B,得到四个三角形。
(2)观察三角形O1AB和O2AB,它们都是等腰三角形,因为OA 和OB是圆的半径。
因此,∠O1AB=∠O1BA=∠O2AB=∠O2BA。
(3)观察三角形O1AC和O2BD,它们都是直角三角形,因为AC 和BD是圆的切线。
因此,∠O1AC=90°-∠O1CA,∠O2BD=90°-
∠O2DB。
(4)观察三角形O1CA和O2DB,它们都是共边三角形,因此它们的边长相等。
具体来说,OC=OD,AC=BD,因此,∠O1CA=∠O2DB。
(5)将上述结果整理,可以得到:
∠O1AB+∠O1CA=∠O2AB+∠O2DB。
由此可知,弧ACB的弧度等于弧
ADB的弧度。
三、应用
相交圆的公共弦定理是解决圆的相交部分的问题时非常有用的一个工具。
具体来说,它可以应用于以下几个方面。
(1)计算圆弧的长度
假设我们要求两个相交圆的公共弦所夹的圆弧长度,那么可以利用相交圆的公共弦定理来求解。
具体来说,可以先求出弦所夹的圆心角的大小,然后根据圆的周长公式(C=2πr)来计算圆弧的长度。
(2)证明圆弧的相等性
假设我们需要证明两个圆弧相等,那么可以利用相交圆的公共弦定理来证明。
具体来说,可以利用公共弦所夹的两个圆心角相等这一事实,来证明两个圆弧相等。
(3)求解三角形的面积
假设我们需要求解一个三角形的面积,其中有两个角是圆心角,那么可以利用相交圆的公共弦定理来求解。
具体来说,可以先求出圆心角所对应的圆弧长度,然后根据三角形面积公式(S=1/2×底×高)来计算三角形的面积。
总之,相交圆的公共弦定理是解决圆的相交部分的问题时非常有用的一个工具。
它可以帮助我们计算圆弧的长度、证明圆弧的相等性以及求解三角形的面积等问题。
因此,在学习圆的相关知识时,我们应该重视相交圆的公共弦定理的学习和应用。
