第12章轮系习 题答案
轮系答案

一 选择题1D 2B 3A 4A 5A 6C 7D 8A二 判断题1√ 2× 3√ 4× 5√ 6√ 7√ 8× 9√ 10√ 11√ 12×三 填空题 1 (1)m -各从动轮齿数连乘积各主动轮齿数连乘积判断外啮合次数来确定 2 各齿轮的轴线相对于机架的位置都是固定的3 至少有一个齿轮的轴线绕另外一个齿轮的固定轴线转动4 蜗杆 螺旋线5 惰轮或介轮6 2 1 太阳轮 行星轮7 太阳轮、行星架、行星轮8 行星轮9 转化机构法10 周转轮系四 简答题1答:常将多对齿轮组合在一起进行传动,这种由多对齿轮组成的传动系统成为轮系。
根据轮系在传动中各个齿轮的轴线在空间的位置是否固定分为定轴轮系、周转轮系、复合轮系。
2 答:所谓定轴轮系是指各齿轮的轴线相对于机架的位置都是固定的。
所谓周转轮系是指至少有一个齿轮的轴线绕另外一个齿轮的固定轴线转动。
3 答:定轴轮系中可以通过判断外啮合次数来确定总传动比的正负号4 答:惰轮齿数不影响传动比的大小,只起改变转向的作用。
5 答:基本周转轮系是由太阳轮、行星架、行星轮组成。
6 行星轮系只有一个中心轮固定不动自由度为1;差动轮系两个中心轮均不固定,自由度为2.7 答:反转法就是在整个轮系中不再以地球作为参照物,而是以行星架作为参照物。
8 答:当从整个轮系中划分出所有单一的周转轮系后,剩下的轴线固定不动的齿轮啮合系统就是定轴轮系。
9 答:根据轴线位置运动的特点找到行星轮,支撑行星轮的是中心架,与行星轮相啮合的是轴线固定不动的中心轮。
10 答:作用:获得很大的传动比;将主动轴的一种转速变换为从动轴的多种转速,改变传动方向;分配运动。
五 计算题五.轮系1.解﹙1﹚空间定轴轮系﹙2﹚由图可知,该轮系包括圆锥齿轮,涡轮蜗杆, 其转动比为3124142123806010836014036z n z z i n z z z ====''故141428808min 360n r n i ===2 略3 解.由图可得,2334B ''----构成行星轮系所以34242372114192418B z z z z i '''⨯=-=-=-⨯得220B i '=又112240401z i z -=-==-、12n n '= 得11224020800B B i i i '==-⨯=-4、解由图分析可得该复合轮系中有蜗杆则齿轮2的转速12239.19min n n r z == 齿轮2′与3′之间是构成定轴轮系 322332255153z n i n z '''==-=-=-22n n '= 23323.51min 5n n r '=-=齿轮3、4和杆H 构成周转轮系则 34344360320h H H n n z i n n z '-====- 其中40n =则3111.75min 2H n n r =-=-5、解由图分析可知该轮系为定轴轮系其中齿轮1为主动轮3532415312343034(1)0.089202622m z z z z z i z z z z z ''⋅⨯=-=-=-⨯⨯ 6解由图分析可得:构件1-2-3-H 构成一套周转轮系则 23113312256051520H H H z z W W i W W z z '⋅-⨯==-=-=--⋅⨯则1356H W W W +=(1) 当1W 、3W 转向相同时13520.95 5.27.8266H W W W rad s ++⨯=== (2) 当1W 、3W 转向相反时,取3W 的转向为正,则 13520.95 5.20.5866H W W W rad s -+-+⨯===7、解由题可知该轮系为周转轮系,经分析可得 1212213311186n z i n z =-=-=-=-2424427826279n z i n z '''==== 12116n n =- 42926n n '= 1416327n n =- 8、解对于符合轮系1、2、3及行星架1H 有 1311133213313H H H z n n i n n z -==-=--30n = 115000n = 14239.13min H n r1H p n n = 4239.13min p n r =对于符合轮系4、5、6及行星架2H得264246624115H H H z n n i n n z -==-=--60n = 4p n n = 21324.728min H n r = 21324.728min H Q n n r ==9、解对于符合轮系1、2、3、及行星架0H 有30n =010********H H H n n z i n n z -==-=-- 01310H n n =对于符合轮系1'、4、5及行星架H 有 511551325H H H z n n i n n z ''-==-=--'50H n n = 11n n '= 18543H n n =118543H H n i n == 10、解由图可知,构件1、3及H 轴线平行,则 2313124020260203H Hz z n n n n z z '-⨯=-=-=--⨯ 图中轮1、轮3转向相反,设轮1转向为正,则轮3为负,故得 4802803H Hn n -=--- 144031602H H n n -=+ 256min H n r =+“+”号说明系杆H 与轮1的转向相同。
机械原理轮系习题参考答案

一、解:(1)判断方向,蜗杆左旋用左手右旋用右手,四指握向蜗杆转动方向,拇指指向的反方向即为涡轮转向。
由此逆向判断图中蜗杆、涡轮和齿轮旋转方向如图中箭头所示。
手柄转向如图所示。
4001
601836186056341265432116=××=••=••=z z z z z z w w w w w w i 二、解:该轮系为周转轮系,由反转法对整个轮系加一个反向旋转角速度H w −,
由于齿轮4为定齿轮,角速度为零,即04=w ,所以H H i i 14
11−=; 又有 2.2)1(3423123
14−=•••−=z z z z z z i H
所以 2.32.211=+=H i
三、解:此轮系中假设轮1的方向向下,则行星轮2、2'和太阳轮4的转向都是
向下。
行星轮2、2'和行星架的角速度相同 在左边行星轮系中,1
3
1H 130z z H H −=−−=ωωωω 在右边行星轮系中,'2
444'2z z H ==ωωωω ∴4114ωω=i ==+4'2131z z z z z 25416
四、解:该轮系可以分为两部分,如图中虚线所分的左右两部分,左边为周转轮系,右边为定轴轮系;
分别求出两个轮系的传动比如下:
周转轮系:=H i 1414
1556601441===++z z n n n n H H ; 定轴轮系:7
63530566556====z z n n i ; 两轮系的关系是:
45n n =; 联立方程组求得min 9.741r n ≈; 转向与齿轮6转向相反。
《机械原理》(于靖军版)第12章习题答案
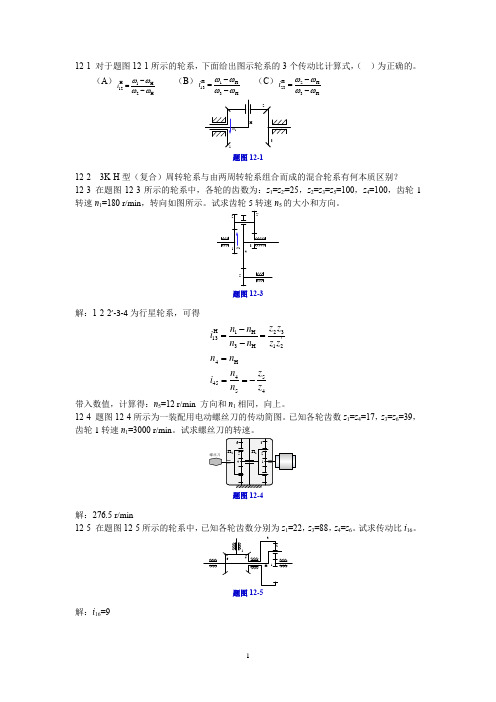
12-1 对于题图12-1所示的轮系,下面给出图示轮系的3个传动比计算式,( )为正确的。
(A )H 1H 122H i ωωωω-=-(B )H 1H 133H i ωωωω-=-(C )H 2H 233H i ωωωω-=-题图12-112-2 3K-H 型(复合)周转轮系与由两周转轮系组合而成的混合轮系有何本质区别?12-3 在题图12-3所示的轮系中,各轮的齿数为:z 1=z 2'=25,z 2=z 3=z 5=100,z 4=100,齿轮1转速n 1=180 r/min ,转向如图所示。
试求齿轮5转速n的大小和方向。
题图12-3解:1-2-2’-3-4为行星轮系,可得H 231H 13'3H 124H 544554z z n n i n n z z n n z n i n z -==-===-带入数值,计算得:n 5=12 r/min 方向和n 1相同,向上。
12-4 题图12-4所示为一装配用电动螺丝刀的传动简图。
已知各轮齿数z 1=z 4=17,z 3=z 6=39,齿轮1转速n 1=3000 r/min 。
试求螺丝刀的转速。
题图12-4解:276.5 r/min12-5 在题图12-5所示的轮系中,已知各轮齿数分别为z 1=22,z 3=88,z 4=z 6。
试求传动比i 16。
题图12-5解:i 16=912-6在题图12-6所示的轮系中,已知各轮齿数z1 =40,z2=z3=100,z4=z5=30,z6=20,z7=80,齿轮1转速n A=1000r/min,方向如图。
试求n B大小及方向。
解:n B=240 r/min 方向向上12-7 下题图12-7所示的轮系中,已知各齿轮的齿数分别为:z1 =80,z2=60,z2'=20,z3=40,z3'=20,z4= 30,z5=80。
轴A和轴B的转速分别为n A=50r/min,n B=60r/min,方向如图所示。
汽车构造课后练习答案第十二章

第12章 汽车转向系
12-1 答:用来改变或恢复汽车行驶方向的机构称为汽车转向系统。
其功用即改变或恢复汽车行驶方向。
机械转向系由转向操纵机构、转向器和转向传动机构三个部分组成。
12-2 答:为了保证汽车转向时所有车轮均作纯滚动,则所有车轮的轴线必须相交于一点,此交点称为转向中心。
应满足的理想关系为
12-3 什么是转向系的传动比?什么是转向器的传动比?什么是转向传动机构的传动比?
答:转向盘偏转角度与转向车轮偏转角度的比值叫转向系传动比。
摇臂轴转动角速度与同侧转向节偏转角速度之比,称为转向传动机构的传动比。
12-4 答:转向盘自由行程是指不使转向轮发生偏转而转向盘所能转过的角度。
转向盘从相应于汽车直线行驶的中间位置向任何一方向的自由行程不应超过10°~15°,当超过25°~30°时,必须及时进行调整。
12-5 答:液压助力转向HPS 系统、电控液压助力转向EHPS 系统和电动助力转向EPS 系统。
12-6 答:常流式动力转向的优点是结构较简单,油泵寿命较长,漏泄较少,消耗功率也较小。
L B +
=βαcot cot。
八年级物理第十二章 简单机械课后习题答案

第十二章 简单机械课后习题新编 《12.1杠杆》1.各式各样的剪刀都是一对对的杠杆。
在图中,哪些是省力杠杆,哪些是费力杠杆?要剪断铁片,应该使用哪种剪刀?剪纸时应该使用哪种剪刀?修剪树枝时应使用哪种剪刀?为什么?AC 是省力杠杆;B 是费力杠杆;要剪铁应使用A ;要剪纸应使用B ;要修剪树枝应使用C 。
2.在图中分别画出钳子、自行车手闸这两个杠杆(图中深色部分)工作时的支点、动力和动力臂、阻力和阻力臂。
3.图为指甲剪刀的示意图,它有几个杠杆?分别是省力杠杆,还是费力杠杆?有三个杠杆。
如图ABC 的动力臂大于阻力臂,是省力杠杆;OBD 、OED 的动力臂小于阻力臂,是费力杠杆;4.搬运砖头的独轮车,车厢和砖头所受的总重力G =1000N ,独轮车的有关尺寸如图所示。
推车时,人手向上的力F 应为多大?FL 1=GL 2F ×1m=1000N×0.3mF =300N《12.2滑轮》1.物体重1000N ,如果用一个定滑轮提起它,需要用多大的力?如果用一个动滑轮提起它,又要用多大的力(不计摩擦及滑轮自重)? F 定=G=1000NF 1 L 1 L 2 F 2 F 2 L 2 F 1 L 1F 动=21G=21×1000N=500N2.仔细观察自行车,看看它上面有几种简单机械,分别说明它们各起到了什么作用。
车把:轮轴——变形杠杆——省力 踏板:轮轴——变形杠杆——省力 前闸、后闸:——杠杆——省力后轮:轮轴——变形杠杆——费力3.解释如图的科学漫画。
一个人要拉起比他体重大的物体,用定滑轮行吗?应该怎么办?不行。
应该使滑轮组。
4.利用如图甲所示的滑轮组提起一个重为2000N 的物体,不计摩擦及滑轮自重,绳子的拉力F 等于多少?如果要用这个滑轮组达到更加省力的效果,绳子应该怎样绕?请在图乙中画出绳子的绕法,并计算此时拉力的大小.F =41G=41×2000N=500NF =51G=51×2000N=400N 《12.3机械效率》 1.有没有机械效率为100%机械?为什么?举例说明,通过什么途径可以提高机械效率。
机械设计基础习题解答第12章

思考题及练习题12.1用轴肩或轴环可以对轴上零件作轴向固定吗?答:轴肩或轴环可以对轴上零件作单向轴向固定12.2圆螺母也可以对轴上零件作周向固定吗?答:圆螺母不能对轴上零件作周向固定,可以轴向固定。
12.3轴肩或轴环的过渡圆角半径是否应小于轴上零件轮毂的倒角高度? 答:轴肩或轴环的过渡圆角半径应小于轴上零件轮毂的倒角高度,以保证装拆方便可靠。
12.4汽车下部变速器与后桥间的轴是否传动轴?答:是传动轴。
12.5轴上零件的轴向固定方法有:1)轴肩和轴环;2)圆螺母与止动垫圈;3)套筒; 4)轴端挡圈和圆锥面;5)弹性挡圈、紧定螺钉或销钉等。
当受轴向力较大时,可采用几种方法?答:轴向力较大时,可采用:1)轴肩和轴环;2)圆螺母与止动垫圈;3)套筒; 4)轴端挡圈和圆锥面。
12.6若轴上的零件利用轴肩来轴向固定,轴肩的圆角半径R 与零件轮毅孔的圆角半径1R 或倒角1C 的关系如何?答:轴肩的圆角半径R 要小于零件轮毅孔的圆角半径1R 或倒角1C 。
12.7为了便于拆卸滚动轴承,轴肩处的直径d (或轴环直径)与滚动轴承内圈外径1D 应保持何种关系?答:1d D <,大约2 mm 。
12.8平键连接的工作原理是什么?主要失效形式是什么?平键的剖面尺寸b ×h 和键的长度L 是如何确定的?举例说明平键连接的标注方法。
答:工作原理:平键的上表面与轮毂键槽顶面留有间隙,依靠键与键槽间的两侧面挤压力 ,传递转矩 。
所以两侧面为工作面。
主要失效形式:键连接的主要失效形式是挤压破坏。
键的剖面尺寸b ×h 和键的长度L 的确定:按照轴的公称直径d ,从国家标准中选择平键的尺寸h b ×。
键的长度L 应略小于轮毂的长度,键长L 应符合标准长度系列。
12.9 圆头(A 型)、方头(B 型)及单圆头(C 型)普通平键各有何优缺点?它们分别用在什么场合?轴上的键槽是如何加工出来的?轮毂上的键槽是如何加工出来的?答:圆头(A 型)对中性好,安装方便,使用广泛;方头(B 型)应力集中小,对轴影响小。
轮系习题答案
n1 转向为正,则
50 nH 0 nH
30 80 20 50
nH 14.7r / min 与 n1 转向相同,方向的判定如图所示。
8-5 如图为标准圆柱直齿轮传动系统,已知 Z1=60 , Z2=20, Z2‘=25 ,各轮模数相等,求:
1) Z3;
2)若已知 n3=200r/min, n 1=50r/min, n3,n1转向如图,求系杆 H转速大小和方向;
解: i ⅠⅡ= i 4H
在周转轮系中:
n1 nH
Z3
n3 nH
Z1
n1' n H n3 ' n H
Z3
3
Z1
在定轴轮系中:
n1' Z 4 n 4 Z 1'
3
n1'
n4 4
n3'
Z4
n3'
3 n4
n4
Z 3'
4
i4H i
n4 nH
8 3
8-10 已知 Z1=12, Z2=51 , Z3=76 , Z4=49, Z5=12 ,Z6=73,求此混合轮系传动比
3)当 n1 方向相反时,以 -50r/min 代入,则
50 nH 200 nH
20 15 60 25
nH 8.33r / min
nH 8.33r / min 转向与 n1 一致
8-6 图示轮系中,已知各轮齿数为 Z 1=60 , Z2=20 , Z2‘=20 , Z3=20 , Z4=20 , Z5=100,试求
题 8-1 图
8-2 已知轮系中各轮齿数, Z1=27 , Z2=17 , Z3=99, n1=6000r/min, 求 i 1H 和 nH。
轮系习题答案

b
2
4、已知
n3
Z1 30 Z 2 25 Z 2 20 Z 3 75
求nH
n1 200r / min n3 50r / min
2′
n1、 n2 反向
n1 1 3
解:
n1 nH Z 2 Z3 6.25 25 75 (-) n3 nH Z1Z 2 2 30 20
200 nH 6.25 50 nH 2
nH ≈10.7(r/min)
5、在图示的电动三爪卡盘转动轮系中,设已知各轮齿数为: Z1=6、 Z2=Z2′=25、 Z3=57、 Z4=56。 试求传动比i14。
2 2′
解: 这是一3k-H 型周转轮系 列方程: 在1-2-3-H中:
1 3
H
4
z3 n1 nH 57 6 n3 nH z1
在4 - 2′-2 -3-H中:
(1)
得: n1
21 NH 2
(2)
1 n4 nH z2 z3 25 57 57 n (3) 得: 4 nH (4) 56 n3 nH z4 z2 56 25 56 n1 21 (2) ÷ (4)得: i14 56 588 n4 2
b
5-6、在图示液压回转台的传动机构中,已知z2=15,液压马 达M的转速Nm=12r/min,回转台H的转速nH=-1﹒5r/min,求 齿轮的齿数。 解:此轮系为行星轮系 1-2-H,列方程:
n2 nH nM
n1 nH Z 2 n2 nH Z1
(1)
n2 nH nM 12r / min,又n1 0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第12章轮系
例1 在图示的轮系中,已知名z 1=z 2=z 4=z 5=20,z 3=z 6=60,齿轮1的转速n l =1440(r /min),求齿轮6的转速(大小及方向)。
解:
传动比
5421653226116)1(z z z z z z z z n n i ⋅⋅⋅⋅⋅⋅-== 920
2060604163=⨯⨯=⋅⋅=z z z z ∴ min)/(1609
14401616r i n n === 齿轮6的转向与齿轮1的转向相同。
注:齿轮6与齿轮1的转向关系也可用标注箭头的方法来确定,
如图所示。
例2 在图示轮系中。
设已知双头右旋蜗杆的转速n l =900r /min ,z 2=60,z 2ˊ=25,z 3=20,z 3ˊ=25,z 4=20,z 4ˊ=30,z 5=35,z 5ˊ=28,z 6=135,求n 6的大小和方向。
解:
10828
30252521353520206054321654326116=⨯⨯⨯⨯⨯⨯⨯⨯=⋅⋅⋅⋅⋅⋅⋅⋅==''''z z z z z z z z z z n n i
m i n )/(33.8108
9001616r i n n === 转向如图所示
例3 在图示轮系中,已知z 1=20,z 2=30,z 3=l 5,z 4=65,n l =150r /min ,求n H 的大小及方向。
解: (1) 该轮系为行星轮系。
(2)
5.615206530)1(31421414
114-=⨯⨯-=⋅⋅-=--==z z z z n n n n n n i H H H H H
04=n
5.611-=+-H
n n m i n /205
.71505.71r n n H === 行星架H 的转向与齿轮1的转向相同。
例4 已知齿轮1的转速n l=120r/min,而z l=40,z2=20,求(1)z3;(2)行星架的转速n H=0时齿轮3的转速n3(大小及方向)。
解:该轮系为差动轮系。
(1)求z3
根据同心条件,轮1和轮2的中心距应等于轮3和轮2的中心距,对于标准齿轮,因互相啮合的齿轮其模数相同,故
r3-r2=r1+r2
r3=r l+2r2
mz3/2=mz1+mz2
z3=z1+2z2=40+2×20=80
(2)当n H=0时,求n3
当n H=0时,即行星架H固定,该轮系成为定轴轮系。
240
80133113-=-=-==z z n n i m i n /6021201313r i n n -=-==
齿轮3的转向与齿轮l 的转向相反。
例5 已知轮系中z 1=60,z 2=15,z 2ˊ=20,各轮的模数均相同,求z 3及i 1H 。
解:
(1) 图示为一行星轮系。
(2) 由同心条件得
)(2)(22321'-=-z z m z z m ∴ 651520602213=-+=-+='z z z z
(3)
1613206065152132313113=⨯⨯=⨯⨯=--=='z z z z n n n n n n i H H H H H 16
3161311=-=H i 齿轮1与行星架H 的转向相同。
例6 在图示周转轮系中,已知各齿轮的齿数为z l =15,z 2=25,z 2ˊ=20,z 3=60,齿轮l 的转速n l =200r /min ,齿轮3的转速n 3=50r /min ,其转向相反,求行星架H 的转速n H 的大小和方向。
解:
(1) 图示为一差动轮系。
(2) 其转化机构的传动比为
520
15602521323113-=⨯⨯-=⨯⨯-=--='z z z z n n n n i H H H (3) 由上式得
3155n n n n H H -=-
6
531n n n H += (4) 设齿轮1的转速为正值,则齿轮3的转速为负值,将已知值代入上式得
m i n /33.86
)50(52006531r n n n H -=-+=+= 行星架H 的转向与齿轮1的转向相反而与齿轮3的转向相同。
