9.3 波的能量 波的能量密度
波的能量知识
A0 r0 r y= cos ω (t − ) r u
r1
式中r为离开波源的距离，A0为r = r0处的振幅。
小结： 小结： 波动能量 u 1 x 2 2 2 d dV内： Wk = ρdVA ω sin ω (t − ) 2 u dV 1 x S 2 2 2 dW p = ρdVA ω sin ω ( t − ) 2 u x 2 2 2 dW = ρdVA ω sin ω (t − ) u 不守恒 dW 1 2 2 平均能量密度： 平均能量密度： w = = ρω A dV 2 1 2 2 2 能流密度（波强）： 能流密度（波强）： I = ρ A ω u ∝ A 2
10、3 波的能量 能流密度 一 波动能量的传播 1 波的能量 波的传播是能量的传播， 波的传播是能量的传播，传播 过程中,媒质中的质点由不动到动， 过程中,媒质中的质点由不动到动， 具只动能 W K ,媒质形变具只势能 W P .
以固体棒传播纵波为例分析波动能量的传播. 固体棒传播纵波为例分析波动能量的传播 传播纵波为例分析波动能量的传播
u= E
2
Sdx = dV dy ∂y 考虑到 y 是 x 和 t 的函数，故 应是 dx ∂x ∂y ω x 1 2 ∂y 2 = A sin ω (t − ) dW P = u ρdV ( ) 而 ∂x u u 2 ∂x
ρ
E = u2ρ
1 x 2 2 2 dWP = ρdVA ω sin ω(t − ) 2 u
E 纵波 u = 固体： 固体：
ρ ρ
G 横波 u =
弹性模量
杨氏模量： 杨氏模量：
应力 F S E= = 应变 ∆L L
x d W = ρ d VA ω sin ω (t − ) u (2) 任一体积元都在不断地接收和 ) 放出能量，即不断地传播能量. 放出能量，即不断地传播能量 任一体 积元的机械能不守恒. 积元的机械能不守恒 波动是能量传递 的一种方式 .
波的能流密度强度公式
波的能流密度强度公式全文共四篇示例，供读者参考第一篇示例：波的能流密度强度公式是描述波动能量传播和传递速率的重要公式。
能流密度强度是指单位面积上通过的波动能量流量，可以用来衡量波在介质中传播的强度和速率。
在物理学和工程学中，波动现象是非常常见的，因此研究波的能流密度强度公式对于理解和控制波动现象非常重要。
波的能流密度强度公式可以根据不同类型的波以及波动现象的特性而有所不同，但一般情况下，波的能流密度强度与波的振幅和频率有关。
在传统的经典力学中，波的能流密度强度可以通过以下公式来表示：\[ P = \frac{1}{2} \sqrt{\frac{u}{\rho}} v^2 \]P表示能流密度强度，u表示波的线密度或者表面密度，ρ表示介质的密度，ν表示波的速度。
在这个公式中，波的振幅对于能流密度强度的影响体现在速度的平方项上。
速度越大，波的振幅对应的能流密度强度就越大。
介质的密度和波的线密度或者表面密度也对能流密度强度起到重要作用。
需要特别说明的是，对于不同类型的波，能流密度强度公式可能需要做适当的修正。
比如对于声波，由于声波是在气体、液体或固体介质中传播的，因此介质密度对于声波的传播会产生不同的影响。
而对于电磁波，介质的电磁性质对于能流密度强度也可能会有所影响。
因此在具体应用中，需要根据波的特性和介质性质做出相应的修正和调整。
在工程学和实际应用中，波的能流密度强度公式可以用来优化波动传输系统的设计，提高能量传播效率，加速数据传输速率，改善声音等波动现象的传播质量。
比如在声学领域中，通过调节声波的振幅和频率，可以控制声音的传播距离和声音质量，进而提高音响设备的性能。
在无线通信领域中，通过优化电磁波的能流密度强度，可以提高无线通信网络的覆盖范围和传输速率。
波的能流密度强度公式是描述波动能量传播和传递速率的重要工具，对于理解和应用波动现象具有重要意义。
在实际应用中，根据波的特性和介质性质，可以对能流密度强度公式进行适当的调整和修正，从而实现对波动现象的优化和控制。
第三节 波的能量 能流密度
§ 9.3 波的能量一、波的能量波是质点振动状态的传播，是质点振动相位的传播，外观上有波形在传播，但在传播过程中并不伴随物质传播，但伴随着能量迁移。
波是能量传递的一种方式。
对于“流动着”的能量，要用由能量密度 和能流密度两个概念来描述。
1 波的振动动能当机械波在媒质中传播时，媒质中各质点均在其平衡位置附近振动，因而具有振动动能。
设在密度为ρ的介质中，有一列沿x 轴传播的平面简谐波。
在波线上坐标为x 处取一个体积元d V ，其质量d m =ρ d V其波方程该体积元的振动速度为该体积元d V 的动能为2 波的势能介质发生弹性形变，因而具有弹性势能。
可以证明，因为介质形变，体积元d V 的势能与动能相等结论：在波的传播过程中，弹性介质体积元中的动能和势能在任何时刻都是相等的，它们同时最大，同时为零。
3 t 时刻体积元d V 的总能量为这一部分介质的能量是不守恒的，它随时间按正弦平方的函数关系而变化，所cos ()x y A ω t u =-ωsin ()y x v A ω t t u ∂==--∂222p k 1d d d sin ()2x E E VA t u ρωω==-k p d d d E E E =+)(sin d 222u x t VA -=ωωρ2222k 11d d ρd ωsin ω()22x E mv VA t u ==-Y x以能量是以波的形式沿着波的传播方向以速度u 传播。
二、能量密度能量密度：单位体积介质中的波动能量称为波的能量密度，用 W 表示平均能量密度：能量密度在一个周期内的平均值称为平均能量密度，用 W 表示三、能流密度波的能量不守恒，它随时间作周期性变化。
波中每个质元左右都和介质中相邻的质元有相互作用的弹性力，在波的传播过程中，通过弹性力做功，质元不断地从波源方向接受能量，又不断地向后传递能量，因此在这部分中，机械能是不守恒的。
将能量的传播与水的流动相比拟，称为能流。
大学物理 波的能量能流密度
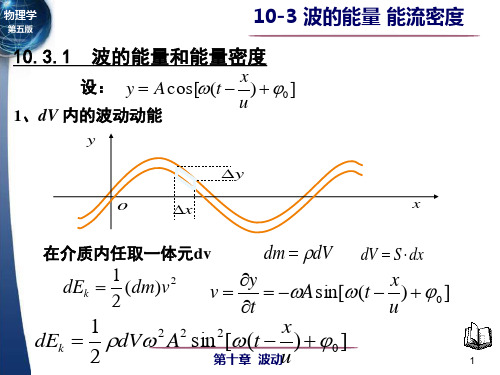
单位体积内的能量 w dE dV
w
dE dV
A2 2 sin2[(t
x u
)
0
]
5、一个周期内的平均能量密度
w 1 T
T wdt 1
0
T
T 0
A2
2
s
in
2[(t
x u
)
0
]dt
1 2 A2
2
sin2 1 1 cos2
2
这说明：w 2、A2
dE
(dV
) A2
2
sin 2[(t
x) u
0 ]
对任一介质体积元来说，不断从波源方向的介质中吸收能
量，又不断地向后面的介质传递能量。这说明波动是传递能
量的一种方式，且能量传播的速度就是波速。
孤立的谐振子系统总能量守恒。
第十章 波动
4
物理学
第4五、版 能量密度
10-3 波的能量 能流密度
dEk
1 2
dV 2 A2
s
in2[(t x
u 第十章 波动
)
0
]
1
物第理五2版、学 dv 内的波动势能
10-3 波的能量 能流密度
体积元因形变而具有弹性势能
在横ห้องสมุดไป่ตู้中，产生切变
y
y
o
x
x
y
x
x
h
lim tg x
h
x0
y y x x
u
A s in
物理学
第五版
大学物理-波的能量
x
y + ∆y
x y = Acosω(t − ) 1）体积元的动能 ） u ∂y x v = = − Aω sin ω(t − ) ∂t u
1 1 x 2 2 2 2 ∆Ek = ∆mi v = ρ∆VA ω sin ω(t − ) 2 2 u
2）体积元的势能 ∆E ）
x
∆x
u
1 x 2 2 2 ρ∆VA ω sin ω(t − ) P = 2 u
形变最小 →0， ， 振动速度最小 →0
y
r u
a
b
x
形变最大， 形变最大，振动 速度最大
r u
y
B P A Q
x
质元A 质元 质元P 质元 质元B 质元 质元Q 质元
（填吸收、释放）能量 填吸收、释放） 填吸收、释放） （填吸收、释放） 能量 填吸收、释放） （填吸收、释放） 能量 （填吸收、释放）能量 填吸收、释放）
结论：在波动过程中能量以波的形式沿 x 方向以 u 向
前传播着。 前传播着。
2、平均能量密度--- 能量密度在一个时间周期内的平均值 、平均能量密度
1 T 2 2 2 x 1 2 2 w = ∫ ρA ω sin ω(t − )dt = ρA ω T 0 u 2
为了定量描述波动过程中能量的传播， 为了定量描述波动过程中能量的传播，引入能流和 能流密度的概念 3、能流---单位时间内通过介质中某面积的能量 、能流 单位时间内通过介质中某面积的能量
形变最小形变最大形变最大振动速度最大填汲取释放能量填汲取释放填汲取释放填汲取释放能量填汲取释放填汲取释放能量填汲取释放能量能流和能流密度波强二能流和能流密ep为了精确地描述波的能量分布为了精确地描述波的能量分布引入能量密度1能量密度介质中单位体积中的波动能量能量密word版本能量密度描述了介质中各点能量即振动能量的分布能量密度描述了介质中各点能量即振动能量由上式可知波的能量密度是随介质的空间坐标能量密度是随介质的空间坐标由上式可知争论
波的能量和干涉
· ·· · · r
折射波传播方向
c c n1 = ，n2 = u1 u2
绝对折射率定义
sin i n2 = sin r n1
即
n1 sin i = n2 sin r 折射定律
11
波的叠加 驻波
一.波传播的独立性与叠加原理
介质中同时有几列波时,每列波都将保持自己原有 介质中同时有几列波时 每列波都将保持自己原有 波传播的独立性。 的特性,不受其它波的影响 不受其它波的影响-----波传播的独立性。 波传播的独立性 的特性 不受其它波的影响 (传播方向、振动方向、振幅、频率等) 传播方向、振动方向、振幅、频率等 传播方向
kx /2类似 与kx2/2
2
1 ∂y wp = E 2 ∂x
∂y 2 ∝ 相对形变( ) ∂x
2 2
能量密度: 能量密度
1 ∂y 1 ∂ y w = wk + wp = ρ + E 2 ∂t 2 ∂x
2
如果： 如果：y(x,t)=Acos(ω t-kx)
λ
4
(n = 0,1,2 L)
相邻波节（或波腹） 相邻波节（或波腹）间距为λ /2， ， 实验中只要测波节间距可得出行波波长。 实验中只要测波节间距可得出行波波长。
19
（2）驻波中的相位 cos ω t ） 驻波。 故相位并不传播 …驻波。 相位中没有x 坐标， 相位中没有 坐标， 驻波是分段的振动，设两相邻波节间为一段。 驻波是分段的振动，设两相邻波节间为一段。 同一段中各点振动相位相同； 同一段中各点振动相位相同； 相位相反。 为什么？ 相邻两段中各点振动 相位相反。 为什么？） （ 因为，相邻两段的 2 A cos 因为，
波的能量
I S u I 2 2 A2 2u
通常
I 2 2 zA2 2
I 1 A2 2u
2
z u 是表征介质特性的一个常量，
——称为介质的特性阻抗
说明：
S u I 2 2 A2 2u
上式根据平面简谐波得到的结论， 但是波的强度与波的振幅、波的频率的 平方成正比的结论对任何弹性波都成立. 波的能量密度表征媒质中某点质元的
一．有波传播时媒质质元的能量
（以平面纵波在固体细长棒中的传播为例）
设有一截面积为 S ，密度为 ρ 的固体细棒，
一平面纵波沿棒长方向传播。
a
b u
o●●
S
x●
●
x
x x
选棒长的方向为 x 轴，在棒上距 o 点 x 处附近 取一长为 Δx 质元 ab ，
a
b u
o●●
S
x●
x
x x
a
W 1 mv2 K2
1 V 2 A2 sin2 (t 2 x )
2
0
1）求势能：
a
b u
o●●
x●
d
●
x
x x
t
a
b u
时
o●
刻
y●
●
y y
x
当有纵波传播时，在应力作用下质元 ab 发生线变,
设 t 时刻质元 ab 正被拉长，
由图上几何关系，质元 ab 长度变化为 Δy
能量的大小. 能流密度表征媒质中某点， 能量传播的多少和快慢.
例:波动的能量与那些物理量有关?比较波动的能量与 简谐运动的能量.
答: 1 V 2 A2
2
物理波的能量
=
3
cos
4πt
(2)以距a点5m处的b点为坐标原 点写出波动方程。
b.
u .a 5m
x
解：(1)以a点为原点在x轴上任取一点P，坐标为x
ya = 3 cos 4πt y =3 cos 4πt +
x
20
(2)以b点为坐标原点
wk
wp
2 A2
sin
2 [ (t
x )] u
平均能量密度（对时间平均)
w 1 T A2 2 sin 2[(t x)]dt
T0
u
w
=
1 2
ρAω2
2
三、波的强度
能流P :单位时间内垂直通过某一截面的 P = w S u 能量称为波通过该截面的能流，或叫能通量。
显然能流是随时间周期性变化的。但它总为正值
(t+
d u
)
π
2
]
y
=
A cos[ω
(
t
+
d u
x u
)
π
2
]
例6、波速 u =400m/s, t = 0 s时刻的波形如图所示。
{ 写出波动方程。
t= 0 (o点)
得：
y 0
=
2
=
A
2
v0
＞0 0=
π
3
2
o
y(m)
4 5
p
u
x (m)
{ t =0
(p点)
2π
=
y 0
=
0
v0＜ 0
p
0
d
λ
得：
平均能流P : 能流在一个周期内的平均值。 P = S w u 波的强度 I（能流密度）:
大学物理-波的能量能流密度
04
电磁波中的能量传播
电磁波概述
电磁波定义
电磁波是由电场和磁场交替变化而产生 的一种波动现象，可以在真空中或物质 中传播。
VS
电磁波分类
根据频率和波长的不同，电磁波可分为无 线电波、红外线、可见光、紫外线、X射线、 γ射线等。
电磁波中电场和磁场能量关系
电场能量
电磁波中电场能量与电场强度的平方成正比，即$W_e = frac{1}{2} epsilon_0 E^2$，其中 $epsilon_0$为真空介电常数，$E$为电场强度。
行波
与驻波不同，行波是向前传播的波形 。在行波中，质点的振动方向与波的 传播方向垂直（横波）或平行（纵波 ）。行波传递能量和动量。
02
能量传播与能流密度
能量传播方式
机械波
通过介质中质点的振动和相互作用传播能量，如声波、水波 等。
电磁波
通过电场和磁场的交替变化传播能量，如光波、无线电波等 。
能流密度定义及表达式
磁场能量
电磁波中磁场能量与磁场强度的平方成正比，即$W_m = frac{1}{2} mu_0 H^2$，其中 $mu_0$为真空磁导率，$H$为磁场强度。
总能量
电磁波的总能量等于电场能量和磁场能量之和，即$W = W_e + W_m$。
电磁波中能量传播特点
01
能流密度矢量
电磁波中的能量传播可以用能流密度矢量$vec{S}$来描述 ，其方向垂直于电磁波的传播方向，大小等于单位时间内 通过单位面积的能量。
光学领域应用
光的传播
01
光波的能量能流密度决定了光的亮度、颜色和温度等特性，是
光学研究的基础。
激光技术
Hale Waihona Puke 02激光具有高能量能流密度的特点，被广泛应用于切割、焊接、
波的能量密度
波的能量密度一、引言波是自然界中广泛存在的物理现象，其能量密度是描述波能量分布的重要参数。
本文将介绍波的能量密度的概念、计算方法以及应用领域。
二、波的能量密度的概念1.定义波的能量密度是指单位体积内所包含的波动能量。
在电磁学中，电磁场中每个点上单位时间内通过单位面积传递的电磁能量称为辐射通量密度，而辐射通量密度除以光速就可以得到电磁场中每个点上单位体积内所包含的电磁辐射能量，即电磁场中的辐射能密度。
2.单位波的能量密度通常用J/m³或者W/m³来表示。
三、计算方法1.机械波对于机械波，其能量密度可以表示为：u = 1/2ρv²其中，u为机械波在介质中传播时所具有的单位体积内储存的总功率；ρ为介质的质量密度；v为机械波在介质中传播时所具有的速率。
2.电磁波对于电磁波，其能量密度可以表示为：u = εE²/2 + 1/2μB²其中，u为电磁波在介质中传播时所具有的单位体积内储存的总功率；ε为介质的介电常数；E为电场强度；μ为介质的磁导率；B为磁感应强度。
四、应用领域1.辐射治疗医学上常用的X射线、γ射线等电离辐射对人体组织产生伤害，而这些伤害与辐射通量密度和能量密度有关。
因此，在医学上，需要精确测量出辐射通量密度和能量密度，以便控制辐射剂量。
2.光学领域在光学领域中，波的能量密度是描述光强的重要参数。
例如，在太阳能电池中，需要精确测量出太阳光的能量密度以确定其转换效率。
3.声学领域在声学领域中，波的能量密度是描述声音强度的重要参数。
例如，在音频设备中，需要精确测量出声音波的能量密度以确定其音质和音响效果。
五、结论波的能量密度是描述波能量分布的重要参数，其计算方法不同于不同类型的波。
在医学、光学和声学领域中，波的能量密度被广泛应用于测量和控制波的强度和剂量。
波的能量
Y ，结合波动表达式 y x A sin t
x u u
2 最后得： 1 x 2 2 2 Wp pu (V ) A 2 sin t 2 u u
1 x 2 2 2 (V ) A sin t 2 u
_____________________________________________
波的能量
Energy in waves
生活中的波
波动学基础
机械波：水波、声波、地震波。其传播需要有介质。
电磁波：无线电波、光波、x射线等，其传播无需介 质。 物质波：近代物理发现实物粒子也具有波性，即物质 波。 各种波性质不同，但又有共性。可以传递能量，可以 产生干涉、衍射等现象。以有限的速率传播。
3
一
波的能量
机械波在弹性媒质中传播时，各质点在其平衡位置 附近振动，因而各质点具有动能； 各质点之间的距离发生改变，媒质发生形变，因而 具有势能；
波的能量是指弹性媒质因波动而具有的动能 和势能的总和
波的能量 = 振动动能 + 形变势能
x x x
y
y y
x
波的能流和能流密度
1、能流 单位时间内沿波传播的方向通过 介质中某一截面积的能量称为该面 积的能流。 u
V udt s
udt
S
E P 瓦 t
如右图所示
wSudt P wSu dt
9
2、波的强度（平均能流密度)I：
单位时间内通过垂直于传播方向单位面积的平均能量， 称为平均能流密度，或称为波的强度。
体积元的总能量为其动能和势能之和，即
x E (V ) A sin t u
波的能量 波的能量密度.ppt
u (2) 任一体积元都在不断地接收和 放出能量，即不断地传播能量. 任一体 积元的机械能不守恒. 波动是能量传递 的一种方式 .
O x dx
x
O
y y dy
x
7
9.3 波的能量 波的能量密度
2 能量密度 单位体积介质中的波动能量
w dW A2 2 sin 2 (t x)
能流相等. w1uS1 w2uS2
即
1 2
A12
2u
4π
r12
1 2
A22 2u4π
r22
A1 r2 A2 r1
s2
s1 r2
y A0r0 cos (t r )
r1
r
u
12
dVA2 2
sin 2 (t
x) u
O x dx
x
O
y y dy
x
5
讨论
9.3 波的能量 波的能量密度
(1)在波动传播的介质中，任一体
积元的动能、势能、总机械能均随x, t
作周期性变化，且变化是同相位的.
体积元在平衡位置时，动能、势能 和总机械能均最大.
体积元的位移最大时，三者均为零.
6
9.3 波的能量 波的能量密度
通过垂直于波传播方向的单位面
积的平均能流.
I P wu S
P wuS u
I 1 A2 2u
2
S udt
10
9.3 波的能量 波的能量密度
例题9-4 见课本
11
9.3 波的能量 波的能量密度
补例 证明球面波的振幅与离开其波源
的距离成反比，并求球面简谐波的波函数. 证 介质无吸收，通过两个球面的平均
波的能流密度
10
超声波、 • 超声波、次声波
* 次声波
特点一 频率在10 频率在 －4～20赫芝之间 赫芝之间 的机械波，人耳听不到。 的机械波，人耳听不到。 特点二 由于它具有衰减极小的特点， 由于它具有衰减极小的特点， 衰减极小的特点 具有远距离传播的突出特点。 具有远距离传播的突出特点。 已形成现代声学的一个新的 分支—次声学 次声学。 分支 次声学。 因为大气湍流、火山爆发、地震、 因为大气湍流、火山爆发、地震、 陨石落地、雷暴、 陨石落地、雷暴、磁暴等大规模自 用途 然活动中，都有次声波产生，因此， 然活动中，都有次声波产生，因此， 它是研究地球、海洋、 它是研究地球、海洋、大气等大规 模运动的有力的工具。 模运动的有力的工具。
y
∆y
A B
o o
A
∆x
B
2
质元形变： 质元形变：
2
∂y 1 ∂y [(∆x) + (∆y) ] − ∆x = ∆x1+ − ∆x ≈ 2 ∂x ∂x 质元的形变势能： 质元的形变势能： 2 1 ∂y = 1 FdxA 2 k 2 sin 2 (ω t − kx ) dE p ≈ F × 2 ∂x 2 ∂x
1 ε = T
∫
T
0
εdt =
ρA2ω 2
T
∫
T
0
1 sin (ω t − kx)dt = ρA 2ω 2 2
2
4
二、波的能流密度 波的强度 单位时间内通过截面 单位时间内通过截面 S 的能量等于体积 uS中的 中的 能量，称为能流 能流。 能量，称为能流。 E = ε uS 单位时间内通过垂直于波的传播方向的 通过垂直于波的传播方向的单位面 单位时间内通过垂直于波的传播方向的单位面 上的能量叫做能流密度 能流密度。 积上的能量叫做能流密度。 r dE 写成矢量式： J= = ε u 写成矢量式： J = ε u dS 一个周期内能流密度大小的平均值称为波的强度 波的强度。 一个周期内能流密度大小的平均值称为波的强度。
波的能量__波的强度
u
P dW wSu d t wSu dt dt
S
uSA2 2 sin 2 (t x u)
u
平均能流：P wSu 1 uSA2 2
2
平均能流密度或波的强度 通过与波传播方向垂直的
单位面积的平均能流，用I 来表示，即
I wu u 2 A2 2 z 2 A2 2
波的强度
介质的特性阻抗 z 。u
x1
1 1n100m 1000
0.0046
m
钢的厚度为
x2
1 ln100m 4
1.15m
可见高频超声波很难透过气体，但极易透过固体。
波的吸收
据题意有 I0 I ，100 得空气的厚度
x1
1 1n100m 1000
0.0046
m
钢的厚度为
x2
1 ln100m 4
1.15m
可见高频超声波很难透过气体，但极易透过固体。
pu
2
(V
)
A2
2
u2
sin2 t
x u
1 2
(V
)
A2
2
sin
2
t
x u
若考虑平面余弦弹性横波,只要把上述计算中的 y x 和 f 分别理解为体积元的切变和切力,用切变模量G 代替 杨氏模量Y，可得到同样的结果。
3. 波的强度
能流 在介质中垂直于波速方向取一面积S ，在单位时
间内通过S 的能量。
解 因 I uA，2所2 以2
A 1
2I pu
2
1 5 105
2 120 107 1103 1.5 103
m
1.27 105 m
可见液体中声振动的振幅实示上是极小的。
§9.4 波的能量 平均能流密度
波是振动状态的传播，相位的传播，同时 也是能量的传播.
波在弹性媒质中传播时，各质元都在振动。 每个质元，有振动速度而具有振动动能；因发生 形变而具有形变势能， 两者之和称此媒质中弹性 波的能量。 对于“流动着”的能量，要由能量密度和 能流密度两个概念来描述。
弹性体的剪切形变
切应变：
y A x sin ( t ) x u u
2 1 1 体元势能：dE p G 2dV GA2 2 sin2 (t x )dV 2 2 u u x 2 2 2 2 1 2 A sin ( t )dV (u G ) u x 体元总能： dE dEk dE p 2 A2 sin 2 ( t )dV u
二、平均能流密度
能流：单位时间内垂直通过某一面积的能量. 平均能流：
P uS
u
平均能流密度 (波的强度 )： 通过垂直于波传播方向的单 位面积的平均能流.
P 1 I u A2 2 u S 2 1 2 2 I 不吸收能量, 显然：
x 位移：y A cos ( t ) u
振动速度：
v y x A sin ( t ) t u
1 2 2 1 2 2 2 2
x 体元动能： dEk dVv A sin ( t )dV u
一、波的能量分布
x 位移：y A cos ( t ) u
2、能量密度与平均能量密度 能量密度：单位体积介质中的波动能量.
dE x 2 2 2 A sin (t ) dV u
平均能量密度：能量密度在一个周期内的平均值.
1 1 x 2 2 2 dt A sin (t )dt T0 T0 u
物理实践：波的功率和能量密度
计算公式： E = ρ c ² u ²/ 2 ， 其 中 E为能量密度，ρ 为介质密度，c为 波速，u为振动 速度
与功率的关系： 能量密度与功率 成正比，即能量 密度越大，功率 越高
功率是单位时间内波所传递的能量， 表示波的强度。
功率和能量密度之间存在一定的关 系，通常功率越高的波具有越高的 能量密度。
波的功率和能量密度对环境的影响 波的传播对生态系统的破坏 波的能量密度对气候变化的影响 波的功率和能量密度对人类生活的影响
波的功率和能量密度在通信技术中的应用 波的能量密度对能源利用的影响 波的功率和能量密度在医疗领域的应用 波的功率和能量密度在军事领域的应用
波的功率和能量密 度未来发展趋势
波的功率和能量密 度对人类生活的影 响
电磁波对生物体的潜在危害
波的功率和能量密度对人体 的辐射影响
微波辐射对人体的伤害 高强度声波对听力的损伤
无线电波：传输 信号，实现远距 离通信
微波：用于卫星 通信和移动通信 网络
光纤：高速、大 容量的信息传输， 提高通信质量
电磁波：用于雷达、 导航和探测等军事 和民用领域
激光雷达技术：利用激光雷达技术实现高精度、高分辨率的波源测量和定位 微波源技术：利用微波源技术实现高效率、高可靠性的波源产生和控制 声波源技术：利用声波源技术实现低成本、高稳定性的波源产生和应用 电磁波源技术：利用电磁波源技术实现高速、高带宽的波源传输和通信
物联网技术：实现波的功率和能量 密度的远程监控和管理
激光技术：利用高能激光束产生高功率和能量密度的光束，可用于医疗、军事等领域。
核聚变技术：通过核聚变反应产生高能量密度，可用于未来能源领域。
纳米技术：利用纳米材料和纳米结构提高能量密度，可用于电池、传感器等领域。
波的能量能流密度
1.波动的动能
以固体棒中传播的纵波为例分析波动能量的传播.
O O
波函数
x
dx
x
y dy
y
x
x y x y A cos ( t ) v A si n ( t ) t u u
•质元的动能
1 1 2 dWk dm v dV v 2 2 2
1 x 2 2 2 dWk dVA si n ( t ) 2 u
① 任一时刻介质元的动能等于势能，且相位相同，与振动系 统的动能与势能总有π/2相位差不同。 ② 振动系统的机械能守恒，而波动过程中，能量不守恒。波 动过程中，沿波的传播方向，介质元不断地通过振动由后面的 质元获得能量，又不断地把能量传播给前面的质元，波是能量 传递的一种形式。 ③ 在平衡位置时质元具有最大动能和势能，在最大振幅处动 能和势能为零。在回到平衡位置时从相邻质元吸收能量，离开 时放出能量。
1 x 2 2 2 dWk dWp dVA si n ( t ) 2 u 表明：质元的总能量随时间作周期性变 3.波动的能量 化，时而达到最大值，时而为零 x dW dWk dWp dVA2 2 si n2 ( t ) u 4.结论 意味着：在由波传播的细棒中有能量在传播
2.波动的势能
弹性势能 O
1 2 dWP k dy 2
F l E S l
F
弹性模量
x
dx
O
y y dy
u E
x x
ES l l
1 1 dy 2 2 dWP k dy ESdx( ) 2 2 dx
SE k dx
1 dy 2 y A si n ( t x ) 2 u dV ( ) x u u 2 dx 1 x 2 2 2 dVA si n ( t ) 2 u
9-3波的能量 能流密度
9-3 波的能量 能流密度 三、能流密度
u
能流：单位时间内垂直通 过某一面积的能量.
P Suw
平均能流： P wuS
u
S
能流密度 ( 波的强度 ) I : 通过垂直于波传播
方向的单位面积的平均能流.
I P S wu
w 1 2 A2
2
能流密度
I 1 A2 2u
2
第九章 机械5波
体积元的总机械能
dE
dEk
dEp
dVA2 2
sin2
(t
x) u
注意
在波动传播的媒质中，任一体积元的动能、 势
能、总机械能均随 x, t作周期性变化，且变化是同
相位的.
体积元在平衡位置时，动能、势能和总机械能 均最大.
体积元的位移最大时，三者均为零. 第九章 机械3波
9-3 波的能量 能流密度
9-3 波的能量 能流密度 思考
例 一平面简谐波动在弹性介质中传播时，在传 播方向上介质中某质元在负的最大位移处，则它的能 量是
（A）动能为零, 势能最大 （B）动能为零, 势能为零 （C）动能最大, 势能最大 （D）动能最大, 势能为零
第九章 机械6波
9-3 波的能量 能流密度
一、波动能量的传播
当机械波在介质中传播时， 介质中各质点均在其
平衡位置附近振动，因而具有振动动能.同时，介质发
生弹性形变，因而具有弹性势能.
任一位置 x 处取一个体积元 dV
dEk
1 2
dm v2
1 2
dV
v2
y Acos(t x ) v y Asin(t x )
电磁波的能量密度与能量传递
电磁波的能量密度与能量传递电磁波是一种由电场和磁场相互作用而形成的能量传播现象。
在物质中，电磁波的能量密度与能量传递是一个非常重要的概念。
本文将探讨电磁波的能量密度、能量传递以及与之相关的一些重要应用。
一、电磁波的能量密度电磁波的能量密度是指单位体积内电磁波所携带的能量。
根据电磁波的性质，我们可以得出电磁波的能量密度与电场强度和磁场强度的关系。
根据麦克斯韦方程组，电磁波的能量密度可以表示为：能量密度= 0.5 * ε0 * E^2 + 0.5 * μ0 * B^2其中，ε0和μ0分别是电场和磁场的介质常数，E和B分别是电场强度和磁场强度。
电磁波的能量密度与电场强度和磁场强度的平方成正比，这意味着电磁波的能量密度与电磁场的强度密切相关。
当电磁场的强度增加时，能量密度也会增加，反之亦然。
二、电磁波的能量传递电磁波的能量传递是指电磁波能量从一个地方传递到另一个地方的过程。
在电磁波的传播过程中，能量以波的形式传递，从而实现能量的传递。
电磁波的能量传递是通过电场和磁场之间的相互作用完成的。
当电磁波传播时，电场和磁场会相互耦合，形成电磁波的传播。
电磁波的能量主要集中在电场和磁场的交界处，即电磁波的传播方向。
电磁波的能量传递速度是光速，即299,792,458米/秒。
这是因为电磁波是由电场和磁场相互作用而形成的，而电场和磁场的相互作用是瞬时的，因此电磁波的传播速度也是瞬时的。
三、电磁波的应用电磁波的能量密度与能量传递在现代科学和技术中有着广泛的应用。
以下是一些重要的应用领域：1. 通信技术：无线电、电视、手机等通信技术都是基于电磁波的传播原理。
电磁波的能量密度和能量传递决定了通信信号的传输质量。
2. 医学影像学：医学影像学中的X射线、CT扫描、核磁共振等技术都是基于电磁波的能量传递原理。
电磁波的能量密度和能量传递决定了医学影像的清晰度和准确性。
3. 太阳能利用：太阳能是一种清洁、可再生的能源，其利用过程依赖于电磁波的能量密度和能量传递。
大学物理- 波的能量能流密度
1 P T
0
1 2 2 wSudt wSu A u s 2
第十章 波动
6
物理学
第五版
3、平均能流密度 （又叫波强）I
10-3 波的能量 能流密度
通过垂直于波传播方向的单位面积的平 均能流. P I w u s
1 2 2 I A u 2
可见波强 （瓦/米2）
10-3 波的能量 能流密度
(5)声压:
在声波传播的空间里，某一点在某一瞬时的压强P与没有 声波时的静压强P0之差dP=P- P0，叫做该点该瞬时的声压。
第十章 波动
10
物理学
第五版
10-3 波的能量 能流密度
因空气波为疏密波，故声压可正、可负，其单位为“帕斯 卡”。
可以证明：声压的振幅
( z u
频率低于20Hz的机械波（如地震、火山爆发、陨石落地、 雷暴等发出…） (1)声强： 1 2 2 I A u 指声波的波强，即声波的平均能流密度 2 (2) 声强级：
以人耳刚能听到的声强 则声强级
IL lg
I 0 10 12 w
m 2为标准，
I I (贝尔) 10lg (分贝 dB) I0 I0
1 y 1 x 2 2 2 E p dV G dV A sin (t ) 0 2 x 2 u
第十章 波动
2
2
物理学
第五版
３、dV内的总波动能量
10-3 波的能量 能流密度 x 2 2 2 dE dE k dE p ( dV ) A sin [ (t ) 0 ] u 以上讨论说明：
y
① 在同一体元dV 内， dEk 、 dEp 是同步的。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
x
dxБайду номын сангаас
y
y dy
x x
2
9.3 波的能量 波的能量密度
弹性势能
杨氏模量
1 2 dWp k dy 2 F l ES E F l S l l
SE k dx
O O
x
dx
y
y dy
x x
3
9.3 波的能量 波的能量密度
弹性势能 1 1 dy 2 2 dWp k dy ES dx( ) 2 2 dx 1 2 dy 2 u dV ( ) 2 dx 1 x 2 2 2 dVA sin (t ) 2 u
2 2 2
O O
x
dx
y
y dy
x x
7
9.3 波的能量 波的能量密度
2 能量密度 单位体积介质中的波动能量 dW x 2 2 2 w A sin (t ) dV u 平均能量密度：能量密度在一个周期内 的平均值 1 T 1 2 2 w wdt A T 0 2
A0 r0 r y cos (t ) r u
r1
12
讨 论 (1)在波动传播的介质中，任一体 积元的动能、势能、总机械能均随 t x, 作周期性变化，且变化是同相位的. 体积元在平衡位置时，动能、势能 和总机械能均最大. 体积元的位移最大时，三者均为零.
6
9.3 波的能量 波的能量密度
x dW dVA sin (t ) u (2) 任一体积元都在不断地接收和 放出能量，即不断地传播能量. 任一体 积元的机械能不守恒. 波动是能量传递 的一种方式 .
O O
x
dx
y
y dy
x x
4
9.3 波的能量 波的能量密度
x dW dVA sin (t ) u
2 2 2
体积元的总机械能
x dW dWk dWp dVA sin (t ) u
2 2 2
O O
x
dx
y
y dy
x x
5
9.3 波的能量 波的能量密度
1 2 2 I A u 2
P wuS
u
udt
S
10
9.3 波的能量 波的能量密度
例题9-4
见课本
11
9.3 波的能量 波的能量密度
补例 证明球面波的振幅与离开其波源 的距离成反比，并求球面简谐波的波函数. 证 介质无吸收，通过两个球面的平均 能流相等. w1uS1 w2uS2 1 1 2 2 2 2 A1 u 4π r1 A2 2u 4π r22 即 2 2 A1 r2 s1 r s2 2 A2 r1
9.3 波的能量 波的能量密度
一
波动能量的传播
1 波的能量 波的传播是能量的传播，传播 过程中,介质中的质点由不动到动， 具有动能 W k ,媒质形变具有势能 W p .
1
9.3 波的能量 波的能量密度
以固体棒中传播的纵波为例分析波动能量 的传播. 1 x 1 2 2 dWk dm v dV v y A cos (t ) u 2 2 y x v A sin (t ) t u 1 x 2 2 2 振动动能 dWk dVA sin (t ) 2 u
O O
x
dx
y
y dy
x x
8
9.3 波的能量 波的能量密度
二
能流和能流密度
能流：单位时间内垂直通过某一面积 的能量. 平均能流：
u
P wu S
udt
S
9
9.3 波的能量 波的能量密度
能流密度 ( 波的强度 )I: 通过垂直于波传播方向的单位面 积的平均能流.
P I wu S