12.1-3波的能量能流密度要点
合集下载
04波的能量能流密度
O O
x
dx
x
y + dy
y
x
5
第十章 波动
物理学
第五版
一
1010-3 波动波动-能量的传播 波的能量
1 2 dWp = k (dy ) 2
能流密度
1 波的能量
弹性势能
SY k = dx
杨氏模量Y 杨氏模量Y
1 x 2 2 2 dWp = ρ dVA ω sin ω (t − ) 2 u
总机械能
x d W = ρ d VA ω sin ω (t − ) u
第十章 波动
7
物理学
第五版
讨 论
1 10-23 2波的能量 x能流密度 10dWk = ρdVA ω sin 2 ω (t − ) 2 u
1 x ρ dVA2ω 2 sin 2 ω (t − ) 2 u x d W = ρ d VA 2ω 2 sin 2 ω (t − ) u dWp =
任一体积元都在不断地接收和放出能量， (2) 任一体积元都在不断地接收和放出能量， 即不断地传播能量. 任一体积元的机械能不 即不断地传播能量. 任一体积元的机械能不 守恒. 守恒. 波动是能量传递的一种方式 .
2 2 2
O O
x
dx
x
y + dy
y
x
6
第十章 波动
物理学
第五版
讨 论
101 10-23 2波的能量 x能流密度 dWk = ρdVA ω sin 2 ω (t − ) 2 u
1 x ρ dVA2ω 2 sin 2 ω (t − ) 2 u x 2 2 2 d W = ρ d VA ω sin ω (t − ) u dWp =
能流密度
x
dx
x
y + dy
y
x
5
第十章 波动
物理学
第五版
一
1010-3 波动波动-能量的传播 波的能量
1 2 dWp = k (dy ) 2
能流密度
1 波的能量
弹性势能
SY k = dx
杨氏模量Y 杨氏模量Y
1 x 2 2 2 dWp = ρ dVA ω sin ω (t − ) 2 u
总机械能
x d W = ρ d VA ω sin ω (t − ) u
第十章 波动
7
物理学
第五版
讨 论
1 10-23 2波的能量 x能流密度 10dWk = ρdVA ω sin 2 ω (t − ) 2 u
1 x ρ dVA2ω 2 sin 2 ω (t − ) 2 u x d W = ρ d VA 2ω 2 sin 2 ω (t − ) u dWp =
任一体积元都在不断地接收和放出能量， (2) 任一体积元都在不断地接收和放出能量， 即不断地传播能量. 任一体积元的机械能不 即不断地传播能量. 任一体积元的机械能不 守恒. 守恒. 波动是能量传递的一种方式 .
2 2 2
O O
x
dx
x
y + dy
y
x
6
第十章 波动
物理学
第五版
讨 论
101 10-23 2波的能量 x能流密度 dWk = ρdVA ω sin 2 ω (t − ) 2 u
1 x ρ dVA2ω 2 sin 2 ω (t − ) 2 u x 2 2 2 d W = ρ d VA ω sin ω (t − ) u dWp =
能流密度
第三节 波的能量 能流密度
§ 9.3 波的能量一、波的能量波是质点振动状态的传播，是质点振动相位的传播，外观上有波形在传播，但在传播过程中并不伴随物质传播，但伴随着能量迁移。
波是能量传递的一种方式。
对于“流动着”的能量，要用由能量密度 和能流密度两个概念来描述。
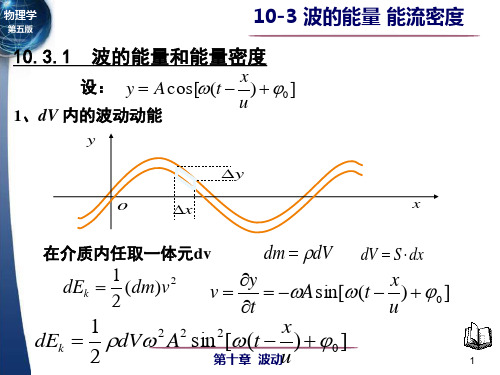
1 波的振动动能当机械波在媒质中传播时，媒质中各质点均在其平衡位置附近振动，因而具有振动动能。
设在密度为ρ的介质中，有一列沿x 轴传播的平面简谐波。
在波线上坐标为x 处取一个体积元d V ，其质量d m =ρ d V其波方程该体积元的振动速度为该体积元d V 的动能为2 波的势能介质发生弹性形变，因而具有弹性势能。
可以证明，因为介质形变，体积元d V 的势能与动能相等结论：在波的传播过程中，弹性介质体积元中的动能和势能在任何时刻都是相等的，它们同时最大，同时为零。
3 t 时刻体积元d V 的总能量为这一部分介质的能量是不守恒的，它随时间按正弦平方的函数关系而变化，所cos ()x y A ω t u =-ωsin ()y x v A ω t t u ∂==--∂222p k 1d d d sin ()2x E E VA t u ρωω==-k p d d d E E E =+)(sin d 222u x t VA -=ωωρ2222k 11d d ρd ωsin ω()22x E mv VA t u ==-Y x以能量是以波的形式沿着波的传播方向以速度u 传播。
二、能量密度能量密度：单位体积介质中的波动能量称为波的能量密度，用 W 表示平均能量密度：能量密度在一个周期内的平均值称为平均能量密度，用 W 表示三、能流密度波的能量不守恒，它随时间作周期性变化。
波中每个质元左右都和介质中相邻的质元有相互作用的弹性力，在波的传播过程中，通过弹性力做功，质元不断地从波源方向接受能量，又不断地向后传递能量，因此在这部分中，机械能是不守恒的。
将能量的传播与水的流动相比拟，称为能流。
波的能量和能流密度
f S
S
x
y
Δy 为 质元 ab 长度变化
与弹簧比较 弹簧的弹性势能 所以时刻质元 ab 的弹性势能
S / x 为常数
f弹簧 Kx
W弹簧P
1 2 Kx 2
1S 2 WP ( y) 2 x
所以 t 时刻质元 ab
的弹性势能
1S WP ( y) 2 2 x
当媒质中有机械波传播时，媒质的质元具有机械能
为了描述媒质中能量分布状况引入——能量密度
二．能量密度
波传播时 ，媒质中单位体积内的能量
——称作波的能量密度
记作 Ω
W 2 2 2 2 A sin (t x 0 ) V
在一个周期内能量密度的平均值称作平均能量密度
W 2 2 2 2 A sin (t x 0 ) V
球面波的平均能流
讨论：在无吸收的理想 媒质中球面波的振幅
通过球面1和球面2的能流应该相等：
I 1 4r12 I 2 4r22
而：
I 1 I 2 A12 A22
r2 r1
A1 A2 r2 r1 Nhomakorabea1 A r
取 : r1 1
——球面波的振幅与距离成反比 球面波的波函数可以写成：
S
2.
能流密度
P S u S
平均能流密度又称波的强度
2 A
2 2
2
记作
I
2
2
2 2
I S u
通常
I 2 A u
1 2 2 I A u 2
S u
说明：
I 2 2 A2 2 u
上式根据平面简谐波得到的结论， 但是波的强度与波的振幅、波的频 率的平方成正比的结论对任何弹性 波都成立 波的能量密度表征媒质中某点质元的 能量的大小 能流密度表征媒质中某点，能量传播的 多少和快慢
3波的能量与能流、声压与声强
例：一球面波源的功率为 100W，则距波源 10m 处， ， 是多少？ 波的平均能流密度 I 是多少？
解：
P P I= = 2 S 4πr 100 = 2 4π × 10 1 = （W •m−2 ） 4π
dengyonghe1@
四.声压、声强与声强级 声压、
1.声波的频率范围
声波频率 超声波频率 20 ~ 20000Hz > 20000Hz 次声波频率 < 20Hz
dengyonghe1@163来自com三.能流、能流密度 能流、
1.平均能流 单位时间内垂直通过介质中某一面积的能 量。 在介质中取体积
V体 V体
u
u
S
波速方向垂直于面积S 波速方向垂直于面积 长为 u ，则能流为
P = wV 体 = w uS
单位：焦耳 秒 单位：焦耳/秒，瓦，J•s-1，W
与功率相同
dengyonghe1@
P = wuS
1 2 2 = ρA ω uS 2
2.平均能流密度----波强I 平均能流密度----波强I ----波强
单位时间内通过垂直于波的传播方向的单位面积 上的平均能量。 上的平均能量。
1 P 2 2 I= = wu = ρA ω u 2 S
单位：J•s−1•m−2 ， W •m−2 单位：
A s2 = A s1
dengyonghe1@
I∝A
2
2 1 2 2
（1）对于平面波： ）对于平面波：
s1 = s2
∴ A1 = A2 ; I1 = I 2
I1 r2 A1 r2 ∴ = ; = I 2 r1 A2 r1 A1 r2 I1 r ∴ = ; = A2 r1 I 2 r
2 2 2 1
3波的能量
●
●
o
x
S
x
在媒质中垂直波传播方向距离原点 x 处
取一面积 ΔS ，考虑 dt 时间通过面积 ΔS 的能量
●
●
o
x
u
S
x
udt
在面积 ΔS 后做一方体，侧面积为 ΔS，宽为 udt
dt时间通过面积 ΔS 的能量就等于方体中的能量
w 设能量密度为 ，方体的体积为 Δs udt
w 方体中的能量 ΔSudt，
动能达到最大时势能为零，势能达到最大时动能为零，两者互相转化， 使得系统的总机械能保持守恒。
在波动过程中，每个质点尽管也是处在振动状态，但是这个振动系统 并不是孤立系统。每个质元动能和势能的变化是同相位的。同时达到 最大，同时达到最小，当此体积元的机械能达到零时，表明它已经把 全部机械能传递给邻近的下一个体积元。接下来它又要从上一个体积 元接收机械能，此能量由波源提供。质元随时和外界作能量的交换和 传递。
S1 4r12
S2 4r22
1 2
u 2 A12r12T
1 2
u 2 A22r22T
波面
A1 r2 A2 r1
球面波振幅与距离成反比。
波线
就越多，表示波动越强烈。描述波的能量强弱.
注意：定义中出现了对方向的要求，即能量密度 是个矢量。有时称为波的强度，则是只取其大小， 也就是说成了一个标量。
分析平面波和球面波的振幅
例 试证明在均匀不吸收能量的媒质中传播的平面波在行进方向 上振幅不变，球面波的振幅与离波源的距离成反比。
证明： 对平面波：
沿着波动的传播方向，该体积元不断从后面的介质获得能量，又不断 地把能量传递给前面的介质。随着波的行进，从介质的这一部分传向 另一部分，所以，波动是能量传递的一种方式。
大学物理 波的能量能流密度
单位体积内的能量 w dE dV
w
dE dV
A2 2 sin2[(t
x u
)
0
]
5、一个周期内的平均能量密度
w 1 T
T wdt 1
0
T
T 0
A2
2
s
in
2[(t
x u
)
0
]dt
1 2 A2
2
sin2 1 1 cos2
2
这说明：w 2、A2
dE
(dV
) A2
2
sin 2[(t
x) u
0 ]
对任一介质体积元来说，不断从波源方向的介质中吸收能
量，又不断地向后面的介质传递能量。这说明波动是传递能
量的一种方式，且能量传播的速度就是波速。
孤立的谐振子系统总能量守恒。
第十章 波动
4
物理学
第4五、版 能量密度
10-3 波的能量 能流密度
dEk
1 2
dV 2 A2
s
in2[(t x
u 第十章 波动
)
0
]
1
物第理五2版、学 dv 内的波动势能
10-3 波的能量 能流密度
体积元因形变而具有弹性势能
在横ห้องสมุดไป่ตู้中，产生切变
y
y
o
x
x
y
x
x
h
lim tg x
h
x0
y y x x
u
A s in
物理学
第五版
3波的能量
2 2 2
2
u
S S
1
2
A A
1
2
球面波振幅： 设球面波在均匀介质中传播，设波源在O点，在 距波源分别为 r1 和 r2处取两个球面，面积分别为S1和 S2，设介质不吸收能量
PP
1
S1 S2
2
所以，球面波波幅A与传播距离 r成反比。即球面 波波幅既使在介质不吸收能量时，也要随距离变小。
一.现象
在波动中，各体积元产生不同程度的 弹性形变， 具有 弹性势能
形变最小 振速 最小 时刻波形 未起振的体积元
上 下
抖 动
形变最大 振速 最大
各体积元以变化的振动速率 v 上下振动，具有振动动能
二、 波的能量
1．介质质元△m的动能
设波速为 u 的简谐波沿x 轴正向传播，波函数为
x y A cos ( t ) u
衍射：受限的尺度与波长相比
障 碍 物
广播和电视 哪个更容易 收到?
更容易听到男 的还是女的说 话的声音？
2.用惠更斯作图法导出了光的折射定律
历史上说明光是波动 • 作图步骤：
入射波 u 法线 1 B 媒质1 u1Dt 折射率n1 i· · E · C · A · 媒质2 F u 折射率n2 2Dt r D u2
2 2
注意：
（1）波的强度与振幅的平方成正比，这一结论不仅 适用于简谐波，而且具有普遍意义。 （2）根据上式和能量守恒概念，可以研究波传播时 振幅的变化。
平面波振幅 如果介质不吸收能量，既单位时间内通过两个截 面的能量相等时，则波在这两个平面处的振幅也相等。
P P
1
2 2 1 1
2
1 1 rA us rA us 2 2
2
u
S S
1
2
A A
1
2
球面波振幅： 设球面波在均匀介质中传播，设波源在O点，在 距波源分别为 r1 和 r2处取两个球面，面积分别为S1和 S2，设介质不吸收能量
PP
1
S1 S2
2
所以，球面波波幅A与传播距离 r成反比。即球面 波波幅既使在介质不吸收能量时，也要随距离变小。
一.现象
在波动中，各体积元产生不同程度的 弹性形变， 具有 弹性势能
形变最小 振速 最小 时刻波形 未起振的体积元
上 下
抖 动
形变最大 振速 最大
各体积元以变化的振动速率 v 上下振动，具有振动动能
二、 波的能量
1．介质质元△m的动能
设波速为 u 的简谐波沿x 轴正向传播，波函数为
x y A cos ( t ) u
衍射：受限的尺度与波长相比
障 碍 物
广播和电视 哪个更容易 收到?
更容易听到男 的还是女的说 话的声音？
2.用惠更斯作图法导出了光的折射定律
历史上说明光是波动 • 作图步骤：
入射波 u 法线 1 B 媒质1 u1Dt 折射率n1 i· · E · C · A · 媒质2 F u 折射率n2 2Dt r D u2
2 2
注意：
（1）波的强度与振幅的平方成正比，这一结论不仅 适用于简谐波，而且具有普遍意义。 （2）根据上式和能量守恒概念，可以研究波传播时 振幅的变化。
平面波振幅 如果介质不吸收能量，既单位时间内通过两个截 面的能量相等时，则波在这两个平面处的振幅也相等。
P P
1
2 2 1 1
2
1 1 rA us rA us 2 2
13-3 波的能量能流密度
系统与外界无能量交换。 系统与外界无能量交换。 波动质元： 波动质元：
∆Ek = ∆Ep ，∆Ek +∆Ep ≠ const.
每个质元都与周围媒质交换能量。 每个质元都与周围媒质交换能量。 特征） （特征）
第十三章 波动
9
物理学
1313-3 波的能量 能流密度
下册
能量密度： 能量密度：单位体积介质中的波动能量 dW x 2 2 2 w= = ρA ω sin ω (t − ) ∝ ω 2 A 2 dV u 平均能量密度 能量密度： 平均能量密度：能量密度在一个周 期内的平均值 1 T 1 2 2 w = ∫ wdt = ρω A T 0 2
ρdV 2 2 2 u 2 ρSdx ∂y x = A ω sin ωt − ω + ϕ = 2 ∂x 2 u
第十三章 波动
4
物理学
下册
1313-3 波的能量 能流密度 x ρdV 2 ρdV 2 2 2 dEk = v = A ω sin ωt − ω + ϕ 2 2 u
A
2
第十三章 波动
14
物理学
1313-3 波的能量 能流密度
下册
例 证明球面波的振幅与离开其波源的 距离成反比，并求球面简谐波的波函数. 距离成反比，并求球面简谐波的波函数 介质无吸收， 证 介质无吸收，通过两个球面的平均 能流相等. 能流相等 w1uS1 = w2uS 2 1 2 2 1 2 2 2 2 即 ρA1 ω u 4π r1 = ρA2 ω u 4π r2 2 2 A1 r2 s1 r s2 = 2 A2 r1
2 2 2
讨 论
(1)在波动传播的介质中，任一体积元的 )在波动传播的介质中， 动能、势能、 动能、势能、总机械能均随 x, t 作周期性变 同相位的 且变化是同相位 化，且变化是同相位的.