16-3 波的能量 能流密度
波的能流密度强度公式

波的能流密度强度公式全文共四篇示例,供读者参考第一篇示例:波的能流密度强度公式是描述波动能量传播和传递速率的重要公式。
能流密度强度是指单位面积上通过的波动能量流量,可以用来衡量波在介质中传播的强度和速率。
在物理学和工程学中,波动现象是非常常见的,因此研究波的能流密度强度公式对于理解和控制波动现象非常重要。
波的能流密度强度公式可以根据不同类型的波以及波动现象的特性而有所不同,但一般情况下,波的能流密度强度与波的振幅和频率有关。
在传统的经典力学中,波的能流密度强度可以通过以下公式来表示:\[ P = \frac{1}{2} \sqrt{\frac{u}{\rho}} v^2 \]P表示能流密度强度,u表示波的线密度或者表面密度,ρ表示介质的密度,ν表示波的速度。
在这个公式中,波的振幅对于能流密度强度的影响体现在速度的平方项上。
速度越大,波的振幅对应的能流密度强度就越大。
介质的密度和波的线密度或者表面密度也对能流密度强度起到重要作用。
需要特别说明的是,对于不同类型的波,能流密度强度公式可能需要做适当的修正。
比如对于声波,由于声波是在气体、液体或固体介质中传播的,因此介质密度对于声波的传播会产生不同的影响。
而对于电磁波,介质的电磁性质对于能流密度强度也可能会有所影响。
因此在具体应用中,需要根据波的特性和介质性质做出相应的修正和调整。
在工程学和实际应用中,波的能流密度强度公式可以用来优化波动传输系统的设计,提高能量传播效率,加速数据传输速率,改善声音等波动现象的传播质量。
比如在声学领域中,通过调节声波的振幅和频率,可以控制声音的传播距离和声音质量,进而提高音响设备的性能。
在无线通信领域中,通过优化电磁波的能流密度强度,可以提高无线通信网络的覆盖范围和传输速率。
波的能流密度强度公式是描述波动能量传播和传递速率的重要工具,对于理解和应用波动现象具有重要意义。
在实际应用中,根据波的特性和介质性质,可以对能流密度强度公式进行适当的调整和修正,从而实现对波动现象的优化和控制。
电磁波能流密度

电磁波能流密度
电磁波能流密度是指单位时间内通过单位面积的能量流密度,它描述了电磁波的能量传递情况。
在经典电磁学中,电磁波的平均能流密度与电场强度的平方成正比。
其定义式通常表示为S=E×H,其中E表示电场强度,H表示磁场强度。
这个公式也
被称为坡印廷矢量。
在实际应用中,电磁波能流密度具有广泛的意义。
在无线通信中,能流密度可以用来评估电磁辐射对人体的潜在危害。
在光学领域,能流密度可以用来描述光束的强度分布。
此外,能流密度还在能源传输、电磁辐射热效应等领域有重要应用。
另外,需要注意的是,由于电磁波频率很高,人眼和现有的探测器通常无法直接观测到电磁波的能量变化,因此实际应用中常常需要考虑电磁波的平均能流密度,即在一个时间周期内的平均能量流密度。
这个平均值才是实际能够观察到的量。
总之,电磁波能流密度是一个重要的物理量,它描述了电磁波在空间中的能量传递情况,对于理解电磁波的性质和应用具有重要意义。
3波的能量

●
●
o
x
S
x
在媒质中垂直波传播方向距离原点 x 处
取一面积 ΔS ,考虑 dt 时间通过面积 ΔS 的能量
●
●
o
x
u
S
x
udt
在面积 ΔS 后做一方体,侧面积为 ΔS,宽为 udt
dt时间通过面积 ΔS 的能量就等于方体中的能量
w 设能量密度为 ,方体的体积为 Δs udt
w 方体中的能量 ΔSudt,
动能达到最大时势能为零,势能达到最大时动能为零,两者互相转化, 使得系统的总机械能保持守恒。
在波动过程中,每个质点尽管也是处在振动状态,但是这个振动系统 并不是孤立系统。每个质元动能和势能的变化是同相位的。同时达到 最大,同时达到最小,当此体积元的机械能达到零时,表明它已经把 全部机械能传递给邻近的下一个体积元。接下来它又要从上一个体积 元接收机械能,此能量由波源提供。质元随时和外界作能量的交换和 传递。
S1 4r12
S2 4r22
1 2
u 2 A12r12T
1 2
u 2 A22r22T
波面
A1 r2 A2 r1
球面波振幅与距离成反比。
波线
就越多,表示波动越强烈。描述波的能量强弱.
注意:定义中出现了对方向的要求,即能量密度 是个矢量。有时称为波的强度,则是只取其大小, 也就是说成了一个标量。
分析平面波和球面波的振幅
例 试证明在均匀不吸收能量的媒质中传播的平面波在行进方向 上振幅不变,球面波的振幅与离波源的距离成反比。
证明: 对平面波:
沿着波动的传播方向,该体积元不断从后面的介质获得能量,又不断 地把能量传递给前面的介质。随着波的行进,从介质的这一部分传向 另一部分,所以,波动是能量传递的一种方式。
大学物理 波的能量能流密度
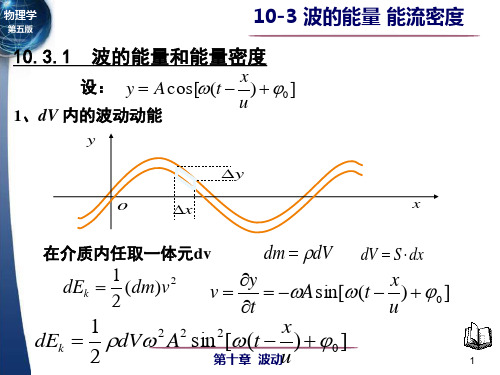
单位体积内的能量 w dE dV
w
dE dV
A2 2 sin2[(t
x u
)
0
]
5、一个周期内的平均能量密度
w 1 T
T wdt 1
0
T
T 0
A2
2
s
in
2[(t
x u
)
0
]dt
1 2 A2
2
sin2 1 1 cos2
2
这说明:w 2、A2
dE
(dV
) A2
2
sin 2[(t
x) u
0 ]
对任一介质体积元来说,不断从波源方向的介质中吸收能
量,又不断地向后面的介质传递能量。这说明波动是传递能
量的一种方式,且能量传播的速度就是波速。
孤立的谐振子系统总能量守恒。
第十章 波动
4
物理学
第4五、版 能量密度
10-3 波的能量 能流密度
dEk
1 2
dV 2 A2
s
in2[(t x
u 第十章 波动
)
0
]
1
物第理五2版、学 dv 内的波动势能
10-3 波的能量 能流密度
体积元因形变而具有弹性势能
在横ห้องสมุดไป่ตู้中,产生切变
y
y
o
x
x
y
x
x
h
lim tg x
h
x0
y y x x
u
A s in
物理学
第五版
大学物理-波的能量

x
y + ∆y
x y = Acosω(t − ) 1)体积元的动能 ) u ∂y x v = = − Aω sin ω(t − ) ∂t u
1 1 x 2 2 2 2 ∆Ek = ∆mi v = ρ∆VA ω sin ω(t − ) 2 2 u
2)体积元的势能 ∆E )
x
∆x
u
1 x 2 2 2 ρ∆VA ω sin ω(t − ) P = 2 u
形变最小 →0, , 振动速度最小 →0
y
r u
a
b
x
形变最大, 形变最大,振动 速度最大
r u
y
B P A Q
x
质元A 质元 质元P 质元 质元B 质元 质元Q 质元
(填吸收、释放)能量 填吸收、释放) 填吸收、释放) (填吸收、释放) 能量 填吸收、释放) (填吸收、释放) 能量 (填吸收、释放)能量 填吸收、释放)
结论:在波动过程中能量以波的形式沿 x 方向以 u 向
前传播着。 前传播着。
2、平均能量密度--- 能量密度在一个时间周期内的平均值 、平均能量密度
1 T 2 2 2 x 1 2 2 w = ∫ ρA ω sin ω(t − )dt = ρA ω T 0 u 2
为了定量描述波动过程中能量的传播, 为了定量描述波动过程中能量的传播,引入能流和 能流密度的概念 3、能流---单位时间内通过介质中某面积的能量 、能流 单位时间内通过介质中某面积的能量
形变最小形变最大形变最大振动速度最大填汲取释放能量填汲取释放填汲取释放填汲取释放能量填汲取释放填汲取释放能量填汲取释放能量能流和能流密度波强二能流和能流密ep为了精确地描述波的能量分布为了精确地描述波的能量分布引入能量密度1能量密度介质中单位体积中的波动能量能量密word版本能量密度描述了介质中各点能量即振动能量的分布能量密度描述了介质中各点能量即振动能量由上式可知波的能量密度是随介质的空间坐标能量密度是随介质的空间坐标由上式可知争论
大学物理第十五章第3,4,5节 波的能量能流密度

∆W = u ⋅ ∆t ⋅ ∆S ⋅ w
u△ t
S
∆W x 2 2 2 P= = u ⋅ ∆S ⋅ w = u∆Sρω A sin [ω(t − )] ∆t u
11
∆W x 2 2 2 P= = u ⋅ ∆S ⋅ w = u∆Sρω A sin [ω(t − )] ∆t u
能流总为正值,并随时间作周期性变化。 能流总为正值,并随时间作周期性变化。 在一个周期内能流的平均值称为平均能流 P
2 2 2
5
波动能量: 波动能量:
Y
能量极小
x
极大 极小
体积元在平衡位置时,动能、 体积元在平衡位置时,动能、势能和总 机械能均最大. 机械能均最大 体积元的位移最大时,三者均为零 体积元的位移最大时,三者均为零.
6
总机械能为: 总机械能为:
x dW= dW +dW = ρdV A sin [ω(t − )] ω k p u
∆ϕ = ϕ 2 − ϕ1 − 2π
r2 − r1
s1 s2
r1 r2
*
P
λ
定值
22
讨 论
A = A + A + 2A A2 cos ∆ϕ 1
2 1 2 2
决定了合振幅的大小. 位相差 ∆ϕ 决定了合振幅的大小. 干涉的位相差条件 当
∆ϕ = 2kπ时(k = 0,±1,±2,±3...)
合振幅最大 当
s1 s2
r1 r2
*
P
21
y P = y1 P + y 2 P = A cos( ω t + ϕ )
tanϕ =
A=
A1 sin(ϕ1 − A1 coA2 sin(ϕ2 −
电磁场的能量密度和能流密度
电磁场的能量密度和能流密度●电磁场能量●电磁场对电荷系统作功●电磁能密度和电磁能流密度的表达式●介质的极化能和磁化能( 1 ) 电磁场能量电磁场是一种物质。
电磁场运动与其他物质运动形式之间能够互相转化,它们都具有共同的运动量度−−能量。
这里,我们通过电磁场与带电物体相互作用过程中,电磁场能量和带电物体运动的机械能之间的相互转化,导出电磁场能量的表达式。
能量是按照一定的方式分布在电磁场内的,而且随着电磁场的运动,能量将在空间中传播。
引进:电磁能密度(体积电磁能) w,表示电磁场单位体积内的能量;电磁能流密度矢量S,表示单位时间内流过与能量传输方向(矢量S方向)垂直的单位横截面积的电磁能量( 2 ) 电磁场对电荷系统作功考虑空间某区域,设其体积为V,表面为A,自由电荷密度为ρe0,电流密度为j0. 以f表示电磁场对电荷的作用力密度,v 表示电荷的运动速度,则电磁场对电荷系统所作功的功率为⎰⎰⎰⋅)(d V V v f ,体积V 内电磁场能量的增加率为 ⎰⎰⎰⎰⎰⎰∂∂=)()(d d d d V V V t w V w t , 通过界面A 流入V 内的电磁能为σ⎰⎰⋅-)(d A S .能量守恒定律要求单位时间内通过界面A 流入V 内的能量,等于场对V 内电荷作功的功率以及V 内电磁场能量的增加率之和,即⎰⎰⎰⎰⎰⎰⎰⎰∂∂+⋅=⋅-)()()(d d d A V V V t w V v f A S . (14.64)利用奥-高斯公式可得,式(14.64)的相应的微分形式是 v f S ⋅-=∂∂+⋅∇tw . (14.65) ( 3 ) 电磁能密度和电磁能流密度的表达式 ① 由洛仑兹力公式可得0)()(j E v E v B v E v f ⋅=⋅=⋅⨯+=⋅ρρρ. (14.66)② 将麦克斯韦方程组中的式t ∂∂-⨯∇=D H j 0 (14.22) 代入上式,可得 t ∂∂⋅-⨯∇⋅=⋅DE H E j E )(0.(14.67) ③ 利用矢量分析中的公式)()()(H E E H H E ⨯∇⋅-⨯∇⋅=⨯⋅∇,及式 t ∂∂-=⨯∇BE ,(14.20)可将式(14.67)化为 t t ∂∂⋅-∂∂-⋅+⨯⋅∇-=⋅DE B H H E j E )()(0,即 t t ∂∂⋅+∂∂⋅+⨯⋅∇=⋅-DE B H H E v f )(.④ 将上式与能量守恒定律所要求的式 v f S ⋅-=∂∂+⋅∇t w(14.65)比较,即=∂∂+⋅∇t w S t t ∂∂⋅+∂∂⋅+⨯⋅∇DE BH H E )(,可得H E S ⨯=, (14.68)tt t w ∂∂⋅+∂∂⋅=∂∂B H D E . (14.69)这就是电磁场能流密度矢量(坡印廷矢量) S 以及能量密度变化率∂w/∂t 的普遍表达式。
3波的能量 能流密度
dW
dWk
dWp
dVA2 2
sin 2 (t
x) u
O x dx
x
O
y y dy
x
3、波的能量 能流密度
波动
讨 论 (1)介质中,任一体积元的动能、势能、总
机械能均随 x,t 作周期性变化,且变化是同相位的。
dW
2dWp
2dWk
dVA22 sin2 (t
x) u
体积元在平衡位置时,动能、势能和总机械能均 最大。因为 y Acos(t x )余弦为零,正弦达到最大。
P wuS
u
2、平均能流: P wuS
3、能流密度 ( 波的强度 )
通过垂直于波传播方向
S udt
的单位面积的平均能流。
I P w幅的平方、角频率的平方、
波速以及介质密度成正比。
波动
2、能量密度:单位体积介质中的波动能量
w dW A2 2 sin 2 (t x)
dV
u
3、平均能量密度:能量密度在一个周期内
的平均值:
w 1 T wdt 1 2 A2
T0
2
O x dx
x
O
y y dy
x
3、波的能量 能流密度
波动
二、能流和能流密度
1、能流:单位时间内垂直通过某一面积的能量.
3、波的能量 能流密度
波动
一、波动能量的传播
1、波的能量
以固体棒中传播的纵波为例:
y Acos(t x )
u
振动动能: v y Asin(t x )
t
u
dWk
1 2
dmv 2
1 2
dV
v 2
dWk
大学物理-波的能量 能流密度
2πr2
)
(1
2πr1
)
如果2 1即相干波源S1、S2同位相
则
2π
r1
r2
2π
r1 r2 称为波程差(波走过的路程之差)
水
的 衍
波 的 衍
射
射
19
三 波的干涉
1 波的叠加原理 波传播的独立性:两列波在某区域相遇
后再分开,传播情况与未相遇时相同,互不 干扰.
波的叠加性:在相遇区,任一质点的振 动为二波单独在该点引起的振动的合成.
20
2 波的干涉
频率相同、振动 方向平行、相位相同 或相位差恒定的两列 波相遇时,使某些地 方振动始终加强,而 使另一些地方振动始 终减弱的现象,称为 波的干涉现象.
波是如何传播的? 传播又有什么现象? 这些现象有什么规律?
一 惠更斯原理
介质中波动传播到的各点都可以看作是 发射子波的波源,而在其后的任意时刻,这 些子波的包络就是新的波前.
ut
平
球
面
面
R1
O
R2
波
波
18
二 波的衍射
波在传播过程中遇到障碍物,能绕过障 碍物的边缘,在障碍物的阴影区内继续传播.
波
一 波动能量的传播
1 波Байду номын сангаас能量
波的传播是能量的传播,传播过程中,
介质中的质点运动,具有动能
W
,介质形变
k
具有势能 W p .
1
以棒dW中k 哪哪传12播里里d的m最最v纵大小2 波,?12为例dV分v析2 波y 动A能co量s的(t 传ux播) .
v y Asin(t x )
t
u
振动动能
大学物理- 波的能量能流密度
3
物理学
第五版
10-3 波的能量 能流密度
相反地,当体积元处在位移为零处(即平衡位置)时,振速、 相对形变均最大,所以弹性势能和动能都同时达到最大值。 这与孤立的谐振子系统不相同,孤立的谐振子系统振动过程中 系统的动能和势能相互转换,且总能保持不变。 ② 体元dV内的机械能不守恒,且作周期性变化。
I 、A
2
2
第十章 波动
7
物理学
第五版
10.3.3
波的吸收
10-3 波的能量 能流密度
波动中一部分机械能因克服内摩擦做功转换成介质内能, 设介质中某处振幅为A,经厚度为dx的介质后,振幅的衰减 量为dA,实验表明 dA
dA Adx dA dx A
A0
dx
A
ln A x c
频率低于20Hz的机械波(如地震、火山爆发、陨石落地、 雷暴等发出…) (1)声强: 1 2 2 I A u 指声波的波强,即声波的平均能流密度 2 (2) 声强级:
以人耳刚能听到的声强 则声强级
IL lg
I 0 10 12 w
m 2为标准,
I I (贝尔) 10lg (分贝 dB) I0 I0
y
① 在同一体元dV 内, dEk 、 dEp 是同步的。
y 0
x
o
x
y
x
以横波为例,当体积元的位移最大时(即波峰、波谷处), 它附近的介质也沿同一方向产生了几乎相等的位移,使该体积 元发生的相对形变为零,即此时有y/x=0,所以此时体积元的 弹性势能为零,而此时体积元的振速也为零,所以动能也为零;
第十章 波动
14
2 2 2
、A
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
讨论 1)在波动传播的媒质中,任一体积元的动能、 )在波动传播的媒质中,任一体积元的动能、 势能、总机械能均随x, 作周期性变化 且变化是同 作周期性变化, 势能、总机械能均随 t作周期性变化,且变化是同 相位的 相位的. 体积元在平衡位置时,动能、 体积元在平衡位置时,动能、势能和总机械能 均最大. 均最大 体积元的位移最大时,三者均为零. 体积元的位移最大时,三者均为零
第十六章 机械波动理论 弹性势能
16-3 波的能量 能流密度 16O O
1 2 dW P = k (dy ) 2 dy F 胡克定律 =Y S dx
x
F
dx
SY k= F = YS dx dx 2 1 1 Y dy 2 dW P = k (d y ) = YS d x u= 2 2 ρ dx ∂y ω 1 dy 2 x 2 = ρu dV ( ) = A sin ω (t − ) 2 dx ∂x u u 1 x 2 2 2 = ρdVA ω sin ω (t − ) 2 u
16-3 波的能量 能流密度 16-
s2
s1
r1
r2
即
w 1 uS1 = w 2 uS2 1 1 2 2 2 ρ A1 ω u 4π r1 = ρ A22ω 2 u 4π r22 2 2 A0 r0 r A1 r2 y= cos ω (t − ) = r u A2 r1
处的振幅。 式中r为离开波源的距离, 式中 为离开波源的距离,A0为r=r0处的振幅。 为离开波源的距离
O O
x
dx
x
y + dy
y
x
第十六章 机械波动理论
16-3 波的能量 能流密度 16-
O O
x
dx
x
y + dy
y
x
1 1 2 dWk = (dm )v = (ρdV )v 2 2 2 ∂y x x y = Acosω(t − ) ∴ v = = −ωA sin ω (t − ) ∂t u u 1 x 2 2 2 dWk = ρdVA ω sin ω (t − ) 振动动能 2 u
P = w uS
能流密度(波的强度 能流密度 波的强度)I: 波的强度 通过垂直于波传播方向的单 位面积的平均能流. 位面积的平均能流
v u
P I = = wu S
udt
S
v 1 2 2v I= ρA ω u 2
单位: 单位: W/m2
第十六章 机械波动理论 例 证明球面波的振幅与 离开其波源的距离成反比, 离开其波源的距离成反比,并 求球面简谐波的波函数。 求球面简谐波的波函数。 介质无吸收, 证:介质无吸收,通过 两个球面的平均能流相等。 两个球面的平均能流相等。
dW x 2 2 2 = ρA ω sin ω (t − ) w= dV u
平均能量密度:能量密度在一个周期内的平均值 平均能量密度:能量密度在一个周期内的平均值. 能量密度
1 T 1 2 2 w = ∫ wdt = ρω A T 0 2
第十六章 机械波动理论
Hale Waihona Puke 16-3 波的能量 能流密度 16-
二 能流和能流密度 能流:单位时间内垂直通过某一面积的能量. 能流:单位时间内垂直通过某一面积的能量 P = wuS 平均能流: 平均能流:
y y + dy dy
x F+dF x
第十六章 机械波动理论
16-3 波的能量 能流密度 16-
1 x 2 2 2 d W k = d W p = ρ d VA ω sin ω (t − ) 2 u
x dW = dWk + dWp = ρdVA ω sin ω (t − ) u
2 2 2
体积元的总机械能
第十六章 机械波动理论 一 波的能量
16-3 波的能量 能流密度 16-
当机械波在媒质中传播时, 当机械波在媒质中传播时,媒质中各质点均在 其平衡位置附近振动,因而具有振动动能. 其平衡位置附近振动,因而具有振动动能 同时,介质发生弹性形变,因而具有弹性势能 同时,介质发生弹性形变,因而具有弹性势能. 以固体棒中传播的纵波为例分析波动能量的传播. 以固体棒中传播的纵波为例分析波动能量的传播
第十六章 机械波动理论
2 2
16-3 波的能量 能流密度 162
x d W = ρ d VA ω sin ω (t − ) u
2) 任一体积元都在不断地接收和放出能量, ) 任一体积元都在不断地接收和放出能量, 即不断地传播能量。任一体积元的机械能不守恒。 即不断地传播能量。任一体积元的机械能不守恒。 波动是能量传递的一种方式。 波动是能量传递的一种方式。 能量密度:介质中单位体积的波动能量。 能量密度:介质中单位体积的波动能量。
第十六章 机械波动理论
16-3 波的能量 能流密度 16-
钢轨中声速为5.1× 例16-4 钢轨中声速为 ×103m·s-1。今有一声波沿钢 轨传播,在某处振幅为1× 轨传播,在某处振幅为 ×10-9m,频率为 ×103Hz。 ,频率为1× 。 钢的密度为7.9× 钢轨的截面积为15cm2。 钢的密度为 ×103kg·m-3,钢轨的截面积为 (1) 试求该声波在该处的强度; 试求该声波在该处的强度; (2) 试求该声波在该处通过钢轨输送的功率。 试求该声波在该处通过钢轨输送的功率。 解: (1) 由强度公式
1 2 2 −4 2 I = ρA ω u = 8.0 ×10 W ⋅ m 2
(2) 通过该处的功率
1 P = wuS = ρA 2ω 2 uS = IS = 1.2 ×10 −6 W 2
作业题: 作业题:16-6
