全排列生成算法
全排列的几种算法

全排列的⼏种算法全排列,我们⾼中时就学过,数学上很简单,可是⽤计算机的算法实现还是有点味道的,今天我将我碰到的⼏种算法如数奉上,欢迎交流!第⼀种:递归最常见的也是最好理解的⽅法:简单点:⽐如"a" ,"b","c"全排列,可以看做事"a" +"b","c"的全排列及"b"+ "a","c"的全排列及"c" + "a","b"的全排列也就是说,遍历原数组中的每个元素,让剩余的元素全排列,这样就找到规律了。
代码如下:public static void main(String[] args) {char buf[]={'a','b','c','d'};perm(buf,0,buf.length-1);}public static void perm(char[] buf,int start,int end){if(start==end){//当只要求对数组中⼀个字母进⾏全排列时,只要就按该数组输出即可(特殊情况)for(int i=0;i<=end;i++){System.out.print(buf[i]);}System.out.println();}else{//多个字母全排列(普遍情况)for(int i=start;i<=end;i++){//(让指针start分别指向每⼀个数)char temp=buf[start];//交换数组第⼀个元素与后续的元素buf[start]=buf[i];buf[i]=temp;perm(buf,start+1,end);//后续元素递归全排列temp=buf[start];//将交换后的数组还原buf[start]=buf[i];buf[i]=temp;}}}第⼆中⽅法:也是递归,但是和第⼀种有所区别,算法:将数据分为两部分,递归将数据从左侧移右侧实现全排列⽐较抽象,如list abcd,遍历每⼀个数,将每个数放到⼀个新的list中,并将该元素从原list删除,然后将剩下的元素继续遍历每个元素继续放到新的list ⾥,这样,当list的长度为原list长度,或者原list长度为0时打印结果!下⾯是简单的⽰意图:// abcd//bcd a//cd ab//d abc//abcd//c abd//abdc//bd ac//d acb//acbd//b acd//acdb//bc ad ...//acd b ...//abd c ...//abc d ...源代码如下:private static void sort(List datas, List target) {//System.out.println("size="+datas.size());if (datas.size()==0) {for (Object obj : target)System.out.print(obj+" ");System.out.print(" ");return;}for (int i = 0; i < datas.size(); i++) {List newDatas = new ArrayList(datas);List newTarget = new ArrayList(target);newTarget.add(newDatas.get(i));newDatas.remove(i);sort(newDatas, newTarget);}}public static void main(String[] args) {List list = new ArrayList();for(int i=0;i<5;i++){list.add(i+1);}sort(list, new ArrayList());}第三种⽅法:⾮递归直接上代码:public static void main(String[] args) {int[] arr = new int[]{1,2,3,4,5,6};for(int i :arr){System.out.print(i + " ");}System.out.println();int totalnum = 1;while(NextNumber(arr,arr.length)){for(int i :arr){System.out.print(i + " ");}System.out.println();totalnum ++;}System.out.println("Total Num: " + totalnum);}private static Boolean NextNumber(int[] arr, int n){//数组最后⼀个元素位置int lastIndex = n-1;//从右向左确定第⼀个数字(前⾯的数字⽐它⼩)int firstIndex = lastIndex;for(;arr[firstIndex-1]>arr[firstIndex];firstIndex--){if(firstIndex == 1){//已经轮询完毕,此数已经是最⼤的那个数return false;}}//从右向左确定⼀个交换数(此数⽐arr[firstIndex]⼩且⽐arr[firstIndex-1]⼤)int swapIndex = lastIndex;for(;swapIndex > firstIndex;swapIndex--){if(arr[swapIndex] < arr[firstIndex] && arr[swapIndex] > arr[firstIndex-1]){break;}}//交换数字swap(arr,firstIndex-1,swapIndex);//将firstIndex右边的数字排序for(;firstIndex < lastIndex;firstIndex++,lastIndex--){if(arr[firstIndex] > arr[lastIndex]){swap(arr,firstIndex,lastIndex);}}return true;}private static void swap(int[] arr,int i, int j){int tmp = arr[i];arr[i] = arr[j];arr[j] = tmp;}如果此⽂对你有帮助,请留个⾔,新⼈需要打架的⽀持和⿎励!。
高三数学计数知识点

高三数学计数知识点计数是数学中非常重要的一个分支,它涉及到对事物的数量进行统计和计算。
在高三数学中,计数是一个基础且关键的知识点。
本文将介绍高三数学中的常见计数知识点,并简要说明其应用。
一、排列组合1. 排列(Permutation)排列是指从一组元素中取出指定数量的元素进行排序的方式。
在高三数学中,常见的排列问题包括全排列和部分排列。
全排列是指从n个元素中取出m个元素进行排序,所有可能的排序个数是m乘以(m-1)乘以(m-2)一直到1,即是n的阶乘除以(n-m)的阶乘。
部分排列是指从n个元素中取出m个元素进行排序,但不要求全部元素都用到,即是n的阶乘除以(n-m)的阶乘。
排列的应用非常广泛,例如在密码学、赛事抽签等领域。
2. 组合(Combination)组合是指从一组元素中取出指定数量的元素,但不考虑其排列顺序的方式。
在高三数学中,常见的组合问题包括组合数的计算和二项式定理的应用。
组合数是指从n个元素中取出m个元素的方式数目,计算公式是n的阶乘除以(m的阶乘乘以(n-m)的阶乘)。
二项式定理是数学中一个非常重要的定理,在组合数的计算、多项式展开等方面有广泛应用。
二、排列组合的应用排列组合在高三数学中具有重要的应用价值。
以下是其中的一些典型应用:1. 图案计数通过排列组合的知识,可以计算出不同颜色、不同形状的图案的数量。
例如,在一副扑克牌中,通过排列组合可计算出各种花色和面值的组合方式的数量。
2. 概率与统计排列组合也广泛应用于概率与统计中。
例如,在抽取一组球的问题中,可以通过排列组合来计算不同颜色的球的概率。
3. 组合优化问题在组合优化问题中,排列组合也扮演着重要的角色。
通过排列组合的计算,可以得到最优解或者解的近似结果。
例如,在货物装箱问题中,可以通过排列组合计算得到最省空间的装箱方案。
三、全排列与循环在高三数学中,全排列与循环也是重要的知识点之一。
1. 全排列生成算法全排列生成算法是一种计算一组元素的全排列的方法。
组合数学 第一章 排列组合5全排列的生成算法合

1.5.2字典序法
[例] 求839647521的下一个排列
找出比右边数字小的标号最大的数4
8397655 72124124517
44><<2157
大小为于于后44的的缀用用橙绿色 色表 表示 示
在 找接后出上即缀其前87中后3缀59比2将861缀4344中此97大、变65找后52的1得5出为缀的标到比对翻7下号84换转一3大2最916个的大5。1数的24数77 5
1.5.2字典序法
对给定的字符集中的字符 规定了一个先后关系,在此基 础上规定两个全排列的先后是 从左到右逐个比较对应的字符 的先后。
1.5.2字典序法
[例]字符集{1,2,3},较小的数字较 先,这样按字典序生成的全排列是: 123,132,213,231,312,321。
※※ 一个全排列可看做一个字符串,字
规则:令n个元素为1,2,…,n. p p1 p2 pn 是 这n个数的任意一个排列,我们可以找到一 个序列和它对应,其中ai 可以看作是排列P中 数i+1所在位置右边比i+1小的数的个数。
例 排列3214,它是元素1,2,3,4的一个 排列, 它对应的序列是什么?
例 序列311对应的排列是什么?
练习
求839763ห้องสมุดไป่ตู้421的下一个排列
1.5.3邻位对换法
序数法和字典排序法,求下一个排列在 不进位的情况下很容易。这就启发我们, 能不能设计一种算法,下一个排列总是 上一个排列某相邻两位对换得到的。
活动状态
以1←2←3←4←为初始排列,箭头所指一侧,相邻 的数比它小时,则称该数组处在活动状态, 1 2 3←4←的←2←,3,4都处于的活动状态。
符串可有前缀、后缀。
排列组合的计算公式和算法

排列组合的计算公式和算法
排列组合的计算公式是:
全排列:A(n,n)=n!
组合:C(n,m)=A(n,m)/A(m,m)=n!/(m!*(n-m)!)
这个计算公式是通过对排列组合的一些基本概念的分析所得,所以其算法就是将排列组合的基本概念结合起来,从而得出最终计算结果。
具体的步骤如下:
1、首先,我们要弄清楚全排列和组合的概念,才能清楚的理解排列组合的计算公式。
2、然后,用这些基本概念去讨论排列组合的情况,得出一个公式去验证排列组合的情况是否正确。
3、接着,我们需要做出正确的推断,将基本概念和判断的概率公式综合起来,形成一个新的公式。
4、最后,用新的公式推导出排列组合的计算公式,并计算出结果。
全排列的几种实现(含字典序排列算法分析)

全排列的⼏种实现(含字典序排列算法分析) 始于⼀个很简单的问题:⽣成{0,1,2,3,...,n-1}的n!种排列,即全排列问题。
下⾯介绍⼏种全排列的实现,以及探讨⼀下其解题思路。
基于枚举/递归的⽅法思路: 基于枚举的⽅法,也可以说是基于递归的⽅法,此⽅法的思路是先将全排列问题的约束进⾏放松,形成⼀个较容易解决的新问题,解新问题,再对新问题进⾏约束,解出当前问题。
以上全排列问题是⽣成{0,1,2,...,n-1}的n!个排列,隐含的⼀个约束是这个n个位置上的数必须是给出的集合中的数,不能重复使⽤。
当我们将此约束放松的时候,问题就变成了n个位置每个位置上有0~n-1种可能出现的数字,列出所有n n种数列,即在每⼀位上枚举所有的可能。
新问题的算法⾮常简单:private Integer[] perm;private void permut(int pos, int n) {if (pos == n) {for (int i = 0; i < perm.length; i++) {System.out.print(perm[i]);}System.out.println();return;}for (int i = 0; i < n; i++) {perm[pos] = i;permut(pos+1, n);}} ⽽我们实际的问题只要保证每⼀位上的数字在其他位置上没有使⽤过就⾏了。
private boolean[] used;private Integer[] perm;private void permut(int pos, int n) {if (pos == n) {for (int i = 0; i < perm.length; i++) {System.out.print(perm[i]);}System.out.println();return;} //针对perm的第pos个位置,究竟使⽤0~n-1中的哪⼀个进⾏循环for (int i = 0; i < n; i++) {if (used[i] == false) {perm[pos] = i;used[i] = true; //i已经被使⽤了,所以把标志位设置为Truepermut(pos+1, n);used[i] = false; //使⽤完之后要把标志复位}}} 或者完全按递归是思想,对{0,1,2,...,n-1}进⾏排列,分别将每个位置交换到最前⾯位,之后全排列剩下的位:private static void PermutationList(int fromIndex, int endIndex){if (fromIndex == endIndex)Output();else{for (int index = fromIndex; index <= endIndex; ++index){// 此处排序主要是为了⽣成字典序全排列,否则递归会打乱字典序Sort(fromIndex, endIndex);Swap(fromIndex, index);PermutationList(fromIndex + 1, endIndex);Swap(fromIndex, index);}}}基于字典序的⽅法 基于字典序的⽅法,⽣成给定全排列的下⼀个排列,所谓⼀个的下⼀个就是这⼀个与下⼀个之间没有其他的。
全排列生成算法的分析
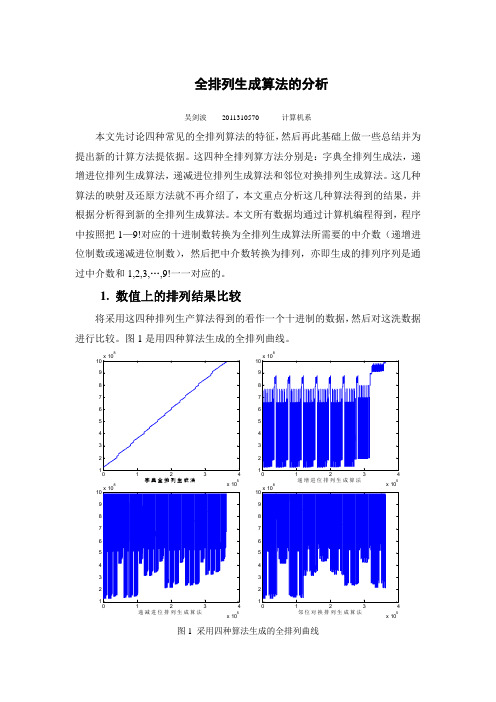
只有三个[0,1,7]。
x 105 2
x 105 2
1.5
1.5
1
1
0.5
0.5
0 0 x 105
4
2
4
6
字典全排列生成法
0
80
2
4
6
8
x 105递 增 进 位 排 列 生 成 算 法
4
3
3
2
2
1
1
0
0
2
4
6
递减进位排列生成算法
0 8
2
4
6
8
邻位对换排列生成算法
图 3. 四种全排列算法生成的相邻排列之间相同的字符个数的直方图
从另一个角度来思考,把生成的排列全部当着一个字符串,然后来比较这些 字符串有多少个位是不同的。比如排列"123456789"和"123456879"其中"78"两个 字符的位置不一样,则认为它们有 2 个位是不同的。上面的每种算法计算的排列 结果分别与上一次计算的排列结果比较,也就是将相邻的两个中介数生成的排列 进行对比,看有多少个字符是不同的,这里可以反映出通过该算法得到的排列在 字符上的变化的情况。
进行比较。图 1 是用四种算法生成的全排列曲线。
x 108 10
9 8 7 6 5 4 3 2 1
0
8
x 10 10
9 8 7 6 5 4 3 2 1
0
1
2
3
字典全排列生成法
1
2
3
递减进位排列生成算法
4
5
x 10
4
5
x 10
x 108 10
9 8 7 6 5 4 3 2 1
组合数学中的全排列生成算法完整版

组合数学全排列生成算法组合数学中的全排列深成算法历来是组合数学考试的重要考察点,因此在这里我简单的介绍一下6种全排列生成算法的详细过程,并借此比较它们之间的优劣之处。
不论是哪种全排列生成算法,都遵循着“原排列”→“原中介数”→“新中介数”→“新排列”的过程。
其中中介数依据算法的不同会的到递增进位制数和递减进位制数。
关于排列和中介数的一一对应性的证明我们不做讨论,这里仅仅给出了排列和中介数的详细映射方法。
相信熟练掌握了方法就可以顺利通过这部分的考察。
递增进位制和递减进位制数所谓递增进位制和递减进位制数字是指数字的进制随着数字位置的不同递增或递减。
通常我们见到的都是固定进制数字,如2进制,10进制等。
m位n进制数可以表示的数字是m*n个。
而m位递增或递减进位制数则可以表示数字m!个。
例如递增进位制数4121,它的进制从右向左依次是2、3、4、5。
即其最高位(就是数字4那位)最大值可能是4;第三高位最大可能是3;第二高位最大可能是2;最末位最大可能是1。
如果将4121加上1的话,会使最末位得到0,同时进位;第二位的2与进位相加,也会得到0,同时进位;第三位的1与进位相加得到2,不再进位。
最终得到结果是4200。
递减进位制的道理是一样的,只不过进制从右向左依次是9、8、7、6……,正好与递增进位制相反。
很明显,递减进位制的一个最大的好处就是加法不易进位,因为它在进行加法最频繁的末几位里(最右边)进制比较大。
接下来要了解的是递增进位制、递减进位制数和其序号的关系。
递增、递减进位制数可以被看作一个有序的数字集合。
如果规定递增进位制和递减进位制数的0的序号是十进制0,递增进位制数的987654321和递减进位制数的123456789对应十进制序号362880(即9!),则可以整理一套对应法则。
其中,递增进位制数(a1 a2 a3 a4 a5 a6 a7 a8 a9)为:a1*9! + a2*8! + ….+ a8*2! + a9*1! =序号例如序号100的递增进位制数就是4020,即4*4!+ 0*3!+ 2*2!+ 0*1!=100。
全排列算法解析(完整版)

void Permutation(int A[], int m, int n) {
int i, int temp; if(m = = n)
{ for(i = 0;i<n;i++) { if(i != n-1) printf("%d ",A[i]); //有加空格 else printf("%d" A[i]); //没加空格 } //直接输出,因为前 n-1 个数已经确定,递归到只有 1 个数。 printf("\n"); return;
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
全排列的生成算法对于给左的字符集,用有效的方法将所有可能的全排列无重复无遗漏地枚举出来。
字典序法按照字典序求下一个排列的算法广例字符集{1,2,3},较小的数字较先,这样按字典序生成的全排列是:123,132,213,231,312,321o注意一个全排列可看做一个字符串,字符串可有前缀、后缀/生成给泄全排列的下一个排列所谓一个全排列的下一个排列就是这一个排列与下一个排列之间没有其他的排列。
这就要求这一个排列与下一个排列有尽可能长的共同前缀,也即变化限制在尽可能短的后缀上。
广例839647521是1—9的排列。
1—9的排列最前而的是123456789,最后而的是987654321,从右向左扫描若都是增的,就到了987654321,也就没有下一个了。
否则找出第一次出现下降的位置。
算法:由P1P2...Pn生成的下一个排列的算法如下:1求j=max{j| Pj-I<pj}2.求|=max{k| Pi-1<Pk }3.交换Pi-1与PI得到P1P2...PI-1 (P i....Pn ),将红色部分顺序逆转,得到结果.例求839647521的下一个排列1.确定i,从左到右两两比较找出后一个数比前一个大的组合,在这里有39 47,然后i 取这些组中最到的位宜号(不是最大的数)在这两组数中7的位置号最大为6,所以i=62.确立I.找岀在i (包括i)后面的所有比i前面那一位大的数的最大的位置号,在此例中7, 5都满足要求,则选5, 5的位置号为7,所以1=73.先将4和5交换,然后将5后的四位数倒转得到结果8396574213 839651247以上算法是在数论课上老师给岀的关于字典序全排列的生成算法,以前也经常要用到全排列生成算法来生成一个全排列对所有的情况进行测试,每次都是现到网上找一个算法,然后直接copy代码,修改一下和自己的程序兼容就行了,也不看是怎么来的,不是我不想看,实在是说的很抽象,那一大堆公式来吓人,一个实例都不给,更有甚者连算法都没有,只是在那里说,想看都看不懂,也没那个耐心取理解那些人写出来的那种让人无法忍受的解释。
不过在说别人的同时我也知道,自己写的也不够好,不过这就是我的理解了,没法子写的再细了。
全排列的生成算法2008年04月25日星期五下午03:23全排列的生成算法就是对于给定的字符集,用有效的方法将所有可能的全排列无重复无遗漏地枚举出來。
任何n个字符集的排列都可以与1〜n的n个数字的排列一一对应,因此在此就以n个数字的排列为例说明排列的生成法。
n个字符的全体排列之间存在一个确定的线性顺序关系。
所有的排列中除最后一个排列外,都有一个后继:除第一个排列外,都有一个前驱。
每个排列的后继都可以从它的前驱经过最少的变化而得到,全排列的生成算法就是从第一个排列开始逐个生成所有的排列的方法。
全排列的生成法通常有以下几种:字典序法递増进位数制法递减进位数制法邻位交换法n进位制法递归类算法1 •字典序法字典序法中,对于数字仁2、3……n的排列.不同排列的先后关系是从左到右逐个比较对应的数字的先后來决定的。
例如对于5个数字的排列12354和12345,排列12345在前,排列12354在后。
按照这样的规定, 5个数字的所有的排列中最前面的是12345,最后面的是54321 o字典序算法如下:设P是1~n的一个全排列:p=p1p2……pn=plp2……pj-lpjpj+1……pk-1pkpk+1……pn1) 从排列的右端开始,找出第一个比右边数字小的数字的序号j (j从左端开始il•算),即j=max{i|pi<pi+1}2) 在pj的右边的数字中,找出所有比pj大的数中报小的数字pk.即k=max{i|pi>pj}(右边的数从右至左是递増的•因此k是所有大干pj的数字中序号最大者)3) 对换pi. pk4) 再将pj+1……pk-lpkpk+lpn倒转得到排列p=plp2••…pj-lpjpn••…pk+1pkpk-1••…pj+1,这就是排列p的下一个下一个排列。
例如839647521是数字1〜9的一个排列。
从它生成下一个排列的步骤如下:自右至左找出排列中第一个比右边数字小的数字4 839647521在该数字后的数字中找出比4大的数中最小的一个5 839647521将5与4交换839657421将7421 倒转839651247所以839647521的下一个排列是839651247。
程序代码如下:Private Sub Dict(p() As Integer, ByVai n As Integer)Dim i As Integer, j As IntegerOutL pi = n -1Do While i > 0If p(i) < p(i + 1) ThenFor j = n To i + 1 Step -1 •从排列右端开始If p(i) <= p(j) Then Exit For ■找出递减子序列i = i + 1NextSwap p(i)t p(j) ■将递减子序列前的数字与序列中比它大的第一个数交换For j = n To 1 Step -1•将这部分排列倒转If i >= j Then Exit ForSwap p(i), p(j)NextOutLp '输出一个排列1 = nEnd Ifi = i -1LoopEnd SubSwap p(i)t p(j)是交换两个元素的子过程.OWL p是输出排列的子过程。
2 •递增进位数制法在递增进位制数法中.从一个排列求另一个排列需雯用到中介数。
如果用ki表示排列plp2...pi...pn中元素pi的右边比pi 小的数的个数.则排列的中介数就是对应的排列ki……ki……kn-l o例如排列839647521的中介数是72642321, 7、2、6 .................分别是排列中数字& 3、9 ................ 的右边比它小的数字个数。
中介数是计算排列的中间环节。
已知一个排列,要求下一个排列,首先确定其中介数.一个排列的后继.其中介数是原排列中介数加仁需要注意的是,如果中介数的末位kn-1+1=2.则要向前进位,一般情形,如果ki+1=n-i+1,则要进位,这就是所谓的递增进位制。
例如排列839647521的中介数是72642321,则下一个排列的中介数是67342221+1=67342300(W为1+1=2,所以向前进位.2+1=3,又发生进位,所以下一个中介数是67342300)。
得到中介数后,可根据它还原对应得排列。
算法如下:中介数k1、k2 ............ kn-1的各位数字顺序表示排列中的数字n、.............. 2在排列中距右端的的空位数•因此,要按k仁k2 ................ kn-1的值从右向左确定n. n-1 .................. 2的位宜•并逐个放置在排列中:i放在右起的ki+1位,如果某位已放有数字,则该位宜不算在内,最后一个空位放仁因此从67342300可得到排列849617523,它就是839647521的后一个排列。
因为9最先放宜,k1=6, 9 放在右起第7位.空出6个空位.然后是放8, k2=7, 8放在右起第8位,但9占用一位,故8应放在右起第9位.余类推。
程序代码如下:Private Sub lncr(p() As Integer, ByVai n As Integer)Dim m() As Integer '保存中介数的数组Dim i As Integer, j As IntegerDim a As IntegerReDim m(n)For i = 1 To n'第一个排列的中介数为000 0i = i + 1For i = 1 To n -1 '计算中介数各位之和•将数字i 放宜在指定位置Next OutLpIf MedN(m) Then Exit Do •汁算下一个中介数,如果是00..0 则全部排列找到Loop End SubPrivate Function MedN(m() As lnteger)As Boolean Dim i As Integer, sum As Integer Dim b As Boolean b = FalseDo While i > 0 m(i) = m(i) + 1If m(i) < n - i + 1 Then Exit Do m(i) = 0 i = i -1 Loop Sum = 0m(i) = 0 NextDo While n > 0 Fori = 1 To n •排列的各位为0P(i) = 0 Next Fori = 1 To n '从右向左察看排列中为0的位 a = m(i) + 1Do While j > 0 If p(j) = 0 ThenIf a = 0 Then Exit Do •0的个数决定数字i 的位宜End IfLoopp(j) = n - i + 1 •讣算中介数函数i = i + 1Sum = Sum + m(i) NextIf Sum = 0 Then b = True MedN = b End Function 3 •递减进位制数法在递増进位制数法中•中介数的最低位是逢2进仁进位频繁.这是一个缺点。
把递增进位制数翻转,就得到 递减进位制数c839647521的中介数是67342221(k1k2...kn-1),倒转成为12224376(kn-1...k2k1),这是递减进位制数的中 介数:ki(i=n-1,n-2,...,2)fe 逢i 向ki-1位进给定排列p, p 的下一个排列的中介数定义为p 的中介数加 例如p=839647521, p 的中介数为12224376, p 的下一个排列的中介数为12224376+1=12224377.由此 得到p 的下一个排列为893647521。
给定中介数.可用与递增进位制数法类似的方法还原出排列。
但在递减进位制数中,可以不先计算中介数就 直接从一个排列求出下一个排列。
具体算法如下:1) 如果p(i)=n 且iv>n,则p(i)与p(i ・l)交换2) 如果p(n)=n.则找出一个连续递减序列9、8 ................... i,将其从排列左端删除,再以相反顺序加在排列右端,然后将PI 与左边的数字交换例如p=893647521的下一个排列是98364752仁 求983647521的下一个排列时•因为9在最左边且第2位 为&第3位不是7,所以将8和9从小到大排于最右端364752189,再将7与其左方数字对调得到983647521 的下一个排列是367452189。
