2021年北京市高考数学压轴题总复习
北京市高考数学压轴题汇编51题(含答案)
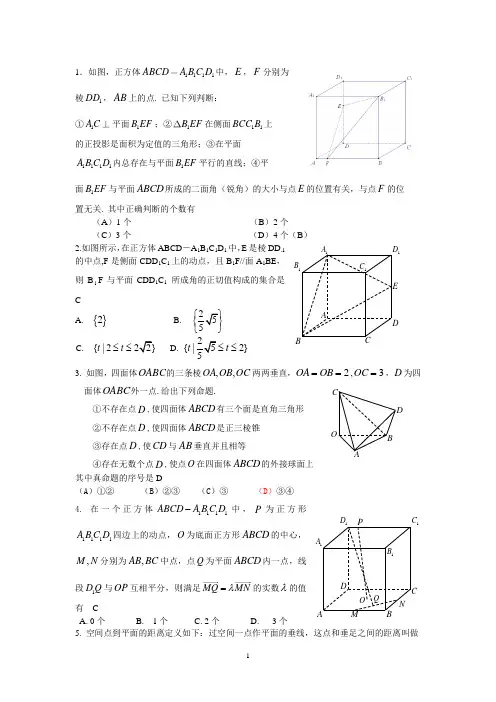
1．如图，正方体1111ABCDA B C D 中，E ，F 分别为棱1DD ，AB 上的点. 已知下列判断： ①1AC 平面1B EF ；②1B EF 在侧面11BCC B 上的正投影是面积为定值的三角形；③在平面1111A B C D 内总存在与平面1B EF 平行的直线；④平面1B EF 与平面ABCD 所成的二面角（锐角）的大小与点E 的位置有关，与点F 的位 置无关. 其中正确判断的个数有（A ）1个 （B ）2个（C ）3个 （D ）4个（B ） 2.如图所示，在正方体ABCD －A 1B 1C 1D 1中，E 是棱DD 1的中点,F 是侧面CDD 1C 1上的动点，且B 1F//面A 1BE ，则B 1F 与平面CDD 1C 1 所成角的正切值构成的集合是 CA. {}2B. 255⎧⎫⎨⎬⎩⎭ C. {|222}t t ≤≤ D. 2{|52}5t t ≤≤3. 如图，四面体OABC 的三条棱OC OB OA ,,两两垂直，2==OB OA ,3=OC ，D 为四面体OABC 外一点.给出下列命题.①不存在点D ,使四面体ABCD 有三个面是直角三角形 ②不存在点D ,使四面体ABCD 是正三棱锥 ③存在点D ,使CD 与AB 垂直并且相等④存在无数个点D ,使点O 在四面体ABCD 的外接球面上 其中真命题的序号是D（A ）①② （B ）②③ （C ）③ （D ）③④ 4. 在一个正方体1111ABCD A B C D -中，P 为正方形1111A B C D 四边上的动点，O 为底面正方形ABCD 的中心，,M N 分别为,AB BC 中点，点Q 为平面ABCD 内一点，线段1D Q 与OP 互相平分，则满足MQ MN λ=的实数λ的值有 CA. 0个B. 1个C. 2个D. 3个5. 空间点到平面的距离定义如下：过空间一点作平面的垂线，这点和垂足之间的距离叫做ABCDE1A 1D 1B1C OABDCA 1D 1A 1C 1B DCB OPN MQM BA图1 图2 图3这个点到这个平面的距离．平面α，β，γ两两互相垂直，点A∈α，点A到平面β，γ的距离都是3，点P是α上的动点，且满足P到β的距离是P到点A距离的2倍，则点P到平面γ的距离的最大值是C（A）3（B）3（C）3+（D）66.已知函数)(xf的定义域为R，若存在常数0>m，对任意x∈R，有|()|||f x m x<，则称)(xf为F函数．给出下列函数：①2)(xxf=；②xxxf cossin)(+=；③1)(2++=xxxxf；④)(xf是定义在R上的奇函数，且满足对一切实数21,xx均有21212)()(xxxfxf-≤-．其中是F函数的序号为 C（A）②④（B）①③（C）③④（D）①②7.定义区间(,)a b，[,)a b，(,]a b，[,]a b的长度均为db a=-，多个区间并集的长度为各区间长度之和，例如, (1, 2)[3, 5)的长度(21)(53)3d=-+-=. 用[]x表示不超过x的最大整数，记{}[]x x x=-，其中x∈R. 设()[]{}f x x x=⋅，()1g x x=-，若用123,,d d d分别表示不等式()()f xg x>，方程()()f xg x=，不等式()()f xg x<解集区间的长度，则当02011x≤≤时，有 B（A）1231,2,2008d d d===（B）1231,1,2009d d d===（C）1233,5,2003d d d===（D）1232,3,2006d d d===8. 下图展示了一个由区间(0,1)到实数集R的映射过程：区间(0,1)中的实数m对应数轴上的点M（如图1）；将线段AB围成一个圆，使两端点A、B恰好重合（从A到B是逆时针，如图2）；再将这个圆放在平面直角坐标系中，使其圆心在y轴上，点A的坐标为(0,1)（如图3），图3中直线AM与x轴交于点,0N n，则m的象就是n，记作f m n．则下列命题中正确的是（）CA ．114f ⎛⎫=⎪⎝⎭B ．()f x 是奇函数C ．()f x 在其定义域上单调递增D ．()f x 的图象关于y 轴对称 9. 用max{}a b ，表示a ，b两个数中的最大数，设2()max{f x x =1()4x ≥，那么由函数()y f x =的图象、x 轴、直线14x =和直线2x =所围成的封闭图形的面积是A A ．3512 B ．5924 C ．578D ．911210. 对于定义域和值域均为[0，1]的函数f (x )，定义1()()f x f x =，21()(())f x f f x =，…，1()(())n n f x f f x -=，n =1，2，3，…．满足()n f x x =的点x ∈[0，1]称为f 的n 阶周期点．设12,0,2()122,1,2x x f x x x ⎧≤≤⎪⎪=⎨⎪-<≤⎪⎩ 则f 的n 阶周期点的个数是C (A) 2n(B) 2(2n -1)(C) 2n(D) 2n 211. 定义在R 上的函数)(x f 满足1)4(=f ，()f x '为)(x f 的导函数，已知)('x f y =的图象如图所示，若两个正数a ，b 满足1)2(<+b a f ，则11++a b 的取值范围是（ C ）12.对于函数①1()45f x x x =+-，②21()log ()2f x x =-，③()cos(2)cos f x x x =+-， 判断如下两个命题的真假：命题甲：()f x 在区间(1,2)上是增函数；命题乙：()f x 在区间(0,)+∞上恰有两个零点12,x x ，且121x x <.能使命题甲、乙均为真的函数的序号是D（A ）① （B ）② （C ）①③ （D ）①②13. 已知函数2()2f x x x =-，()2g x ax =+(a >0)，若1[1,2]x ∀∈-，2[1,2]x ∃∈-，使得f (x 1)= g (x 2)，则实数a 的取值范围是 DA ．)31,51(B ．1(,)(5,)3-∞+∞C ．)5,31(D ．)3,(-∞(A) 1(0,]2(B) 1[,3]2(C) (0,3] (D) [3,)+∞14.已知函数21,0,()log ,0,x x f x x x +≤⎧=⎨>⎩则函数1)]([+=x f f y 的零点个数是 A（A ）4 （B ）3 （C ）2 （D ）115. 已知点P 是ABC ∆的中位线EF 上任意一点，且//EF BC ，实数x ，y 满足PA xPB yPC ++=0．设ABC ∆，PBC ∆，PCA ∆，PAB ∆的面积分别为S ，1S ，2S ，3S ， 记11S S λ=，22SS λ=，33S Sλ=．则23λλ⋅取最大值时，2x y +的值为 A（A ）32 （B ）12（C ） 1 （D ）2 16. 已知抛物线M ：24yx ，圆N ：222)1(r y x =+-（其中r 为常数，0>r ）.过点（1，0）的直线l 交圆N 于C 、D 两点，交抛物线M 于A 、B 两点，且满足BD AC =的直线l 只有三条的必要条件是 DA ．(0,1]r ∈B ．(1,2]r ∈C ．3(,4)2r ∈ D ．3[,)2r ∈+∞ 17. 设点(1,0)A ，(2,1)B ，如果直线1ax by +=与线段AB 有一个公共点，那么22a b +（A ）（A ）最小值为15（B（C ）最大值为15（D18. 已知数列*{} ()n a nN 满足：*1log (2) ()n n a n n N +=+∈，定义使123......k a a a a ⋅⋅⋅⋅为整数的数*()k k N ∈叫做企盼数，则区间[1, 2011]内所有的企盼数的和为 . 2026 19. 在平面直角坐标系xOy 中，O 为坐标原点.定义11,P x y 、22,Q x y 两点之间的“直角距离”为1212(,)d P Q x x y y .若点1,3A -，则(,)d A O = ；已知点1,0B ，点M 是直线30(0)kxykk上的动点，(,)d B M 的最小值为 . 4 32 (1)2 3 (01)k kk k ⎧+≥⎪⎨⎪+<<⎩20. 在平面直角坐标系中，定义1212(,)d P Q x x y y =-+-为两点11(,)P x y ,22(,)Q x y 之间的“折线距离”. 则坐标原点O与直线20x y +-=上一点的“折线距离”的最小值是____；圆221x y +=上一点与直线20x y +-=上一点的“折线距离”的最小值是____.，25 21. 已知函数2)1ln()(x x a x f -+=，在区间)1,0(内任取两个实数,p q ，且q p ≠，不等式1)1()1(>-+-+qp q f p f 恒成立，则实数a 的取值范围是 ．[15,)+∞22. 定义方程()()f x f x '=的实数根x 0叫做函数()f x 的“新驻点”，如果函数()g x x =，()ln(1)h x x =+，()cos x x ϕ=（()x π∈π2，）的“新驻点”分别为α，β，γ，那么α，β，γ的大小关系是 ．γ>α>β23．将全体正奇数排成一个三角形数阵： 1 3 5 7 9 11 13 15 17 19 ……按照以上排列的规律，第n 行（n ≥3）从左向右的第3个数为 ．24.已知函数399)(+=x x x f ，则(0)(1)f f += ，若112()()k S f f k k-=+31()()(2,k f f k k kk-+++≥∈Z)，则1k S -= （用含有k 的代数式表示）．1，12k - 25.已知数列{}n a 的各项均为正整数，对于⋅⋅⋅=,3,2,1n ，有1135,2n n n nn n k k a a a a a a +++⎧⎪=⎨⎪⎩为奇数为偶数.其中为使为奇数的正整数，, 当111a =时，100a =______；若存在*m ∈N ，当n m >且n a 为奇数时，n a 恒为常数p ，则p 的值为______.62；1或526.已知数列{}n a ，满足：123451,2,3,4,5a a a a a =====，且当5n ≥时，1121n n a a a a +=-，若数列{}n b 满足对任意*n ∈N ，有2221212n n n b a a a a a a =----，则5b = ；当5n ≥时，=n b ．65 n -7027．数列{}n a 满足11a =，11n n n a a n λ+-=+，其中λ∈R ， 12n =，，．①当0λ=时，20a =_____；②若存在正整数m ，当n m >时总有0n a <，则λ的取值范围是_____.120；(21,2),k k k -∈*N 28．函数)0(2>=x x y 的图象在点2(,)n n a a 处的切线与x 轴交点的横坐标为1n a +，n N *∈，若161=a ，则=+53a a ，数列{}n a 的通项公式为 ．5， 52n-29.对任意x ∈R ，函数()f x 满足1(1)2f x +=，设)()]([2n f n f a n -=，数列}{n a 的前15项的和为3116-，则(15)f = ．3430. 如图，线段AB =8，点C 在线段AB 上，且AC =2，P 为线段CB 上一动点，点A 绕点C 旋转后与点B 绕点P 旋转后重合于点D .设CP =x ， △CPD 的面积为()f x .则()f x 的定义域为 ； '()f x 的零点是 . (2,4); 331.已知函数sin ()x f x x=（1）判断下列三个命题的真假：①()f x 是偶函数；②()1f x < ；③当32x π=时，()f x 取得极小值. 其中真命题有____________________；（写出所有真命题的序号） （2）满足()()666n n f f πππ<+的正整数n 的最小值为___________.①② , 9 32．如图所示，∠AOB =1rad ，点A l ，A 2，…在OA 上，点B 1，B 2，…在OB 上，其中的每一个实线段和虚线段的长均为1个长度单位，一个动点M 从O 点出发，沿着实线段和以O 为圆心的圆弧匀速运动，速度为l 长度单位／秒，则质点M 到达A 3点处所需要的时间为__ACP BD秒，质点M 到达A n 点处所需要的时间为__秒．6，(1),2(3),2n n n n a n n n +⎧⎪⎪=⎨+⎪⎪⎩为奇数，为偶数.33．已知函数2()(1)1f x ax b x b =+++-，且(0, 3)a ∈，则对于任意 的b ∈R ，函数()()F x f x x =-总有两个不同的零点的概率是 .1334. 对于各数互不相等的整数数组),,,,(321n i i i i (n 是不小于3的正整数)，对于任意的,{1,2,3,,}p q n ∈，当q p <时有q p i i >，则称p i ，q i 是该数组的一个“逆序”，一个数组中所有“逆序”的个数称为该数组的“逆序数”，则数组（2，4，3，1）中的逆序数等于 ；若数组123(,,,,)n i i i i 中的逆序数为n ，则数组11(,,,)n n i i i -中的逆序数为 .4；232n n -35. 已知集合},,,{21n a a a A =中的元素都是正整数，且n a a a <<< 21，对任意的,,A y x ∈且x y ≠，有25xyy x ≥-． （Ⅰ）求证：251111-≥-n a a n ； （Ⅱ）求证：9≤n ；（Ⅲ）对于9=n ，试给出一个满足条件的集合A ． (Ⅰ) 证明：依题意有)1,,2,1(2511-=≥-++n i a a a a i i i i ，又n a a a <<< 21， 因此)1,,2,1(2511-=≥-++n i a a a a i i i i ． OA 1A 2 A 3 A 4B 1 B 2 B 3 B 4 AB可得)1,,2,1(251111-=≥-+n i a a i i ． 所以12231111111111125i i n n n a a a a a a a a +---+-+-++-≥． 即251111-≥-n a a n ． …………………4分 （Ⅱ）证明：由(Ⅰ)可得25111->n a ． 又11≥a ，可得2511->n ，因此26<n ． 同理2511i n a a n i -≥-，可知251i n a i ->． 又i a i ≥，可得251in i ->， 所以)1,,2,1(25)(-=<-n i i n i 均成立． 当10≥n 时，取5=i ，则25)5(5)(≥-=-n i n i ， 可知10<n ．又当9≤n 时，25)2()2()(22<=-+≤-ni n i i n i ． 所以9≤n ． …………………9分（Ⅲ）解：对于任意n j i ≤<≤1，j i i a a a ≤<+1，由)1,,2,1(251111-=≥-+n i a a i i 可知， 25111111≥-≥-+i i j i a a a a ，即25j i j i a a a a ≥-． 因此，只需对n i <≤1，251111≥-+i i a a 成立即可． 因为251211≥-；2513121≥-；2514131≥-；2515141≥-， 因此可设11=a ；22=a ；33=a ；44=a ；55=a ． 由2511165≥-a a ，可得4256≥a ，取76=a ． 由2511176≥-a a ，可得181757≥a ，取107=a ．由2511187≥-a a ，可得3508≥a ，取208=a ． 由2511198≥-a a ，可得1009≥a ，取1009=a ． 所以满足条件的一个集合{}100,20,10,7,5,4,3,2,1=A ．……………14分 36. 已知集合{}1,2,3,,2A n =*()n N ∈.对于A 的一个子集S ，若存在不大于n 的正整数m ，使得对于S 中的任意一对元素12,s s ，都有12s s m -≠，则称S 具有性质P.（Ⅰ）当10n =时，试判断集合{}9B x A x =∈>和{}*31,C x A x k k N =∈=-∈是否具有性质P ？并说明理由.（Ⅱ）若1000n =时① 若集合S 具有性质P ，那么集合{}2001T x x S =-∈是否一定具有性质P ？并说明理由；②若集合S 具有性质P ，求集合S 中元素个数的最大值． 解：（Ⅰ）当10n =时，集合{}1,2,3,,19,20A =,{}{}910,11,12,,19,20B x A x =∈>=不具有性质P ．...................................1分 因为对任意不大于10的正整数m ，都可以找到该集合中两个元素110b =与210b m =+，使得12b b m -=成立．...............2分 集合{}*31,C x A x k k N =∈=-∈具有性质P ． ................................................3分 因为可取110m =<，对于该集合中任意一对元素112231,31c k c k =-=-，*12,k k N ∈ 都有121231c c k k -=-≠． .....................................................................4分 （Ⅱ）当1000n =时，则{}1,2,3,,1999,2000A =①若集合S 具有性质P ，那么集合{}2001T x x S =-∈一定具有性质P ．...................5分 首先因为{}2001T x x S =-∈，任取02001,t x T =-∈ 其中0x S ∈， 因为S A ⊆，所以0{1,2,3,...,2000}x ∈，从而0120012000x ≤-≤，即,t A ∈所以T A ⊆. ...........................6分 由S 具有性质P ，可知存在不大于1000的正整数m ， 使得对S 中的任意一对元素12,s s ，都有12s s m -≠． 对于上述正整数m ，从集合{}2001T x x S =-∈中任取一对元素11222001,2001t x t x =-=-，其中12,x x S ∈， 则有1212t t x x m -=-≠,所以集合{}2001T x x S =-∈具有性质P ． .............................8分 ②设集合S 有k 个元素．由第①问知，若集合S 具有性质P ，那么集合{}2001T x x S =-∈一定具有性质P ．任给x S ∈，12000x ≤≤，则x 与2001x -中必有一个不超过1000， 所以集合S 与T 中必有一个集合中至少存在一半元素不超过1000，不妨设S 中有t 2k t ⎛⎫≥ ⎪⎝⎭个元素12,,,t b b b 不超过1000．由集合S 具有性质P ，可知存在正整数1000m ≤， 使得对S 中任意两个元素12,s s ，都有12s s m -≠， 所以一定有12,,,t b m b m b m S +++∉.又100010002000i b m +≤+=，故12,,,t b m b m b m A +++∈,即集合A 中至少有t 个元素不在子集S 中， 因此2k k +≤2000k t +≤，所以20002kk +≤，得1333k ≤， 当{}1,2,,665,666,1334,,1999,2000S =时，取667m =，则易知对集合S 中任意两个元素12,y y ， 都有12||667y y -≠，即集合S 具有性质P ，而此时集合Ｓ中有1333个元素．因此集合S 元素个数的最大值是1333． .....................................14分 37. 已知函数2()1f x x=+，数列{}n a 中，1a a =，1()n n a f a +=*()n ∈N ．当a 取不同的值时，得到不同的数列{}n a ，如当1a =时，得到无穷数列1，3，53，115，…；当2a =时，得到常数列2，2，2，…；当2a =-时，得到有穷数列2-，0．（Ⅰ）若30a =，求a 的值；（Ⅱ）设数列{}n b 满足12b =-，1()n n b f b +=*()n ∈N ．求证：不论a 取{}n b 中的任何数，都可以得到一个有穷数列{}n a ；（Ⅲ）若当2n ≥时，都有533n a <<，求a 的取值范围． 解：（Ⅰ）因为 30a =，且3221a a =+， 所以22a =-．同理可得123a =-，即23a =-． ………………………3分（Ⅱ）证明：假设a 为数列{}n b 中的第*()i i ∈N 项，即1i a a b ==；则211()()i i a f a f b b -===； 3212()()i i a f a f b b --===；………121()()2i i a f a f b b -====-；12()10i i ia f a a +==+=， 即1()(2)0i i a f a f +==-=。
2021.1北京高三数学期末分类汇编-新定义压轴题(含参考答案)
（Ⅲ）设数列{an} 为等比数列，公比为 q ，项数为 N (N ≥3) ．判定数列{an} 是否存在长 度为 3 的递增子列：1，16，81？若存在，求出 N 的最小值；若不存在，说明理由穷数列．给出两个性质： ①对于{an} 中任意两项 ai , a j (i > j) ，在{an} 中都存在一项 am ，使得 2ai − a j = am ； ②对于{an} 中任意项 an (n 3) ，在{an} 中都存在两项 ak ,al (k > l) ，使得= an 2ak − al . (Ⅰ)若= an 2= n (n 1, 2,) ，判断数列{an} 是否满足性质①，说明理由； (Ⅱ)若= an n= (n 1, 2,) ，判断数列{an} 是否同时满足性质①和性质②，说明理由； (Ⅲ)若{an} 是递增数列， a1 = 0 ，且同时满足性质①和性质②，证明：{an} 为等差数列.
（Ⅱ）对于任意“ 5 阶非负数表” A ，记 R(s) 为 A 的第 s 行各数之和（1 ≤ s ≤ 5），证明：存
在 {i, j, k}⊆ {1,2,3,4,5}，使得 R(i) + R( j) + R(k) ≥ 3 ；
（Ⅲ）当 n = 2k(k ∈ N*) 时，证明：对与任意“ n 阶非负数表” A ，均存在 k 行 k 列，使得 这 k 行 k 列交叉处的 k 2 个数之和不小于 k .
设{an*} 的前 n 项和为 Sn* .
（Ⅰ）设 an
=
n 2n
，写出 a1* ， a2* ， a3* ， a4* ；
（Ⅱ）证明：“对任意 n ∈ N* ，有= Sn* an+1 − a1 ”的充要条件是“对任意 n ∈ N* ，有 | an+1 − an |= 1 ”；
2021年高考数学高考数学压轴题 立体几何多选题分类精编附答案
2021年高考数学高考数学压轴题 立体几何多选题分类精编附答案一、立体几何多选题1．已知正方体1111ABCD A B C D -的棱长为2，点E ，F 在平面1111D C B A 内，若||5AE =，AC DF ⊥，则（ ）A ．点E 的轨迹是一个圆B ．点F 的轨迹是一个圆C ．EF 21-D ．AE 与平面1A BD 所成角的正弦值的最大值为153015【答案】ACD 【分析】对于A 、B 、C 、D 四个选项，需要对各个选项一一验证. 选项A ：由2211||5AE AA A E =+=1||1A E =，分析得E 的轨迹为圆；选项B ：由AC DBF ⊥，而点F 在11B D 上，即F 的轨迹为线段11B D ，； 选项C ：由E 的轨迹为圆，F 的轨迹为线段11B D ，可分析得min ||EF d r =-； 选项D ：建立空间直角坐标系，用向量法求最值. 【详解】 对于A:2211||5AE AA A E =+=221|25A E +=1||1A E =，即点E 为在面1111D C B A 内，以1A 为圆心、半径为1 的圆上；故A 正确；对于B: 正方体1111ABCD A B C D -中，AC ⊥BD ，又AC DF ⊥，且BD ∩DF=D ，所以AC DBF ⊥，所以点F 在11B D 上，即F 的轨迹为线段11B D ，故B 错误；对于C:在平面1111D C B A 内，1A 到直线11B D 的距离为2,d=当点E ，F 落在11A C 上时，min ||21EF =-；故C 正确； 对于D:建立如图示的坐标系，则()()()()10,0,0,2,0,0,0,0,2,0,2,0A B A D因为点E 为在面1111D C B A 内，以1A 为圆心、半径为1 的圆上，可设()cos ,sin ,2E θθ 所以()()()1cos ,sin ,2,2,0,2,2,2,0,AE A B BD θθ==-=-设平面1A BD 的法向量(),,n x y z =，则有1·220·220n BD x y n A B x z ⎧=-+=⎪⎨=-=⎪⎩不妨令x =1，则()1,1,1n =， 设AE 与平面1A BD 所成角为α，则：22|||sin |cos ,|||||5315n AE n AE n AE πθα⎛⎫++ ⎪⎝⎭====⨯⨯当且仅当4πθ=时，sin α2215301515=， 故D 正确故选：CD 【点睛】多项选择题是2020年高考新题型，需要要对选项一一验证．2．如图，直三棱柱11,ABC A B C -，ABC 为等腰直角三角形，AB BC ⊥，且12AC AA ==，E ，F 分别是AC ，11A C 的中点，D ，M 分别是1AA ，1BB 上的两个动点，则（ ）A ．FM 与BD 一定是异面直线B ．三棱锥D MEF -的体积为定值14C ．直线11B C 与BD 所成角为2π D ．若D 为1AA 中点，则四棱锥1D BB FE -55【答案】CD 【分析】A 当特殊情况M 与B 重合有FM 与BD 相交且共面；B 根据线面垂直、面面垂直判定可证面1BEFB ⊥面11ACC A ，可知EMFS、D 到面1BEFB 的距离，可求D EMF V -；C 根据线面垂直的判定及性质即可确定11B C 与BD 所成角；D 由面面垂直、勾股、矩形性质等确定外接球半径，进而求体积，即可判断各项的正误. 【详解】A ：当M 与B 重合时，FM 与BD 相交且共面，错误； B ：由题意知：BE AC ⊥，AC EF ⊥且BEEF E =，则AC ⊥面1BEFB ，又AC ⊂面11ACC A ，面1BEFB ⋂面11ACC A EF =，所以面1BEFB ⊥面11ACC A ，又1121122EMFSEF BE =⋅⋅=⨯⨯=，D 到面1BEFB 的距离为1h =，所以1133D EMF EMFV h S-=⋅⋅=，错误； C ：由AB BC ⊥，1BC B B ⊥，1B BAB B =，所以BC ⊥面11ABB A ，又11//BC B C ，即11B C ⊥面11ABB A ，而BD ⊂面11ABB A ，则11BD B C ⊥，正确；D ：由B 中，面1BEFB ⊥面11ACC A ，即面DEF ⊥面1BEFB ，则D 到面1BEFB 的距离为1h =，又D 为1AA 中点，若1,BF EB 交点为O ，G 为EF 中点，连接,,OG GD OD ，则OG GD ⊥，故225OD OG GD =+=，由矩形的性质知：152OB OE OF OB ====，令四棱锥1D BB FE -的外接球半径为R ，则5R =，所以四棱锥1D BB FE -的外接球体积为354356V R π==，正确. 故选：CD. 【点睛】关键点点睛：利用线面、面面关系确定几何体的高，结合棱锥体积公式求体积，根据线面垂直、勾股定理及矩形性质确定外接球半径，结合球体体积公式求体积.3．已知正方体1111ABCD A B C D -的棱长为2，点O 为11A D 的中点，若以O 6为半径的球面与正方体1111ABCD A B C D -的棱有四个交点E ，F ，G ，H ，则下列结论正确的是（ ）A ．11//A D 平面EFGHB ．1AC ⊥平面EFGHC ．11A B 与平面EFGH 所成的角的大小为45°D ．平面EFGH 将正方体1111ABCD A B C D -分成两部分的体积的比为1:7 【答案】ACD 【分析】如图，计算可得,,,E F G H 分别为所在棱的中点，利用空间中点线面的位置关系的判断方法可判断A 、B 的正确与否，计算出直线AB 与平面EFGH 所成的角为45︒后可得C 正确，而几何体BHE CGF -为三棱柱，利用公式可求其体积，从而可判断D 正确与否.【详解】如图，连接OA ，则2115OA AA =+=，故棱1111,,,A A A D D D AD 与球面没有交点.同理，棱111111,,A B B C C D 与球面没有交点. 因为棱11A D 与棱BC 之间的距离为26>BC 与球面没有交点.因为正方体的棱长为2，而26<球面与正方体1111ABCD A B C D -的棱有四个交点E ，F ，G ，H ， 所以棱11,,,AB CD C C B B 与球面各有一个交点， 如图各记为,,,E F G H .因为OAE △为直角三角形，故22651AE OE OA -=-=，故E 为棱AB 的中点. 同理,,F G H 分别为棱11,,CD C C B B 的中点.由正方形ABCD 、,E F 为所在棱的中点可得//EF BC ， 同理//GH BC ，故//EF GH ，故,,,E F G H 共面. 由正方体1111ABCD A B C D -可得11//A D BC ，故11//A D EF因为11A D ⊄平面EFGH ，EF ⊂平面EFGH ，故11//A D 平面EFGH ，故A 正确. 因为在直角三角1BA C 中，122A B =2BC = ，190A BC ∠=︒， 1A C 与BC 不垂直，故1A C 与GH 不垂直，故1A C ⊥平面EFGH 不成立，故B 错误.由正方体1111ABCD A B C D -可得BC ⊥平面11AA B B ，而1A B ⊂平面11AA B B ， 所以1BC A B ⊥，所以1EF A B ⊥在正方形11AA B B 中，因为,E H 分别为1,AB BB 的中点，故1EH A B ⊥， 因为EFEH E =，故1A B ⊥平面EFGH ，所以BEH ∠为直线AB 与平面EFGH 所成的角，而45BEH ∠=︒， 故直线AB 与平面EFGH 所成的角为45︒，因为11//AB A B ，故11A B 与平面EFGH 所成的角的大小为45°.故C 正确. 因为,,,E F G H 分别为所在棱的中点，故几何体BHE CGF -为三棱柱，其体积为111212⨯⨯⨯=，而正方体的体积为8， 故平面EFGH 将正方体1111ABCD A B C D -分成两部分的体积的比为1:7，故D 正确. 故选：ACD. 【点睛】本题考查空间中线面位置的判断、空间角的计算和体积的计算，注意根据球的半径确定哪些棱与球面有交点，本题属于中档题.4．在长方体1111ABCD A B C D -中，AB =12AD AA ==，,,P Q R 分别是11,,AB BB AC 上的动点，下列结论正确的是（ ） A ．对于任意给定的点P ，存在点Q 使得1D P CQ ⊥ B ．对于任意给定的点Q ，存在点R 使得1D R CQ ⊥ C ．当1AR A C ⊥时，1AR D R ⊥D ．当113AC A R =时，1//D R 平面1BDC 【答案】ABD 【分析】如图所示建立空间直角坐标系，计算142D P CQ b ⋅=-，()12222D R CQ b λλ⋅=--，134AR D R ⋅=-，10D R n ⋅=，得到答案.【详解】如图所示，建立空间直角坐标系，设()2,,0P a ，a ⎡∈⎣，()Q b ，[]0,2b ∈，设11A R AC λ=，得到()22,22R λλ--，[]0,1λ∈. ()12,,2P a D -=，()2,0,CQ b =，142D P CQ b ⋅=-，当2b =时，1D P CQ ⊥，A 正确；()122,2D R λλ=--，()12222D R CQ b λλ⋅=--，取22bλ=+时，1D R CQ ⊥，B 正确； 1AR A C ⊥，则()()12,222212440AR AC λλλλλ⋅=--⋅--=-+-+=，14λ=，此时113313022224AR D R ⎛⎫⎛⎫⋅=-⋅-=-≠ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭，C 错误；113AC A R =，则4234,,33R ⎛⎫ ⎪ ⎪⎝⎭，14232,,33D R ⎛⎫=- ⎪ ⎪⎝⎭，设平面1BDC 的法向量为(),,n x y z =，则10n BD n DC ⎧⋅=⎪⎨⋅=⎪⎩，解得()3,1,3n =-，故10D R n ⋅=，故1//D R 平面1BDC ，D 正确. 故选：ABD .【点睛】本题考查了空间中的线线垂直，线面平行，意在考查学生的计算能力和空间想象能力，推断能力.5．在边长为2的等边三角形ABC 中，点,D E 分别是边,AC AB 上的点，满足//DE BC 且AD ACλ=，（()01λ∈，），将ADE 沿直线DE 折到A DE '△的位置.在翻折过程中，下列结论不成立的是（ ）A ．在边A E '上存在点F ，使得在翻折过程中，满足//BF 平面A CD 'B ．存在102λ∈⎛⎫⎪⎝⎭,，使得在翻折过程中的某个位置，满足平面A BC '⊥平面BCDEC ．若12λ=，当二面角A DE B '--为直二面角时，||10A B '= D ．在翻折过程中，四棱锥A BCDE '-体积的最大值记为()f λ，()f λ23【答案】ABC 【分析】对于A.在边A E '上点F ，在A D '上取一点N ，使得//FN ED ，在ED 上取一点H ，使得//NH EF ，作//HG BE 交BC 于点G ，即可判断出结论.对于B ，102λ∈⎛⎫⎪⎝⎭,，在翻折过程中，点A '在底面BCDE 的射影不可能在交线BC 上，即可判断出结论. 对于C ，12λ=，当二面角A DE B '--为直二面角时，取ED 的中点M ，可得AM ⊥平面BCDE .可得22A B AM BM '=+，结合余弦定理即可得出.对于D.在翻折过程中，取平面AED ⊥平面BCDE ，四棱锥A BCDE '-体积()3133BCDE f S λλλλ=⋅⋅=-，()01λ∈，，利用导数研究函数的单调性即可得出.【详解】对于A.在边A E '上点F ，在A D '上取一点N ，使得//FN ED ，在ED 上取一点H ，使得//NH EF ，作//HG BE 交BC 于点G ，如图所示，则可得FN 平行且等于BG ，即四边形BGNF 为平行四边形， ∴//NG BE ，而GN 始终与平面ACD 相交，因此在边A E '上不存在点F ，使得在翻折过程中，满足//BF 平面A CD '，A 不正确.对于B ，102λ∈⎛⎫⎪⎝⎭,，在翻折过程中，点A '在底面BCDE 的射影不可能在交线BC 上，因此不满足平面A BC '⊥平面BCDE ，因此B 不正确. 对于C.12λ=，当二面角A DE B '--为直二面角时，取ED 的中点M ，如图所示：可得AM ⊥平面BCDE ，则A B '===≠，因此C 不正确；对于D.在翻折过程中，取平面AED ⊥平面BCDE ，四棱锥A BCDE '-体积()313BCDE f S λλλ=⋅=-，()01λ∈，，()213f λλ'=-，可得3λ=时，函数()f λ取得最大值()113f λ⎫=-=⎪⎝⎭，因此D 正确. 综上所述，不成立的为ABC. 故选：ABC. 【点睛】本题考查了利用运动的观点理解空间线面面面位置关系、四棱锥的体积计算公式、余弦定理、利用导数研究函数的单调性极值与最值，考查了推理能力空间想象能力与计算能力，属于难题.6．如果一个棱锥的底面是正方形，且顶点在底面内的射影是底面的中心，那么这样的棱锥叫正四棱锥．若一正四棱锥的体积为18，则该正四棱锥的侧面积最小时，以下结论正确的是（ ）．A ．棱的高与底边长的比为2B ．侧棱与底面所成的角为4πC D ．侧棱与底面所成的角为3π 【答案】AB 【分析】设四棱锥S ABCD -的高为h ，底面边长为a ，由21183V a h ==得254h a=，然后可得侧a =时侧面积取得最小值，此时3h =，然后求出棱锥的高与底面边长的比和SAO ∠即可选出答案. 【详解】设四棱锥S ABCD -的高为h ，底面边长为a 可得21183V a h ==，即254h a= 所以其侧面积为2222244215410842244a a a h a a a⋅⋅+=+=+令()242108f a a a =+，则()23321084f a a a⨯'=- 令()233210840f a a a⨯'=-=得32a = 当(0,32a ∈时()0f a '<，()f a 单调递减当()32,a ∈+∞时()0f a '>，()f a 单调递增所以当32a =时()f a 取得最小值，即四棱锥的侧面积最小 此时3h =所以棱锥的高与底面边长的比为22，故A 正确，C 错误 侧棱与底面所成的角为SAO ∠，由3h =，32a =可得3AO = 所以4SAO π∠=，故B 正确，D 错误故选：AB 【点睛】本题考查的知识点有空间几何体的体积和表面积、线面角及利用导数求最值，属于综合题.7．如图，在正方体ABCD ﹣A 1B 1C 1D 1中，点P 在线段B 1C 上运动，则（ ）A ．直线BD 1⊥平面A 1C 1DB ．三棱锥P ﹣A 1C 1D 的体积为定值C ．异面直线AP 与A 1D 所成角的取值范用是[45°，90°]D ．直线C 1P 与平面A 1C 1D 6 【答案】ABD【分析】在A 中，推导出A 1C 1⊥BD 1，DC 1⊥BD 1，从而直线BD 1⊥平面A 1C 1D ；在B 中，由B 1C ∥平面 A 1C 1D ，得到P 到平面A 1C 1D 的距离为定值，再由△A 1C 1D 的面积是定值，从而三棱锥P ﹣A 1C 1D 的体积为定值；在C 中，异面直线AP 与A 1D 所成角的取值范用是[60°，90°]；在D 中，以D 为原点，DA 为x 轴，DC 为y 轴，DD 1为z 轴，建立空间直角坐标系，利用向量法能求出直线C 1P 与平面A 1C 1D 6． 【详解】解：在A 中，∵A 1C 1⊥B 1D 1，A 1C 1⊥BB 1，B 1D 1∩BB 1＝B 1，∴A 1C 1⊥平面BB 1D 1，∴A 1C 1⊥BD 1，同理，DC 1⊥BD 1，∵A 1C 1∩DC 1＝C 1，∴直线BD 1⊥平面A 1C 1D ，故A 正确；在B 中，∵A 1D ∥B 1C ，A 1D ⊂平面A 1C 1D ，B 1C ⊄平面A 1C 1D ，∴B 1C ∥平面 A 1C 1D ，∵点P 在线段B 1C 上运动，∴P 到平面A 1C 1D 的距离为定值，又△A 1C 1D 的面积是定值，∴三棱锥P ﹣A 1C 1D 的体积为定值，故B 正确；在C 中，异面直线AP 与A 1D 所成角的取值范用是[60°，90°]，故C 错误；在D 中，以D 为原点，DA 为x 轴，DC 为y 轴，DD 1为z 轴，建立空间直角坐标系， 设正方体ABCD ﹣A 1B 1C 1D 1中棱长为1，P （a ，1，a ），则D （0，0，0），A 1（1，0，1），C 1（0，1，1），1DA ＝（1，0，1），1DC ＝（0，1，1），1C P ＝（a ，0，a ﹣1），设平面A 1C 1D 的法向量(),,n x y z =，则1100n DA x z n DC y z ⎧⋅=+=⎪⎨⋅=+=⎪⎩，取x ＝1，得1,1,1n ，∴直线C 1P 与平面A 1C 1D 所成角的正弦值为： 11||||||C P n C P n ⋅⋅＝22(1)3a a +-⋅＝21132()22a ⋅-+， ∴当a ＝12时，直线C 1P 与平面A 1C 1D 所成角的正弦值的最大值为63，故D 正确． 故选：ABD ．【点睛】求直线与平面所成的角的一般步骤：（1）、①找直线与平面所成的角，即通过找直线在平面上的射影来完成；②计算，要把直线与平面所成的角转化到一个三角形中求解；（2）、用空间向量坐标公式求解.8．如图所示，正方体ABCD A B C D ''''-的棱长为1，E ，F 分别是棱AA '，CC '的中点，过直线EF 的平面分别与棱BB '，DD '交于点M ，N ，以下四个命题中正确的是（ ）A ．0MN EF ⋅=B ．ME NE =C ．四边形MENF 的面积最小值与最大值之比为2:3D ．四棱锥A MENF -与多面体ABCD EMFN -体积之比为1:3【答案】ABD【分析】证明EF ⊥平面BDD B ''，进而得EF MN ⊥，即可得A 选项正确；证明四边形MENF 为菱形即可得B 选项正确；由菱形性质得四边形MENF 的面积12S MN EF =⋅，再分别讨论MN 的最大值与最小值即可；根据割补法求解体积即可.【详解】对于A 选项，如图，连接BD ，B D ''，MN ．由题易得EF BD ⊥，EF BB '⊥，BD BB B '⋂=，所以EF ⊥平面BDD B ''，又MN ⊂平面BDD B ''，所以EF MN ⊥，因此0MN EF ⋅=，故A 正确．对于B 选项，由正方体性质得：平面''//BCC B 平面''ADD A ，平面''BCC B 平面EMFN MF =，平面''ADD A 平面EMFN EN =， 所以//MF EN ，同理得//ME NF ，又EF MN ⊥，所以四边形MENF 为菱形， 因此ME NE =，故B 正确．对于C 选项，由B 易得四边形MENF 的面积12S MN EF =⋅， 所以当点M ，N 分别为BB '，DD '的中点时，四边形MENF 的面积S 最小，此时MN EF ==，即面积S 的最小值为1； 当点M ，N 分别与点B （或点B '），D （或D ）重合时，四边形MENF 的面积S 最大，此时MN =，即面积S 的最大值为2所以四边形MENF 的面积最小值与最大值之比为2C 不正确．对于D 选项，四棱锥A MENF -的体积11113346M AEF N AEF AEF V V V DB S --=+=⋅==△； 因为E ，F 分别是AA '，CC '的中点，所以BM D N '=，DN B M '=，于是被截面MENF 平分的两个多面体是完全相同的，则它们的体积也是相同的，因此多面体ABCD EMFN -的体积21122ABCD A B C D V V ''''-==正方体， 所以四棱锥A MENF -与多面体ABCD EMFN -体积之比为1:3，故D 正确． 故选：ABD ．【点睛】本题考查立体几何与向量的综合、截面面积的最值、几何体的体积，考查空间思维能力与运算求解能力，是中档题.本题解题的关键在于证明四边形MENF 为菱形，利用割补法将四棱锥A MENF -的体积转化为三棱锥M AEF - 和N AEF -的体积之和，将多面体ABCD EMFN -的体积转化为正方体的体积的一半求解.9．如图所示，在棱长为1的正方体1111ABCD A B C D -中，过对角线1BD 的一个平面交棱1AA 于点E ，交棱1CC 于点F ，得四边形1BFD E ，在以下结论中，正确的是（ ）A ．四边形1BFD E 有可能是梯形B ．四边形1BFD E 在底面ABCD 内的投影一定是正方形C ．四边形1BFDE 有可能垂直于平面11BB D DD ．四边形1BFDE 面积的最小值为62【答案】BCD【分析】四边形1BFD E 有两组对边分别平行知是一个平行四边形四边形；1BFD E 在底面ABCD 内的投影是四边形ABCD ；当与两条棱上的交点是中点时，四边形1BFD E 垂直于面11BB D D ；当E ，F 分别是两条棱的中点时，四边形1BFD E 的面积最小为62. 【详解】过1BD 作平面与正方体1111ABCD A B C D -的截面为四边形1BFD E ， 如图所示，因为平面11//ABB A 平面11DCC D ，且平面1BFD E平面11ABB A BE =. 平面1BFD E 平面1111,//DCC D D F BE D F =，因此，同理1//D E BF ，故四边形1BFD E 为平行四边形，因此A 错误；对于选项B ，四边形1BFD E 在底面ABCD 内的投影一定是正方形ABCD ，因此B 正确； 对于选项C ，当点E F 、分别为11,AA CC 的中点时，EF ⊥平面11BB D D ，又EF ⊂平面1BFD E ，则平面1BFD E ⊥平面11BB D D ，因此C 正确；对于选项D ，当F 点到线段1BD 的距离最小时，此时平行四边形1BFD E 的面积最小，此时点E F 、分别为11,AA CC 的中点，此时最小值为16232⨯⨯=，因此D 正确. 故选：BCD【点睛】关键点睛：解题的关键是理解想象出要画的平面是怎么样的平面，有哪些特殊的性质，考虑全面即可正确解题.10．半正多面体（semiregularsolid ）亦称“阿基米德多面体”，是由边数不全相同的正多边形围成的多面体，体现了数学的对称美．二十四等边体就是一种半正多面体，是由正方体切截而成的，它由八个正三角形和六个正方形构成（如图所示），若它的所有棱长都为2 ）A ．BF ⊥平面EABB ．该二十四等边体的体积为203C ．该二十四等边体外接球的表面积为8πD ．PN 与平面EBFN 2 【答案】BCD【分析】 A 用反证法判断；B 先补齐八个角成正方体，再计算体积判断；C 先找到球心与半径，再计算表面积判断；D 先找到直线与平面所成角，再求正弦值判断．【详解】解：对于A ，假设A 对，即BF ⊥平面EAB ，于是BF AB ⊥，90ABF ∠=︒，但六边形ABFPQH 为正六边形，120ABF ∠=︒，矛盾，所以A 错；对于B ，补齐八个角构成棱长为2的正方体， 则该二十四等边体的体积为3112028111323-⋅⋅⋅⋅⋅=， 所以B 对；对于C ，取正方形ACPM 对角线交点O ，即为该二十四等边体外接球的球心， 其半径为2R =248R ππ=，所以C 对；对于D ，因为PN 在平面EBFN 内射影为NS ，所以PN 与平面EBFN 所成角即为PNS ∠， 其正弦值为22PS PN =，所以D 对． 故选：BCD ．【点睛】本题考查了正方体的性质，考查了直线与平面所成角问题，考查了球的体积与表面积计算问题．。
2021-2023北京高考真题数学汇编：压轴选择(第10题)
证明：当 n = 1 时， a1 − 6 =−3 ≤ −3 ，此时不等关系 an ≤ 3 成立；
设当 n = k 时， ak − 6 ≤ −3 成立，
则
ak +1
−
6
=
1 4
( ak
−
6)3
∈
−54, −
27 4
，故
ak +1
−
6
≤
−3
成立，
由数学归纳法可得 an ≤ 3 成立.
而 an+1 − a=n
2021-2023 北京高考真题数学汇编
压轴选择（第 10 题）
一、单选题
1．（2023·北京·统考高考真题）已知数列{an} 满足 an+1=
1 4
(
an
−
6)3
+
6(n=
1, 2,3,) ，则（
）
A．当 a1 = 3时，{an} 为递减数列，且存在常数 M ≤ 0 ，使得 an > M 恒成立
B．当 a1 = 5 时，{an} 为递增数列，且存在常数 M ≤ 6 ，使得 an < M 恒成立
1 4
x3
−
9 2
x2
+
26x
−
47 (
x
≤
3)
，判断得
an+1
<
an
−1，
进而取 m = −[M ] + 4 推得 an > M 不恒成立；对于 B，证明 an 所在区间同时证得后续结论；对于 C，记
m0
log3
2 log1
(M
− 6)
+ 1
，取=m
[m0 ] +1推得 an > M 不恒成立；对于 D，构造
2021年北京市高考数学总复习：数列
a1，a6，a21依次成等比数列，可得
a62＝a1a21，即（a1+10）2＝a1（a1+40），
解得a1＝5，
则an＝5+2（n﹣1）＝2n+3；
（2） （ ），
即有前n项和为Sn （ ）
（ ） ，
数列{bn}的前n项和Sn ．
3．已知等比数列{an}的前n项和为Sn，且a1＝m，an+1＝Sn+1（n∈N*）．
（1）求{an}和{bn}的通项公式；
（2）求数列{anbn}的前n项和Tn．
【解答】解：（1）设公差为d的等差数列{bn}满足b1＝1，b2+b5＝b8，
则b1+d+b1+4d＝b1+7d，解得d ，
所以 ．
数列{an}前n项和为Sn且2a1＝a2＝2，且b2Sn+1+b5Sn﹣1＝b8Sn，
整理得 ，
6．已知正项等比数列{an}中，a1，2a2，a3+6成等差数列，且a42＝4a1a5．
（1）求数列{an}的通项公式；
（2）若Sn是数列{an}的前n项和，设bn ，求数列{bn}的前n项和Tn．
【解答】解：（1）设公比为q的正项等比数列{an}中，a1，2a2，a3+6成等差数列，且a42＝4a1a5．
＝（101+102+…+10n）+2×（1+2+…+n）﹣1×n
2 n
（10n﹣1）+n2．
2．已知数列{an}为等差数列，a7﹣a2＝10，且a1，a6，a21依次成等比数列．
（1）求数列{an}的通项公式；
北京高考数学压轴题试题集锦(含详细解析)
北京高考数学压轴题试题集锦第1讲 真题分析【例1】 （2007北京理）已知集合{}12(2)k A a a a k =，，，≥，其中(12)i a i k ∈=Z ，，，，由A 中的元素构成两个相应的集合：{}()S a b a A b A a b A =∈∈+∈，，，，{}()T a b a A b A a b A =∈∈-∈，，，．其中()a b ，是有序数对，集合S 和T 中的元素个数分别为m 和n ． 若对于任意的a A ∈，总有a A -∉，则称集合A 具有性质P ．（I ）检验集合{}0123，，，与{}123-，，是否具有性质P 并对其中具有性质P 的集合，写出相应的集合S 和T ； （II ）对任何具有性质P 的集合A ，证明：(1)2k k n -≤； （III ）判断m 和n 的大小关系，并证明你的结论．（I ）解：集合{}0123，，，不具有性质P ． 集合{}123-，，具有性质P ，其相应的集合S 和T 是{}(13)(31)S =--，，，， {}(21)23T =-()，，，．（II ）证明：首先，由A 中元素构成的有序数对()i j a a ，共有2k 个．因为0A ∉，所以()(12)i i a a T i k ∉=，，，，； 又因为当a A ∈时，a A -∉时，a A -∉，所以当()i j a a T ∈，时，()(12)j i a a T i j k ∉=，，，，，． 从而，集合T 中元素的个数最多为21(1)()22k k k k --=，即(1)2k k n -≤． （III ）解：m n =，证明如下：（1）对于()a b S ∈，，根据定义，a A ∈，b A ∈，且a b A +∈，从()a b b T +∈，．如果()a b ，与()c d ，是S 的不同元素，那么a c =与b d =中至少有一个不成立，从而a b c d +=+与b d =中也至少有一个不成立．故()a b b +，与()c d d +，也是T 的不同元素．可见，S 中元素的个数不多于T 中元素的个数，即m n ≤，（2）对于()a b T ∈，，根据定义，a A ∈，b A ∈，且a b A -∈，从而()a b b S -∈，．如果()a b ，与()c d ，是T 的不同元素，那么a c =与b d =中至少有一个不成立，从而a b c d -=-与b d =中也不至少有一个不成立，故()a b b -，与()c d d -，也是S 的不同元素．可见，T 中元素的个数不多于S 中元素的个数，即n m ≤， 由（1）（2）可知，m n =．【例2】 （2009北京文）设数列{}n a 的通项公式为(,0)n a pn q n N p *=+∈>. 数列{}n b 定义如下：对于正整数m ，m b 是使得不等式n a m ≥成立的所有n 中的最小值.（Ⅰ）若11,23p q ==-，求3b ； （Ⅰ）若2,1p q ==-，求数列{}m b 的前2m 项和公式；（Ⅰ）是否存在,p q 使得32()m b m m N *=+∈？如果存在，求,p q 的取值范围；如果不存在，请说明理由.本题主要考查数列的概念、数列的基本性质，考查运算能力、推理论证能力、分类讨论等数学思想方法．本题是数列与不等式综合的较难层次题.（Ⅰ）由题意，得1123n a n =-， 解11323n -≥，得203n ≥. Ⅰ11323n -≥成立的所有n 中的最小正整数为7，即37b =. （Ⅰ）由题意，得21n a n =-， 对于正整数m ，由n a m ≥，得12m n +≥. 根据m b 的定义可知当21m k =-时，()*m b k k N =∈； 当2m k =时，()*1m b k k N =+∈.Ⅰ()()1221321242m m m b b b b b b b b b -+++=+++++++()()1232341m m =++++++++++⎡⎤⎣⎦()()213222m m m m m m ++=+=+. （Ⅰ）假设存在p 和q 满足条件，由不等式pn q m +≥及0p >得m qn p-≥. Ⅰ32()m b m m N *=+∈,根据m b 的定义可知，对于任意的正整数m 都有3132m qm m p-+<≤+， 即()231p q p m p q --≤-<--对任意的正整数m 都成立. 当310p ->（或310p -<）时，得31p q m p +<--（或231p qm p +≤--），这与上述结论矛盾！当310p -=，即13p =时，得21033q q --≤<--，解得2133q -≤<-.（经检验符合题意） Ⅰ 存在p 和q ，使得32()m b m m N *=+∈；p 和q 的取值范围分别是13p =，2133q -≤<-. 【例3】 （2009北京理）已知数集{}()1212,,1,2n n A a a a a a a n =≤<<≥具有性质P ：对任意的(),1i j i j n ≤≤≤，i j a a 与j ia a 两数中至少有一个属于A .（Ⅰ）分别判断数集{}1,3,4与{}1,2,3,6是否具有性质P ，并说明理由； （Ⅰ）证明：11a =，且1211112nn na a a a a a a ---+++=+++； （Ⅰ）证明：当5n =时，12345,,,,a a a a a 成等比数列.本题主要考查集合、等比数列的性质，考查运算能力、推理论证能力、分类讨论等数学思想方法．本题是数列与不等式的综合题，属于较难层次题.（Ⅰ）由于34⨯与43均不属于数集{}1,3,4，Ⅰ该数集不具有性质P. 由于66123612,13,16,23,,,,,,231236⨯⨯⨯⨯都属于数集{}1,2,3,6，Ⅰ该数集具有性质P. （Ⅰ）Ⅰ{}12,,n A a a a =具有性质P ，Ⅰn n a a 与nna a 中至少有一个属于A ， 由于121n a a a ≤<<<，Ⅰn n n a a a >，故n n a a A ∉.从而1nna A a =∈，Ⅰ11a = Ⅰ121n a a a =<<<， Ⅰk n n a a a >，故()2,3,,k n a a A k n ∉=.由A 具有性质P 可知()1,2,3,,nka A k n a ∈=.又Ⅰ121n nn nn n a a a a a a a a -<<<<， Ⅰ121121,,,n nn n n n n n a a a aa a a a a a a a --====， 从而121121n nn nn n n n a a a a a a a a a a a a --++++=++++，Ⅰ1211112nn na a a a a a a ---+++=+++. （Ⅰ）由（Ⅰ）知，当5n =时，有552343,a a a a a a ==，即25243a a a a ==，Ⅰ1251a a a =<<<，Ⅰ34245a a a a a >=，Ⅰ34a a A ∉，由A 具有性质P 可知43a A a ∈. 由2243a a a =，得3423a a A a a =∈，且3321a a a <<，Ⅰ34232a aa a a ==， Ⅰ534224321a a a a a a a a a ====， 即12345,,,,a a a a a 是首项为1，公比为2a 成等比数列.【例4】 （2010北京理）已知集合12{|(,,),{0,1},1,2,,}(2)n n i S X X x x x x i n n ==∈=≥…，…对于12(,,,)n A a a a =…，12(,,,)n n B b b b S =∈…，定义A 与B 的差为 1122(||,||,||);n n A B a b a b a b -=---…A 与B 之间的距离为=1(,)||i i i d A B a b =-∑（Ⅰ）证明：,,,n n A B C S A B S ∀∈-∈有，且(,)(,)d A C B C d A B --=; （Ⅰ）证明：,,,(,),(,),(,)n A B C S d A B d A C d B C ∀∈三个数中至少有一个是偶数 (Ⅰ) 设P n S ⊆，P 中有m (m ≥2)个元素，记P 中所有两元素间距离的平均值为()P d，证明：()P d≤2(1)mnm -.证明：（I ）设12(,,...,)n A a a a =，12(,,...,)n B b b b =，12(,,...,)n C c c c =n S ∈因为i a ，{}0,1i b ∈，所以{}0,1i i a b -∈,(1,2,...,)i n = 从而1122(||,||,...,||)n n n A B a b a b a b S -=---∈ 又1(,)||||||niiiii d A C B C a c b c =--=---∑由题意知i a ，i b ，i c {}0,1∈(1,2,...,)i n =. 当0i c =时，|||||||||i i i i i i a c b c a b ---=-;当1i c =时，|||||||(1)(1)|||i i i i i i i i a c b c a b a b ---=---=- 所以1(,)||(,)niii d A C B C a b d A B =--=-=∑(II)设12(,,...,)n A a a a =，12(,,...,)n B b b b =，12(,,...,)n C c c c =n S ∈(,)d A B k =，(,)d A C l =，(,)d B C h =.记(0,0,...,0)n O S =∈，由（I ）可知(,)(,)(,)d A B d A A B A d O B A k =--=-= (,)(,)(,)d A C d A A C A d O C A l =--=-=(,)(,)d B C d B A C A h =--=所以||(1,2,...,)i i b a i n -=中1的个数为k ，||(1,2,...,)i i c a i n -=的1的个数为l 。
北京高考数学压轴题
【例1】如果存在常数a使得数列{}n a满足：若x是数列{}n a中的一项，则a x-也是数列{}n a中的一项，称数列{}n a为“兑换数列”，常数a是它的“兑换系数”．（1）若数列：1,2,4,(4)m m>是“兑换系数”为a的“兑换数列”，求m和a的值；（2）已知有穷．．等差数列{}nb的项数是00(3)n n≥，所有项之和是B，求证：数列{}n b是“兑换数列”，并用n和B表示它的“兑换系数”；（3）对于一个不少于3项，且各项皆为正整数的递增数列{}n c，是否有可能它既是等比数列，又是“兑换数列”？给出你的结论并说明理由．压轴题【例2】 已知集合121{|(,,),{0,1},1,2,,}(2)n n S X X x x x x i n n ==∈=≥…，…对于12(,,,)n A a a a =…，12(,,,)n n B b b b S =∈…，定义A 与B 的差为1122(||,||,||)n n A B a b a b a b -=---…； A 与B 之间的距离为111(,)||i d A B a b -=-∑（Ⅰ）证明：,,,n n A B C S A B S ∀∈-∈有，且(,)(,)d A C B C d A B --=；（Ⅱ）证明：,,(,)(,)(,)n A B C S d A B d A C d B C ∀∈，，，三个数中至少有一个是偶数（Ⅲ） 设n P S ⊆，P 中有(2)m m …个元素，记P 中所有两元素间距离的平均值为()d P ．【例3】 已知集合{}12(2)k A a a a k = ，，，≥，其中(12)i a i k ∈=Z ，，，，由A 中的元素构成两个相应的集合：{}()S a b a A b A a b A =∈∈+∈，，，，{}()T a b a A b A a b A =∈∈-∈，，，．其中()a b ，是有序数对，集合S 和T 中的元素个数分别为m 和n ．若对于任意的a A ∈，总有a A -∉，则称集合A 具有性质P ．（I ）检验集合{}0123，，，与{}123-，，是否具有性质P 并对其中具有性质P 的集合，写出相应的集合S 和T ； （II ）对任何具有性质P 的集合A ，证明：(1)2k k n -≤； （III ）判断m 和n 的大小关系，并证明你的结论．【例4】 设A 是由m n ⨯个实数组成的m 行n 列的数表，如果某一行（或某一列）各数之和为负数，则改变该行（或该列）中所有数的符号，称为一次“操作”．(Ⅰ) 数表A 如表1所示，若经过两次“操作”，使得到 的数表每行的各数之和与每列的各数之和均为非负实数，请写出每次“操作”后所得的数表（写出一种方法即可）；表1(Ⅱ) 数表A 如表2所示，若必须经过两次“操作”，才可使得到的数表每行的各数之和与每列的各数之和均为非负整数，求整数．．a 的所有可能值；(Ⅲ)对由m n ⨯个实数组成的m 行n 列的任意一个数表A ，能否经过有限次“操作”以后，使得到的数表每行的各数之表2和与每列的各数之和均为非负整数？请说明理由．1 2 3 7-2-1122221212a a a a a a a a ------【例5】 若12(0n n i A a a a a == 或1,1,2,,)i n = ，则称n A 为0和1的一个n 位排列．对于n A ，将排列121n n a a a a - 记为1()n R A ；将排列112n n n a a a a -- 记为2()n R A ；依此类推，直至()n n n R A A =．对于排列n A 和()i n R A (1,2,,1)i n =- ，它们对应位置数字相同的个数减去对应位置数字不同的个数，叫做n A 和()i n R A 的相关值，记作(,())i n n t A R A ．例如3110A =，则13()011R A =， 133(,())1t A R A =-．若(,())1(1,2,,1)i n n t A R A i n =-=- ，则称n A 为最佳排列． （Ⅰ）写出所有的最佳排列3A ； （Ⅱ）证明：不存在最佳排列5A ；（Ⅲ）若某个21(k A k +是正整数)为最佳排列，求排列21k A +中1的个数．【例6】 设(,),(,)A A B B A x y B x y 为平面直角坐标系上的两点，其中,,,A A B B x y x y ∈Z .令B A x x x ∆=-，B A y y y ∆=-，若x ∆+=3y ∆,且||||0x y ∆⋅∆≠，则称点B 为点A 的“相关点”，记作：()B A τ=. 已知0P 0000(,)(,)x y x y ∈ Z 为平面上一个定点，平面上点列{}i P 满足：1()i i P P τ-=，且点i P 的坐标为(,)i i x y ，其中1,2,3,...,i n =.（Ⅰ）请问：点0P 的“相关点”有几个？判断这些“相关点”是否在同一个圆上，若在同一个圆上，写出圆的方程；若不在同一个圆上，说明理由； （Ⅱ）求证：若0P 与n P 重合，n 一定为偶数；（Ⅲ）若0(1,0)P ，且100n y =，记0ni i T x ==∑，求T 的最大值.。
高考数学压轴题精选精编附详细解答试题
2021年高考数学压轴题精选精编附详细解答1、〔本小题满分是14分〕如图，点(4,0)N p -〔p >0,p 是常数〕，点T 在y 轴上，0MT NT ⋅=，MT 交x 轴于点Q ，且2TM QM =.〔Ⅰ〕当点T 在y 轴上挪动时，求动点M 的轨迹E 的方程；(4分) 〔Ⅱ〕设直线l 过轨迹E 的焦点F,且与该轨迹交于A 、B 两点，过A 、B 分别作该轨迹的对称轴的垂线，垂足分别为12,,A A 求证：OF 是1OA 和2OA 的等比中项；〔5分〕(Ⅲ) 对于该轨迹E ，能否存在一条弦CD 被直线l 垂直平分？假设存在，求出直线CD 的方程；假设不存在，试说明理由。
〔5分〕2、〔本小题满分是14分〕设函数)(x f 的定义域为R ，当0<x 时，0()1f x <<，且对任意的实数x 、R y ∈，有).()()(y f x f y x f =+ 〔Ⅰ〕求)0(f ；〔2分〕(Ⅱ)试判断函数)(x f 在(,0]-∞上是否存在最大值，假设存在，求出该最大值，假设不存在说明理由；〔5分〕〔Ⅲ〕设数列{}n a 各项都是正数，且满足1(0),a f =22111(),()(32)n n n n f a a n N f a a *++-=∈--又设1322121111,,)21(++++=+++==n n n n n an a a a a a a T b b b S b n ，试比拟S n 与 n T 的大小.〔7分〕3、〔此题满分是13分〕椭圆221:36(0)x c y t t+=>的两条准线与双曲线222:536c x y -=的两条准线所围成的四边形之面积为直线l 与双曲线2c 的右支相交于,P Q 两点(其中点P 在第一象限)，线段OP 与椭圆1c 交于点,A O 为坐标原点(如下图). 〔I 〕务实数t 的值；〔II 〕假设3OP OA =⋅，PAQ ∆的面积26tan S =-⋅∠求直线l 的方程.4、〔此题满分是14分〕数列{}n a 的前n项和nS 满足11,S =-121(),n n S S n N *++=-∈数列{}n b 的通项公式34().n b n n N *=-∈〔I 〕求数列{}n a 的通项公式；〔II 〕试比拟n a 与n b 的大小,并加以证明；〔III 〕是否存在圆心在x 轴上的圆C 及互不相等的正整数n m k 、、，使得三点(,),(,),(,)n n n m m m k k k A b a A b a A b a 落在圆C 上?说明理由.5、(本小题满分是14分)一次国际乒乓球比赛中，甲、乙两位选手在决赛中相遇，根据以往经历，单局比赛甲选手胜乙选手的概率为０．６，本场比赛采用五局三胜制，即先胜三局的选手获胜，比赛完毕．设全局比赛互相间没有影响，令ξ为本场比赛甲选手胜乙选手的局数〔不计甲负乙的局数〕，求ξ〕．6、(本小题满分是14分)数列{}n a 的前n 项和为S n *()n N ∈，点〔a n ，S n 〕在直线y =2x -3n 上．〔1〕假设数列{}的值求常数成等比数列C c a n ,+；〔5分〕〔2〕求数列}{n a 的通项公式；〔3分〕〔3〕数列{}请求出一组若存在它们可以构成等差数列中是否存在三项,?,n a 合适条件的项；假设不存在，请说明理由．〔6分〕7、〔本小题14分〕数列}{n a 的前n 项和为n S ，且满足211=a ，)2(021≥-n S S a n n n ＝＋． 〔1〕问：数列}1{nS 是否为等差数列？并证明你的结论；(5分) 〔2〕求n S 和n a ；(5分)〔3〕求证：nS S S S n 41212232221-≤+⋅⋅⋅+++ (4分)8、〔本小题满分是14分〕函数f (x )＝ln x ，g(x )＝21ax 2＋b x ，a ≠0. 〔Ⅰ〕假设b ＝2，且h (x )＝f (x )－g (x )存在单调递减区间，求a 的取值范围；(7分) 〔Ⅱ〕设函数f (x )的图象C 1与函数g (x )图象C 2交于点P 、Q ，过线段PQ 的中点作x 轴的垂线分别交C 1，C 2于点M 、N ，证明C 1在点M 处的切线与C 2在点N 处的切线不平行. (7分)9、〔本小题满分是14分〕设抛物线214C y mx =：(0)m >的准线与x 轴交于1F ，焦点为2F ；以12F F 、为焦点，离心率12e =的椭圆2C 与抛物线1C 的一个交点为P . 〔Ⅰ〕当1m =时，直线l 经过椭圆2C 的右焦点2F ，与抛物线1C 交于12A A 、，假如弦长12A A 等于三角形12PF F 的周长，求直线l 的斜率.〔Ⅱ〕求最小实数m ，使得三角形12PF F 的边长是自然数．10、〔本小题满分是14分〕〔Ⅰ〕函数：1()2()(),([0,),)n n n f x x a x a x n N -*=+-+∈+∞∈求函数()f x 的最小值;〔Ⅱ〕证明:()(0,0,)22n n na b a b a b n N *++≥>>∈；〔Ⅲ〕定理:假设123,,ka a a a 均为正数,那么有123123()n n nn n kka a a a a a a a kk++++++++≥ 成立(其中2,,)k k N k *≥∈为常数．请你构造一个函数()g x ，证明： 当1231,,,,,k k a a a a a +均为正数时，12311231()11n n nn n k k a a a a a a a a k k ++++++++++≥++．11、本小题满分是14分〕如图，在OAB ∆中，||||4OA OB ==，点P 分线段AB 所成的比3:1，以OA 、OB 所在 直线为渐近线的双曲线M 恰好经过点P ，且离心率为2．〔Ⅰ〕求双曲线M 的HY 方程；〔Ⅱ〕假设直线y kx m =+〔0k ≠，0m ≠〕与双曲线M 交于不同的两点E 、F ，且E 、F 两点都在以(0,3)Q -为圆心的同一圆上，务实数m 的取值范围．12、本小题满分是14分函数()f x 是定义在[,0)(0,]e e -上的奇函数，当(0,]x e ∈时，有()ln f x ax x =+〔其中e 为自然对数的底，a ∈R 〕．〔Ⅰ〕求函数()f x 的解析式； 〔Ⅱ〕设ln ||()||x g x x =〔[,0)(0,]x e e ∈-〕，求证：当1a =-时，1|()|()2f xg x >+； 〔Ⅲ〕试问：是否存在实数a ，使得当[,0)x e ∈-，()f x 的最小值是3？假如存在，求出实数a 的值；假如不存在，请说明理由．13、〔小题满分是14分〕锐角α、β满足sin cos()m βαβ=+〔0m >，2παβ+≠〕，令tan y β=，tan x α=。
2021年高考数学压轴题100题精选含答案
∴若其内切圆半径为 r ，则有 3
3 ，即 3 ，所以内切球的表面积为
3 .故
错误.
D：正方体 ABCD ABCD 中，点 P 在底面 ABCD（所在的平面）上运动且 MAC PAC ，
即 P 的轨迹为面 ABCD 截以 AM、AP 为母线，AC’为轴的圆锥体侧面所得曲线，如下图曲线 GPK ，
利用面面垂直的判定定理与性质定理得到 A' 到平面面 BCED 的高 A'H,并根据二面角的平面角，在直
角三角形中计算求得 A'H 的值，从而判定 A;根据异面直线所成角的定义找到∠A'DN 就是直线 A'D 与 CE 所成的角，利用余弦定理计算即可判定 B;利用勾股定理检验可以否定 C;先证明底面的外接圆 的圆心为 N,在利用外接球的球心的性质进行得到四棱锥 A'-BCED 的外接球的球心为 O,则 ON⊥平面 BCED,且 OA'=OC,经过计算求解可得半径从而判定 D. 【详解】 如图所示，作 AM⊥DE，交 DE 于 M,延长 AM 交 BC 于 N,连接 A'M,A'N. 则 A'M⊥DE,MN⊥DE, ,
B1N B1M
4 3
1
，故错误；
对于 D.同 A 选项证明方法一样可证的 GC1 //B1M ，
因为
E
为棱 CC1 上的中点， C1 为棱 B1N
GC1 =
上的中点，所以
1 2
B1M
3 2
所以
D1G=
1 2
，所以
D1G
:
GC1
1:
3
，故正确.
故选：ABD 【点睛】 求体积的常用方法： （1）直接法：对于规则的几何体，利用相关公式直接计算； （2）等体积法：选择合适的底面来求几何体体积，常用于求三棱锥的体积，即利用三棱锥的任一 个面可作为三棱锥的底面进行等体积变换； （3）割补法：首先把不规则的几何体分割成规则的几何体，然后进行体积计算；或者把不规则的 几何体补成规则的几何体，不熟悉的几何体补成熟悉的几何体，便于计算.
北京首都师范大学附属中学2021年高考数学高考数学压轴题 多选题分类精编附解析
一、函数的概念与基本初等函数多选题1．已知函数222,0()log ,0x x x f x x x ⎧--≤⎪=⎨>⎪⎩，若x 1<x 2<x 3<x 4，且f (x 1)＝f (x 2)＝f (x 3)＝f (x 4)，则下列结论正确的是（ ） A ．x 1＋x 2＝－1 B ．x 3x 4＝1 C ．1<x 4<2 D ．0<x 1x 2x 3x 4<1【答案】BCD 【分析】由解析式得到函数图象，结合函数各分段的性质有122x x +=-，341x x =，341122x x <<<<，即可知正确选项. 【详解】由()f x 函数解析式可得图象如下：∴由图知：122x x +=-，121x -<<-，而当1y =时，有2|log |1x =，即12x =或2， ∴341122x x <<<<，而34()()f x f x =知2324|log ||log |x x =：2324log log 0x x +=， ∴341x x =，21234121(1)1(0,1)x x x x x x x ==-++∈.故选：BCD 【点睛】关键点点睛：利用分段函数的性质确定函数图象，由二次函数、对数运算性质确定1234,,,x x x x 的范围及关系.2．已知函数()()()22224x x f x x x m m ee --+=-+-+（e 为自然对数的底数）有唯一零点，则m 的值可以为（ ） A ．1 B ．1-C ．2D ．2-【答案】BC【分析】由已知，换元令2t x =-，可得()()f t f t -=，从而f t 为偶函数，()f x 图象关于2x =对称，结合函数图象的对称性分析可得结论. 【详解】∵22222222()4()()(2)4()()x x x x f x x x m m e e x m m e e --+--+=-+-+=--+-+， 令2t x =-，则22()4()()ttf t t m m e e -=-+-+，定义域为R ，22()()4()()()t t f t t m m e e f t --=--+-+=，故函数()f t 为偶函数，所以函数()f x 的图象关于2x =对称， 要使得函数()f x 有唯一零点，则(2)0f =， 即2482()0m m -+-=，解得1m =-或2 ①当1m =-时，2()42()t t f t t e e -=-++ 由基本不等式有2t t e e -+≥，当且仅当0t =时取得2()4t t e e -∴+≥故2()42()0ttf t t e e -=-++≥，当且仅当0t =取等号 故此时()f x 有唯一零点2x =②当2m =时，2()42()t t f t t e e -=-++，同理满足题意. 故选：BC ． 【点睛】方法点睛：①函数轴对称：如果一个函数的图像沿一条直线对折，直线两侧的图像能够完全重合，则称该函数具备对称性中的轴对称，该直线称为该函数的对称轴.②()y f x =的图象关于直线x a =对称 ()()f a x f a x ⇔-=+()()2f x f a x ⇔-=+3．已知函数()1y f x =-的图象关于1x =对称，且对(),y f x x R =∈，当12,(,0]x x ∈-∞时，()()21210f x f x x x -<-成立，若()()2221f ax f x <+对任意的x ∈R 恒成立，则a 的可能取值为（ ）A ．B ．1-C ．1 D【答案】BC 【分析】由已知得函数()f x 是偶函数，在[0,)+∞上是单调增函数，将问题转化为2|2||21|ax x <+对任意的x ∈R 恒成立，由基本不等式可求得范围得选项． 【详解】因为函数()1y f x =-的图象关于直线1x =对称，所以函数()y f x =的图象关于直线0x =（即y 轴）对称，所以函数()f x 是偶函数.又12,(,0]x x ∈-∞时，()()21210f x f x x x -<-成立，所以函数()f x 在[0,)+∞上是单调增函数.且()()2221f ax f x <+对任意的x ∈R 恒成立，所以2|2||21|ax x <+对任意的x ∈R 恒成立，当0x =时，01<恒成立，当0x ≠时，2|21|11|||||||||2|22x a x x x x x+<=+=+，又因为1||||2x x +=≥||2x =时，等号成立，所以||a <，因此a <<，故选：BC. 【点睛】方法点睛：不等式恒成立问题常见方法：① 分离参数()a f x ≥恒成立(()max a f x ≥即可)或()a f x ≤恒成立（()min a f x ≤即可）；② 数形结合(()y f x = 图象在()y g x = 上方即可)；③ 讨论最值()min 0f x ≥或()max 0f x ≤恒成立.4．函数()()1xf x x R x=∈+，以下四个结论正确的是（ ） A ．()f x 的值域是()1,1- B ．对任意x ∈R ，都有()()12120f x f x x x ->-C ．若规定()()()()()11,n n f x f x f x f f x +==，则对任意的(),1n xn N f x n x*∈=+ D ．对任意的[]1,1x ∈-，若函数()2122f x t at ≤-+恒成立，则当[]1,1a ∈-时，2t ≤-或2t ≥【答案】ABC 【分析】由函数解析式可得函数图象即可知其值域、单调性；根据C 中的描述结合数学归纳法可推得结论成立；由函数不等式恒成立，利用变换主元法、一元二次不等式的解法即可求参数范围. 【详解】由函数解析式可得11,01()11,01x x f x x x⎧-≥⎪⎪+=⎨⎪-<⎪-⎩，有如下函数图象：∴()f x 的值域是()1,1-，且单调递增即()()12120f x f x x x ->-(利用单调性定义结合奇偶性也可说明)，即有AB 正确； 对于C ，有()11x f x x =+，若()1,1(1)n x n N f x n x*-∈=+-， ∴当2n ≥时，11(1)||()(())1||1||1(1)||n n xx n x f x f f x x n x n x -+-===+++-，故有(),1n xn N f x n x*∈=+.正确. 对于D ，[]1,1x ∈-上max 1()(1)2f x f ==，若函数()2122f x t at ≤-+恒成立，即有211222t at -+≥，220t at -≥恒成立，令2()2h a at t =-+，即[]1,1a ∈-上()0h a ≥， ∴0t >时，2(1)20h t t =-+≥，有2t ≥或0t ≤（舍去）；0t =时，()0h a 故恒成立；0t <时，2(1)20h t t -=+≥，有2t ≤-或0t ≥（舍去）；综上，有2t ≥或0t =或2t ≤-；错误. 故选：ABC 【点睛】 方法点睛：1、对于简单的分式型函数式画出函数图象草图判断其值域、单调性.2、数学归纳法：当1n =结论成立，若1n -时结论也成立，证明n 时结论成立即可.3、利用函数不等式恒成立，综合变换主元法、一次函数性质、一元二次不等式解法求参数范围.5．下列结论正确的是（ ）A ．函数()y f x =的定义域为[]1,3，则函数()21y f x =+的定义域为[]0,1B ．函数()f x 的值域为[]1,2，则函数()1f x +的值域为[]2,3C ．若函数24y x ax =-++有两个零点，一个大于2，另一个小于-1，则a 的取值范围是()0,3D ．已知函数()23,f x x x x R =+∈，若方程()10f x a x --=恰有4个互异的实数根，则实数a 的取值范围为()()0,19,⋃+∞ 【答案】ACD 【分析】根据抽象函数定义域及代换的方法可求函数的定义域，判断A ，利用函数图象的平移可判断函数值域的变换情况，判断B ，利用数形结合及零点的分布求解判断C ，作出函数()23f x x x =+与1y a x =-的图象，数形结合即可判断D.【详解】对于A, ()y f x =的定义域为[]1,3，则由1213x ≤+≤可得()21y f x =+定义域为[]0,1，故正确；对于B ，将函数()f x 的图象向左平移一个单位可得函数()1f x +的图象，故其值域相同，故错误；对于C, 函数2()4y g x x ax ==-++有两个零点，一个大于2，另一个小于-1只需(2)0(1)0g g >⎧⎨->⎩，解得0<<3a ，故正确； 对于D, 作出函数()23f x x x =+与1y a x =-的图象，如图，由图可以看出，0a ≤时，不可能有4个交点，找到直线与抛物线相切的特殊位置1a =或9a =，观察图象可知，当01a <<有4个交点，当9a <时，两条射线分别有2个交点，综上知方程()10f x a x --=恰有4个互异的实数根时，()()0,19,a ∈+∞正确.故选：ACD关键点点睛：对于方程实根问题，可转化为函数图象交点问题，本题中，()23f x x x=+图象确定，而1y a x =-是过(1,0)关于1x =对称的两条射线，参数a 确定两射线张角的大小，首先结合图形找到关键位置，即1a =时左边射线与抛物线部分相切，9a =时右边射线与抛物线相切，然后观察图象即可得出结论.6．设[]x 表示不超过x 的最大整数，如：[]1.21=，[]1.22-=-，[]y x =又称为取整函数，在现实生活中有着广泛的应用，诸如停车收费，出租车收费等均按“取整函数”进行计费，以下关于“取整函数”的描述，正确的是（ ） A ．x R ∀∈，[][]22x x =B ．,x y R ∀∈，若[][]x y =，则1x y ->-C ．x R ∀∈，[][]122x x x ⎡⎤++=⎢⎥⎣⎦D ．不等式[][]2230x x --≥的解集为{|0x x <或}2x ≥ 【答案】BCD 【分析】通过反例可得A 错误，根据取整函数的定义可证明BC 成立，求出不等式2230t t --≥的解后可得不等式[][]2230x x --≥的解集，从而可判断D 正确与否. 【详解】对于A ， 1.5x =-，则[][][]()233,2224x x =-=⨯--==-，故[][]22x x ≠，故A 不成立.对于B ，[][]x y m ==，则1,1m x m m y m ≤<+≤<+， 故1m y m --<-≤-，所以1x y ->-，故B 成立. 对于C ，设x m r =+，其中[),0,1m Z r ∈∈， 则[]11222x x m r ⎡⎤⎡⎤++=++⎢⎥⎢⎥⎣⎦⎣⎦，[][]222x m r =+， 若102r ≤<，则102r ⎡⎤+=⎢⎥⎣⎦，[]20r =，故[][]122x x x ⎡⎤++=⎢⎥⎣⎦； 若112r <<，则112r ⎡⎤+=⎢⎥⎣⎦，[]21r =，故[][]122x x x ⎡⎤++=⎢⎥⎣⎦，故C 成立. 对于D ，由不等式[][]2230x x --≥可得[]1x ≤-或[]32x ≥， 故0x <或2x ≥，故D 正确. 故选：BCD本题考查在新定义背景下恒等式的证明与不等式的解法，注意把等式的证明归结为整数部分和小数部分的关系，本题属于较难题.7．已知函数21,01()(1)1,1x x f x f x x ⎧-≤<=⎨-+≥⎩，方程()0f x x -=在区间0,2n⎡⎤⎣⎦(*n N ∈)上的所有根的和为n b ，则（ ） A ．()20202019f = B ．()20202020f = C ．21122n n n b --=+D ．(1)2n n n b +=【答案】BC 【分析】先推导出()f x 在[)()*,1n n n N+∈上的解析式，然后画出()f x 与y x =的图象，得出()f x x =时，所有交点的横坐标，然后得出n b .【详解】因为当[)0,1x ∈时，()21xf x =-，所以当[)1,2x ∈时，[)10,1x -∈，则()1121x f x --=-，故()()11112112x x f x f x --=-+=-+=，即[)10,1x -∈时，[)10,1x -∈，()12x f x -= 同理当[)2,3x ∈时，[)11,2x -∈，()()21121x f x f x -=-+=+；当[)3,4x ∈时，[)12,3x -∈，则()()31122x f x f x -=-+=+；………故当[),1x n n ∈+时，()()21x nf x n -=+-，当21,2nnx ⎡⎤∈-⎣⎦时，()()()21222n x n f x --=+-.所以()20202020f =，故B 正确；作出()f x 与y x =的图象如图所示，则当()0f x x -=且0,2n⎡⎤⎣⎦时，x 的值分别为：0,1,2,3,4,5,6,,2n则()()121122101222221222n n n n n n n n b ---+=+++++==+=+，故C 正确.故选：BC.【点睛】本题考查函数的零点综合问题，难度较大，推出原函数在每一段上的解析式并找到其规律是关键.8．设函数g (x )=sinωx (ω＞0)向左平移5πω个单位长度得到函数f (x )，已知f (x )在[0，2π]上有且只有5个零点，则下列结论正确的是（ ）A ．f (x )的图象关于直线2x π=对称B ．f (x )在(0，2π)上有且只有3个极大值点，f (x )在(0，2π)上有且只有2个极小值点C ．f (x )在(0,)10π上单调递增 D ．ω的取值范围是[1229,510) 【答案】CD 【分析】利用正弦函数的对称轴可知，A 不正确；由图可知()f x 在(0,2)π上还可能有3个极小值点，B 不正确；由2A B x x π≤<解得的结果可知，D 正确；根据()f x 在3(0,)10πω上递增，且31010ππω<，可知C 正确. 【详解】依题意得()()5f x g x πω=+sin[()]5x πωω=+sin()5x πω=+， 2T πω=，如图：对于A ，令52x k ππωπ+=+，k Z ∈，得310k x ππωω=+，k Z ∈，所以()f x 的图象关于直线310k x ππωω=+(k Z ∈)对称，故A 不正确； 对于B ，根据图象可知，2A B x x π≤<，()f x 在(0,2)π有3个极大值点，()f x 在(0,2)π有2个或3个极小值点，故B 不正确， 对于D ，因为5522452525A x T ππππωωωω=-+=-+⨯=，22933555B x T ππππωωωω=-+=-+⨯=，所以2429255πππωω≤<，解得1229510ω≤<，所以D 正确；对于C ，因为1123545410T ππππωωωω-+=-+⨯=，由图可知()f x 在3(0,)10πω上递增，因为29310ω<<，所以33(1)0101010πππωω-=-<，所以()f x 在(0,)10π上单调递增，故C 正确；故选：CD. 【点睛】本题考查了三角函数的相位变换，考查了正弦函数的对称轴和单调性和周期性，考查了极值点的概念，考查了函数的零点，考查了数形结合思想，属于中档题.9．已知直线2y x =-+分别与函数x y e =和ln y x =的图象交于点()()1122,,,A x y B x y ，则下列结论正确的是( ) A ．122x x +=B ．122x x e e e +>C ．1221ln ln 0x x x x +<D ．122x x >【答案】ABC 【分析】根据互为反函数的性质可得()()1122,,,A x y B x y 的中点坐标为()1,1，从而可判断A ；利用基本不等式可判断B 、D ；利用零点存在性定理以及对数的运算性质可判断C. 【详解】函数xy e =与ln y x =互为反函数， 则xy e =与ln y x =的图象关于y x =对称，将2y x =-+与y x =联立，则1,1x y ==，由直线2y x =-+分别与函数xy e =和ln y x =的图象交于点()()1122,,,A x y B x y ，作出函数图像：则()()1122,,,A x y B x y 的中点坐标为()1,1， 对于A ，由1212x x +=，解得122x x +=，故A 正确； 对于B ，12121222222x x x x x x e e e e e e e +≥=+⋅==， 因为12x x ≠，即等号不成立，所以122x x e e e +>，故B 正确；对于C ，将2y x =-+与xy e =联立可得2x x e -+=，即20x e x +-=，设()2xf x e x =+-，且函数为单调递增函数，()010210f =+-=-<，112211320222f e e ⎛⎫=+-=-> ⎪⎝⎭，故函数的零点在10,2⎛⎫⎪⎝⎭上，即1102x <<，由122x x +=，则212x <<，122112211ln ln ln lnx x x x x x x x +=- ()1222122ln ln ln 0x x x x x x x <-=-<，故C 正确；对于D ，由12122x x x x +≥，解得121x x ≤， 由于12x x ≠，则121x x <，故D 错误； 故选：ABC 【点睛】本题考查了互为反函数的性质、基本不等式的应用、零点存在性定理以及对数的运算性质，考查了数形结合的思想，属于难题.10．狄利克雷是德国著名数学家，是最早倡导严格化方法的数学家之一，狄利克雷函数()1,0,x Q f x x Q∈⎧=⎨∉⎩（Q 是有理数集）的出现表示数学家对数学的理解开始了深刻的变化，从研究“算”到研究更抽象的“概念、性质、结构”．关于()f x 的性质，下列说法正确的是（ ）A ．函数()f x 是偶函数B ．函数()f x 是周期函数C ．对任意的1x R ∈，2x ∈Q ，都有()()121f x x f x +=D ．对任意的1x R ∈，2x ∈Q ，都有()()121f x x f x ⋅= 【答案】ABC 【分析】利用函数奇偶性的定义可判断A 选项的正误；验证()()1f x f x +=，可判断B 选项的正误；分1x Q ∈、1x Q ∉两种情况讨论，结合函数()f x 的定义可判断C 选项的正误；取20x =，1x Q ∉可判断D 选项的正误.【详解】对于A 选项，任取x Q ∈，则x Q -∈，()()1f x f x ==-； 任取x Q ∉，则x Q -∉，()()0f x f x ==-.所以，对任意的x ∈R ，()()f x f x -=，即函数()f x 为偶函数，A 选项正确； 对于B 选项，任取x Q ∈，则1x Q +∈，则()()11f x f x +==； 任取x Q ∉，则1x Q +∉，则()()10f x f x +==.所以，对任意的x ∈R ，()()1f x f x +=，即函数()f x 为周期函数，B 选项正确； 对于C 选项，对任意1x Q ∈，2x ∈Q ，则12x Q x +∈，()()1211f x x f x +==； 对任意的1x Q ∉，2x ∈Q ，则12x x Q +∉，()()1210f x x f x +==. 综上，对任意的1x R ∈，2x ∈Q ，都有()()121f x x f x +=，C 选项正确； 对于D 选项，取20x =，若1x Q ∉，则()()()12101f x x f f x ⋅==≠，D 选项错误. 故选：ABC. 【点睛】关键点点睛：本题解题的关键在于根据已知函数的定义依次讨论各选项，分自变量为无理数和有理数两种情况讨论，对于D 选项，可取1x Q ∉，20x =验证.二、导数及其应用多选题11．对于定义城为R 的函数()f x ，若满足：①(0)0f =；②当x ∈R ，且0x ≠时，都有()0xf x '>；③当120x x <<且12||||x x <时，都有12()()f x f x <，则称()f x 为“偏对称函数”.下列函数是“偏对称函数”的是（ ）A ．()321f x x x =-+B ．()21xf x e x =--C ．()3ln 1,0()2,x x f x x x ⎧-+≤=⎨>⎩D ．4()sin f x x x =【答案】BC 【分析】运用新定义，分别讨论四个函数是否满足三个条件，结合奇偶性和单调性，以及对称性，即可得到所求结论． 【详解】解：经验证，1()f x ，2()f x ，3()f x ，4()f x 都满足条件①；0()0()0x xf x f x >⎧'>⇔⎨'>⎩，或0()0x f x <⎧⎨'<⎩；当120x x <<且12||||x x <时，等价于21120x x x x -<<<-<，即条件②等价于函数()f x 在区间(,0)-∞上单调递减，在区间(0,)+∞上单调递增； A 中，()321f x x x =-+，()2132f x x x '=-+，则当0x ≠时，由()()321232230x x x x f x x =-+=-≤'，得23x ≥，不符合条件②，故1()f x 不是“偏对称函数”；B 中，()21xf x e x =--，()21xf x e '=-，当0x >时，e 1x >，()20f x '>，当0x <时，01x e <<，()20f x '<，则当0x ≠时，都有()20xf x '>，符合条件②， ∴函数()21xf x e x =--在(),0-∞上单调递减，在()0,∞+上单调递增，由2()f x 的单调性知，当21120x x x x -<<<-<时，()2122()f x f x <-， ∴22212222222()()()()2x x f x f x f x f x e e x --<--=-++，令()2x x F x e e x -=-++，0x >，()220x x F x e e -'=--+≤-=， 当且仅当x x e e -=即0x =时，“=”成立，∴()F x 在[0，)+∞上是减函数，∴2()(0)0F x F <=，即2122()()f x f x <，符合条件③， 故2()f x 是“偏对称函数”；C 中，由函数()3ln 1,0()2,0x x f x x x ⎧-+≤=⎨>⎩，当0x <时，31()01f x x =<-'，当0x >时，3()20f x '=>，符合条件②，∴函数3()f x 在(),0-∞上单调递减，在()0,∞+上单调递增， 有单调性知，当21120x x x x -<<<-<时，()3132()f x f x <-， 设()ln(1)2F x x x =+-，0x >，则1()201F x x '=-<+，()F x 在(0,)+∞上是减函数，可得()(0)0F x F <=，∴1222()()()()f x f x f x f x -<--()()222ln 1()0F x x f x =+-=<， 即12()()f x f x <，符合条件③，故3()f x 是“偏对称函数”；D 中，4()sin f x x x =，则()44()sin ()f x x x f x -=--=，则4()f x 是偶函数，而4()sin cos f x x x x '=+ ()x ϕ=+（tan x ϕ=），则根据三角函数的性质可知，当0x >时，4()f x '的符号有正有负，不符合条件②，故4()f x 不是“偏对称函数”； 故选：BC ． 【点睛】本题主要考查在新定义下利用导数研究函数的单调性与最值，考查计算能力，考查转化与划归思想，属于难题．12．已知函数()xf x e =，()1ln22x g x =+的图象与直线y m =分别交于A 、B 两点，则（ ）A ．AB 的最小值为2ln2+B ．m ∃使得曲线()f x 在A 处的切线平行于曲线()g x 在B 处的切线C ．函数()()f x g x m -+至少存在一个零点D ．m ∃使得曲线()f x 在点A 处的切线也是曲线()g x 的切线 【答案】ABD 【分析】求出A 、B 两点的坐标，得出AB 关于m 的函数表达式，利用导数求出AB 的最小值，即可判断出A 选项的正误；解方程()12ln 2m f m g e -⎛⎫''= ⎪⎝⎭，可判断出B 选项的正误；利用导数判断函数()()y f x g x m =-+的单调性，结合极值的符号可判断出C 选项的正误；设切线与曲线()y g x =相切于点()(),C n g n ，求出两切线的方程，得出方程组，判断方程组是否有公共解，即可判断出D 选项的正误.进而得出结论. 【详解】令()xf x e m ==，得ln x m =，令()1ln22x g x m =+=，得122m x e -=， 则点()ln ,A m m 、122,m B e m -⎛⎫ ⎪⎝⎭，如下图所示：由图象可知，122ln m AB e m -=-，其中0m >，令()122ln m h m em -=-，则()1212m h m em-'=-，则函数()y h m '=单调递增，且102h ⎛⎫'= ⎪⎝⎭，当102m <<时，0h m，当12m >时，0h m.所以，函数()122ln m h m e m -=-在10,2⎛⎫ ⎪⎝⎭上单调递减，在1,2⎛⎫+∞⎪⎝⎭上单调递增， 所以，min 112ln 2ln 222AB h ⎛⎫==-=+⎪⎝⎭，A 选项正确； ()x f x e =，()1ln 22x g x =+，则()x f x e '=，()1g x x'=，曲线()y f x =在点A 处的切线斜率为()ln f m m '=，曲线()y g x =在点B 处的切线斜率为1212122m m g e e --⎛⎫'= ⎪⎝⎭，令()12ln 2m f m g e -⎛⎫''= ⎪⎝⎭，即1212m m e -=，即1221m me -=， 则12m =满足方程1221m me -=，所以，m ∃使得曲线()y f x =在A 处的切线平行于曲线()y g x =在B 处的切线，B 选项正确；构造函数()()()1ln22xx F x f x g x m e m =-+=-+-，可得()1x F x e x'=-， 函数()1xF x e x '=-在()0,∞+上为增函数，由于120F e e ⎛⎫'=< ⎪⎝⎭，()110F e -'=>，则存在1,12t ⎛⎫∈⎪⎝⎭，使得()10t F t e t '=-=，可得ln t t =-，当0x t <<时，()0F x '<；当x t >时，()0F x '>.()()min 1111ln ln ln 2ln 22222t t t F x F t e m e t m t m t ∴==-+-=-++-=+++-13ln 2ln 2022m m >+-=++>，所以，函数()()()F x f x g x m =-+没有零点，C 选项错误；设曲线()y f x =在点A 处的切线与曲线()y g x =相切于点()(),C n g n ， 则曲线()y f x =在点A 处的切线方程为()ln ln my m ex m -=-，即()1ln y mx m m =+-，同理可得曲线()y g x =在点C 处的切线方程为11ln 22n y x n =+-， 所以，()111ln ln 22m nn m m ⎧=⎪⎪⎨⎪-=-⎪⎩，消去n 得()11ln ln 202m m m --++=，令()()11ln ln 22G x x x x =--++，则()111ln ln x G x x x x x-'=--=-， 函数()y G x '=在()0,∞+上为减函数，()110G '=>，()12ln 202G '=-<，则存在()1,2s ∈，使得()1ln 0G s s s'=-=，且1s s e =. 当0x s <<时，()0G x '>，当x s >时，()0G x '<.所以，函数()y G x =在()2,+∞上为减函数，()5202G =>，()17820ln 202G =-<， 由零点存在定理知，函数()y G x =在()2,+∞上有零点， 即方程()11ln ln 202m m m --++=有解. 所以，m ∃使得曲线()y f x =在点A 处的切线也是曲线()y g x =的切线. 故选：ABD. 【点睛】本题考查导数的综合应用，涉及函数的最值、零点以及切线问题，计算量较大，属于难题.13．对于函数2ln ()xf x x =，下列说法正确的有（ ）A ．()f x在x =12eB ．()f x 有两个不同的零点 C．(2)f f f <<D ．若21()f x k x >-在(0,)+∞上有解，则2e k <【答案】ACD 【分析】利用导数求出函数的单调区间，进一步求出函数的极值可判断A ；利用函数的单调性和函数值的范围判断B ；利用函数的单调性比较出函数值的大小关系判断C ；利用不等式有解问题的应用判断D ． 【详解】函数2ln ()x f x x =，所以2431ln 212ln ()(0)x x xx x f x x x x ⨯-⨯-'==>， 令()0f x '=，即2ln 1x =，解得x =当0x <<()0f x '>，故()f x在上为单调递增函数．当x >()0f x '<，故()f x在)+∞上为单调递减函数．所以()f x在x =12f e=，故A 正确；当0x <<()0f x '>，()f x在上为单调递增函数，因为()10f =，所以函数()f x在上有唯一零点，当x ≥2ln ()0xf x x=>恒成立，即函数()f x在)+∞上没有零点， 综上，()f x 有唯一零点，故B 错误．由于当x >()0f x '<，()f x在)+∞上为单调递减函数，因为2>>>(2)f f f <<，故C 正确；由于21()f x k x>-在(0,)+∞上有解，故221ln 1()x k f x x x +<+=有解， 所以2ln 1()max x k x +<，设2ln 1()x g x x +=，则32ln 1()x g x x --'=，令()0g x '=，解得x =当x >()0f x '<，故()f x在)+∞上为单调递减函数．当0x <<时，()0f x '>，故()f x在上为单调递增函数．所以()22max e e g x g e ==-=． 故2ek <，故D 正确． 故选：ACD ． 【点睛】方法点睛：本题通过对多个命题真假的判断，综合考查导数的应用，这种题型综合性较强，也是高考的命题热点，同学们往往因为某一处知识点掌握不好而导致“全盘皆输”，因此做这类题目更要细心、多读题，尽量挖掘出题目中的隐含条件，另外，要注意从简单的自己已经掌握的知识点入手，然后集中精力突破较难的命题.14．对于定义域为R 的函数()f x ，()'f x 为()f x 的导函数，若同时满足：①()00f =；②当x ∈R 且0x ≠时，都有()0xf x '>；③当120x x <<且12x x =时，都有()()12f x f x <，则称()f x 为“偏对称函数”.下列函数是“偏对称函数”的是（ ）A ．21()xx f x ee x =--B ．2()1xf x e x =+-C ．31,0(),0x e x f x x x ⎧-≥=⎨-<⎩D ．42,0()ln(1),0x x f x x x >⎧=⎨-≤⎩【答案】ACD 【分析】结合“偏对称函数”的性质，利用导数的方法，分别讨论四个函数是否满足三个条件，即可得到所求结论． 【详解】条件①()00f =；由选项可得：001(0)00f e e =--=，02(0)010f e =+-=，03(0)10f e =-=，4()ln(10)0f x =-=，即ABCD 都符合；条件②0()0()0x xf x f x >⎧'>⇔⎨'>⎩，或0()0x f x <⎧⎨'<⎩；即条件②等价于函数()f x 在区间(,0)-∞上单调递减，在区间(0,)+∞上单调递增； 对于21()xx f x ee x =--，则()()21()11212x x x xf x e e e e =-+-=-'，由0x >可得，()()120(1)1x xf x e e '-=+>，即函数1()f x 单调递增；由0x <可得，()()120(1)1xxf x ee '-=+<，即函数1()f x 单调递减；满足条件②；对于2()1xf x e x =+-，则2()10x f x e =+>'显然恒成立，所以2()1xf x e x =+-在定义域上单调递增，不满足条件②；对于31,0(),0x e x f x x x ⎧-≥=⎨-<⎩，当0x <时，3()f x x =-显然单调递减；当0x ≥时，3()1x f x e =-显然单调递增；满足条件②；对于42,0()ln(1),0x x f x x x >⎧=⎨-≤⎩，当0x ≤时，4()ln(1)f x x =-显然单调递减；当0x >时，4()2f x x =显然单调递增，满足条件②； 因此ACD 满足条件②；条件③当120x x <<且12x x =时，12x x -=，都有()()12f x f x <，即()()()()21220f x f x f x f x -=-->，对于21()xx f x ee x =--，()()212122211211x x x x f x f x e e e e x x -=-+--+()()()()22222222222222x x x x x x x x x e e e e e e e x e ----=----=-+-，因为222x x e e -+≥=，当且仅当22x x e e -=，即20x =时，等号成立， 又20x >，所以222x x e e -+>， 则()()()()2222122211222xx x x f x f x e ee e xx ----=--->令()xxg x e ex -=--，0x >，所以()1110x x e e g x -'=+->=>在0x >上显然恒成立， 因此()xxg x e ex -=--在0x >上单调递增，所以()()00g x g >=，即()()()222121120xx f x f x e ex -->-->，所以()()1211f x f x >满足条件③；对于31,0(),0x e x f x x x ⎧-≥=⎨-<⎩，()()2232311211x xf x f x e x x e -=--=-+，令()1xh x e x =--，0x >，则()10xh x e '=->在0x >上显然恒成立，所以()()00h x h >=，则()()23231210xf x f x e x --=>-，即()()3231f x f x >满足条件③；对于42,0()ln(1),0x x f x x x >⎧=⎨-≤⎩，()()()()212122442ln 12ln 1f x f x x x x x -=--=-+，令()()2ln 1u x x x =-+，0x >， 则()1221101u x x'=->-=>+在0x >上显然恒成立，所以()()00u x u >=， 则()()()1422422ln 10f x f x x x -=-+>，即()()1442f x f x >满足条件③； 综上，ACD 选项是“偏对称函数”，故选：ACD. 【点睛】 思路点睛：求解此类函数新定义问题时，需要结合函数新定义的概念及性质，结合函数基本性质，利用导数的方法，通过研究函数单调性，值域等，逐项判断，即可求解.（有时也需要构造新的函数，进行求解.）15．定义在(0,)+∞上的函数()f x 的导函数为()'f x ，且()()f x f x x'<，则对任意1x 、2(0,)x ∈+∞，其中12x x ≠，则下列不等式中一定成立的有（ ）A ．()()()1212f x x f x f x +<+B ．()()()()21121212x xf x f x f x f x x x +<+ C ．()1122(1)x x f f <D ．()()()1212f x x f x f x <【答案】ABC 【分析】构造()()f x g x x=，由()()f x f x x '<有()0g x '<，即()g x 在(0,)+∞上单调递减，根据各选项的不等式，结合()g x 的单调性即可判断正误.【详解】 由()()f x f x x '<知：()()0xf x f x x'-<， 令()()f x g x x =，则()()()20xf x f x g x x '-='<， ∴()g x 在(0,)+∞上单调递减，即122112121212()()()()0()g x g x x f x x f x x x x x x x --=<--当120x x ->时，2112()()x f x x f x <；当120x x -<时，2112()()x f x x f x >； A ：121()()g x x g x +<，122()()g x x g x +<有112112()()x f x x f x x x +<+，212212()()x f x x f x x x +<+，所以()()()1212f x x f x f x +<+； B:由上得21121212()()()()x f x x x x f x x x -<-成立，整理有()()()()21121212x xf x f x f x f x x x +<+； C ：由121x >，所以111(2)(1)(2)(1)21x x x f f g g =<=，整理得()1122(1)x x f f <； D ：令121=x x 且121x x >>时，211x x =，12111()()()()g x g x f x f x =，12()(1)(1)g x x g f ==，有121()()g x x g x >，122()()g x x g x <，所以无法确定1212(),()()g x x g x g x 的大小. 故选：ABC 【点睛】思路点睛：由()()f x f x x '<形式得到()()0xf x f x x'-<， 1、构造函数：()()f x g x x =，即()()()xf x f x g x x'-'=. 2、确定单调性：由已知()0g x '<，即可知()g x 在(0,)+∞上单调递减.3、结合()g x 单调性，转化变形选项中的函数不等式，证明是否成立.16．定义在R 上的函数()f x ，若存在函数()g x ax b =+（a ，b 为常数），使得()()f x g x ≥对一切实数x 都成立，则称()g x 为函数()f x 的一个承托函数，下列命题中正确的是（ ）A ．函数()2g x =-是函数ln ,0()1,0x x f x x >⎧=⎨⎩的一个承托函数B ．函数()1g x x =-是函数()sin f x x x =+的一个承托函数C ．若函数()g x ax = 是函数()x f x e =的一个承托函数，则a 的取值范围是[0,]eD ．值域是R 的函数()f x 不存在承托函数 【答案】BC 【分析】由承托函数的定义依次判断即可. 【详解】解：对A ，∵当0x >时，()ln (,)f x x =∈-∞+∞， ∴()()2f x g x ≥=-对一切实数x 不一定都成立，故A 错误；对B ，令()()()t x f x g x =-，则()sin (1)sin 10t x x x x x =+--=+≥恒成立， ∴函数()1g x x =-是函数()sin f x x x =+的一个承托函数，故B 正确； 对C ，令()xh x e ax =-，则()xh x e a '=-， 若0a =，由题意知，结论成立， 若0a >，令()0h x '=，得ln x a =，∴函数()h x 在(,ln )a -∞上为减函数，在(ln ,)a +∞上为增函数， ∴当ln x a =时，函数()h x 取得极小值，也是最小值，为ln a a a -， ∵()g x ax =是函数()x f x e =的一个承托函数， ∴ln 0a a a -≥， 即ln 1a ≤， ∴0a e <≤，若0a <，当x →-∞时，()h x →-∞，故不成立，综上，当0a e 时，函数()g x ax =是函数()x f x e =的一个承托函数，故C 正确； 对D ，不妨令()2,()21f x x g x x ==-，则()()10f x g x -=≥恒成立， 故()21g x x =-是()2f x x =的一个承托函数，故D 错误. 故选：BC . 【点睛】方法点睛：以函数为载体的新定义问题，是高考命题创新型试题的一个热点，常见的命题形式有新概念、新法则、新运算等，这类试题中函数只是基本的依托，考查的是考生创造性解决问题的能力．17．设函数()()1x af x a x a =->的定义域为()0,∞+，已知()f x 有且只有一个零点，下列结论正确的有（ ） A ．a e =B ．()f x 在区间()1,e 单调递增C ．1x =是()f x 的极大值点D ．()f e 是()f x 的最小值【答案】ACD 【分析】()f x 只有一个零点，转化为方程0x a a x -=在(0,)+∞上只有一个根，即ln ln x ax a=只有一个正根．利用导数研究函数ln ()xh x x=的性质，可得a e =，判断A ，然后用导数研究函数()x e f x e x =-的性质，求出()'f x ，令()0f x '=，利用新函数确定()'f x 只有两个零点1和e ，并证明出()'f x 的正负，得()f x 的单调性，极值最值．判断BCD ．【详解】()f x 只有一个零点，即方程0x a a x -=在(0,)+∞上只有一个根，x a a x =，取对数得ln ln x a a x =，即ln ln x ax a=只有一个正根． 设ln ()xh x x =，则21ln ()x h x x-'=，当0x e <<时，()0h x '>，()h x 递增，0x →时，()h x →-∞，x e >时，()0h x '<，()h x 递减，此时()0h x >，max 1()()h x h e e==． ∴要使方程ln ln x ax a =只有一个正根．则ln 1a a e =或ln 0a a<，解得a e =或0a <，又∵1a >，∴a e =．A 正确；()x e f x e x =-，1()x e f x e ex -'=-，1()0x e f x e ex -'=-=，11x e e x --=，取对数得1(1)ln x e x -=-，易知1x =和x e =是此方程的解．设()(1)ln 1p x e x x =--+，1()1e p x x-'=-，当01x e <<-时，()0p x '>，()p x 递增，1x e >-时，()0p x '<，()p x 递减，(1)p e -是极大值，又(1)()0p p e ==， 所以()p x 有且只有两个零点，01x <<或x e >时，()0p x <，即(1)ln 1e x x -<-，11e x x e --<，1e x ex e -<，()0f x '>，同理1x e <<时，()0f x '<，所以()f x 在(0,1)和(,)e +∞上递增，在(1,)e 上递减，所以极小值为()0f e =，极大值为(1)f ，又(0)1f =，所以()f e 是最小值．B 错，CD 正确． 故选：ACD ． 【点睛】关键点点睛：本题考用导数研究函数的零点，极值，单调性．解题关键是确定()'f x 的零点时，利用零点定义解方程，1()0xe f x e ex-'=-=，11x e e x --=，取对数得1(1)ln x e x -=-，易知1x =和x e =是此方程的解．然后证明方程只有这两个解即可．18．已知函数1()2ln f x x x=+，数列{}n a 的前n 项和为n S ，且满足12a =，()()*1N n n a f a n +=∈，则下列有关数列{}n a 的叙述正确的是（ ）A ．21a a <B ．1n a >C ．100100S <D ．112n n n a a a +⋅+<【答案】AB 【分析】A ．计算出2a 的值，与1a 比较大小并判断是否正确；B ．利用导数分析()f x 的最小值，由此判断出1n a >是否正确；C ．根据n a 与1的大小关系进行判断；D ．构造函数()()1ln 11h x x x x =+->，分析其单调性和最值，由此确定出1ln 10nn a a +->，将1ln 10n na a +->变形可得112n n a a ++>，再将112n n a a ++>变形可判断结果.【详解】A 选项，3221112ln 2ln 4ln 2222a e =+=+<+=，A 正确；B 选项，因为222121()x f x x x x='-=-，所以当1x >时，()0f x '>，所以()f x 单增，所以()(1)1f x f >=，因为121a =>，所以()11n n a f a +=>，所以1n a >，B 正确； C 选项，因为1n a >，所以100100S >，C 错误；D 选项，令1()ln 1(1)h x x x x =+->，22111()0x h x x x x-='=->， 所以()h x 在(1,)+∞单调递增，所以()(1)0h x h >=，所以1ln 10nna a +->， 则22ln 20n n a a +->，所以112ln 2n n n a a a ⎛⎫++> ⎪⎝⎭，即112n n a a ++>，所以112n n n a a a ++>，所以D 错误. 故选：AB. 【点睛】易错点睛：本题主要考查导数与数列的综合问题，属于难题.解决该问题应该注意的事项： （1）转化以函数为背景的条件时，应该注意题中的限制条件，如函数的定义域，这往往是很容易被忽视的问题；（2）利用函数的方法研究数列中的相关问题时，应准确构造相应的函数，注意数列中相关限制条件的转化.19．已知()2sin x f x x x π=--.（ ）A ．()f x 的零点个数为4B ．()f x 的极值点个数为3C ．x 轴为曲线()y f x =的切线D ．若()12()f x f x =，则12x x π+=【答案】BC 【分析】首先根据()0f x '=得到21cos xx π-=，分别画出21xy π=-和cos y x =的图像，从而得到函数的单调性和极值，再依次判断选项即可得到答案. 【详解】()21cos xf x x π'=--，令()0f x '=，得到21cos xx π-=.分别画出21xy π=-和cos y x =的图像，如图所示：由图知：21cos xx π-=有三个解，即()0f x '=有三个解，分别为0，2π，π. 所以(),0x ∈-∞，()21cos 0xf x x π'=-->，()f x 为增函数，0,2x π⎛⎫∈ ⎪⎝⎭，()21cos 0x f x x π'=--<，()f x 为减函数，,2x ππ⎛⎫∈ ⎪⎝⎭，()21cos 0x f x x π'=-->，()f x 为增函数，(),x π∈+∞，()21cos 0xf x x π'=--<，()f x 为减函数.所以当0x =时，()f x 取得极大值为0，当2x π=时，()f x 取得极小值为14π-，当x π=时，()f x 取得极大值为0，所以函数()f x 有两个零点，三个极值点，A 错误，B 正确.因为函数()f x 的极大值为0，所以x 轴为曲线()y f x =的切线，故C 正确. 因为()f x 在(),0-∞为增函数，0,2π⎛⎫⎪⎝⎭为减函数， 所以存在1x ，2x 满足1202x x π<<<，且()()12f x f x =，显然122x x π+<，故D 错误.故选：BC 【点睛】本题主要考查导数的综合应用，考查利用导数研究函数的零点，极值点和切线，属于难题.20．已知函数()21,0log ,0kx x f x x x +≤⎧=⎨>⎩，下列是关于函数()1y f f x =+⎡⎤⎣⎦的零点个数的判断，其中正确的是（ ） A ．当0k >时，有3个零点 B ．当0k <时，有2个零点 C ．当0k >时，有4个零点 D ．当0k <时，有1个零点【答案】CD【分析】令y ＝0得()1f f x =-⎡⎤⎣⎦，利用换元法将函数分解为f （x ）＝t 和f （t ）＝﹣1，作出函数f （x ）的图象，利用数形结合即可得到结论． 【详解】令()10y f f x =+=⎡⎤⎣⎦，得()1f f x =-⎡⎤⎣⎦，设f （x ）＝t ，则方程()1f f x =-⎡⎤⎣⎦等价为f （t ）＝﹣1，①若k ＞0，作出函数f （x ）的图象如图：∵f （t ）＝﹣1，∴此时方程f （t ）＝﹣1有两个根其中t 2＜0，0＜t 1＜1，由f （x ）＝t 2＜0，此时x 有两解，由f （x ）＝t 1∈（0，1）知此时x 有两解，此时共有4个解， 即函数y ＝f [f （x ）]+1有4个零点．②若k ＜0，作出函数f （x ）的图象如图：∵f （t ）＝﹣1，∴此时方程f （t ）＝﹣1有一个根t 1，其中0＜t 1＜1，由f （x ）＝t 1∈（0，1），此时x 只有1个解，即函数y ＝f [f （x ）]+1有1个零点． 故选：CD ．【点睛】本题考查分段函数的应用，考查复合函数的零点的判断，利用换元法和数形结合是解决本题的关键，属于难题．三、三角函数与解三角形多选题21．知函数()()sin 04f x x πωω⎛⎫=+> ⎪⎝⎭，则下述结论中正确的是（ ） A ．若()f x 在[]0,2π有且仅有4个零点，则()f x 在[]0,2π有且仅有2个极小值点 B ．若()f x 在[]0,2π有且仅有4个零点，则()f x 在20,15π⎛⎫⎪⎝⎭上单调递增 C ．若()f x 在[]0,2π有且仅有4个零点，则ω的范是1519,88⎡⎫⎪⎢⎣⎭D ．若()f x 的图象关于4x π=对称，且在5,1836ππ⎛⎫⎪⎝⎭单调，则ω的最大值为9 【答案】ACD 【分析】 令4t x πω=+，由[]0,2x π∈，可得出,244t ππωπ⎡⎤∈+⎢⎥⎣⎦，作出函数sin y t =在区间,244ππωπ⎡⎤+⎢⎥⎣⎦上的图象，可判断A 选项正误；根据已知条件求出ω的取值范围，可判断C 选项正误；利用正弦型函数的单调性可判断B 选项的正误；利用正弦型函数的对称性与单调性可判断D 选项的正误. 【详解】 令4t x πω=+，由[]0,2x π∈，可得出,244t ππωπ⎡⎤∈+⎢⎥⎣⎦，作出函数sin y t =在区间,244ππωπ⎡⎤+⎢⎥⎣⎦上的图象，如下图所示：对于A 选项，若()f x 在[]0,2π有且仅有4个零点，则()f x 在[]0,2π有且仅有2个极小值点，A 选项正确；对于C 选项，若()f x 在[]0,2π有且仅有4个零点，则4254ππωππ≤+<，解得151988ω<≤，C 选项正确； 对于B 选项，若151988ω<≤，则2192154604πππππω≤+<+， 所以，函数()f x 在区间20,15π⎛⎫⎪⎝⎭上不单调，B 选项错误； 对于D 选项，若()f x 的图象关于4x π=对称，则()442k k Z ωππππ+=+∈，()14k k Z ω∴=+∈.52361812T ππππω∴=≥-=，12ω∴≤，()41k k Z ω=+∈，max 9ω∴=. 当9ω=时，()sin 94f x x π⎛⎫=+⎪⎝⎭，当5,1836x ππ⎛⎫∈⎪⎝⎭时，339442x πππ<+<，此时，函数()f x 在区间5,1836ππ⎛⎫⎪⎝⎭上单调递减，合乎题意，D 选项正确. 故选：ACD. 【点睛】方法点睛：求较为复杂的三角函数的单调区间时，首先化简成()sin y A ωx φ=+形式，再求()sin y A ωx φ=+的单调区间，只需把x ωϕ+看作一个整体代入sin y x =的相应单调区间内即可，注意要先把ω化为正数．22．已知函数()(|sin |cos )(sin cos )f x x x x x =-+，x ∈R ，则（ ） A ．()f x 在0,3π⎛⎫⎪⎝⎭上单调递减B ．()f x 是周期为2π的函数C ．()f x 有对称轴D ．函数()f x 在(0,2)π上有3个零点【答案】BD 【分析】先判断出()f x 是周期为2π的函数，再在给定的范围上研究()f x 的单调性和零点，从而可判断BCD 的正误，再利用反证法可判断C 不正确. 【详解】因为[][]()(2)|sin(2)|cos(2)(sin(2)cos(2))f x x x x x f x πππππ+=+-+⋅+++=， 故()f x 是周期为2π的函数，故B 正确.当0,3x π⎛⎫∈ ⎪⎝⎭时，22()sin cos cos 2f x x x x =-=-， 因为220,3x π⎛⎫∈ ⎪⎝⎭，而cos y u =-在20,3π⎛⎫⎪⎝⎭为增函数， 故()cos2f x x =-在0,3π⎛⎫⎪⎝⎭为增函数，故A 错误.由(sin cos )(sin cos )002x x x x x π⎧-+=⎨<<⎩可得4x π=或34x π=或74x π=，故D 正确. 若()f x 的图象有对称轴x a =，因为()f x 的周期为2π，故可设[)0,2a π∈， 则()()2f x f a x =-对任意的x ∈R 恒成立，所以()()02f f a =即1(|sin 2|cos 2)(sin 2cos 2)a a a a -=-+①， 也有222f f a ππ⎛⎫⎛⎫=-⎪ ⎪⎝⎭⎝⎭即1(|cos 2|sin 2)(cos 2sin 2)a a a a =--+②， 也有222f f a ππ⎛⎫⎛⎫-=+ ⎪ ⎪⎝⎭⎝⎭即1(|cos 2|sin 2)(cos 2sin 2)a a a a -=+-③，。
北京市高考数学压轴题
北京市高考数学压轴题近日，北京市的高考数学压轴题引起了广泛关注。
这道数学题目名为“寻找戴帽子的人”，题目难度相对较大，甚至有人形容它是“有史以来最难的高考数学题目之一”。
下面我们就来详细解析这道数学题目。
第一步：题目要求题目在第一句话中就明确了要求：“现有A、B、C三人戴着白色或黑色的帽子，其中每人戴一顶，三顶帽子中恰有一顶是白色的，现分别给A、B、C三人发出信号，让他们猜戴着白帽子的人是谁，已知：”在题目中，为了描述方便，把戴白色帽子的人称为“白帽子”，把戴黑色帽子的人称为“黑帽子”。
第二步：已知条件- 有A、B、C三人，每人戴一顶帽子；- 三顶帽子恰有一顶是白色的，即有一人戴白帽子；- A、B、C三人猜测戴白帽子的人。
第三步：分析对于每个人来说，他能看到别人戴的帽子的颜色，但看不到自己戴的帽子的颜色。
在这种情况下，每个人都要根据别人戴的帽子的颜色来推断出自己的帽子的颜色。
在题目中，已知三人中有一个人戴白帽子，假设他是A，那么A能看到的是B和C戴的是黑帽子，而B和C看到的是A戴的是白帽子。
因此，他们会这样推断：A：如果我戴的是黑帽子，那么B和C戴的都是黑帽子，而B和C 却看到了A的帽子是白色的，这是不可能的，因为三个人中必须有一个人戴白帽子。
所以，我戴的是白帽子。
B：如果我戴的是黑帽子，那么C戴的必是白帽子，因为A戴的帽子已经确定是白色的。
但是，C并没有确定是戴白帽子还是戴黑帽子，因为他无法判断他自己的帽子是什么颜色的。
因此，根据题目条件，C的帽子肯定是黑色的，这样三个人中就不会有人戴白帽子了，这显然与题目条件矛盾。
所以，我戴的也是白帽子。
C：与B的分析类似，我戴的也是白帽子。
这样，三个人都猜测出了戴白帽子的人是自己。
第四步：答案因此，戴白帽子的人是A、B、C都有可能，每个人都不能排除自己是戴白帽子的人。
所以，这道题目的答案是不确定的，考生只需要在解题过程中清晰地表达出自己的思路和推断过程即可。
2021年北京市高考数学压轴题预测附答案
2021年高考数学压轴题预测1．已知函数f（x）＝x+a+1x−alnx，a∈R．（1）求f（x）的单调性；（2）若a＞0，且f（x）的最小值小于4﹣2ln3，求a的取值范围．【分析】（1）求出导函数，判断函数在①当a≤﹣1时，②当a＞﹣1时，判断导函数的符号，判断函数的单调性．（2）求解函数的单调区间，求出函数的最小值，再构造函数，判断函数的单调性，结合零点存在定理即可求解．【解答】解：（1）f′（x）＝1−a+1x2−a x=x2−ax−(a+1)x2=(x+1)[x−(a+1)]x2，（x＞0），①当a≤﹣1时，f′（x）≥0恒成立，∴f（x）在（0，+∞）上单调递增，②当a＞﹣1时，令f′（x）＜0，则0＜x＜a+1，令f′（x）＞0，则x＞a+1，∴f（x）在（0，a+1）上单调递减，在（a+1，+∞）上单调递增，综上：当a≤﹣1时，f（x）在（0，+∞）上单调递增，当a＞﹣1时，f（x）在（0，a+1）上单调递减，在（a+1，+∞）上单调递增，（2）由（1）知f（x）min＝f（a+1）＝a+1+1﹣aln（a+1），则a﹣aln（a+1）＜2﹣2ln3，令g（x）＝x﹣xln（x+1），则g′（x）＝1﹣ln（x+1）−xx+1=−ln（x+1）+1x+1，令h（x）＝﹣ln（x+1）+1x+1，∵h′（x）=−1x+1−1(x+1)2＜0，∴h（x）在（﹣1，+∞）上单调递减，又h（0）＝1＞0，h（1）=12−ln2＜0，∴存在x0∈（0，1），使得h（x0）＝0，即g′（x0）＝0，g（x）在（0，x0）上单调递增，在（x0，+∞）上单调递减，又g（0）＝0＞2﹣2ln3，g（2）＝2﹣2ln3，∴g（a）＜2﹣2ln3⇔a＞2．∴a的取值范围为（2，+∞）．【点评】本题考查函数的导数的应用，函数的最值的求法，考查分析问题解决问题的能力，是难题．2．已知函数f（x）＝lnx+bx−a（a∈R，b∈R）有最小值M，且M≥0．（Ⅰ）求e a﹣1﹣b+1的最大值；第1页共2页。
2021年北京市高考数学解三角形复习题 (42)
2021年北京市高考数学解三角形复习题42．如图，边长为2的等边三角形ABC中，O是BC的中点，D，E分别是边AB，AC上的动点（不含端点），记∠BOD＝θ．（1）在图①中，∠DOE＝120°，试将AD，AE分别用含θ的关系式表示出来，并证明AD+AE为定值；（2）在图②中，∠DOE＝60°，问此时AD+AE是否为定值？若是，请给出证明；否则，求出AD+AE的取值范围．【解答】解：（1）由∠DOE＝120°，∠BOD＝θ，则∠BDO＝120°﹣θ，∠COE＝60°﹣θ，∠CEO＝60°+θ，在△BOD和△COE中，分别应用正弦定理可得，BDsinθ=BOsin(120°−θ)，CEsin(60°−θ)=COsin(60°+θ)，故BD=sinθsin(120°−θ)，CE=sin(60°−θ)sin(60°+θ)，所以AD=2−sinθsin(120°−θ)，AE=2−sin(60°−θ)sin(60°+θ)，θ∈（0，60°）．从而AD+AE=4−sinθsin(120°−θ)−sin(60°−θ)sin(60°+θ)=4−sinθsin(60°+θ)−sin(60°−θ)sin(60°+θ)=4−sinθ+sin(60°−θ) sin(60°+θ)=4−sinθ+√32cosθ−12sinθ32cosθ+12sinθ=3，从而AD+AE＝3为定值；（2）当∠DOE＝60°，∠BOD＝θ，则∠BDO＝120°﹣θ，∠COE＝120°﹣θ，∠CEO ＝θ，在△BOD和△COE中，分别应用正弦定理可得，BDsinθ=BOsin(120°−θ)，CEsin(120°−θ)=CO sinθ，故BD =sinθsin(120°−θ)，CE =sin(120°−θ)sinθ，所以AD =2−sinθsin(120°−θ)，AE =2−sin(120°−θ)sinθ，θ∈（30°，90°），AD +AE =4−sinθsin(120°−θ)−sin(120°−θ)sinθ，θ∈（30°，90°）．令y =sinθsin(120°−θ)+sin(120°−θ)sinθ，θ∈（30°，90°）， 下面先求y 的取值范围： 解法一：y =sinθsin(120°−θ)+sin(120°−θ)sinθ=√32cosθ+12sinθ+√32cosθ+12sinθsinθ=sin 2θ+(√32cosθ+12sinθ)2√32sinθcosθ+12sin 2=54sin 2θ+34cos 2θ+√32sinθcosθ√32sinθcosθ+12sin 2=1+34√32sinθcosθ+12sin 2=1+34√34sin2θ−14cos2θ+14=1+3412sin(2θ−30°)+14=1+32sin(2θ−30°)+1，由于θ∈（30°，90°），2θ﹣30°∈（30°，150°），2sin （2θ﹣30°）+1∈（2，3]， 所以1+32sin(2θ−30°)+1∈[2，52)， 因此AD +AE =4−y ∈(32，2]； 解法二：y =sinθsin(120°−θ)+sin(120°−θ)sinθ，设u =sin(120°−θ)sinθ，则y =u +1u，u =sin(120°−θ)sinθ=√32cosθ+12sinθsinθ=√32⋅1tanθ+12， 由θ∈（30°，90°），tanθ∈(√33，+∞)，1tanθ∈(0，√3)，u =√32⋅1tanθ+12∈(12，2)，又y =u +1u 在(12，1)上单调递减，在（1，2）上单调递增， 而当u =12或2时，y =52，当u ＝1时，y ＝2，所以y ∈[2，52)， 因此AD +AE =4−y ∈(32，2]．。
北京市2021年高考数学压轴卷含解析
市2021年高考数学压轴卷（含解析）本试卷共5页，150分，考试时长120分钟．考试务必将答案答在答题卡上，在试卷上作答无效．考试结束后，将本试卷和答题卡一并交回．第一部分（选择题 共40分）一、选择题10小题，每小题4分，共40分．在每小题列出的四个选项中，选出符合题目要求的一项．1．设集合{(1)(2)0}M x x x =-+<|，{1}N x x =-|，则M N =（ ）A ．(2,1)-B ．[1,1)-C ．[1,)-+∞D ．(1,1)- 2．设复数z 满足(1)1i z i -=+，则z 等于（ ） A ．i -B ．i C ．2i -D ．2i3．在61x ⎫⎪⎭的展开式中，常数项为（ ）A ．15B ．30C ．20D ．404．已知两条直线m ，n 和平面α，且//n α，则“m n ⊥”是“m α⊥”的（ ） A ．充分必要条件B ．充分而不必要条件C ．必要而不充分条件D ．既不充分也不必要条件5．在平面直角坐标系xOy 中，直线l 的方程为(1)3y k x =++，以点(1,1)为圆心且与直线l 相切的所有圆中，半径最大的圆的半径为（ ） A ．2B ．．4D ．86．在ABC 中，90,4,3C AC BC =︒==，点P 是AB 的中点，则CB CP ⋅=（ ） A ．94B ．4C ．92D ．67．已知函数211,0,()221,0,x x f x x x x ⎧+≤⎪=⎨⎪-++>⎩则不等式()20xf x ->的解集是（ ） A ．(1,0)(0,1)-B ．(1,1)-C ．(0,1)D ．(1,)-+∞8．将函数()sin f x x ω=（0>ω）的图象向左平移2π个单位长度后得到函数()g x 的图象，且()01g =，下列说法错误．．的是（ ） A ．()g x 为偶函数 B ．02g π-=⎛⎫⎪⎝⎭C ．当5ω=时，()g x 在0,2π⎡⎤⎢⎥⎣⎦上有3个零点D ．若()g x 在0,5π⎡⎤⎢⎥⎣⎦上单调递减，则ω的最大值为9 9．数列{}n a 是等差数列，{}n b 是各项均为正数的等比数列，公比1q >，且44a b =，则（ ） A ．2635a a b b +>+B ．2635a a b b +=+C ．2635a a b b +<+D ．26a a +与35b b +大小不确定10．形状､节奏､声音或轨迹，这些现象都可以分解成自复制的结构.即相同的形式会按比例逐渐缩小，并无限重复下去，也就是说，在前一个形式中重复出现被缩小的相同形式，依此类推，如图所示，将图1的正三角形的各边都三等分，以每条边中间一段为边再向外做一个正三角形，去掉中间一段得到图2，称为“一次分形”；用同样的方法把图2中的每条线段重复上述操作，得到图3，称为“二次分形”；依次进行“n 次分形”，得到一个周长不小于初始三角形周长100倍的分形图，则n 最小值是（ ）(取lg30.4771,lg 20.3010≈≈)A ．15B ．16C ．17D ．18第二部分（非选择题 共110分）二、填空题共5小题，每小题5分，共25分。
2021-2023北京高考真题数学汇编：压轴填空(第15题)
【点睛】关键点点睛：本题在推断②④的正误时，利用正面推理较为复杂时，可采用反证法来进行推导.
3．①②④
【分析】由 f ( x) = 0 可得出 lg x= kx + 2 ，考查直线 =y kx + 2 与曲线 g ( x) = lg x 的左、右支分别相切的情
形，利用方程思想以及数形结合可判断各选项的正误.
②当 a ≥ 1 时， f (x) 存在最大值；
③设 M ( x1, f ( x1 ))( x1 ≤ a), N ( x2, f ( x2 ))( x2 > a) ，则| MN |> 1；
④设
P
(
x3 ,
f
(
x3
))(
x3
<
−a),Q
(
x4
,
f
(
x4
))(
x4
≥
−a)
．若 |
PQ
| 存在最小值，则
a
an an −1
)
>
0 ，可得 an
<
an−1 ，所以，数列{an} 为递减数列，③对；
假设对任意的
n∈
N∗
，
an
≥
1 100
，则
S100000
≥ 100000× 1 100
= 1000
，
所以， a100000 =
9 S100000
≤9 1000
<1 100
，与假设矛盾，假设不成立，④对.
故答案为：①③④.
④
{an
}
中存在小于
1 100
的项．
其中所有正确结论的序号是
．
3．（2021·北京·统考高考真题）已知函数 f (x)= lg x − kx − 2 ，给出下列四个结论：
北京首都师范大学附属中学2021年高考数学高考数学压轴题 三角函数与解三角形多选题分类精编附解析
北京首都师范大学附属中学2021年高考数学高考数学压轴题 三角函数与解三角形多选题分类精编附解析一、三角函数与解三角形多选题1．知函数()()sin 04f x x πωω⎛⎫=+> ⎪⎝⎭，则下述结论中正确的是（ ）A ．若()f x 在[]0,2π有且仅有4个零点，则()f x 在[]0,2π有且仅有2个极小值点B ．若()f x 在[]0,2π有且仅有4个零点，则()f x 在20,15π⎛⎫⎪⎝⎭上单调递增 C ．若()f x 在[]0,2π有且仅有4个零点，则ω的范是1519,88⎡⎫⎪⎢⎣⎭D ．若()f x 的图象关于4x π=对称，且在5,1836ππ⎛⎫⎪⎝⎭单调，则ω的最大值为9 【答案】ACD 【分析】 令4t x πω=+，由[]0,2x π∈，可得出,244t ππωπ⎡⎤∈+⎢⎥⎣⎦，作出函数sin y t =在区间,244ππωπ⎡⎤+⎢⎥⎣⎦上的图象，可判断A 选项正误；根据已知条件求出ω的取值范围，可判断C 选项正误；利用正弦型函数的单调性可判断B 选项的正误；利用正弦型函数的对称性与单调性可判断D 选项的正误. 【详解】 令4t x πω=+，由[]0,2x π∈，可得出,244t ππωπ⎡⎤∈+⎢⎥⎣⎦，作出函数sin y t =在区间,244ππωπ⎡⎤+⎢⎥⎣⎦上的图象，如下图所示：对于A 选项，若()f x 在[]0,2π有且仅有4个零点，则()f x 在[]0,2π有且仅有2个极小值点，A 选项正确；对于C 选项，若()f x 在[]0,2π有且仅有4个零点，则4254ππωππ≤+<，解得151988ω<≤，C 选项正确； 对于B 选项，若151988ω<≤，则2192154604πππππω≤+<+，所以，函数()f x 在区间20,15π⎛⎫⎪⎝⎭上不单调，B 选项错误； 对于D 选项，若()f x 的图象关于4x π=对称，则()442k k Z ωππππ+=+∈，()14k k Z ω∴=+∈.52361812T ππππω∴=≥-=，12ω∴≤，()41k k Z ω=+∈，max 9ω∴=. 当9ω=时，()sin 94f x x π⎛⎫=+ ⎪⎝⎭，当5,1836x ππ⎛⎫∈⎪⎝⎭时，339442x πππ<+<， 此时，函数()f x 在区间5,1836ππ⎛⎫⎪⎝⎭上单调递减，合乎题意，D 选项正确. 故选：ACD. 【点睛】方法点睛：求较为复杂的三角函数的单调区间时，首先化简成()sin y A ωx φ=+形式，再求()sin y A ωx φ=+的单调区间，只需把x ωϕ+看作一个整体代入sin y x =的相应单调区间内即可，注意要先把ω化为正数．2．函数()sin()f x x ωϕ=+的部分图像如图中实线所示，图中的M 、N 是圆C 与()f x 图像的两个交点，其中M 在y 轴上，C 是()f x 图像与x 轴的交点，则下列说法中正确的是（ ）A ．函数()y f x =的一个周期为56B ．函数()f x 的图像关于点4,03成中心对称C ．函数()f x 在11,26⎛⎫-- ⎪⎝⎭上单调递增 D ．圆C 的面积为3136π【答案】BD 【分析】根据图象，结合三角函数的对称性、周期性、值域以及圆的中心对称性，可得,,C M N 的坐标，进而可得()f x 的最小正周期、对称中心、单调减区间，及圆的半径，故可判断选项的正误.【详解】由图知：1(,0)3C，M，2(3N ， ∴()f x 中111()2362T =--=，即1T =；对称中心为1,0,23k k Z ⎛⎫+∈ ⎪⎝⎭；单调减区间为17,,1212k k k Z ⎡⎤++∈⎢⎥⎣⎦；圆的半径6r ==，则圆的面积为3136π； 综上，知：AC 错误，而BD 正确. 故选：BD. 【点睛】本题考查了三角函数的性质，结合了圆的中心对称性质判断三角函数的周期、对称中心、单调区间及求圆的面积，属于难题.3．ABC 中，2BC =，BC 边上的中线2AD =，则下列说法正确的有（ ） A ．AB AC →→⋅为定值B ．2210AC AB += C ．co 415s A << D ．BAD ∠的最大值为30【答案】ABD 【分析】A 利用向量的加减法及向量的数量积公式运算即可，B 根据余弦定理及角的互补运算即可求值，C 利用余弦定理及基本不等式求出cos A 范围即可，D 根据余弦定理及基本不等式求出cos BAD ∠的最小值即可. 【详解】 对于A ，22413AB AC AD DB AD DB AD DB →→→→→→→→⎛⎫⎛⎫⋅=+-=-=-= ⎪⎪⎝⎭⎝⎭，AB AC →→∴⋅为定值，A 正确； 对于B ，cos cos ADC ADB∠=-∠2222222cos 2cos AC AB AD DC AD DC ADC AD DB AD DB ADB ∴+=+-⋅⋅∠++-⋅⋅∠2222AD DB DC =++ 2221110=⨯++=，故B 正确；对于C ，由余弦定理及基本不等式得224242122b c bc cosA bc bc bc+--=≥=-（当且仅当b c =时，等号成立）,由A 选项知cos 3bc A =，22cos cos 1133cos AA A∴≥-=-，解得3cos 5A ≥，故C 错误； 对于D ，2222213233cos 4442c c c BAD c c c +-+∠==≥=（当且仅当3c =时，等号成立），因为BAD ABD ∠<∠， 所以(0,)2BAD π∠∈，又3cos 2BAD ∠≥，所以BAD ∠的最大值30，D 选项正确. 故选：ABD 【点睛】本题主要考查了向量的数量积运算，余弦定理，基本不等式，考查了推理能力，属于难题.4．（多选题）如图，设ABC 的内角、、A B C 所对的边分别为a b c 、、，若a b c 、、成等比数列，、、A B C 成等差数列，D 是ABC 外一点，1,3DC DA ==，下列说法中，正确的是（ ）A ．3B π=B ．ABC 是等边三角形C ．若A B CD 、、、四点共圆，则13AC =D ．四边形ABCD 面积无最大值 【答案】ABC 【分析】根据等差数列的性质和三角形内角和可得3B π=，根据等比中项和余弦定理可得a c =，即ABC 是等边三角形，若A B C D 、、、四点共圆，根据圆内接四边形的性质可得23D π=，再利用余弦定理可求13AC =211sin sin 223ACD ABC S S S AD CD D AC π∆∆=+=⋅+和2222cos AC AD CD AD CD D 可得3335353sin 3sin()23S D D D π=-+=-+. 【详解】由、、A B C 成等差数列可得，2A+C =B ，又A B C π++=，则3B π=，故A 正确；由a b c 、、成等比数列可得，2b ac =，根据余弦定理，2222cos b a c ac B =+-，两式相减整理得，2()0a c -=，即a c =，又3B π=，所以，ABC 是等边三角形，故B 正确；若A B C D 、、、四点共圆，则B D π+=，所以，23D π=， ADC 中，根据余弦定理，2222cos AC AD CD AD CD D ，解得AC =C 正确； 四边形ABCD 面积为：211sin sin 223ACD ABC S S S AD CD D AC π∆∆=+=⋅+23sin 2D AC = 又2222cos 106cos AC AD CD AD CD D D =+-⋅=-，所以，3sin 3sin()22232S D D D π=-+=-+， 因为(0,)D π∈，当四边形面积最大时，sin()13D π-=，此时max 3S =，故D 错误. 故选：ABC 【点睛】本题考查解三角形和平面几何的一些性质，同时考查了等差等比数列的基本知识，综合性强，尤其是求面积的最大值需要一定的运算，属难题.5．函数()cos |cos |f x x x =+，x ∈R 是（ ） A ．最小正周期是π B ．区间[0，1]上的减函数 C ．图象关于点(k π，0)()k Z ∈对称 D ．周期函数且图象有无数条对称轴 【答案】BD 【分析】根据绝对值的意义先求出分段函数的解析式，作出函数图象，利用函数性质与图象关系分别对函数的周期、单调区间、对称中心和对称轴进行判断求解. 【详解】2cos (22)22()30(22)22x k x k f x k x k ππππππππ⎧-+⎪⎪=⎨⎪+<≤+⎪⎩，则对应的图象如图：A 中由图象知函数的最小正周期为2π，故A 错误，B 中函数在[0,]2π上为减函数，故B 正确，C 中函数关于x k π=对称，故C 错误，D 中函数由无数条对称轴，且周期是2π，故D 正确 故正确的是B D 故选：BD【点睛】本题考查由有解析式的函数图象的性质. 有关函数图象识别问题的思路:①由函数的定义域，判断图象左右的位置，由函数的值域，判断图象的上下位置； ②由函数的单调性，判断图象的变化趋势； ③由函数的奇偶性，判断图象的对称性； ④由函数的周期性，判断图象的循环往复．6．函数()()()2sin 0,f x x ωϕωϕπ=+><的部分图象如图所示，则下列结论正确的是（ ）A ．1()2sin 36f x x π⎛⎫=-⎪⎝⎭ B ．若把()f x 的横坐标缩短为原来的23倍，纵坐标不变，得到的函数在[],ππ-上是增函数C ．若把函数()f x 的图像向左平移2π个单位，则所得函数是奇函数 D ．函数()y f x =的图象关于直线4x π=-对称【答案】ACD 【分析】根据函数的图象求出函数的解析式，得选项A 正确； 求出213263x πππ--得到函数在[],ππ-上不是增函数，得选项B 错误；求出图象变换后的解析式得到选项C 正确； 求出函数的对称轴方程，得到选项D 正确. 【详解】 A, 如图所示：1732422T πππ=-=， 6T π∴=，∴2163πωπ==，(2)2f π=，∴2(2)2sin()23f ππϕ=+=，即2sin()13πϕ+=， ∴22()32k k Z ππϕπ+=+∈， ∴2()6k k Z πϕπ=-∈，||ϕπ<，∴6πϕ=-，∴1()2sin()36f x x π=-，故选项A 正确；B, 把()y f x =的横坐标缩短为原来的23倍，纵坐标不变，得到的函数12sin()26y x π=-，[x π∈-，]π，∴213263x πππ--，∴12sin()26y x π=-在[π-，]π上不单调递增，故选项B 错误；C, 把()y f x =的图象向左平移2π个单位，则所得函数12sin[()]2sin 3223xy x ππ=-+=，是奇函数，故选项C 正确； D, 设1,,32,362x k k Z x k πππππ-=+∈∴=+当24k x π=-⇒=-，所以函数()y f x =的图象关于直线4x π=-对称，故选项D 正确.故选：ACD 【点睛】方法点睛：求三角函数的解析式，一般利用待定系数法，一般先设出三角函数的解析式sin()y A wx k ，再求待定系数,,,A w k ，最值确定函数的,A k ,周期确定函数的w ,非平衡位置的点确定函数的φ.7．设函数()sin()(0)4f x x πωω=+>，已知()f x 在[]02π，有且仅有5个零点，则下列结论成立的有（ ）A ．()1y f x =+在()02π，有且仅有2个零点 B ．()f x 在023π⎛⎫⎪⎝⎭，单调递增C ．ω的取值范围是192388⎡⎫⎪⎢⎣⎭，D ．将()f x 的图象先右移4π个单位，再纵坐标不变，横坐标扩大为原来的2倍，得到函数1()sin()2g x x ω=【答案】BC 【分析】首先利用图象直接判断A 选项；再利用函数()f x 在[]02π，有且仅有5个零点，求得ω的范围，并利用整体代入的方法判断B 选项；最后利用图象的变换规律，求得变换之后的解析式，判断D. 【详解】A.如图，[]0,2π上函数仅有5个零点，但有3个最小值点，这3个最小值点就是()1y f x =+在()0,2π上的3个零点；B.[]0,2x π∈时，,2444t x πππωωπ⎡⎤=+∈⋅+⎢⎥⎣⎦ 若函数()f x 在[]02π，有且仅有5个零点，则5264ππωππ≤⋅+<，得192388ω≤<，当023x π⎛⎫∈ ⎪⎝⎭，时，,448t x πππω⎛⎫=+∈ ⎪⎝⎭，此时函数单调递增，故BC 正确； D. 函数()f x 的图象先右移4π个单位后得到sin sin 4444y x x ππωππωω⎡⎤⎛⎫⎛⎫=-+=-+ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦，再将横坐标扩大为原来的2倍，得到()1sin 244g x x ωππω⎛⎫=-+ ⎪⎝⎭，故D 不正确；故选：BC 【点睛】关键点点睛：本题的关键是求出ω的取值范围，首先根据函数在区间[]0,2π有5个零点，首先求4t x πω=+的范围，再分析sin y t =的图象，求得ω的范围.8．已知函数()()()2sin 0,0f x x ωϕωϕπ=+><<的部分图象如图所示，则下列说法正确的是（ ）A ．23ϕπ=B ．()f x 的最小正周期为πC ．()f x 的图象关于直线12x π=对称D ．()f x 的图象关于点5,06π⎛⎫⎪⎝⎭对称 【答案】BCD 【分析】利用图象，把(3代入求ϕ,利用周期求出2ω=，从而2n 2)3(si f x x π⎛⎫=+ ⎪⎝⎭，研究对称轴和对称中心. 【详解】由图可知2sin 3ϕ=3sin 2ϕ=，根据图象可知0x =在()f x 的单调递增区间上，又0ϕπ<<，所以3πϕ=，A 项错误；因为()2sin 3f x x πω⎛⎫=+ ⎪⎝⎭，所以结合图像，由五点法得33ωπππ+=，解得2ω=，则()f x 的最小正周期2T ππω==，B 项正确；将12x π=代入2n 2)3(si f x x π⎛⎫=+ ⎪⎝⎭，得2sin 21263f πππ⎛⎫⎛⎫=+= ⎪ ⎪⎝⎭⎝⎭，所以()f x 的图象关于直线12x π=对称，C 项正确﹔将56x π=代入可得552sin 0633f πππ⎛⎫⎛⎫=+= ⎪ ⎪⎝⎭⎝⎭，所以点5,06π⎛⎫ ⎪⎝⎭是()f x 图象的一个对称中心，D 项正确. 故选：BCD. 【点睛】求三角函数解析式的方法： (1)求A 通常用最大值或最小值； (2)求ω通常用周期；()求φ通常利用函数上的点带入即可求解.9．设函数()()sin f x A x =+ωϕ，x ∈R （其中0A >，0>ω，2πϕ<），在,62ππ⎛⎫ ⎪⎝⎭上既无最大值，也无最小值，且()026f f f ππ⎛⎫⎛⎫-== ⎪ ⎪⎝⎭⎝⎭，则下列结论错误的是（ ）A ．若()()()12f x f x f x ≤≤对任意x ∈R ，则21min x x π-=B ．()y f x =的图象关于点,03π⎛-⎫ ⎪⎝⎭中心对称 C ．函数()f x 的单调减区间为()7,1212k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦D ．函数()()y f x x R =∈的图象相邻两条对称轴之间的距离是2π 【答案】ABD【分析】根据条件先求函数的解析式，对于A:判断出()1f x 为最小值，()2f x 为最大值，即可；对于B:根据函数的对称性进行判断；对于C:求出角的范围，结合三角函数的单调性进行判断；对于D:根据函数的对称性即对称轴之间的关系进行判断.【详解】因为函数()f x 在,62ππ⎛⎫⎪⎝⎭上既无最大值，也无最小值， 所以,62ππ⎛⎫ ⎪⎝⎭是函数的一个单调区间，区间长度为263πππ-=， 即函数的周期2233T ππ≥⨯=，即223ππω≥，则03ω<≤ 因为()06f f π⎛⎫= ⎪⎝⎭，所以06212ππ+=为函数的一条对称轴； 则1223πππωϕωϕπ+=+=①② 由①②解得：=2=3πωϕ，，即()sin 23f x A x π⎛⎫=+ ⎪⎝⎭，函数的周期=T π. 对于A: 若()()()12f x f x f x ≤≤对任意x ∈R 恒成立，则()1f x 为最小值，()2f x 为最大值，所以12||22T k x x k π-==,则21x x -必为2π的整数倍，故A 错误，可选A; 对于B:3x π=-时，()sin 03f x A π⎛⎫=-≠ ⎪⎝⎭，故,03π⎛-⎫ ⎪⎝⎭不是()y f x =的对称中心，B 错误，可选B; 对于C:当7,1212x k k ππππ⎡⎤∈++⎢⎥⎣⎦时，322,2322x k k πππππ⎡⎤+∈++⎢⎥⎣⎦，此时()y f x =单调递减，C 正确，不选C;对于D: 函数()()y f x x R =∈的图象相邻两条对称轴之间的距离是44T π=,故D 错误，可选D故选:ABD【点睛】（1）求三角函数解析式的方法：①求A 通常用最大值或最小值；②(2)求ω通常用周期；③求φ通常利用函数上的点带入即可求解；（2）三角函数问题通常需要把它化为“一角一名一次”的结构，借助于sin y x =或cos y x =的性质解题.10．在ABC 中，下列说法正确的是（ ）A ．若AB >，则sin sin A B >B ．若2C π>，则222sin sin sin C A B >+C ．若sin cos A B <，则ABC 为钝角三角形D ．存在ABC 满足cos cos 0A B +≤【答案】ABC【分析】根据大角对大边，以及正弦定理，判断选项A ；利用余弦定理和正弦定理边角互化，判断选项B ；结合诱导公式，以及三角函数的单调性判断CD.【详解】A.A B >，a b ∴>，根据正弦定理sin sin a b A B =，可知sin sin A B >，故A 正确；B.2C π>，222cos 02a b c C ab +-∴=<，即222a b c +<，由正弦定理边角互化可知222sin sin sin C A B >+，故B 正确； C.当02A π<<时，sin cos cos cos 2A B A B π⎛⎫<⇔-< ⎪⎝⎭，即22A B A B ππ->⇒+<，即2C π>，则ABC 为钝角三角形，若2A π>，sin cos cos cos 2A B A B π⎛⎫<⇔-< ⎪⎝⎭，即22A B A B ππ->⇒>+成立，A 是钝角，当2A π=是，sin cos A B >，所以综上可知：若sin cos A B <，则ABC 为钝角三角形，故C 正确；D.A B A B ππ+<⇒<-，0,0A B πππ<<<-<，()cos cos cos A B B π∴>-=-，即cos cos 0A B +>，故D 不正确.故选：ABC【点睛】关键点点睛：本题考查判断三角形的形状，关键知识点是正弦定理和余弦定理，判断三角形形状，以及诱导公式和三角函数的单调性.。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2021年北京市高考数学压轴题总复习
1．若方程f （x ）＝x 有实数根x 0，则称x 0为函数f （x ）的一个不动点．已知函数f （x ）＝
e x ﹣lnx +（a +1）x ﹣alnx （e 为自然对数的底数）a ∈R ．
（1）当a ≥0时f （x ）是否存在不动点？并证明你的结论；
（2）若a ＝﹣e ，求证f （x ）有唯一不动点．
【解答】解：（1）当a ≥0时f （x ）不存在不动点，
证明：由f （x ）＝x 可得，
e x x +ax −alnx =0， 令F （x ）=e x x +ax −alnx ，x ＞0，
则F ′（x ）=xe x −e x x 2+a −a x =(x−1)(e x +ax)x 2
， 当x ∈（0，1）时，F ′（x ）＜0，函数单调递减，当x ∈（1，+∞）时，F ′（x ）＞0，函数单调递增，
故当x ＝1时，函数取得最小值F （1）＝a +e ＞0
故方程，e x x +ax −alnx =0没有实数根，即f （x ）不存在不动点；
（2）当a ＝﹣e 时，F （x ）=e x x
−ex +elnx ， 则F′(x)=(x−1)(e x −ex)x 2
， 令g （x ）＝e x ﹣ex 则g ′（x ）＝e x ﹣e ，
当x ∈（0，1）时，g ′（x ）＜0，函数单调递减，当x ∈（1，+∞）时，g ′（x ）＞0，函数单调递增，
故g （x ）≥g （1）＝0，
当x ∈（0，1）时，F ′（x ）＜0，函数单调递减，当x ∈（1，+∞）时，F ′（x ）＞0，函数单调递增，
故当x ＝1时，函数取得最小值F （1）＝a +e ＝0，
所以e x x −ex +elnx =0有唯一的实数根1，
故f （x ）有唯一的不动点．
2．已知抛物线y 2＝2px （p ＞0）经过点（3，2√3），点A ，B ，C 为抛物线上不同的三点，F
为抛物线的焦点，且满足FA →+FB →+FC →=0→
，过点C 作y 轴的垂线且垂足为M ． （Ⅰ）若直线AB ，FM 的斜率都存在，求证：k AB •k FM 为定值；
（Ⅱ）已知直线AB 过点（﹣1，0），抛物线上任意一点N （异于点A ，B ），直线NA ，NB 分别交直线x ＝1交于P ，Q 两点，O 为坐标原点，求证：OP →•OQ →
为定值．
【解答】解：（Ⅰ）依题意有（2√3）2＝6p ，解得p ＝2，
所以抛物线的方程为y 2＝4x ，
所以焦点F （1，0），
设点A （x 1，y 1），B （x 2，y 2），C （x 3，y 3），M （0，y 3），
由FA →+FB →+FC →=0→，得x 1+x 2＝3﹣x 3，y 1+y 2＝﹣y 3，
又因为{y 12=4x 1y 22=4x 2
， 两式相减得，（y 1+y 2）（y 1+y 2）＝4（x 1﹣x 2），
k AB =
y 1−y 2x 1−x 2=4y 1+y 2=−4y 3， k FM =0−y 31−0=−y 3， 所以k AB •k FM ＝4，
即k AB •k FM 为定值．
（Ⅱ）证明：设点N （x 0，y 0），A （x 1，y 1），B （x 2，y 2），
由{y 02=4x 0y 12=4x 1
，得y 0−y 1x 0−x 1=4y 0+y 1， 则直线l NA ：y ﹣y 0=4y 0+y 1
（x ﹣x 0）， 即（y 0+y 1）y ＝4x +y 0y 1，
其与x ＝1的交点P （1，y 0y 1+4
y 0+y 1），
同理直线l NB 与直线x ＝1的交点Q （1，
y 0y 2+4
y 0+y 2）， 所以OP →⋅OQ →=1+y 0y 1+4y 0+y 1+y 0y 2+4y 0+y 2
=1+y 02y 1y 2+4y 0(y 1+y 2)+16y 02+y 0(y 1+y 2)+y 1y 2① 设直线AB 的方程为y ＝k （x +1），
联立{y 2=4x y =k(x +1)
，消y 整理得k 2x 2+（2k 2﹣4）x +k 2＝0， 则x 1x 2＝1，y 1y 2=√16x 1x 2=4，
代入①得1+4y 02+4y 0(y 1+y 2)+16y 02+y 0(y 1+y 2)+4
=1+4＝5， 所以OP →•OQ →为定值．。