π的简介

合集下载

圆周圆周率

圆周圆周率圆周率（π）简介圆周率是一个数学常数，为一个圆的周长和其直径的比率，近似值约等于3.，常用符号π （读作pài）来表示。

圆周率（π）是一个无理数，它不能用分数完全表示出来（即它的小数部分是一个无限不循环小数）。

π 的数字序列被认为是随机分布的，有一种统计上特别的随机性，但至今未能证明。

此外，π 还是一个超越数——它不是任何有理数系数多项式的根。

在日常生活中，通常都用3.14代表圆周率去进行近似计算。

圆周率的定义π 常用定义为圆的周长C与直径d的比值：π=C/d无论圆的大小如何，比值C/d为恒值。

如果一个圆的直径变为原先的二倍，它的周长也将变为二倍，比值C/d不变。

圆周率的近似值圆周率近似等于以下几个分数的值（依准确度顺序排列）：22/7、333/106、355/113、52163/16604、103993/33102、/圆周率怎么算圆周率计算方法1：通过测量圆的周长和直径来计算 Pi 值1.找到标准的圆形物体。

2.尽量精确地测量圆的周长。

3. 尽量精确地测量圆的直径。

4. 用周长除以直径，就可以得到圆周率的近似值。

并且周长和直径测量得越精确，圆周率的计算值就越精确。

圆周率计算方法2：通过无穷级数来计算 Pi 值 1. 使用格雷戈里 - 莱布尼茨无穷级数进行计算，公式如下：π = (4/1) - (4/3) + (4/5) - (4/7) + (4/9) - (4/11) + (4/13) - (4/15) ...2. 使用尼拉坎特级数进行计算，公式如下：π = 3 +4/(2*3*4) - 4/(4*5*6) + 4/(6*7*8) - 4/(8*9*10) + 4/(10*11*12) - (4/(12*13*14) ...圆周率计算方法3：通过反正弦函数来计算 Pi 值 1. 选一个介于-1和1之间的数。

因为反正弦函数不能用于大于1或小于-1的参数。

2. 将选好的数字代入以下公式，其结果将约等于Pi 值。

圆弧长度计算公式

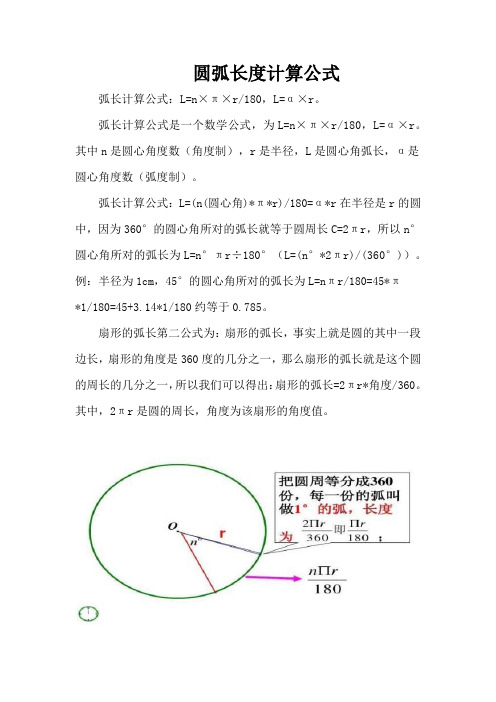
圆弧长度计算公式弧长计算公式：L=n×π×r/180，L=α×r。

弧长计算公式是一个数学公式，为L=n×π×r/180，L=α×r。

其中n是圆心角度数（角度制），r是半径，L是圆心角弧长，α是圆心角度数（弧度制）。

弧长计算公式：L=(n(圆心角)*π*r)/180=α*r在半径是r的圆中，因为360°的圆心角所对的弧长就等于圆周长C=2πr，所以n°圆心角所对的弧长为L=n°πr÷180°（L=(n°*2πr)/(360°)）。

例：半径为1cm，45°的圆心角所对的弧长为L=nπr/180=45*π*1/180=45+3.14*1/180约等于0.785。

扇形的弧长第二公式为：扇形的弧长，事实上就是圆的其中一段边长，扇形的角度是360度的几分之一，那么扇形的弧长就是这个圆的周长的几分之一，所以我们可以得出：扇形的弧长=2πr*角度/360。

其中，2πr是圆的周长，角度为该扇形的角度值。

π简介：圆周率π简介：圆周率用希腊字母π（读作pài）表示，是一个常数（约等于3.141592654），是代表圆周长和直径的比值。

它是一个无理数，即无限不循环小数。

在日常生活中，通常都用3.14代表圆周率去进行近似计算。

而用十位小数3.141592654便足以应付一般计算。

即使是工程师或物理学家要进行较精密的计算，充其量也只需取值至小数点后几百个位。

弧形面积计算：弧长、两弧点间的距离、弧高这三个条件知道任意两个就够了。

1、由已知弧长和已知弦长（两弧点间的距离）求得圆半径和弧所对的圆心角的度数；2、由半径和圆心角求得扇形面积和三角形面积；3、扇形面积减去三角形的面积的弧形的面积。

浅谈“数学分析”课程中的常数π

的面积等于百。
证令括ｌ则ｎ３，＿５于黑十当－时ｎ４。是ｎＪ，＞ｔｏ￣
２《数学分析》中关于的几个重要结果
ｔｔａ＝ｎｎ
从而、，
上咖一ｔｎ＞ａ觚１ｔ－ｔ’ ）ａ＋ … ｎｆｎ
ｓ（１ｓｔｓ。ｔ拉ｉ￡ｓ＋誉 ≤ ｉｌ）ｉｔｓｉｓｃｔ）ｎ＋扭ｎｃ十ｎｎｎ。（ｆｎｏｃｓｎ１
。
ｘ
［华东师范大学数学系．学分析（１】数第三版）．［北京：Ｍ】高等教育出版社。０３２０．［］日）２（堀场芳数．的奥秘［．７ｒＭ】北京：学出版社，９８科１９．［齐民有．温微积分［＿京：３】重Ｍ】匕高等教育出版社，０４｜２０．［朱静航激学分析［．４】Ｍ］长春：吉林教育出版社，９６１８．
ｎ＋ｌ
—
—
・互、
ｓｎｘｉ
ｘ
一
＝普。
证利用ｓｘ的幂级数展开，以得到ｉｎ可
ｓｎ．ｉｎｆ
所以，当力３，ｌｓ＞－时Ｌｎｉ＝ｎ
Ｌ什。１
（１ｉ１０ｎ）ｎ８＋ｓ０
一
ｓ
皿十
寺争一。另我有（）萼争… 外们ｈ＋ｕ斗，１＝ｕ一ｌ＋ｕ＋一代上，Ｃｓ，ｎｕ一孚… 人式Ｅ－ｉ＝（）手１＝ｐＩｘ（ｉｎｘ一ｎ
（）ｓ的全部零点为 ±７，丁Ｔ２ｃｘ。１ ±３－ｑ…， Nhomakorabea，
±

圆的周长怎么求公式是什么_1

圆的周长怎么求公式是什么
圆的周长公式：周长L=2πr（其中r为圆的半径，π为圆周率，通常状况下取3.14）。

圆周率π是圆的周长与直径的比值，一般用希腊字母π表示，是一个在数学及物理学中普遍存在的数学常数。

圆的周长算法
圆的周长=3.14x圆的直径=2x3.14x圆的半径，即：C=πd=2πr。

其中，C代表周长，π代表圆周率，d代表直径，r代表半径。

圆的简介:
圆是一种几何图形。

平面上到定点的距离等于定长的全部点组成的图形叫做圆。

当一条线段围着它的一个端点在平面内旋转一周时，它的另一个端点的轨迹叫做圆。

圆的面积和体积计算公式:
1、计算圆的面积公式是：半径×半径×3.14。

2、计算圆的体积公式是：半径×半径×3.14×高。

圆周率π介绍
后来的数学家们就想方法算出这个π的详细值，数学家刘徽用的是“割圆术”的方法，也就是用圆的内接正多边形和外切正多边形的周长靠近圆周长，求得圆接近192边型，求得圆周率大约是3.14。

割圆术的大致方法在中学的数学教材上就有。

然而必需看到，它很大程度上只是计算圆周率的方法，而圆周长是C=π*d好像已经是事
实了，这一方法仅仅是定出π的值来。

认真想想就知道这样做有问题，由于他们并没有从规律上证明圆的周长的确正比于直径，更进一步说他们甚至对周长的概念也仅是直观上的、非理性的。

π牌游戏规则

π牌（圆周率牌）棋牌游戏规则（以一副牌为例）Tags：π牌（圆周率牌）
发明人：戴建昌
【游戏简介】
π牌是一种以圆周率（一般取31415）为基数，组成若干种牌型，获取积分的扑克牌游戏。

【游戏规则】
一、牌的大小
本游戏牌不分大小，不分花色。

二、牌类
π外：大王、小王、K、Q、J、10、9、8、7、6、2
π干：3、4、5
π基：1（A）
三、牌型组合
天π型：由π干3、4、5和2个π基组成的牌型叫天π。

得分公式：基注X10倍=得分
地π型：由4个相同π干和一个π基组成或3个相同π干和2个π基组成或2个相同π干和3个π基组成或1个相同π干和4个π基组成的牌型叫地π。

得分公式：基注X8倍=得分
人π型：由4个相同π外和1个π基或3个相同π外和2个π基或2个相同π外和3个π基或4个相同π外和1个π基
组成的牌型叫人π。

得分公式：基注X4倍=得分
和π型：除天π、地π、人π以外，任意五张牌组成的牌型叫和π。

得分公式：（π干个数+π基个数）X基注=得分
四、游戏方法
游戏玩家分为庄家（一家），闲家（若干），由庄家轮流发牌，每家每次一张，共计五张牌，然后庄家和闲家分别各自按天π、地π、人π、和π得分公式计分。

每计分一次算一局牌，每局结束后，必须将所有牌重新洗牌方可开始下一局。

五、输赢判定
庄家在每局牌中获得的分数和闲家各自获得的分数互减，得正分方获胜，且或得减后得分。

六、逃跑扣分
1、庄家逃跑
庄家逃跑须向闲家赔分，庄家逃跑赔分=闲家个数X基注。

2、闲家逃跑
闲家逃跑须向庄家赔分，每个闲家逃跑赔分=每个闲家基注。

圆的周长公式是什么周长怎么算出来的

圆的周长公式是什么周长怎么算出来的圆的周长怎么求公式是什么圆的周长算法圆的周长=3.14x圆的直径=2x3.14x圆的半径，即：C=πd=2πr。

其中，C代表周长，π代表圆周率，d代表直径，r代表半径。

圆的简介:圆是一种几何图形。

平面上到定点的距离等于定长的所有点组成的图形叫做圆。

当一条线段绕着它的一个端点在平面内旋转一周时，它的另一个端点的轨迹叫做圆。

圆的面积和体积计算公式1、计算圆的面积公式是：半径×半径×3.14。

2、计算圆的体积公式是：半径×半径×3.14×高。

割圆术的大致方法在中学的数学教材上就有。

然而必须看到，它很大程度上只是计算圆周率的方法，而圆周长是C=π__d似乎已经是事实了，这一方法仅仅是定出π的值来。

什么是圆周率割圆术的大致方法在中学的数学教材上就有。

然而必须看到，它很大程度上只是计算圆周率的方法，而圆周长是C = π __ d似乎已经是事实了，这一方法仅仅是定出π的值来。

圆的定义及相关概念1、圆的一些概念(1) 圆的定义：在平面中，线段$OA$绕其固定端点$o$旋转一个圆，由另一端点$a$形成的图形称为圆。

固定端点$o$称为圆心，线段$OA$称为半径。

以点$o$为中心的圆记录为“$⊙o$”，读作“圆$o$”。

此外，圆心为$o$、半径为$R$的圆可以看作是到固定点$o$的距离等于固定长度$R$的所有点的集合。

π—超可解群

别声明的术语和记号参见文献［］１．
１７ｔ可解群的基本结论＂．超
定义１１对任意Ｐ ∈ 丌，均有Ｇ为Ｐ超可解群，则称Ｇ为丌超可解群．．．．
显然有：（）Ｇ为丌超可解群当且仅当Ｇ的主因子或为丌．或为Ｐ阶循环群，１．群Ｐ∈ 丌；丌超可解群必．
为丌．可解群－．２．可解群的Ｈｌ丌ｌ（）丌超Ｊａｌ．子群为超可解群．
定义１２若为Ｃ的极大子群，且Ｉ：Ｉ ≠ １则称为Ｇ的丌极大子群．．ＧＭ，．
丌超可解群与丌幂零群Ｃ紧密相关．由文献［］．．３］３定理１和定理２知：１可（）Ｇ为丌幂零群等价于对任．
群．
收稿日期：０２— ３８２００ —２
基金项目：国家自然科学基金资助项目（０７０４；教育部优秀青年教师资助计划．１１１７）
作者简介：陈顺民（９８一）１６，男，重庆壁山人．士研究生。要从事有限群论的研究硕主
摘要：给出了．可解群的若干刻画，过强．群得到了超可解群相应的特征性质超通闭
一
关
键
词：一可解群；一超幂零群：强一群闭文献标识码：Ａ
中图分类号：Ｏ５．１２１
－
维普资讯

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

地平线上的不同高度和不同角度观察宇宙射线的强度巧妙地推断出平均寿命的，后来F．拉赛蒂直接测出了平均寿命。

但是进行宇宙射线实验的人员在开始观察时，并不知道汤川的工作。

战争使这项实验工作延缓了，并且使日本和西方隔绝开来。

日本物理学家对存在着质量和汤川假定的粒子的质量相近的粒子根感兴趣，然而他们也注意到，要把μ介子和汤川粒子等同起来仍然有些困难：首先μ介子的平均寿命太长了；其次，μ介子在物质中受阻止时，它们与阻止物质的原子核发生相互作用显得很平常，虽然并不总是这样，三个年轻的意大利物理学家：M．康弗西(M．Conversi)，E.潘锰尼(E．Pancini)和O.皮西奥尼克(O.Piccionic)，通过研究这个现象，有了一个重要的实验发现。

这三个年轻人那时正在躲避德国人，因为德国人要把他们流放到德国去进行强制劳动。

他们三个人躲在罗马的一个地下室中秘密地工作，他们发现，正μ介子和负μ介子在物质中受阻止时的行为不一样。

正μ介子的衰变或多或少象在真空中一样，而负μ介子如果被重核所阻止，则被其俘获并产生蜕变，但当它们被象碳这样的轻核所俘获时，则它们的衰变大部份就象在真空中一样，这不是汤川粒子所应具有的特性，因为一旦介子距离原子核足够近时，特定的核力就应当产生蜕变，所以汤川粒子应当与轻的或重的原子核都发生剧烈的反应。

实验证明情况并非如此，因此μ介子不大会是汤川粒子。

情况确实非常奇怪。

汤川已经预言存在着质量约等于300个电子质量的粒子，有人也已找到了它们，但这种粒子却又不是汤川所预言的那种粒子。

理论物理学家对康弗西、潘锡尼和皮西奥尼克的结果感到迷惑不解，而这些结果从实验观点来看，却又非常可靠。

理论家们决心找出答案。

日本的谷川、坂田和井上及美国的H．A．贝特和R．马沙克(R．Marshak)，各自独立地提出了一个可以解决已存在的困难的假设。

他们提出，观察到的μ介子是汤川介子的衰变产物，而尚没有人观察到汤川介子。

作出吸引人的、看起来是合理的假设是一回事，而要确证—个事实又是另一回事了。

这时，一个新的实验技术，或者应当说一个老的实验的改进，为解决这个难题提供了一个有力的工具。

早在第一次世界大战前，卢瑟福实验室的一位日本物理学家树下就已证明，通过照相乳胶的α粒子在它们的运动轨迹上留下了一组可显影的乳胶颗粒，所以人们能够看到粒子的轨迹。

(我们可能会问：量子力学怎么办？测不准原理呢?粒子的波动性呢?读者可以放心，这些问题都有令人满意的解答，例如海森堡就曾作过详细的解释)树下用的乳胶仅对电离作用较大的粒子才灵敏，电子是探测不到的。

π键
根据分子轨道理论，两个原子的p轨道线性组合能形成两个分子轨道。

能量低于原来原子轨道的成键轨道π和能量高于原来原子轨道的反键轨道π*，相应的键分别
型巨型电子计算机计算出π值小数点后4.8亿位数，后又继续算到小数点后10.1亿位数，创下新的纪录。

至今，最新纪录是小数点后12411亿位。

除π的数值计算外，它的性质探讨也吸引了众多数学家。

1761年瑞士数学家兰伯特第一个证明π是无理数。

1794年法国数学家勒让德又证明了π^2也是无理数。

到1882年德国数学家林德曼首次证明了π是超越数，由此否定了困惑人们两千多年的“化圆为方”尺规作图问题。

还有人对π的特征及与其它数字的联系进行研究。

如1929年苏联数学家格尔丰德证明了e^π 是超越数等等。

编辑本段圆周率的计算
古今中外，许多人致力于圆周率的研究与计算。

为了计算出圆周率的越来越好的近似值，一代代的数学家为这个神秘的数贡献了无数的时间与心血。

十九世纪前，圆周率的计算进展相当缓慢，十九世纪后，计算圆周率的世界纪录频频创新。

整个十九世纪，可以说是圆周率的手工计算量最大的世纪。

进入二十世纪，随着计算机的发明，圆周率的计算有了突飞猛进。

借助于超级计算机，人们已经得到了圆周率的2061亿位精度。

历史上最马拉松式的计算，其一是德国的Ludolph Van Ceulen，他几乎耗尽了一生的时间，计算到圆的内接正262边形，于1609年得到了圆周率的35位精度值，以至于圆周率在德国被称为Ludolph数；其二是英国的威廉·山克斯，他耗费了15年的光阴，在1874年算出了圆周率的小数点后707位。

可惜，后人发现，他从第528位开始就算错了。

把圆周率的数值算得这么精确，实际意义并不大。

现代科技领域使用的圆周率值，有十几位已经足够了。

如果用鲁道夫算出的35位精度的圆周率值，来计算一个能把太阳系包起来的一个圆的周长，误差还不到质子直径的百万分之一。

以前的人计算圆周率，是要探究圆周率是否是循环小数。

自从1761年兰伯特证明了圆周率是无理数，1882年林德曼证明了圆周率是超越数后，圆周率的神秘面纱就被揭开了。

现在的人计算圆周率, 多数是为了验证计算机的计算能力的，还有，就是为了兴趣。

编辑本段圆周率的运算方法
古人计算圆周率，一般是用割圆法。

即用圆的内接或外切正多边形来逼近圆的周长。

阿基米德用正96边形得到圆周率小数点后3位的精度；刘徽用正3072边形得到5位精度；鲁道夫用正262边形得到了35位精度。

这种基于几何的算法计算量大，速度慢，吃力不讨好。

随着数学的发展，数学家们在进行数学研究时有意无意地发现了许多计算圆周率的公式。

下面挑选一些经典的常用公式加以介绍。

除了这些经典公式外，还有很多其它公式和由这些经典公式衍生出来的公式，就不一一列举了。