信号与线性系统分析吴大正习题答案1_2
信与线性系统分析吴大正第四版习题答案
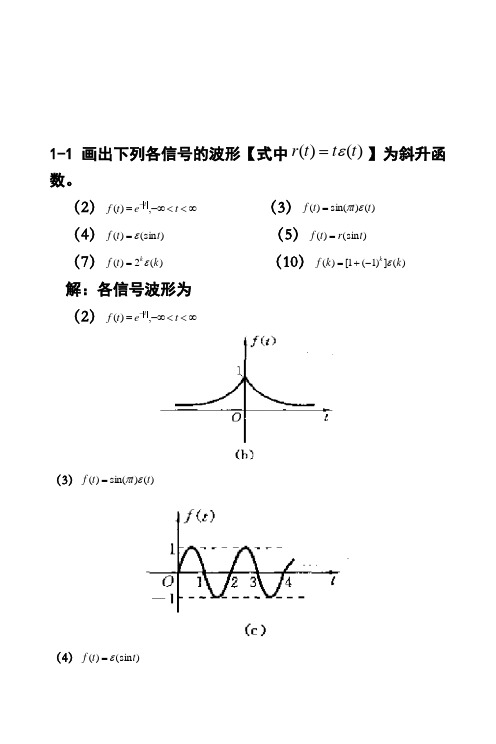
1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。
(2)∞<<-∞=-t et f t,)( (3))()sin()(t t t f επ=(4))(sin )(t t f ε= (5))(sin )(t r t f = (7))(2)(k t f kε= (10))(])1(1[)(k k f kε-+=解:各信号波形为 (2)∞<<-∞=-t et f t,)((3))()sin()(t t t f επ=(4))(sin )(t t f ε=(5))rt f=)(t(sin(7))(t f kε)(k2=(10))(])1kf kε(k)(1[=-+1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。
(1))2()1(3)1(2)(-+--+=t t t t f εεε (2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε (8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(k k k f k ---=εε解:各信号波形为(1))2()1(3)1(2)(-+--+=t t t t f εεε(2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε(8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(k k k f k ---=εε1-3 写出图1-3所示各波形的表达式。
1-4 写出图1-4所示各序列的闭合形式表达式。
1-5 判别下列各序列是否为周期性的。
如果是,确定其周期。
(2))63cos()443cos()(2ππππ+++=k k k f (5))sin(2cos 3)(5t t t f π+=解:1-6 已知信号)(t f 的波形如图1-5所示,画出下列各函数的波形。
信号与线性系统分析-(吴大正-第四版)习题答案

信号与线性系统分析-(吴大正-第四版)习题答案1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。
(1))2()1(3)1(2)(-+--+=t t t t f εεε (2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε (8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(k k k f k ---=εε解:各信号波形为(1))2()1(3)1(2)(-+--+=t t t t f εεε(2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε(8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(k k k f k---=εε1-3 写出图1-3所示各波形的表达式。
1-4 写出图1-4所示各序列的闭合形式表达式。
1-5 判别下列各序列是否为周期性的。
如果是,确定其周期。
(2))63cos()443cos()(2ππππ+++=k k k f (5))sin(2cos 3)(5t t t f π+=解:1-6 已知信号)(t f 的波形如图1-5所示,画出下列各函数的波形。
(1))()1(t t f ε- (2))1()1(--t t f ε (5))21(t f- (6))25.0(-t f(7)dtt df )( (8)dx x f t ⎰∞-)(解:各信号波形为(1))()1(t t f ε-(2))1()1(--t t f ε(5))21(t f -(6))25.0(-t f(7)dt t df )((8)dx x f t⎰∞-)(1-7 已知序列)(k f 的图形如图1-7所示,画出下列各序列的图形。
信号与线性系统分析课后答案吴大正

1-1画出下列各信号的波形(式中 )为斜升函数。
解:各信号波形为
(2)
(3)
(4)
(5)
(7)
(10)
1-2画出下列各信号的波形[ 为斜升函数]。
(1) (2)
(5) (8)
(11) (12)
解:各信号波形为
(1)
(2)
(5)
(8)
(11)
(12)
1-3写出图1-3所示各波形的表达式。
1-4写出图1-4所示各序列的闭合形式表达式。
(3) (4)
(5) (6)
解:
1-9已知信号的波形如图1-11所示,分别画出 和 的波形。
解:由图1-11知, 的波形如图1-12(a)所示( 波形是由对 的波形展宽为原来的两倍而得)。将 的波形反转而得到 的波形,如图1-12(b)所示。再将 的波形右移3个单位,就得到了 ,如图1-12(c)所示。 的波形如图1-12(d)所示。
图4-30
4.33某LTI系统,其输入为 ,输出为
式中a为常数,且已知 ,求该系统的频率响应 。
(1) (2) (3) (4)
3.13、求题3.9图所示各系统的阶跃响应。
3.14、求图所示系统的单位序列响应和阶跃响应。
3.15、若LTI离散系统的阶跃响应 ,求其单位序列响应。
3.16、如图所示系统,试求当激励分别为(1) (2) 时的零状态响应。
3.18、如图所示的离散系统由两个子系统级联组成,已知 , ,激励 ,求该系统的零状态响应 。(提示:利用卷积和的结合律和交换律,可以简化运算。)
(3) (4)
(5)
1-25设激励为 ,下列是各系统的零状态响应 。判断各系统是否是线性的、时不变的、因果的、稳定的?
线性系统分析_(吴大正_第四版)习题答案

专业课习题解析课程西安电子科技大学844信号与系统专业课习题解析课程第1讲第一章信号与系统(一)专业课习题解析课程第2讲第一章信号与系统(二)1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。
(2)∞<<-∞=-t et f t,)( (3))()sin()(t t t f επ=(4))(sin )(t t f ε= (5))(sin )(t r t f = (7))(2)(k t f kε= (10))(])1(1[)(k k f kε-+=解:各信号波形为 (2)∞<<-∞=-t et f t,)((3))()sin()(t t t f επ=(4))fεt=(sin)(t(5))trf=(sin)(t(7))t(kf kε=)(2(10))f kεk-=(k+(])1(1[)1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。
(1))2()1(3)1(2)(-+--+=t t t t f εεε (2))2()1(2)()(-+--=t r t r t r t f (5))2()2()(t t r t f -=ε (8))]5()([)(--=k k k k f εε (11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(k k k f k---=εε 解:各信号波形为(1))2()1(3)1(2)(-+--+=t t t t f εεε(2))2()1(2)()(-+--=t rt rt rtf(5))2()2()(ttrtf-=ε(8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(kkkf k---=εε1-3 写出图1-3所示各波形的表达式。
1-4 写出图1-4所示各序列的闭合形式表达式。
线性系统分析_(吴大正_第四版)习题答案

专业课习题解析课程西安电子科技大学844信号与系统专业课习题解析课程第1讲第一章信号与系统(一)专业课习题解析课程第2讲第一章信号与系统(二)1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。
(2)∞<<-∞=-t et f t,)( (3))()sin()(t t t f επ=(4))(sin )(t t f ε= (5))(sin )(t r t f = (7))(2)(k t f kε= (10))(])1(1[)(k k f kε-+=解:各信号波形为 (2)∞<<-∞=-t et f t,)((3))()sin()(t t t f επ=(4))fεt=(sin)(t(5))trf=(sin)(t(7))t(kf kε=)(2(10))f kεk-=(k+(])1(1[)1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。
(1))2()1(3)1(2)(-+--+=t t t t f εεε (2))2()1(2)()(-+--=t r t r t r t f (5))2()2()(t t r t f -=ε (8))]5()([)(--=k k k k f εε (11))]7()()[6sin()(--=k k k k f εεπ (12))]()3([2)(k k k f k---=εε解:各信号波形为(1))2()1(3)1(2)(-+--+=t t t t f εεε(2))2()1(2)()(-+--=t rt rt rtf(5))2()2()(ttrtf-=ε(8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(kkkf k---=εε1-3 写出图1-3所示各波形的表达式。
1-4 写出图1-4所示各序列的闭合形式表达式。
信号与线性系统分析-(吴大正-第四版)习题答案第二章

第二章2-1 已知描述系统的微分方程和初始状态如下,试求其零输入响应。
(1)1)0(',1)0(),()(6)('5)(''-===++-y y t f t y t y t y(4)0)0(',2)0(),()()(''===+-y y t f t y t y2-2 已知描述系统的微分方程和初始状态如下,试求其+0值)0(+y 和)0('+y 。
(2))()(,1)0(',1)0(),('')(8)('6)(''t t f y y t f t y t y t y δ====++--(4))()(,2)0(',1)0(),(')(5)('4)(''2t e t f y y t f t y t y t y t ε====++--解:2-4 已知描述系统的微分方程和初始状态如下,试求其零输入响应、零状态响应和全响应。
(2))()(,2)0(',1)0(),(3)(')(4)('4)(''t e t f y y t f t f t y t y t y t ε---===+=++解:2-8 如图2-4所示的电路,若以)(t i S 为输入,)(t u R 为输出,试列出其微分方程,并求出冲激响应和阶跃响应。
2-12 如图2-6所示的电路,以电容电压)(tuC为响应,试求其冲激响应和阶跃响应。
2-16 各函数波形如图2-8所示,图2-8(b)、(c)、(d)均为单位冲激函数,试求下列卷积,并画出波形图。
(1))(*)(21t f t f (2))(*)(31t f t f (3))(*)(41t f t f(4))(*)(*)(221t f t f t f (5))3()(2[*)(341--t f t f t f波形图如图2-9(a)所示。
信号与线性系统分析吴大正习题答案1_2

1-1画出下列各信号的波形【式中r(t) t (t)】为斜升函数。
(2) f(t) e N, t (4) f(t) (si nt) (7) f(t) 2k (k) 解:各信号波形为(2) f(t) e N, t (3) f(t) sin( t) (t) (5) f (t) r(sint) (10) f(k) [1 ( 1)k] (k)(hl(3) f(t) sin( t) (t)(4) f(t) (si nt)(d)(5) f(t) r(si nt)(7) f(t) 2k (k)(10) f(k) [1 ( 1)k] (k)2卜〔■■ 4* *0::2 3 4 5( 5 21-2画出下列各信号的波形[式中r(t)t (t)为斜升函数]。
(1) f(t) 2 (t 1) 3 (t1) (t 2)(2) f (t) r(t)2r(t1) r(t 2)(5) f(t)r(2t) (2 t)(8) f(k)k[ (k)(k 5)](11) f(k)k(k 7)](12) f(k)2k[ (3k) ( k)] sin( )[ (k)6解:各信号波形为⑴ f(t) 2 (t 1) 3 (t 1) (t 2)(5)f(t) r(2t) (2 t)r(t) 2r(t 1)r(t 2)j/O)Z\1 a7(b)⑵ f(t)4P -OF ■"■(8)f(k) k[ (k) (k 5)]O3)2 13,2<k(11)f(k) sin(~6)[ (k) (k 7)]fa)■MB -»r1.4 1 L_ K _o! 2 3 4 5 6(k)(12)f(k) 2k[ (3k) ( k)]g 8.I~o| 1 2 3 k(I)1-3写出图仁3所示各波形的表达式解图示各波形的表示式分别为:(a) /(f) — 2e(z — 1)—€(『一1) — F (t — 2.) (b)/ (t ) — (t —1)e (r — 1)—2(/—1)c ( f —1) — (t — 3)c ( / 一3)(= 10sint7rZ )_£(?) 一 M — 1 丿_= 1 — 2(r + 2) £(? + 2) — £(r + l)] + (r — 1) c(t H-l) —— 1)12.Ar>1.LIo i tb/(r)正菠函數—1 O l 23(b) I AO(d)1-4写出图1-4所示各序列的闭合形式表达式解图示各序列的闭台形式表示式分别为:(a)/(A)=讥+ 2) (b)/(A) = —3)——7)(c)/«) =e(-^+2) (d)f(k)= (一1)¥⑷1-5判别下列各序列是否为周期性的。
信号与线性系统分析-(吴大正-第四版)习题答案

信号与系统习题解析C1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。
(2)∞<<-∞=-t et f t,)( (3))()sin()(t t t f επ=(4))(sin )(t t f ε= (5))(sin )(t r t f = (7))(2)(k t f kε= (10))(])1(1[)(k k f kε-+=解:各信号波形为 (2)∞<<-∞=-t et f t,)((3))()sin()(t t t f επ=(4))fεt=(sin)(t(5))trf=(sin)(t(7))t(kf kε=)(2(10))f kεk-=(k+(])1(1[)1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。
(1))2()1(3)1(2)(-+--+=t t t t f εεε (2))2()1(2)()(-+--=t r t r t r t f (5))2()2()(t t r t f -=ε (8))]5()([)(--=k k k k f εε (11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(k k k f k---=εε 解:各信号波形为(1))2()1(3)1(2)(-+--+=t t t t f εεε(2))2()1(2)()(-+--=t rt rt rtf(5))2()2()(ttrtf-=ε(8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(kkkf k---=εε1-3 写出图1-3所示各波形的表达式。
1-4 写出图1-4所示各序列的闭合形式表达式。
1-5 判别下列各序列是否为周期性的。
如果是,确定其周期。
(2))63cos()443cos()(2ππππ+++=k k k f(5))sin(2cos 3)(5t t t f π+=解:1-6 已知信号)(t f 的波形如图1-5所示,画出下列各函数的波形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1-1画出下列各信号的波形【式中r(t) t (t)】为斜升函数。
(2) f(t) e N, t (4) f(t) (si nt) (7) f(t) 2k (k) 解:各信号波形为(2) f(t) e N, t (3) f(t) sin( t) (t) (5) f (t) r(sint) (10) f(k) [1 ( 1)k] (k)(hl(3) f(t) sin( t) (t)(4) f(t) (si nt)(d)(5) f(t) r(si nt)(7) f(t) 2k (k)(10) f(k) [1 ( 1)k] (k)2卜〔■■ 4* *0::2 3 4 5( 5 21-2画出下列各信号的波形[式中r(t)t (t)为斜升函数]。
(1) f(t) 2 (t 1) 3 (t1) (t 2)(2) f (t) r(t)2r(t1) r(t 2)(5) f(t)r(2t) (2 t)(8) f(k)k[ (k)(k 5)](11) f(k)k(k 7)](12) f(k)2k[ (3k) ( k)] sin( )[ (k)6解:各信号波形为⑴ f(t) 2 (t 1) 3 (t 1) (t 2)(5)f(t) r(2t) (2 t)r(t) 2r(t 1)r(t 2)j/O)Z\1 a7(b)⑵ f(t)4P -OF ■"■(8)f(k) k[ (k) (k 5)]O3)2 13,2<k(11)f(k) sin(~6)[ (k) (k 7)]fa)■MB -»r1.4 1 L_ K _o! 2 3 4 5 6(k)(12)f(k) 2k[ (3k) ( k)]g 8.I~o| 1 2 3 k(I)1-3写出图仁3所示各波形的表达式解图示各波形的表示式分别为:(a) /(f) — 2e(z — 1)—€(『一1) — F (t — 2.) (b)/ (t ) — (t —1)e (r — 1)—2(/—1)c ( f —1) — (t — 3)c ( / 一3)(= 10sint7rZ )_£(?) 一 M — 1 丿_= 1 — 2(r + 2) £(? + 2) — £(r + l)] + (r — 1) c(t H-l) —— 1)12.Ar>1.LIo i tb/(r)正菠函數—1 O l 23(b) I AO(d)1-4写出图1-4所示各序列的闭合形式表达式解图示各序列的闭台形式表示式分别为:(a)/(A)=讥+ 2) (b)/(A) = —3)——7)(c)/«) =e(-^+2) (d)f(k)= (一1)¥⑷1-5判别下列各序列是否为周期性的。
如果是,确定其周期(2) f2(k) cos(务k 4) cos(- k -) (5) f5(t) 3cost 2sin( t)解:⑵ 该序列的周期应为亡叫沪+手]和g打尹+話的最小公倍数C叫—和的周期为8,心(爭一劄的周期为6化该序列的周期为24.⑸该序列不是周期的忙。
视的周期为益,sin(nz)的周期为Z若序列周期为八则T是2的整数倍,也是%的整数倍,这不成立,二不是周期的事1-6已知信号f(t)的波形如图1-5所示,画出下列各函数的波形■/C)*42[ --2O J图1-5 .>■9t(1)f(t 1) (t)(2)f(t1) (t 1)(5)f(12t)(7)df(t) dt(8)tf (x)dx⑹ f(0.5t 2)解:各信号波形为(1) f(t 1) (t)(6) f(0・5t 2)df(t) ⑺ dti</(I- 2f)X…I 1 1 3 tM ___Ao. 5r—2)O 4 t? t(f)1-7已知序列f(k)的图形如图1-7所示,画出下列各序列的图形f(ky-4-3-2-10 1 2 3 4 b k图1-7(1)f(k2) (k)(2)f(k2) (k 2)(3)f(k2)[ (k)(k 4)](4)f(k 2)(5)f( k2) ( k1)(6)f(k)f(k 3)解:/O — ?:£(▲3•—•■01234567 呂(h)3i12Io1 3 :3 4 9 6 B-31Cf) a〉1-9已知信号的波形如图1-11所示,分别画出f(t)和黔的波形-2 0 23 1-11解:由图1-11知,f(3 t)的波形如图1-12(a)所示(f (3 t)波形是由对f(3 2t)的波形展宽为原来的两倍而得)。
将f(3 t)的波形反转而得到f(t 3)的波形,如图1- 12(b)所示。
再将f(t 3)的波形右移3个单位,就得到了f(t),如图1- 12(c)所示。
蛭的波形如图1-12(d)所示。
dt1-10计算下列各题。
d2(2)(1八d rt(1)2 cost sin(2t)dt2(t)t) [e dt(t)](5)[t2sine;)] (t42)dt(8)t(1 x)'(x)dx—4 (J13O7|d/Q) Cl)山J2 _ 解 (1)护{[cosr + sin(27),(T )} =sinl + 2cos(2r)〉(r) + [cosl + sin(2r )2^(Z)} =£{[— sinz + 2cos(2r)~€(z) +5(7)}=_— cost — 4sin(2r )_£(f) + _— sin/ -r 2cos( 2f) _5( r) + F( D=[一 cosr — 4sin(2d (r)十 2&(r) +*⑷(2) (1 -r)护-0(C]首先求 扌[刊⑺]=-刊⑴+ E ⑴=一5(刀+/(门+5(门 =^(z )这里注意尹丫⑴=5\t ) +M )=y (n 一於心=/&)+/&) 这里注意力'(门=_"则(1 —(5) t2一宇)]次(F 十2)df = 严十sint^)] = 3”―。
o 4 - 4 —2fV -(8) | (1 -x)y(x)dx叩-5C=I E(?'(z) —(— 1 )tJ(jr)Zdjr = 扩(工】血十| S(jc)dj=8U)m1-12如图1-13所示的电路,写出(1)以u c(t)为响应的微分方程<(2)以i L(t)为响应的微分方程图1-13解 由KVL 可得 心(z ) = zz L (r ) +々(J 由 KCL 可得 z L (r )= 〃(" + %(『) 各元件端电流和端电压的关系为稍加整理得以心门为响应的微分方程々:"([)+ ^72((/(匸)+C2)选定以订(i )为响应°联立各式消去其余中间参量可得M 執⑺+拾⑴+皿) R dr1RLC Us稍加整理得以i"为响应的微分方程<1)选定uc<t )为响应,联立以上各式消去其余中间参量得 1 (、 LCWs (Z )1-20写出图1-18各系统的微分或差分方程。
图 1-18解(“系统框图中含有两个积分器•则该系统是二阶系统,设最下方积分器输出则co各积分器输入为才"(“山'(J 3左方加法器的输出为『⑺=“ 一2") —3/⑺即*a)+3/(r) +2jr(r) = /(r)由右方加法器的输出,得y(C =工"⑺一2") 由上式得/(r)=[九)了—2[")了3y (r) = [3才"(门丁一2[3/'(z)了2y(f)= [2x\t^ — 2[2<r'(r)]将以上三式相加,得/(7) +3$(" + 2》心)=[『(7)+ 3x7?) + 2z(r) — 2[『(门 + 3x z(?) + 2x(r)T考虑到/(/)= f (f) + 3工£) +力⑺,上式右端等于/(Z) -2/</),故得『(门 + 3$(门+幼(门=/(7) -2/(/)此即为系统的微分方程。
(b)系统框图中含有三个积分器,则该系统为三阶系统。
设最下方积分器输出为文(门・则各积分器输人为才⑺,Z(r) 。
左端加法器的输出为x w<t) = /⑺一2/⑺一3文⑺即才少(/〉一2才'(力 + 3;r(r) = f(t')由右方加法器的输出得yCt) = T'(r) — 4 工(r)由上式得/(F) = ⑺]"一4/(门2y(r) = [2F(C]" — 4[2T(r)] 3y(F) = —4[3彳(刀]将以上三式相加得y w(n+2y(n +3)⑴=Lr"(f) + 2,( f) + 3J T(/)T — 4[工气『)+ 2,(r) + 3z(f)]即y"(r) + 2j/(r)+3y(D = /(r) -4/(z)此即为系统的微分方程,9则各个迟延单元的输出为讥一1)"(—2)。
左方加法器的输出为= fCk) + 2x(k —1) — 4乂(怡一2) 即工(走)一2工以-1)十4工^一2) = g右方加法器的输出为yCk) =2乞"一1) 一乂"一2)由上式移位可得—2y(k — 1) = 2 [—2x(k— 2)[ —2x(k— 3匸4曲一2) = 2[4工4一3)] — [4工(〃一4)]将以上三式相加得$4) -2y4 — l)+4y徒一2)=2\_x{k— 1) —— 2)十4工(& —3)] —— 2) —2x(k— 3)十4才(斤—4)2 考虑到式上(小一2乂(怡一1)+4艾(怡一2〉= fS及其迟延项9町得y<k) - 2y(.k - 1) + iy<k - 2) = 2用一1〉一用一2)此即为框图中系统的差分方程,各个迟延单元的输出为一1)山仏一2)左方加法器输出为x(k') = f(k) — 2x(k — 2)即工5 — 2工 5 —2、= fCk)右方加法器输出为_y(&) = 2彳仏)+3;r (怡一1) — 4«r (斤一2)由上式移位得— 2),"-2) = 2[—2文(&一2)] + 3[—2文(&一3〉]一4[一2幺仏一4)] 将以上两式相加得〉乂力〉一2》(怡一2)=2[文(&) —2x(k— 2)] + 3[«r (& — 1) —2x(.k— 3)_ — 4^( k— 2) —2x(.k— 4)] 考虑到式x(k)-2xCk-2) = fg及其迟延项,町得,(耐一2,仏一2) = 2f(k} +3/(^- 1) -4/(^-2)此即为框图中系统的差分方程’1-23 设系统的初始状态为 x(0) ,激励为 f ( ) ,各系统的全响应 y() 与激励和初始状 态的关系如下,试分析各系统是否是线性的。
