六年级数学上册 《比较线段的长短》同步练习2 鲁教版
鲁教版(五四制)》六年级下册5.2比较线段的长短学案

鲁教版(五四制)》六年级下册5.2比较线段的长短学案第 2 页第 3 页第 4 页AD=( )+( )=( )-( ) BC=( )+( )=( )-( )2、在直线AB 上有一点C ,若AB=5cm,BC=3cm,则AC=( )一、 线段的中点 如图,点M 把线段AB 分成两条线段AM 、MB,且AM=MB 此时,点M 叫线段AB 的中点。
语言叙述为:把一条线段分成相等的两条线段的点, 叫这条线段的中点。
如上图,因为 M 是AB 的中点 所以 AM=BM=AB 21 或AB=2AM=2BM 应用练习: 1、EF=6cm,点P 是EF 的中点,则PE= ,PF= 2、如图,AB=9,BC=3,点M 是AC 的中点, 则AM= ,BM= 3、以下给出的四个语句中,结论不正确的有( ) A 、延长线段AB 到C B 、如果线段AB=BC ,则B 是线段AC 的中点 C 、线段和射线都可以看作直线上的一部分 D 、如果线段AB+BC=AC ,那么A ,B ,C 在同一直线上4、下列说法正确的是( )A 、两点之间的连线中,直线最短B 、若P 是线段AB 的中点,则AP=BPC 、若AP=BP ,则P 是线段AB 的中点D 、两点之间的线段叫做者两点之间的距离 5、已知如图,点C 在线段AB 上,线段AC =10,BC =6,点M 、N 分别是AC 、BC 的中点,(1)求MN 的长度。
(2)根据⑴的计算过程与结果,设AC +BC = ,其它条件不变,你能猜想出MN 的长度吗?请用一句简洁的语言表达你发现的规律。
(3)若把⑴中的“点C 在线段AB 上”改为“点C 在直线AB 上”,结论又如何?请说明理由。
二、 课堂小结 1、 两点之间的距离 2、 比较线段大小 3、 尺规作图 4、 线段的中点 三、 集中练习 1、已知两根木条,一根长60cm ,一根长100cm ,将它们的一端重合,放在同一条直线上,此时两根木条的中点之间的距离是 。
新鲁教版五四制六年级数学下册基本平面图形(比较线段的长短)同步测试及答案.docx

鲁教版(五四制)六年级下册知能提升作业(二)(30分钟50分)一、选择题(每小题4分,共12分)AB,若D为AC的中点,则BD等于1.已知线段AB=8,延长AB到C,使BC=12( )(A)1 (B)2 (C)3 (D)42.已知,如图,AD>BC,则AC与BD的关系为( )(A)AC>BD (B)AC=BD(C)AC<BD (D)以上情况都有可能3.如图,在数轴上有A,B,C,D,E五个整数点(即各点均表示整数),且AB=2BC=3CD=4DE,若A,E两点表示的数分别为-13和12,那么,该数轴上上述五个点所表示的整数中,离线段AE的中点最近的整数是( )(A)-2 (B)-1 (C)0 (D)2二、填空题(每小题4分,共12分)4.已知线段AB=8 cm,在直线AB上画线段BC使BC=3 cm,则线段AC=_________.5.已知线段AB被顺次分为1∶2∶3三部分,已知第一部分的中点和第三部分的中点之间的距离是6.4 cm,那么线段AB的长为_________.6.已知线段AB=10 cm,直线AB上有一点C,且BC=4 cm,M是线段AC的中点,则AM=cm.三、解答题(共26分)7.(8分)已知线段a,b,c(a>c)(如图所示).作线段AB,使AB=a+b-c.8.(8分)如图所示,已知AB=80,M为AB的中点,P在AB上,N为PB的中点,且NB=14,求PA的长.【拓展延伸】9.(10分)情景一:如图①,从教室门口B到图书馆A,总有不少同学不走人行道而横穿草坪.情景二:如图②,A,B是河流l两旁的两个村庄,现要在河边修一个引水站P向两村供水,为了使所需的管道最短,点P需建在A,B连线与l的交点处.这是为什么?请你用所学知识来说明.你赞同以上哪种做法?你认为应用科学知识为人们服务应注意什么?答案解析AB,AB=8,1.【解析】选B.如图,BC=12所以BC=4,AC=AB+BC=12,AC=6,因为D为AC的中点,所以CD=12所以BD=CD-BC=2.2.【解析】选A.因为AD>BC,所以AD-CD>BC-CD,即AC>BD.3.【解析】选B.根据图示知,AE=25,AE=12.5,所以12所以AE的中点所表示的数是-0.5;因为AB=2BC=3CD=4DE,所以AB∶BC∶CD∶DE=12∶6∶4∶3;而12+6+4+3恰好是25,就是A点和E点之间的距离,所以AB=12,BC=6,CD=4,DE=3,所以这5个点的坐标分别是-13,-1,5,9,12,所以在上面的5个点中,距离-0.5最近的整数是-1.4.【解析】根据题意,分类讨论.点C可能在线段AB上,也可能在AB的延长线上.若点C在线段AB上,则AC=AB-BC=8-3=5(cm);若点C在AB的延长线上,则AC=AB+BC=8+3=11(cm).答案:5 cm或11 cm5.【解析】设三部分长分别为x cm,2x cm,3x cm,再根据中点定义可得0.5x+2x+1.5x=6.4,所以x=1.6,所以线段AB的长为1.6×(1+2+3)=9.6(cm).答案:9.6 cm6.【解析】分两种情况:如图(1),点C在线段AB右边:因为AB=10 cm,BC=4 cm,所以AC=AB+BC=10+4=14(cm).AC=7 cm.因为M为AC的中点,所以AM=12如图(2),点C在线段AB之间:因为AB=10 cm,BC=4 cm,所以AC=AB-BC=10-4=6(cm).AC=3 cm.因为M为AC的中点,所以AM=12综上可得AM=7 cm或3 cm.答案:7或37.【解析】画法:(1)画射线AE.(2)在射线AE上顺次截取AC,CD,使AC=a,CD=b.(3)在线段AD上截取线段DB,使DB=c,则线段AB为所画线段(如图).8.【解析】因为N为PB的中点,所以PB=2NB.又因为NB=14,所以PB=2×14=28.又因为AP=AB-PB,AB=80,所以AP=80-28=52.9.【解析】两个情景都是根据两点之间线段最短的原理来做的.我赞同第二种做法.我们在利用科学的同时,必须注意保护我们周围赖以生存的生态环境.。
六年级数学上册4.2比较线段长短练习鲁教版五四学制.doc

4.2 比较线段的长短1、两点之间的全部连线中,______最短.2、如图,点C是线段AB上的点,点E是线段CB的中点,D是线段AC的中点.(1)若AC 2cm,BC 3cm,则DE=______cm.(2)若AB 5cm,AD 1cm,则EB ______cm.A D C E B2cm 3cm3、如图,AB ___ ___ ___;AB a ___ ___.A m b a B4、平面上M、N两点间的距离指( )经过M、N两点的直线B.射线MNM、N两点间的线段D.M、N两点间的线段长5、已知点C是线段AB上的点,则以下条件中不能够确立C是AB中点的是()A.ACCB 1B.ACABC.AB2CBD.ACCBAB 26、以下说法中,不正确的选项是( )A.任何线段都能胸怀它们的长短B.由于线段有长度,因此它们之间能比较长短C.利用圆规配合刻度尺能够进行线段的胸怀,也能比较它们的长短D.两条直线也能进行胸怀和比较大小7、请目测图中线段AB和CD的长短,再用刻度尺检测一下你目测的结果能否正确.CA D B8、如图,点P在线段AB上,点M、N分别是线段AB、AP的中点,若AB 16cm,BP 6cm,求线专心爱心专心1段MN的长.A NMP B9、如图,AB8cm,AC=13cm,设点E、F分别是线段AB、AC的中点,求EF.A E FB C10、某旅馆在从头装饰后,准备在大厅的主楼梯上铺设某种红色地毯,已知这类地毯每平方米售价30元,主楼梯道宽2米,其侧面以下图,求购置地毯起码需要多少元?2.65.8米11、如图,是一个由8根火柴棒摆成的长方形,再取多少根火柴棒从头摆一个长方形,使新长方形的面积是原长方形面积的3倍.12、如图,线段CB=4cm,DB7cm,且D是AC的中点,则AB______cm,AC=______cm.A D C B13、已知M是线段AB的中点,AM10厘米,若在直线AB上有一点C,使AB:BC5:2,求MC的长度.14、假如点B在线段AC上,那么以下式子中,ABBC,AB 1BCAC中AC,AC2AB,AB2能表示B是线段AC的中点的有()A.1个B.2个C.3个D.4个15、已知线段AB5厘米,在直线AB上画BC2厘米,则AC的长是___________.16、以以下图所示,在一条笔挺的公路l双侧,分别有A,B两个乡村,此刻要在公路l上建一供电站C,使供电站C到A,B两村所用电线之和最短.问供电站C的地点应当怎样确立?lB17、在一条直线上按序有n个点A1,A2,A3,A n,且A1A2A2A3A3A4=A n1A n,把以这n个专心爱心专心2点为端点的全部线段的中点都染成红色,那么红色点有多少个?为何?18、以以下图所示,以A1,A2,A3,,A n为端点的线段有多少条?若线段A i A i1的长度为a i(i1,2,,n1),试求出全部线段长的总和.A1A2A3An1A n19、点A,B在直线l上,AB5cm,画点C,使点C是在直线l上到点A的距离是3的点,则点C到点B的距离是____________cm.20、已知线段AB,延伸AB到C,使BC1AB,D为AC中点,若BD3cm,求AB的长.421、从县城O出发的一条直线公路两旁共有10个村需要安装自来水(从县城出发),县城与A村的距离是30千米,其他各村之间的距离以以下图所示.现有粗细两种水管能够采用,粗管能够足够供给全部各村用水,细管只好供一个村用水.安装花费,粗管每千米8000元,细管每千米2000元.把粗管和细管相互搭配,相互连结,能够降低工程总花费.请你设计一种最节俭的安装方案,并求出所需总花费.30524232225O AB C DEF G HM22、以以下图所示是某城市街道图,纵横各有 5条路,假如从A处走到H处(只好由北到南,由西向东),那么共有多少种不一样的走法.AH23、以以下图所示,甲、乙两人同时从A,B两地相向而行,甲骑自行车,乙步行,出发后40min在P1处相遇;而后甲、乙持续前行,甲到B地后立刻返回向A地骑行,从P1处起40min后甲又在P2处追上乙;今后两人持续前行,甲从A地再返回的路上第二次在P处相遇.求证:P,P,P 是AB的四平分点.3 1 2 3A P P P B3 2 124、已知线段AB 15cm,点C在直线AB上,BC 5cm,则线段AC为()A.20cm B.10cm专心爱心专心3C.20cm或10cm D.不确立25、已知线段AB,在AB的延伸线上取一点C,使AC 2BC,在AB的反向延伸线上取一点D,使DA 2AB,那么线段AC是线段DB的_____________.26、在连结两点的全部线中,最短的是.答案:1、线段2、(1)2.5(2)1.53、m,b,a,m,b4、D5、D6、D7、CD和AB相等.8、MN3cm、2.5cm10、(2.6 5.8)230504元9EF11、再取4根摆成以下图12、10,6 13 、18厘米或2厘米14、C15 、7厘米或3厘米16、直线AB与l的交点上17、(2n3)个18、1g(n1)a12g(n2)a23g(n3)a3(n2)g2a n2(n1)ga n1.19、8或22、8cm21、414000元22、7023、B用到P也用B P.到,用,3乙由40min,由1240min,故P1P甲从1再到240min共行PP到1212∴甲速是乙速的3倍由第三次相遇知PA AP 3PP2 3 2 3即P2P32AP3 3P2P3,P2P3AP3又由第一次相遇知AP 3PB1 1即2PP PP 3PB,得PP PB2 3 1 2 1 2 3 1专心爱心专心4故AP PP PP PB3 3 2 2 1 1即PPP是AB的四平分点.1 2 324、C 25 、226 、线段3专心爱心专心5。
2020-2021鲁教版(五四制)数学六年级下册-5.2 比较线段的长短 课堂练习含答案

2020-2021学年鲁教版数学六年级下册-5.2 比较线段的长短课堂练习一、选择题1.如果A、B、C在同−条直线上,线段AB=6cm,BC=2cm,则A、C两点间的距离是()A. 8 cmB. 4 cmC. 8 cm或4 cmD. 无法确定2.如图,已知点C在线段AB上,线段AC=4,线段BC的长是线段AC长的两倍,点D是线段AB的中点,则线段CD的长是()A. 1B. 2C. 3D. 43.点E在线段CD上,下面的等式:①CE=DE;②DE=12CD;③CD=2CE;④CD=12DE,其中能表示E是CD中点的有()A. 4个B. 3个C. 2个D. 1个4.在直线l上顺次取A、B、C三点,使得AB=5cm,BC=3cm,如果O是线段AC的中点,那么线段OB的长度是()A. 0.5cmB. 1 cmC. 1.5cmD. 2 cm5.将一根拉直的绳子用线段AB表示,现从绳子上的一点C处将绳子剪断,剪断后的两段绳子中较长的一段是20cm,若AC=45BC,则这段绳子的原长是()A. 45cmB. 36cmC. 25cmD. 16cm6.如图,C是AB的中点,D是BC的中点,则下列等式中正确的是()①DB=3AD−2AB;②CD=13AB;③DB=2AD−AB;④CD=AD−CB.A. ①②B. ③④C. ①④D. ②③7.如图,线段BD=14AB=15CD,点E,F分别是线段AB,CD的中点,EF=14cm,则线段AB长()A. 16B. 12C. 10D. 148.下列说法正确的个数是()①射线MN与射线NM是同一条射线;②两点确定一条直线;③两点之间直线最短;④若2AB=AC,则点B是AC的中点A. 1个B. 2个C. 3个D. 4个9.某同学用剪刀沿直线将一片平整的银杏叶剪掉一部分(如图),发现剩下的银杏叶的周长比原银杏叶的周长要小,能正确解释这一现象的数学知识是()A. 两点之间线段最短B. 两点确定一条直线C. 垂线段最短D. 经过直线外一点,有且只有一条直线与这条直线平行10.图中下列从A到B的各条路线中最短的路线是()A. A→C→G→E→BB. A→C→E→BC. A→D→G→E→BD. A→F→E→B11.下列生活实例中,数学原理解释错误的一项是()A. 从一条河向一个村庄引一条最短的水渠,其中数学原理是:在同一平面内,过一点有且只有一条直线垂直于已知直线B. 两个村庄之间修一条最短的公路,其中的数学原理是:两点之间线段最短C. 把一个木条固定到墙上需要两颗钉子,其中的数学原理是:两点确定一条直线D. 从一个货站向一条高速路修一条最短的公路,其中的数学原理是:连结直线外一点与直线上各点的所有线段中,垂线段最短12.下列四个日常现象:①用两根钉子就可以把一根木条固定在墙上;②把弯曲的公路改直,就能够缩短路程;③用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长要小;④沿桌子的一边看,可将桌子排整齐.其中,可以用“两点之间,线段最短”来解释的现象是().A. ①③B. ②③C. ①④D. ②④二、填空题13.把一段弯曲的河流改直,可以缩短航程,其理由是______ .14.如下图,从小华家去学校共有4条路,第______条路最近,理由是______.15.如图所示,在一条笔直公路p的两侧,分别有甲、乙两个村庄,现要在公路p上建一个汽车站,使汽车站到甲、乙两村的距离之和最小,你认为汽车站应该建在______处(填A或B或C),理由是______.16.如图,点B是线段AC上一点,点O是线段AC的中点,且AB=20,BC=8.则线段OB的长为______.17.在直线上顺次取A、B、C三点,使得AB=5cm,BC=3cm.如果O是线段AC的中点,那么线段OC的长度是______.AB,D、E分别是BC、AB的中点,则18.如图,已知AB=6,C是线段AB上一点,且AC=23DE=________.三、解答题19.已知线段AB=20,M是线段AB的中点,P是线段AB上任意一点,N是线段PB的中点.(1)当P是线段AM的中点时,求线段NB的长;(2)当线段MP=1时,求线段NB的长;20.如图,已知线段a和线段AB,(1)延长线段AB到C,使BC=a(尺规作图,不写作法,保留作图痕迹);(2)在(1)的条件下,若AB=5,BC=3,点O是线段AC的中点,求线段OB的长.答案1.【答案】C2.【答案】B3.【答案】B4.【答案】B5.【答案】B6.【答案】C7.【答案】A8.【答案】A9.【答案】A10.【答案】D11.【答案】A12.【答案】B13.【答案】两点之间,线段最短14.【答案】③;两点之间,线段最短15.【答案】B两点之间线段最短16.【答案】617.【答案】4cm18.【答案】219.【答案】解:(1)如图,∵M是线段AB的中点,AB=20,AB=10,∴MA=12∵P是线段AM的中点,AM=5,∴AP=12∴PB=AB−AP=20−5=15,∵N是线段PB的中点,∴NB=1PB=7.5;2(2)由(1)知MB=MA=10,∵MP=1,①当P在M左边时,如图:∴BP=MB+MP=11,∵N是线段PB的中点,∴NB=1PB=5.5,2②当P在M右边时,如图:∴BP=MB−MP=9,∵N是线段PB的中点,∴NB=1PB=4.5.220.【答案】解:(1)如图:(2)∵AB=5,BC=3,∴AC=8,∵点O是线段AC的中点,∴AO=CO=4,∴BO=AB−AO=5−4=1,∴OB长为1.。
《4.2 第2课时 线段长短的比较与运算》教案、同步练习、导学案(3篇)
《第2课时线段长短的比较与运算》教案【教学目标】1.会画一条线段等于已知线段,会比较线段的长短;2.体验两点之间线段最短的性质,并能初步应用;(重点)3.知道两点之间的距离和线段中点的含义;(重点)4.在图形的基础上发展数学语言,体会研究几何的意义.【教学过程】一、情境导入比较两名同学的身高,可以有几种比较方法?向大家说说你的想法.二、合作探究探究点一:线段长度的比较和计算【类型一】比较线段的长短为比较两条线段AB与CD的大小,小明将点A与点C重合使两条线段在一条直线上,点B在CD的延长线上,则( )A.AB<CD B.AB>CDC.AB=CD D.以上都有可能解析:由点A与点C重合使两条线段在一条直线上,点B在CD的延长线上,得AB>CD,故选B.方法总结:比较线段长短时,叠合法是一种较为常用的方法.【类型二】根据线段的中点求线段的长如图,点C是线段AB上一点,点M是AC的中点,点N是BC的中点,如MC比NC长2cm,AC比BC长( )A.2cm B.4cm C.1cm D.6cm解析:点M是AC的中点,点N是BC的中点,∴AC=2MC,BC=2NC,∴AC -BC=(MC-NC)×2=4cm,即AC比BC长4cm,故选B.方法总结:根据线段的中点表示出线段的长,再根据线段的和、差求未知线段的长度.【类型三】已知线段的比求线段的长如图,B、C两点把线段AD分成2∶3∶4的三部分,点E是线段AD的中点,EC=2cm,求:(1)AD的长;(2)AB∶BE.解析:(1)根据线段的比,可设出未知数,根据线段的和差,可得方程,根据解方程,可得x的值,根据x的值,可得AD的长度;(2)根据线段的和差,可得线段BE的长,根据比的意义,可得答案.解:(1)设AB=2x,则BC=3x,CD=4x,由线段的和差,得AD=AB+BC+CD=9x.由E为AD的中点,得ED=12AD=92x.由线段的和差得CE=DE-CD=92x-4x=x2=2.解得x=4.∴AD=9x=36(cm);(2)AB=2x=8(cm),BC=3x=12(cm).由线段的和差,得BE=BC-CE=12-2=10(cm).∴AB∶BE=8∶10=4∶5.方法总结:在遇到线段之间比的问题时,往往设出未知数,列方程解答.【类型四】当图形不确定时求线段的长如果线段AB=6,点C在直线AB上,BC=4,D是AC的中点,那么A、D两点间的距离是( )A.5 B.2.5 C.5或2.5 D.5或1解析:本题有两种情形:(1)当点C在线段AB上时,如图:AC=AB-BC,又∵AB=6,BC=4,∴AC=6-4=2,D是AC的中点,∴AD=1;(2)当点C在线段AB的延长线上时,如图:AC=AB+BC,又∵AB=6,BC=4,∴AC=6+4=10,D是AC的中点,∴AD =5.故选D.方法总结:解答本题关键是正确画图,本题渗透了分类讨论的思想,体现了思维的严密性,在今后解决类似的问题时,要防止漏解.探究点二:有关线段的基本事实如图,把弯曲的河道改直,能够缩短航程,这样做的根据是( )A.两点之间,直线最短B.两点确定一条线段C.两点确定一条直线D.两点之间,线段最短解析:把弯曲的河道改直缩短航程的根据是:两点之间,线段最短.故选D.方法总结:本题考查了线段的性质,熟记两点之间线段最短是解题的关键.三、板书设计1.线段的比较与性质(1)比较线段:度量法和叠合法.(2)两点之间线段最短.2.线段长度的计算(1)中点:把线段AB分成两条相等线段的点.(2)两点间的距离:两点间线段的长度.【教学反思】本节课通过比较两个人的高矮这一生活中的实例让学生进行思考,从而引出课题,极大地激发了学生的学习兴趣;并通过动手操作,亲身体验用叠合法比较线段的长短.教师要尝试让学生自主学习,优化课堂教学中的反馈与评价.通过评价,激发学生的求知欲,坚定学生学习的自信心.《第2课时线段长短的比较与运算》同步练习能力提升1.如图所示,要在直线PQ上找一点C,使PC=3CQ,则点C应在( )A.P,Q之间B.点P的左边C.点Q的右边D.P,Q之间或在点Q的右边2.如果线段AB=5 cm,BC=3 cm,那么A,C两点间的距离是( )A.8 cmB.2 cmC.4 cmD.不能确定3.C为线段AB的一个三等分点,D为线段AB的中点,若AB的长为6.6 cm,则CD的长为( )A.0.8 cmB.1.1 cmC.3.3 cmD.4.4 cm4.如图所示,C是线段AB的中点,D是CB上一点,下列说法中错误的是( )A.CD=AC-BDB.CD=BCC.CD=AB-BDD.CD=AD-BC5.下面给出的4条线段中,最长的是( )A.dB.cC.bD.a6.已知A,B是数轴上的两点,点A表示的数是-1,且线段AB的长度为6,则点B表示的数是.7.已知线段AB=7 cm,在线段AB所在的直线上画线段BC=1 cm,则线段AC= .8.如图所示,设A,B,C,D为4个居民小区,现要在四边形ABCD内建一个购物中心,试问把购物中心建在何处,才能使4个居民小区到购物中心的距离之和最小?请说明理由.9.如图所示,点C是线段AB上一点,点M是线段AC的中点,点N是线段BC的中点.(1)如果AB=20 cm,AM=6 cm,求NC的长;(2)如果MN=6 cm,求AB的长.10.在桌面上放了一个正方体的盒子,如图所示,一只蚂蚁在顶点A处,它要爬到顶点B处找食物,你能帮助蚂蚁设计一条最短的爬行路线吗?要是食物在顶点C处呢?★11.已知线段AB=12 cm,直线AB上有一点C,且BC=6 cm,M是线段AC的中点,求线段AM的长.创新应用★12.在同一条公路旁,住着5人,他们在同一家公司上班,如图,不妨设这5人的家分别住在点A,B,D,E,F所示的位置,公司在点C处,若AB=4 km,BC=2 km,CD=3 km,DE=3 km,EF=1 km,他们全部乘出租车上班,车费单位报销.出租车收费标准是:起步价6元(3 km以内,包括3 km),超过3 km超出的部分每千米1.5元(不足1 km,以1 km计算),每辆车能容纳3人.(1)若他们分别乘出租车去上班,公司应支付车费多少元?(2)如果你是公司经理,你对他们有没有什么建议?参考答案能力提升1.D 注意本题中的条件是在直线PQ上找一点C,所以C可以在P,Q之间,也可以在点Q的右侧.2.D A,B,C三点位置不确定,可能共线,也可能不共线.3.B如图,AD=AB=3.3cm,AC=AB=2.2cm,所以CD=AD-AC=3.3-2.2=1.1(cm).4.B5.A6.-7或5 点B可能在点A的左侧,也有可能在点A的右侧.若点B在点A的左侧,则点B表示的数比点A表示的数小6,此时点B表示的数为-7;若点B在点A的右侧,则点B表示的数比点A表示的数大6,此时点B表示的数为5.7.8 cm或6 cm 分两种情况:①点C在线段AB内,②点C在线段AB的延长线上.8.解:连接AC,BD,交点P即为购物中心的位置.理由:根据公理“两点之间,线段最短”,要使购物中心到A,B,C,D的距离和最小,购物中心既要在AC上,又要在BD上.9.解:(1)因为M为AC的中点,所以MC=AM.又因为AM=6cm,所以AC=2×6=12(cm).因为AB=20cm,所以BC=AB-AC=20-12=8(cm).又因为N为BC的中点,所以NC=BC=4(cm).(2)因为M为AC的中点,所以MC=AM.因为N为BC的中点,所以CN=BN.所以AB=AC+BC=2(MC+CN)=2MN=2×6=12(cm).10.解:如图所示,是该正方体的侧面展开图.食物在B处时的最短路线为线段AB,食物在C处时的最短路线为线段AC.11.解:(1)当点C在线段AB上时,如图①,图①因为M是AC的中点,所以AM=AC.又因为AC=AB-BC,AB=12cm,BC=6cm,所以AM=(AB-BC)=×(12-6)=3(cm).(2)当点C在线段AB的延长线上时,如图②,图②因为M是AC的中点,所以AM=AC.又因为AC=AB+BC,AB=12cm,BC=6cm,所以AM=AC=(AB+BC)=×(12+6)=9(cm).故AM的长度为3cm或9cm.创新应用12.解:(1)在A处乘车的车费为6+(4+2-3)×1.5=10.5(元);在B处乘车的车费为6元;在D处乘车的车费为6元;在E处乘车的车费为6+(3+3-3)×1.5=10.5(元);在F处乘车的车费为6+(1+3+3-3)×1.5=12(元),合计45元.(2)A,B同乘一辆车,从A开出,D,E,F同乘一辆车,从F开出,合计22.5元.第四章几何图形初步4.2 直线、射线、线段《第1课时直线、射线、线段》导学案【学习目标】:1. 会用尺规画一条线段等于已知线段,会比较两条线段的长短.2. 理解线段等分点的意义.3. 能够运用线段的和、差、倍、分关系求线段的长度.4. 体会文字语言、符号语言和图形语言的相互转化.5. 了解两点间距离的意义,理解“两点之间,线段最短”的线段性质,并学会运用.【重点】:作一条线段等于已知线段,理解线段的和、差,掌握线段中点的概念,理解“两点之间,线段最短”的线段性质.【难点】:利用尺规作图作一条线段等于两条线段的和、差,利用线段的和、差、倍、分求线段的长度,“两点之间,线段最短”的实际运用.【课堂探究】一、要点探究探究点1:线段长短的比较合作探究:问题1 做手工时,在没有刻度尺的条件下,如何从较长的木棍上截下一段,使截下的木棒等于另一根短木棒的长?问题2 画在黑板上的线段是无法移动的,在只有圆规和无刻度的直尺的情况下,如何再画一条与它相等的线段?要点归纳:尺规作图:作一条线段(AB)等于已知线段(a)的作法:1.画射线AC;2.在射线AC上截取AB=a.问题3 若要比较两个同学的身高,有哪些办法?你能从比身高的方法中得到启示来比较两条线段的长短吗?试一试:比较线段AB,CD的长短.(1)度量法:分别测量线段AB、CD的长度,再进行比较:AB=_________;BC=_______,________>_______,所以_______>_______;(2)叠合法:将点A与点C重合,再进行比较:①若点 A 与点 C 重合,点 B 落在C,D之间,那么 AB_____CD.②若点 A 与点 C 重合,点 B 与点 D________,那么 AB = CD.③若点 A 与点 C 重合,点 B 落在 CD 的延长线上,那么 AB_________CD.探究点2:线段的和、差、倍、分画一画:在直线上画出线段AB=a,再在AB的延长线上画线段BC=b,线段AC就是与的和,记作AC= . 如果在AB上画线段BD=b,那么线段AD就是与的差,记作AD= .观察与思考:在一张纸上画一条线段,折叠纸片,使线段的端点重合,折痕与线段的交点处于线段的什么位置?要点归纳:如图,点 M 把线段 AB 分成相等的两条线段AM 与 BM,点 M 叫做线段 AB 的中点.几何语言:∵ M 是线段 AB 的中点∴ AM = MB = AB,或 AB = AM = MB例1 若AB = 6cm,点C是线段AB的中点,点D是线段CB的中点,求:线段AD的长是多少?例2 如图,B、C是线段AD上两点,且AB:BC:CD=3:2:5,E、F分别是AB、CD的中点,且EF=24,求线段AB、BC、CD的长.变式训练:如图,已知线段AB和CD的公共部分BD=13AB=14CD,线段AB、CD的中点E、F之间距离是10cm,求AB,CD的长方法总结:求线段的长度时,当题目中涉及到线段长度的比例或倍分关系时,通常可以设未知数,运用方程思想求解.例3 A,B,C三点在同一直线上,线段AB=5cm,BC=4cm,那么A,C两点的距离是()A.1cm B.9cm C.1cm或9cm D.以上答案都不对变式训练:已知A,B,C三点共线,线段AB=25cm,BC=16cm,点E,F分别是线段AB,BC的中点,则线段EF的长为()A.21cm或4cm B.20.5cm C.4.5cm D.20.5cm或4.5cm方法总结:无图时求线段的长,应注意分类讨论,一般分以下两种情况:①点在某一线段上;②点在该线段的延长线.针对训练1.如图,点B ,C 在线段AD 上则AB +BC =____;AD -CD =___;BC = ___ -___= ___ - ___.第1题图 第2题图 第3题图2.如图,点C 是线段AB 的中点,若AB =8cm ,则AC = cm.3.如图,下列说法,不能判断点C 是线段AB 的中点的是 ( )A. AC =CBB. AB =2ACC. AC +CB =ABD. CB =21AB 4. 如图,已知线段a ,b ,画一条线段AB ,使AB =2a -b .5.如图,线段AB =4cm ,BC =6cm ,若点D 为线段AB 的中点,点E 为线段BC 的中点,求线段DE 的长.探究点3:有关线段的基本事实议一议:如图:从A 地到B 地有四条道路,除它们外能否再修一条从A 地到B 地的最短路?如果能,请你联系以前所学的知识,在图上画出最短路线.想一想:1.如图,这是A,B两地之间的公路,在公路工程改造计划时,为使A,B 两地行程最短,应如何设计线路?请在图中画出,并说明理由.2. 把原来弯曲的河道改直,A,B两地间的河道长度有什么变化?第1题图第2题图要点归纳:1.两点的所有连线中,_____最短.简称:两点之间,_____最短.2.连接两点间的线段的_______,叫做这两点的距离.针对训练1.如图,AB+BC AC,AC+BC AB,AB+AC BC(填“>”“<”或“=”). 其中蕴含的数学道理是 .2.在一条笔直的公路两侧,分别有A,B两个村庄,如图,现在要在公路l 上建一个汽车站C,使汽车站到A,B两村庄的距离之和最小,请在图中画出汽车站的位置.二、课堂小结1. 基本作图:作一条线段等于已知线段.2. 比较两条线段大小 (长短) 的方法:度量法;叠合法.3. 线段的中点.因为点M 是线段AB 的中点,所以AM =BM =21AB . (反过来说也是成立的) 4. 两点之间的所有连线中,线段最短;两点之间线段的长度 ,叫做这两点之间的距离.【当堂检测】1. 下列说法正确的是 ( )A. 两点间距离的定义是指两点之间的线段B. 两点之间的距离是指两点之间的直线C. 两点之间的距离是指连接两点之间线段的长度D. 两点之间的距离是两点之间的直线的长度2. 如图,AC =DB ,则图中另外两条相等的线段为_____________.第2题图 第3题图3.已知线段AB = 6 cm ,延长AB 到C ,使BC =2AB ,若D 为AB 的中点,则线段DC 的长为_____________.4.点A ,B ,C 在同一条数轴上,其中点A ,B 表示的数分别是-3,1,若BC=5,则AC=_________.5. 如图:AB =4cm ,BC =3cm ,如果点O 是线段AC 的中点.求线段OB 的长度.6.已知,如图,B,C两点把线段AD分成2:5:3三部分,M为AD的中点,BM=6,求CM和AD的长.。
六年级数学上册《比较线段的长短》同步练习2鲁教版

1
① MN=GC ② GN= (AC-BC)
2
A.1 B.2 C.3 D.4
③MG=BN ④ MC=AG+BN
3. 下列说法中 , 错误的是 ( )
1
①若 AC=BC则, C是线段 AB的中点 ; ②若 BD= AB,则 D 是线段 AB的中点 ;
2
③若 AE=BE=1 AB, 则 E 是线段 AB 的中点 . 2
5
8. 如图 5,AB:BC:CD=2:3:4,AB 的中点 M?与 CD?的中点 N?的距离是 3cm,?则 BC=______.
三、解答题 :
9. 已知 C 是线段 AB 上一点 ,D 是线段 BC的中点 ,F 图中所有线段的长度之和为 23, 线段 AC的
长度与 BC的长度都是正整数 , 求线段 AC的长 .
10. 线段 AB 上有 P、 Q两点 ,AB=26,AP=14,PQ=11, 试求 BQ的值 .
11. 如图 , 设 A、B、C、D为 4 个居民小区 , 现要在四边形 ABCD?内建一个购物中心 , 试问把购物 中心建在何处 , 才能使 4 个居民小区到购物中心的距离之和最小 ?说明理由 .
A D
∵PB=AB-AP=26-14=12,PQ=11,
∴BQ=PB+PQ=12+11=23
(2) 当 Q在线段 PB上时 ,BQ=PB-PQ=12-11=1
11. 连 AC、BC,交点即自来水厂的位置 ,? 根据公理“两点之间,线段最短” , 要使自来水
厂到 A、 B、 C、D 的距离和最小 , 故自来水厂既要在 AC上 , 又要在 BD上.
第二节 比较线段的长短
一、选择题 : 1. 如图 1, 下列关系中与图中不符合的是 ( )
六年级数学上册 《角的比较》同步练习2 鲁教版
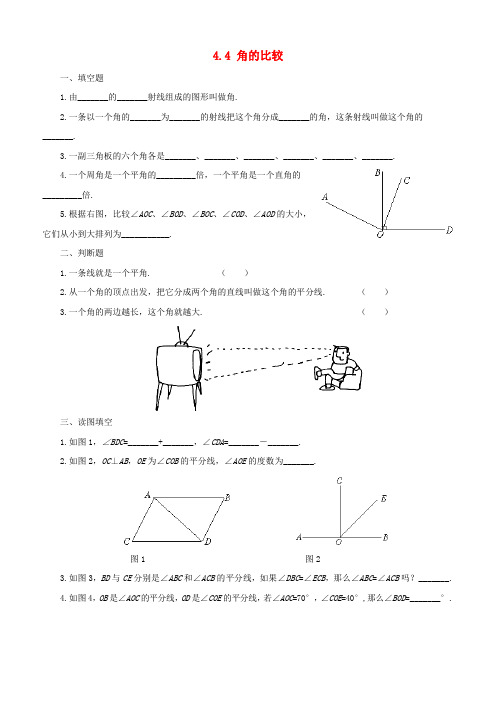
4.4 角的比较一、填空题1.由_______的_______射线组成的图形叫做角.2.一条以一个角的_______为_______的射线把这个角分成_______的角,这条射线叫做这个角的_______.3.一副三角板的六个角各是_______、_______、_______、_______、_______、_______.4.一个周角是一个平角的_________倍,一个平角是一个直角的_________倍.5.根据右图,比较∠AOC、∠BOD、∠BOC、∠COD、∠AOD的大小,它们从小到大排列为___________.二、判断题1.一条线就是一个平角. ()2.从一个角的顶点出发,把它分成两个角的直线叫做这个角的平分线. ()3.一个角的两边越长,这个角就越大. ()三、读图填空1.如图1,∠BDC=_______+_______,∠CDA=_______-_______.2.如图2,OC⊥AB,OE为∠COB的平分线,∠AOE的度数为_______.图1 图23.如图3,BD与CE分别是∠ABC和∠ACB的平分线,如果∠DBC=∠ECB,那么∠ABC=∠ACB吗?_______.4.如图4,OB是∠AOC的平分线,OD是∠COE的平分线,若∠AOC=70°,∠COE=40°,那么∠BOD=_______°.图3 图4做一做在一张透明纸上画一个角,记为∠PQR,折线使射线QR与射线QP重合,把纸展开,以Q为端点,沿折痕画一条射线,这条射线就是∠PQR的平分线.说说为什么这条线平分∠PQR?答案:一、1.略 2.略 3.45° 45° 90° 90° 30° 60° 4.2 25.∠BOC<∠COD<∠AOC=∠BOD=90°<∠AOD二、1.× 2.× 3.×三、1.∠BDA∠ADC∠CDB∠BDA 2.135° 3.相等 4.55°做一做略。
2017年春季鲁教版五四制六年级数学下学期5.2比较线段的长短同步练习2

5.2比较线段的长短训练题一、填空题1、 连结_______的_______叫作两点间的距离.2、 点B 把线段AC 分成两条相等的线段,点B 就叫做线段AC 的_______,这时,有AB =_______,AC =_______BC ,AB =BC =_______AC .点B 和点C 把线段AD 分成三条相等的线段,则点B 和点C 就叫做AD 的_______.3、 比较两个人的身高,我们有_______种方法. 一种为直接用卷尺量出,另一种可以让两人站在 一块平地上,再量出差.这两种方法都是把身高看成一条______,方法(1)是直接量出线段的_______, 再作比较.方法(2)是把两条线段的一端_______,再观察另一个_______.4、 如图,点C 分AB 为2∶3,点D 分AB 为1∶4,若AB 为5 cm,则AC =_____cm, BD =_____cm,CD =______cm.5、 下面线段中,_____最长,_____最短.按从长到短的顺序用“>”号排列如下:① ② ③ ④6、若线段AB =a ,C 是线段AB 上任一点,MN 分别是AC 、BC 的中点,则MN =_______+_______=_______AC +_______BC =_______.7、 已知线段AB ,在AB 的延长线上取一点C ,使BC=2AB ,再在BA 的延长线上取一点D ,使DA=AC , 则线段DC=______AB ,BC=_____CD8、 已知线段AB=10㎝,点C 是AB 的中点,点D 是AC 中点,则线段CD=_______㎝。
二、选择题:9、 如图9,CB=21AB ,AC=31AD ,AB=31AE 若CB=2㎝,则AE=( ) A 、6㎝ B 、8㎝ C 、10㎝ D 、12㎝10、如图10,O 是线段AC 中点,B 是AC 上任意一点,M 、N 分别是AB 、BC 的中点,下列四个等式中, 不成立的是( )A 、MN=OC B 、MO=21(AC -BC) C 、ON=21(AC-BC) D 、MN=21(AC-BC)O 、P 、Q 是平面上的三点,PQ=20㎝,OP+OQ=30㎝,那么下列正确的是( )A 、O 是直线PQ 外B 、O 点是直线PQ 上C 、O 点不能在直线PQ 上D 、O 点不能在直线PQ 上12、如图11,M 是线段的EF 中点,N 是线段FM 上一点,如果EF=2a, NF=b,则下面结论中错误是( )A 、MN=a -b B.MN=21aC.EM=aD.EN=2a -b 三、比较下列各组线段的长短 13、⑴ 线段OA 与OB . 答:_________________ ⑵线段AB 与AD . 答:_________________ ⑶ 线段AB 、BC 与AC . 答:________________四、解答题14、已知两条线段的差是10 cm ,这两条线段的比是2∶3,求这两条线段的长.15、在直线AB 上,有AB =5 cm , BC =3 cm ,求AC 的长.解:⑴当C 在线段AB 上时,AC =_______.(2)当C 在线段AB 的延长线上时,AC =_______.A CB D E 图9A CB D N 图10M A F图11MN16、 已知线段AB ,延长AB 到C ,使BC=21AB ,反向延长AC 到D ,使DA=21AC ,若AB=8㎝,求DC 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
④③
②①
乙甲第二节 比较线段的长短
一、选择题:
1.如图1,下列关系中与图中不符合的是( )
A.AC+CD=AB-DB
B.AB-CB=AD-BC;
C.AC+CB=AD+DB
D.AD+BC=AB+CD
(1) (2) (3)
2.如图2,B 是AC 上一点,M 、N 分别是AB 、BC 的中点,AG=GC,则下列各式中,正确的有( )个 ①MN=GC ②GN=12
(AC-BC) ③MG=BN ④MC=AG+BN A.1 B.2 C.3 D.4
3.下列说法中,错误的是( )
①若AC=BC,则C 是线段AB 的中点; ②若BD=
12AB,则D 是线段AB 的中点; ③若AE=BE=12
AB,则E 是线段AB 的中点. A.①② B.①③ C.②③ D.①②③
4.如图3,C 、D 是线段AB 上的两点,E 是AC 的中点,F 是BD 的中点,若EF=18,CD=6,则AB=( )
A.24
B.12
C.30
D.42
二、填空题
5.如图4,已知B 、C 是线段AD 上的两点,M 是AB 的中点,N 是CD 的中点,若MN=a,BC=b,则线段AD=________(2002年重庆竞赛题) B (4) (5)
6.如图6,从甲地到乙地有四条道路,其中______最近,理由是:_______. (6)
7.P 为线段AB 上一点,且PA=25
AB,M 是AB 的中点,若PM=2cm,则AB=________. 8.如图5,AB:BC:CD=2:3:4,AB 的中点M•与CD•的中点N•的距离是3cm,•则BC=______.
三、解答题:
9.已知C 是线段AB 上一点,D 是线段BC 的中点,F 图中所有线段的长度之和为23,线段AC 的长度与BC 的长度都是正整数,求线段AC 的长.
10.线段AB上有P、Q两点,AB=26,AP=14,PQ=11,试求BQ的值.
11.如图,设A、B、C、D为4个居民小区,现要在四边形ABCD•内建一个购物中心,试问把购物
中心建在何处,才能使4个居民小区到购物中心的距离之和最小?说明理由.
D
B
答案:
一、1.B 2.D 3.A(点拨:①,②中C或D可能在直线AB上) 4.C
二、5.2a-b 点拨:AD=AB+BC+CD=2BM+BC+2CN)=2(MB+BC+CN)-BC=2MN-BC=2a-b •
6.③;两点之间的连线中,线段最短
7.20cm
8.1.5cm
9.如图,设AC=y,CD=DB=•x
图中所有线段和为 y+(x+y)+(y+2x)+x+2x=23,即7x+3y=23
∵x,y均为正整数 •3y=23-7x
∴23-7x>0 x<37 7
∴x=1,2,3
经检验知:x=2时,y=3满足条件,故AC=3 •
10.(1)当Q在线段AP上时,
∵PB=AB-AP=26-14=12,PQ=11,
∴BQ=PB+PQ=12+11=23
(2)当Q在线段PB上时,BQ=PB-PQ=12-11=1
11.连AC、BC,交点即自来水厂的位置,•根据公理“两点之间,线段最短”,要使自来水
厂到A、B、C、D的距离和最小,故自来水厂既要在AC上,又要在BD上.。
