控制论论文
学会控制自己议论文600字
学会控制自己议论文600字学会控制自己议论文1著名教育专家马卡连柯说：“不会控制自己的人就像一台损坏的机器。
”时刻存在被淘汰的危险。
因此，作为现实社会中的人，我们都要学会控制自己，才能保全自己，并进一步获得发展。
学会控制自己，首先要控制自己的情绪。
喜、怒、哀、乐是人的基本情绪，然而又有多少次人是真正发自内心地传达出这一情绪呢?究其原因，在于人是社会的人，人的各种情绪不仅对自己产生影响，而且还往往涉及他人，影响自己与他人的关系。
因此，我们在和别人交往时要时刻注意自己的情绪，以利于双方交往的顺利进行。
至于人们常说的“情寓于衷而发之于外”，往往也是委婉为之吧。
学会控制自己，其次要控制自己的欲望。
每个人都有自己的好恶，都愿意做自己喜欢的事情。
但是我们还得考虑现实情况，不能“率性而为”。
例如，某个人喜欢上网打游戏，并且正在打游戏，但是还有工作没有完成。
这时他就需要控制自己打游戏的欲望，先完成工作。
这样才能有充分的时间去做工作，工作的质量和效率才会高。
否则，打完游戏，身心俱疲，匆忙地完成工作，其效果未必尽如人意。
而工作的成效，也影响着下一次打游戏的时间和心情。
因此，我们要学会控制自己的欲望，当前时间做紧要的事情，这才是我们做事情的正确方法。
学会控制自己，还要控制自己的行动。
思想是花朵，行动是果实。
没有实际行动，没有丰硕的果实，再灿烂的花朵也只是昙花一现，空留下遗憾。
人们常常喜欢幻想，描绘自己美好未来的图景。
有了这些美好的愿景以后，有些人能够积极积极行动，为实现理想而努力。
如战国时期的苏秦为了实现自己游说天下，谋取功名的目标，常常读书至深夜，“头悬梁，锥刺股”。
最终成为受国君重视的一代谋士。
再如爱迪生为了找到合适的灯丝原料进行了上千次实验，最后才找到了金属钨。
这些成功的人士为了实现理想都进行了坚持不懈的努力，同时，这也是他们在有意识地控制自己的行为过程。
现实中也有另外一些人，他们喜欢整天沉溺于幻想，却怠于付出行动。
控制论初探新生课论文
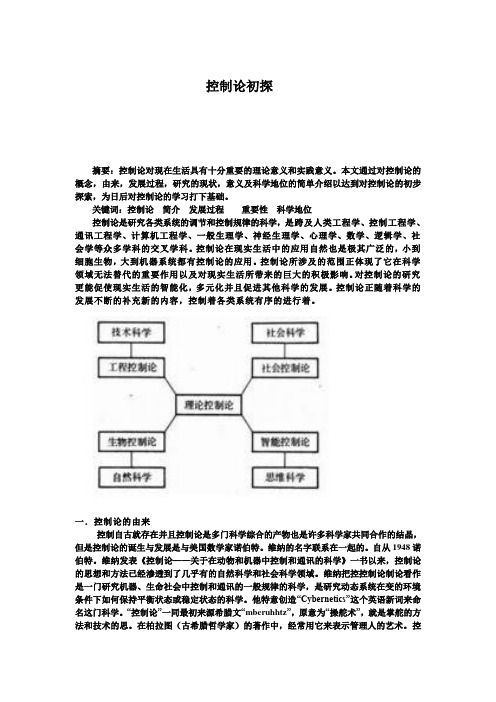
控制论初探摘要：控制论对现在生活具有十分重要的理论意义和实践意义。
本文通过对控制论的概念，由来，发展过程，研究的现状，意义及科学地位的简单介绍以达到对控制论的初步探索，为日后对控制论的学习打下基础。
关键词：控制论简介发展过程重要性科学地位控制论是研究各类系统的调节和控制规律的科学，是跨及人类工程学、控制工程学、通讯工程学、计算机工程学、一般生理学、神经生理学、心理学、数学、逻辑学、社会学等众多学科的交叉学科。
控制论在现实生活中的应用自然也是极其广泛的，小到细胞生物，大到机器系统都有控制论的应用。
控制论所涉及的范围正体现了它在科学领域无法替代的重要作用以及对现实生活所带来的巨大的积极影响。
对控制论的研究更能促使现实生活的智能化，多元化并且促进其他科学的发展。
控制论正随着科学的发展不断的补充新的内容，控制着各类系统有序的进行着。
一．控制论的由来控制自古就存在并且控制论是多门科学综合的产物也是许多科学家共同合作的结晶，但是控制论的诞生与发展是与美国数学家诺伯特。
维纳的名字联系在一起的。
自从1948诺伯特。
维纳发表《控制论——关于在动物和机器中控制和通讯的科学》一书以来，控制论的思想和方法已经渗透到了几乎有的自然科学和社会科学领域。
维纳把控控制论制论看作是一门研究机器、生命社会中控制和通讯的一般规律的科学，是研究动态系统在变的环境条件下如何保持平衡状态或稳定状态的科学。
他特意创造“Cybernetics”这个英语新词来命名这门科学。
“控制论”一同最初来源希腊文“mberuhhtz”，原意为“操舵术”，就是掌舵的方法和技术的思。
在柏拉图（古希腊哲学家）的著作中，经常用它来表示管理人的艺术。
控制论由此不断发展成为一门学科。
二．控制论的简介在控制论中，“控制”的定义是：为了“改善”某个或某些受控对象的功能或发展，需要获得并使用信息，以这种信息为基础而选出的、于该对象上的作用，就叫作控制。
控制论的基本部分：1.信息论：主要是关于各种通路（包括机器、生物机体）中信息的加工传递和贮存的统计理论。
自动控制原理论文
自动控制原理论文自动控制原理，也被称为控制理论，是研究和设计控制系统的一门学科。
控制系统是用来改变或维持被控对象的状态或行为的一组设备和过程。
自动控制原理通过分析系统的数学模型和反馈机制来设计和优化控制系统，以实现期望的系统行为。
首先是系统建模。
系统建模是自动控制原理的第一步，其目的是将被控对象抽象为一个数学模型。
常见的数学模型有差分方程模型、微分方程模型和传递函数模型等。
对于线性时不变系统，传递函数模型是最常用的一种表示方法。
通过建立合适的数学模型，可以更好地理解系统的动态特性，并为控制器设计提供基础。
接下来是控制器设计。
控制器是自动控制系统的核心部分，其作用是根据系统的输入和输出信号实时调整控制量，使被控对象的输出信号与期望信号尽可能接近。
常见的控制器设计方法有比例控制、比例积分控制和比例积分微分控制等。
控制器设计的目标是在满足系统稳定性和鲁棒性的前提下，使系统的响应速度快、稳定性好。
然后是性能评估。
性能评估是对控制系统在不同工况下的性能进行定量分析。
常见的性能指标有超调量、调整时间和稳态误差等。
性能评估可以帮助我们了解控制系统的优缺点，进一步提高系统的控制性能。
最后是仿真分析。
仿真分析是在计算机上建立控制系统的数学模型，并进行模拟实验。
通过仿真分析，可以评估不同控制策略的性能，进行参数调整和优化。
仿真分析还可以帮助我们理解控制系统的动态特性，预测系统的行为。
总之，自动控制原理论文需要包含系统建模、控制器设计、性能评估和仿真分析等方面的内容。
在撰写论文时，需要深入研究自动控制原理的基本理论和方法，并结合实际案例进行分析和探讨。
同时，还需要运用数学建模和计算机仿真技术来验证理论结果，并提出进一步的优化方案。
现代控制理论综述—课程论文
论文题目现代控制理论综述姓名 *** 学号 ***学科(专业) ***所在学院机械工程学院任课教师*** 提交日期***目录摘要 (1)Abstract (1)1绪论 (2)现代控制理论 (2)现代控制理论的发展历程 (2)现代控制理论与经典控制理论的异同 (3)2 现代控制理论的基本内容 (5)线性系统理论 (5)非线性系统理论 (5)最优控制理论 (6)最优估计理论 (6)随机控制理论 (6)适应控制理论 (7)2.7 系统辨识理论 (7)3现代控制理论的其他研究方向 (8)智能控制 (8)鲁棒性分析与鲁棒控制 (8)模糊控制 (9)神经网络控制 (9)实时专家控制 (9)分布参数系统控制 (10)预测控制 (10)4 现代控制理论的发展趋势和展望 (11)现代控制理论的发展趋势 (11)现代控制理论的前景展望 (11)5 参考文献 (13)摘要本文首先介绍了现代控制理论的发展历程以及现代控制理论和经典控制理论二者的异同点，然后介绍了现代控制技术的基本内容,之后又对现代控制理论目前研究的一些方向作了简要说明，包括智能控制、鲁棒控制、模糊控制、神经网络控制及实时专家控制等。
最后总结了现代控制技术的发展特点以及发展趋势。
关键词:现代控制理论控制概述发展内容AbstractThe paper introduces the development process of modern control at first. And then it compares the differences and similarities between modern control and classical control . Besides,it introduces the basic content of modern control technology and some new research directions , such us Intelligent control,robust control, fuzzy control, neural network control and real-time expert control ,etc. At last , this paper pointesout the development characteristics and development trend of modern control technology.Keywords: modern control technology control overview development content1绪论1.1现代控制理论现代控制理论是在经典控制理论基础上逐步发展起来的，建立在状态空间法基础上的一种控制理论，研究多输入多输出、变参数、非线性、高精度、高效能等控制系统的分析与设计问题，是自动控制理论的一个主要组成部分。
现代控制理论的论文
第一章经典控制理论和现代控制理论本学期学习了现代控制理论课程的主要内容，现代控制理论建立在状态空间法基础上的一种控制理论，是自动控制理论的一个主要组成部分。
在现代控制理论中，对控制系统的分析和设计主要是通过对系统的状态变量的描述来进行的，基本的方法是时间域方法。
现代控制理论比经典控制理论所能处理的控制问题要广泛得多，包括线性系统和非线性系统，定常系统和时变系统，单变量系统和多变量系统。
它所采用的方法和算法也更适合于在数字计算机上进行。
现代控制理论还为设计和构造具有指定的性能指标的最优控制系统提供了可能性。
现代控制理论的名称是在1960年以后开始出现的，用以区别当时已经相当成熟并在后来被称为经典控制理论的那些方法。
现代控制理论已在航空航天技术、军事技术、通信系统、生产过程等方面得到广泛的应用。
现代控制理论的某些概念和方法，还被应用于人口控制、交通管理、生态系统、经济系统等的研究中。
以下是经典控制理论和现代控制理论的比较：1、经典控制理论：(1)理论基础：Evens的根轨迹，Nyquist稳定判据。
(2)研究对象：线性定常SISO系统分析与设计。
(3)分析问题：稳、准、快(4)采用方法：是以频率域中传递函数为基础的外部描述方法。
(5)数学描述：高阶微分方程、传递函数、频率特性;方块图、信号流图、频率特性曲线。
(6)研究方法：时域法、根轨迹法、频率法。
2、现代控制理论：(1)理论基础：李雅普诺夫稳定性理论，Bellman动态规划，Понтрягин极值原理，Kalman 滤波。
(2)研究对象：MIMO系统分析与设计（复杂系统：多变量、时变、非线性）(3)分析问题：稳、准、快(4)设计（综合）问题：1)采用方法：是以时域中（状态变量）描述系统内部特征的状态空间方法为基础的内部描述方法。
2)数学描述：状态方程及输出方程、传递函数阵、频率特性；状态图、信号流图、频率特性曲线。
3)研究方法：状态空间法（时域法）、频率法。
现代控制理论结课论文
现代控制理论方法综述研电1610 秦晓 1162201332摘要：本文将控制理论方法分为现代控制理论基础，线性最优控制，非线性最优控制三大部分，查阅文献，综述了每一部分中的经典控制方法，以及每种控制方法的优缺点和在工业中的应用，最后提出了目前在现代控制理论中依旧存在的问题。
1.引言电力系统是一个复杂的非线性动态大系统，对于这个规模庞大的系统，研究其运行的动态特性进而构建先进的安全控制系统是极富挑战性的课题。
同时，各种新技术的应用，一方面增强了系统的调控能力和经济效益，另一方面也极大的增加了电网控制的复杂性，对电力系统的安全稳定运行提出了更严格的要求。
因此，改善与提高我国电力系统的动态品质、安全稳定和经济性成为了电力工作者的首要任务。
提高电力系统稳定性的最经济和最有效的手段之一是采用先进的控制理论和方法。
在过去的时间里，电力工作者们为改进与发展电力系统控制技术进行了大量研究。
本文主要梳理总结电力系统在现代控制方面的研究成果，分析了电力系统控制技术的发展趋势，并总结了目前现代控制理论还需要解决的问题。
2.现代控制的基础现代控制理论的基础是经典控制理论，在20世纪20年代到50年代间，为了满足第二次世界大战前后军事技术和工业发展的需求，经典控制理论有了飞速的发展。
经典控制理论主要研究线性时不变、单输入单输出的控制问题。
在分析和设计大型反馈控制系统时，经典控制论主要采用频域法，其中以 Nyquist 判据、Bode 图和根轨迹法最为广泛[1~2]。
经典控制理论的设计目标是使闭环系统特征方程的特征根全部位于左半开平面上。
上述设计目标可以描述为一类无目标函数的优化问题，即约束满足问题。
由于使系统稳定的控制器解并不唯一，所以根据经典控制理论设计的PID 控制器往往带有较大的冗余性[3]。
也正是由于经典控制理论设计目标及方向简单明确，计算方便，特别适合需要依赖工程经验或现场测试进行控制器设计的系统，所以至今仍在工业中广泛应用。
企业内部控制论文（通用15篇）
企业内部控制论文（通用15篇）企业内部控制论文1一、企业内部会计控制的内涵在不同的国家，对内部控制的概念也不同。
从内部控制理论发展过程来看，最早提出的是在1963年，美国注册会计师协会发布的公告。
内部会计控制包括组织的计划和与保护该组织的财产、保证财务记录的可信性有直接关系的所有协调方法和步骤。
这时的内部会计控制主要是指授权和批准制度、会计记录，财务报告编制、企业资产保管等方面的职责分工以及内部审计。
1973年，该委员会在第1号审计准则公告中对内部会计控制又进行了重新表述，认为内部会计控制包括组织的计划和与保护该组织的财产、保证财务记录的可信性有关的程序和记录。
而我国对内部会计控制的定义是：“单位为了提高会计信息质量，保护资产的安全、完整，确保有关法律法规和规章制度的贯彻执行等而制定和实施的一系列控制方法、措施和程序。
”从两国的概念可以可以看出：内部会计控制是指为了保护资产的安全、完整和会计信息的真实、可靠而制定的各种方法和程序。
二、企业内部会计控制存在的问题（一）企业内部会计缺乏控制意识一个企业的内部控制成不成功，主要是看员工的意识和行为。
不过员工的意识和行为都是领导和管理者带动的，如果领导者都没有这样内控的意识，员工更加没有，因此，领导者内控意识是最主要的。
当今社会，一般的企业都没有认识到内控的重要性，而是仅仅停留在内控的表面。
人们都有一种不想改变的懒惰心理，管理者总是满足于传统的管理模式，他们思想上认为只要按照模式来做就可以，其实不是这样，落后的模式总有它的弊端。
我们从广东的国投的破产的实例还有郑州亚细亚的关门这两个实例就能发现：领导者的内部控制意识直接关系到企业的成功与否。
（二）内控制度有待加强长期以来，很多企业普遍存在着内部控制制度不健全，財务管理薄弱的现象，大多数的都是内控制度不够完善，比如一个企业内部很多员工都没有意识去内控，很多的业务也没有涉及内控，这就意味着一个企业内部很多的环节都会出现浪费的现象，造成企业内成本增加，蒙受经济损失。
现代控制理论小论文
现代控制理论小论文1. 引言现代控制理论是控制理论的一个重要分支，它在工程控制领域有着广泛的应用。
随着科技的发展，控制系统越来越复杂，要求控制系统具备更高的性能指标和更强的鲁棒性。
现代控制理论的研究和应用为工程控制带来了很大的推动力，以提升系统的控制性能和鲁棒性。
本篇小论文将介绍现代控制理论的基本概念、方法和应用，并讨论其在实际系统中的应用情况。
2. 现代控制理论的基本概念现代控制理论是基于数学模型的控制理论，其核心概念包括控制系统、系统模型和控制器等。
2.1 控制系统控制系统是由一组相互作用的组件组成的系统，旨在通过对系统输入进行调节以达到预期的输出。
控制系统通常包括传感器、执行器、控制算法和反馈环路等。
2.2 系统模型系统模型是控制系统的数学描述，可分为传递函数模型和状态空间模型。
传递函数模型描述了系统的输入与输出之间的关系，而状态空间模型描述了系统的状态随时间的变化。
2.3 控制器控制器是控制系统中的关键组件，根据系统的输入和输出信息，使用控制算法来生成控制信号，以调节系统的行为。
常见的控制器包括比例-积分-微分（PID）控制器、模糊控制器和自适应控制器等。
3. 现代控制理论的方法现代控制理论提供了多种方法来设计控制系统，以满足不同的控制需求。
3.1 线性控制线性控制是现代控制理论的重要方法之一，它基于线性系统的模型和理论，通过设计线性控制器来实现对系统的控制。
线性控制具有较好的稳定性和可调节性，在许多工业应用中得到广泛应用。
3.2 非线性控制非线性控制是应对非线性系统的控制方法，它考虑系统的非线性特性，并设计相应的非线性控制器来实现对系统的控制。
非线性控制可用于对复杂系统进行建模和控制，具有更强的适应性和鲁棒性。
3.3 鲁棒控制鲁棒控制是一种针对不确定性和扰动的控制方法，通过设计具有鲁棒性的控制器来使控制系统对不确定因素具有一定的容忍能力。
鲁棒控制可以提高系统的稳定性和鲁棒性，适用于对不确定因素较多的系统进行控制。
控制论的征文
控制论的征文控制论是一种系统论的分支学科，它研究的是如何通过控制改变系统的行为。
它的基本思想是通过建立数学模型来描述系统的动态过程，并设计控制策略来引导系统朝着期望的状态演化。
控制论的应用领域非常广泛，涵盖了自动化控制、经济管理、交通运输、生态环境等多个领域。
在自动化控制领域，控制论的应用可以追溯到上世纪40年代。
当时，随着工业自动化的发展，人们开始关注如何通过控制手段提高生产效率和质量。
控制论的出现为解决这一问题提供了理论基础。
通过对系统的建模和分析，可以确定系统的状态和行为，进而设计控制器来实现对系统的控制。
这种方法不仅可以提高生产效率，还可以减少人为干预对系统的干扰，提高系统的稳定性和可靠性。
除了自动化控制领域，控制论在经济管理中也有广泛的应用。
在市场经济条件下，企业面临着各种各样的不确定性和风险。
控制论提供了一种理论框架，可以帮助企业制定合理的经营策略和控制措施。
通过对市场需求、成本结构和竞争环境等因素进行建模和分析，可以确定最优的经营决策，实现企业的长期发展目标。
此外，控制论还在交通运输领域发挥着重要作用。
随着城市化进程的加快，交通拥堵问题日益突出。
控制论可以用来优化交通系统的运行，提高交通效率。
通过对交通流的建模和分析，可以确定最优的交通信号控制策略，减少交通拥堵和排放量，提高交通运输的效益。
此外，控制论还可以应用于生态环境领域。
生态系统是一个复杂的动态系统，受到多种因素的影响。
控制论可以用来研究生态系统的演化规律，设计合理的保护措施。
通过对生态系统的建模和分析，可以确定最优的资源配置和管理策略，实现生态环境的可持续发展。
综上所述，控制论是一种研究系统行为和控制方法的学科，具有广泛的应用领域。
它通过建立数学模型和设计控制策略来改变系统的行为，提高系统的效率和稳定性。
在自动化控制、经济管理、交通运输和生态环境等领域，控制论都发挥着重要作用，为解决实际问题提供了理论支持和技术手段。
随着科学技术的不断发展，控制论的应用前景将更加广阔，为人类社会的发展做出更大的贡献。
控制_关于自控的议论文700字
控制_关于自控的议论文700字"一个人最难战胜的不是别人，而是自己。
"这条真理想必谁都知晓。
而在繁乱纷扰的现代社会，随着世界的大流，人人都急着投入一场轰轰烈烈的人生浩歌中，多少人被迷失得不知所踪。
面对生活中的大小事，能做到很好地控制自己的情感，才能战胜自己，战胜生活。
"古之立大事者，不惟有超世之才，亦必有坚忍不拔之志。
"这些人之所以成为伟人，想必他们每个人都有着极强的控制力。
在失败时控制自己的伤感，拾起勇气；在成功时，控制过度的喜悦，一路前行；面对别人的嘲笑，控制愤怒，一往无前......在人生的每一个关卡，他们都能控制喜怒哀乐，给人生的每个阶段都画上一个完整的句号。
回望历史长河，那些伟人身上都彰显着控制克己的魅力。
有"士可杀不可辱"的士大夫；有不为五斗米折腰的陶渊明；有自我放逐，对权贵嗤之以鼻的竹林七贤；更有为正义而牺牲的俄国贵族......他们的感人事迹都在告诫我们：控制自己的情感欲念，不管世界如何改变，也要坚持自我，不为所动。
然而，高速化的现代社会以排山倒海之势向人们袭来，有多少不知所措之人被卷入其中！微博控，苹果控，沙发控......我不禁感慨，这样一些小小的欲念就能将人活活生生禁锢住，人的高贵从何谈起？想到那个在故宫铜缸上刻字的梁齐齐，愤怒他素质低下的同时，我也为现代人克制力的缺失而心寒。
所以，从今天起做个精神贵族吧！学会控制自己的感情，让自己看清人生之路。
我们不妨学学杨绛先生，她已逾百岁。
一个人能经历人生喜怒哀乐、爱恨情愁，健康地踏过一百多个春秋是很不容易的，从做钱家媳妇的诸事含忍，到国难中的忍生活之苦，以及在名利面前深自敛抑，"甘当一个零"，杨绛先生善于控制内心，淡然处世，忍生活之苦，保存天真，最终让她的生活如此幸福。
佛语有云，心随境转是凡夫，境随心转是圣人。
学会控制并不是要让你成为卫道士，而是要让你成为清心寡欲、淡然处世的精神贵族。
现代控制理论综述论文
论文题目：现代控制理论综述摘要本文是对现代控制理论课程的完整综述，现代控制理论的主要内容包括控制系统的状态空间表达式及其解，线性控制系统的能控性和能观性，稳定性与李雅普诺夫方法，线性定常系统的综合以及最优控制理论等部分。
本文通过对控制理论各部分的阐述，构出了现代控制理论的主要框架及各部门的基本内容。
关键词：现代控制；状态方程；稳定性；最优控制；AbstractThis article is a complete review of modern control theory course, the main contents of the modern control theory, including the control system of the state space expression and its solution, the controllability of linear control systems and can view, stability and Lyapunov method, the synthesis of linear time-invariant system and optimal control theory. This article through to all parts of the control theory, compose the main framework of modern control theory and the basic content of each department.Keywords: Modern control; State equation;Stability;Optimal control目录摘要 (I)Abstract........................................................... I I一、控制理论的发展历史 (1)二、现代控制理论的基本内容 (2)2.1 控制系统的状态空间表达式 (3)2.2 线性控制系统的能控性和能观性 (3)2.2.1 线性控制系统的能控性 (3)2.2.2 线性控制系统的能观性 (4)2.3 自动控制系统的稳定性 (5)2.4 最优控制 (6)三、控制理论的发展展望 (6)四、总结 (6)参考文献 (8)一、控制理论的发展历史控制理论是关于各种系统的一般性控制规律的科学，它研究如何通过信号反馈来修正动态系统的行为和性能，以达到预期的控制目的。
现代控制理论论文
摘要最优控制，又称无穷维最优化或动态最优化，是现代控制理论的最基本，最核心的部分。
它所研究的中心问题是：如何根据受控系统的动态特性，去选择控制规律，才能使得系统按照一定的技术要求进行运转，并使得描述系统性能或品质的某个“指标”在一定的意义下达到最优值。
最优控制问题有四个关键点：受控对象为动态系统；初始与终端条件（时间和状态）；性能指标以及容许控制。
一个典型的最优控制问题描述如下：被控系统的状态方程和初始条件给定，同时给定目标函数。
然后寻找一个可行的控制方法使系统从输出状态过渡到目标状态，并达到最优的性能指标。
系统最优性能指标和品质在特定条件下的最优值是以泛函极值的形式来表示。
因此求解最优控制问题归结为求具有约束条件的泛函极值问题，属于变分学范畴。
变分法、最大值原理（最小值原理）和动态规划是最优控制理论的基本内容和常用方法。
庞特里亚金极大值原理、贝尔曼动态规划以及卡尔曼线性二次型最优控制是在约束条件下获得最优解的三个强有力的工具，应用于大部分最优控制问题。
尤其是线性二次型最优控制，因为其在数学上和工程上实现简单，故其有很大的工程实用价值。
关键词：最优控制；控制规律；最优性能指标；线性二次型AbstractThe optimal control, also called dynamic optimization or infinite dimension, optimization of modern control theory, the most basic part of the core. It is the center of the research question: how to control system based on the dynamic characteristics, to choose, can control system according to certain technical requirements, and makes the operation performance of the system or the quality of describing a "index" in certain significance to achieve optimal value. The optimal control problem has four points for dynamic systems, controlled, The initial and terminal conditions (state) and, Performance index and allow control.A typical of optimal control problem is described as follows: the state equation and initial conditions are given, and given the objective function. Then a feasible method for the control system of the output state transition to the target state and optimum performance. The optimal performance index and quality in the specific conditions of the optimal value is functional form. Therefore solution of optimal control problem is due to the constraint condition of functional, belongs to the category of variational learning. The variational method, the maximum principle (minimum principle) and dynamic planning is the optimal control theory, the basic contents and methods. The Pontryagin maximum principle, Behrman dynamic programming and Kaman linear quadratic optimal control is obtained in the constraint condition of the optimal solution of the three powerful tools, used in the most optimal control problem. Especially the linear quadratic optimal control, because its in mathematics and engineering implementation is simple, so it has great practical value.Key words: The optimal control, Control rule, optimal performance indicators, The linear quadratic一绪论1.1背景和意义要求将最优控制问题典型解决方法变分法、极值原理和动态规划及其在时间最短控制问题的应用和线性二次型最优控制问题（包括线性二次型实验及仿真结果）作为主要内容。
控制理论与控制工程毕业论文范文
控制理论与控制工程毕业论文范文一、论文说明本团队专注于毕业论文写作与辅导服务，擅长案例分析、编程仿真、图表绘制、理论分析等，论文写作300起，具体价格信息联系二、论文参考题目现代控制工程基础虚拟实验系统的研究思路：“现代控制工程”是机械类专业的一门必修课程,其中状态空间法的应用,加深了人们对控制领域的一些重要问题的认识,也使人们能较容易的解决多输入—多输出系统的问题,并且提供了将线性定常系统中的结论推广到复杂系统中的手段。
但是在教学中学生很难掌握在其状态空间中的数学模型-状态方程。
因此迫切需要通过实验的方式将抽象的理论可视化,加。
题目：电力建设工程管理公司合同管理控制制度的建立思路：本文是针对国家电力体制改革后，重组成立的电力建设工程管理公司运行中存在着合同管理控制制度不健全的问题，运用内部控制理论并结合企业的具体情况，设计了一套完整的合同管理控制制度框架，为企业提供了合同管理控制的工作制度（标准）和程序，并制定了相应的测试体系，以备定期对企业进行测试（复评），检查对合同管理控制制度的执行情况和合。
题目：工程机械液压系统动力匹配及控制技术研究思路：液压系统动力优化匹配控制技术是现代工程机械重要核心技术之一,它将现代液压控制理轮,自动控制理论,计算机技术及发动机技术等有机地连成一个不可分割的整体。
液压系统动力优化匹配控制技术应用到工程机械上以后,大大地提高了机器的很多性能,如工作效率、节能效果等,提高了机器对各种作业工况和作业环境的适应性,使机器操作、使用及维护更。
题目：基于内部控制理论的贵阳市城市轨道交通项目工程价款结算控制制度研究思路：贵阳市城市轨道交通公司采用DBB平行发包管理模式，这种管理模式工作界面清晰，业主选择承包商的范围较广，可节约投资，但对业主的管理水平要求高，目前公司仅有的《建设工程款拨付管理办法》无法满足工程价款结算控制要求，制定一套DBB模式下适用于贵阳市城市轨道交通项目的工程价款结算控制制度成为一个亟待解决的现实问题。
[工学]现代控制理论论文
![[工学]现代控制理论论文](https://img.taocdn.com/s3/m/4036b3aebceb19e8b9f6ba0c.png)
最优控制方法及其应用摘要：主要阐述了关于最优控制问题的基本概念，最优控制是最优化方法的一个应用。
最优化一般可以分为最优设计、最优计划、最优管理和最优控制四个方面。
而最优控制理论是研究和解决从一切可能的控制方案中寻找最优解的一门学科，解决最优控制问题的主要方法有变分法、极大值原理和动态规划。
常使用到的主要有时间最短控制问题和线性二次型最优控制问题等。
通过以上知识的了解和应用可以使初学者能够快速掌握最优控制的问题。
关键字：最优化最优控制极值时间最优控制线性二次型目录第一章最优控制的基础 (4)1.1 最优控制理论 (4)1.2 最优控制问题的一般形式 (5)1.3 最优控制方法 (6)第二章变分法 (7)2.1 变分法基础 (7)2.2 变分法应用 (7)第三章极大值原理 (10)3.1 极大值原理的提出和形式 (10)3.2 极大值原理的应用 (11)第四章动态规划方法 (13)4.1 动态规划概念及意义 (13)4.2 动态规划算法的基本思想和结构 (13)4.3 动态规划算法的运用 (14)第五章时间最优控制问题 (16)第六章线性二次型最优控制问题 (20)6.1 线性二次型最优控制问题的提出 (20)6.2 应用MATLAB求解二次型最优控制问题（实验部分） (22)第七章关于倒立摆的最优控制 (34)结束语 (39)参考文献 (39)第一章最优控制的基础§ 1.1 最优控制理论最优控制理论是研究和解决从一切可能的控制方案中寻找最优解的一门学科。
它是现代控制理论的重要组成部分。
最优控制是最优化方法的一个应用，如果想了解最优控制必须知道什么是最优化方法。
所谓最优化方法为了达到最优化目的所提出的各种求解方法。
从数学意义上说，最优化方法是一种求极值的方法，即在一组约束为等式或不等式的条件下，使系统的目标函数达到极值，即最大值或最小值。
从经济意义上说，是在一定的人力、物力和财力资源条件下，使经济效果达到最大（如产值、利润），或者在完成规定的生产或经济任务下，使投入的人力、物力和财力等资源为最少。
现代控制理论论文
[3]程鹏，王艳东编著.现代控制理论基础.第二版.北京：北京航空航天大学出版社，2010
学年论文
题目四阶系统稳定性判定
院系
专业
学生姓名
学号
指导教师
二Ｏ一二年五月二十日
一.背景介绍
1997年7月4日,以太阳能作动力的”逗留者号”漫游车在火星上着陆.漫游车全重10.4kg，可由地球上发出的路径控制信号r(t)实施遥控。漫游车的两组车轮以不同的速度运行，以便实现整个装置的转向。为了进一步探测火星上是否有水，2004年美国国家宇航局又发射了“勇气号”火星探测器。“勇气号”上的装备更为先进。在此，仅仅研究“逗留者号”漫游车的转向控制。
2.控制系统设计
车轮力矩
操纵右C(s)
调速阀门左漫游方向
3.结构图
R(s) + C(s)
预期的_
转动方向
3.仿真
由上可知,可设K1=50,a=0.84。所以
在Matlab中执行以下命令
运行结果为
即状态空间模型为
x +
(1)用MATLAB编程来分析
原系统的能控性、能观测性、稳定性分析，程序如下:
运行结果为：
（2）用MATLAB确定系统的零输入响应曲线
在MATLAB中执行以下命令
运行结果为
(3)用MATLAB分析所设计系统的单位阶跃响应特性
假设作用在小车上的输入为阶跃函数，所有的初始条件为0，确定了反馈增益矩
阵和积分增益常数，小车的转矩对阶跃输入的响应为
运行结果为：
4.控制信号图
5．参考文献
[1]胡寿松主编.自动控制原理.第五版.北京：科学出版社，2007
自我控制论文(5篇)
自我控制论文(5篇)自我掌握论文(5篇)自我掌握论文范文第1篇【关键词】内部掌握管理理论公司治理企业文化重视人1936年美国会计师协会（美国注册会计师协会的前身）了《注册会计师对财务报表的审查》文告，首次使用了“内部掌握”这个名称。
此时对内部掌握的定义侧重于内部牵引，内部牵引在会计制度中的应用从而有利于财务报表的牢靠性评测。
1972年美国注册会计师协会对于内部掌握的定义进行了改进，以内部会计掌握和内部管理掌握来综合表述内部掌握的概念。
1988年aicpasas no.55中用内部掌握结构取代之前的“制度二分法”定义。
我们目前大多数学者定义的概念coso的内部掌握整合框架。
美国coso 的定义：内部掌握是由企业董事会、经理阶层以及其他员工影响实施的，旨在保证财务报告的牢靠性、经营的效果和效率以及现行法规的遵循而供应合理保证的过程。
本人无意于争论内部掌握的明确定义，但从管理学理论看待内部掌握，内部掌握仅仅是实现某种目标的一个工具或者说是一种机制、一种策略甚至是一项明确的政策。
当然这个工具是动态性的，会依据外部环境的变化不断调整的。
一、内部掌握的管理定位从成熟期的内部掌握理论来看，学术界受到coso和sox法案的影响最大，几乎是每个讨论内部掌握的学者必需提及到的内容。
但是无论是coso还是sox都仅仅是在一系列财务欺诈案件之后，相关部门所做出来的合理的反应而已。
coso报告和sox法案仅仅是这一系列案件后果中的一小部分成果，从公司制的进展历史上来看，财务造假与反财务虚假报告就从未停止过，内部掌握仅仅是他们两派斗争之后的副产品而已。
内部掌握作为世界任何国家审计部门或者相关财务政策管理部门亲密关注的焦点，从本质上来看仅仅反应了两个方面内容：（1）对于受托责任的监控，公司全部者要求资产的保值与增值，不盼望管理者有太大的冒险行为，更不盼望看到虚假的受托报告。
（2）决策有用，无论是“安稳”“世通”还是“银广夏”等公司的失败，最终买单的都是投资者，内部掌握有利于保证投资者的权益。
现代控制理论课程论文浙江大学Word版
现代控制理论课程论文现代控制理论综述姓名XXXX学号XXXX学院机械工程学院班级XXXXX专业机械设计及理论学位类型学术型2014年11月21日摘要本文对现代控制理论做了一次完整综述,主要讲了现代控制理论的起源、内容、发展及其特点。
本文简要说明了现代控制理论的主要内容，对系统的状态和状态方程、线性控制系统的能控性和能观性、系统的稳定性分析、线性定常系统的常规综合、最优控制做了简要概述。
最后介绍了一下现代控制技术在21世纪的发展趋势，主要包括信息技术与控制技术的结合、虚拟现实及计算机仿真技术、集成控制技术。
关键词：现代控制理论，综述，主要内容，发展趋势AbstractThis paper made a complete summary modern control theory, concerning the origin, content, development and characteristics of modern control theory. This paper made a brief description of the main elements of modern control theory, including the system's status and state equations, linear control system controllability and observability, the stability analysis, conventional integrated of linear time-invariant systems and optimal control. Finally we made a introduction about the trends of modern control theory in modern control technology of the 21st century, including the combination of information technology and control technology, virtual reality and computer simulation technology and integrated control technology.Key words:Modern control theory, summary, main content, development trend目录第一章绪论 (1)1.1现代控制理论的起源与发展 (1)1.2现代控制理论的特点及主要内容简介 (1)1.3现代控制理论的学习意义 (1)第二章现代控制理论的主要内容 (2)2.1系统的状态和状态方程 (2)2.2线性控制系统的能控性和能观性 (2)2.3系统的稳定性分析 (2)2.4线性定常系统的常规综合 (3)2.5最优控制 (4)第三章现代控制技术在21世纪的发展趋势 (5)3.1信息技术与控制技术的结合 (5)3.2虚拟现实及计算机仿真技术 (6)3.3集成控制技术 (6)第四章总结与展望 (7)参考文献 (8)第一章绪论1.1现代控制理论的起源与发展经典控制理论考虑的对象比较简单，对象为单输入单输出、线性、时不变系统；使用图形化方法，从而依赖于设计人员的经验；不能具有处理多目标，不能揭示系统的内部特性。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
最优控制理论简单研究
姓名：学号：
内容摘要
最优控制理论（optimal control theory），是现代控制理论的一个主要分支，着重于研究使控制系统的性能指标实现最优化的基本条件和综合方法。
最优控制理论是研究和解决从一切可能的控制方案中寻找最优解的一门学科。
它是现代控制理论的重要组成部分。
其所研究的问题可以概括为：对一个受控的动力学系统或运动过程，从一类允许的控制方案中找出一个最优的控制方案，使系统的运动在由某个初始状态转移到指定的目标状态的同时，其性能指标值为最优。
这类问题广泛存在于技术领域或社会问题中。
这类问题广泛存在于技术领域或社会问题中。
例如，确定一个最优控制方式使空间飞行器由一个轨道转换到另一轨道过程中燃料消耗最少，选择一个温度的调节规律和相应的原料配比使化工反应过程的产量最多。
因此最优控制理论对于解决实际问题和促进科学的发展具有重要的意义和作用。
关键字：最优控制；状态方程；稳定性
引言
控制工程领域早期的经典控制方法和技术早已被工程师们所熟知并进行广泛的应用。
一般而言经典控制非常适合解决单输入单输出线性定长系统的控制器设计问题。
然而对于高阶系统或多输入多输出系统，采用经典控制方法很难获得令人满意的控制性能。
在这种情况下，控制学者于20世纪60年代初开始研究状态空间方法，并依此发展出现代控制的理论框架。
其中最优控制则是现代控制理论的主要分支，解决最优控制问题的主要方法有变分法、极值原理和动态规划。
从数学的观点来看，最优控制研究的问题是求解一类带有约束条件的泛函极值问题，属于变分学的范畴，但它只能解决一类简单的最优控制问题，因为它只对无约束或开集性约束是有效的，而无法解决工程实际中经常碰到的容许控制属于闭集的一类最优控制问题。
这就促使了控制学者们开辟求解最优控制问题的新途径。
苏
联学者Л.С.庞特里亚金1958年提出的极大值原理和美国学者R.贝尔曼1956年提出的动态规划，对最优控制理论的形成和发展起了重要的作用，而这两种理论则被称作是最优控制理论的两大基石，它们对现代控制理论的发展起了重要的推动作用。
理论形成阶段：
自动控制联合会(IFAC)第一届世界大会于1960年召开,卡尔曼（Kalman ）、贝尔曼（R.Bellman ）和庞特里亚金（Pontryagin ）分别在会上作了“控制系统的一般理论”、“动态规划”和“最优控制理论”的报告,宣告了最优控制理论的诞生,人们也称这三个工作是现代控制理论的三个里程碑。
1953－1957年，贝尔曼(R.E.Bellman)创立“动态规划”原理。
为了解决多阶段决策过程逐步创立的，依据最优化原理，用一组基本的递推关系式使过程连续地最优转移。
“动态规划”对于研究最优控制理论的重要性，表现于可得出离散时间系统的理论结果和迭代算法。
1956－1958年，庞特里亚金创立“极小值原理”。
它是最优控制理论的主要组成部分和该理论发展史上的一个里程碑。
对于“最大值原理”，由于放宽了有关条件的使得许多古典变分法和动态规划方法无法解决的工程技术问题得到解决，所以它是解决最优控制问题的一种最普遍的有效的方法。
同时，庞特里亚金在《最优过程的数学理论》著作中已经把最优控制理论初步形成了一个完整的体系。
此外，构成最优控制理论及现代最优化技术理论基础的代表性工作，还有不等式约束条件下的非线性最优必要条件(库恩—图克定理)以及卡尔曼的关于随机控制系统最优滤波器等。
最优控制问题的描述
1、系统的状态方程。
对连续系统，其状态方程为： 对离散系统，其状态方程为：
X(k+1)=f( X(k), u(k), k )
系统状态方程给出了系统内部状态随系统控制输入的变化关系，或者说是内部状态的一种约束关系，或者说是系统状态在整个控制过程的转移约束关系。
2、系统状态的始端和终端条件。
始端和终端条件给出了系统状态在系统控制开始和结束时刻的约束条件。
端点条件一般有三种类型：固定端、自由端和可变端。
固定端就是时间和状态值都是固定的端点。
例如初始时间t 0及其初始状态X(t 0)都固定就称始端固定条件，而终端时间t 1及其终端状态X(t 1)都固定就称终端固定条件。
一般来说，两端固定是最简单的情况。
自由端是指端点时间固定，但端点状态值不受任何限制的端点。
有始端自由和终端自由两种。
可变端就是端点时间及其状态值都可变的端点。
但一般它满足一定条件，如满足C(t 1)=0，或N[X(t 1), t 1]=0。
3、系统控制域。
在实际控制系统中，控制输入u (t )往往是受限制地任意取值的，例如作为作为汽车控制的发动机，其输出功率就有最大功率的限制。
所以在许多最优控制问题中，需要规定一个)),(),((t t u t X f X
允许的控制域，即控制允许取值的范围，在此范围取值的控制称为允许控制。
如果系统目标泛函只取式中的第一项，即：
或 则称为终端型或迈耶（Mayer ）型。
如果系统目标泛函只取式中的第二部分，即 或 则称为积分型或拉格朗日(Lagrange)型。
最优控制问题就是在满足上述1、2、3点的条件下，找到一个控制u (t )，使得系统目标泛函J 达到最大或最小。
这样的控制u (t )就称系统的最优控制u *(t )，将u *(t )代入系统状态方程就可解得系统的状态轨迹X(t )，称之为最优状态轨迹X*(t )。
一个最优控制问题的复杂程度，或者说其求解和实现的难易程度是由上述四方面的具体规定，特别是系统的性能指标的具体形式来决定的。
一般来说，两端固定的线性系统，其控制不受限制，且系统性能指标为积分型时，最优控制问题是比较简单的。
结论
常见的实际物理系统，性能指标的提法合理则一般存在最优解，而且在一定的范围内有唯一解。
但是，对于一个比较复杂的问题，最优控制问题解的存在性和唯一性的判定是比较复杂的，有时甚至是不可能的。
现在的研究一般都假定是有唯一解的最优控制问题，即可以求出一个最优的解来。
我们还应该了解，我们希望找到的是“整体”的最优控制，也就是在允许的范围内，寻找的控制作用使动态系统的性能指标达到最小或者最大。
但是，在实际情况中除二次型性能指标的最优控制问题外，一般是很难用定量方法求得整体最优控制的，因此常常是求出许多局部最优控制，再挑选整体最优控制。
21世纪是科技迅猛发展的时代，各门学术都将有令人耳目一新的成就出现。
而最优控制仍是一个十分活跃的研究领域，在理论和实践两方面都得到了充分的发展，为科学的发展和人类的进步作出了巨大的贡献。
参考文献:
[1]胡寿松，王执铨，胡维礼. 最优控制理论与应用[M].北京：科学出本社,2005.
[2]王青，陈宇. 最优控制--理论、方法与应用[M]. 北京：高等教育出版社,2011.
[3]孙文瑜,徐成贤. 最优化方法，高等教育出版社[M],2004
[4]王孝武. 现代控制理论基础，（第二版），机械工业出版社[M],2006
[5]顾立钧.最优控制系统[M].北京：水利电力出版社，1993.
))((1t X J Φ=))((l X J Φ=⎰=10)),(),((t t dt t t u t X F J ∑
-==1)),(),((l h k k k u k X F J。