结构力学第五章习题集与答案解析
结构力学结构力学第三版王焕定第5章习题及参考答案
4-1 答：可用解除约束、暴露未知力和求计算自由度的方法判断超静定次数。
（a ）7次；（b ）3次；（c ）3次；（d ）4次；（e ）7次；（f ）10次；（g ）7次；（h ）6次；（i ）21次。
4-2 (a) 答：一次超静定，可如下做单位与荷载弯矩图：可由图乘求系数，由力法方程求解并由叠加做弯矩图：1111P 23111041P1P 01P 11d 3d 838ll X M l x EI EIM M ql x EI EI ql X M M X M δ∆δ∆+===−====+∑∫∑∫本题也可将B 处解除约束变成铰，以简支梁为基本体系，两者工作量相当（从略）。
这说明力法由于基本体系不唯一，对应解法也不唯一，只要不出错都可获得问题的解答，真实解答是唯一的。
ql 22 A B M P 图 q A lA /8M 图在上述荷载及单位弯矩图下，可图乘求系数、建立力法方程并求解，最后叠加出最终弯矩图，有关过程如下：2211P P2P 122P 1P 22211211222212112121118,816,36,300M X M X M M l F X l F X EI l F EI l EI l EI l X X X X P P P ++===−=∆=∆=====∆++=∆++δδδδδδδδ 本题也可利用对称性，在轴力为零前提下按一次超静定结构计算（过程参见（c ）题），最终结果完全一样。
P M P 图 1F P l /8F P l /8 B A M 图21M 图F P l /44-2(c) 答：横向荷载轴力为零，可按一次求解（实际（b ）可用对称性化成本题形式）由单位、荷载弯矩图苛求习俗，建立力法方程并求解，叠加可得最终弯矩图如下。
11P P 1P111P 1111220X M M l F X EI lF EI l X P +=−==∆==∆+δδ 考虑到本题荷载及杆长是上题（b ）对称性后的一倍，可将两者结果一样。
结构力学 第五章(07.8.28)
( ) θ A1
= θ B1
=−
ql 2 4 l 3EI
ql/2
q
AB
D
C
l/2
l
wA1
=
−θ B1
⋅ ⎜⎛ ⎝
l ⎟⎞ 2⎠
=
ql 4 24EI
( ) wD1
=−
ql 2 4 l 2 16EI
ql2/4 （1）
AB
D
C
θ A2
= θB2
=
ql 3 24EI
wA2
=
−θ B2
⋅ ⎜⎛ l ⎟⎞ ⎝2⎠
− (qa 2)(3a)3
3EI
= 135qa 4 24EI
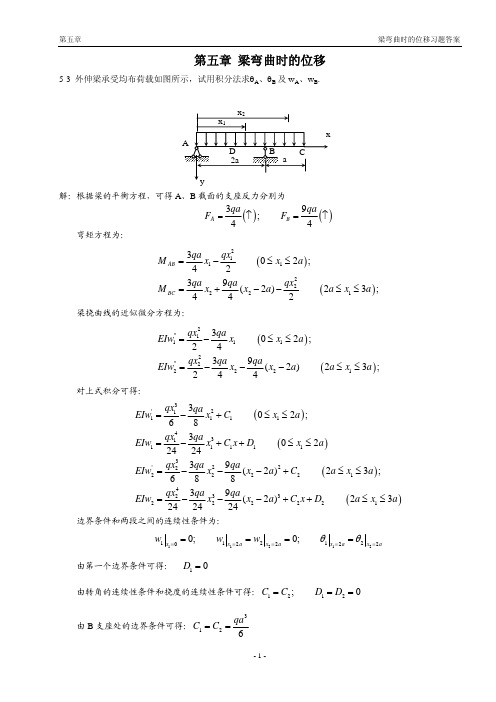
将 AC 段刚化，梁的挠曲线如图（2）所示，此时 C 点挠度为零。
故 wC
=
wC1
= 135qa 4 24EI
作梁的弯矩图如图所示，由弯矩图的正负可确定挠曲线的大致形状。
q
（a） A 3a
qa
C
BD
2a a
qa/2
（1）
C
A
（2）
C
3qa2
EIw2
=
qx24 24
−
3qa 24
x23
−
9qa 24
( x2
−
2a)3
+
C2 x
+
D2
(2a ≤ x1 ≤ 3a)
边界条件和两段之间的连续性条件为：
w1 x1=0 = 0;
w1 x1=2a = w2 x2 =2a = 0;
θ = θ 1 x1=2a
2 x2 =2a
由第一个边界条件可得： D1 = 0
θB = 0
结构力学第5章答案(完整版)
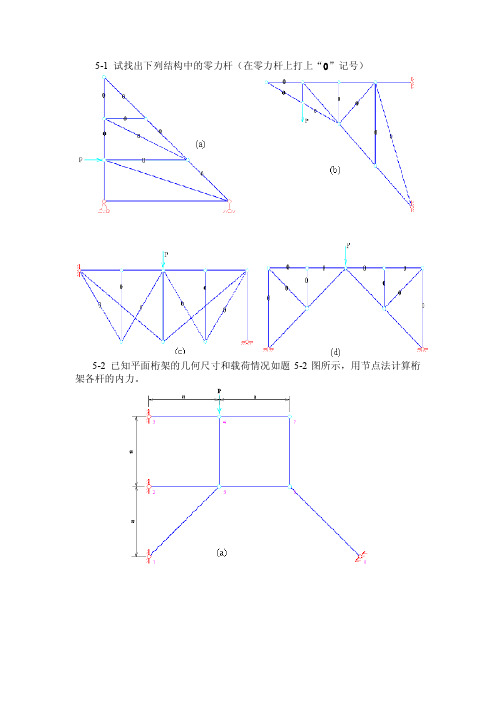
5-1试找出下列结构中的零力杆（在零力杆上打上“0”记号）5-2 已知平面桁架的几何尺寸和载荷情况如题5-2图所示，用节点法计算桁架各杆的内力。
解：(a)、零力杆：74，76，65，68，43分析节点4，得P N -=45分析节点5，得 ２－ １P N P N ==552,(b)、零力杆：26，61，63，48，83，85，37，71分析节点7：P N -=75 分析节点5：5254P N =1221233234434554N N N N N N N N =======(c)、支座反力：均为0分析节点1： P N P N 2,31512-== 分析节点2： P N P N 2,32523== 分析节点3： P N 235-= 分析节点4： 04543==N N (d)、零力杆：12，15，52，83，43，49支座反力：P R P R P R y x y 3.1,8.0,3.2223=-==分析节点5： P N 8.056-=分析节点6： P N P N -=-=6267,8.0 分析节点9： P N P N 6.0,26.09893=-= 分析节点8： P N 6.087=分析节点3： P N P N 1.1,27.13237=-= 分析节点7： P N 23.072-=5-3 用分解成平面桁架的方法求如题5-3图所示空间桁架各杆的内力。
解：零力杆：26，48，34，24，28122152316213337317383N P a N P P cN P N P N P N P NP ==-=-=-===-３ 5-4 已知平面桁架的几何尺寸和受载情况如题5-4图所示。
求图中用粗线所示的杆件①，②，③的内力。
解：(a)、零力杆如图所示1340,3P M N ==∑由得 3210,M N P ==-∑由得310,3y F N P ==∑由得 (b)、2140,2M N P ==∑由得230,x F N P ==-∑由得250,y F N ==∑由得(c)、支座反力：均为0，结构简化为：PN F P N F PN M x y 31,032,032,03213====-==∑∑∑得由得由得由5-5 求如题5-5图所示平面桁架的内力。
哈工大结构力学题库五章
第五章位移法一判断题1. 图a为对称结构，用位移法求解时可取半边结构如图b所示。
答：（×）题1图2. 图示结构，用位移法求解，有三个结点角位移和二个结点线位移未知数。
（×）。
题2图题3图ϕ=所施加的弯矩相同。
（×）3. 以下两个单跨梁左端产生14. 用位移法计算刚架，常引入轴向刚度条件，即“受弯直杆在变形后两端距离保持不变”。
此结论是由下述假定导出的：（D）A 忽略受弯直杆的轴向变形和剪切变形；B 弯曲变形是微小的；C 变形后杆件截面仍与变形曲线相垂直；D 假定A与B同时成立。
5. 用位移法计算图示结构时，独立的基本未知数数目是4 。
（×）题5图题6图6. 图示结构用位移法计算时，其基本未知量的数目为3个（√）。
7. 在位移法典型方程的系数和自由项中，数值范围可为正、负实数的有：（D）A 主系数；B 主系数和副系数；C 主系数和自由项D 负系数和自由项。
8. 用位移法计算超静定结构时考虑了到的条件是：（A）A物理条件、几何条件、和平衡条件；B平衡条件117C平衡条件与物理条件D平衡条件与几何条件9. 规定位移法的杆端弯矩正负时，对杆端而言，以顺时针为正，对结点则以逆时针为正，这一规定也适合于杆端剪力的符号规定。
（×）10. 图a对称结构可简化为图（b）来计算。
（×）题10图题11图11. 图示结构用位移法求解时，基本未知量个数是相同的（√）12. 图示结构用位移法求解时，只有一个未知数（√）题12图题13图题14图13. 图示结构横梁无弯曲变形，故其上无弯矩。
（×）14. 图ａ对称结构可简化为图ｂ来计算，EI均为常数。
（×）15. 图示结构用位移法求解的基本未知量数目最少为3。
（√）题15图题16图16. 图示结构EI＝常数，用位移法求解时有一个基本未知量。
（√）。
17. 位移法中固端弯矩是当其基本未知量为零时由外界因数所产生的杆端弯矩（√）18. 位移法的典型方程与力法的典型方程一样，都是变形协调方程。
地质大学远程网络继续教育结构力学习题集以及答案解读
1、杆系结构中梁、刚架、桁架及拱的分类，是根据结构计算简图来划分的。
(正确)2、定向支座总是存在—个约束反力矩(正确)和一个竖向约束反力。
(错误)3静力和动力荷载的区别，主要是取决于它随时间变化规律、加载速度的快慢。
其定性指标由结构的自振周期来确定。
(正确)4、铰结点的特性是被连杆件在连接处既不能相对移动，(正确)又不能相对转动。
(错误)5、线弹性结构是指其平衡方程是线性的，(正确)变形微小，(正确)且应力与应变之间服从虎克定律。
(正确)1、学习本课程的主要任务是：研究结构在各种外因作用下结构内力与（）计算，荷载作用下的结构反应；研究结构的（）规则和（）形式等问题。
正确答案：位移，动，组成，合理2、支座计算简图可分为刚性支座与弹性支座，其中刚性支座又可分为（）、（）、（）和（）。
正确答案：链杆，固定铰支座，固定支座，滑动支座3、永远作用在结构上的荷载称为固定荷载，暂时作用在结构上的荷载称为（）它包括（）、（）、（）、（）和（）等正确答案：活载，风，雪，人群，车辆，吊车4、刚节点的特性是被连接的杆件载连接处既无（）又不能相对（）；既可传递（），也可传递（）正确答案：移动，转动，力，力矩第二章平面体系的几何构成分析1、图中链杆1和2的交点O可视为虚铰。
（）O正确答案：正确2、两刚片或三刚片组成几何不变体系的规则中，不仅指明了必需的约束数目，而且指明了这些约束必须满足的条件。
（）正确答案：正确3、在图示体系中，去掉1-5，3-5，4-5，2-5，四根链杆后，的简支梁12，故该体系具有四个多余约束的几何不变体系。
（）12345正确答案：错误4、几何瞬变体系产生的运动非常微小并很快就转变成几何不变体系，因而可以用作工程结构。
（）正确答案：错误5、图示体系是几何不变体系。
()正确答案：错误2-2几何组成分析1．正确答案：几何不变，且无多余联系。
2．(图中未编号的点为交叉点。
)A B CDEF正确答案：铰接三角形BCD视为刚片I，AE视为刚片II，基础视为刚片III；I、II间用链杆AB、EC构成的虚铰(在C点)相连，I、III间用链杆FB和D处支杆构成的虚铰(在B点)相联，II、III 间由链杆AF和E处支杆构成的虚铰相联3．(图中未画圈的点为交叉点。
结构力学章节习题及参考答案
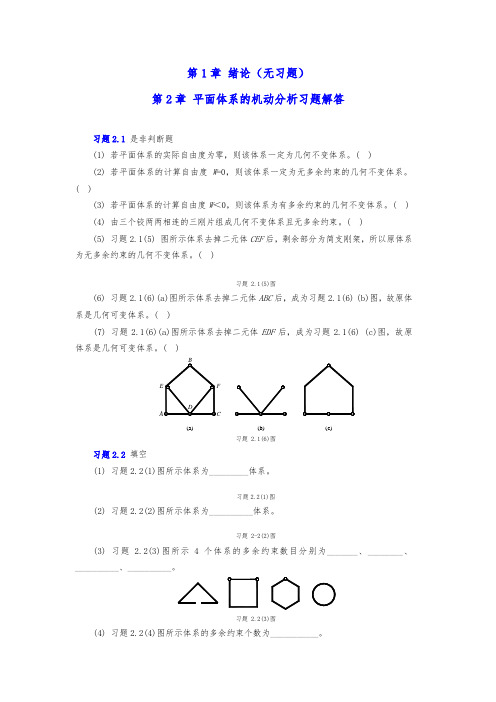
第1章绪论（无习题）第2章平面体系的机动分析习题解答习题2.1是非判断题(1) 若平面体系的实际自由度为零，则该体系一定为几何不变体系。
( )(2) 若平面体系的计算自由度W=0，则该体系一定为无多余约束的几何不变体系。
( )(3) 若平面体系的计算自由度W＜0，则该体系为有多余约束的几何不变体系。
( )(4) 由三个铰两两相连的三刚片组成几何不变体系且无多余约束。
( )(5) 习题2.1(5) 图所示体系去掉二元体CEF后，剩余部分为简支刚架，所以原体系为无多余约束的几何不变体系。
( )习题 2.1(5)图(6) 习题2.1(6)(a)图所示体系去掉二元体ABC后，成为习题2.1(6) (b)图，故原体系是几何可变体系。
( )(7) 习题2.1(6)(a)图所示体系去掉二元体EDF后，成为习题2.1(6) (c)图，故原体系是几何可变体系。
( )(a)(b)(c)习题 2.1(6)图习题2.2填空(1) 习题2.2(1)图所示体系为_________体系。
习题2.2(1)图(2) 习题2.2(2)图所示体系为__________体系。
习题 2-2(2)图(3) 习题 2.2(3)图所示4个体系的多余约束数目分别为_______、________、__________、__________。
习题 2.2(3)图(4) 习题2.2(4)图所示体系的多余约束个数为___________。
习题 2.2(4)图(5) 习题2.2(5)图所示体系的多余约束个数为___________。
习题 2.2(5)图(6) 习题2.2(6)图所示体系为_________体系，有_________个多余约束。
习题 2.2(6)图(7) 习题2.2(7)图所示体系为_________体系，有_________个多余约束。
习题 2.2(7)图习题2.3 对习题2.3图所示各体系进行几何组成分析。
(a)(b)(c)(d)(e)(f)(h)(g)(i)(j)(k)(l)习题2.3图第3章 静定梁与静定刚架习题解答习题3.1 是非判断题(1) 在使用力图特征绘制某受弯杆段的弯矩图时，必须先求出该杆段两端的端弯矩。
结构力学 第五章 作业参考答案
结构力学 第五章习题 参考答案2005级 TANG Gui-he （整理）5－1 试用结点法计算图示桁架各杆的内力。
5－2 试用结点法计算图示桁架各杆的内力。
解:由整体平衡条件可解得支座反力 F A =1.5F F B =1.5F 取结点A 为隔离体,如图,用数解法可解得 F A C =-2.12F F A B =1.5F 同理,依次取结点B 、C 、 D 、E 为隔离体,并由对称性可得各杆的内力如图。
4 * 8m60k N60k N6M 2MA B C D E FG H 解：由 M H =0 可得支座F a y=75kN.由 F Y=0 得 F h y=45kN 取 A 结点为隔离体，利用数解法可得 F N AB=-100kN. F NAC=125kN. 再取 C 点为隔离体，利用投影法和力平衡 可得 F N BC=-50,F NCE=103.1kN.同理依次取 B ， D ， E ， G ， F 可得各杆内力（如图所标）AC-60k N -90k N -100k N 45k N75k N125k N 75k N 42.4k N61.8k N 103.1k N -60k N -50k N -30k N55－4试判断图示桁架中的零杆。
解：图中红色的杆件为零杆在杆中标有 为零杆其中用到K 型和T 型结构判断原理5－5试用截面法计算图示桁架中指定杆件的内力。
2解:（1）求出支座竖向反力为2.5F (↑),（2）作截面I -I ，由∑M A=0得: 2.5F ×15-10F -5F +6F N 1=0 → F N 1=-3.75F （3）由∑M B=0得: 2.5F ×10-F ×5-F N 2×6=0 → F N 2=3.33F （4）利用勾股定理求出A B 杆长7.8F N 4x =5F N 4/3.84 由∑M C=0得: 2.5F ×10-5F +F N 1×6+6×5F N 4/7.8=0 → F N 4=0.65F （5）取结点B 为分析对象,由∑F Y=0得: F N 4×6/7.8+F N 3=0 → F N 3=-0.5F5－6试用截面法计算图示桁架中指定杆件的内力。
同济大学 结构力学课后习题及答案解析(完整版)
R=2m
4m
A O
M ( ) 1 (R sin )2 1 2 R(1 cos ) 2
M ( ) 1
B
1 EI
2 1 [1 (R sin )2 1 2 R(1 cos )]Rd 02
= (8-3 ) -1.42 (逆时针)
EI
EI
(d) A q
R EI=常数
O
B
5-7 试用图乘法计算图示梁和刚架的位移：（a） ΔyC ；（b） ΔyD ；（c） ΔxC ；（d） ΔxE ；（e） D ；（f） ΔyE 。 (a)
5-5 已知桁架各杆的 EA 相同，求 AB、BC 两杆之间的相对转角 ΔB 。 5-6 试用积分法计算图示结构的位移：（a） ΔyB ；（b） ΔyC ；（c） B ；（d） ΔxB 。
(a)
q2 q1
A
EI
B
l
以B点为原点，向左为正方向建立坐标。
q( x)
q2
l
q1
x
q1
M
p(x)
1 2
52.17
M
248.49
104.37 52.14
6-6 试用力法求解图示超静定桁架，并计算 1、2 杆的内力。设各杆的 EA 均相同。
(a)
(b)
1
1
2
FP
FP
a
a
a
2m
题 6-6 图
6-7 试用力法计算图示组合结构，求出链杆轴力并绘出 M 图。
2
30kN 2m
(a)
a 1.5m
l
A
kθ=
12EI l
2 3
2 3
6 1 20 62 8
3 2
1 6180 3 2
结构力学课后习题答案
结构力学课后习题答案结构力学是一门研究结构在外力作用下的内力、变形和稳定性的学科。
课后习题是帮助学生巩固理论知识和提高解题技巧的重要环节。
以下是一些结构力学课后习题的参考答案，供学习者参考：第一章：结构力学基础1. 静定结构与超静定结构的区别：静定结构是指在已知外力作用下，其内力和位移可以通过静力平衡方程和几何关系唯一确定的结构。
超静定结构则是指静力平衡方程和几何关系不足以唯一确定其内力和位移的结构。
2. 弯矩图的绘制方法：绘制弯矩图首先需要确定结构的支反力，然后通过截面平衡条件，逐步求出各截面的弯矩值，并将其绘制成图形。
第二章：静定梁的内力分析1. 简支梁的内力计算：对于简支梁，可以通过静力平衡条件和截面平衡条件来计算梁的内力，包括剪力和弯矩。
2. 悬臂梁的内力计算：悬臂梁的内力计算需要考虑梁端的外力和力矩，通过静力平衡条件求解。
第三章：静定桁架的内力分析1. 节点法的应用：节点法是通过在桁架的节点上施加平衡条件来求解节点的反力，进而求得杆件的内力。
2. 截面法的应用：截面法是通过选取桁架的某一截面，对该截面进行平衡分析，求得截面两侧杆件的内力。
第四章：静定拱的内力分析1. 三铰拱的内力计算：三铰拱的内力计算通常需要利用静力平衡条件和几何关系，计算出拱的反力和弯矩。
2. 双铰拱和无铰拱的内力特点：双铰拱和无铰拱的内力计算更为复杂，需要考虑更多的平衡条件和几何关系。
第五章：超静定结构的内力分析1. 力法的应用：力法是通过建立力的平衡方程来求解超静定结构的内力，通常需要引入多余未知力。
2. 位移法的应用：位移法是通过建立位移的平衡方程来求解超静定结构的内力，通常需要引入位移未知数。
第六章：结构的稳定性分析1. 欧拉临界载荷的计算：欧拉临界载荷是指细长杆件在轴向压力作用下失稳的临界载荷，可以通过欧拉公式计算。
2. 非线性稳定性分析：对于非线性问题，稳定性分析需要考虑材料的非线性特性和几何非线性，通常需要采用数值方法求解。
结构力学第五章习题参考解答
ql 2 8
? 1? l
1 2
l
????
?
ql 3 24EI
代入力法典型方程
?11 X1 ? ?12 X2 ? ? 1P ? 0
得：
X1
?
3ql 28
X2
?
ql 2 28
? 21 X1 ? ? 22 X2 ? ? 2P ? 0
1 ql 2 14
1 ql 2 8
3 ql 28
作结构的弯矩图如图。
3
9 98
M图
5－3 试利用可能简便的方法计算图示对称结构的内力， 并绘出弯矩图。
（a）解：由于该结构上下、左右均为正对称荷载， 故可取 1/4部分，对称轴处简化为定向支座如图。 去掉水平支座的一根链杆，代之以多余约束力矩 X1 ， 得到基本体系如图。
q
q
q
D
C
X1 EI ? 常数 l
A
B
lq
作 M P 图、M 图，则有：
B D
25.54
E
F
M图
MC
?
X1 ?
2 ? 80 ?
2?
1 q ? 22 2
? 67.23? 2 ? 160 ? 40 ? 14.46?KN ?m?
M中
?
X1 ? 2 ?
1 q ? 82 8
?
67.23 ?
2 ? 160
?
?25.54?KN ?m?
5－6 试用力法计算图示桁架，各杆 EA ? 常数 。
X1 、X2，得到
q
q
C
B
EI
X1
EI
l
A
X2
l
作 M P图、M 1图、M 2图 ，
《结构力学习题集》5-力法
第五章 力法一、是非题1、图示结构用力法求解时，可选切断杆件2、4后的体系作为基本结构。
123452、力法典型方程的实质是超静定结构的平衡条件。
3、图a结构，取图b 为力法基本结构，则其力法方程为δ111X c=。
(a)(b)X 14、图a 所示结构，取图b 为力法基本体系，线胀系数为α，则∆1= t t l h -322α()。
lo +2t 1X (a)(b)5、图a 所示梁在温度变化时的M 图形状如图b 所示。
(a)(b)0C 图 -50C +15M6、超静定结构在荷载作用下的反力和内力，只与各杆件刚度的相对数值有关。
7、在温度变化、支座移动因素作用下，静定与超静定结构都有内力。
8、图示结构中，梁AB 的截面EI 为常数，各链杆的E A 1相同，当EI 增大时，则梁截面D 弯矩代数值M D 增大。
9、图示对称桁架，各杆EA l ,相同，N P AB =。
二、选择题1、图a 所示结构 ，EI =常数 ，取图b 为力法基本体系，则下述结果中错误的是： A ．δ230= ； B ．δ310= ；C ．∆20P = ；D ．δ120= 。
()llll/2(a)P (b)2、图示连续梁用力法求解时, 简便的基本结构是： A ．拆去B 、C 两支座；B ．将A 支座改为固定铰支座，拆去B 支座；C ．将A 支座改为滑动支座，拆去B 支座；D ．将A 支座改为固定铰支座 ，B 处改为完全铰。
()3、图示结构H B 为：A ．P ；B ．-P 2 ； C ．P ； D ．-P 。
()4、在力法方程δij j c i X ∑+=∆∆1中：A B.C. D .;;;.∆∆∆i i i =><000前三种答案都有可能。
()5、图示两刚架的EI 均为常数，并分别为EI = 1和EI = 10，这两刚架的内力关系为：()A．M图相同；B．M图不同；C．图a刚架各截面弯矩大于图b刚架各相应截面弯矩；D．图a刚架各截面弯矩小于图b刚架各相应截面弯矩。
结构力学结构力学第三版王焕定第5章习题及参考答案
X1
I1/I2=k
I2 B E
I2 F
基本体系
q
l/4
C
I1 A
I1 D
ql2/8
I2 B
I2
E
F
MP图
C
I1 A
I1 D
X1 =1
I2 B
I2
E
l/4
F
M 1图
δ11X1 + ∆1P = 0
δ11
=
l3 24EI1
+
l3 24EI2
=
l3 24EI1
(1 + k)
C
(1 − 5 )ql2 8 64(1 + k)
更多教材下载: 更多考研资料下载：
4-1 答：可用解除约束、暴露未知力和求计算自由度的方法判断超静定次数。（a）7 次；（b） 3 次；（c）3 次；（d）4 次；（e）7 次；（f）10 次；（g）7 次；（h）6 次；（i）21 次。
FP
A B
l
FP
A
B
基本体系
X1
FPl
1
1
FP
A B
MP 图
A B
M1图
X1 =1
由单位、荷载弯矩图苛求习俗，建立力法方程并求解，叠加可得最终弯矩图如下。
δ11X1 + ∆1P = 0
δ11
=
l EI
∆1P
=
FPl 2EI
X1
=
−
FPl 2
FPl/2 A
B
M图
FPl/2
M = MP + X1M1
考虑到本题荷载及杆长是上题（b）对称性后的一倍，可将两者结果一样。
基本体系
结构力学第五章习题集与答案解析
结构⼒学第五章习题集与答案解析第五章习题5—2 试⽤⼒法计算下列结构，并会出弯矩图。
解：1.判断超静定次数：n=12. 确定(选择)基本结构。
3.写出变形(位移)条件：（a ）根据叠加原理，式（a ）可写成(a)基本体系M P 图F P l 01=?（b ）4 .建⽴⼒法基本⽅程将?11=δ11x1代⼊(b)得（c ）5. 计算系数和常数项EI l ll l EI 332)21(1311==δ6. 将d11、 ?11代⼊⼒法⽅程式（c ）1111=?+?=?P 01111=?+P X δEIl F l F l l l F l l EI P P P P485)2322212312221(131=+?=?) (1651111↑=?-=PPF X δpM X M M +=17.作弯矩图3FP P l /16(b)基本体系M P 图F P (l -a ）1632165l F l F l F M P P P A =-?=解：1.判断超静定次数：n=12. 确定(选择)基本结构。
3.写出变形(位移)条件：（a ）根据叠加原理，式（a ）可写成（b ）4 .建⽴⼒法基本⽅程将?11=δ11x1代⼊(b)得（c ）5. 计算系数和常数项1=?01111=?+?=?P 01111=?+P X δ133)3221(1)]332()(21)332()(21[132331211EI a EI a l a a a EI a l a a l l a a a l EI + -=++??-?++??-?=δ22216)2()(]3)(2)(213)()(21[1EI a l a l F a l F a a l a l F a a l EI P P P P+--=-??-?+-??-?=?6. 将d11、 ?11代⼊⼒法⽅程式（c ）31233231)1(322aI I l a al l F X P --+-=7.作弯矩图（d ）解：超静定次数为2选择基本结构如图（1）所⽰⼒法pM X M M +=11(a)。
西北工业大学(王生楠)结构力学课后题答案第五章位移法
2 − 2 0 −4 0 0 0 0 − 2 4+ 2 0
4 0 0 8+ 2 0 − 2 0 −4 0 0 0 0
0 − 2 −4 4+ 2 0 0 8+ 2 0 − 2 0 −4
⎤ ⎥ ⎥ − 2 ⎥ ⎥ 2 ⎥ 0 ⎥ ⎥ 0 ⎥ ⎥ 0 ⎥ 0 ⎥ ⎥ −4 ⎥ 0 ⎥ ⎥ 4 + 2⎦ ⎥ 0 0
K 1− 4
⎡ 1 3 −1 − 3⎤ ⎢ ⎥ 3 3 − 3 −3 ⎥ 3 EA ⎢ = 8l ⎢ − 1 − 3 1 3 ⎥ ⎢ ⎥ 3 3 ⎥ ⎢− 3 − 3 ⎣ ⎦
�
杆元 1-5，长度为 2l , θ = 30 , λ = cos θ =
3
2
, µ = sin θ = 1 . 2
K 1−5
2
4
6
60°
7
1 a
3 a
5 a
(b)
解：以节点 1 为原点，建立如图所示的总体坐标系。 建立元素刚度矩阵。杆元 1-3， l = a, θ = 0 , λ = cos θ = 1, µ = sin θ = 0.
�
K 1−3
⎡1 ⎢0 EA ⎢ = a ⎢− 1 ⎢ ⎣0
0 −1 0 0 0 1 0 0
0 0⎤ 0 − 1⎥ ⎥ 0 0⎥ ⎥ 0 1⎦
杆元 1-5，长度为 2l
θ = 60 � , λ = cos θ = 1 , µ = sin θ = 3 , 2 2 3,
K 1−5
⎡ 1 3 −1 − 3⎤ ⎢ ⎥ 3 3 − 3 −3 ⎥ 3 EA ⎢ = 8l ⎢ − 1 − 3 1 3 ⎥ ⎢ ⎥ 3 3 ⎥ ⎢− 3 − 3 ⎣ ⎦
K 1− 2
结构力学章节习题及参考答案
第1章绪论（无习题）第2章平面体系的机动分析习题解答习题2.1是非判断题(1) 若平面体系的实际自由度为零，则该体系一定为几何不变体系。
( )(2) 若平面体系的计算自由度W=0，则该体系一定为无多余约束的几何不变体系。
( )(3) 若平面体系的计算自由度W＜0，则该体系为有多余约束的几何不变体系。
( )(4) 由三个铰两两相连的三刚片组成几何不变体系且无多余约束。
( )(5) 习题2.1(5) 图所示体系去掉二元体CEF后，剩余部分为简支刚架，所以原体系为无多余约束的几何不变体系。
( )习题2.1(5)图(6) 习题2.1(6)(a)图所示体系去掉二元体ABC后，成为习题2.1(6) (b)图，故原体系是几何可变体系。
( )(7) 习题2.1(6)(a)图所示体系去掉二元体EDF后，成为习题2.1(6) (c)图，故原体系是几何可变体系。
()(a)(b)(c)习题2.1(6)图习题2.2填空(1) 习题2.2(1)图所示体系为_________体系。
习题2.2(1)图(2) 习题2.2(2)图所示体系为__________体系。
习题2-2(2)图(3) 习题 2.2(3)图所示4个体系的多余约束数目分别为_______、________、__________、__________。
习题2.2(3)图(4) 习题2.2(4)图所示体系的多余约束个数为___________。
习题2.2(4)图(5) 习题2.2(5)图所示体系的多余约束个数为___________。
习题2.2(5)图(6) 习题2.2(6)图所示体系为_________体系，有_________个多余约束。
习题2.2(6)图(7) 习题2.2(7)图所示体系为_________体系，有_________个多余约束。
习题2.2(7)图习题2.3对习题2.3图所示各体系进行几何组成分析。
(a)(b)(c)(d)(e)(f)(h)(g)(i)(j)(k)(l)习题2.3图第3章 静定梁与静定刚架习题解答习题3.1 是非判断题(1) 在使用内力图特征绘制某受弯杆段的弯矩图时，必须先求出该杆段两端的端弯矩。
结构力学第五章习题及答案
结构力学第五章习题及答案第五章 习题5—2 试用力法计算下列结构，并会出弯矩图。
解：1.判断超静定次数：n=12. 确定(选择)基本结构。
3.写出变形(位移)条件：（a ）根据叠加原理，式（a ）可写成（b ）4 .建立力法基本方程 将∆11=δ11x1代入(b)得(a)基本体系M P 图F P l 01=∆01111=∆+∆=∆P（c ）5. 计算系数和常数项EI l ll l EI 332)21(1311=⨯⨯⨯=δ6. 将δ11、 ∆11代入力法方程式（c ）7.作弯矩图3FP P l /16P 01111=∆+P X δEIl F l F l l l F l l EI P P P P 485)2322212312221(131=⨯⨯⨯+⨯⨯⨯⨯=∆)(1651111↑=∆-=PP F X δpM X M M +=11632165l F l F l F M P P P A =-⨯=解：1.判断超静定次数：n=12. 确定(选择)基本结构。
3.写出变形(位移)条件：（a ）根据叠加原理，式（a ）可写成（b ）4 .建立力法基本方程 将∆11=δ11x1代入(b)得 （c ）5. 计算系数和常数项(b)基本体系M P 图F P (l -a ）1=∆01111=∆+∆=∆P 01111=∆+P X δ133)3221(1)]332()(21)332()(21[132331211EI a EI a l a a a EI a l a a l l a a a l EI +-=⨯⨯⨯++⨯⨯-⨯++⨯⨯-⨯=δ22216)2()(]3)(2)(213)()(21[1EI a l a l F a l F a a l a l F a a l EI P P P P+--=-⨯⨯-⨯+-⨯⨯-⨯=∆6. 将δ11、 ∆11代入力法方程式（c ）31233231)1(322aI I l a al l F X P --+-=7.作弯矩图（d ）解：超静定次数为2选择基本结构如图（1）所示力法典型方程为： δ11X 1+δ12X 2+△1P =0δ21X 1 + δ22X 2+△2P =0计算系数和常数项，为此作作出X 1=1、X 2=1和荷载单独作用下的弯矩图如（2）（3）（4）所示计算结果如下pM X M M +=11(a)EI l l l l l l l EI 34)3221(1311=⨯⨯+⨯⨯⨯=δEI l l l l EI 2)2(1312=⨯⨯=δ1212δδ=EI l l l l EI 3)3221(1322=⨯⨯⨯=δEIql l l ql l ql l EI P85)243231(14221-=⨯⨯+⨯⨯⨯-=∆EIql l l ql EI P4)22(1422-=⨯⨯-=∆将以上各系数代入方程(a)0432*******231342313=-+=-+EI ql X EI l X EI l EI ql X EI l X EI l解联立方程得X 1=3ql/7 (↑) X 2=3ql/28(←) 最后绘制弯矩图M 如（5）所示。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第五章 习题
5—2 试用力法计算下列结构，并会出弯矩图。
解：1.判断超静定次数：n=1
2. 确定(选择)基本结构。
3.写出变形(位移)条件：
（a ）
根据叠加原理，式（a ）可写成
(a)
基本体系
M P 图
F P l 0
1=∆
（b ）
4 .建立力法基本方程 将∆11=δ11x
1代入(b)得
（c ）
5. 计算系数和常数项
EI l l
l l EI 332)21(1311=
⨯⨯⨯=δ
6. 将d11、 ∆11代入力法方程式（c ）
1111=∆+∆=∆P 0
1111=∆+P X δEI
l F l F l l l F l l EI P P P P
485)2322212312221(131=⨯⨯⨯+⨯⨯⨯⨯=∆)
(16
511
11↑=∆-
=P
P
F X δp
M X M M +=1
7.作弯矩图
3FP P l /16
(b)
基本体系
M P 图
F P (l -a ）
16
32165l F l F l F M P P P A =
-⨯=
解：1.判断超静定次数：n=1
2. 确定(选择)基本结构。
3.写出变形(位移)条件：
（a ）
根据叠加原理，式（a ）可写成
（b ）
4 .建立力法基本方程 将∆11=δ11x
1代入(b)得
（c ）
5. 计算系数和常数项
1=∆0
1111=∆+∆=∆P 0
1111=∆+P X δ
1
33)3
221(1)]332()(21)332()(21[13
2331211EI a EI a l a a a EI a l a a l l a a a l EI +
-=⨯⨯⨯++⨯⨯-⨯++⨯⨯-⨯=
δ2
2216)2()(]3
)(2)(213)()(21
[1EI a l a l F a l F a a l a l F a a l EI P P P P
+--=
-⨯⨯-⨯+-⨯⨯-⨯=∆
6. 将d11、 ∆11代入力法方程式（c ）
31
23
3
231)1(322a
I I l a al l F X P --+-=
7.作弯矩图
（d ）解： 超静定次数为2
选择基本结构如图
（1）所示力法
p
M X M M +=1
1(a)
典型方程为： d 11X 1+d 12X 2+△1P =0 d 21X 1 + d 22X 2+△2P =0
计算系数和常数项，为此作作出X 1=1、X 2=1和荷载单独作用下的弯矩图如（2）（3）（4）所示计算结果如下
EI l l l l l l l EI 34)3221(1311=
⨯⨯+⨯⨯⨯=δ
EI l l l l EI 2)2(13
12
=⨯⨯=δ
1212δδ=
EI l l l l EI 3)3221(1322
=⨯⨯⨯=δ
EI
ql l l ql l ql l EI P
85)243231(14
221-=
⨯⨯+⨯⨯⨯-=∆
EI
ql l l ql EI P
4)22(14
22-=
⨯⨯-=∆
将以上各系数代入方程(a)
0432*******
23134
2313=-+=-+EI ql X EI l X EI l EI ql X EI l X EI l
解联立方程得
X 1=3ql/7 (↑) X 2=3ql/28(←) 最后绘制弯矩图M 如（5）所示。
q
（2）
q
ql 2/2
ql /2
M P 图
5—3 试用可能简便的方法计算图示对称结构的力，并绘出弯矩图。
解：①根据结构和荷载的对称性取1/4结构为研究对象如（b ）所示，为1次超静定； ②作出1/4结构的基本结构如图（c ）所示， ③力法典型方程为
q
B
C
D
A
取1/4结构
基本结构
ql 2
(b)
(c)
1111=∆+P X δ
④分别作出单位多余未知力和荷载单独作用下的弯矩图如图（d ）所示
EI
l l l EI )121121(111⨯⨯+⨯⨯=
δ
EI
ql ql l ql l EI p
12)18218231(13221-=⨯⨯-⨯⨯⨯-=∆
⑤将系数和自由项带入典型方程解出X 1=ql 2/12
⑥利用叠加法作出原结构的弯矩图为图（f ）
ql 2
/12
ql 2/12
ql 2/12
ql 2/12
(f)
p
M X M M +=1。