传热学-第七章
《传热学》第七章 凝结与沸腾换热

适用范围:
水平管:
适用范围:
(由于管径不会很大, 一般不会到达紊流)
进行修正后,得到:
垂直壁层流膜状凝结换热平均表面传热系数:
垂直壁与水平管凝结换热强度的比较—— 由于垂直壁定型尺寸远大于水平管,因而水平管凝结换热性能 更好,在实际管外凝结式冷凝器设计中多采用水平管。
垂直壁层流膜状凝结换热另一准则方程:
层流膜状凝结换热 速度变化规律:
蒸气静止,且对液膜无黏滞应力作用
层流膜状凝结换热 温度变化规律:
ts为蒸气饱和温度
可采用对流换热微分方程组对垂直壁层流膜状凝结换热加以研究
1.X方向液膜动量方程: 将: 代入,得:
v为蒸汽密度
假定液膜流动缓慢,则惯性力项可忽略,动量方程可简化为:
一般情况下:
从而:
已知壁温:
二、管内沸腾换热
特征:由于流体温度随流向逐渐 升高,沸腾状态随流向不断改变
液相单相流 h较低
垂 直 管 内 沸 腾
Байду номын сангаас
泡状流
h升高
块状流
h高
环状流
h高
气相单相流
h急剧降低
水平管内沸腾
液 相 单 相 流
泡 状 流
块 状 流
波 浪 流
环 状 流
气 相 单 相 流
汽水分层,管上半部局部换热较差
第七章重点: 1.膜状凝结换热特征和计算方法
2.沸腾换热的四个阶段 3.热管的工作原理
谢谢观看
三、水平管束管外凝结换热
上一层管子的凝液流到下一层管 子上,使下一层管面的膜层增厚
下层管上的h比上层管的h低
计算方法:用nd代替d代入水平单管管外凝结换热计算式
(完整版)《传热学》第7章_相变对流传热

5
第7章 相变对流传热
7.2 膜状凝结分析解及计算关联式
7.2.1 努塞尔的蒸气层流膜状凝结分析解(温度、传热系数及动量分布)
1. 对实际问题的简化假设
努塞尔的分析是对纯净的饱和蒸气在均匀壁温的竖直表面上的层流
x
1/
4
整个竖壁上的温差ts-tw为常数,因此,整个
竖壁的平均表面传热系数为:
hV
1 l
l 0
hx dx
34hxl
0.943lgl rts 3ltl2w
1/ 4
液膜层流时竖壁膜状凝结的努塞尔理论解,
如果有倾角φ的话,直接改为gsin φ即可。
8
第7章 相变对流传热
7.2.2 竖直管与水平管的比较及实验验证
第7章 相变对流传热
7.1 凝结传热的模式 7.2 膜状凝结分析解及计算关联式 7.3 膜状凝结的影响因素及其传热
强化 7.4 沸腾传热的模式 7.5 大容器沸腾传热的实验关联式 7.6 沸腾传热的影响因素及强化 7.7 热管简介
1
第7章 相变对流传热
引入:
对流传热
强制对流传热 自然对流传热 无相变
膜状凝结的热阻通常比珠状凝结大一个数量级以上,
膜状凝结的表面传热系数的数量级为“成千上万”,而
珠状凝结的表面传热系数可以高达几十万!
g
tw ts
tw ts
4
第7章 相变对流传热
珠状凝结的关键问题是在常规金属表面上难 以产生与维持!! 7.1.3 膜状凝结是工程设计的依据 常用蒸气在洁净的条件下都能得到膜状凝结。 实现起来较容易且计算简单,因此,采用膜状 凝结的计算式作为设计的依据。 强化传热的主要途径是减薄液膜的厚度!!! 珠状和膜状凝结的异同:
《传热学》第7章-凝结与沸腾换热
补充例题3
v 思路: 膜态沸腾换热套用公式计算即可。
稳定的膜态沸腾时,金属丝的电流的发热量 一部分通过沸腾换热传给了水,其余部分则 使金属丝的内能增加(温度升高),这是一 个能量平衡。
补充例题3
v 解:膜态沸腾换热系数的计算套教材中的公式,略 去。结果为: h=236.70 W/(m2.℃)
每米长金属丝的传热量为:
理论解的修正
h
=
0.943
gγρ
µH (ts
2λ3 − tw
1/ 4
)
实验证实: Re < 20
时,实验结果与理论解相吻合
Re > 20 时,实验结果比理论解高20%
所以在工程计算时将该式的系数加大20%
h
=
1.13
gγρ 2λ3
µl(ts − tw
)
1/
4
定性温度
tm
传热学
第7章 凝结与沸腾换热 Condensation and boiling
简介
蒸气被冷却凝结成液体的换热过程称为凝结换热; 液体被加热沸腾变成蒸气的换热过程称为沸腾换热
——有相变的对流换热
一般情况下,凝结和沸腾换热的表面传热系数要比单相 流体的对流换热高出几倍甚至几十倍。
7-1 凝结换热现象
膜状凝结换热 的主要阻力
=
1 2
(ts
+
tw
)
其他
单根水平圆管外壁面上的层流膜状凝结换热平均表面传热系数
h=
( ) 紊流膜状凝结换热
0.729
gγρ µd ts
2λ3 − tw
1/ 4
( ) 整个垂直壁面的平均表面传热系数
传热学第七章
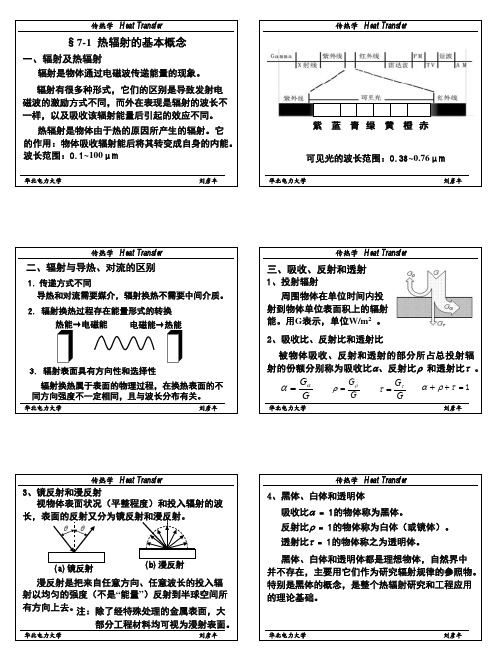
由黑体辐射函数表可查得
Fb(0−λ1 ) = 9.94% 可见光所占的比例为
Fb(0−λ2 ) = 54.59%
Fb(λ1−λ2 ) = Fb(0−λ2 ) − Fb(0−λ2 ) = 44.65%
华北电力大学
刘彦丰
传热学 Heat Transfer
被物体吸收、反射和透射的部分所占总投射辐
射的份额分别称为吸收比α、反射比ρ 和透射比τ 。
α = Gα G
华北电力大学
ρ = Gρ G
τ = Gτ G
α +ρ+τ =1
刘彦丰
传热学 Heat Transfer 3、镜反射和漫反射
视物体表面状况(平整程度)和投入辐射的波 长,表面的反射又分为镜反射和漫反射。
dA cosθ
华北电力大学
n θ
dA
p
可见辐射 面积
刘彦丰
传热学 Heat Transfer
(3) 定向辐射强度
是指单位时间内在空间指定方向的单位立体角内
离开表面单位看见辐射面积的全波段辐射能量。
用符号 L(θ )表示。
L(θ ) = dΦ(θ ) W/(m2 ⋅sr)
dA cos θdΩ
n
dΦ(θ )
如果仅考虑某特定
θ
p
波长的辐射,那么相应
可见辐射
的量被称为定向光谱辐
面积
射强度 L(λ,θ ) 。
dA
华北电力大学
刘彦丰
传热学 Heat Transfer
(4) 定向辐射力
是指单位时间、单位辐射面积向空间指定方向
所在的单位立体角内发射的全波段辐射能量。用
传热学第七章

C : 电磁波传播速度
在真空中,C 3 108 m / s 在大气中,略低于此值
第七章 辐射传热
第一节 基本概念 一、热辐射的本质
3、波长范围(如图7-1所示)
图7-1 电磁波谱
第七章 辐射传热
第一节 基本概念 一、热辐射的本质
3、波长范围(如图7-1所示)
(1)热辐射产生的电磁波称为热射线。从理论上讲,其波长 包括整个电磁波谱,即波长从零到无穷大。 (2)实用中,通常把波长在0.1~100μm范围内的电磁波称为 热射线。它包括部分紫外线、全部可见光和部分红外线: ①部分紫外线(0.1~0.38μm) 热射线(0.1~100μm) ②全部可见光(0.38~0.76μm) ③部分红外线(0.76~100μm)
第七章 辐射传热
第一节 基本概念 五、黑体、白体和透明体
1、理想模型 (1)把吸收比α=1的物体称为绝对黑体,简称黑体。 (2)把反射比ρ=1的物体称为绝对白体,简称白体。
(3)把透射比σ=1的物体称为绝对透明体,简称透明体
※ 黑体、白体、透明体都是理想模型,
是理论研究的基础,自然界中并不存在。
第七章 辐射传热
第七章 辐射传热
第二节 黑体辐射的基本定律 二、普朗克定律
⑤当黑体的T>800K时,其辐射能中才明显地具有波长为 0.38~0.76μm的可见光射线。
※随着温度的升高,可见光射线增加。
※当温度达到5800K时,Ebλ的峰值才位于可见光范围。 ※太阳可近似认为是表面温度为5800K的黑体,根据计算,
图7-3 物体表面的反射 a)镜面反射;b)漫反射
第七章 辐射传热
第一节 基本概念 四、漫射表面
1、当物体表面较光滑,其粗糙不平的尺度小于热射线的波长时, 物体表面对投射辐射呈镜面反射,入射角等于反射角,该表 面称为镜面,如图7-3a)所示。 2、当物体表面粗糙不平的尺度大于热射线的波长时,物体表面 对投射辐射呈漫反射,其吸收比大于镜面,该表面称为漫反 射表面,如图7-3b)所示。 ※一般工程材料的表面均可近似作为漫反射表面。 3、若漫反射表面同时能向周围半球空间均匀发射辐射能,则称 该表面为漫射表面。
传热学-第七章热辐射基本定律及物体的辐射特性

定律 表示式 说明
韦恩位移定律 λmax = b / T 黑体辐射波长与温度的关系
理想黑体的辐射特性
理想黑体具有尽可能高的吸收率和发射率,同时它是完美的热辐射体,能够根据其温度和波长分布发射出连续 的辐射能量。
实际物体的辐射特性
实际物体的辐射特性受到其表面性质的影响。反射率与吸收率、发射率与辐射率以及雷诺茨定律帮助我们了解 和描述实际物体的辐射情况。
反射率与吸收率
实际物体吸收和反射辐射能量 的能力
发射率与辐射率
实际物体辐射能量的发出能力
雷诺茨定律
物体在达到热平衡后,各表面 温度和总发射能力一致
热辐射的应用和实例
热辐射广泛应用于热工技术、太阳能技术、计算机热管理等领域。例如,太阳能电池利用光照下的热辐射转换 为电能。
太阳能电池
利用光照下的热辐射转换为电能
传热学-第七章热辐射基 本定律及物体的辐射特性
了解热辐射的基本概念和定义,掌握热辐射的三大基本定律:斯特藩-玻尔兹 曼定律,基尔霍夫定律和韦恩位移定律。
斯特藩-玻尔兹曼定律
斯特藩-玻尔兹曼定律揭示了黑体辐射功率与温度的关系,P = εσT4,其中P为辐射功率,ε为辐射率,σ为斯特 藩-玻尔兹曼常数。
定律 表示式 说明
斯特藩-玻尔兹曼定律 P = εσT4 黑体辐射功率与温度的关系
基尔霍夫定律
基尔霍夫定律阐明了一个物体表面的吸收率和发射率相等,α = ε。
1 基尔霍夫定律
物体表面的吸收率和发射率相等
韦恩位移定律
韦恩位移定律描述了黑体辐射波长与黑体温度之间的关系,λmax = b / T,其中λmax是峰值辐射波长,b是韦恩 位移常数。
总结和要点
• 热辐射包括斯特藩-玻尔兹曼定律、基尔霍夫定律和韦恩位移定律 • 理
第七章凝结及沸腾换热_传热学
23
3 大空间饱和沸腾曲线:
表征了大容器饱和沸腾的全部过程,共包括4个换热规律不 同的阶段:自然对流、泡态沸腾、过渡沸腾和稳定膜态沸腾, 如图所示:
qmax
qmin
24
4.几点说明: (1)上述热流密度的峰值qmax 有重大意义,称为临界 热流密度,亦称烧毁点。一般用核态沸腾转折点DNB作 为监视接近qmax的警戒。这一点对热流密度可控和温度 可控的两种情况都非常重要。 (2)对稳定膜态沸腾,因为热量必须穿过的是热阻较 大的汽膜,所以换热系数比凝结小得多。
25
三. 大空间泡态沸腾表面传热系数计算
沸腾换热也是对流换热的一种,因此,牛顿冷却公式仍 然适用,即
q h(tw ts ) ht
但对于沸腾换热的h却又许多不同的计算公式 影响泡态沸腾的因素主要是过热度和汽化核心数,而汽 化核心数受表面材料、表面状况、压力等因素的支配,所 以沸腾换热的情况液比较复杂,导致了个计算公式分歧较 大。目前存在两种计算是,一种是针对某一种液体,另一 种是广泛适用于各种液体的。
与膜状凝结换热不同,液体中的不凝结气体会使沸腾换热 得到某种程度的强化 2 过冷度
只影响过冷沸腾,不影响饱和沸腾,因自然对流换热时,
h (tw, 因t f 此)n ,过冷会强化换热。
30
3.液位高度
当传热表面上的液位足够高时, 沸腾换热表面传热系数与液位 高度无关。但当液位降低到一 定值时,表面传热系数会明显 地随液 位的降低而升高(临界 液位)。
2t y 2
5
考虑(3)液膜的惯性力忽略
l (u
u x
v
u y
)
0
考虑(7)忽略蒸汽密度
dp 0 dx
考虑(5) 膜内温度线性分布, 即热量转移只有导热
传热学-第七章
(2)罗森诺公式——广泛适用的强制对流换热公式
既然沸腾换热也属于对流换热,那么,st = f ( Re, Pr )也 应该适用。罗森诺正是在这种思路下,通过大量实验得 出了如下实验关联式:
S 1 tC wlR0 .3 e3 Plsr
式中,St Nu r RePr Cplt
r — 汽化潜热; Cpl — 饱和液体的比定压热容
共包括4个换热规律不同的阶段:自然对流、核态沸腾、过渡沸 腾和稳定膜态沸腾,如图所示:
qmax
qmin
几点说明:
(1)上述热流密度的峰值qmax 有重大意义,称为临界热流 密度,亦称烧毁点。一般用核态沸腾转折点DNB作为 监视接近qmax的警戒。这一点对热流密度可控和温度 可控的两种情况都非常重要。
实验表明,通常情况下,沸腾时汽泡只发生在加热面的某些点
点,而不是整个加热面上,这些产生气泡的点被称为汽化核心
,增加气化核心是强化沸腾换热的主要途径。较普遍的看法认
为,加热壁面上的凹穴和裂缝易残留气体,是最好的汽化核心
(三个原因)。
(2) 汽泡的存在条件
汽泡半径R必须满足下列条件才能存活(克拉贝龙方程)
第七章 相变对流传热
Boiling and Condensation
第六章我们分析了无相变的对流换热,包括强制对 流换热和自然对流换热
下面我们即将遇到的是有相变的对流换热,也称之为 相变换热,目前涉及的是凝结换热和沸腾换热两种。
相变换热的特点:由于有潜热释放和相变过程的复 杂性,比单相对流换热更复杂,因此,目前,工程 上也只能助于经验公式和实验关联式。
1 凝结过程
tw ts
g
膜状凝结
沿整个壁面形成一层薄膜,并且在重力 的作用下流动,凝结放出的汽化潜热必 须通过液膜,因此,液膜厚度直接影响 了热量传递。
传热学第七章
7. 单相流体对流换热及其实验关联式7.1 知识结构1. 实验关联式应用条件:适用范围,定性温度,特征尺度,特征流速,修正系数(入口、弯道、特性)。
2. 常用实验关联式:管内强制对流(紊流、层流及过渡流)(非圆形管道的当量直径计算); 外掠(平板、单管、管束)强制对流; 自然对流(大空间、有限空间)。
7.2 重点内容剖析由于对流换热问题的复杂性,大多数工程问题不能依靠分析解,而是依靠相似理论指导下的实验解。
在应用实验关联式(准则方程)时要注意以下几个方面:(1) 实验范围(已定准则范围)内的相似现象一般不能外推; (2) 注意关联式所规定的定性温度、特征尺度、特征流速; (3) 正确选用各种修正系数(物性,入口,弯管……)7.2.1 强制对流换热及其实验关联式 一、管槽内强制对流换热特征 1.流动状态Re :0 2300 10000层流 过渡流 湍流 2.速度分布温度对流速分布的影响是通过粘性作用的。
液体粘性随温度升高而降低,气体粘性随温度升高而增加。
相同切应力作用下,粘度越大,速度在壁面法线方向的变化率越小。
3.典型边界条件恒热流:边界处热流密度恒定不变,如电加热器。
恒壁温:边界处温度恒定不变,如冷凝器。
湍流时(除液态金属外)两种边界条件对传热系数的影响可忽略不计,但对层流和低Pr 介质,两种边界条件下传热系数的差别不容忽视。
4.原则性准则方程()Pr Re,f Nu = (7-1)5.入口效应:入口段:从入口至流动边界层在管道中心汇合处。
层流入口段长径比(比湍流大):Pr Re 05.0≈d l 湍流入口段长径比:60<d l 充分发展段:流动边界汇合处下游。
入口效应:由于入口段边界层较薄,平均表面传热系数比充分发展段大,入口段有强化传热的作用。
(短管强化传热)6.努塞尔特准则的物性修正系数: (温度场不均匀→物性场不均匀)nw f nwf nwf T T ⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛Pr Pr ,,ηη下标:f ——流体温度下参数w ——壁面温度下参数二、管内湍流换热实验关联式nf ff Nu Pr Re 023.08.0= (7-2)加热液体时:n=0.4 冷却液体时:n=0.3定性温度:流体平均温度(管道进出口平均温度)特性尺度:管道内径(由关联式分析可知:h~d -0.2 →小管强化传热) 适用范围:Ref=104~1.2⨯105,Prf=0.7~120,l/d>60, 对于短管或弯管:乘以相应修正系数对于非圆形管道:用当量直径代替管道直径气体:不超过50 ℃ 传热温差 水:不超过30 ℃ 油:不超过10 ℃温差超出范围时,参考文献[1]P165有推荐公式和使用条件 注:① 非圆形管道(当量直径):UAde d 4== (7-3) A ——流动截面积 U ——湿周长② 入口效应修正系数(l/d<60)7.01⎪⎭⎫⎝⎛+=l d c l (7-4)③ 弯管修正(二次环流强化传热)(弯管强化传热)对于气体Rdc r 77.11+= (7-5) R 为弯道半径(曲率半径)对于液体33.101⎪⎭⎫⎝⎛+=R d c r (7-6)三、管内层流换热实验关联式(层流充分发展段) 对于恒热流边界条件:36.4=Nu 对于恒壁温边界条件:66.3=Nu(对于非圆形管道参见参考文献[1]P168~169表5-3、4) 管内层流换热实验关联式的应用要注意以下几点: (1) 对于同一截面形状的通道,恒热流Nu>恒壁温Nu(2) 等截面直通道内的层流充分发展段Nu 与Re 无关(自模化)(3) 对于层流,当量直径只是一几何参数,不能用它来统一不同截面通道的换热和阻力计算表达式。
传热学-第7章 传热过程的分析和计算2
四、强化传热的考虑
kAtf1 tf 2
• 为强化传热,有三条途径:
★方法1:提高温差 ★方法2:提高传热系数
14
★如何提高传热系数?
k
1 h1
1 h2
1
1 h1
1 h2
1
数学上可以证明
k min( h1, h2 )
提高较小的表面传热系数值,强化薄弱环节,效果最好
15
• h1=1000,h2=10,没有强化前:k=9.90 W/(m2.K)
t m in
Δtmax、Δtmin 均指端差,即同一端热流体与冷流体间的温差。 Δtmax 是其中大温差, Δtmin 则是其中小温差。
26
平均温差的另一种更为简单的形式是算术平均温差,即
tm,算术
tmax
2
tmin
tm,对数
t max tmin ln t max
t m in
t1' t1"
t
' 2
温差 t f 1 沿t f 2整 个壁面不是常数,必须采用整个面积上的平均温差
t m
kAtm
25
(一)简单顺流及逆流换热器的对数平均温差
t1'
t1"
t1'
t
' 2
t
" 2
t
" 2
t1"
t
' 2
顺流
逆流
换热器中流体温度沿程变化的示意图
可以推导出顺流和逆流的平均温差公式为
对数平均温差
tm
t max tmin ln t max
第7章 传热过程与换热器
导热
Φ
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
考虑(5) 膜内温度线性分布,即热量转移只有导热 ⇒ 膜内温度线性分布, 考虑(
∂t ∂t u +v =0 ∂x ∂y
只有u 两个未知量, 只有u 和 t 两个未知量,于 上面得方程组化简为: 是,上面得方程组化简为:
2 ∂ u = 0 ρlg +ηl 2 ∂y ∂ 2t a =0 l 2 ∂y
0
固相冰温度变化时显热焓量变化 ∆Q1 ∆Q2 = 1=C冰Q3 0-t1)kJ/kg,∆QC冰=2.09kJ/kg·℃ ∆Q 335 ∆ (t ∆Q4 = 2257 5 热焓量(kJ 不同状态下水的显热与相变潜热比较
3
2011-6-7
§7-1 凝结传热的模式
1 珠状凝结与膜状凝结
1.1 凝结换热实例 •电站的凝汽器 电站的凝汽器 •制冷空调装置中的冷凝器 制冷空调装置中的冷凝器 •寒冷冬天窗户上的冰花 寒冷冬天窗户上的冰花 1.2 凝结传热的关键点
1 努塞尔的蒸汽层流膜状凝结分析解
1916年 Nusselt提出的简单膜状凝结传热分析是近代 1916年,Nusselt提出的简单膜状凝结传热分析是近代 膜状凝结理论和传热分析的基础。 1916年以来 年以来, 膜状凝结理论和传热分析的基础。自1916年以来,各种修 正或发展都是针对Nusselt分析的限制性假设而进行了, Nusselt分析的限制性假设而进行了 正或发展都是针对Nusselt分析的限制性假设而进行了,并 形成了各种实用的计算方法。所以,我们首先得了解 形成了各种实用的计算方法。所以, Nusselt对纯净饱和蒸汽膜状凝结换热的分析 对纯净饱和蒸汽膜状凝结换热的分析。 Nusselt对纯净饱和蒸汽膜状凝结换热的分析。 8个假定:1)常物性;2)蒸气静止;3)液膜的惯性力忽 个假定: )常物性; )蒸气静止; ) 个假定 略;4)气液界面上无温差,即液膜温度等于饱和温度;5) )气液界面上无温差,即液膜温度等于饱和温度; ) 膜内温度线性分布,即热量转移只有导热; ) 膜内温度线性分布,即热量转移只有导热;6)液膜的过冷 度忽略; )忽略蒸汽密度; ) 度忽略; 7)忽略蒸汽密度;8)液膜表面平整无波动
4
2011-6-7
1.3 凝结换热中的重要参数 • • • • 蒸汽的饱和温度与壁面温度之差( 蒸汽的饱和温度与壁面温度之差(ts - tw) 汽化潜热 r 特征尺度 其他标准的热物理性质,如动力粘度、 其他标准的热物理性质,如动力粘度、导热系 数、比热容等
2011-6-7
5
1.4
凝结过程
tw < ts
xc xc h=h + h 1− l t l l
式中: 为层流段的传热系数; 为湍流段的传热系数; 式中:hl 为层流段的传热系数; ht 为湍流段的传热系数; xc 为层流转变为湍流时转折点的高度 l 为竖壁的总高度 本教材没有介绍
2011-6-7 14
2 水平圆管及球的表面传热系数
努塞尔的理论分析可推广到水平圆管及球表面上的层流 膜状凝结
grρ λ hH = 0.729 ηl d(ts − tw )
2 3 l l
1/ 4
grρ λ hS = 0.826 ηl d(ts − tw )
下脚标 l 表示液相
2011-6-7
对应于p211页(5-15),(5-16),(5-17) 对应于 页 , ,
9
考虑( ) 考虑(3)液膜的惯性力忽略 ⇒ ∂u ∂u ρ l (u + v ) = 0 ∂x ∂y 考虑(7)忽 ⇒ 考虑( 略蒸汽密度
dp =0 dx
∂u ∂v ∂x + ∂y = 0 dp ∂u ∂u ∂ 2u ρl (u ∂x + v ∂y ) = − dx + ρl g + ηl 2 ∂y ∂t ∂t ∂ 2t ρv g u + v = al 2 ∂x ∂y ∂y
2011-6-7 8
tw < ts
g
m(x) ɺ
微元控制体
边界层微分方程组: 边界层微分方程组:
t(y)
x
Thermal boundary layers
u(y)
Velocity boundary layers
∂u ∂v ∂x + ∂y = 0 ∂u ∂u dp ∂ 2u ρ l (u ∂x + v ∂y ) = − dx + ρ l g + v ∂y = al 2 ∂y
4hl(ts − tw ) Re = ηr
4hπd (t s − t w ) ηr
对水平管, 对水平管,用πd代替上式中的l即可。 代替上式中的l即可。
Re =
并且横管一般都处于层流状态
2011-6-7 18
3.2 湍流膜状凝结传热 液膜从层流转变为湍流的临界雷诺数可定为1600。 液膜从层流转变为湍流的临界雷诺数可定为1600。横管因 1600 直径较小,实践上均在层流范围。 直径较小,实践上均在层流范围。 对湍流液膜, 对湍流液膜,除了靠近壁面的层流底层仍依靠导热来传递 热量外,层流底层之外以湍流传递为主, 热量外,层流底层之外以湍流传递为主,换热大为增强 对竖壁的湍流凝结传热,其沿整个壁面的平均表面传热 竖壁的湍流凝结传热,其沿整个壁面的平均表面传热 系数计算式为 计算式为: 系数计算式为:
10
2011-6-7
边界条件: 边界条件:
y = 0 时, u = 0, t = t w du y = δ 时, = 0, t = t s dy δ
求解上面方程可得: 求解上面方程可得: (1) 液膜厚度
4ηl λl (ts − tw )x δ = gρl2r
tm ts + tw = 2
• • • • •
凝结可能以不同的形式发生,膜状凝结和珠状凝结 凝结可能以不同的形式发生, 冷凝物相当于增加了热量进一步传递的热阻 层流和湍流膜状凝结换热的实验关联式 影响膜状凝结换热的因素 会分析竖壁和横管的换热过程, Nusselt膜状凝结理论 会分析竖壁和横管的换热过程,及Nusselt膜状凝结理论
2 3 l l
1/ 4
式中:下标“ ”表示水平管 表示水平管, ”表示球 表示球; 式中:下标“ H ”表示水平管,“ S ”表示球; 特征长 为水平管或球的直径。 度d 为水平管或球的直径。 定性温度与前面的公式相同
tm
ts + tw = 2
15
2011-6-7
在其它条件相同时,横管与竖管的平均对流传热系数之比: 在其它条件相同时,横管与竖管的平均对流传热系数之比:
tw < ts
g
2011-6-7
6
虽然珠状凝结换热远大于膜状凝结,但可惜的是, 虽然珠状凝结换热远大于膜状凝结,但可惜的是,珠状凝 结很难保持,因此, 结很难保持,因此,大多数工程中遇到的凝结换热大多属 于膜状凝结,因此, 于膜状凝结,因此,教材中只简单介绍了膜状凝结 接触 角
2011-6-7
7
§7-2 膜状凝结分析解及计算关联式
湍流
式中: 式中: ul 为 x = l 处液膜层的平均流速; 处液膜层的平均流速; 为该截面处液膜层的当量直径。 de 为该截面处液膜层的当量直径。
2011-6-7
17
如图
由热平衡 所以
de = 4A / P = 4bδ / b = 4δ c 4δρul 4qml Re = = η η h(ts −tw )l = rqml
1/ 4
定性温度: 定性温度: 注意: 注意:r
2011-6-7
按 ts 确定
11
(2) 局部对流传热系数
( ∆t = ts − tw = C)
grρ λ hx = 4 l (ts − tw )x η
2 l 3 l
1/ 4
整个竖壁的平均表面传热系数
grρ λ 1 l h = ∫ hxdx = 0.943 V l 0 ηll(ts − tw ) ts + tw 定性温度: 定性温度: t m = 注意: 注意:r 按 ts 确定 2
液相水汽化成气相蒸汽的潜热阶段 ∆Q4=2257kJ/kg t
3
F E
水蒸气
tk = 100 t2 t0 = 0
t1
D
B
C
液相水温度变化时显热焓量变化 ∆Q3=C水(t2-t0)kJ/kg, C水=4.187kJ/kg·℃ 从0到100℃,共吸收显热量为418kJ/kg
A
固相冰融化成液相水的潜热阶段 ∆Q2=335kJ/kg
h Hg h Vg l = 0 . 77 d
1 4
如果取l/d=50,则横管的平均表面传热系数是竖管的2 如果取l/d=50,则横管的平均表面传热系数是竖管的2倍 l/d=50 课堂讨论:试解释为什么冷凝器(凝汽器)通常都采用横 课堂讨论:试解释为什么冷凝器(凝汽器) 管的布置方式? 管的布置方式?
2011-6-7
16
3
3.1
湍流膜状凝结
边界层内的流态
无波动层流
凝结液体流动也分层流和湍流, 凝结液体流动也分层流和湍流,并且 其判断依据仍然是Re Re, 膜层Re Re数 其判断依据仍然是Re,叫膜层Re数
Re = 20
有波动层流
Re =
ul d e
ν
=
ρul d e η
Re c = 1600
第七章 相变对流传热
Boiling and Condensation
能源工程系 黄金
2011-6-7 1
第五章我们分析了无相变的对流换热, 第五章我们分析了无相变的对流换热,包括强制对 流换热和自然对流换热 下面我们即将遇到的是有相变的对流传热, 下面我们即将遇到的是有相变的对流传热,也称之为 相变传热,目前涉及的是凝结传热和沸腾传热两种。 凝结传热和沸腾传热两种 相变传热,目前涉及的是凝结传热和沸腾传热两种。 相变传热的特点: 相变传热的特点:由于有潜热释放和相变过程的复 特点 杂性,比单相对流传热更复杂,因此,目前, 杂性,比单相对流传热更复杂,因此,目前,工程 上也只能助于经验公式和实验关联式。 上也只能助于经验公式和实验关联式。
