平行线中添加辅助线
平行线中常见作辅助线的技巧的九种类型

( 2 ) 如 图 ① , 在 AB ∥ DE 的 条 件 下 , 你 能 得 出 ∠ B , ∠BCD,∠D之间的数量关系吗?请说明理由. 解:∠B+∠BCD+∠D=360°.理由如下: 因为CF∥AB,所以∠B+∠BCF=180°. 因为AB∥DE,所以CF∥DE. 所以∠FCD+∠D=180°. 所以∠B+∠BCF+∠FCD+∠D=180°+ 180°,即∠B+∠BCD+∠D=360°.
6.如图,AB∥DE,则∠BCD,∠B,∠D有何关系?为什么?
解:∠BCD=∠B-∠D.理由如下: 如图,过点C作CF∥AB,所以∠B=∠BCF. 因为AB∥DE,CF∥AB,所以CF∥DE. 所以∠DCF=∠D.所以∠B-∠D=∠BCF-∠DCF. 因为∠BCD=∠BCF-∠DCF, 所以∠BCD=∠B-∠D.
解:AB∥CD.理由如下: 如图,连接 BD. 在三角形 BDE 中,∠1+∠2+∠E=180°. 因为∠E=∠3+∠4, 所以∠1+∠2+∠3+∠4=180°, 即∠ABD+∠CDB=180°. 所以 AB∥CD.
2.【2020·攀枝花】如图,平行线AB,CD被直线EF所截, 过点B作BG⊥EF于点G,已知∠1=50°,则∠B= ( C) A.20° B.30° C.40° D.50°
BS版平行线中常见作辅助线的技巧的九种
类型
提示:点击 进入习题
1 见习题 2C 3 见习题 4 见习题
5 见习题 6 见习题 7 见习题 8 见习题 9 见习题
答案显示
1.如图,∠E=∠B+∠D,猜想AB与CD有怎样的位 置关系,并说明理由.
【点拨】本题可通过连接 B,D 两点构造截线,进而利用平行线 的判定说明 AB∥CD.
4 . ( 1 ) 如 图 ① , 若 AB ∥ DE , ∠ B = 135° , ∠ D = 145°,求∠BCD的度数.
平行线中添辅助线的方法

平行线中添辅助线的方法在几何学中,平行线是指在同一个平面内,永远不会相交的线。
平行线可以用于解决许多几何问题。
有时,为了更好地理解和解决问题,我们可能需要在已知的平行线中添加辅助线。
这篇文章将介绍一些经常在平行线中添加辅助线的方法,以及如何利用这些辅助线解决几何问题。
方法一:创建平行线之间的等距线段这是最常见的方法之一,可以通过创建平行线之间的等距线段来添加辅助线。
这个方法可以在几何证明中使用,以创建所需的形状或角度。
下面是一个例子:假设有两个平行线AB和CD,在这两条平行线上选择两个等距点E和F。
然后,通过连接EF,你就创建了一个辅助线,使得EF平行于AB和CD。
这样,你就可以利用这个平行四边形来证明或解决其他几何问题。
方法二:使用交叉线段这个方法涉及到在平行线上选择一个点,并通过它绘制一条与其他平行线相交的线段。
这种方法通常用于证明几何性质。
例如,假设有两个平行线AB和CD,我们可以在AB上选择一个点E,并通过它绘制一条线段EF与CD相交。
然后,通过观察EF与AB的关系,可以证明一些三角形的性质或者其他几何关系。
方法三:利用平行线之间的相似三角形利用平行线之间的相似三角形是另一种常用的方法。
通过观察平行线和与它们相交的第三条线,可以找到相似的三角形。
然后,利用这些相似三角形的性质来解决几何问题。
例如,假设有两个平行线AB和CD,以及一条与它们相交的第三条线EF。
通过观察,可以发现三角形ADE与三角形BCF相似。
这意味着可以使用相似三角形的性质来计算未知角度或线段的长度。
方法四:利用中位线和对角线这个方法通常涉及到在平行线形成的平行四边形中绘制中位线或对角线。
中位线是连接平行四边形两对相对顶点的线段,对角线是连接两对非相邻顶点的线段。
这些辅助线可以帮助我们找到形状的性质,或计算线段的长度。
例如,假设有一个平行四边形ABCD,你可以通过绘制对角线AC来创建两个互相重叠的三角形ABC和ADC。
通过观察这些三角形的性质,可以得出许多结论,例如它们的面积相等或角度相等。
添加辅助线解决平行线中角的问题 PPT

提问:
1、我们学过的直线平行的条件有哪些? 2、平行线的性质又有哪些呢? 3、练习:如图,AB//CD//EF,那么 B A AE E EC C ( CD)
(A) 180 (B) 270 (C) 360 (D) 540
A E
C
B F
D
若将上图做一下变化,我们来观察一下:
已知:如图,AB//CD,那么 A、C与AEC 有什么关系?为什么?
A
B
1
2
F
C
3 4
E
D
A
B
E
F
C
D
理由: 过E做EF//AB
EF //AB (所作)
AB//CD(已知) EF//CD(平行于同一直线的两直线平行) C CE 1F 8 (两0 直线平行,同旁内角互补) E/F /AB(已知)
A AE 1F 8(0 两直线平行,同旁内角互补)
即 A C AEC
返回
感谢您的聆听!
添加辅助线解决平行线中角的问题
两直线平行
请注意:
性质
{1.同位角相等 2.内错角相等 判定 3.同旁内角互补
1.由_角__的__关__系__得到_两__直__线__平__行__的结 论是平行线的判定; 用途:说明直线平行
2.由_两__直__线__平__行___得到_角__相__等__或__互__补___的 结论是平行线的性质. 用途:说明角相等或互补
A
B
E
E
C
D
答: A C A E 3 C 60
理由
如果点E的位置发生变化,如图,已知:AB//CD,A、 C与 AEC 又有
什么样的关系呢?
A
B
E
C
初中平面几何常见添加辅助线的方法

初中平面几何常见添加辅助线的方法平面几何是数学中的一个重要分支,通过在平面上描述和研究几何图形之间的关系和性质。
在解决平面几何问题中,添加辅助线是一种常见且有效的方法,可以帮助我们更好地理解和分析问题。
下面是初中平面几何常见的添加辅助线的方法:1.使用垂直辅助线:垂直辅助线是指与已知线段垂直的辅助线,可以用来分割和构造几何图形。
比如,在矩形中,可以通过连接矩形的对角线来构造一条垂直辅助线,从而将矩形分割为两个等腰直角三角形。
2.使用平行辅助线:平行辅助线是指与已知线段平行的辅助线,可以用来帮助构造平行线段和证明平行性质。
例如,在平行四边形中,可以通过连接相邻顶点和平行线段的端点来构造平行辅助线,从而证明平行四边形的对边相等。
3.使用角平分线:角平分线是指将一个角平分为两个等角的辅助线。
在解决涉及角的等分、相等或相似性质问题时,添加角平分线是非常有用的方法。
例如,在等腰三角形中,可以通过连结底边中点和顶角顶点的直线来构造角平分线,从而证明等腰三角形的顶角相等。
4.使用中线:中线是指连接一个几何图形的两边中点的辅助线。
在解决涉及几何图形的中点、平行四边形和三角形性质问题时,添加中线是一种常见的方法。
例如,在四边形中,可以通过连接相对边的中点来构造中线,从而证明中线互相平分。
5.使用高线:高线是指从多边形的一个顶点向对边所引的垂线。
在解决多边形的高、重心、垂心和外心问题时,添加高线是非常有用的方法。
例如,在三角形中,可以通过从一个顶点向对边引垂线来构造高线,从而证明高线汇聚于三角形的垂心。
6.使用辅助图形:有时,我们可以通过在平面上添加一些辅助图形来辅助解决几何问题。
例如,在求解平行四边形的面积时,可以通过添加一个垂直边和一个三角形来将平行四边形划分为两个高度相等的矩形,从而方便计算面积。
在实际应用中,我们可以根据具体问题的要求来灵活地选择合适的辅助线方法。
添加辅助线不仅可以帮助我们更好地理解和分析问题,还可以提高解题效率和准确性。
第3讲 平行线辅助线(学生版)

第3讲平行线辅助线一、知识回顾:在解决平行线的问题时,当无法直接得到角的关系或两条线之间的位置关系时,通常借助辅助线来帮助解答,如何作辅助线需根据已知条件确定,辅助线的添加既可以产生新的条件,又能将题目中原有的条件联系在一起.一、加截线(连接两点或延长线段)1.如图,已知AB∥CD,∠ABF=∠DCE.∠BFE与∠FEC有何关系?并说明理由.(第1题)【解析】:∠BFE=∠FEC.理由一:连接BC,如图①.∵AB∥CD,∴∠ABC=∠BCD(两直线平行,内错角相等).又∵∠ABF=∠DCE,∴∠ABC-∠ABF=∠BCD-∠DCE,即∠FBC=∠ECB.∴BF∥CE(内错角相等,两直线平行).∴∠BFE=∠FEC(两直线平行,内错角相等).(第1题)理由二:延长AB,CE相交于点G,如图②.∵AB∥CD,∴AG∥CD.∴∠DCE=∠G(两直线平行,内错角相等).又∵∠ABF=∠DCE,∴∠ABF=∠G.∴BF∥CG(同位角相等,两直线平行).∴∠BFE=∠FEC(两直线平行,内错角相等).二、过“拐点”作平行线a.“”形图2.如图,AB∥CD,P为AB,CD之间的一点,已知∠1=32°,∠2=25°,求∠BPC的度数.(第2题)【解析】:方法一:过点P作射线PN∥AB,如图①.∵AB∥CD,∴PN∥CD.∴∠4=∠2=25°.∵PN∥AB,∴∠3=∠1=32°.∴∠BPC=∠3+∠4=57°.(第2题)方法二:过点P作射线PM∥AB,如图②.∵AB∥CD,∴PM∥CD.∴∠4=180°-∠2=180°-25°=155°.∵AB∥PM,∴∠3=180°-∠1=180°-32°=148°.∴∠BPC=360°-∠3-∠4=360°-148°-155°=57°. 方法三:连接BC,略。
初二几何辅助线添加方法

初二几何辅助线添加方法几何辅助线是在解决几何问题时,通过添加额外的线段或线条来帮助我们更好地理解和解决问题。
在初二阶段的几何学中,辅助线的使用是非常重要的,可以帮助我们找到问题的关键点,简化问题的分析和解决过程。
下面将介绍几个常见的初二几何辅助线添加方法。
第一种方法是绘制垂直辅助线。
在解决一些关于垂直关系的问题时,我们可以通过添加垂直辅助线来辅助解题。
例如,在求两条平行直线之间的距离时,我们可以通过在两条直线上分别取一点,然后通过添加垂直辅助线来构建一个直角三角形,从而求出距离。
第二种方法是绘制平行辅助线。
在求两条直线平行或相交关系时,我们可以通过添加平行辅助线来辅助解题。
例如,在求两条平行线之间的距离时,我们可以通过添加一条与两条平行线相交的直线,然后构建一个平行四边形,从而求出距离。
第三种方法是绘制角平分线。
在解决涉及到角度的问题时,我们可以通过添加角平分线来辅助解题。
例如,在求一个角的角平分线时,我们可以通过画出这个角的两条边的延长线,然后通过它们的交点来构建角平分线。
第四种方法是绘制对称线。
在求对称形状或对称位置的问题时,我们可以通过添加对称线来辅助解题。
例如,在求一个图形的对称轴时,我们可以通过添加对称线来找到对称轴的位置。
除了上述介绍的四种常见的几何辅助线添加方法外,还有许多其他的方法。
例如,绘制中垂线来求三角形的垂心和外心,绘制角的角平分线来求多边形的内角和,等等。
每个问题都有其特定的解题方法和特定的辅助线添加方法。
总结起来,初二几何辅助线的添加方法是非常多样的。
通过合理地添加辅助线,可以帮助我们更好地理解和解决几何问题。
在解题过程中,我们应该根据问题的特点和要求,选择合适的辅助线添加方法。
同时,多进行几何练习,多掌握不同的辅助线添加方法,可以提高我们的解题能力和思维灵活性。
平行线中添辅助线的方法
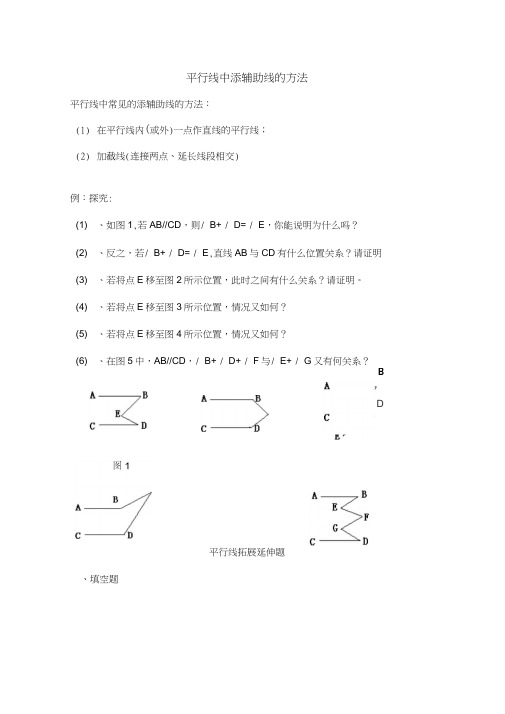
平行线中添辅助线的方法平行线中常见的添辅助线的方法:(1) 在平行线内(或外)一点作直线的平行线;(2) 加截线(连接两点、延长线段相交)例:探究:(1) 、如图1,若AB//CD ,则/ B+ / D= / E ,你能说明为什么吗?(2) 、反之,若/ B+ / D= / E ,直线AB 与CD 有什么位置关系?请证明(3) 、若将点E 移至图2所示位置,此时之间有什么关系?请证明。
(4) 、若将点E 移至图3所示位置,情况又如何?(5) 、若将点E 移至图4所示位置,情况又如何?(6) 、在图5中,AB//CD ,/ B+ / D+ / F 与/ E+ / G 又有何关系?平行线拓展延伸题、填空题BDA 、10° B 、15° C 、20° A L ________ ~B A —-------------------- B \E ZP C z f --------------------— — C D CD图1图2 1 如图,已知 AB // CD ,若/ A=20。
,/ E=35°,则/ C 等于____________2、如图,I 1//I 2,/ 1=120°,/ 2=100°,则/ 3= ________________ 。
4、如图,AB // CD , 1 50°, 2 110°,则 3 ______________ 。
6、如图,已知 AB // EF ,/ BAC=p ,/ ACD=x ,/ CDE=y ,/ DEF=q,用 p 、q 、 y 来表示x 得 ___________________________ 。
、选择题如图1, AB / CD ,且/BAP=60° —a ,Z APC=45° + a ,2、 如图2, AB//CD ,且 A 25 , C 45,贝U E 的度数是(A. 60B. 70C. 110D. 80 3、如图3,已知AB // CD ,则角a 、B 、丫之间的关系为( )BD/ PCD=30°—a ,贝U a (),证明:BC丄CD。
平行线分线段成比例中的常用技巧

平行线分线段成比例中的常用技巧一、直接用例1 如图1,在△ABC 中,AD 平分∠BAC ,按如下步骤作图:第一步,分别以点A ,D 为圆心,以大于12AD 的长为半径在AD 两侧作弧,交于两点M ,N ; 第二步,连接MN ,分别交AB ,AC 于点E ,F ;第三步,连接DE ,DF .若BD=6,AF=4,CD=3,求BE 的长.解析:由作法可知,MN 是线段AD 的垂直平分线.∴AE=DE ,AF=DF.∴∠EAD=∠EDA.∵AD 平分∠BAC ,∴∠BAD=∠CAD.∴∠EDA=∠CAD.∴DE ∥AC.同理DF ∥AE.∴四边形AEDF 是菱形.∴AE=AF=4.∵DE ∥AC ,∴BD CD =BE AE ,即63=4BE ,解得BE=8. 二、连续用例2 如图2,在△ABC 中,点D ,E ,F 分别在AB ,AC ,BC 上,DE ∥BC ,EF ∥AB .若AB =8,BD =3,BF =4,则FC 的长为 .解析:由已知可得AD =AB -BD =5.ECB D AF 图2图1∵DE∥BC,∴BDAD=ECAE.∵EF∥AB,∴FCBF=ECAE.∴BDAD=FCBF,即35=4FC,解得FC=125.三、添加辅助线后再用例3 如图3,在直角梯形ABCD中,DC∥AB,∠DAB=90°,AC⊥BC,AC=BC,∠ABC的平分线分别交AD,AC于点E,F,则BFEF的值是()A.2-1 B.2+2C.1+2D.2解析:过点F作FG⊥AB于点G.∵∠DAB=90°,∴AE∥FG.∴BFEF=BGAG.∵AC⊥BC,∴∠ACB=90°.又∵BE是∠ABC的平分线,∴FG=FC.∴Rt△BGF≌Rt△BCF.∴BG=BC.∵AC=BC,∴∠CBA=45°.∴AB=2BC.∴BFEF=BGAG=2BCBC BC-=121-=1+2.故选C.例4 如图4,BDDC=53,E为AD的中点,求BEEF的值.图3解析:过D作DG∥AC,则BDDC=BGGF=53,GEEF=DEAE=1.设EF=a,则GE=a,GF=2a,BG=103a,∴BEEF=103a aa=133.图4。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
• 例1:如图,已知∠ 1=∠2+ ∠3,试 判断CD是否平行于BE,写出2:已知:如图,AB//CD,
AB//CD,∠A=100° ∠C=110 1
°求∠AEC的度数
E2
C
D
解法一:过点E作EF//AB
∵AB//CD,EF//AB(已知)
∴ CD // EF (平行于同一直线的两直线平行)
又∵ ∠2=110°, ∠1=100° ∴∠AEC =360 °—∠1—∠2=150° (等量代换)
4
试一试
如图,已知AB//CD,为了说明 ∠A= 60°,∠C=40°,求∠AEC的度数是多少? 请写出2种辅助线的作法
F
作法:过点E作 EF∥AB
F 作法:延长AE交CD于点F
5
回顾前面辅助线的作法
则∠ =
。
⑵如图,已知AB∥CD,∠ABE=120°,
∠DCE=35°,则∠BEC= 。
A
P1
B
120°
C
BA
B
E
D
C
D
11
3如图,已知AB∥DE,∠ABC=80°, ∠CDE=140°,求∠BCD? 4如图,CD∥BE,则∠2+∠3-∠1 的度数等于 ()
A
B
C
D
A
2
E
1 3
C
FB
D E
12
如图,直线AB∥CD,∠EFA=30°,
F F
6
1.如图,已知AB∥CD,∠1=30°,∠2=90°, 求∠3
过点E作EF∥AB
F 2.如图,已知AB∥CD,∠BAE=135°, ∠AED =80°,∠EDC的度数是( )
过点E作EF∥AB
F
7
3.如图,AB∥CD,∠B=105°, ∠DCE =40°,则∠CEF的为( )
F 4.如图,AB∥CD,EF⊥AB于点O,FG与CD交于点M, 若∠1=43°,则∠2=___1_3_3_°____
G
8
5.如图,已知AB∥CD,∠B=120°,∠D=110°则 ∠E=__1_3_0_°_____
9
6,如图,一条公路修到湖边时,需拐弯绕湖而过, 如果第一次拐的角∠A是120°,第二次拐的角是 150°,第三次拐的角是∠C,这时的道路恰好和 第一次拐弯前的道路平行,求∠C的度数。
A
B
C
10
⑴如图,已知AB∥CD,∠1=100°,∠2=120°,
∠FGH=90°,∠HMN=30°,∠CNP=50°,
则∠GHM的大小是
。
E
A
F G
B
H
M
C N
P
D
13
如图,AB∥EF,∠C=90°,则 , , 的
关系是( )
A. 18o0
B.9 0 o
A
C. 18o0
C
D.
E
B
D F
14
(方法应用反馈) 如∠E图C,D,AB1试∥探C求D,∠A∠FECA与F=∠A∠14EECA的B关,系∠E。CF=
4
A
B
EF
C
D
15
16
∴∠A+∠1=180o,∠C+∠2 =180o
(两直线平行,同旁内角互补)
又∵∠A=100°,∠C=110°(已知)
∴∠ 1 = 80 ° ∠2=70° (等量代换)
∴∠AEC=∠1+∠2= 80 ° + 70° = 150 °
3
1 2
解法二:过点E作EF//AB ∵AB//CD,EF//AB(已知) ∴EF//CD(平行于同一条直线的两直线平行) ∴∠1=∠A=100°,∠2=∠C=110° (两直线平行,内错角相等) ∵∠1+∠2+∠AEC=360 ° (周角的定义)
