3-5高考真题汇编
近5年有机化学高考真题汇编带答案

近5年有机化学高考真题汇编带答案2019年高考化学有机真题汇编1.(2019年高考化学全国III卷) [化学——选修5:有机化学基础] (15分)氧化白藜芦醇W具有抗病毒等作用。
下面是利用Heck反应合成W的一种方法:回答下列问题:(1)A的化学名称为(2)中的官能团名称是(3)(4)上述实验探究了和对反应产率的影响。
还可以进一步探究等对反应产率的影响(5)X为D的同分异构体,写出满足如下条件的X的结构简式①含有苯环②有三种不同化学环境的氢,个数比为6∶2∶1③1 mol的X与足量金属Na反应可生成2 g H2(6)利用Heck反应,由苯和溴乙烷为原料制备,写出合成路线。
(无机试剂任选)2.(2019年高考化学全国II卷) [化学——选修5:有机化学基础] (15分)环氧树脂因其具有良好的机械性能、绝缘性能以及与各种材料的粘结性能,已广泛应用于涂料和胶黏剂等领域。
下面是制备一种新型环氧树脂G的合成路线:已知以下信息:回答下列问题:(1)A是一种烯烃,化学名称为,C中官能团的名称为、(2)由B生成C的反应类型为(3)由C生成D的反应方程式为(4)E的结构简式为(5)E的二氯代物有多种同分异构体,请写出其中能同时满足以下条件的芳香化合物的结构简式、①能发生银镜反应;②核磁共振氢谱有三组峰,且峰面积比为3∶2∶1(6)假设化合物D、F和NaOH恰好完全反应生成1 mol单一聚合度的G,若生成的NaCl和H2O的总质量为765g,则G的n值理论上应等于3.(2019年高考化学全国I卷15分) [化学——选修5:有机化学基础]化合物G是一种药物合成中间体,其合成路线如下:回答下列问题:(1)A中的官能团名称是(2)碳原子上连有4个不同的原子或基团时,该碳称为手性碳。
写出B的结构简式,用星号(*)标出B中的手性碳(3)写出具有六元环结构、并能发生银镜反应的B的同分异构体的结构简式____________________________________________________________(不考虑立体异构,只需写出3个)(4)反应④所需的试剂和条件是(5)⑤的反应类型是(6)写出F到G的反应方程式(7)设计由甲苯和乙酰乙酸乙酯(CH3COCH2COOC2H5)制备的合成路线(无机试剂任选)4. (2019年高考化学北京卷15分)抗癌药托瑞米芬的前体K的合成路线如下。
2023全国高考真题语文汇编:文言文阅读

2023全国高考真题语文汇编文言文阅读一、文言文阅读(2023·北京·统考高考真题)阅读下面的文言文,完成下面小题。
贵廉汉元帝时,贡禹上书言:“孝文皇帝时,贵廉洁,贱贪污,贾人、赘婿及吏坐赃者,皆禁锢不得为吏。
赏善罚恶,不阿亲戚,罪白者伏其诛,疑者以与民,无赎罪之法。
故令行禁止,海内大化,天下断狱仅四百,与刑措亡异。
“武帝始临天下,尊贤用士,辟地广境数千里。
自见功大威行,遂从.嗜欲。
用度不足,乃行一切之.变,使犯法者赎罪,入谷者补吏。
是以.天下奢侈,官乱民贫,盗贼并起,亡命者众。
郡国恐其诛,则.择便巧史书①、习于计簿、能欺上府者,以为右职;奸宄不胜,则取勇猛能操切..百姓者、以苛暴威服下者,使居大位。
故亡义而有财者显于世,欺谩而善书者尊于朝,悖逆而勇猛者贵于官。
故俗皆曰:何以孝弟为?财多而光荣。
何以礼义为?史书而仕宦。
何以谨慎为?勇猛而临官。
’故黥劓而髡钳者,犹复攘臂为政于世,行虽犬彘,家富势足,目指气使,是为贤耳。
故谓居官而置富者为雄杰,处奸而得利者为壮士。
兄劝其弟,父勉其子,俗之败坏,乃至于是!察其所以然者,皆以犯法得赎罪,求士不得真贤,相守②崇财利而诛不行之所致也。
“今欲兴至治,致太平,宜除赎罪之法。
相守选举不以实及有赃者,辄行其诛,亡但免官,则.争尽力为善,贵孝弟,贱贾人,进真贤,举实廉,而天下治矣。
”呜呼,今日之变,有甚于.此!自神宗③以来,黩.货之风日甚一日。
国维不张,而人心大坏,数十年于.此矣。
《书》曰:“不肩好货,敢恭生生,鞠人谋人之保居,叙钦。
”④必如是而后可以立太平之本。
贡禹又言:“欲令近臣自诸曹侍中以上,家亡得私贩卖,与民争利。
犯者辄免官削爵,不得仕宦。
”此议今亦可行。
自万历以后,天下水利碾硙,场渡市集,无不属之.豪绅,相沿以.为常事矣。
(取材于顾炎武⑤《日知录》)【注】①便巧史书:这里指善于舞文弄墨。
②相守:诸侯国相、郡守。
③神宗:明朝皇帝,年号万历。
三年高考生物真题分类汇编5(分子与细胞)-细胞中无机物、生物大分子(含解析)

2023届二轮备考-2020-2022三年高考生物真题分类汇编5(分子与细胞)- 细胞中无机物、生物大分子(含解析)一、单选题1.(2022·辽宁·统考高考真题)二甲基亚砜(DMSO)易与水分子结合,常用作细胞冻存的渗透性保护剂。
干细胞冻存复苏后指标检测结果见下表。
下列叙述错误的是()注:细胞分裂间期分为G1期、S期(DNA复制期)和G2期A.冻存复苏后的干细胞可以用于治疗人类某些疾病B.G1期细胞数百分比上升,导致更多干细胞直接进入分裂期C.血清中的天然成分影响G1期,增加干细胞复苏后的活细胞数百分比D.DMSO的作用是使干细胞中自由水转化为结合水2.(2022·海南·统考高考真题)种子萌发过程中,储藏的淀粉、蛋白质等物质在酶的催化下生成简单有机物,为新器官的生长和呼吸作用提供原料。
下列有关叙述错误..的是()A.种子的萌发受水分、温度和氧气等因素的影响B.种子萌发过程中呼吸作用增强,储藏的有机物的量减少C.干燥条件下种子不萌发,主要是因为种子中的酶因缺水而变性失活D.种子子叶切片用苏丹Ⅲ染色后,显微镜下观察到橘黄色颗粒,说明该种子含有脂肪3.(2022·湖北·统考高考真题)水是生命的源泉,节约用水是每个人应尽的责任,下列有关水在生命活动中作用的叙述,错误的是()A.水是酶促反应的环境B.参与血液中缓冲体系的形成C.可作为维生素D等物质的溶剂D.可作为反应物参与生物氧化过程4.(2022·全国·高考真题)钙在骨骼生长和肌肉收缩等过程中发挥重要作用。
晒太阳有助于青少年骨骼生长,预防老年人骨质疏松。
下列叙述错误的是()A.细胞中有以无机离子形式存在的钙B.人体内Ca2+可自由通过细胞膜的磷脂双分子层C.适当补充维生素D可以促进肠道对钙的吸收D.人体血液中钙离子浓度过低易出现抽搐现象5.(2021·湖北·统考高考真题)采摘后的梨常温下易软化。
2023全国高考真题英语汇编:完形填空2

2023全国高考真题英语汇编完形填空2(2023·全国·高考真题)Recently I was very busy and I needed a timeout. So I decided to drive to the supermarket and pick up dinner instead of doing my usual 1 .In the supermarket, I took fat and juicy chicken and some warm cornbread. As the cashier began processing my items, I 2 my bag for my credit card. However, I realized my wallet was not there. In 3 , I told the cashier I had left my money at home and apologized sincerely, offering to 4 my items to where I 5 them. Just at that moment the supermarket owner appeared, saying “Please, take everything home and 6 the dinner. It’s on the house tonight!” I tried to 7 the lovely offer but he 8 a dark chocolate bar near the counter and said, “Here! Take this, too!” His act of 9 lifted everybody present. I thanked him 10 for making my day.When I approached home, as I 11 into my driveway, I saw my next-door neighbor had just mowed my lawn (草坪). He was putting on the finishing touches, clearing the cut grass. Feeling 12 , I jumped out of my car and asked him how much he wanted for his 13 , to which he replied,“Nothing at all. The lawn needed doing.” He 14 me off summarily as he returned to his home. A second scoop of good 15 had landed in my lap, which again reminded me kindness is everywhere in the world.1.A.walking B.cooking C.shopping D.teaching2.A.reached into B.stared at C.put aside D.watched over3.A.anger B.amazement C.satisfaction D.embarrassment4.A.clear B.show C.pack D.return5.A.bought B.put C.took D.ate6.A.enjoy B.prepare C.donate D.deliver7.A.appreciate B.withdraw C.decline D.ensure8.A.looked at B.picked up C.showed off D.put away9.A.courage B.generosity C.faith D.bravery10.A.hurriedly B.curiously C.hesitantly D.sincerely11.A.searched B.dug C.crashed D.pulled12.A.regretful B.excited C.nervous D.energetic13.A.efforts B.talent C.guidance D.goods14.A.sent B.drove C.waved D.turned15.A.appetite B.deal C.fortune D.reputation(2023·全国·高考真题)The sun was beginning to sink as I set off into the Harenna Forest. I was on my way to 16 a unique honey harvest. Here, in south-east Ethiopia, hand-carved beehives(蜂箱)are placed in the17 . Reaching them to get the honey is difficult—and often 18 .I 19 beekeeper Ziyad over a wide stretch of grassland before entering a thick jungle. Ziyad began preparations. He 20 handfuls of damp tree leaves, wrapped them with string, and 21 the bunch to create a torch(火把). Then, with one end of a rope tied to his waist and the other end around the trunk of a tree, Ziyadlooked puzzled, and then 126 :“Oh this isn’t for the 127 I had. I take that as a 128 . No, this is for setting my hair yesterday.”And there you have it. To many people, 129 lives is part of the job but styling hair is an 130 and should be rewarded.111.A.cleaner B.chemist C.nurse D.doctor112.A.grades B.meanings C.needs D.expectations113.A.brushed aside B.put to the test C.brought under discussion D.taken into account 114.A.departing B.escaping C.retiring D.recovering115.A.attempting B.choosing C.pausing D.promising116.A.eventually B.fortunately C.casually D.secretly117.A.assessing B.requiring C.forming D.proving118.A.slightly B.accidentally C.slowly D.happily119.A.grateful B.thoughtful C.sorrowful D.fearful120.A.surprise B.delight C.curiosity D.disappointment 121.A.operating B.thinking C.hesitating D.leaving122.A.sorry B.hello C.goodbye D.yes123.A.reached B.consulted C.introduced D.persuaded124.A.wished B.pretended C.failed D.refused125.A.enjoying B.doing C.securing D.starting126.A.repeated B.recited C.replied D.reported127.A.courage B.patience C.duty D.care128.A.goal B.given C.push D.greeting129.A.risking B.changing C.saving D.building130.A.honour B.ability C.opening D.extra参考答案1.B 2.A 3.D 4.D 5.C 6.A 7.C 8.B 9.B 10.D 11.D 12.B 13.A 14.C 15.C【导语】本文是一篇记叙文。
高中物理近5年高考全国卷真题分类汇编01 直线运动
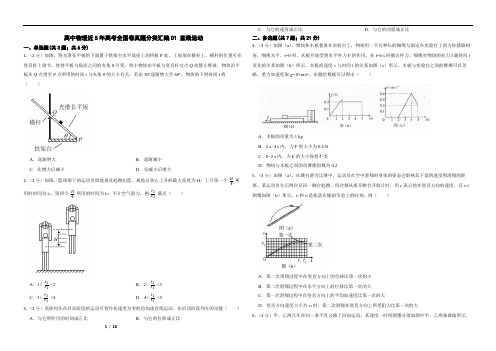
高中物理近5年高考全国卷真题分类汇编01 直线运动一、单选题(共3题;共6分)1.(2分)如图,将光滑长平板的下端置于铁架台水平底座上的挡板P处,上部架在横杆上。
横杆的位置可在竖直杆上调节,使得平板与底座之间的夹角θ可变。
将小物块由平板与竖直杆交点Q处静止释放,物块沿平板从Q点滑至P点所用的时间t与夹角θ的大小有关。
若由30°逐渐增大至60°,物块的下滑时间t将()A.逐渐增大B.逐渐减小C.先增大后减小D.先减小后增大2.(2分)如图,篮球架下的运动员原地垂直起跳扣篮,离地后重心上升的最大高度为H。
上升第一个H4所用的时间为t1,第四个H4所用的时间为t2。
不计空气阻力,则t2t1满足()A.1< t2t1<2B.2<t2t1<3C.3< t2t1<4D.4<t2t1<53.(2分)高铁列车在启动阶段的运动可看作初速度为零的均加速直线运动,在启动阶段列车的动能()A.与它所经历的时间成正比B.与它的位移成正比C.与它的速度成正比D.与它的动量成正比二、多选题(共7题;共21分)4.(3分)如图(a),物块和木板叠放在实验台上,物块用一不可伸长的细绳与固定在实验台上的力传感器相连,细绳水平。
t=0时,木板开始受到水平外力F的作用,在t=4 s时撤去外力。
细绳对物块的拉力f随时间t 变化的关系如图(b)所示,木板的速度v与时间t的关系如图(c)所示。
木板与实验台之间的摩擦可以忽略。
重力加速度取g=10 m/s2。
由题给数据可以得出()A.木板的质量为1 kgB.2 s~4 s内,力F的大小为0.4 NC.0~2 s内,力F的大小保持不变D.物块与木板之间的动摩擦因数为0.25.(3分)如图(a),在跳台滑雪比赛中,运动员在空中滑翔时身体的姿态会影响其下落的速度和滑翔的距离。
某运动员先后两次从同一跳台起跳,每次都从离开跳台开始计时,用v表示他在竖直方向的速度,其v-t 图像如图(b)所示,t1和t2是他落在倾斜雪道上的时刻。
2024全国高考真题数学汇编:集合

2024全国高考真题数学汇编集合一、单选题1.(2024全国高考真题)已知集合{}355,{3,1,0,2,3}A x x B =-<<=--∣,则A B = ()A .{1,0}-B .{2,3}C .{3,1,0}--D .{1,0,2}-2.(2024天津高考真题)集合{}1,2,3,4A =,{}2,3,4,5B =,则A B = ()A .{}1,2,3,4B .{}2,3,4C .{}2,4D .{}13.(2024全国高考真题)若集合{}1,2,3,4,5,9A =,{}1B x x A =+∈,则A B = ()A .{}1,3,4B .{}2,3,4C .{}1,2,3,4D .{}0,1,2,3,4,94.(2024北京高考真题)已知集合{|31}M x x =-<<,{|14}N x x =-≤<,则M N ⋃=()A .{}11x x -≤<B .{}3x x >-C .{}|34x x -<<D .{}4x x <5.(2024全国高考真题)已知集合{}{}1,2,3,4,5,9,A B A ==,则()A A B ⋂=ð()A .{}1,4,9B .{}3,4,9C .{}1,2,3D .{}2,3,5参考答案1.A【分析】化简集合A ,由交集的概念即可得解.【详解】因为{{}|,3,1,0,2,3A x x B =<=--,且注意到12<<,从而A B = {}1,0-.故选:A.2.B【分析】根据集合交集的概念直接求解即可.【详解】因为集合{}1,2,3,4A =,{}2,3,4,5B =,所以{}2,3,4A B = ,故选:B3.C【分析】根据集合B 的定义先算出具体含有的元素,然后根据交集的定义计算.【详解】依题意得,对于集合B 中的元素x ,满足11,2,3,4,5,9x +=,则x 可能的取值为0,1,2,3,4,8,即{0,1,2,3,4,8}B =,于是{1,2,3,4}A B ⋂=.故选:C4.C【分析】直接根据并集含义即可得到答案.【详解】由题意得{}|34M x x N ⋃=-<<.故选:C.5.D【分析】由集合B 的定义求出B ,结合交集与补集运算即可求解.【详解】因为{}{}1,2,3,4,5,9,A B A ==,所以{}1,4,9,16,25,81B =,则{}1,4,9A B = ,(){}2,3,5A A B = ð故选:D。
【高考生物】2023高考生物真题汇编——变异、育种与进化

2023高考生物真题汇编——变异、育种与进化一、单选题1.(2023·山东·高考真题)溶酶体膜上的H+载体蛋白和Cl-/H+转运蛋白都能运输H+,溶酶体内H+浓度由H+载体蛋白维持,Cl-/H+转运蛋白在H+浓度梯度驱动下,运出H+的同时把Cl-逆浓度梯度运入溶酶体。
Cl-/H+转运蛋白缺失突变体的细胞中,因Cl-转运受阻导致溶酶体内的吞噬物积累,严重时可导致溶酶体破裂。
下列说法错误的是()A.H+进入溶酶体的方式属于主动运输B.H+载体蛋白失活可引起溶酶体内的吞噬物积累C.该突变体的细胞中损伤和衰老的细胞器无法得到及时清除D.溶酶体破裂后,释放到细胞质基质中的水解酶活性增强1.D【分析】1. 被动运输:简单来说就是小分子物质从高浓度运输到低浓度,是最简单的跨膜运输方式,不需能量。
被动运输又分为两种方式:自由扩散:不需要载体蛋白协助,如:氧气,二氧化碳,脂肪,协助扩散:需要载体蛋白协助,如:氨基酸,核苷酸,特例...2.主动运输:小分子物质从低浓度运输到高浓度,如:矿物质离子,葡萄糖进出除红细胞外的其他细胞需要能量和载体蛋白。
3.胞吞胞吐:大分子物质的跨膜运输,需能量。
【详解】A、Cl-/H+转运蛋白在H+浓度梯度驱动下,运出H+的同时把Cl-逆浓度梯度运入溶酶体,说明H+浓度为溶酶体内较高,因此H+进入溶酶体为逆浓度运输,方式属于主动运输,A正确;B、溶酶体内H+浓度由H+载体蛋白维持,若载体蛋白失活,溶酶体内pH改变导致溶酶体酶活性降低,进而导致溶酶体内的吞噬物积累,B正确;C、Cl-/H+转运蛋白缺失突变体的细胞中,因Cl-转运受阻导致溶酶体内的吞噬物积累,该突变体的细胞中损伤和衰老的细胞器无法得到及时清除,C正确;D、细胞质基质中的pH与溶酶体内不同,溶酶体破裂后,释放到细胞质基质中的水解酶可能失活,D错误。
故选D。
2.(2023·湖北·统考高考真题)现有甲、乙两种牵牛花,花冠的颜色由基因A、a控制。
2024年高考真题汇编(数学)(新课标卷+全国卷)PDF版含答案

2024年高考真题汇编数学(新课标卷+全国卷)目录2024年普通高等学校招生全国统一考试(新课标I卷)数学2024年普通高等学校招生全国统一考试(新课标II卷)数学2024年普通高等学校招生全国统一考试(全国甲卷)理科数学2024年普通高等学校招生全国统一考试(全国甲卷)文科数学(部分)参考答案2024年普通高等学校招生全国统一考试(新课标I 卷)数学一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一个选项是正确的.请把正确的选项填涂在答题卡相应的位置上.1.已知集合{}355,{3,1,0,2,3}A xx B =-<<=--∣,则A B = ()A.{1,0}-B.{2,3}C.{3,1,0}--D.{1,0,2}-2.若1i 1zz =+-,则z =()A.1i -- B.1i -+ C.1i- D.1i+3.已知向量(0,1),(2,)a b x == ,若(4)b b a ⊥-,则x =()A.2- B.1- C.1D.24.已知cos(),tan tan 2m αβαβ+==,则cos()αβ-=()A.3m- B.3m -C.3m D.3m5.,则圆锥的体积为()A. B. C. D.6.已知函数为22,0()e ln(1),0x x ax a x f x x x ⎧---<=⎨++≥⎩,在R 上单调递增,则a 取值的范围是()A.(,0]-∞B.[1,0]-C.[1,1]- D.[0,)+∞7.当[0,2]x πÎ时,曲线sin y x =与2sin 36y x π⎛⎫=- ⎪⎝⎭的交点个数为()A.3B.4C.6D.88.已知函数为()f x 的定义域为R ,()(1)(2)f x f x f x >-+-,且当3x <时()f x x =,则下列结论中一定正确的是()A.(10)100f > B.(20)1000f >C.(10)1000f <D.(20)10000f <二、多项选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对得6分,部分选对的得部分分,选对但不全的得部分分,有选错的得0分.9.为了解推动出口后的亩收入(单位:万元)情况,从该种植区抽取样本,得到推动出口后亩收入的样本均值 2.1x =,样本方差20.01s =,已知该种植区以往的亩收入X 服从正态分布()21.8,0.1N ,假设推动出口后的亩收入Y 服从正态分布()2,N x s ,则()(若随机变量Z 服从正态分布()2,N u σ,()0.8413P Z u σ<+≈)A.(2)0.2P X >>B.(2)0.5P X ><C.(2)0.5P Y >> D.(2)0.8P Y ><10.设函数2()(1)(4)f x x x =--,则()A.3x =是()f x 的极小值点B.当01x <<时,()2()f x f x<C.当12x <<时,4(21)0f x -<-< D.当10x -<<时,(2)()f x f x ->11.造型可以做成美丽的丝带,将其看作图中曲线C 的一部分.已知C 过坐标原点O .且C 上的点满足横坐标大于2-,到点(2,0)F 的距离与到定直线(0)x a a =<的距离之积为4,则()A.2a =- B.点在C 上C.C 在第一象限的点的纵坐标的最大值为1D.当点()00,x y 在C 上时,0042y x ≤+三、填空题:本题共3小题,每小题5分,共15分.12.设双曲线2222:1(0,0)x y C a b a b-=>>的左右焦点分别为12F F 、,过2F 作平行于y 轴的直线交C 于A ,B 两点,若1||13,||10F A AB ==,则C 的离心率为___________.13.若曲线e x y x =+在点()0,1处的切线也是曲线ln(1)y x a =++的切线,则=a __________.14.甲、乙两人各有四张卡片,每张卡片上标有一个数字,甲的卡片上分别标有数字1,3,5,7,乙的卡片上分别标有数字2,4,6,8,两人进行四轮比赛,在每轮比赛中,两人各自从自己持有的卡片中随机选一张,并比较所选卡片上数字的大小,数字大的人得1分,数字小的人得0分,然后各自弃置此轮所选的卡片(弃置的卡片在此后的轮次中不能使用).则四轮比赛后,甲的总得分不小于2的概率为_________.四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.15.记ABC 内角A 、B 、C 的对边分别为a ,b ,c ,已知sin C B =,222a b c +-=(1)求B ;(2)若ABC 的面积为3c .16.已知(0,3)A 和33,2P ⎛⎫ ⎪⎝⎭为椭圆2222:1(0)x yC a b a b+=>>上两点.(1)求C 的离心率;(2)若过P 的直线l 交C 于另一点B ,且ABP 的面积为9,求l 的方程.17.如图,四棱锥P ABCD -中,PA ⊥底面ABCD ,2PA AC ==,1,BC AB ==.(1)若AD PB ⊥,证明://AD 平面PBC ;(2)若AD DC ⊥,且二面角A CP D --的正弦值为427,求AD .18.已知函数3()ln(1)2xf x ax b x x=++--(1)若0b =,且()0f x '≥,求a 的最小值;(2)证明:曲线()y f x =是中心对称图形;(3)若()2f x >-当且仅当12x <<,求b 的取值范围.19.设m 为正整数,数列1242,,...,m a a a +是公差不为0的等差数列,若从中删去两项i a 和()j a i j <后剩余的4m 项可被平均分为m 组,且每组的4个数都能构成等差数列,则称数列1242,,...,m a a a +是(),i j -可分数列.(1)写出所有的(),i j ,16i j ≤<≤,使数列126,,...,a a a 是(),i j -可分数列;(2)当3m ≥时,证明:数列1242,,...,m a a a +是()2,13-可分数列;(3)从1,2,...,42m +中一次任取两个数i 和()j i j <,记数列1242,,...,m a a a +是(),i j -可分数列的概率为m P ,证明:18m P >.2024年普通高等学校招生全国统一考试(新课标II 卷)数学一、单项选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一个选项是正确的.请把正确的选项填涂在答题卡相应的位置上.1.已知1i z =--,则z =()A.0B.1C.D.22.已知命题p :x ∀∈R ,|1|1x +>;命题q :0x ∃>,3x x =,则()A.p 和q 都是真命题B.p ⌝和q 都是真命题C.p 和q ⌝都是真命题D.p ⌝和q ⌝都是真命题3.已知向量,a b满足1,22a a b =+= ,且()2b a b -⊥ ,则b = ()A.12B.22C.32D.14.某农业研究部门在面积相等的100块稻田上种植一种新型水稻,得到各块稻田的亩产量(单位:kg )并部分整理下表亩产量[900,950)[950,1000)[1000,1050)[1100,1150)[1150,1200)频数612182410据表中数据,结论中正确的是()A.100块稻田亩产量的中位数小于1050kgB.100块稻田中亩产量低于1100kg 的稻田所占比例超过80%C.100块稻田亩产量的极差介于200kg 至300kg 之间D.100块稻田亩产量的平均值介于900kg 至1000kg 之间5.已知曲线C :2216x y +=(0y >),从C 上任意一点P 向x 轴作垂线段PP ',P '为垂足,则线段PP '的中点M 的轨迹方程为()A.221164x y +=(0y >)B.221168x y +=(0y >)C.221164y x +=(0y >)D.221168y x +=(0y >)6.设函数2()(1)1f x a x =+-,()cos 2g x x ax =+,当(1,1)x ∈-时,曲线()y f x =与()y g x =恰有一个交点,则=a ()A.1- B.12C.1D.27.已知正三棱台111ABC A B C -的体积为523,6AB =,112A B =,则1A A 与平面ABC 所成角的正切值为()A.12B.1C.2D.38.设函数()()ln()f x x a x b =++,若()0f x ≥,则22a b +的最小值为()A.18B.14C.12D.1二、多项选择题:本大题共3小题,每小题6分,共18分.在每小题给出的四个选项中,有多项符合题目要求.全部选对得6分,选对但不全的得部分分,有选错的得0分.9.对于函数()sin 2f x x =和π()sin(2)4g x x =-,下列正确的有()A.()f x 与()g x 有相同零点B.()f x 与()g x 有相同最大值C.()f x 与()g x 有相同的最小正周期D.()f x 与()g x 的图像有相同的对称轴10.抛物线C :24y x =的准线为l ,P 为C 上的动点,过P 作22:(4)1A x y +-=⊙的一条切线,Q 为切点,过P 作l 的垂线,垂足为B ,则()A.l 与A 相切B.当P ,A ,B 三点共线时,||PQ =C.当||2PB =时,PA AB ⊥D.满足||||PA PB =的点P 有且仅有2个11.设函数32()231f x x ax =-+,则()A.当1a >时,()f x 有三个零点B.当0a <时,0x =是()f x 的极大值点C.存在a ,b ,使得x b =为曲线()y f x =的对称轴D.存在a ,使得点()()1,1f 为曲线()y f x =的对称中心三、填空题:本大题共3小题,每小题5分,共15分.12.记n S 为等差数列{}n a 的前n 项和,若347a a +=,2535a a +=,则10S =________.13.已知α为第一象限角,β为第三象限角,tan tan 4αβ+=,tan tan 1αβ=+,则sin()αβ+=_______.14.在如图的4×4方格表中选4个方格,要求每行和每列均恰有一个方格被选中,则共有________种选法,在所有符合上述要求的选法中,选中方格中的4个数之和的最大值是________.四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.15.记ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,已知sin 2A A =.(1)求A .(2)若2a =,sin sin 2C c B =,求ABC 的周长.16.已知函数3()e x f x ax a =--.(1)当1a =时,求曲线()y f x =在点()1,(1)f 处的切线方程;(2)若()f x 有极小值,且极小值小于0,求a 的取值范围.17.如图,平面四边形ABCD 中,8AB =,3CD =,AD =,90ADC ︒∠=,30BAD ︒∠=,点E ,F 满足25AE AD = ,12AF AB =,将AEF △沿EF 对折至PEF !,使得PC =.(1)证明:EF PD ⊥;(2)求面PCD 与面PBF 所成的二面角的正弦值.18.某投篮比赛分为两个阶段,每个参赛队由两名队员组成,比赛具体规则如下:第一阶段由参赛队中一名队员投篮3次,若3次都未投中,则该队被淘汰,比赛成员为0分;若至少投中一次,则该队进入第二阶段,由该队的另一名队员投篮3次,每次投中得5分,未投中得0分.该队的比赛成绩为第二阶段的得分总和.某参赛队由甲、乙两名队员组成,设甲每次投中的概率为p ,乙每次投中的概率为q ,各次投中与否相互独立.(1)若0.4p =,0.5q =,甲参加第一阶段比赛,求甲、乙所在队的比赛成绩不少于5分的概率.(2)假设0p q <<,(i )为使得甲、乙所在队的比赛成绩为15分的概率最大,应该由谁参加第一阶段比赛?(ii )为使得甲、乙,所在队的比赛成绩的数学期望最大,应该由谁参加第一阶段比赛?19.已知双曲线()22:0C x y m m -=>,点()15,4P 在C 上,k 为常数,01k <<.按照如下方式依次构造点()2,3,...n P n =,过1n P -作斜率为k 的直线与C 的左支交于点1n Q -,令n P 为1n Q -关于y 轴的对称点,记n P 的坐标为(),n n x y .(1)若12k =,求22,x y ;(2)证明:数列{}n n x y -是公比为11kk+-的等比数列;(3)设n S 为12n n n P P P ++ 的面积,证明:对任意的正整数n ,1n n S S +=.2024年普通高等学校招生全国统一考试(全国甲卷)理科数学一、选择题:本题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.设5i z =+,则()i z z +=()A.10iB.2iC.10D.2-2.集合{}{}1,2,3,4,5,9,A B A ==,则()A A B ⋂=ð()A.{}1,4,9 B.{}3,4,9C.{}1,2,3 D.{}2,3,53.若实数,x y 满足约束条件43302202690x y x y x y --≥⎧⎪--≤⎨⎪+-≤⎩,则5z x y =-的最小值为()A.5B.12C.2- D.72-4.等差数列{}n a 的前n 项和为n S ,若510S S =,51a =,则1a =()A.2- B.73C.1D.25.已知双曲线的两个焦点分别为(0,4),(0,4)-,点(6,4)-在该双曲线上,则该双曲线的离心率为()A.4B.3C.2D.6.设函数()2e 2sin 1x xf x x+=+,则曲线()y f x =在()0,1处的切线与两坐标轴围成的三角形的面积为()A.16B.13C.12D.237.函数()()2e esin xxf x x x -=-+-在区间[ 2.8,2.8]-的大致图像为()A.B.C. D.8.已知cos cos sin ααα=-πtan 4α⎛⎫+= ⎪⎝⎭()A.1+ B.1- C.32D.19.已知向量()()1,,,2a x x b x =+=,则()A.“3x =-”是“a b ⊥”的必要条件B.“3x =-”是“//a b”的必要条件C.“0x =”是“a b ⊥”的充分条件 D.“1x =-+”是“//a b”的充分条件10.设αβ、是两个平面,m n 、是两条直线,且m αβ= .下列四个命题:①若//m n ,则//n α或//n β②若m n ⊥,则,n n αβ⊥⊥③若//n α,且//n β,则//m n ④若n 与α和β所成的角相等,则m n⊥其中所有真命题的编号是()A.①③ B.②④C.①②③D.①③④11.在ABC 中内角,,A B C 所对边分别为,,a b c ,若π3B =,294b ac =,则sin sin A C +=()A.32B.C.72D.212.已知b 是,a c 的等差中项,直线0ax by c ++=与圆22410x y y ++-=交于,A B 两点,则AB 的最小值为()A.2B.3C.4D.二、填空题:本题共4小题,每小题5分,共20分.13.1013x ⎛⎫+ ⎪⎝⎭的展开式中,各项系数的最大值是______.14.已知甲、乙两个圆台上、下底面的半径均为1r 和2r ,母线长分别为()212r r -和()213r r -,则两个圆台的体积之比=V V 甲乙______.15.已知1a >,8115log log 42a a -=-,则=a ______.16.有6个相同的球,分别标有数字1、2、3、4、5、6,从中不放回地随机抽取3次,每次取1个球.记m 为前两次取出的球上数字的平均值,n 为取出的三个球上数字的平均值,则m 与n 差的绝对值不超过12的概率是______.三、解答题:共70分.解答应写出文字说明,证明过程或演算步骤.第17题~第21题为必考题,每个考题考生必须作答.第22、23题为选考题,考生根据要求作答.(一)必考题:共60分.17.某工厂进行生产线智能化升级改造,升级改造后,从该工厂甲、乙两个车间的产品中随机抽取150件进行检验,数据如下:优级品合格品不合格品总计甲车间262450乙车间70282100总计96522150(1)填写如下列联表:优级品非优级品甲车间乙车间能否有95%的把握认为甲、乙两车间产品的优级品率存在差异?能否有99%的把握认为甲,乙两车间产品的优级品率存在差异?(2)已知升级改造前该工厂产品的优级品率0.5p=,设p为升级改造后抽取的n件产品的优级品率.如果p p>+则认为该工厂产品的优级品率提高了,根据抽取的150件产品的数据,能否认为生产线智能化升级改造后,该工厂产品的优级品率提高了?12.247≈)附:22()()()()()n ad bcKa b c d a c b d-=++++()2P K k≥0.0500.0100.001 k 3.841 6.63510.82818.记n S为数列{}n a的前n项和,且434n nS a=+.(1)求{}n a的通项公式;(2)设1(1)nn nb na-=-,求数列{}n b的前n项和为n T.19.如图,在以A,B,C,D,E,F为顶点的五面体中,四边形ABCD与四边形ADEF均为等腰梯形,//,//BC AD EF AD,4,2AD AB BC EF====,ED FB==M为AD的中点.(1)证明://BM 平面CDE ;(2)求二面角F BM E --的正弦值.20.设椭圆2222:1(0)x y C a b a b+=>>的右焦点为F ,点31,2M ⎛⎫ ⎪⎝⎭在C 上,且MF x ⊥轴.(1)求C 的方程;(2)过点()4,0P 的直线与C 交于,A B 两点,N 为线段FP 的中点,直线NB 交直线MF 于点Q ,证明:AQ y ⊥轴.21.已知函数()()()1ln 1f x ax x x =-+-.(1)当2a =-时,求()f x 的极值;(2)当0x ≥时,()0f x ≥恒成立,求a 的取值范围.(二)选考题:共10分,请考生在第22、23题中任选一题作答,并用2B 铅笔将所选题号涂黑,多涂、错涂、漏涂均不给分,如果多做,则按所做的第一题计分.[选修4-4:坐标系与参数方程]22.在平面直角坐标系xOy 中,以坐标原点O 为极点,x 轴的正半轴为极轴建立极坐标系,曲线C 的极坐标方程为cos 1ρρθ=+.(1)写出C 的直角坐标方程;(2)设直线l :x ty t a =⎧⎨=+⎩(t 为参数),若C 与l 相交于A B 、两点,若2AB =,求a 的值.[选修4-5:不等式选讲]23.实数,a b 满足3a b +≥.(1)证明:2222a b a b +>+;(2)证明:22226a b b a -+-≥.2024年普通高等学校招生全国统一考试(全国甲卷)文科数学(部分)一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.集合{}1,2,3,4,5,9A =,{}1B x x A =+∈,则A B = ()A.{}1,2,3,4 B.{}1,2,3C.{}3,4 D.{}1,2,92.设z =,则z z ⋅=()A.-iB.1C.-1D.23.若实数,x y 满足约束条件43302202690x y x y x y --≥⎧⎪--≤⎨⎪+-≤⎩,则5z x y =-的最小值为()A.5B.12C.2- D.72-4.等差数列{}n a 的前n 项和为n S ,若91S =,37a a +=()A.2- B.73C.1D.295.甲、乙、丙、丁四人排成一列,丙不在排头,且甲或乙在排尾的概率是()A.14B.13C.12D.236.已知双曲线的两个焦点分别为(0,4),(0,4)-,点(6,4)-在该双曲线上,则该双曲线的离心率为()A.4B.3C.2D.7.曲线()631f x x x =+-在()0,1-处的切线与坐标轴围成的面积为()A.16B.32C.12D.8.函数()()2e esin xxf x x x -=-+-在区间[ 2.8,2.8]-的大致图像为()A.B.C.D.9.已知cos cos sin ααα=-πtan 4α⎛⎫+= ⎪⎝⎭()A.1+B.1- C.32D.1原10题略10.设αβ、是两个平面,m n 、是两条直线,且m αβ= .下列四个命题:①若//m n ,则//n α或//n β②若m n ⊥,则,n n αβ⊥⊥③若//n α,且//n β,则//m n ④若n 与α和β所成的角相等,则m n⊥其中所有真命题的编号是()A.①③ B.②④C.①②③D.①③④11.在ABC 中内角,,A B C 所对边分别为,,a b c ,若π3B =,294b ac =,则sin sin A C +=()A.32B.C.72D.2二、填空题:本题共4小题,每小题5分,共20分.原13题略12.函数()sin f x x x =在[]0,π上的最大值是______.13.已知1a >,8115log log 42a a -=-,则=a ______.14.曲线33y x x =-与()21y x a =--+在()0,∞+上有两个不同的交点,则a 的取值范围为______.三、解答题:共70分.解答应写出文字说明,证明过程或演算步骤.第17题第21题为必考题,每个考题考生必须作答.第22、23题为选考题,考生根据要求作答.(一)必考题:共60分.15.已知等比数列{}n a 的前n 项和为n S ,且1233n n S a +=-.(1)求{}n a 的通项公式;(2)求数列{}n S 的通项公式.16.如图,在以A ,B ,C ,D ,E ,F 为顶点的五面体中,四边形ABCD 与四边形ADEF 均为等腰梯形,//,//BC AD EF AD ,4,2AD AB BC EF ====,ED FB ==M 为AD 的中点.(1)证明://BM 平面CDE ;(2)求点M 到ABF 的距离.17.已知函数()()1ln 1f x a x x =--+.(1)求()f x 的单调区间;(2)若2a ≤时,证明:当1x >时,()1ex f x -<恒成立.18.设椭圆2222:1(0)x y C a b a b+=>>的右焦点为F ,点31,2M ⎛⎫ ⎪⎝⎭在C 上,且MF x ⊥轴.(1)求C 的方程;(2)过点()4,0P 的直线与C 交于,A B 两点,N 为线段FP 的中点,直线NB 交直线MF 于点Q ,证明:AQ y ⊥轴.(二)选考题:共10分.请考生在第22、23题中任选一题作答,并用2B 铅笔将所选题号涂黑,多涂、错涂、漏涂均不给分,如果多做,则按所做的第一题计分.19.在平面直角坐标系xOy 中,以坐标原点O 为极点,x 轴的正半轴为极轴建立极坐标系,曲线C 的极坐标方程为cos 1ρρθ=+.(1)写出C 的直角坐标方程;(2)设直线l :x ty t a =⎧⎨=+⎩(t 为参数),若C 与l 相交于A B 、两点,若2AB =,求a 的值.20.实数,a b 满足3a b +≥.(1)证明:2222a b a b +>+;(2)证明:22226a b b a -+-≥.参考答案2024年普通高等学校招生全国统一考试(新课标I 卷)数学参考答案一、单项选择题【答案】1.A 【解析】【详解】因为{{}|,3,1,0,2,3A x x B =<<=--,且注意到12<<,从而A B = {}1,0-.故选:A.【答案】2.C 【解析】【详解】因为11111i 111z z z z z -+==+=+---,所以111i i z =+=-.故选:C.【答案】3.D 【解析】【详解】因为()4b b a ⊥- ,所以()40b b a ⋅-=,所以240b a b -⋅=即2440x x +-=,故2x =,故选:D.【答案】4.A 【解析】【详解】因为()cos m αβ+=,所以cos cos sin sin m αβαβ-=,而tan tan 2αβ=,所以sin sin 2cos cos αβαβ=,故cos cos 2cos cos m αβαβ-=即cos cos m αβ=-,从而sin sin 2m αβ=-,故()cos 3m αβ-=-,故选:A.【答案】5.B 【解析】【详解】设圆柱的底面半径为r而它们的侧面积相等,所以2ππr r=即=,故3r=,故圆锥的体积为1π93⨯=.故选:B.【答案】6.B【解析】【详解】因为()f x在R上单调递增,且0x≥时,()()e ln1xf x x=++单调递增,则需满足()2021e ln1aa-⎧-≥⎪⨯-⎨⎪-≤+⎩,解得10a-≤≤,即a的范围是[1,0]-.故选:B.【答案】7.C【解析】【详解】因为函数siny x=的的最小正周期为2πT=,函数π2sin36y x⎛⎫=-⎪⎝⎭的最小正周期为2π3T=,所以在[]0,2πx∈上函数π2sin36y x⎛⎫=-⎪⎝⎭有三个周期的图象,在坐标系中结合五点法画出两函数图象,如图所示:由图可知,两函数图象有6个交点.故选:C【答案】8.B【解析】【详解】因为当3x<时()f x x=,所以(1)1,(2)2f f==,又因为()(1)(2)f x f x f x>-+-,则(3)(2)(1)3,(4)(3)(2)5f f f f f f>+=>+>,(5)(4)(3)8,(6)(5)(4)13,(7)(6)(5)21f f f f f f f f f>+>>+>>+>,(8)(7)(6)34,(9)(8)(7)55,(10)(9)(8)89f f f f f f f f f >+>>+>>+>,(11)(10)(9)144,(12)(11)(10)233,(13)(12)(11)377f f f f f f f f f >+>>+>>+>(14)(13)(12)610,(15)(14)(13)987f f f f f f >+>>+>,(16)(15)(14)15971000f f f >+>>,则依次下去可知(20)1000f >,则B 正确;且无证据表明ACD 一定正确.故选:B.二、多项选择题【答案】9.BC 【解析】【详解】依题可知,22.1,0.01x s ==,所以()2.1,0.1Y N ,故()()()2 2.10.1 2.10.10.84130.5P Y P Y P Y >=>-=<+≈>,C 正确,D 错误;因为()1.8,0.1X N ,所以()()2 1.820.1P X P X >=>+⨯,因为()1.80.10.8413P X <+≈,所以()1.80.110.84130.15870.2P X >+≈-=<,而()()()2 1.820.1 1.80.10.2P X P X P X >=>+⨯<>+<,B 正确,A 错误,故选:BC .【答案】10.ACD 【解析】【详解】对A ,因为函数()f x 的定义域为R ,而()()()()()()22141313f x x x x x x =--+-=--',易知当()1,3x ∈时,()0f x '<,当(),1x ∞∈-或()3,x ∞∈+时,()0f x '>函数()f x 在(),1∞-上单调递增,在()1,3上单调递减,在()3,∞+上单调递增,故3x =是函数()f x 的极小值点,正确;对B ,当01x <<时,()210x x x x -=->,所以210x x >>>,而由上可知,函数()f x 在()0,1上单调递增,所以()()2f x f x>,错误;对C ,当12x <<时,1213x <-<,而由上可知,函数()f x 在()1,3上单调递减,所以()()()1213f f x f >->,即()4210f x -<-<,正确;对D,当10x -<<时,()()()()()()222(2)()12141220f x f x x x x x x x --=------=-->,所以(2)()f x f x ->,正确;故选:ACD.【答案】11.ABD 【解析】【详解】对于A :设曲线上的动点(),P x y ,则2x >-4x a -=,04a -=,解得2a =-,故A 正确.对于B24x +=,而2x >-,()24x+=.当0x y ==()2844=-=,故()在曲线上,故B 正确.对于C :由曲线的方程可得()()2221622y x x =--+,取32x =,则2641494y =-,而64164525624510494494494---=-=>⨯,故此时21y >,故C 在第一象限内点的纵坐标的最大值大于1,故C 错误.对于D :当点()00,x y 在曲线上时,由C 的分析可得()()()220022001616222y x x x =--≤++,故0004422y x x -≤≤++,故D 正确.故选:ABD.三、填空题【答案】12.32【解析】【详解】由题可知2,,A B F 三点横坐标相等,设A 在第一象限,将x c =代入22221x ya b-=得2b y a =±,即22,,,b b A c B c a a ⎛⎫⎛⎫- ⎪ ⎪⎝⎭⎝⎭,故2210b AB a ==,225b AF a ==,又122AF AF a -=,得1222513AF AF a a =+=+=,解得4a =,代入25ba=得220b =,故22236,c a b =+=,即6c =,所以6342c e a ===.故答案为:32【答案】13.ln 2【解析】【详解】由e x y x =+得e 1x y '=+,00|e 12x y ='=+=,故曲线e x y x =+在()0,1处的切线方程为21y x =+;由()ln 1y x a =++得11y x '=+,设切线与曲线()ln 1y x a =++相切的切点为()()00,ln 1x x a ++,由两曲线有公切线得0121y x '==+,解得012x =-,则切点为11,ln 22a ⎛⎫-+ ⎪⎝⎭,切线方程为112ln 21ln 222y x a x a ⎛⎫=+++=++- ⎪⎝⎭,根据两切线重合,所以ln 20a -=,解得ln 2a =.故答案为:ln 2【答案】14.12【解析】【详解】设甲在四轮游戏中的得分分别为1234,,,X X X X ,四轮的总得分为X .对于任意一轮,甲乙两人在该轮出示每张牌的概率都均等,其中使得甲获胜的出牌组合有六种,从而甲在该轮获胜的概率()631448k P X ===⨯,所以()()31,2,3,48k E X k ==.从而()()()441234113382kk k E X E X X X X E X ===+++===∑∑.记()()0,1,2,3k p P X k k ===.如果甲得0分,则组合方式是唯一的:必定是甲出1,3,5,7分别对应乙出2,4,6,8,所以04411A 24p ==;如果甲得3分,则组合方式也是唯一的:必定是甲出1,3,5,7分别对应乙出8,2,4,6,所以34411A 24p ==.而X 的所有可能取值是0,1,2,3,故01231p p p p +++=,()1233232p p p E X ++==.所以121112p p ++=,1213282p p ++=,两式相减即得211242p +=,故2312p p +=.所以甲的总得分不小于2的概率为2312p p +=.故答案为:12.四、解答题【答案】15.(1)由余弦定理有2222cos a b c ab C +-=,对比已知222a b c +-=,可得22222cos 222a b c C ab ab +-===,因为()0,πC ∈,所以sin 0C >,从而sin 2C ==,又因为sin C B =,即cos 2B =,注意到()0,πB ∈,所以π3B =.(2)由(1)可得π3B =,2cos 2C =,()0,πC ∈,从而π4C =,ππ5ππ3412A =--=,而5πππ232162sin sin sin 124622224A ⎛⎫⎛⎫==+=⨯=⎪ ⎪⎝⎭⎝⎭,由正弦定理有5πππsin sin sin 1234a b c==,从而623136,4222a c b c +====,由三角形面积公式可知,ABC 的面积可表示为211316233sin 222228ABC S ab C c c c +==⋅⋅= ,由已知ABC 的面积为3+,可得2338c =,所以c =【答案】16.(1)由题意得2239941b a b =⎧⎪⎪⎨⎪+=⎪⎩,解得22912b a ⎧=⎨=⎩,所以12e ==.(2)法一:3312032APk -==--,则直线AP 的方程为132y x =-+,即260x y +-=,352AP ==,由(1)知22:1129x y C +=,设点B 到直线AP 的距离为d ,则1255352d ==,则将直线AP 沿着与AP 垂直的方向平移1255单位即可,此时该平行线与椭圆的交点即为点B ,设该平行线的方程为:20x y C ++=,1255=,解得6C =或18C =-,当6C =时,联立221129260x y x y ⎧+=⎪⎨⎪++=⎩,解得03x y =⎧⎨=-⎩或332x y =-⎧⎪⎨=-⎪⎩,即()0,3B -或33,2⎛⎫--⎪⎝⎭,当()0,3B -时,此时32l k =,直线l 的方程为332y x =-,即3260x y --=,当33,2B ⎛⎫--⎪⎝⎭时,此时12lk =,直线l 的方程为12y x =,即20x y -=,当18C =-时,联立2211292180x y x y ⎧+=⎪⎨⎪+-=⎩得22271170y y -+=,227421172070∆=-⨯⨯=-<,此时该直线与椭圆无交点.综上直线l 的方程为3260x y --=或20x y -=.法二:同法一得到直线AP 的方程为260x y +-=,点B 到直线AP 的距离1255d =,设()00,B x y,则220012551129x y =⎪+=⎪⎩,解得00332x y =-⎧⎪⎨=-⎪⎩或0003x y =⎧⎨=-⎩,即()0,3B -或33,2⎛⎫--⎪⎝⎭,以下同法一.法三:同法一得到直线AP 的方程为260x y +-=,点B 到直线AP的距离5d =,设(),3sin B θθ,其中[)0,2θ∈π1255=,联立22cos sin 1θθ+=,解得cos 21sin 2θθ⎧=-⎪⎪⎨⎪=-⎪⎩或cos 0sin 1θθ=⎧⎨=-⎩,即()0,3B -或33,2⎛⎫--⎪⎝⎭,以下同法一;法四:当直线AB 的斜率不存在时,此时()0,3B -,16392PAB S =⨯⨯= ,符合题意,此时32l k =,直线l 的方程为332y x =-,即3260x y --=,当线AB 的斜率存在时,设直线AB 的方程为3y kx =+,联立椭圆方程有2231129y kx x y =+⎧⎪⎨+=⎪⎩,则()2243240k x kx ++=,其中AP k k ≠,即12k ≠-,解得0x =或22443k x k -=+,0k ≠,12k ≠-,令22443k x k -=+,则2212943k y k -+=+,则22224129,4343k k B k k ⎛⎫--+ ⎪++⎝⎭同法一得到直线AP 的方程为260x y +-=,点B 到直线AP 的距离1255d =,5=,解得32k =,此时33,2B ⎛⎫-- ⎪⎝⎭,则得到此时12lk =,直线l 的方程为12y x =,即20x y -=,综上直线l 的方程为3260x y --=或20x y -=.法五:当l 的斜率不存在时,3:3,3,,3,2l x B PB A ⎛⎫=-= ⎪⎝⎭到PB 距离3d =,此时1933922ABP S =⨯⨯=≠ 不满足条件.当l 的斜率存在时,设3:(3)2PB y k x -=-,令()()1122,,,P x y B x y ,223(3)21129y k x x y ⎧=-+⎪⎪⎨⎪+=⎪⎩,消y 可得()()22224324123636270k x k k x k k +--+--=,()()()2222Δ24124433636270k kk k k =--+-->,且AP k k ≠,即12k ≠-,21222122241243,36362743k k x x k PB k k x x k ⎧-+=⎪⎪+==⎨--⎪=⎪+⎩,A 到直线PB距离192PAB d S ==⋅ ,12k ∴=或32,均满足题意,1:2l y x ∴=或332y x =-,即3260x y --=或20x y -=.法六:当l 的斜率不存在时,3:3,3,,3,2l x B PB A ⎛⎫=-= ⎪⎝⎭到PB 距离3d =,此时1933922ABP S =⨯⨯=≠ 不满足条件.当直线l 斜率存在时,设3:(3)2l y k x =-+,设l 与y 轴的交点为Q ,令0x =,则30,32Q k ⎛⎫-+⎪⎝⎭,联立223323436y kx k x y ⎧=-+⎪⎨⎪+=⎩,则有()2223348336362702k x k k x k k ⎛⎫+--+--= ⎪⎝⎭,()2223348336362702k x k k x k k ⎛⎫+--+--= ⎪⎝⎭,其中()()22223Δ8343436362702k k k k k ⎛⎫=--+--> ⎪⎝⎭,且12k ≠-,则2222363627121293,3434B B k k k k x x k k ----==++,则211312183922234P B k S AQ x x k k +=-=+=+,解的12k =或32k =,经代入判别式验证均满足题意.则直线l 为12y x =或332y x =-,即3260x y --=或20x y -=.【答案】17.(1)因为PA ⊥平面ABCD ,而AD ⊂平面ABCD ,所以PA AD ⊥,又AD PB ⊥,PB PA P = ,,PB PA ⊂平面PAB ,所以AD ⊥平面PAB ,而AB ⊂平面PAB ,所以AD AB ⊥.因为222BC AB AC +=,所以BC AB ⊥,根据平面知识可知//AD BC ,又AD ⊄平面PBC ,BC ⊂平面PBC ,所以//AD 平面PBC .(2)如图所示,过点D 作DE AC ⊥于E ,再过点E 作EF CP ⊥于F ,连接DF ,因为PA ⊥平面ABCD ,所以平面PAC ⊥平面ABCD ,而平面PAC 平面ABCD AC =,所以DE ⊥平面PAC ,又EF CP ⊥,所以⊥CP 平面DEF ,根据二面角的定义可知,DFE ∠即为二面角A CP D --的平面角,即sin 7DFE ∠=,即tan DFE ∠=因为AD DC ⊥,设AD x =,则CD =,由等面积法可得,2DE =,又242xCE -==,而EFC 为等腰直角三角形,所以2EF =,故242tan 4DFE x∠==x =AD =.【答案】18.(1)0b =时,()ln 2xf x ax x=+-,其中()0,2x ∈,则()()()112,0,222f x a x x x x x =+=+∈--',因为()22212x x x x -+⎛⎫-≤= ⎪⎝⎭,当且仅当1x =时等号成立,故()min 2f x a '=+,而()0f x '≥成立,故20a +≥即2a ≥-,所以a 的最小值为2-.,(2)()()3ln12x f x ax b x x=++--的定义域为()0,2,设(),P m n 为()y f x =图象上任意一点,(),P m n 关于()1,a 的对称点为()2,2Q m a n --,因为(),P m n 在()y f x =图象上,故()3ln 12m n am b m m=++--,而()()()()3322ln221ln 122m m f m a m b m am b m a m m -⎡⎤-=+-+--=-++-+⎢⎥-⎣⎦,2n a =-+,所以()2,2Q m a n --也在()y f x =图象上,由P 的任意性可得()y f x =图象为中心对称图形,且对称中心为()1,a .(3)因为()2f x >-当且仅当12x <<,故1x =为()2f x =-的一个解,所以()12f =-即2a =-,先考虑12x <<时,()2f x >-恒成立.此时()2f x >-即为()()3ln21102x x b x x +-+->-在()1,2上恒成立,设()10,1t x =-∈,则31ln 201t t bt t+-+>-在()0,1上恒成立,设()()31ln 2,0,11t g t t bt t t+=-+∈-,则()()2222232322311tbtbg t bt t t -++=-+=-'-,当0b ≥,232332320bt b b b -++≥-++=>,故()0g t '>恒成立,故()g t 在()0,1上为增函数,故()()00g t g >=即()2f x >-在()1,2上恒成立.当203b -≤<时,2323230bt b b -++≥+≥,故()0g t '≥恒成立,故()g t 在()0,1上为增函数,故()()00g t g >=即()2f x >-在()1,2上恒成立.当23b <-,则当01t <<<时,()0g t '<故在⎛ ⎝上()g t 为减函数,故()()00g t g <=,不合题意,舍;综上,()2f x >-在()1,2上恒成立时23b ≥-.而当23b ≥-时,而23b ≥-时,由上述过程可得()g t 在()0,1递增,故()0g t >的解为()0,1,即()2f x >-的解为()1,2.综上,23b ≥-.【答案】19.(1)首先,我们设数列1242,,...,m a a a +的公差为d ,则0d ≠.由于一个数列同时加上一个数或者乘以一个非零数后是等差数列,当且仅当该数列是等差数列,故我们可以对该数列进行适当的变形()111,2,...,42k ka a a k m d-=+=+',得到新数列()1,2, (42)a k k m ==+',然后对1242,,...,m a a a +'''进行相应的讨论即可.换言之,我们可以不妨设()1,2,...,42k a k k m ==+,此后的讨论均建立在该假设下进行.回到原题,第1小问相当于从1,2,3,4,5,6中取出两个数i 和()j i j <,使得剩下四个数是等差数列.那么剩下四个数只可能是1,2,3,4,或2,3,4,5,或3,4,5,6.所以所有可能的(),i j 就是()()()1,2,1,6,5,6.(2)由于从数列1,2,...,42m +中取出2和13后,剩余的4m 个数可以分为以下两个部分,共m 组,使得每组成等差数列:①{}{}{}1,4,7,10,3,6,9,12,5,8,11,14,共3组;②{}{}{}15,16,17,18,19,20,21,22,...,41,4,41,42m m m m -++,共3m -组.(如果30m -=,则忽略②)故数列1,2,...,42m +是()2,13-可分数列.(3)定义集合{}{}410,1,2,...,1,5,9,13,...,41A k k m m =+==+,{}{}420,1,2,...,2,6,10,14,...,42B k k m m =+==+.下面证明,对142i j m ≤<≤+,如果下面两个命题同时成立,则数列1,2,...,42m +一定是(),i j -可分数列:命题1:,i A j B ∈∈或,i B j A ∈∈;命题2:3j i -≠.我们分两种情况证明这个结论.第一种情况:如果,i A j B ∈∈,且3j i -≠.此时设141i k =+,242j k =+,{}12,0,1,2,...,k k m ∈.则由i j <可知124142k k +<+,即2114k k ->-,故21k k ≥.此时,由于从数列1,2,...,42m +中取出141i k =+和242j k =+后,剩余的4m 个数可以分为以下三个部分,共m 组,使得每组成等差数列:①{}{}{}11111,2,3,4,5,6,7,8,...,43,42,41,4k k k k ---,共1k 组;②{}{}{}11111111222242,43,44,45,46,47,48,49,...,42,41,4,41k k k k k k k k k k k k ++++++++--+,共21k k -组;③{}{}{}2222222243,44,45,46,47,48,49,410,...,41,4,41,42k k k k k k k k m m m m ++++++++-++,共2m k -组.(如果某一部分的组数为0,则忽略之)故此时数列1,2,...,42m +是(),i j -可分数列.第二种情况:如果,i B j A ∈∈,且3j i -≠.此时设142i k =+,241j k =+,{}12,0,1,2,...,k k m ∈.则由i j <可知124241k k +<+,即2114k k ->,故21k k >.由于3j i -≠,故()()2141423k k +-+≠,从而211k k -≠,这就意味着212k k -≥.此时,由于从数列1,2,...,42m +中取出142i k =+和241j k =+后,剩余的4m 个数可以分为以下四个部分,共m 组,使得每组成等差数列:①{}{}{}11111,2,3,4,5,6,7,8,...,43,42,41,4k k k k ---,共1k 组;②{}112121241,31,221,31k k k k k k k +++++++,{}121212232,222,32,42k k k k k k k +++++++,共2组;③全体{}11212124,3,22,3k p k k p k k p k k p +++++++,其中213,4,...,p k k =-,共212k k --组;④{}{}{}2222222243,44,45,46,47,48,49,410,...,41,4,41,42k k k k k k k k m m m m ++++++++-++,共2m k -组.(如果某一部分的组数为0,则忽略之)这里对②和③进行一下解释:将③中的每一组作为一个横排,排成一个包含212k k --个行,4个列的数表以后,4个列分别是下面这些数:{}111243,44,...,3k k k k +++,{}12121233,34,...,22k k k k k k +++++,{}121212223,223,...,3k k k k k k +++++,{}1212233,34,...,4k k k k k ++++.可以看出每列都是连续的若干个整数,它们再取并以后,将取遍{}11241,42,...,42k k k +++中除开五个集合{}1141,42k k ++,{}121231,32k k k k ++++,{}1212221,222k k k k ++++,{}121231,32k k k k ++++,{}2241,42k k ++中的十个元素以外的所有数.而这十个数中,除开已经去掉的142k +和241k +以外,剩余的八个数恰好就是②中出现的八个数.这就说明我们给出的分组方式满足要求,故此时数列1,2,...,42m +是(),i j -可分数列.至此,我们证明了:对142i j m ≤<≤+,如果前述命题1和命题2同时成立,则数列1,2,...,42m +一定是(),i j -可分数列.然后我们来考虑这样的(),i j 的个数.首先,由于A B ⋂=∅,A 和B 各有1m +个元素,故满足命题1的(),i j 总共有()21m +个;而如果3j i -=,假设,i A j B ∈∈,则可设141i k =+,242j k =+,代入得()()2142413k k +-+=.但这导致2112k k -=,矛盾,所以,i B j A ∈∈.设142i k =+,241j k =+,{}12,0,1,2,...,k k m ∈,则()()2141423k k +-+=,即211k k -=.所以可能的()12,k k 恰好就是()()()0,1,1,2,...,1,m m -,对应的(),i j 分别是()()()2,5,6,9,...,42,41m m -+,总共m 个.所以这()21m +个满足命题1的(),i j 中,不满足命题2的恰好有m 个.这就得到同时满足命题1和命题2的(),i j 的个数为()21m m +-.当我们从1,2,...,42m +中一次任取两个数i 和()j i j <时,总的选取方式的个数等于()()()()424121412m m m m ++=++.而根据之前的结论,使得数列1242,,...,m a a a +是(),i j -可分数列的(),i j 至少有()21m m +-个.所以数列1242,,...,m a a a +是(),i j -可分数列的概率m P 一定满足()()()()()()()()()22221111124214121412142221218m m m m m m m m P m m m m m m m m ⎛⎫+++ ⎪+-++⎝⎭≥=>=++++++++.这就证明了结论.2024年普通高等学校招生全国统一考试(新课标II 卷)数学参考答案一、单项选择题【答案】1.C 【解析】【详解】若1i z =--,则z ==.故选:C.【答案】2.B 【解析】【详解】对于p 而言,取=1x -,则有101x +=<,故p 是假命题,p ⌝是真命题,对于q 而言,取1x =,则有3311x x ===,故q 是真命题,q ⌝是假命题,综上,p ⌝和q 都是真命题.故选:B.【答案】3.B 【解析】【详解】因为()2b a b -⊥ ,所以()20b a b -⋅= ,即22b a b =⋅,又因为1,22a a b =+=,所以22144164a b b b +⋅+=+= ,从而22=b .故选:B.【答案】4.C 【解析】【详解】对于A,根据频数分布表可知,612183650++=<,所以亩产量的中位数不小于1050kg ,故A 错误;对于B ,亩产量不低于1100kg 的频数为341024=+,所以低于1100kg 的稻田占比为1003466%100-=,故B 错误;对于C ,稻田亩产量的极差最大为1200900300-=,最小为1150950200-=,故C 正确;对于D ,由频数分布表可得,亩产量在[1050,1100)的频数为100(612182410)30-++++=,所以平均值为1(692512975181025301075241125101175)1067100⨯⨯+⨯+⨯+⨯+⨯+⨯=,故D 错误.故选;C.【答案】5.A 【解析】【详解】设点(,)M x y ,则0(,),(,0)P x y P x ',因为M 为PP '的中点,所以02y y =,即(,2)P x y ,又P 在圆2216(0)x y y +=>上,所以22416(0)x y y +=>,即221(0)164x y y +=>,即点M 的轨迹方程为221(0)164x y y +=>.故选:A 【答案】6.D 【解析】【详解】解法一:令()()f x g x =,即2(1)1cos 2a x x ax +-=+,可得21cos a x ax -=+,令()()21,cos a x F x ax G x =-=+,原题意等价于当(1,1)x ∈-时,曲线()y F x =与()y G x =恰有一个交点,注意到()(),F x G x 均为偶函数,可知该交点只能在y 轴上,可得()()00F G =,即11a -=,解得2a =,若2a =,令()()F x G x =,可得221cos 0x x +-=因为()1,1x ∈-,则220,1cos 0x x ≥-≥,当且仅当0x =时,等号成立,可得221cos 0x x +-≥,当且仅当0x =时,等号成立,则方程221cos 0x x +-=有且仅有一个实根0,即曲线()y F x =与()y G x =恰有一个交点,所以2a =符合题意;综上所述:2a =.解法二:令()()()2()1cos ,1,1h x f x g x ax a x x =-=+--∈-,原题意等价于()h x 有且仅有一个零点,因为()()()()221cos 1cos h x a x a x ax a x h x -=-+---=+--=,则()h x 为偶函数,根据偶函数的对称性可知()h x 的零点只能为0,即()020h a =-=,解得2a =,若2a =,则()()221cos ,1,1h x x x x =+-∈-,又因为220,1cos 0x x ≥-≥当且仅当0x =时,等号成立,可得()0h x ≥,当且仅当0x =时,等号成立,即()h x 有且仅有一个零点0,所以2a =符合题意;故选:D.【答案】7.B 【解析】【详解】解法一:分别取11,BC B C 的中点1,D D ,则11AD A D ==可知111131662222ABC A B C S S =⨯⨯⨯==⨯= 设正三棱台111ABC A B C -的为h ,则(11115233ABC A B C V h -=++=,解得433h =,如图,分别过11,A D 作底面垂线,垂足为,M N ,设AM x =,。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第页即墨实验高中卓峰班物理3-5测试题选择题(本题共36个小题,每题4分,共144分。
每题给出的选项中,1-26只有一个选项符合题意,27-36题有多个选项符合题意,全部选对的得4分,选对但不全的得2分,有选错或不答的得0分)1.下列说法中正确的是 ( ) A.质子与中子的质量不等,但质量数相等B.两个质子之间,不管距离如何,核力总是大于库仑力C.同一种元素的原子核有相同的质量数,但中子数可以不同D.除万有引力外,两个中子之间不存在其它相互作用力2.铀裂变的产物之一氪90(Kr9036)是不稳定的,它经过一系列衰变最终成为稳定的锆90(Zr 9040),这些衰变是 ( ) A.1次α衰变,6次β衰变 B.4次β衰变 C.2次α衰变D.2次α衰变,2次β衰变3.原子从一个能级跃迁到一个较低的能级时,有可能不发射光子。
例如在某种条件下,铬原子的n =2能级上的电子跃迁到n =1能级上时并不发射光子,而是将相应的能量转交给n =4能级上的电子,使之脱离原子,这一现象叫做俄歇效应。
以这种方式脱离了原子的电子叫做俄歇电子。
已知铬原子的能级公式可简化表示为2n A E n -=,式中n=1,2,3…表示不同的能级,A 是正的已知常数。
上述俄歇电子的动能是 ( ) A.A 163 B.A 167 C.A 1611 D.A 16134.在核反应方程(X)O N He 17814742+→+的括弧中,X 所代表的粒子是 ( )A.H 11 B.H 21 C.e 01- D.n 15.爱因斯坦由光电效应的实验规律,猜测光具有粒子性,从而提出光子说。
从科学研究的方法来说,这属于 ( ) A.等效替代 B.控制变量 C.科学假说 D.数学归纳6.下面列出的是一些核反应方程 ( )X P +→30143015Y B H Be +→+1052194 Z Li He He +→+734242 其中A. X 是质子,Y 是中子,Z 是正电子B. X 是正电子,Y 是质子,Z 是中子C. X 是中子,Y 是正电子,Z 是质子D. X 是正电子,Y 是中子,Z 是质子 7.如图,当电键K 断开时,用光子能量为2.5eV 的一束光照射阴极P ,发现电流表读数不为零。
合上电键,调节滑线变阻器,发现当电压表读数小于0.60V 时,电流表读数仍不为零;当电压表读数大于或等于0.60V 时,电流表读数为零。
由此可知阴极材料的逸出功为 ( ) A.1.9eV B.0.6eVC.2.5eVD.3.1eV8.下面是一核反应方程X He H H +→+423121用c 表示光速,则 ( )A .X 是质子,核反应放出的能量等于质子质量乘c 2B .X 是中子,核反应放出的能量等于质子质量乘c 2C .X 是质子,核反应放出的能量等于氘核与氚核的质量和减去氦核与质子的质量和,再乘c 2D . X 是中子,核反应放出的能量等于氘核与氚核的质量和减去氦核与中子的质量和,再乘c 2 9.一根粗细均匀长1.0m 的直玻璃管,上端封闭,下端开口,将它竖直地缓慢插入深水池中,直到管内水面距管上端0.50m 为止。
已知水的密度为1.0×103kg/m 3,重力加速度为10m/s 2,1.0×105Pa ,则这时管内、外水面的高度差为 ( ) A .9mB .9.5mC .10mD .0.5m10.图中画出了氢原子的4个能级,并注明了相应的能量E 。
处在n=4的能级的一群氢原子向低能级跃迁时,能够发出若干种不同频率的光波。
已知金属钾的逸出功为2.22eV 。
在这些光波中,能够从金属钾的表面打出光电子的总共有( )A .二种B .三种C .四种D .五种11.为纪念爱因斯坦对物理学的巨大贡献,联合国将2005年定为“国际物理年”。
对于爱因斯坦提出的质能方程E=mc 2,下列说法中不正确的是 A.E=mc 2表明物体具有的能量与其质量成正比 B.根据ΔE =Δmc 2可计算核反应的能量C.一个质子和一个中子结合成一个氘核时释放能量,表明此过程出现了质量亏损第2页D.E=mc 2中的E 是发生核反应中释放的核能12.某光电管的阴极是用金属钾制成的,它的逸出功为2.21eV ,用波长为2.5×10-7m 的紫外线照射阴极,已知真空中光速为3.0×108m/s ,元电荷为1.6×10-19C ,普朗克常量为6.63×10-34J s ,求得钾的极限频率和该光电管发射的光电子的最大动能应分别是A.5.3×1014H Z ,2.2J B.5.3×1014H Z ,4.4×10-19J C.3.3×1033H Z ,2.2J D.3.3×1033H Z ,4.4×10-19J13.某原子核AZ X 吸收一个中子后,放出一个电子,分裂为两个α粒子。
由此可知 A .A=7,Z =3 B .A=7,Z =4 C .A=8,Z =3 D .A=8,Z =4 14.现有三个核反应:①2311Na 24121Mg e →+ ②23592U 11419210563603n Ba Kr e +→++③23411120H H He n +→+ 下列说法正确的是A .①是裂变,②是β衰变,③是聚变B .①是聚变,②是裂变,③是β衰变C .①β衰变,②裂变,③聚变D .①是β衰变,②是聚变,③是裂变 15.目前核电站利用的核反应是A .裂变,核燃料为铀B .聚变,核燃烧为铀C .裂变,核燃烧为氘D .聚变,核燃料为氘16.使用电的金属球靠近不带电的验电器,验电器的箔片开。
下列各图表示验电器上感应电荷的分布情况,正确的是A B C D17.一个质子和一个中子聚变结合成一个氘核,同时辐射一个γ光子。
已知质子、中子、氘核的质量分别为m 1、m 2、m 3,普朗克常量为h ,真空中的光速为c 。
下列说法正确的是A.核反应方程是11H+10n →31H+γB.聚变反应中的质量亏损m m ∆=1+m 2-m 1C.辐射出的γ光子的能量E=(m 3-m 1-m 2)cD. γ光子的波长2123()hm m m c λ=+-18.一个23592U 原子核在中子的轰击下发生一种可能的裂变反应,其裂变方程为23519419203802U n X Sr n +→++,则下列说法正确的是A .X 是原子核中含有86个中子B .X 是原子核中含有141个核子C .因为裂变释放能量,根据E =mc 2,所以裂变后的总质量数增加D .因为裂变释放能量,出现质量亏损,所以裂变后的总质量数减少19.14C 是一种半衰期为5730年的放射性同位素。
若考古工作者探测某古木中14C 的含量为原来的14,则该古树死亡时间口中距今大约为 A .22920年 B .11460年 C . 5730年 D .2865年20.现有a 、b 、c 三束单光λa >λ>b λc 。
用b 光束照射某种金属时,恰能发生光电效应。
若分别用a 光束和c 光束照射该金属,则可以断定 A .a 光束照射时,不能发生光电效应 B .c 光束照射时,不能发生光电效应 C .a 光束照射时,释放出的光电子数目最多D .c 光束照射时,释放出的光电子的最大初动能最小21.某核反应方程为234112H+H He+x →。
已知21H 的质量为2.0136u ,31H 的质量为3.0180,42He 质量为4.0026u ,x 的质量为1.0087u 。
则下列说法中正确是A .x 是质子,该反应释放能量B .x 是中子,该反应释放能量C .x 是质子,该反应吸收能量D .x 是中子,该反应吸收能量 22.卢瑟福通过对a 粒子散射实验结果的分析,提出 (A )原子的核式结构模型. (B )原子核内有中子存在.第3页(C )电子是原子的组成部分.(D )原子核是由质子和中子组成的. 23.质子(p )和α粒子以相同的速率在同一匀强磁场中作匀速圆周运动,轨道半径分别为 R P 和 R α,周期分别为 T P 和 T α ,则下列选项正确的是A .R P ∶R α=1∶2,T P ∶T α=1∶2B . R P ∶R α=1∶1,T P ∶T α=1∶1C .R P ∶R α=1∶1,T P ∶T α=1∶2D . R P ∶R α=1∶2,T P ∶T α=1∶124..氢原子的能级如图所示,已知可见的光的光子能量范围约为1.62eV —3.11e V ,下列说法错误的是A .处于n = 3能级的氢原子可以吸收任意频率的紫外线,并发生电离B .大量氢原子从高能级向n = 3能级跃迁时,发出的光具有显著的热效应C .大量处于n =4能级的氢原子向低能级跃迁时,可能发出6种不同频率的光D .大量处于n =4是能级的氢原子向低能级跃迁时,可能发出3种不同频率的可见光25.研究光电效应规律的实验装置如图所示,以频率为ν的光照射光电管阴极K 时,有光电子产生。
由于光电管K 、A 间加的是反向电压,光电子从阴极 K 发射后将向阳极A 作减速运动。
光电流i 由图中电流计G 测出,反向电压U 由电压表V 测出。
当电流计示数恰好为零时,电压表的示数称为反向截止电压U 0。
在下列表示光电效应实验规律的图象中,错误的是26.下列说法中正确的是 ( )A .原子核由质子和中子组成B .原子核由质子和电子组成C .质子和中子都带正电D .原子核的质量数一定等于电荷数27.据新华社报道,由我国自行设计、研制的世界第一套全超导核聚变实验装置(又称“人造太阳”)已完成了首次工程调试。
下列关于“人造太阳”的说法正确的是 A .“人造太阳”的核反应方程是n He H H 10423121+→+ B .“人造太阳”的核反应方程是n Kr Ba n U 1092361415610235923++→+C .“人造太阳”释放的能量大小的计算公式是2mc E ∆=∆ D .“人造太阳”核能大小的计算公式是221mc E =28.铝箔被α粒子轰击后发生了以下核反应:2713Al+42He →+10n .下列判断正确的是A .10n 是质子B .10n 是中子 C .X 是2814Si 的同位素 D .X 是3115P 的同位素29.有关氢原子光谱的说法正确的是 A .氢原子的发射光谱是连续谱B .氢原子光谱说明氢原子只发出特定频率的光C .氢原子光谱说明氢原子能级是分立的D .氢原子光谱的频率与氢原子能级的能量差无关30.三个原子核X 、Y 、Z ,X 核放出一个正电子后变为Y 核,Y 核与质子发生核反应后生成Z 核并放出一个个氦(42He ),则下面说法正确的是 A.X 核比Z 核多一个原子 B.X 核比Z 核少一个中子C.X 核的质量数比Z 核质量数大3D.X 核与Z 核的总电荷是Y 核电荷的2倍31.中子和质子结合成氘核时,质量亏损为△m ,相应的能量△E =△mc 2=2.2 MeV 是氘核的结合能。
