3-5高考真题汇编
2024_2025三年高考英语真题分项汇编专题01冠词名词

专题01 冠词、名词2024年高考真题1.(2024新高考I卷)Covering an area about three times __________ size of Yellowstone National Park, the GPNP will be one of the first national parks in the country. 答案:the解析:考查冠词。
句意:该公园占地面积约为黄石国家公园的三倍,将成为中国首批国家公园之一。
本句的结构为:倍数+ the size of +比较成份。
故填the。
2.(2024全国甲卷)____________ friend of his, Wu Fan, volunteered to be his companion during the trip.答案:A解析:考查冠词。
句意:他的一位挚友吴凡在旅行中自愿成为他的同伴。
依据句意可知,此处泛指“他的一个挚友”,应用不定冠词,friend以辅音音素开头,应用a,空处位于句首,首字母大写。
故填A。
3.(2024全国乙卷)To celebrate ___________ festival, a number of events took place at the Chinese Businessman Museum in Beijing on Thursday.答案:the解析:考查非谓语动词。
句意:为了庆祝这一节日,周四在北京的中国商人博物馆实行了一系列活动。
特指International Tea Day这一节日,所以用定冠词the。
故填the。
4.(2024年浙江 1月真题)Cobb, for her party, started to ask conference organizers who invited her to speak if she could do so remotely; about three-quarters of ___________ time, they agreed.答案:the解析:考查冠词。
2024_2025三年高考英语真题分项汇编专题06动词的时态语态和主谓一致

专题06 动词的时态、语态和主谓一样2024年高考真题1.(2024新高考I卷)The plan will extend protection to a significant number of areas that __________ (be)previously unprotected,答案:were解析:考查时态和主谓一样。
句意:该安排将把爱护范围扩大到大量以前未受爱护的地区,将很多现有的大熊猫爱护区纳入一个管理机构,以提高效率,削减管理上的不一样性。
设空处在that引导的限制性定语从句中作谓语,先行词为a significant number of areas,先行词在从句中作主语,依据“previously (之前地)”可知从句的时态应为一般过去时,依据主谓一样,从句主语复数,从句谓语复数形式。
故填were。
2.(2024新高考I卷)After a three-year pilot period, the GPNP will be officially set up next year. The GPNP __________ (design)to reflect the guiding principle of “protecting the authenticity and integrity(完整性)of natural ecosystems, preserving biological diversity, protecting ecological buffer zones, and leaving behind precious natural assets(资产)for future generations”.答案:is designed解析:考查时态语态和主谓一样。
句意:GPNP旨在体现“爱护自然生态系统的真实性和完整性,爱护生物多样性,爱护生态缓冲区,为子孙后代留下珍贵的自然资产”的指导原则。
2023全国高考真题语文汇编:文言文阅读

2023全国高考真题语文汇编文言文阅读一、文言文阅读(2023·北京·统考高考真题)阅读下面的文言文,完成下面小题。
贵廉汉元帝时,贡禹上书言:“孝文皇帝时,贵廉洁,贱贪污,贾人、赘婿及吏坐赃者,皆禁锢不得为吏。
赏善罚恶,不阿亲戚,罪白者伏其诛,疑者以与民,无赎罪之法。
故令行禁止,海内大化,天下断狱仅四百,与刑措亡异。
“武帝始临天下,尊贤用士,辟地广境数千里。
自见功大威行,遂从.嗜欲。
用度不足,乃行一切之.变,使犯法者赎罪,入谷者补吏。
是以.天下奢侈,官乱民贫,盗贼并起,亡命者众。
郡国恐其诛,则.择便巧史书①、习于计簿、能欺上府者,以为右职;奸宄不胜,则取勇猛能操切..百姓者、以苛暴威服下者,使居大位。
故亡义而有财者显于世,欺谩而善书者尊于朝,悖逆而勇猛者贵于官。
故俗皆曰:何以孝弟为?财多而光荣。
何以礼义为?史书而仕宦。
何以谨慎为?勇猛而临官。
’故黥劓而髡钳者,犹复攘臂为政于世,行虽犬彘,家富势足,目指气使,是为贤耳。
故谓居官而置富者为雄杰,处奸而得利者为壮士。
兄劝其弟,父勉其子,俗之败坏,乃至于是!察其所以然者,皆以犯法得赎罪,求士不得真贤,相守②崇财利而诛不行之所致也。
“今欲兴至治,致太平,宜除赎罪之法。
相守选举不以实及有赃者,辄行其诛,亡但免官,则.争尽力为善,贵孝弟,贱贾人,进真贤,举实廉,而天下治矣。
”呜呼,今日之变,有甚于.此!自神宗③以来,黩.货之风日甚一日。
国维不张,而人心大坏,数十年于.此矣。
《书》曰:“不肩好货,敢恭生生,鞠人谋人之保居,叙钦。
”④必如是而后可以立太平之本。
贡禹又言:“欲令近臣自诸曹侍中以上,家亡得私贩卖,与民争利。
犯者辄免官削爵,不得仕宦。
”此议今亦可行。
自万历以后,天下水利碾硙,场渡市集,无不属之.豪绅,相沿以.为常事矣。
(取材于顾炎武⑤《日知录》)【注】①便巧史书:这里指善于舞文弄墨。
②相守:诸侯国相、郡守。
③神宗:明朝皇帝,年号万历。
三年高考生物真题分类汇编5(分子与细胞)-细胞中无机物、生物大分子(含解析)

2023届二轮备考-2020-2022三年高考生物真题分类汇编5(分子与细胞)- 细胞中无机物、生物大分子(含解析)一、单选题1.(2022·辽宁·统考高考真题)二甲基亚砜(DMSO)易与水分子结合,常用作细胞冻存的渗透性保护剂。
干细胞冻存复苏后指标检测结果见下表。
下列叙述错误的是()注:细胞分裂间期分为G1期、S期(DNA复制期)和G2期A.冻存复苏后的干细胞可以用于治疗人类某些疾病B.G1期细胞数百分比上升,导致更多干细胞直接进入分裂期C.血清中的天然成分影响G1期,增加干细胞复苏后的活细胞数百分比D.DMSO的作用是使干细胞中自由水转化为结合水2.(2022·海南·统考高考真题)种子萌发过程中,储藏的淀粉、蛋白质等物质在酶的催化下生成简单有机物,为新器官的生长和呼吸作用提供原料。
下列有关叙述错误..的是()A.种子的萌发受水分、温度和氧气等因素的影响B.种子萌发过程中呼吸作用增强,储藏的有机物的量减少C.干燥条件下种子不萌发,主要是因为种子中的酶因缺水而变性失活D.种子子叶切片用苏丹Ⅲ染色后,显微镜下观察到橘黄色颗粒,说明该种子含有脂肪3.(2022·湖北·统考高考真题)水是生命的源泉,节约用水是每个人应尽的责任,下列有关水在生命活动中作用的叙述,错误的是()A.水是酶促反应的环境B.参与血液中缓冲体系的形成C.可作为维生素D等物质的溶剂D.可作为反应物参与生物氧化过程4.(2022·全国·高考真题)钙在骨骼生长和肌肉收缩等过程中发挥重要作用。
晒太阳有助于青少年骨骼生长,预防老年人骨质疏松。
下列叙述错误的是()A.细胞中有以无机离子形式存在的钙B.人体内Ca2+可自由通过细胞膜的磷脂双分子层C.适当补充维生素D可以促进肠道对钙的吸收D.人体血液中钙离子浓度过低易出现抽搐现象5.(2021·湖北·统考高考真题)采摘后的梨常温下易软化。
2023全国高考真题英语汇编:完形填空2

2023全国高考真题英语汇编完形填空2(2023·全国·高考真题)Recently I was very busy and I needed a timeout. So I decided to drive to the supermarket and pick up dinner instead of doing my usual 1 .In the supermarket, I took fat and juicy chicken and some warm cornbread. As the cashier began processing my items, I 2 my bag for my credit card. However, I realized my wallet was not there. In 3 , I told the cashier I had left my money at home and apologized sincerely, offering to 4 my items to where I 5 them. Just at that moment the supermarket owner appeared, saying “Please, take everything home and 6 the dinner. It’s on the house tonight!” I tried to 7 the lovely offer but he 8 a dark chocolate bar near the counter and said, “Here! Take this, too!” His act of 9 lifted everybody present. I thanked him 10 for making my day.When I approached home, as I 11 into my driveway, I saw my next-door neighbor had just mowed my lawn (草坪). He was putting on the finishing touches, clearing the cut grass. Feeling 12 , I jumped out of my car and asked him how much he wanted for his 13 , to which he replied,“Nothing at all. The lawn needed doing.” He 14 me off summarily as he returned to his home. A second scoop of good 15 had landed in my lap, which again reminded me kindness is everywhere in the world.1.A.walking B.cooking C.shopping D.teaching2.A.reached into B.stared at C.put aside D.watched over3.A.anger B.amazement C.satisfaction D.embarrassment4.A.clear B.show C.pack D.return5.A.bought B.put C.took D.ate6.A.enjoy B.prepare C.donate D.deliver7.A.appreciate B.withdraw C.decline D.ensure8.A.looked at B.picked up C.showed off D.put away9.A.courage B.generosity C.faith D.bravery10.A.hurriedly B.curiously C.hesitantly D.sincerely11.A.searched B.dug C.crashed D.pulled12.A.regretful B.excited C.nervous D.energetic13.A.efforts B.talent C.guidance D.goods14.A.sent B.drove C.waved D.turned15.A.appetite B.deal C.fortune D.reputation(2023·全国·高考真题)The sun was beginning to sink as I set off into the Harenna Forest. I was on my way to 16 a unique honey harvest. Here, in south-east Ethiopia, hand-carved beehives(蜂箱)are placed in the17 . Reaching them to get the honey is difficult—and often 18 .I 19 beekeeper Ziyad over a wide stretch of grassland before entering a thick jungle. Ziyad began preparations. He 20 handfuls of damp tree leaves, wrapped them with string, and 21 the bunch to create a torch(火把). Then, with one end of a rope tied to his waist and the other end around the trunk of a tree, Ziyadlooked puzzled, and then 126 :“Oh this isn’t for the 127 I had. I take that as a 128 . No, this is for setting my hair yesterday.”And there you have it. To many people, 129 lives is part of the job but styling hair is an 130 and should be rewarded.111.A.cleaner B.chemist C.nurse D.doctor112.A.grades B.meanings C.needs D.expectations113.A.brushed aside B.put to the test C.brought under discussion D.taken into account 114.A.departing B.escaping C.retiring D.recovering115.A.attempting B.choosing C.pausing D.promising116.A.eventually B.fortunately C.casually D.secretly117.A.assessing B.requiring C.forming D.proving118.A.slightly B.accidentally C.slowly D.happily119.A.grateful B.thoughtful C.sorrowful D.fearful120.A.surprise B.delight C.curiosity D.disappointment 121.A.operating B.thinking C.hesitating D.leaving122.A.sorry B.hello C.goodbye D.yes123.A.reached B.consulted C.introduced D.persuaded124.A.wished B.pretended C.failed D.refused125.A.enjoying B.doing C.securing D.starting126.A.repeated B.recited C.replied D.reported127.A.courage B.patience C.duty D.care128.A.goal B.given C.push D.greeting129.A.risking B.changing C.saving D.building130.A.honour B.ability C.opening D.extra参考答案1.B 2.A 3.D 4.D 5.C 6.A 7.C 8.B 9.B 10.D 11.D 12.B 13.A 14.C 15.C【导语】本文是一篇记叙文。
2024年高考数学真题分类汇编(三角函数篇,解析版)

专题三角函数1(新课标全国Ⅰ卷)已知cos (α+β)=m ,tan αtan β=2,则cos (α-β)=()A.-3mB.-m3C.m 3D.3m【答案】A【分析】根据两角和的余弦可求cos αcos β,sin αsin β的关系,结合tan αtan β的值可求前者,故可求cos α-β 的值.【详解】因为cos α+β =m ,所以cos αcos β-sin αsin β=m ,而tan αtan β=2,所以=12×2b ×kb ×sin A 2+12×kb ×b ×sin A2,故cos αcos β-2cos αcos β=m 即cos αcos β=-m ,从而sin αsin β=-2m ,故cos α-β =-3m ,故选:A .2(新课标全国Ⅰ卷)当x ∈[0,2π]时,曲线y =sin x 与y =2sin 3x -π6 的交点个数为()A.3B.4C.6D.8【答案】C【分析】画出两函数在0,2π 上的图象,根据图象即可求解【详解】因为函数y =sin x 的的最小正周期为T =2π,函数y =2sin 3x -π6 的最小正周期为T =2π3,所以在x ∈0,2π 上函数y =2sin 3x -π6有三个周期的图象,在坐标系中结合五点法画出两函数图象,如图所示:由图可知,两函数图象有6个交点.故选:C3(新课标全国Ⅱ卷)设函数f (x )=a (x +1)2-1,g (x )=cos x +2ax ,当x ∈(-1,1)时,曲线y =f (x )与y =g (x )恰有一个交点,则a =()A.-1B.12C.1D.22024年高考数学真题分类汇编——三角函数篇【分析】解法一:令F x =ax 2+a -1,G x =cos x ,分析可知曲线y =F (x )与y =G (x )恰有一个交点,结合偶函数的对称性可知该交点只能在y 轴上,即可得a =2,并代入检验即可;解法二:令h x =f (x )-g x ,x ∈-1,1 ,可知h x 为偶函数,根据偶函数的对称性可知h x 的零点只能为0,即可得a =2,并代入检验即可.【详解】解法一:令f (x )=g x ,即a (x +1)2-1=cos x +2ax ,可得ax 2+a -1=cos x ,令F x =ax 2+a -1,G x =cos x ,原题意等价于当x ∈(-1,1)时,曲线y =F (x )与y =G (x )恰有一个交点,注意到F x ,G x 均为偶函数,可知该交点只能在y 轴上,可得F 0 =G 0 ,即a -1=1,解得a =2,若a =2,令F x =G x ,可得2x 2+1-cos x =0因为x ∈-1,1 ,则2x 2≥0,1-cos x ≥0,当且仅当x =0时,等号成立,可得2x 2+1-cos x ≥0,当且仅当x =0时,等号成立,则方程2x 2+1-cos x =0有且仅有一个实根0,即曲线y =F (x )与y =G (x )恰有一个交点,所以a =2符合题意;综上所述:a =2.解法二:令h x =f (x )-g x =ax 2+a -1-cos x ,x ∈-1,1 ,原题意等价于h x 有且仅有一个零点,因为h -x =a -x 2+a -1-cos -x =ax 2+a -1-cos x =h x ,则h x 为偶函数,根据偶函数的对称性可知h x 的零点只能为0,即h 0 =a -2=0,解得a =2,若a =2,则h x =2x 2+1-cos x ,x ∈-1,1 ,又因为2x 2≥0,1-cos x ≥0当且仅当x =0时,等号成立,可得h x ≥0,当且仅当x =0时,等号成立,即h x 有且仅有一个零点0,所以a =2符合题意;故选:D .4(全国甲卷数学(理)(文))已知cos αcos α-sin α=3,则tan α+π4=()A.23+1 B.23-1C.32D.1-3【答案】B【分析】先将cos αcos α-sin α弦化切求得tan α,再根据两角和的正切公式即可求解.【详解】因为cos αcos α-sin α=3,所以11-tan α=3,⇒tan α=1-33,所以tan α+π4 =tan α+11-tan α=23-1,故选:B .5(新高考北京卷)已知f x =sin ωx ω>0 ,f x 1 =-1,f x 2 =1,|x 1-x 2|min =π2,则ω=()A.1B.2C.3D.4【分析】根据三角函数最值分析周期性,结合三角函数最小正周期公式运算求解.【详解】由题意可知:x 1为f x 的最小值点,x 2为f x 的最大值点,则x 1-x 2 min =T 2=π2,即T =π,且ω>0,所以ω=2πT=2.故选:B .6(新高考天津卷)已知函数f x =sin3ωx +π3ω>0 的最小正周期为π.则函数在-π12,π6 的最小值是()A.-32B.-32C.0D.32【答案】A【分析】先由诱导公式化简,结合周期公式求出ω,得f x =-sin2x ,再整体求出x ∈-π12,π6时,2x 的范围,结合正弦三角函数图象特征即可求解.【详解】f x =sin3ωx +π3 =sin 3ωx +π =-sin3ωx ,由T =2π3ω=π得ω=23,即f x =-sin2x ,当x ∈-π12,π6 时,2x ∈-π6,π3,画出f x =-sin2x 图象,如下图,由图可知,f x =-sin2x 在-π12,π6上递减,所以,当x =π6时,f x min =-sin π3=-32故选:A7(新高考上海卷)下列函数f x 的最小正周期是2π的是()A.sin x +cos xB.sin x cos xC.sin 2x +cos 2xD.sin 2x -cos 2x【答案】A【分析】根据辅助角公式、二倍角公式以及同角三角函数关系并结合三角函数的性质一一判断即可 .【详解】对A ,sin x +cos x =2sin x +π4,周期T =2π,故A 正确;对B ,sin x cos x =12sin2x ,周期T =2π2=π,故B 错误;对于选项C ,sin 2x +cos 2x =1,是常值函数,不存在最小正周期,故C 错误;对于选项D ,sin 2x -cos 2x =-cos2x ,周期T =2π2=π,故D 错误,故选:A .8(新课标全国Ⅱ卷)对于函数f(x)=sin2x和g(x)=sin2x-π4,下列说法正确的有() A.f(x)与g(x)有相同的零点 B.f(x)与g(x)有相同的最大值C.f(x)与g(x)有相同的最小正周期D.f(x)与g(x)的图像有相同的对称轴【答案】BC【分析】根据正弦函数的零点,最值,周期公式,对称轴方程逐一分析每个选项即可.【详解】A选项,令f(x)=sin2x=0,解得x=kπ2,k∈Z,即为f(x)零点,令g(x)=sin2x-π4=0,解得x=kπ2+π8,k∈Z,即为g(x)零点,显然f(x),g(x)零点不同,A选项错误;B选项,显然f(x)max=g(x)max=1,B选项正确;C选项,根据周期公式,f(x),g(x)的周期均为2π2=π,C选项正确;D选项,根据正弦函数的性质f(x)的对称轴满足2x=kπ+π2⇔x=kπ2+π4,k∈Z,g(x)的对称轴满足2x-π4=kπ+π2⇔x=kπ2+3π8,k∈Z,显然f(x),g(x)图像的对称轴不同,D选项错误.故选:BC9(新课标全国Ⅱ卷)已知α为第一象限角,β为第三象限角,tanα+tanβ=4,tanαtanβ=2+1,则sin(α+β)=.【答案】-22 3【分析】法一:根据两角和与差的正切公式得tanα+β=-22,再缩小α+β的范围,最后结合同角的平方和关系即可得到答案;法二:利用弦化切的方法即可得到答案.【详解】法一:由题意得tanα+β=tanα+tanβ1-tanαtanβ=41-2+1=-22,因为α∈2kπ,2kπ+π2,β∈2mπ+π,2mπ+3π2,k,m∈Z,则α+β∈2m+2kπ+π,2m+2kπ+2π,k,m∈Z,又因为tanα+β=-22<0,则α+β∈2m+2kπ+3π2,2m+2kπ+2π,k,m∈Z,则sinα+β<0,则sinα+βcosα+β=-22,联立sin2α+β+cos2α+β=1,解得sinα+β=-223.法二:因为α为第一象限角,β为第三象限角,则cosα>0,cosβ<0,cosα=cosαsin2α+cos2α=11+tan2α,cosβ=cosβsin2β+cos2β=-11+tan2β,则sin(α+β)=sinαcosβ+cosαsinβ=cosαcosβ(tanα+tanβ)=4cosαcosβ=-41+tan2α1+tan2β=-4(tanα+tanβ)2+(tanαtanβ-1)2=-442+2=-223故答案为:-22 3.10(全国甲卷数学(文))函数f x =sin x-3cos x在0,π上的最大值是.【答案】2【分析】结合辅助角公式化简成正弦型函数,再求给定区间最值即可.【详解】f x =sin x -3cos x =2sin x -π3 ,当x ∈0,π 时,x -π3∈-π3,2π3,当x -π3=π2时,即x =5π6时,f x max =2.故答案为:2一、单选题1(2024·宁夏石嘴山·三模)在平面直角坐标系中,角θ的顶点与原点重合,始边与x 轴的非负半轴重合,终边经过点P 1,2 ,则7cos 2θ-2sin2θ=()A.-15B.15C.-2D.2【答案】A【分析】由题意可知:tan θ=2,根据倍角公式结合齐次化问题分析求解.【详解】由题意可知:tan θ=2,所以7cos 2θ-2sin2θ=7cos 2θ-4sin θcos θsin 2θ+cos 2θ=7-4tan θtan 2θ+1=7-4×222+1=-15.故选:A .2(2024·广东茂名·一模)已知cos α+π =-2sin α,则sin 2α-3cos α+π2cos αcos2α+1=()A.-1B.-25C.45D.78【答案】D【分析】根据给定条件,求出tan α,再结合诱导公式及二倍角的余弦公式,利用正余弦齐次式法计算得解.【详解】由cos α+π =-2sin α,得cos α=2sin α,则tan α=12,所以sin 2α-3cos α+π2 cos αcos2α+1=sin 2α+3sin αcos α2cos 2α=12tan 2α+32tan α=18+34=78.故选:D3(2024·河北保定·二模)函数f (x )=1-e x1+e xcos2x 的部分图象大致为()A. B.C. D.【答案】A【分析】根据函数的奇偶性判断即可.【详解】设g x =1-e x1+e x,则g-x=1-e-x1+e-x=e x-11+e x=-g x ,所以g x 为奇函数,设h x =cos2x,可知h x 为偶函数,所以f x =1-e x1+e xcos2x为奇函数,则B,C错误,易知f0 =0,所以A正确,D错误.故选:A.4(2024·山东济宁·三模)已知函数f(x)=(3sin x+cos x)cos x-12,若f(x)在区间-π4,m上的值域为-3 2,1,则实数m的取值范围是()A.π6,π2B.π6,π2C.π6,7π12D.π6,7π12【答案】D【分析】利用二倍角公式、辅助角公式化简函数f(x),再借助正弦函数的图象与性质求解即得.【详解】依题意,函数f(x)=3sin x cos x+cos2x-12=32sin2x+12cos2x=sin2x+π6,当x∈-π4,m时,2x+π6∈-π3,2m+π6,显然sin-π3=sin4π3=-32,sinπ2=1,且正弦函数y=sin x在π2,4π3上单调递减,由f(x)在区间-π4,m上的值域为-32,1,得π2≤2m+π6≤4π3,解得π6≤m≤7π12,所以实数m的取值范围是π6,7π12.故选:D5(2024·江西景德镇·三模)函数f x =cosωx x∈R在0,π内恰有两个对称中心,fπ=1,将函数f x 的图象向右平移π3个单位得到函数g x 的图象.若fα +gα =35,则cos4α+π3=()A.725B.1625C.-925D.-1925【答案】A【分析】根据y轴右边第二个对称中心在0,π内,第三个对称中心不在0,π内可求得32≤ω<52,结合fπ=1可得ω=2,再利用平移变换求出g x ,根据三角变换化简fα +gα =35可得sin2α+π6=35,然后由二倍角公式可解.【详解】由x∈0,π得ωx∈0,ωπ,因为函数f x 在0,π内恰有两个对称中心,所以3π2≤ωπ5π2>ωπ,解得32≤ω<52,又fπ=cosωπ=1,所以ωπ=kπ,k∈Z,即ω=k,k∈Z,所以ω=2,将函数f x 的图象向右平移π3个单位得到函数y=cos2x-π3=cos2x-2π3,即g x =cos2x-2π3,因为fα +gα =cos2α+cos2α-2π3=32sin2α+12cos2α=sin2α+π6=35,所以cos4α+π3=1-2sin22α+π6=1-2×35 2=725.故选:A6(2024·安徽马鞍山·三模)已知函数f(x)=sin2ωx+cos2ωx(ω>1)的一个零点是π2,且f(x)在-π6,π16上单调,则ω=()A.54B.74C.94D.114【答案】B【分析】整理可得f(x)=2sin2ωx+π4,以2ωx+π4为整体,根据单调性分析可得1<ω≤2,再结合零点分析求解.【详解】因为f(x)=sin2ωx+cos2ωx=2sin2ωx+π4,x∈-π6,π16,且ω>1时,可得2ωx+π4∈-π3ω+π4,π8ω+π4,且-π3ω+π4<0<π8ω+π4,若f(x)在-π6,π16上单调,则-π3ω+π4≥-π2π8ω+π4≤π2,解得1<ω≤2,又因为f(x)的一个零点是π2,则πω+π4=kπ,k∈Z,解得ω=k-14,k∈Z,所以k=2,ω=7 4 .故选:B.7(2024·山东临沂·二模)已知函数f x =sin2x+φϕ <π2图象的一个对称中心为π6,0,则()A.f x 在区间-π8,π3上单调递增B.x=5π6是f x 图象的一条对称轴C.f x 在-π6,π4上的值域为-1,32D.将f x 图象上的所有点向左平移5π12个长度单位后,得到的函数图象关于y轴对称【答案】D【分析】借助整体代入法结合正弦函数的性质可得A、B;结合正弦函数最值可得C;得到平移后的函数解析式后借助诱导公式即可得D.【详解】由题意可得2×π6+φ=kπk∈Z,解得φ=-π3+kπk∈Z,又ϕ <π2,故φ=-π3,即f x =sin2x-π3;对A :当x ∈-π8,π3 时,2x -π3∈-7π12,π3,由函数y =sin x 在-7π12,π3上不为单调递增,故f x 在区间-π8,π3上不为单调递增,故A 错误;对B :当x =5π6时,2x -π3=4π3,由x =4π3不是函数y =sin x 的对称轴,故x =5π6不是f x 图象的对称轴,故B 错误;对C :当x ∈-π6,π4 时,2x -π3∈-2π3,π6,则f x ∈-1,12,故C 错误;对D :将f x 图象上的所有点向左平移5π12个长度单位后,可得y =sin 2x +2×5π12-π3 =sin 2x +π2=cos2x ,该函数关于y 轴对称,故D 正确.故选:D .8(2024·广东广州·二模)已知函数f (x )=2sin (ωx +φ)ω>0,|φ|<π2的部分图象如图所示,若将函数f (x )的图象向右平移θ(θ>0)个单位后所得曲线关于y 轴对称,则θ的最小值为()A.π8B.π4C.3π8D.π2【答案】A【分析】根据给定的图象特征,结合五点法作图列式求出ω和φ,再根据图象的平移变换,以及图象的对称性即可得解.【详解】由f π4=1,得sin π4ω+φ =22,又点π4,1 及附近点从左到右是上升的,则π4ω+φ=π4+2k π,k ∈Z ,由f 5π8 =0,点5π8,0 及附近点从左到右是下降的,且上升、下降的两段图象相邻,得5π8ω+φ=π+2k π,k ∈Z ,联立解得ω=2,φ=-π4+2k π,k ∈Z ,而|φ|<π2,于是φ=-π4,f (x )=2sin 2x -π4,若将函数f (x )的图像向右平移θ(θ>0)个单位后,得到y =sin 2x -2θ-π4,则-2θ-π4=π2-k π,k ∈Z ,而θ>0,因此θ=-3π8+k π2,k ∈N ,所以当k =1时,θ取得最小值为π8.故选:A9(2024·四川雅安·三模)已知函数f x =sin ωx +3cos ωx (ω>0),则下列说法中正确的个数是()①当ω=2时,函数y =f x -2log πx 有且只有一个零点;②当ω=2时,函数y =f x +φ 为奇函数,则正数φ的最小值为π3;③若函数y =f x 在0,π3 上单调递增,则ω的最小值为12;④若函数y =f x 在0,π 上恰有两个极值点,则ω的取值范围为136,256.A.1 B.2C.3D.4【答案】B【分析】利用辅助角公式化简函数,由图象分析判断①;由正弦函数的性质判断②③;由极大值的意义结合正弦函数的性质判断④.【详解】依题意,ω>0,函数f (x )=212sin ωx +32cos ωx =2sin ωx +π3,对于①:f (x )=2sin 2x +π3,令y =f x -2log πx =0,即f x =2log πx ,作出函数y =f (x )和函数y =2log πx 的图象,如图,观察图象知,两个函数在0,7π12 上只有一个零点,f 13π12 =2sin 5π2=2,当x =13π12时,y =2log π13π12=2log π1312+2log ππ=2+2log π1312>2,当x >13π12时,2log πx >2≥f (x ),因此函数y =f x 与函数y =2log πx 的图象有且只有一个交点,①正确;对于②:f (x +φ)=2sin 2x +2φ+π3 为奇函数,则2φ+π3=k π,k ∈Z ,φ=-π6+k π2,k ∈Z ,即正数φ的最小值为π3,②正确;对于③:当x ∈0,π3 时,ωx +π3∈π3,π(ω+1)3,由y =f x 在0,π3 上单调递增,得π(ω+1)3≤π2ω>0,解得0<ω≤12,正数ω有最大值12,③错误;对于④:当x ∈(0,π)时,ωx +π3∈π3,ωπ+π3,而y =f x 在(0,π)上恰有两个极值点,由正弦函数的性质得3π2<ωπ+π3≤5π2,解得76<ω≤136,因此ω的取值范围是76,136,④错误.综上,共2个正确,故选:B .10(2024·河北保定·二模)已知tan α=3cos αsin α+11,则cos2α=()A.-78B.78C.79D.-79【答案】B【分析】利用切化弦和同角三角函数的关系,解出sin α,再结合二倍角公式即可求解.【详解】因为sin αcos α=3cos αsin α+11,所以4sin 2α+11sin α-3=0,解得sin α=14或sin α=-3(舍去),所以cos2α=1-2sin 2α=78.故选:B .11(2024·河北衡水·三模)已知sin (3α-β)=m sin (α-β),tan (2α-β)=n tan α,则m ,n 的关系为()A.m =2nB.n =m +1mC.n =m m -1D.n =m +1m -1【答案】D【分析】利用和差角的正弦公式化简,结合已知列出方程即可求解.【详解】依题意,sin (3α-β)=sin [(2α-β)+α]=sin (2α-β)cos α+cos (2α-β)sin α,sin (α-β)=sin [(2α-β)-α]=sin (2α-β)cos α-cos (2α-β)sin α,则sin (2α-β)cos α+cos (2α-β)sin α=m sin (2α-β)cos α-m cos (2α-β)sin α,即sin (2α-β)cos αcos (2α-β)sin α=m +1m -1,即tan (2α-β)tan α=m +1m -1=n .故选:D12(2024·辽宁沈阳·三模)已知tan α2=2,则sin 2α2+sin α的值是()A.25B.45C.65D.85【答案】D【分析】利用二倍角公式和同角之间的转化,进行求解判断选项【详解】当tan α2=2,则sin 2α2+sin α=sin 2α2+2sin α2cos α2sin 2α2+cos 2α2=tan 2α2+2tan α2tan 2α2+1=22+2×222+1=85故选:D13(2024·贵州黔东南·二模)已知0<α<β<π,且sin α+β =2cos α+β ,sin αsin β-3cos αcos β=0,则tan α-β =()A.-1 B.-32C.-12D.12【答案】C【分析】找出tan α和tan β的关系,求出tan α和tan β即可求解.【详解】∵sin αsin β-3cos αcos β=0,∴sin αsin β=3cos αcos β,∴tan αtan β=3①,∵sin α+β =2cos α+β ,∴tan α+β =2⇒tan α+tan β1-tan αtan β=2⇒tan α+tan β1-3=2,∴tan α+tan β=-4②,由①②解得tan α=-1tan β=-3或tan α=-3tan β=-1 ,∵0<α<β<π,∴tan α<tan β,∴tan α=-3tan β=-1 ,∴tan α-β =tan α-tan β1+tan αtan β=-12.故选:C .二、多选题14(2024·河北张家口·三模)已知函数f (x )=23cos 2x +2sin x cos x ,则下列说法正确的是()A.函数f (x )的一个周期为2πB.函数f (x )的图象关于点π3,0 对称C.将函数f (x )的图象向右平移φ(φ>0)个单位长度,得到函数g (x )的图象,若函数g (x )为偶函数,则φ的最小值为5π12D.若f 12α-5π24 -3=12,其中α为锐角,则sin α-cos α的值为6-308【答案】ACD【分析】利用三角恒等变换公式化简,由周期公式可判断A ;代入验证可判断B ;根据平移变化求g (x ),由奇偶性可求出φ,可判断C ;根据已知化简可得sin α-π12 =14,将目标式化为2sin α-π12 -π6 ,由和差角公式求解可判断D .【详解】对于A ,因为f (x )=31+cos2x +sin2x =2sin 2x +π3+3,所以f (x )的最小值周期T =2π2=π,所以2π是函数f (x )的一个周期,A 正确;对于B ,因为f π3 =2sin 2×π3+π3 +3=3,所以,点π3,0 不是函数f (x )的对称中心,B 错误;对于C ,由题知,g x =f (x -φ)=2sin 2(x -φ)+π3 +3=2sin 2x +π3-2φ +3,若函数g (x )为偶函数,则π3-2φ=π2+k π,k ∈Z ,得φ=-π12-k π2,k ∈Z ,因为φ>0,所以φ的最小值为5π12,C 正确;对于D ,若f 12α-5π24-3=2sin 212α-5π24 +π3 =2sin α-π12 =12,则sin α-π12 =14,因为α为锐角,-π12<α-π12<5π12,所以cos α-π12 =154,所以sin α-cos α=2sin α-π4 =2sin α-π12 -π6=232sin α-π12 -12cos α-π12=232×14-12×154=6-308,D 正确.故选:ACD 15(2024·辽宁鞍山·模拟预测)已知函数f x =sin x ⋅cos x ,则()A.f x 是奇函数B.f x 的最小正周期为2πC.f x 的最小值为-12D.f x 在0,π2上单调递增【答案】AC【分析】首先化简函数f x =12sin2x ,再根据函数的性质判断各选项.【详解】f x =sin x ⋅cos x =12sin2x ,函数的定义域为R ,对A ,f -x =-12sin2x =-f x ,所以函数f x 是奇函数,故A 正确;对B ,函数f x 的最小正周期为2π2=π,故B 错误;对C ,函数f x 的最小值为-12,故C 正确;对D ,x ∈0,π2 ,2x ∈0,π ,函数f x 不单调,f x 在0,π4 上单调递增,在π4,π2上单调递减,故D 错误.故选:AC16(2024·安徽·三模)已知函数f x =sin x -3cos x ,则()A.f x 是偶函数B.f x 的最小正周期是πC.f x 的值域为-3,2D.f x 在-π,-π2上单调递增【答案】AC【分析】对于A ,直接用偶函数的定义即可验证;对于B ,直接说明f 0 ≠f π 即可否定;对于C ,先证明-3≤f x ≤2,再说明对-3≤u ≤2总有f x =u 有解即可验证;对于D ,直接说明f -5π6>f -2π3 即可否定.【详解】对于A ,由于f x 的定义域为R ,且f -x =sin -x -3cos -x =-sin x -3cos x =sin x -3cos x =f x ,故f x 是偶函数,A 正确;对于B ,由于f 0 =sin0 -3cos0=-3,f π =sinπ -3cosπ=3,故f 0 ≠f π ,这说明π不是f x 的周期,B 错误;对于C ,由于f x =sin x -3cos x ≤sin x +3cos x =sin x +3cos x 2≤sin x +3cos x 2+3sin x -cos x 2=sin 2x +3cos 2x +23sin x cos x +3sin 2x +cos 2x -23sin x cos x =4sin 2x +4cos 2x =4=2,且f x =sin x -3cos x ≥-3cos x ≥-3,故-3≤f x ≤2.而对-3≤u ≤2,有f 0 =-3≤u ,f 5π6 =2≥u ,故由零点存在定理知一定存在x ∈0,5π6使得f x =u .所以f x 的值域为-3,2 ,C 正确;对于D ,由于-π<-5π6<-2π3<-π2,f -5π6 =2>3=f -2π3 ,故f x 在-π,-π2上并不是单调递增的,D 错误.故选:AC .17(2024·山西太原·模拟预测)已知函数f x =sin 2x +φ 0<φ<π2 的图象关于直线x =π12对称,且h x =sin2x -f x ,则()A.φ=π12B.h x 的图象关于点π6,0中心对称C.f x 与h x 的图象关于直线x =π4对称 D.h x 在区间π6,5π12内单调递增【答案】BCD【分析】根据正弦函数的对称性求解φ判断A ,先求出h x =sin 2x -π3,然后利用正弦函数的对称性求解判断B ,根据对称函数的性质判断C ,结合正弦函数的单调性代入验证判断D .【详解】由题意得2×π12+φ=π2+k π,k ∈Z ,解得φ=π3+k π,k ∈Z ,又因为0<φ<π2,所以φ=π3,A 错误;由φ=π3可知f x =sin 2x +π3,则h x =sin2x -sin 2x +π3 =12sin2x -32cos2x =sin 2x -π3,令2x -π3=k π,k ∈Z ,解得x =π6+k π2,k ∈Z ,令k =0,得x =π6,所以点π6,0 是曲线y =h x 的对称中心,B 正确;因为f π2-x =sin 2π2-x +π3 =sin 4π3-2x =sin 2x -π3=h x ,所以f x 与h x 的图象关于直线x =π4对称,C 正确;当x ∈π6,5π12 时,2x -π3∈0,π2 ,故h x 在区间π6,5π12内单调递增,D 正确.故选:BCD 18(2024·浙江金华·三模)已知函数f x =sin2ωx cos φ+cos2ωx sin φω>0,0<φ<π2的部分图象如图所示,则()A.φ=π6B.ω=2C.f x +π6为偶函数 D.f x 在区间0,π2的最小值为-12【答案】ACD【分析】先由正弦展开式,五点法结合图象求出f x =sin 2x +π6,可得A 正确,B 错误;由诱导公式可得C 正确;整体代入由正弦函数的值域可得D 正确.【详解】由题意得f x =sin 2ω+φ ,由图象可得f 0 =12⇒sin φ=12,又0<φ<π2,所以φ=π6,由五点法可得ω×4π3+π6=3π2⇒ω=1,所以f x =sin 2x +π6 .A :由以上解析可得φ=π6,故A 正确;B :由以上解析可得ω=1,故B 错误;C :f x +π6 =sin 2x +π6 +π6=cos2x ,故C 正确;D :当x ∈0,π2 ⇒2x +π6∈π6,7π6 时,sin 2x +π6 ∈-12,1,所以最小值为-12,故D 正确;故选:ACD .19(2024·浙江温州·二模)已知角α的顶点为坐标原点,始边与x 轴的非负半轴重合,P -3,4 为其终边上一点,若角β的终边与角2α的终边关于直线y =-x 对称,则()A.cos π+α =35B.β=2k π+π2+2αk ∈Z C.tan β=724D.角β的终边在第一象限【答案】ACD【分析】根据三角函数的定义,可求角α的三角函数,结合诱导公式判断A 的真假;利用二倍角公式,求出2α的三角函数值,结合三角函数的概念指出角2α的终边与单位圆的交点,由对称性确定角β终边与单位圆交点,从而判断BCD 的真假.【详解】因为角α的顶点为坐标原点,始边与x 轴的非负半轴重合,终边经过点P -3,4 ,所以:OP =5,所以sin α=45,cos α=-35,所以cos π+α =-cos α=35,故A 对;又sin2α=2sin α⋅cos α=2×45×-35 =-2425,cos2α=cos 2α-sin 2α=-35 2-45 2=-725,所以2α的终边与单位圆的交点坐标为:-725,-2425 ,因为角β的终边与角2α的终边关于直线y =-x 对称,所以角β的终边与单位圆的交点为2425,725,所以tan β=724,且β的终边在第一象限,故CD 正确;又因为终边在直线y =-x 的角为:k π-π4,k ∈Z ,角2α的终边与角β的终边关于y =-x 对称,所以2α+β2=k π-π4⇒β=2k π-π2-2αk ∈Z ,故B 错误.故选:ACD20(2024·广东佛山·二模)已知函数f x =sin x +cos2x 与g x =sin2x +cos x ,记h x =λf x +μg x ,其中λ,μ∈R 且λ2+μ2≠0.下列说法正确的是()A.h x 一定为周期函数B.若λ⋅μ>0,则h x 在0,π2上总有零点C.h x 可能为偶函数 D.h x 在区间0,2π 上的图象过3个定点【答案】ABD【分析】对于A :计算h x +2π ,化简即可;对于B :求出h x ,然后计算h 0 h π2的正负即可;对于C :计算h x ,h -x 是否恒相等即可;对于D :令f x =0g x =0,求解x 即可.【详解】对于A ,∀x ∈R ,h x +2π =λf x +2π +μg x +2π =λf x +μg x =h x ,A 正确;对于B ,h x =λcos x -2sin2x +μ2cos2x -sin x ,则h 0 =λ+2μ,h π2=-3μ,因为λμ>0,即λ,μ同号,所以h 0 h π2<0,由零点存在定理知h x 在0,π2上总有零点,故B 正确;对于C ,h x =λsin x +λcos2x +μsin2x +μcos x ,h -x =-λsin x +λcos2x -μsin2x +μcos x ,由h x =h -x 得2λsin x +2μsin2x =2λsin x +2μ⋅2sin x cos x =2sin x λ+2μcos x =0对x ∈R 恒成立,则λ=μ=0与题意不符,故C 错误;对于D ,令f x =0g x =0 ,则sin x +cos2x =1-2sin 2x +sin x =-sin x -1 2sin x +1 =0sin2x +cos x =cos x 2sin x +1 =0 ⇒sin x =1或sin x =-12cos x =0或sin x =-12,即x ∈-π6+2k π,π2+2k π,7π6+2k π ,k ∈Z ,故所有定点坐标为-π6+2k π,0 ,π2+2k π,0 ,7π6+2k π,0 ,k ∈Z ,又因为x ∈0,2π ,所以函数h x 的图象过定点π2,0 ,7π6,0 ,11π6,0 ,故D 正确;故选:ABD .21(2024·湖南·二模)已知函数f x =12cos 2x -π3 ,把y =f x 的图象向右平移π3个单位长度,得到函数y =g x 的图象,以下说法正确的是()A.x =π6是y =f x 图象的一条对称轴B.f x 的单调递减区间为k π+π6,k π+2π3k ∈Z C.y =g x 的图象关于原点对称D.f x +g x 的最大值为12【答案】ABD【分析】根据题意,求得g x =-12cos2x 的图象,结合三角函数的图象与性质,以及两角差的正弦公式,逐项判定,即可求解.【详解】将函数f x =12cos 2x -π3 的图象向右平移π3个单位长度,得到函数y =g x =12cos 2x -π =-12cos2x 的图象,对于A 中,令x =π6,求得f x =12,即为函数y =f x 最大值,所以直线x =π6是函数f x 图象的一条对称轴,所以A 正确;对于B 中,令2k π≤2x -π3≤2k π+π,k ∈Z ,解得k π+π6≤x ≤k π+2π3,k ∈Z ,可得f x 的单调减区间为k π+π6,k π+2π3,k ∈Z ,所以B 正确.对于C 中,由于g x =-12cos2x 是偶函数,可得函数g x 的图象关于y 轴对称,所以C 错误.对于D 中,由f x +g x =12cos 2x -π3 +-12cos2x =1212cos2x +32sin2x -12cos2x =34sin2x -14cos2x =12sin 2x -π6 ≤12,即f x +g x 的最大值为12,所以D 正确.故选:ABD .22(2024·广东江门·一模)已知函数f (x )=sin 2ωx +π3 +sin 2ωx -π3+23cos 2ωx -3(ω>0),则下列结论正确的是()A.若f x 相邻两条对称轴的距离为π2,则ω=2B.当ω=1,x ∈0,π2时,f x 的值域为-3,2 C.当ω=1时,f x 的图象向左平移π6个单位长度得到函数解析式为y =2cos 2x +π6D.若f x 在区间0,π6上有且仅有两个零点,则5≤ω<8【答案】BCD【分析】根据三角恒等变换化简f x =2sin 2ωx +π3,进而根据周期可判断A ,根据整体法求解函数的值域判断B ,根据函数图象的平移可判断C ,根据零点个数确定不等式满足的条件可判断D .【详解】f (x )=sin 2ωx +π3 +sin 2ωx -π3+23cos 2ωx -3=sin2ωx cos π3+cos2ωx sin π3+sin2ωx cos π3-cos2ωx sin π3+3cos2ωx=sin2ωx +3cos2ωx =2sin 2ωx +π3,对于A ,若f x 相邻两条对称轴的距离为π2,则T =2×π2=π=2π2ω,故ω=1,A 错误,对于B ,当ω=1,f x =2sin 2x +π3 ,当x ∈0,π2 时,2x +π3∈π3,4π3,则f x 的值域为-3,2 ,B 正确,对于C ,当ω=1,f x =2sin 2x +π3,f x 的图象向左平移π6个单位长度得到函数解析式为f x +π6 =2sin 2x +π6 +π3 =2sin 2x +2π3 =2cos 2x +π6,C 正确,对于D ,当x ∈0,π6 时,2ωx +π3∈π3,2ωπ6+π3,若f x 在区间0,π6 上有且仅有两个零点,则2π≤2ωπ6+π3<3π,解得5≤ω<8,故D 正确,故选:BCD 三、填空题23(2024·北京·三模)已知函数f (x )=sin x cos ωx ,x ∈R .①若ω=1,则f (x )的最小正周期是;,②若ω=2,则f (x )的值域是.【答案】π[-1,1]【分析】把ω=1代入,t 明智二倍角的正弦,结合正弦函数的周期求出f (x )的最小正周期;把ω=2代入,利用二倍角的余弦公式,借助换元法,利用导数求出f (x )的值域.【详解】当ω=1时,f (x )=sin x cos x =12sin2x ,函数f (x )的最小正周期为2π2=π;当ω=2时,f (x )=sin x cos2x =sin x (1-2sin 2x ),令sin x =t ∈[-1,1],g (t )=t (1-2t 2)=-2t 3+t ,求导得g (t )=-6t 2+1,当-1≤t <-66或66<t ≤1时,g (t )<0,当-66<t <66时,g (t )>0,函数g (t )在-1,-66 ,66,1 上单调递减,在-66,66上单调递增,g (-1)=1,g 66 =69,g (1)=-1,g -66 =-69,所以g (t )min =-1,g (t )max =1,f (x )的值域是[-1,1].故答案为:π;[-1,1]24(2024·北京·模拟预测)已知函数f (x )=sin ωx -2cos ωx (ω>0),且f α+x =f α-x .若两个不等的实数x 1,x 2满足f x 1 f x 2 =5且x 1-x 2 min =π,则sin4α=.【答案】-45/-0.8【分析】利用辅助角公式化简f (x )的解析式,再由题意可得函数关于x =α对称,且最小正周期T =π,即可求出ω的值,从而得到2α=φ+π2+k π,k ∈Z ,再由二倍角公式及同角三角函数的基本关系计算可得.【详解】因为f (x )=sin ωx -2cos ωx =5sin ωx -φ ,其中tan φ=2,由f α+x =f α-x ,可得f x 关于x =α对称,又两个不等的实数x 1,x 2满足f x 1 f x 2 =5且x 1-x 2 min =π,所以f x 的最小正周期T =π,又ω>0,所以2πω=π,解得ω=2,所以f x =5sin 2x -φ ,所以2α-φ=π2+k π,k ∈Z ,则2α=φ+π2+k π,k ∈Z ,所以sin4α=sin2φ+π2+k π =sin 2φ+π+2k π =-sin2φ=-2sin φcos φsin 2φ+cos 2φ=-2tan φtan 2φ+1=-2×222+1=-45.故答案为:-4525(2024·湖北荆州·三模)设0<α<β<π2,tan α=m tan β,cos α-β =35,若满足条件的α与β存在且唯一,则m =,tan αtan β=.【答案】191【分析】由tan α=m tan β得到sin αcos β=m cos αsin β,再结合cos α-β =35,利用sin α-β =-45,得到cos αsin β=-45m -1 ,sin αcos β=-4m5m -1 ,从而sin α+β =-4m +1 5m -1,再由满足条件的α与β存在且唯一,得到α+β唯一,从而sin α+β =-4m +15m -1=1,求得m 即可.【详解】解:由tan α=m tan β,得sin αcos α=m sin βcos β,即sin αcos β=m cos αsin β,因为0<α<β<π2,tan α=m tan β,所以-π2<α-β<0,0<m <1,又cos α-β =35,所以sin α-β <0,从而sin α-β =sin αcos β-cos αsin β=m -1 cos αsin β=-45,所以cos αsin β=-45m -1,所以sin αcos β=m cos αsin β=-4m5m -1,所以sin α+β =sin αcos β+cos αsin β=-4m +15m -1,因为α,β∈0,π2,所以α+β∈0,π ,因为满足条件的α与β存在且唯一,所以α+β唯一,所以sin α+β =-4m +1 5m -1=1,所以m =19,经检验符合题意,所以tan α=19tan β,则tan α-β =-43=tan α-tan β1+tan αtan β=tan α-9tan α1+9tan 2α,解得tan α=13,所以tan αtan β=9tan 2α=1.故答案为:19,1【点睛】关键点点睛:关键是结合已知得出sin α+β =-4m +15m -1 =1,求出m ,由此即可顺利得解.。
高中物理近5年高考全国卷真题分类汇编01 直线运动
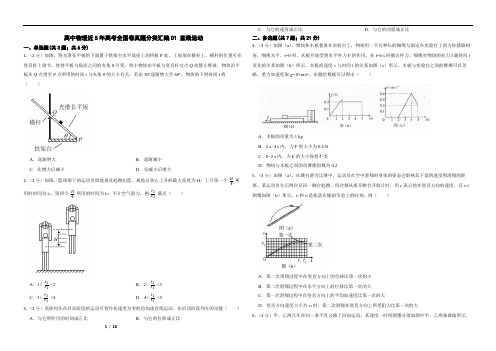
高中物理近5年高考全国卷真题分类汇编01 直线运动一、单选题(共3题;共6分)1.(2分)如图,将光滑长平板的下端置于铁架台水平底座上的挡板P处,上部架在横杆上。
横杆的位置可在竖直杆上调节,使得平板与底座之间的夹角θ可变。
将小物块由平板与竖直杆交点Q处静止释放,物块沿平板从Q点滑至P点所用的时间t与夹角θ的大小有关。
若由30°逐渐增大至60°,物块的下滑时间t将()A.逐渐增大B.逐渐减小C.先增大后减小D.先减小后增大2.(2分)如图,篮球架下的运动员原地垂直起跳扣篮,离地后重心上升的最大高度为H。
上升第一个H4所用的时间为t1,第四个H4所用的时间为t2。
不计空气阻力,则t2t1满足()A.1< t2t1<2B.2<t2t1<3C.3< t2t1<4D.4<t2t1<53.(2分)高铁列车在启动阶段的运动可看作初速度为零的均加速直线运动,在启动阶段列车的动能()A.与它所经历的时间成正比B.与它的位移成正比C.与它的速度成正比D.与它的动量成正比二、多选题(共7题;共21分)4.(3分)如图(a),物块和木板叠放在实验台上,物块用一不可伸长的细绳与固定在实验台上的力传感器相连,细绳水平。
t=0时,木板开始受到水平外力F的作用,在t=4 s时撤去外力。
细绳对物块的拉力f随时间t 变化的关系如图(b)所示,木板的速度v与时间t的关系如图(c)所示。
木板与实验台之间的摩擦可以忽略。
重力加速度取g=10 m/s2。
由题给数据可以得出()A.木板的质量为1 kgB.2 s~4 s内,力F的大小为0.4 NC.0~2 s内,力F的大小保持不变D.物块与木板之间的动摩擦因数为0.25.(3分)如图(a),在跳台滑雪比赛中,运动员在空中滑翔时身体的姿态会影响其下落的速度和滑翔的距离。
某运动员先后两次从同一跳台起跳,每次都从离开跳台开始计时,用v表示他在竖直方向的速度,其v-t 图像如图(b)所示,t1和t2是他落在倾斜雪道上的时刻。
2024全国高考真题数学汇编:集合

2024全国高考真题数学汇编集合一、单选题1.(2024全国高考真题)已知集合{}355,{3,1,0,2,3}A x x B =-<<=--∣,则A B = ()A .{1,0}-B .{2,3}C .{3,1,0}--D .{1,0,2}-2.(2024天津高考真题)集合{}1,2,3,4A =,{}2,3,4,5B =,则A B = ()A .{}1,2,3,4B .{}2,3,4C .{}2,4D .{}13.(2024全国高考真题)若集合{}1,2,3,4,5,9A =,{}1B x x A =+∈,则A B = ()A .{}1,3,4B .{}2,3,4C .{}1,2,3,4D .{}0,1,2,3,4,94.(2024北京高考真题)已知集合{|31}M x x =-<<,{|14}N x x =-≤<,则M N ⋃=()A .{}11x x -≤<B .{}3x x >-C .{}|34x x -<<D .{}4x x <5.(2024全国高考真题)已知集合{}{}1,2,3,4,5,9,A B A ==,则()A A B ⋂=ð()A .{}1,4,9B .{}3,4,9C .{}1,2,3D .{}2,3,5参考答案1.A【分析】化简集合A ,由交集的概念即可得解.【详解】因为{{}|,3,1,0,2,3A x x B =<=--,且注意到12<<,从而A B = {}1,0-.故选:A.2.B【分析】根据集合交集的概念直接求解即可.【详解】因为集合{}1,2,3,4A =,{}2,3,4,5B =,所以{}2,3,4A B = ,故选:B3.C【分析】根据集合B 的定义先算出具体含有的元素,然后根据交集的定义计算.【详解】依题意得,对于集合B 中的元素x ,满足11,2,3,4,5,9x +=,则x 可能的取值为0,1,2,3,4,8,即{0,1,2,3,4,8}B =,于是{1,2,3,4}A B ⋂=.故选:C4.C【分析】直接根据并集含义即可得到答案.【详解】由题意得{}|34M x x N ⋃=-<<.故选:C.5.D【分析】由集合B 的定义求出B ,结合交集与补集运算即可求解.【详解】因为{}{}1,2,3,4,5,9,A B A ==,所以{}1,4,9,16,25,81B =,则{}1,4,9A B = ,(){}2,3,5A A B = ð故选:D。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3-5高考真题汇编(光电效应、原子物理、原子核物理)1.【(单选),2019·新课标Ⅰ卷T14,6分】氢原子能级示意图如图所示.光子能量在1.63eV ~3.10eV 的光为可见光,要使处于基态(n=1)的氢原子被激发后可辐射出可见光光子,最少应给氢原子提供的能量为( ) A.12.09eV B.10.20eV C.1.89eV D.1.51eV 答案:A解析:氢原子从高能级向基态跃迁时,所辐射光子能量为:E=﹣3.40eV-(﹣13.6eV)=10.2eV >3.10eV ,故可知要产生可见光,氢原子吸收能量后,最起码要跃迁到n >2能级;由于E ´=E 3﹣E 2=﹣1.51eV ﹣(﹣3.40eV)=1.89eV ,则有1.63eV <E ´<3.10eV ,可知要使处于基态(n=1)的氢原子被激发后可辐射出可见光光子;氢原子最起码应该跃迁到n =3能级,则氢原子吸收的最小能为:E m =E 3﹣E 1=﹣1.51eV ﹣(﹣13.6eV)=12.09eV ,A 正确,BCD 错误.2.【(单选),2019·新课标Ⅱ卷T15,6分】太阳内部核反应的主要模式之一是质子﹣质子循环,循环的结果可表示为411H →42He+201e+2υ,已知11H 和42He 的质量分别为m p =1.0078u 和m α=4.0026u ,1u =931MeV/C 2,C 为光速.在4个11H 转变成1个42He 的过程中,释放的能量约为( ) A .8MeV B .16MeV C .26MeV D .52MeV 答案:C解析:反应过程中的质量亏损约为△m =4m p ﹣m α=4×1.0078u ﹣4.0026u =0.0286u ,由于1u =931MeV/c 2,由爱因斯坦质能方程有△E =△mc 2=26MeV ,C 正确,ABD 错误.3.(多选) (2019·海南卷T7,5分)对于钠和钙两种金属,其遏止电压U c 与入射光频率v 的关系如图所示,用h 、e 分别表示普朗克常量和电子电荷量,则()A.钠的逸出功小于钙的逸出功B.图中直线的斜率为heC.在得到这两条直线时,必须保证入射光的光强相同D.若这两种金属产生的光电子具有相同的最大初动能,则照射到钠的光频率较高 答案:AB解析:由爱因斯坦光电效应方程有h υ=E km +W 及-eU c =0-E km ,可得U c =h υe -We ,由图线可知,图中直线的斜率为h e ,B 正确;纵轴的截距b=We ,钙的逸出功大于钠的逸出功,A 正确;由图可知钙的极限频率大于钠的,即钙的逸出功大于钠,再由h υ=E km +W 可知,E km 相同,W 钙>W 钠,则υ钙>υ钠,D 错误;两条直线的斜率相同,只能说明频率相同,无法知道入射光的强度大小,C 错误.4.【(单选) 2019·北京卷T14,6分】利用图1所示的装置(示意图),观察光的干涉、衍射现象,在光屏上得到如图2中甲和乙两种图样.下列关于P 处放置的光学元件说法正确的是 A.甲对应单缝,乙对应双缝 B.甲对应双缝,乙对应单缝 C.都是单缝,甲对应的缝宽较大D.都是双缝,甲对应的双缝间距较大 答案:A解析:单缝衍射图样为中央亮条纹最宽最亮,往两边变窄,双缝干涉图样是明暗相间的条纹,条纹间距相等,条纹宽度相等,结合图甲、乙可知,甲对应单缝,乙对应双缝,A 正确,BCD 错误.5.【(单选) 2019·北京卷T19,6分】光电管是一种利用光照射产生电流的装置,当入射光照在管中金属板上时,可能形成光电流,表中给出了6次实验的结果.由表中数据得出的论断中不正确的是 A.两组实验采用了不同频率的入射光 B.两组实验所用的金属板材质不同C.若入射光子的能量为5.0 eV ,逸出光电子的最大动能为1.9 eVD.若入射光子的能量为5.0 eV ,相对光强越强,光电流越大 答案:B解析:由题表格中数据可知,两组实验所用的入射光的能量不同,由公式E=h υ可知,两组实验中所用的入射光的频率不同,A 正确;由爱因斯坦质能方程E k =h υ-W 0可得:第一组实验:0.9=4.0-W 01,第二组实验:2.9=6.0- W 02,解得W 02=W 02=3.1eV ,即两种材料的逸出功相同也即材料相同,B 错误;由爱因斯坦质能方程E k =h υ-W 0可得E k =(5.0-3.1)eV=1.9eV ,C 正确; 由题表格中数据可知,入射光能量相同时,相对光越强,光电流越大,D 正确. 6.【(单选) 2019·北京卷T20,6分】国际单位制(缩写SI )定义了米(m )、秒(s )等7个基本单位,其他单位均可由物理关系导出,例如,由m 和s 可以导出速度单位m/s.历史上,曾用“米原器”定义米,用平均太阳日定义秒.但是,以实物或其运动来定义基本单位会受到环境和测量方式等因素的影响,而采用物理常量来定义则可避免这种困扰.1967年用铯–133原子基态的两个超精细能级间跃迁辐射的频率∆ν=9 192 631 770 Hz 定义s ;1983年用真空中的光速c=299 792 458m/s 定义m.2018年第26届国际计量大会决定,7个基本单位全部用基本物理常量来定义(对应关系如图,例如,s 对应∆ν,m 对应c ).新SI 自2019年5月20日(国际计量日)正式实施,这将对科学和技术发展产生深远影响,下列选项不正确的是A. 7个基本单位全部用物理常量定义,保证了基本单位的稳定性B. 用真空中的光速c (m/s )定义m ,因为长度L 与速度v 存在L=vt ,而s 已定义C. 用基本电荷e (C )定义安培(A ),因为电荷量与电流I 存在I=qt ,而s 已定义D. 因为普朗克常量h (J·s)的单位中没有kg ,所以无法用它来定义质量单位 答案:D解析:由题意可知,如果以实物或其运动来定义基本单位会受到环境和测量方式等因素的影响,所以7个基本单位全部用物理常量定义,保证了基本单位的稳定性,A 正确;用真空中的光速定义m ,即光在真空中传播299792458分之一秒的距离,且s 早已定义,B 正确;由公式I=qt 可知,安培即为1s 时间内通过的电荷量,C 正确;由题意可知,h 对应的单位为J·s,而能量的单位单位中包含质量,故可以对Kg 进行定义,D 错误. 7.【2019·江苏卷T12,12分】(1)质量为M 的小孩站在质量为m 的滑板上,小孩和滑板均处于静止状态,忽略滑板与地面间的摩擦.小孩沿水平方向跃离滑板,离开滑板时的速度大小为v ,此时滑板的速度大小为A. m M vB.M mv C.m M+m v D. MM+mv 答案:B解析:忽略滑板与地面间的摩擦,小孩和滑板系统动量守恒,取小孩跃起的方向为正,根据动量守恒定律得0=Mv-mv ´,解得滑板的速度为v ´=Mm v ,B 正确,ACD 错误.(2)100年前,卢瑟福用α粒子轰击氮核打出了质子,后来人们用α粒子轰击6028Ni 核也打出了质子42He+6028Ni →6229Cu+11H +X ;该反应中的X 是______(选填“电子”“正电子”或“中子”).此后,对原子核反应的持续研究为核能利用提供了可能.目前人类获得核能的主要方式是_______(选填“核衰变”“核裂变”或“核聚变”).答案:(1)中子(2)核裂变解析:由质量数守恒和电荷数守恒,可知4+60=62+1+A ,2+28=29+1+Z ,解得A=1,Z=0即X是中子10n ;目前人类获得核能的主要方式是核裂变,我们可以通过链式反应,反应条件比较简单,反应速度比较容易控制;核衰变不能人为控制,是自然衰变的;而核聚变反应条件苛刻,而且反应速度比较难以控制.(3)在“焊接”视网膜的眼科手术中,所用激光的波长λ=6.4×10-7m ,每个激光脉冲的能量E=1.5×10-2J .求每个脉冲中的光子数目.(已知普朗克常量h=6.63×l0-34J·s,光速C =3×108m/s .计算结果保留一位有效数字) 答案:5×1016解析:光子的能量为ɛ=h C λ=6.63×10−34×3×1086.4×10-7J=3.1×10-19J.每个脉冲中的光子数目为N=E ɛ=1.5×10-23.1×10-19≈5×1016个 8.【(多选),2019·浙江4月份选考卷T14,2分】【加试题】波长为λ1和λ2的两束可见光入射到双缝,在光屏上观察到干涉条纹,其中波长为λ1的光的条纹间距大于波长为λ2的条纹间距.则(下列表述中,脚标“1”和“2”分别代表波长为λ1和λ2的光所对应的物理量)A. 这两束光的光子的动量P 1>P 2B. 这两束光从玻璃射向真空时,其临界角C 1>C 2C. 这两束光都能使某种金属发生光电效应,则遏止电压U 1>U 2D. 这两束光由氢原子从不同激发态跃迁到n=2能级时产生,则相应激发态的电离能△E 1>△E 2答案:BD解析:由光子的动量P=h λ,则P 1<P 2,A 错误;由υ=Cλ可知两种光子的频率关系为υ1<υ2,即2的频率较大,根据介质的折射率与频率的关系可知它们的折射率n 1<n 2,由临界角与折射率的关系sinC=1n,则这两束光从玻璃射向真空时,其临界角C1>C2,B正确;这两束光都能使某种金属发生光电效应,由光电效应方程E km=hυ-W,其中W为金属的逸出功,可知频率越大的光对应的光电子的最大初动能越大;又由E km=e•U遏止则频率越大,遏止电压越大,所以遏止电压U2>U1,C错误;根据玻尔理论,当发生跃迁时辐射出的光子的能量:E=E m-E n;都是跃迁到n=2能级,则n相同,m越大,则放射出的光子的能量值越大,由于λ1>λ2,则υ1<υ2,所以E1<E2,E m1<E m2,即2的能级更大,结合氢原子电离时需要的能量为能级对应能量值的负值可知,相应激发态的电离能△E1>△E2,D正确.9.【(多选),2019·浙江4月份选考卷T15,2分】【加试题】静止在匀强磁场中的原子核X 发生α衰变后变成新原子核Y,已知核X的质量数为A,电荷数为Z,核X、核Y和α粒子的质量分别为m X、m Y和mα,α粒子在磁场中运动的半径为R,则A.衰变方程可表示为A Z X→A-4Z-2Y+42HeB.核Y的结合能为(m x-m Y-mα)C2C.核Y在磁场中运动的半径为2RZ-2 D.核Y的动能为E kY=m Y(m X-m Y-mα)C2m Y+mα答案:AC解析:根据电荷数守恒和质量数守恒,核衰变反应方程为A Z X→A-4Z-2Y+42He,A正确;该过程中亏损的质量为△m=(m x-m Y-mα),所以释放的核能为(m x-m Y-mα)C2,由于原子核也有一定的结合能,则核Y的结合能一定大于(m x-m Y-mα)C2,B错误;在衰变过程中遵守动量守恒,根据动量守恒定律得0=P Y-Pα,则P Y=Pα,根据半径公式r=mvqB,又mv=P(动量),则得r=PqB联立可得R Y=2RZ-2,C正确;由动能与动量的关系E k=P22m,得原子核Y与α粒子的动能之比为E KYE Kα=mαm Y=4A-4,由题原子核X衰变时释放的核能全部转化为动能,则有释放的核能为E=E kα+E kY=(m x-m Y-mα)C2,联立可得E kY=mα(m x-m Y-mα)C2m Y+mα,D错误.10.【(多选) 2019·天津卷T6,6分】我国核聚变反应研究大科学装置“人造太阳”2018年获得重大突破,等离子体中心电子温度首次达到1亿度,为人类开发利用核聚变能源奠定了重要的技术基础.下列关于聚变的说法正确的是()A.核聚变比核裂变更为安全、清洁B.任何两个原子核都可以发生聚变C.两个轻核结合成质量较大的核,总质量较聚变前增加D.两个轻核结合成质量较大的核,核子的比结合能增加答案:AD解析:核聚变的最终产物时氦气无污染,与裂变相比轻核聚变辐射极少,废物容易处理,更为安全、清洁,A正确;自然界中最容易实现的聚变反应是氢的同位素,氘与氚的聚变,大核不能发生核聚变,不是任意的原子核就能发生核聚变,B错误;两个轻核结合成质量较大的核,平均质量减小,则总质量较聚变前减小,出现质量亏损,结合时放出能量,C错误;两个轻核结合成质量较大的核,聚变反应放出能量,总的结合能增加,因此反应前的比结合能小于反应后的比结合能, D正确.3-5高考真题汇编(光电效应、原子物理、原子核物理)1.【(单选),2019·新课标Ⅰ卷T14,6分】氢原子能级示意图如图所示.光子能量在1.63eV ~3.10eV 的光为可见光,要使处于基态(n=1)的氢原子被激发后可辐射出可见光光子,最少应给氢原子提供的能量为( ) A.12.09eV B.10.20eV C.1.89eV D.1.51eV2.【(单选),2019·新课标Ⅱ卷T15,6分】太阳内部核反应的主要模式之一是质子﹣质子循环,循环的结果可表示为411H →42He+201e+2υ,已知11H 和42He 的质量分别为m p =1.0078u 和m α=4.0026u ,1u =931MeV/C 2,C 为光速.在4个11H 转变成1个42He 的过程中,释放的能量约为( ) A .8MeV B .16MeV C .26MeV D .52MeV3.(多选) (2019·海南卷T7,5分)对于钠和钙两种金属,其遏止电压U c 与入射光频率v 的关系如图所示,用h 、e 分别表示普朗克常量和电子电荷量,则() A.钠的逸出功小于钙的逸出功 B.图中直线的斜率为h eC.在得到这两条直线时,必须保证入射光的光强相同D.若这两种金属产生的光电子具有相同的最大初动能,则照射到钠的光频率较高4.【(单选) 2019·北京卷T14,6分】利用图1所示的装置(示意图),观察光的干涉、衍射现象,在光屏上得到如图2中甲和乙两种图样.下列关于P 处放置的光学元件说法正确的是 A.甲对应单缝,乙对应双缝 B.甲对应双缝,乙对应单缝 C.都是单缝,甲对应的缝宽较大D.都是双缝,甲对应的双缝间距较大5.【(单选) 2019·北京卷T19,6分】光电管是一种利用光照射产生电流的装置,当入射光照由表中数据得出的论断中不正确的是A.两组实验采用了不同频率的入射光B.两组实验所用的金属板材质不同C.若入射光子的能量为5.0 eV ,逸出光电子的最大动能为1.9 eVD.若入射光子的能量为5.0 eV ,相对光强越强,光电流越大6.【(单选) 2019·北京卷T20,6分】国际单位制(缩写SI )定义了米(m )、秒(s )等7个基本单位,其他单位均可由物理关系导出,例如,由m 和s 可以导出速度单位m/s.历史上,曾用“米原器”定义米,用平均太阳日定义秒.但是,以实物或其运动来定义基本单位会受到环境和测量方式等因素的影响,而采用物理常量来定义则可避免这种困扰.1967年用铯–133原子基态的两个超精细能级间跃迁辐射的频率∆ν=9 192 631 770 Hz 定义s ;1983年用真空中的光速c=299 792 458m/s 定义m.2018年第26届国际计量大会决定,7个基本单位全部用基本物理常量来定义(对应关系如图,例如,s 对应∆ν,m 对应c ).新SI 自2019年5月20日(国际计量日)正式实施,这将对科学和技术发展产生深远影响,下列选项不正确的是A. 7个基本单位全部用物理常量定义,保证了基本单位的稳定性B. 用真空中的光速c (m/s )定义m ,因为长度L 与速度v 存在L=vt ,而s 已定义C. 用基本电荷e (C )定义安培(A ),因为电荷量与电流I 存在I=qt ,而s 已定义D. 因为普朗克常量h (J·s)的单位中没有kg ,所以无法用它来定义质量单位 7.【2019·江苏卷T12,12分】(1)质量为M 的小孩站在质量为m 的滑板上,小孩和滑板均处于静止状态,忽略滑板与地面间的摩擦.小孩沿水平方向跃离滑板,离开滑板时的速度大小为v ,此时滑板的速度大小为A. m M vB.M mv C.m M+m v D. MM+mv (2)100年前,卢瑟福用α粒子轰击氮核打出了质子,后来人们用α粒子轰击6028Ni 核也打出了质子42He+6028Ni →6229Cu+11H +X ;该反应中的X 是______(选填“电子”“正电子”或“中子”).此后,对原子核反应的持续研究为核能利用提供了可能.目前人类获得核能的主要方式是_______(选填“核衰变”“核裂变”或“核聚变”).(3)在“焊接”视网膜的眼科手术中,所用激光的波长λ=6.4×10-7m ,每个激光脉冲的能量E=1.5×10-2J .求每个脉冲中的光子数目.(已知普朗克常量h=6.63×l0-34J·s,光速C =3×108m/s .计算结果保留一位有效数字)8.【(多选),2019·浙江4月份选考卷T14,2分】【加试题】波长为λ1和λ2的两束可见光入射到双缝,在光屏上观察到干涉条纹,其中波长为λ1的光的条纹间距大于波长为λ2的条纹间距.则(下列表述中,脚标“1”和“2”分别代表波长为λ1和λ2的光所对应的物理量)A. 这两束光的光子的动量P 1>P 2B. 这两束光从玻璃射向真空时,其临界角C 1>C 2C. 这两束光都能使某种金属发生光电效应,则遏止电压U 1>U 2D. 这两束光由氢原子从不同激发态跃迁到n=2能级时产生,则相应激发态的电离能△E 1> 9.【(多选),2019·浙江4月份选考卷T15,2分】【加试题】静止在匀强磁场中的原子核X 发生α衰变后变成新原子核Y ,已知核X 的质量数为A ,电荷数为Z ,核X 、核Y 和α粒子的质量分别为m X 、m Y 和m α,α粒子在磁场中运动的半径为R ,则A.衰变方程可表示为A Z X →A-4Z-2Y+42HeB.核Y 的结合能为(m x -m Y -m α)C 2C.核Y 在磁场中运动的半径为2R Z-2D.核Y 的动能为E kY =m Y (m X -m Y -m α)C 2m Y +m α10.【(多选) 2019·天津卷T6,6分】我国核聚变反应研究大科学装置“人造太阳”2018年获得重大突破,等离子体中心电子温度首次达到1亿度,为人类开发利用核聚变能源奠定了重要的技术基础.下列关于聚变的说法正确的是( )A.核聚变比核裂变更为安全、清洁B.任何两个原子核都可以发生聚变C.两个轻核结合成质量较大的核,总质量较聚变前增加D.两个轻核结合成质量较大的核,核子的比结合能增加。
