电路各章重点题型解答 第二章
《电路与模拟电子技术》第二版第二章习题解答
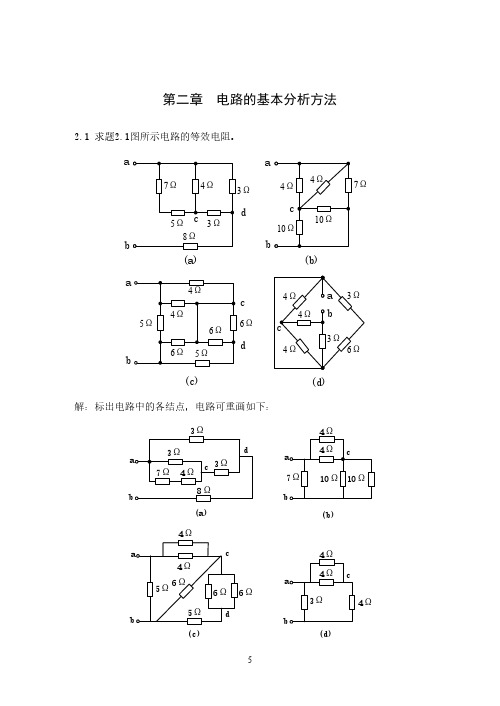
第二章电路的基本分析方法2.1 求题2.1图所示电路的等效电阻。
解：标出电路中的各结点，电路可重画如下：(b)(a)(c)(d)6Ω7Ω3Ωa aabbbddcb(a)(d)(c)(b)6Ωb4Ω（a ）图 R ab =8+3||[3+4||（7+5）]=8+3||（3+3）=8+2=10Ω（b ）图 R ab =7||(4||4+10||10)=7||7=3.5Ω（c ）图 R ab =5||[4||4+6||(6||6+5)]=5||(2+6||8)=5||(2+3.43)=2.6Ω（d ）图 R ab =3||(4||4+4)=3||6=2Ω（串联的3Ω与6Ω电阻被导线短路）2.2 用电阻的丫-△的等效变换求题2.2图所示电路的等效电阻。
解：为方便求解，将a 图中3个6Ω电阻和b 图中3个2Ω电阻进行等效变换，3个三角形连接的6Ω电阻与3个星形连接的2Ω电阻之间可进行等效变换，变换后电路如图所示。
（a ）R ab =2+(2+3)||(2+3)=4.5Ω（b ） R ab =6||(3||6+3||6)=6||4=2.4Ω2.3 将题2.3图所示电路化成等效电流源电路。
baba(b)(a)题2.2图(b)(a)题2.3图b abΩ(b)解：（a ）两电源相串联，先将电流源变换成电压源，再将两串联的电压源变换成一个电压源，最后再变换成电流源；等效电路为（b ）图中与12V 恒压源并联的6Ω电阻可除去（断开），与5A 恒流源串联的9V 电压源亦可除去（短接）。
两电源相并联，先将电压源变换成电流源，再将两并联的电流源变换成一个电流源，等效电路如下：2.4 将题2.4图所示电路化成等效电压源电路。
解：（a ）与10V 电压源并联的8Ω电阻除去（断开），将电流源变换成电压源，再将两串联的电压源变换成一个电压源，再变换成电流源，最后变换成电压源，等效电路如下：（b ）图中与12V 恒压源并联的6Ω电阻可除去（断开），与2A 恒流源串联的4Ω亦可(a)(b)题2.4图aa bababababbbb b除去（短接），等效电路如下：2.5 用电源等效变换的方法，求题2.5图中的电流I 。
《电路原理导论》第二章习题解答
习题二2-1图2-1所示为万用表的直流毫安档，表头内阻R p =650Ω，满量程电流为50μA 。
欲把它的量程扩大到1/10/100mA ，试计算分流电阻R 1、 R 2 、R 3。
答：Ω=3421.01R Ω=0789.32R Ω=7895.303R解： pd dp R R R II +=分流比 dp dpd pR R R R R I I n +=+==1p d R n R 11-=各档分流比1．2005.01= ； 2. 20005.010= ； 3. 200005.0100= ∴〔1〕 d p R R n R R R ∑=Ω==-=-=++2105.34650191650120111321 ()2132105.34R R R +-Ω=〔2〕 ()3321005025126.026633.36501200111R R R n R R p+=+-='-=+ ()33213005025126.094417.30005025126.026633.32105.34R R R R R R d -=--=+-=∑Ω==78945.30005025126.194417.303R〔3〕42105.378945.302105.34321=-=-=+∑R R R R d()()2323211050025.0340565.065078945.30199911999111R R R R R R n R P p-⨯+=++=++=''-= ()2321050025.0340565.042105.3R R ⨯⨯+-=-图2-1 习题2-1题图图2-1 习题2-1题图Ω==-=078945.300050025.10805.300050025.1340565.042105.32RΩ=-=3421.0078945.342105.31R验： 05.02105.6842105.3416502105.342105.34==⨯+=p I05.02105.6842105.34106502105.3442105.3==⨯+=p I05.02105.6842105.341006502105.34342105.0==⨯+=p I2-2把上题所用表头做成电压表，量程为1/10/100V ，内阻指标为20K Ω/V ，试求分压电阻R 1 、R 2 、R 3。
电路第二章习题详解
P (4) 2 8W
6 . 求一端口网络的输入电阻RabA. 3ΩB. 4ΩC.7Ω
D. 10Ω
7. 求一端口网络的等效电阻。 i0
us +
+
含受控源， “外加电源”法 由定义式求取
u0
_
A. 1Ω
B. 3Ω
C. 4Ω
D. 5Ω
i0 i 2i
3i0 2i u0 0
i0 u0
习题
1、求图所示电路中电流值I ； 若电流源为10A，则I 又为多少？
+ 15V _
5A
I 5Ω
I 3A
2、求等效电阻Rab。
10Ω 10Ω a 10Ω 10Ω b b R a
R
R
R
R R
R
3、电路如图所示，求： 1) 电流I2 ； 2) 10V电压源的功率。 R1
I 2 2.5A
B. -2V
C. 2V
D.-12V
2 5 2 U ab 0
4. 一端口的短路电流Iab 。
Iab
A. 1A B. -1A
I ab 5 5
C. -5A
D. 5A
2
5. 求2A电流源发出的功率
+
D. 16W
A. 4W
B. -4W
C. -8W
3 2 10 u 0
u 4V
3I I a +
U _ b
Rab
2 3
书中的一道题： 求一端口的等效电阻Rab。
此处u1为开路电压
N
业精于勤，荒于嬉；
行成于思，毁于随。 ——韩愈
第2章习题
1. 求电路中电压U 。
电路(第版)第二章习题答案
–
b 图（2）
Uab 4 Rab 4 5 20V
【2-13】图示电路中R1 =R3= R4 ，R2=2 R1， uc=4R1i1 ，利用电源的等效变换求电压 u10 。
【解】 在图（2）中：
ic
uc R2
4i1 R1 2 R1
2i1
R R2 /（ / R3 R4） R1
i1 R1 ① R3
+
+
uS
–
u10
–
R2
+
uc
–
R4
0
图（1）
u10 3i1R1
i1 R1 ① 3i1
uS i1R1 3i1R1 4i1R1
所以：
u10
3 4
uS
0.75uS
+
+ ic
uS
–
u10
–
0
R
图（2）
由电压源变换为电流源：
i 1
us
u
R
转换
u /R s
i
Ru
1'
由电流源变换为电压源：
Rab= (R1+ R3) ∥(R2+R4)
3 1.5
2
a
R1
R2
S
R3
b
R5
R4
（c）
桥形连接
惠斯通电桥
R1
I5
R3
R5
若： R1R4 = R2R3 则： I5 = 0
R2
R4
RS +
U_ S
电桥平衡
所以： 可将 R5 开路或短路。
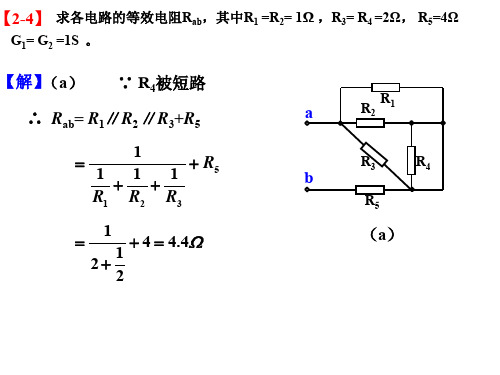
【2-4】 求各电路的等效电阻Rab，其中R1 =R2= 1Ω ，R3= R4 =2Ω， R5=4Ω
电路分析答案解析第二章
电路分析答案解析第二章第二章习题2.1 如题2.1割集与基本回路。
(a) 树一1T 如图所示。
基本割集为：c1{1,2,4}, c2{1,3,7}, c3{1,3,6,8}, c4{1,3,6,5,4} 基本回路为：l1{5,6,8}, l2{2,4,5}, l3{3,5,8,7}, l4{1,2,5,8,7}(b) 树二2T 如图所示。
基本割集为：c1{4,5,8}, c2{5,7,8}, c3{1,3,7}, c4{4,2,3,7} 基本回路为：l1{2,4,5}, l2{5,6,8}, l3{1,2,3}, l4{1,2,6,7}2.2 题2.2图示电路，求支路电流1I 、2I 、I 解：列两个KVL 回路方程：051)54211=-+++I I I （021)510212=-+++I II （整理为： 45921=+I I 115521=+I I 解得：A I 5.01= A I 1.02-= 而 A I I I 4.0)213-=+-=（2.3 如题2.3图所示电路，已知电流A I 21=解：可列KVL 回路方程： 2I+2+(i-3)R=3已知 i=2A ，代入上式可得：R=3Ω2.4 如题2.4方程求解电流i。
解：10(i-6)+5(0.4i+i)+13i=0解得：i=2A2.5 如题2.5图所示电路，试选一种树，确定基本割集，仅用一个基本割集方程求解电压u程求电压u。
解：①② 选3为参考节点，列方程如下： 52018120124-=-+u u ）（已知V u 122-=，代入上式，有： 52012812014-=++u ）（解得节点点位： V u 324-=又可知 0124=++u u 得： V u u 201232124=-=--=2.6 如题2.6图所示电路，已知电流A i 21=电压源S u 。
解：列三个网孔方程28)6=-+B A Ri i R （①33)43(-=-+++-C B A i i R Ri ②S C B u i i -=++3)323-（③ 可知： 12==i i B 21==-i i i B A 可得： 32=+=B Ai i由①式可得：283)6=-+R R （解得：Ω=5R 由②式有：33)57(35-=-++?-C i 解得： 0=C i 由③式有： S u -=33- 解得： V u S 6= 根据KVL 有： V i u bc 7432-=--=2.7 如题2.7解该电路的网孔方程。
电工电子第二章试题及答案
电工电子第二章试题及答案一、选择题1.电流的单位是（）A.伏特B.欧姆C.安培D.瓦特答案：C2.简单电路中，电流的方向是（）A.电子流动的方向B.阳极到阴极的方向C.阴极到阳极的方向D.无法确定的方向答案：C3.伏特表的作用是（）A.测量电流B.测量电阻C.测量电压D.测量功率答案：C4.电流的大小受到（）的影响。
A.单位时间内通过导体的电荷数B.导体的长度C.导体的截面积D.导体的材料答案：A5.电阻的单位是（）A.安培B.瓦特C.欧姆D.伏特答案：C二、填空题1.在串联电路中，总电阻等于各个电阻的（）之和。
答案：电阻2.在并联电路中，总电阻等于各个电阻的（）之倒数再取倒数。
答案：电阻3.如果电源电压为12伏特，电路中的总电阻为3欧姆，根据欧姆定律可求出电路中的电流为（）安培。
答案：44.如果电路中的电阻为10欧姆，电路中通过的电流为5安培，根据欧姆定律可求出电路中的电压为（）伏特。
答案：505.根据欧姆定律，电阻与电流成（）关系。
答案：反比三、解答题1.请解释什么是欧姆定律，并列举几个符合欧姆定律的电路现象。
答：欧姆定律是指在一定温度下，电流通过的导体两端的电压与导体两端的电阻成正比关系。
符合欧姆定律的电路现象包括：串联电路中，电流通过的各个电阻之和等于总电压；并联电路中，不同电阻上的电压相等；恒流源电路中，电流经过电阻时，电压与电阻成正比。
2.请简述串联电路和并联电路的区别。
答：串联电路是指电子元件按照一条路径连接起来，电流在元件之间只有一条通路。
并联电路是指电子元件按照多条路径连接起来，电流可以通过不同的路径流过不同的元件。
3.一根电阻为5欧姆的导线接在电源上，通过导线的电流为2安培。
求导线两端的电压。
答：根据欧姆定律，电压等于电阻乘以电流。
所以，导线两端的电压等于5欧姆乘以2安培，即10伏特。
4.某电路中，两个电阻分别为8欧姆和12欧姆，电源电压为20伏特。
请计算电路中的总电阻和电流。
电工技术第二章 电路的分析方法习题解答
第二章电路的分析方法本章以电阻电路为例，依据电路的基本定律，主要讨论了支路电流法、弥尔曼定理等电路的分析方法以及线性电路的两个基本定理：叠加定理和戴维宁定理。
1．线性电路的基本分析方法包括支路电流法和结点电压法等。
（1）支路电流法：以支路电流为未知量，根据基尔霍夫电流定律（KCL）和电压定律(KVL)列出所需的方程组，从中求解各支路电流，进而求解各元件的电压及功率。
适用于支路较少的电路计算。
（2）结点电压法：在电路中任选一个结点作参考结点，其它结点与参考结点之间的电压称为结点电压。
以结点电压作为未知量，列写结点电压的方程，求解结点电压，然后用欧姆定理求出支路电流。
本章只讨论电路中仅有两个结点的情况，此时的结点电压法称为弥尔曼定理。
2 ．线性电路的基本定理包括叠加定理、戴维宁定理与诺顿定理，是分析线性电路的重要定理，也适用于交流电路。
（1）叠加定理：在由多个电源共同作用的线性电路中，任一支路电压（或电流）等于各个电源分别单独作用时在该支路上产生的电压（或电流）的叠加（代数和）。
①“除源”方法（a）电压源不作用：电压源短路即可。
（b）电流源不作用：电流源开路即可。
②叠加定理只适用于电压、电流的叠加，对功率不满足。
（2）等效电源定理包括戴维宁定理和诺顿定理。
它们将一个复杂的线性有源二端网络等效为一个电压源形式或电流源形式的简单电路。
在分析复杂电路某一支路时有重要意义。
①戴维宁定理：任何一个线性含源的二端网络，对外电路来说，可以用一个理想电压源和一个电阻的串联组合来等效代替，其中理想电压源的电压等于含源二端网络的开路电压，电阻等于该二端网络中全部独立电源置零以后的等效电阻。
②诺顿定理：任何一个线性含源的二端网络，对外电路来说，可以用一个理想电流源和一个电阻的并联组合来等效代替。
此理想电流源的电流等于含源二端网络的短路电流，电阻等于该二端网络中全部独立电源置零以后的等效电阻。
3 ．含受控源电路的分析对含有受控源的电路，根据受控源的特点，选择相应的电路的分析方法进行分析。
电工学-第二章习题答案
第二章 电路的分析方法2.1.1 在图2.01的电路中，V 6=E ，Ω=61R ，Ω=32R ，Ω=43R ，Ω=34R ，Ω=15R 。
试求3I 和4I 。
4I ↓图2.01解：图2.01电路可依次等效为图（a ）和图（b ）。
R 3R 1R(b)Ω=+×=+×=23636414114R R R R R Ω=+++×=+++×=2243)24(3)(14321432R R R R R R R A 22165=+=+=R R E IA 322363)(214323=×+=++=I R R R R IA 943263631414−=×+−=+−=I R R R I2.3.3 计算图2.12中的电流3I 。
Ω=1R A2S =图2.12解：根据电压源与电流源的等效变换，图2.12所示电路可依次等效为图（a ）和图（b ），由图（b ）可求得A 2.15.023=+=I由图（a ）可求得：A 6.02.121213=×==I IΩ=1R V22=Ω=14R(b)Ω=12R2.6.1 在图2.19中，（1）当将开关S 合在a 点时，求电流1I ，2I 和3I ；（2）当将开关S 合在b 点时，利用（1）的结果，用叠加定理计算电流321,I I I 和 。
I图2.19I (a)I (b)解：（1）当将开关S 合在a 点时，图2.19所示电路即为图（a ），用支路电流法可得：=+=+=+12042130423231321I I I I I I I 解得：===A 25A 10A 15321I I I(2)开关S 合在b 点时，利用叠加原理图2.19所示电路可等效为图（a ）和图（b ），其中图（a ）电路中130V 和120V 两个电压源共同作用时所产生的电流已在（1）中求得，即：A 151=,I A 102=,I A 253=,I由图3（b ）可求得：A 642422202=+×+=,,I A 464241−=×+−=,,IA26422=×+=则：A 11415111=−=+=,,,I I IA 16610,222=+=+=,,I I IA 27225333=+=+=,,,I I I2.6.2 电路如图2.20（a ）所示，V 10ab ,,V 124321=====U R R R R E 。
电工第二章习题答案
I1
a
I2
I3
1
R2
d
c
R3
U S2
b 图 2.1 支路电流法
返 返回 回 上 上页 页 下 下页 页
第2章 电路的基本分析方法
2. 支路电流法求解电路的步骤 (1) 选定各支路电流的参考方向；
(2) 根据KCL对n个节点列写n-1节点电流方程； (3) 选定网孔绕行方向，对l-(n-1)个网孔列写 KVL方程； (4) 联立方程求解各支路电流。
R1
a
I 2'
IS
US
U
R2
US
R2
US I2 R1 R2
返 返回 回 上 上页 页 下 下页 页
b
(a) 完整电路
b
（b）电压源单独作用
图 2.3 叠加原理示意图
第2章 电路的基本分析方法
I1
R1
(2)Is单独作用时产生的电流
a
I2
I 1'
R1
a
I 2'
I 1"
R1
a
" I2
US
U
R I1 R2 IS R 1 R 2
1
a
1
U 例2.7电路如图 2.10所示，用戴维 南定理求电压U。 b (1)求开路电压U图 。 解： OC 2.9 戴维南定理求解例 2.4
S
R2
U OC
R2
R0
R0
U OC
I
R3
（1）开路电压
3
S
U 15 S U R 10 7 . 5 V OC 2 R R 10 10 1 2
b 2.8 图 2.8图 例 2.4 图
电路分析试题及答案（第二章）
电路分析试题及答案（第⼆章）节点、回路、⽀路分析法：1、如下图所⽰，应⽤节点电压法计算。
已知U s 1=60V ，U s 2=40V ，R 1=6Ω, 23456Ω，求I 1，I 2，I 3，I 4，I 5，I 6的值。
解：114432111111R U U R U R R R R s b a =-+++ 6246541111R U U R U R R R s a b =-???? ??++ U a =U b =24V ；I 1=6A ；I 2=2A ；I 3=4A ；I 4=0A ；I 5=4A ；I 6=-4A ；2、求下图电路的电压U.解：利⽤戴维南等效做，先求ab 两端开路电压：只有24V 的电压源⼯作时： U ‘ab =24/（6+3）=8V ；只有4A 的电流源⼯作时： U ‘‘ab =4×4=16V ； U ab = U ‘ab +U ‘‘ab =24V ；等效电阻R 0=6Ω；U= U ab /（6+2）×2=6V3、计算下图电路中的电压U 1与U 2.解：U 1=8×[4+(6//3)]/[18+4+(6//3)] ×18=36V; U 2=8×18/[18×4+(6//3)] ×3=12V .4、已知下图电路的回路⽅程为2I 1+I 2=4V 和4I 2=8V ，式中各电流的单位为安培。
求：（1）各元件的参数；（2）各电压源供出的功率；（3）改变U和U 的值，使各电阻的功率增加⼀倍。
解：（1）1+ R 3)I 1+R 3I 2+k U 1=Us 1 1+ R 3-k R 1)I 1+R 3I 2 =Us 1-k Us 1R 3I 1 + (R 2+ R 3)I 2+k U 1=Us 2U 1=Us 1- R 1I 1 3-k R 1) I 1+ (R 2+ R 3)I 2+k U 1=Us 2-k Us 1R 1=2Ω, R 2=3Ω, R 3=1Ω, Us 1=8V , Us 1=12V , k =0.5 （2）求解⽅程式，得到：I 1=1A, I 2=2A ，计算各电源功率：Us 1：P 1= Us 1 I 1=8W ； (发出) Us 2：P 2= Us 2 I 2=24W ；（发出） Ucs ：Pcs= Ucs (I 1+I 2)=9W ；（吸收）（3）各电源增加2倍，则各电阻上的电流相应增加2倍，即可实现⽬的。
电路理论习题答案 第二章
习题22.1选择题（1）C （2）D （3）A （4）C （5）B （6）C2.2简答题（1）因为P 1=100W I s2=-4A所以U s2=50VI 1=10A I r2=5AI A =2-（10-4+5）=-9A（2）11101020111136152020R =+=+=++ 所以i=6020=3 i 1＋i 2＝330 i 1＝15i 2i 2=2i 1i 1=1 i 2 =2i 1’=i 2’i 1’=(60-30)/20=1.5i 1+I=i 1’所以I=0.5A(3) ①有三个电容组成一个网络时有SCU(s)+SCU 1(s)=SC ’U(s)得 C ’=3/2C依次 可得如图所示输入端电容Ci=(n+1)/2(n 为电容所组成的网孔数) ②同理可得 Ri ＝2/(n+1) (n 为电阻所组成的网孔数)(4) L=L 11+L 22+2 M =16H(5) 设放大器副端电压为U 3 电流为i 2 正端为i 1 从R 1,R 2端流出得电流为i 则有图可得U 3＝0， i 1＝i 2＝001212+=fU U U i R R R =- 所以01212ff R R U U U R R =--R f /R 1=4 R f /R 2=7由此得R 1＝2.5K Ω,R 2＝10/7（K Ω）（6）设理想变压器输入端线圈电压为U1，输出端线圈电压为U2 有n 1/u 1= n 2/u 2得 u 1＝(n 1/n 2)×u 2＝3u 2n 1i 1+n 2i 2＝0得 i 1＝－（1/3）i 2Ri ＝U/i 1＝4i 1+U 1=4+(3U 2)/(－1/3 i 2)=4－9×（-23/3）=73 K Ω2.3（1）LTI ，双向、单调、有源电阻（2）非线性、时变、单调、有源电阻（3）非线性时不变、单调、单向、有源电容（4）非线性、时不变、单向、流控、有源电感（5）非线性、时不变、有向、有源电感、单调（6）非线性、时不变、单调、单向、有源电阻（7）非线性、时不变、压控、单向、无源电（电流）（8）非线性、时不变、单调、单向、有源电容（9）非线性、时不变、单调、有源电阻（10）非线性、时不变、单调、流控、有源电阻（11）非线性、时不变、荷控、有源电容（12）非线性、时不变、单调、有源电阻2.4①2121U ()U ()1 ()()2t t L di t di t dt dt=== ∴元件1 为电感 ②又2L C 1(0)(0)(0)25(0)252C W W W CU =+=+= 故Uc(0)=0,i 1(0)=i 1(t)t =0= -10A.设元件2 为电阻，则(0)(0) 1.5(0)C L U U R i --==Ω ③元件3 为电容，2111()(0)()(1010)0t t C C t U t U i d e e C Cττ--==-+⎰ 由KVL 又可得：Uc(t)=-U L (t)－U R (t)= －10e-t+10e-2t比较两式系数得C=1F .2.52.6（a ）P R =34 (w),P v =32 (w),P 1= －2（w ）,消耗功率来源于电流源。
电路分析答案 第二章
R2
∞
R1 us
R1
uo R2 us
∞
R3
uo
题图 2.32 解 u+ = u− = u S 由分压公式
题图 2.33
u− =
R2 uo R1 + R2
uo R = 1+ 1 uS R2
2.33 求图示电路的输入电压与输出电压的关系。 解：因为 Rin = ∞ ，所以
2.7 求题图 2.7 电路的等效电阻 Rx 。
R
Rx
R
Rx
10Ω
10Ω
∞
r
r
Rx
7.5Ω
7.5Ω
(a) 图题 2.7 解：(a) Rx = R + r // Rx 得到一个一元二次方程，求解后即有（仅取正根）
(b)
Rx = ( R + R 2 + 4 Rr ) / 2
(b)利用上面的公式，求得
Rx = 15Ω
t = 1s 时， i (1) = i (0) + t = 2 s 时， i (2) = i (1) + t = 3s 时， i (3) = i (2) + t = 4 s 时， i (4) = i (3) +
1 3 1 3 u (t )dt = 5 + ∫ 0dt = 5 A ∫ L 2 4 2
1 4 1 4 u (t )dt = 5 + ∫ (10dt − 40)dt = 3.75 A ∫ L 3 4 3 2.25 题图 2.25 为三端网络， 端子用 a , d , e 标记， 已知 R = 1Ω ，C = 0.1 F，L = 0.5 H，u ab = sin(10t ) V，
(完整版)电工2章
第2章 习题解答(部分)2.3.3 计算图2.13中的电流 I 3。
解: 用电源等值互换法将电流源变换成电压源，将电阻R 2和R 3合并成电阻R 23，其中 V R I U R S S 2125.043,2=⨯=⨯=Ω=参考方向如图2.34所示。
求电路中电流IA R R R U U I S 2.115.012143,211=+++=+++= I 即为原电路中R 1上流过的电流，用分流公式，可求原电路中I 3A I R R R I 6.02.11113223=⨯+=⨯+= 2.4.1 图2.16是两台发电机并联运行的电路。
已知E 1=230V , R 01=0.5Ω，E 2=226V , R 02=0.3 Ω,负载电阻R L =5.5Ω，试分别用支路电流法和结点电压法求各支路电流 。
解:（1）用支路电流法：各支路电流参考方向已画在图2.16中。
列结点电压方程 L I I I =+21列回路电压方程L L 0222LL 0111R I R I E R I R I E +=+=S Ω 图 2.13 习题2.3.3的图U S U 图解 2.34101202图2.16 习题2.4.1的图联立求解上述三各方程式组成的方程组，可得A 40A2021===L I I I验算：按非独立回路方程进行02201121R I R I E E -=-代入数据443.0205.020226230==⨯-⨯=- （正确！）（2）用结点电压法求解：先求端电压U ，有V 2205.513.015.013.02265.02301110201022011=+++=+++=L R R R R E R E U A 405.0220A 205.0220226A 205.022023002220111====-=-==-=-=L L R U I R U E I R U E I 结果与上相同。
2.5.1 试用结点电压法求图2.18所示电路中的各支路电流解:在原图2.18中用O 和O ’标明两个结点，则有A 5.0505025V 505015015015025501005025a O ,O'-=-==++++=I U A 5.0505025A 15050100c b -=-==-=I I 2.6.1 用叠加原理计算图2.19中各支路的电流。
《电力电子技术》第二章习题解答
2-1.一个开关器件的数据表的详细开关时间如下（对应图2.7(a)）所示固定感应开关的线性特性）：t ri =100ns ，t fv =50ns ，t rv =100ns ，t fi =200ns 。
试计算当频率范围为25~100khz 时的开关能量损失，并绘图。
假设图2.7(a)的电路中U d =300V ，I 0=4A 。
解：(1)先求出25s f kH z =时的开关能量损失T P 1)开关损耗：由： 7()150 1.510c on ri fv t t t ns s -=+==⨯7()300310c off rv fi t t t ns s -=+==⨯4()() 4.510s on off t tc tc s -=+=⨯得：470113004 2.510 4.5106.7522s d S s P U I f t w-=∙∙∙=⨯⨯⨯⨯⨯⨯=2)导通损耗：000on on on on s sU Vt P U I f t =∴=∙∙∙=3)关断损耗：01 4.52offd s off P U I f t w=∙∙∙=开关的平均能量损耗： 6.75T s o n s P P P P w =+== 开关损耗如图2-1(2)同理：当100s f K H z =时： 1)开关损耗：由： 7()150 1.510c on ri fv t t t ns s -=+==⨯7()300310c off rv fi t t t ns s -=+==⨯4()() 4.510s on off t tc tc s -=+=⨯570113004110 4.5102722s d S s P U I f t w-=∙∙∙=⨯⨯⨯⨯⨯⨯=2)导通损耗：000on on on on s sU Vt P U I f t =∴=∙∙∙=3)关断损耗：01182offd s off P U I f t w=∙∙∙=开关的平均能量损耗： 27T s on s P P P P w =+== 开关损耗如图2-2图2-1 图2-22-2.在下图的开关电路中，有U d =300V ，f V =100kHz ，R =75Ω。
电路分析第二章习题解答
i1
=
50 ＝5A R总
i2
=
−5 × 15 15 + 10
=
−3A
6．化简图题 2-6 所示各二端电路。
a
- 7Ω
3Ω
5V
+ 3A
1A b
（a）
a
3A
-
5V
+
+
2V
15Ω
-
b
（b）
a
a
-
5Ω
18Ω
5V
7Ω 12Ω
+
1A
10Ω
7A
+ 2A
10V -
20Ω
b
b
（c）
解： a) 电路等效为
图题 2-6
（d）
R
4Ω
25V
15Ω
6Ω 24Ω
4Ω
4Ω
图题 2-4
解： 原电路可等效为
R
I +
25V
i
+
u 15Ω
10Ω
Q P = 15 = i 2 ×15
根据分流公式
∴i = 1A u = 15V i = I × 10 = 2 I
15 + 10 5
∴ I = 5 i = 2.5A 2
R = 25 −15 = 4Ω 2.5
5．求图题 2-5 所示电路的i1和i2。
32Ω
6Ω
i1 4Ω
12Ω
50V 解： 原电路可等效为
15Ω i2 2Ω
图题 2-5
40Ω 30Ω 6Ω
i1
4Ω
50V
4Ω
15Ω
i2 2Ω
72Ω 5Ω
i1 4Ω
电工学第2章习题及答案
2.4.1 图所示电路原 已稳定。在 t = 0 时将开关 S 从 a 端换接到 b 端。试 求换路后的响应 iL 和 uL。24 V
2Ω
US
R2
6Ω
uL
iL L
1H
返 回
第2章 电路的暂态分析
2.4.2 图所示电路原 已处于稳态。试求 S 闭合 后的 i2 、iL 和 uL，并画出 其变化曲线。
i1
S
IS
R1
24 A
i2
1.5 Ω 3Ω
7Ω
R3
R2
iL L uL 0.4 H
a
S
b
R1
3Ω
2.4.3 图所示电路 原已处于稳态。在 t = 0 时将开关 S 从 a 端改合 到 b 端。试求换路后的 iL 和 uL，并说明是什么 响应。
U S1
6V
US2
6V 6Ω
3Ω
R3
iL L
R2 6 i1 (0) i L ( 0) 3 A 1.8 A R1 R2 46 R1 4 i 2 ( 0) i L ( 0) 3 A 1.2 A R1 R2 46
返 回练习题题集 下一页 上一题 下一题
U S 12 uL (0) A 3A R1 4
返 回练习题题集 上一页 上一题 下一题
第2章 电路的暂态分析
2.3.3 图所示电路原已稳定，求开关 S 闭合后的响应 uC 和 i1、 i2 ，并画出其变化曲线。
S
R1
i1
20 V
4kΩ
R3 iC
R2
1.6kΩ
US
uC
iC
C 2.5F
6kΩ
电工电子学第二章习题答案(2)
第二章电路分析基础2-1 电路如图所示，已知US1=24V，US2=16V，IS=1A，R1=R2=8Ω，R3=4Ω。
试用支路电流法求各支路电流。
解：该题有四条支路其中一条支路是恒流源（设恒流源两端电压为U IS），应列四个方程。
有两个节点，按KCL定理可列一个节点方程： I1+I2 =I S+I3有三个网孔按KVL定理可列三个回路方程：I1R1 =U S1+U ISI2R2 =U S2+U IS I2R2+I3R3 =U S2 U IS=I3R3 解之 I1=2A I2=1A I3=2A U S=8V2-2 电路如图所示。
已知I S=2A，U S=6V，R1=R2=3Ω，R3=R4=6Ω，用叠加原理求a、b两点之间电压U ab。
解：当电压源U S单独作用时，题图变如右图：Uab1=当电流源I S单独作用时，题图变如右图Uab2=3V Uab=Uab1+Uab2=2-3 电路如图所示。
已知R1=6Ω，R2=12Ω，R3=8Ω，R4=4Ω，R5=1电路中流经R3的电流I当电流源I S单独作用时，题图变如右图)(13844434AIRRRI=⨯+=+=''I=)(211AII=+=''+'2-4 在图示电路中，当U S=24V时，Uab=8v. 试用叠加原理求U S=0时的UabIs。
解：当电压源U S单独作用时，题图变如右图)(1841243ARRUI S=+=+='解：以知U S=24V时，Uab=8v.当U S、、I S1、I S2、单独作用时题图分别变作变作下图1、图2、图3由图1可得：Uab1=)(64244VRRUS-=-=⨯；由图2可得：Uab2=)(212411VRIRRISS=⨯；由图3可得：Uab3=)(41422VRIRISS=⨯；UabIs=Uab2+Uab3=8+6=14（V）2-5 用电源等效变换法求图示电路中6Ω电阻中的电流I。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第二章
2－2电路如图所示，其中电阻、电压源和电流源均已给定。
求： （1）电压u 2和电流i 2 ；
（2）若电阻R 1增大，问对哪些元件的电压、电流有影响？影响如何？
解： (1)
S
3232i R R R i += S
323
2222i R R R R i R u +=
=
(2) 若R 1增大，则 R 1上的电压增大，另外，R 1增大时还会影响电 流源电压，因为
S 2R i u u u u 1S -+= 2－4求图示各电路的等效电阻R ab ，其中R 1= R 2=1Ω，R 3= R 4=2Ω，R 5=4Ω，G 1= G 2=1S ，
R=2Ω。
解： (a)图中R 4短路，原电路等效为
Ω
=+
++=4.4R 1
R 1R 11R R 3215ab
(c) 原电路可变换为 i S
3 4 a R
5 (a) b R 3 a b
R 2
R 4
( f ) a b 2Ω
由于21R R ＝，43R R ＝，故K 闭合时的等效电阻ab R 与K 打开时的相等。
()()Ω=++=5.1R R R R R 4231ab
(f)将图中1Ω，1Ω，2Ω的Y 形（兰线示之），2Ω，2Ω，1Ω的Y 形分 别转化成等值的△形，则这个等值△形的电阻分别为
Ω=
⎪⎭⎫ ⎝⎛⨯++⎪⎭⎫ ⎝⎛
⨯++=∆9202212112121R ab
Ω=
⎪⎭⎫ ⎝⎛⨯++⎪⎭⎫ ⎝⎛
⨯++=∆21401222221111R ac Ω
==∆∆920
R R ab bc
则该电路的等效电阻为
Ω=++⎪⎭⎫ ⎝⎛+⨯=
+⨯+
+⎪
⎪⎭⎫ ⎝⎛+⨯+=∆
∆∆∆∆∆∆∆269.11920
214092019202140920R 2R 2R R R 2R 2R R R bc bc ac ab bc bc ac ab ab
2－9试问：
(1) 图a 中，R ab <16Ω还是R ab >16Ω； (2) 图b 中，R ab <16Ω还是R ab >16Ω；
(3) 图c 中，R ab <16Ω还是R ab >16Ω；为什么？
解：(1)利用电源的等效变换，图(a)电路可用下图电路等效。
其中
16u 98.0105i 98.0105u ab
33d ⨯⨯-=⨯⨯-= ab u 25.306-=
若u ab >0，则()3
d
ab 1105100u u i ⨯+-=>0 故R ab <16Ω
(2) 这时u d =306.25u ab >u ab ,则i 1<0，故R ab >16Ω
a 5K Ω
( c) a b 5K Ω (a) a b 5K Ω (b)
a b Ω
u d
(3)因16Ω与105K Ω电阻并联，显然 R ab <16Ω
2－10求图示电路的输入电阻R in ，其中全部电阻均为1Ω。
解：电路可按图(a) 、(b)进行等效转换
2i
由KVL 得 1ab i 1i 1u ⨯+⨯=
()i 3i 5.01i 1u 2ab -⨯++⨯=
又 i u R ab
in = 解方程得 Ω=4.0R in
0.5Ω (a)
0.5Ω
(b) i 2
a。