高考数学总复习 25 对数与对数函数但因为测试新人教B版

合集下载

高中数学第三章Ⅰ3.2对数与对数函数1第二课时同步练习新人教B版必修1

3.2 对数与对数函数（1）第2课时1．对于a>0，a≠1，下列说法中正确的是… ( )①若M ＝N ，则log a M ＝log a N ； ②若log a M ＝log a N ，则M ＝N ；③若log a M 2＝log a N 2，则M ＝N ；④若M ＝N ，则log a M 2＝log a N 2. A ．①与③ B．②与④ C ．② D．①②③④2．log 28＋log 218等于( )A.103B.83C ．0D ．6 3．若a>0，a≠1，x>0，y>0，x>y ，下列式子中正确的个数是( ) ①log a x·log a y ＝log a (x ＋y)； ②log a x －log a y ＝log a (x －y)；③log a xy＝log a x÷log a y ；④log a xy ＝log a x·log a y. A ．0 B ．1 C ．2 D ．34．若a ＝log 32，则用a 表示log 38－2log 36为________． 5．设log 34·log 48·log 8m ＝log 416，则m ＝________.1．若a>0，a≠1，x>y>0，n∈N *,则下列各式中：①(log a x)n ＝n·log a x ；②(log a x)n ＝log a x n；③log a x ＝－log a 1x ；④log a x log a y ＝log a x y ；⑤n log a x ＝1n ·log a x ；⑥1n log a x ＝log a n x ；⑦log a x ＝loga n x n；⑧log a x －y x ＋y ＝－log a x ＋y x －y.其中成立的有( )A ．3个B ．4个C ．5个D ．6个2．若y ＝log 56·log 67·log 78·log 89·log 910，则有( ) A ．y∈(0,1) B．y∈(1,2) C ．y∈(2,3) D．y ＝13．已知a 、b 、c 为非零实数，且3a ＝4b ＝6c，那么……( )A.1c ＝1a ＋1bB.2c ＝2a ＋1bC.1c ＝2a ＋2bD.2c ＝1a ＋2b4．若lg(x －y)＋lg(x ＋2y)＝lg2＋lgx ＋lgy ，则xy＝________.5．若lg2＝a ，lg3＝b ，则log 512＝________.6．已知lg2＝0.301 0，lg3＝0.477 1，求lg 45的值．7．已知log 3(x －1)＝log 9(x ＋5)，求x.1．(lg2)3＋(lg5)3＋3lg2·lg5的值为( ) A ．4 B ．1 C ．6 D ．32．若lnx －lny ＝a ，则ln(x 2)3－ln(y 2)3等于( )A.a 2 B ．a C.3a2D ．3a 3．如果方程lg 2x ＋(lg2＋lg3)lgx ＋lg2·lg3＝0的两根为lgx 1、lgx 2，那么x 1·x 2的值为… ( )A ．lg2·lg3 B．lg2＋lg3 C.16D ．－64.若x·log 34＝1，则4x ＋4－x等于( ) A.103 B ．6 C.83 D.1635．已知函数f(x)＝alog 2x ＋blog 3x ＋2且f(1200)＝4，则f(200)＝________.6．lg25＋23lg8＋lg5·lg20＋lg 22＝________.7．a>1，b>1，p ＝log b (log b a)log b a ，则a p＝________.8．设3x ＝4y＝36，求2x ＋1y的值．9．如果lgx ＋lgy lgx ＋lgx ＋lgy lgy ＋[lg(x －y)]2lgx·lgy＝0，求x ，y 及log 2(xy)的值．10．设a>0，a≠1，x 、y 满足log a x ＋3log x a －log x y ＝3，用log a x 表示log a y ，并求出当x 为何值时，log a y 取得最小值．答案与解析课前预习1．C 在①中，当M ＝N≤0时，log a M 与log a N 无意义，故①不成立；在②中，当log a M＝log a N 时，必有M ＝N>0成立，故②成立；在③中，当log a M 2＝log a N 2时，有M≠0，N≠0，且M 2＝N 2，即|M|＝|N|，但未必有M ＝N ，例如：M ＝2，N ＝－2时，有log a M 2＝log a N 2，但M≠N，∴③不成立；在④中，若M ＝N ＝0时，log a M 2与log a N 2均无意义，∴④不成立．2．C log 28＋log 218＝log 28×18＝log 21＝0.3．A4．a －2 log 38－2log 36＝3log 32－2(log 32＋log 33)＝3a －2(a ＋1)＝a －2.5．9 log 34·log 48·log 8m ＝lg4lg3·lg8lg4·lgm lg8＝lgmlg3，又log 416＝2，∴lgmlg3＝2.∴lgm＝2lg3＝lg32＝lg9.∴m＝9. 课堂巩固1．B 其中③⑥⑦⑧正确．①式中nlog a x ＝log a x n；②式中log a x n＝n·log a x ；④式中log a x y ＝log a x －log a y ；⑤式中1nlog a x ＝log a n x.2．B y ＝lg6lg5·lg7lg6·lg8lg7·lg9lg8·lg10lg9＝1lg5，∵lg5≈0.699 0，∴y≈1.43∈(1,2)．3．B 设3a ＝4b ＝6c＝k ，则a ＝log 3k ，b ＝log 4k ，c ＝log 6k ，得1a ＝log k 3，1b ＝log k 4，1c＝log k 6.所以2c ＝2a ＋1b.4．2 由对数的定义得⎩⎪⎨⎪⎧x －y>0，x ＋2y>0，x>0，y>0，又由原式可得(x －y)(x ＋2y)＝2xy ，即x 2－xy －2y 2＝0，∴(x y )2－xy －2＝0，解得x y ＝2或xy ＝－1(舍去)．5.2a ＋b 1－a log 512＝lg12lg5＝lg4＋lg3lg5＝2lg2＋lg31－lg2＝2a ＋b 1－a. 6．解：方法一：lg 45＝12lg45＝12lg 902＝12(lg90－lg2) ＝12(lg9＋lg10－lg2) ＝12(2lg3＋1－lg2) ＝lg3＋12－12lg2＝0.477 1＋0.5－0.150 5 ＝0.826 6.方法二：lg 45＝12lg45＝12lg(5×9)＝12(lg5＋lg9) ＝12(lg5＋2lg3)＝12(1－lg2＋2lg3) ＝12－12lg2＋lg3 ＝0.826 6. 点评：运算过程中要注意对数运算法则的正确运用，体会lg2＋lg5＝1性质的灵活运用．7．解：原方程可化为log 9(x －1)2＝log 9(x ＋5)，∴(x－1)2＝x ＋5. ∴x 2－3x －4＝0.∴x＝－1或x ＝4.将x ＝－1，x ＝4分别代入方程检验知：x ＝－1不合题意，舍去，∴x＝4.点评：对简单的对数方程，同底法是最基本的求解方法，利用log a N ＝loga n N n(N>0，n≠0)可得，计算过程中要注意等价变形，如本题中将log 3(x －1)化为log 9(x －1)2实质上是非等价变形，扩大了x 的取值范围，因此在解对数方程后要验根．课后检测1．B 原式＝(lg2＋lg5)(lg 22－lg2·lg5＋lg 25)＋3lg2·lg5＝lg 22－lg2·lg5＋lg 25＋3lg2·lg5＝(lg2＋lg5)2－3lg2·lg5＋3lg2·lg5 ＝1.2．D ln(x 2)3－ln(y 2)3＝3(ln x 2－ln y2)＝3(lnx －ln2－lny ＋ln2)＝3(lnx －lny)＝3a.3．C 由已知得lgx 1＝－lg2，lgx 2＝－lg3，∴x 1＝12，x 2＝13，∴x 1·x 2＝16.4．A ∵x·log 34＝1，∴x＝log 43，则4x ＋4－x＝4log 43＋4－log 43＝3＋13＝103.5．0 由f(1200)＝a·log 21200＋blog 31200＋2＝－alog 2200－blog 3200＋2＝4得alog 2200＋blog 3200＝－2，∴f(200)＝a·log 2200＋blog 3200＋2＝0.6．3 原式＝lg25＋lg823＋lg 102·lg(10×2)＋lg 22＝lg25＋lg4＋(lg10－lg2)(lg10＋lg2)＋lg 22＝lg100＋lg 210－lg 22＋lg 22＝2＋1＝3.点评：对于对数的运算性质要熟练掌握，并能够灵活运用，在求值过程中，要注意公式的正用和逆用．7．log b a 由对数换底公式，得log b (log b a)log b a＝log a (log b a)，∴p＝log a (log b a)．∴a p＝log b a.8．解：由3x ＝4y＝36，得x ＝log 336，y ＝log 436， ∴1x ＝1log 336＝log 363，1y ＝1log 436＝log 364. ∴2x ＋1y＝2log 363＋log 364＝log 36(32×4)＝1. 9．解：去分母得lgy(lgx ＋lgy)＋lgx(lgx ＋lgy)＋[lg(x －y)]2＝0，即(lgx ＋lgy)2＋[lg(x －y)]2＝0， ∴⎩⎪⎨⎪⎧lgx ＋lgy ＝0，lg(x －y)＝0. ∴⎩⎪⎨⎪⎧xy ＝1，x －y ＝1. ∴x，－y 是方程t 2－t －1＝0的两个实根．又x ，y>0，且x≠1，y≠1，x>y ，∴x＝5＋12，y ＝5－12.∴log 2(xy)＝log 21＝0.10．解：由换底公式得log a x ＋3·1log a x －log a y log a x ＝3，整理得log 2a x ＋3－log a y ＝3log a x ，∴log a y ＝log 2a x －3log a x ＋3＝(log a x －32)2＋34.∴当log a x ＝32，即x ＝a 32时，log a y 取最小值34.。

高中数学第三章基本初等函数(Ⅰ)3.2对数与对数函数(1)第一课时同步练习新人教B版必修1

3．2.1 对数及其运算第1课时1．若a 2＝N(a>0且a≠1)，则有( )A ．log 2N ＝aB ．log 2a ＝NC ．log N a ＝2D ．log a N ＝22．若log x 7y ＝z ，则( )A ．y 7＝x zB ．y ＝x 7zC ．y ＝7x zD ．y ＝z 7x3．21＋log 272的值等于( )A ．272B ．7 C.47D ．144．若log 16x ＝－14，则x ＝________；若(2)x＝12，则x ＝________.5．若log 2(x 2－4x ＋6)＝1，则x ＝________.1．有下列说法：①零和负数无对数；②3log 3(－5)＝－5成立；③任何一个指数式都可以化为对数式；④以10为底的对数叫做常用对数．其中正确命题的个数为( )A ．1个B ．2个C ．3个D ．4个2．下列指数式与对数式的互化中，不正确的一组是( )A ．100＝1与lg1＝0B ．27－13＝13与log 2713＝－13C ．log 39＝2与912＝3D ．log 55＝1与51＝53．在b ＝log (a －2)(5－a)中，实数a 的取值范围为…( ) A ．a>5或a<2 B ．2<a<5 C ．2<a<3或3<a<5 D ．3<a<44．计算3log 35＋3log315＝________.5．已知log 7[log 3(log 2x)]＝0，那么x －12＝________.6．已知log a 2＝m ，log a 3＝n ，求a 2m ＋n的值．7．求alog a b·log b c·log c N 的值．1．给出下列式子：①5log 512＝12；②πlogπ3－1＝13；③4log 4(－3)＝－3；④xlog x 6＝6.其中不正确的是( )A ．①③ B．②③ C．③④ D．②④ 2．下列命题正确的是( )①对数式log a N ＝b(a>0，且a≠1)和指数式a b＝N(a>0，且a≠1)是同一关系式的两种不同表达形式；②在同底条件下，对数式log a N ＝b 与指数式a b＝N 可以互相转化；③若a b＝N(a>0，且a≠1)，则alog a N ＝N 一定成立； ④对数的底数是任意正实数． A ．①② B．①②③④ C ．①②③ D．④3．以6为底，216336的对数等于( )A.73B.113C.92D ．2 4.设5lgx＝25，则x 的值等于( ) A ．10 B ．±10 C．100 D ．±100 5．log 6(log 4(log 381))＝________.6．log 3(1－2x9)＝1，则x ＝________.7．(1)求对数值：log 4381＝________；log 354625＝________.(2)求真数：log 3x ＝－34，则x ＝________；log 2x ＝78，则x ＝________.(3)求底数：log x 3＝－35，则x ＝________；log x 2＝78，则x ＝________.8．已知二次函数f(x)＝(lga)x 2＋2x ＋4lga 的最大值是3，求a 的值．9．已知log a b ＝log b a(a>0，a≠1；b>0，且b≠1)，求证：a ＝b 或a ＝1b.10．已知lga 和lgb 是关于x 的方程x 2－x ＋m ＝0的两个根，而关于x 的方程x 2－(lga)x －(1＋lga)＝0有两个相等的实数根，求实数a ，b 和m 的值．答案与解析课前预习1．D 由对数式与指数式的互化易得．2．B log x 7y ＝z ⇔x z ＝7y ，∴x 7z＝y.3．B 21＋log 272＝2·2log 272＝2·72＝7.4.12 －2 log 16x ＝－14⇔x ＝16－14＝12，(2)x ＝12⇔x ＝log 212＝log 2(2)－2＝－2. 5．2 由log 2(x 2－4x ＋6)＝1得x 2－4x ＋6＝2，即x 2－4x ＋4＝0，即(x －2)2＝0，∴x ＝2. 课堂巩固1．B ③错误，如(－1)2＝1就不能写成对数式．②错误，log 3(－5)无意义．2．C log 39＝2的指数式应为32＝9. 3．C 由对数的定义知⎩⎪⎨⎪⎧5－a>0，a －2>0，a －2≠1，解得⎩⎪⎨⎪⎧a<5，a>2，a≠3，∴2<a<3或3<a<5.4.655 ∵3log 35＝5，3log 315＝(3log 315)12＝(15)12＝55. ∴原式＝5＋55＝655. 5.24由已知得log 3(log 2x)＝1， ∴log 2x ＝3，则x ＝23.∴x－12＝2－32＝122＝24.6．解：∵log a 2＝m ，∴a m＝2.又log a 3＝n ，∴a n＝3. ∴a 2m ＋n ＝(a m )2·a n ＝22·3＝12.7．解：原式＝(alog a b)log b c·log c N ＝blog b c·log c N ＝(blog b c)log c N ＝clog c N ＝N. 点评：重复使用对数恒等式即可得解；对数恒等式alog a N ＝N 中要注意书写格式．课后检测1．C ③不正确，log 4(－3)无意义，∵负数和零无对数；④不正确，应在条件“x>0，且x≠1”的前提下计算．2．C ④中的底数应满足“大于0且不等于1”．3．A ∵216336＝63623＝63－23＝673，∴log 6216336＝log 6673＝73.4．C 5lgx ＝25，∴lgx＝2，即102＝x. ∴x＝100.5．0 原式＝log 6[log 4(log 334)] ＝log 6(log 44) ＝log 61＝0.6．－13 由已知得1－2x9＝3，∴x＝－13.7．(1)16 3 (2)1427278 (3)3－53 287(1)(43)16＝34＝81，∴log 4381＝16；∵(354)3＝625，∴log 354625＝3.(2)由题意可得x ＝3－34＝1427；由已知得x ＝278.(3)由已知得x －35＝3，∴x＝3－53；x 78＝2，∴x＝287.点评：对于对数和对数的底数与真数三者之间，已知其中两个就可求另外一个，关键是指数式与对数式的互化．8．解：∵f(x)的最大值为3，∴⎩⎪⎨⎪⎧lga<0，16lg 2a －44lga＝3⇒(4lga ＋1)(lga －1)＝0.∴lga＝1(舍去)或lga ＝－14.∴a＝10－14.9．证明：设log a b ＝log b a ＝k ，则b ＝a k ，a ＝b k，从而有b ＝(b k )k ＝bk 2.∵b>0，b≠1，∴k 2＝1，即k ＝±1.当k ＝－1时，a ＝1b；当k ＝1时，a ＝b.∴a＝b 或a ＝1b ，命题得证．10．解：由题意，得⎩⎪⎨⎪⎧ lga ＋lgb ＝1，lga·lgb＝m ，(lga)2＋4(1＋lga)＝0，①②③由③得(lga ＋2)2＝0，∴lga＝－2.∴a ＝1100.代入①得lgb ＝1－lga ＝3，∴b＝103＝1 000. 代入②得m ＝lga·lgb＝(－2)×3＝－6.∴a＝1100，b ＝1 000，m ＝－6.。

2023年人教版高考数学总复习第一部分考点指导第三章函数及其应用第六节对数、对数函数

eln x·eln y＝eln x＋ln y＝xy，故 D 错误．
2．(2021·开封模拟)若 2a＝5b＝zc，且1a ＋1b ＝1c ，则 z 的值可能为(
)
A． 7 B． 10 C．7 D．10
【解析】选 D.设 2a＝5b＝zc＝k，则 a＝log2k，b＝log5k，c＝logzk，所以a1 ＋1b ＝lo1g2k ＋log15k ＝logk2＋logk5＝logk(2×5)＝logk10＝1c ＝logkz，所以 z ＝10.
3．换底公式【1】 logab＝llooggccba (a>0，且 a≠1；c>0，且 c≠1；b>0).
换底公式的推论：①logab·logba＝1； ② logam bn ＝mn logab.
4．对数函数的图象与性质
y=logax
a>1
图象
定义域值域
性质
___(0__,+_∞__)___
过定点__(_1_,_0_)__,即x=1时,y=0 当x>1时,___y_>_0___;
1．如图，若 C1，C2 分别为函数 y＝logax 和 y＝logbx 的图象，则( )
A．0<a<b<1 C．a>b>1
B．0<b<a<1 D．b>a>1
【解析】选 B.作直线 y＝1，则直线与 C1，C2 的交点的横坐标分别为 a，b 易知 0<b<a<1.
2．函数 y＝2log4(1－x)的图象大致是( )
b a
lg c ·lg b
lg 3 ·lg c
＝2，即llgg
3 a
＝2，
所以 lg 3＝2lg a，所以 a2＝3，a＝ 3 .

2025年高考数学总复习课件13第二章第六节对数与对数函数

对数与对数函数
必备知识
落实“四基”
核心考点
提升“四能”
课时质量评价
【常用结论】
1.换底公式的变形
(1)logab·logba ＝ 1 ，即 logab ＝
1
a
，b均大于0且不等于1 ； 2 log am bn ＝
log b a
n
log M
log M
logab(a，b均大于0且不等于1，m≠0，n∈R)；(3)logNM＝ a ＝ b (a，
√
B．第二象限
C．第三象限
D．第四象限
A
核心考点
解析：函数f (x)＝loga(x＋2)(0<a<1)的图象如图所示．故选A．
课时质量评价
第六节
对数与对数函数
必备知识
落实“四基”
核心考点
提升“四能”
课时质量评价
(4，－1)
4．已知函数y＝loga(x－3)－1的图象恒过定点P，则点P的坐标是__________．
a
x单调递减，故排除B，D.
1
a
对于A，C，由函数f (x)＝ x 的图象，可知0<a<1，对于函数g(x)＝lg ，g(1)＝lg
a
a<0，故A正确，C错误．
x
第六节
对数与对数函数
必备知识
落实“四基”
核心考点
提升“四能”
2．已知函数f (x)＝|ln x|.若0<a<b，且f (a)＝f (b)，则2a＋b的取值范围是(
移、伸缩、对称变换得到所要求的函数图象．特别地，当底数与1的大小关系不
确定时应注意分类讨论．
第六节
对数与对数函数

2024届高考一轮复习数学教案(新人教B版)：对数与对数函数

§2.8对数与对数函数考试要求1.理解对数的概念及运算性质，能用换底公式将一般对数转化成自然对数或常用对数.2.通过实例，了解对数函数的概念，会画对数函数的图象，理解对数函数的单调性与特殊点.3.了解指数函数y ＝a x (a >0，且a ≠1)与对数函数y ＝log a x (a >0，且a ≠1)互为反函数．知识梳理1．对数的概念在表达式a b ＝N (a >0且a ≠1，N ∈(0，＋∞))中，当a 与N 确定之后，只有唯一的b 能满足这个式子，此时，幂指数b 称为以a 为底N 的对数，记作b ＝log a N ，其中a 称为对数的底数，N 称为对数的真数．以10为底的对数叫做常用对数，记作lg N .以e 为底的对数叫做自然对数，记作ln N .2．对数的性质与运算性质(1)对数的性质：log a 1＝0，log a a ＝1，log a N a ＝N (a >0，且a ≠1，N >0)．(2)对数的运算性质如果a >0，且a ≠1，M >0，N >0，那么：①log a (MN )＝log a M ＋log a N ；②log a MN ＝log a M －log a N ；③log a M n ＝n log a M (n ∈R ).(3)对数换底公式：log a b ＝log c blog c a (a >0，且a ≠1；b >0；c >0，且c ≠1)．3．对数函数的图象与性质a >10<a <1图象定义域(0，＋∞)值域R性过定点(1,0)，即x ＝1时，y ＝0质当x >1时，y >0；当0<x <1时，y <0当x >1时，y <0；当0<x <1时，y >0在(0，＋∞)上是增函数在(0，＋∞)上是减函数4.反函数一般地，如果在函数y ＝f(x )中，给定值域中任意一个y 的值，只有唯一的x 与之对应，那么x 是y 的函数，这个函数称为y ＝f (x )的反函数．常用结论1．log a b ·log b a ＝1，log m nab ＝n m log a b .2．如图给出4个对数函数的图象则b >a >1>d >c >0，即在第一象限，不同的对数函数图象从左到右底数逐渐增大．3．对数函数y ＝log a x (a >0，且a ≠1)的图象恒过点(1,0)，(a ,1)思考辨析判断下列结论是否正确(请在括号中打“√”或“×”)(1)若M ＝N ，则log a M ＝log a N .(×)(2)函数y ＝log a 2x (a >0，且a ≠1)是对数函数．(×)(3)对数函数y ＝log a x (a >0，且a ≠1)在(0，＋∞)上是增函数．(×)(4)函数y ＝log 2x 与y ＝121log x的图象重合．(√)教材改编题1．若函数f (x )＝log 2(x ＋1)的定义域是[0,1]，则函数f (x )的值域为()A ．[0,1]B ．(0,1)C ．(－∞，1]D ．[1，＋∞)答案A解析根据复合函数单调性同增异减可知f (x )在[0,1]上单调递增，因为0≤x ≤1，所以1≤x ＋1≤2，则log 21≤log 2(x ＋1)≤log 22，即f (x )∈[0,1]．2．函数y ＝log a (x －2)＋2(a >0，且a ≠1)的图象恒过点________．答案(3,2)解析∵log a 1＝0，令x －2＝1，∴x ＝3，y ＝2，∴函数的图象过定点(3,2)．3．e ln 2＋log 202216log 20224＝________.答案4解析e ln 2＋log 202216log 20224＝2＋log 416＝2＋2＝4.题型一对数式的运算例1(1)若2a ＝5b ＝10，则1a ＋1b 的值是()A ．－1 B.12C.710D ．1答案D解析由2a ＝5b ＝10，∴a ＝log 210，b ＝log 510，∴1a ＝lg 2，1b ＝lg 5，∴1a ＋1b＝lg 2＋lg 5＝lg 10＝1.(2)计算：log 535＋122log －log 5150－log 514＝________.答案2解析原式＝log 535－log 5150－log 514＋212log ＝log 535150×14＋12log 2＝log 5125－1＝log 553－1＝3－1＝2.思维升华解决对数运算问题的常用方法(1)将真数化为底数的指数幂的形式进行化简．(2)将同底对数的和、差、倍合并．(3)利用换底公式将不同底的对数式转化成同底的对数式，要注意换底公式的正用、逆用及变形应用．跟踪训练1(1)(2022·保定模拟)已知2a ＝3，b ＝log 85，则4a－3b＝________.答案925解析因为2a ＝3，所以a ＝log 23，又b ＝log 85，所以b ＝13log 25，所以a －3b ＝log 235，4a －3b ＝232log 52＝925.(2)(lg 5)2＋lg 2lg 5＋12lg 4－log 34×log 23＝________.答案－1解析原式＝lg 5(lg 5＋lg 2)＋12lg 4－2lg 2lg 3×lg 3lg 2＝lg 5＋lg 2－2＝1－2＝－1.题型二对数函数的图象及应用例2(1)已知函数f (x )＝log a (2x ＋b －1)(a >0，且a ≠1)的图象如图所示，则a ，b 满足的关系是()A ．0<a －11.函数图象与y 轴的交点坐标为(0，log a b )，由函数图象可知－1<log a b <0，解得1a 0，所以0<a <1，b >1，所以－ln a ＝ln b ，所以ln a ＋ln b ＝ln(ab )＝0，所以ab ＝1，则b ＝1a ，所以a ＋2b ＝a ＋2a ，令g (x )＝x ＋2x (0<x <1)，则g (x )在(0,1)上单调递减，所以g (x )>g (1)＝1＋2＝3，所以a ＋2b >3，所以a ＋2b 的取值范围为(3，＋∞)．思维升华对数函数图象的识别及应用方法(1)在识别函数图象时，要善于利用已知函数的性质、函数图象上的特殊点(与坐标轴的交点、最高点、最低点等)排除不符合要求的选项．(2)一些对数型方程、不等式问题常转化为相应的函数图象问题，利用数形结合法求解．跟踪训练2(1)已知lg a ＋lg b ＝0(a >0且a ≠1，b >0且b ≠1)，则函数f (x )＝a x 与g (x )＝1log bx的图象可能是()答案B解析∵lg a ＋lg b ＝0(a >0且a ≠1，b >0且b ≠1)，∴ab ＝1，∴a ＝1b，∴g (x )＝1log bx ＝log a x ，函数f (x )＝a x 与函数g (x )＝1log bx 互为反函数，x的图象关于直线y＝x对称，且具有相同的单调性．log∴函数f(x)＝a x与g(x)＝1b(2)(2023·濮阳模拟)已知a>0且a≠1，函数y＝a x的图象如图所示，则函数f(x)＝log a(－x＋1)的部分图象大致为()答案D解析由函数y＝a x的图象可得a>1.当a>1时，y＝log a x经过定点(1,0)，为增函数．因为y＝log a x与y＝log a(－x)关于y轴对称，所以y＝log a(－x)经过定点(－1,0)，为减函数．而f(x)＝log a(－x＋1)可以看作y＝log a(－x)的图象向右平移一个单位得到的，所以f(x)＝log a(－x＋1)的图象经过定点(0,0)，为减函数．结合选项可知选D.题型三对数函数的性质及应用命题点1比较对数式的大小例3(2023·武汉质检)已知a＝log30.5，b＝log3π，c＝log43，则a，b，c的大小关系是() A．a<b<c B．b<a<cC．a<clog33＝1，即b>1；0＝log41<log43<log44＝1，即0<c<1，∴a<c<b.命题点2解对数方程、不等式例4若log a(a＋1)<log a(2a)<0(a>0，且a≠1)，则实数a的取值范围是________．答案解析由题意log a(a＋1)<log a(2a)<log a1，>1，＋1<2a <1a <1，＋1>2a >1，解得14<a <1.命题点3对数函数的性质及应用例5(2023·郑州模拟)设函数f (x )＝ln|x ＋3|＋ln|x －3|，则f (x )()A ．是偶函数，且在(－∞，－3)上单调递减B ．是奇函数，且在(－3,3)上单调递减C ．是奇函数，且在(3，＋∞)上单调递增D ．是偶函数，且在(－3,3)上单调递增答案A解析函数f (x )的定义域为{x |x ≠±3}，f (x )＝ln|x ＋3|＋ln|x －3|＝ln|x 2－9|，令g (x )＝|x 2－9|，则f (x )＝ln g (x )，函数g (x )的单调区间由图象(图略)可知，当x ∈(－∞，－3)，x ∈(0,3)时，g (x )单调递减，当x ∈(－3,0)，x ∈(3，＋∞)时，g (x )单调递增，由复合函数单调性同增异减得单调区间．由f (－x )＝ln|(－x )2－9|＝ln|x 2－9|＝f (x )得f (x )为偶函数．思维升华求与对数函数有关的函数值域和复合函数的单调性问题，必须弄清三个问题：一是定义域；二是底数与1的大小关系；三是复合函数的构成．跟踪训练3(1)(2023·开封模拟)已知函数f (x )＝log a (6－ax )(a >0，且a ≠1)在(0,2)上单调递减，则实数a 的取值范围是()A ．(1,3]B ．(1,3)C ．(0,1)D ．(1，＋∞)答案A解析令t (x )＝6－ax ，因为a >0，所以t (x )＝6－ax 为减函数．又由函数f (x )＝log a (6－ax )在(0,2)上单调递减，可得函数t (x )＝6－ax >0在(0,2)上恒成立，且a >1，>1，－2a ≥0，解得1<a ≤3.(2)(2022·惠州模拟)若函数f (x )＝log 2－ax a >0，且a ≠1)有最小值，则实数a 的取值范围是________．答案(1，2)解析令u (x )＝x 2－ax ＋12＝＋12－a 24，则u (x )有最小值12－a 24，欲使函数f (x )＝log 2－ax ，－a 24>0，解得1<a <2，即实数a 的取值范围为(1，2)．课时精练1．函数f (x )＝log 0.5(2x －1)的定义域为()1 B.12，－∞，12D ．[1，＋∞)答案A解析由题意，要使函数f (x )＝log 0.5(2x －1)有意义，则满足log 0.5(2x －1)≥0，所以0<2x －1≤1，解得12<x ≤1，即函数f (x )1.2．若函数f (x )＝log a x (a >0，且a ≠1)的反函数的图象过点(1,3)，则f (log 28)等于()A ．－1B ．1C ．2D ．3答案B解析依题意，函数f (x )＝log a x (a >0，且a ≠1)的反函数，即函数y ＝a x 的图象过点(1,3)，则a ＝3，f (x )＝log 3x ，于是得f (log 28)＝log 3(log 28)＝log 33＝1，所以f (log 28)＝1.3．函数f (x )＝log 2(|x |－1)的图象为()答案A解析函数f (x )＝log 2(|x |－1)的定义域为(－∞，－1)∪(1，＋∞)，排除B ，C ；由f (－x )＝log 2(|－x |－1)＝log 2(|x |－1)＝f (x )，可知函数f (x )为偶函数，其图象关于y 轴对称，排除D.4．按照“碳达峰”“碳中和”的实现路径，2030年为碳达峰时期，2060年实现碳中和，到2060年，纯电动汽车在整体汽车中的渗透率有望超过70%，新型动力电池迎来了蓬勃发展的风口．Peukert 于1898年提出蓄电池的容量C (单位：Ah)，放电时间t (单位：h)与放电电流I (单位：A)之间关系的经验公式：C ＝I n ·t ，其中n 为Peukert 常数，为了测算某蓄电池的Peukert 常数n ，在电池容量不变的条件下，当放电电流I ＝20A 时，放电时间t ＝20h ；当放电电流I ＝30A 时，放电时间t ＝10h ．则该蓄电池的Peukert 常数n 大约为()(参考数据：lg 2≈0.30，lg 3≈0.48)A.43B.53C.83D ．2答案B解析根据题意可得C ＝20n ·20，C ＝30n ·10，两式相比得20n ·2030n ·10＝1，即23n ＝12，所以n ＝23321log log 22＝lg 2lg 32＝lg 2lg 3－lg 2≈0.30.48－0.3＝53.5．已知函数f (x )＝log 2(x ＋1)－|x |，则不等式f (x )>0的解集是()A ．(－1,1)B ．(0,1)C ．(－1,0)D ．∅答案B解析不等式f (x )>0⇔log 2(x ＋1)>|x |，分别画出函数y ＝log 2(x ＋1)和y ＝|x |的图象，由图象可知y ＝log 2(x ＋1)和y ＝|x |的图象有两个交点，分别是(0,0)和(1,1)，由图象可知log 2(x ＋1)>|x |的解集是(0,1)，即不等式f (x )>0的解集是(0,1)．6．(多选)已知函数f (x )＝|log a (x ＋1)|(a >1)，下列说法正确的是()A ．函数f (x )的图象恒过定点(0,0)B ．函数f (x )在区间(0，＋∞)上单调递减C ．函数f (x )在区间－12，1上的最小值为0D ．若对任意x ∈[1,2]，f (x )≥1恒成立，则实数a 的取值范围是(1,2]答案ACD解析将(0,0)代入函数f (x )＝|log a (x ＋1)|(a >1)，成立，故A 正确；当x ∈(0，＋∞)时，x ＋1∈(1，＋∞)，又a >1，所以f (x )＝|log a (x ＋1)|＝log a (x ＋1)，由复合函数单调性可知，当x ∈(0，＋∞)时，f (x )＝|log a (x ＋1)|＝log a (x ＋1)单调递增，故B 错误；当x ∈－12，1时，x ＋1∈12，2，所以f (x )＝|log a (x ＋1)|≥log a 1＝0，故C 正确；当x ∈[1,2]时，f (x )＝|log a (x ＋1)|＝log a (x ＋1)≥1恒成立，所以由函数为增函数知log a 2≥1，解得1<a ≤2，故D 正确．7．(2023·淮北模拟)2＋log 4＝______.答案10解析2＋4log 2log 2422＝＋＝4＋2＋4＝10.8．函数f (x )＝()log 2x 的最小值为________．答案－14解析依题意得f (x )＝12log 2x ·(2＋2log 2x )＝(log 2x )2＋log 2x 2x －14≥－14，当且仅当log 2x ＝－12，即x ＝22时等号成立，所以函数f (x )的最小值为－14.9．已知f (x )＝()213log 5.x ax a －＋(1)若a ＝2，求f (x )的值域；(2)若f (x )在(1，＋∞)上单调递减，求a 的取值范围．解(1)当a ＝2时，f (x )＝()213log 210x x －＋，令t ＝x 2－2x ＋10＝(x －1)2＋9，∴t ≥9，f (x )≤13log 9＝－2，∴f (x )的值域为(－∞，－2]．(2)令u (x )＝x 2－ax ＋5a ，∵y ＝13log u (x )为减函数，∴u (x )＝x 2－ax ＋5a 在(1，＋∞)上单调递增，1，4a >0，解得－14<a ≤2，∴a －14，2.10．(2023·南昌模拟)已知函数f (x )＝log 3(9x ＋1)＋kx 是偶函数．(1)求k ；(2)解不等式f (x )≥log 3(7·3x －1)．解(1)∵f (x )是偶函数，∴f (－x )＝f (x )，即log 3(9－x ＋1)－kx ＝log 3(9x ＋1)＋kx 对任意x ∈R 恒成立，∴2kx ＝log 3(9－x ＋1)－log 3(9x ＋1)＝log 39－x ＋19x ＋1＝log 33－2x ＝－2x ，∴k ＝－1.(2)由(1)得f (x )＝log 3(9x ＋1)－x ＝log 3(9x ＋1)－log 33x＝log 39x ＋13x ＝log 3(3x ＋3－x )，则不等式f (x )≥log 3(7·3x －1)等价于3x ＋3－x ≥7·3x －1>0，由7·3x －1>0，解得x >－log 37；由3x ＋3－x ≥7·3x －1，得6·(3x )2－3x －1≤0，得0<3x ≤12，即x ≤－log 32，综上，不等式的解集为(－log 37，－log 32]．11．若非零实数a ，b ，c 满足2a ＝3b ＝6c ＝k ，则()A.1a ＋1b ＝1c B.2a ＋2b ＝1cC.1a ＋1b ＝2cD.2a ＋1b ＝2c答案A 解析由已知，得2a ＝3b ＝6c ＝k ，得a ＝log 2k ，b ＝log 3k ，c ＝log 6k ，所以1a ＝log k 2，1b ＝log k 3，1c＝log k 6，而2×3＝6，所以1a ＋1b ＝1c.12．(多选)关于函数f (x )＝log 2x ＋log 2(4－x )，下列说法正确的是()A ．f (x )的最大值为1B ．f (x )在区间(0,2)上为增函数C ．f (x )的图象关于直线x ＝2对称D ．f (x )的图象关于点(2,0)对称答案BC 解析函数f (x )＝log 2x ＋log 2(4－x )＝log 2(4x －x 2)(0<x <4)，当x ＝2时，4x －x 2取到最大值4，故此时f (x )＝log 2x ＋log 2(4－x )取到最大值log 24＝2，A 错误；f (x )＝log 2(4x －x 2)(0<x <4)可以看作是由函数y ＝log 2u ，u ＝－x 2＋4x (0<x <4)复合而成，而y ＝log 2u 是定义域上的增函数，u ＝－x 2＋4x (0<x <4)在(0,2)上单调递增，在(2,4)上单调递减，故f (x )在区间(0,2)上为增函数，在(2,4)上为减函数，故B 正确；因为函数f (4－x )＝log 2(4－x )＋log 2x ＝f (x )，故f (x )的图象关于直线x ＝2对称，C 正确；因为f (4－x )＝log 2(4－x )＋log 2x ＝f (x )≠－f (x )，故f (x )的图象不关于点(2,0)对称，D 错误．13．已知函数f (x )的定义域为R ，图象恒过点(0,1)，对任意x 1，x 2∈R ，x 1≠x 2，都有f (x 1)－f (x 2)x 1－x 2>1，则不等式f (ln(e x －1))<1＋ln(e x －1)的解集为()A ．(ln 2，＋∞)B ．(－∞，ln 2)C ．(ln 2,1)D ．(0，ln 2)答案D 解析因为f (x 1)－f (x 2)x 1－x 2>1，不妨设x 1>x 2，则f (x 1)－x 1>f (x 2)－x 2，令g (x )＝f (x )－x ，则g (x )在R 上单调递增，又f (0)＝1，则不等式f (ln(e x －1))<1＋ln(e x －1)，等价于f (ln(e x －1))－ln(e x －1)<1＝f (0)－0，即g (ln(e x －1))<g (0)，所以ln(e x －1)<0，则0<e x －1<1，解得0<x <ln 2.14．(多选)已知函数f (x )2x |，0<x <2，2－8x ＋13，x ≥2，若f (x )＝a 有四个解x 1，x 2，x 3，x 4且满足x 1<x 2<x 3<x 4，则下列命题正确的是()A ．0<a <1B ．x 1＋2x 2∈(3，＋∞)C ．x 1＋x 2＋x 3＋x 4D ．x 4∈[4，＋∞)答案AC解析作函数f (x )2x |，0<x <2，2－8x ＋13，x ≥2的图象如图所示，f (x )＝a 有四个解，即y ＝a 与y ＝f (x )的图象有4个交点x 1，x 2，x 3，x 4且x 1<x 2<x 3<x 4，可得0<a <1，故选项A 正确；由图象可得x 1·x 2＝1，则1x 1＝x 2，∴x 1＋2x 2＝x 1＋2x 1，∵12<x 1<1，且1<x 2<2，对勾函数y ＝x ＋2x 在区间上单调递减，故当12<x 1<1时，x 1＋2x 2＝x 1＋2x 1∈B 错误；x 1＋x 2＝1x 1＋x 1，∵12<x 1<1，∴1x 1＋x 1∵x 3＋x 4＝8，∴x 1＋x 2＋x 3＋x 4C 正确；令x2－8x＋13＝0，解得x＝4±3，由图象可知x4∈(4＋3，6)，故选项D错误．。

高考数学总复习 2-5 对数与对数函数但因为测试新人教B版

高考数学总复习 2-5 对数与对数函数但因为测试新人教B 版1.(2011·广东高州市大井中学模拟)函数y ＝x ＋－x 2－3x ＋4的定义域为( )A ．(－4，－1)B ．(－4,1)C ．(－1,1)D ．(－1,1][答案] C[解析] 要使函数有意义，须⎩⎪⎨⎪⎧x ＋1>0－x 2－3x ＋4>0，∴⎩⎪⎨⎪⎧x >－1－4<x <1，∴－1<x <1. 2．函数y ＝l og 2|x |的图象大致为( )[答案] C[解析] 由|x |＝1时，y ＝0排除A 、B ；由x >0时，y ＝log 2x 为增函数，排除D ，选C. 3．(2011·浙江省“百校联盟”交流联考)已知0<a <1，log a (1－x )<log a x ，则( ) A ．0<x <1 B ．x <12C ．0<x <12D.12<x <1 [答案] C[解析] 由⎩⎪⎨⎪⎧1－x >0x >01－x >x解得0<x <12.4．(文)(2011·山东实验中学模拟)已知函数f (x )＝⎩⎪⎨⎪⎧13x ，x ≥3fx ＋，x <3，则f (2＋log 32)的值为( )A ．－227B.154C.227 D ．－54[答案] B[解析] ∵0＜log 32<1，∴2<2＋log 32<3，∴f (2＋log 32)＝f (3＋log 32)＝f (log 354)＝(13)log 354＝154.(理)(2011·北京朝阳一模)已知函数y ＝f (x )是奇函数，当x >0时，f (x )＝lg x ，则f (f (1100))的值等于( )A.1lg2 B ．－1lg2C ．lg2D ．－lg2[答案] D[解析] 当x <0时，－x >0，则f (－x )＝lg(－x )．又函数为奇函数，f (－x )＝－f (x )，∴f (x )＝－lg(－x )． ∴f (1100)＝lg 1100＝－2，f (f (1100))＝f (－2)＝－lg2.5．(文)(2011·天津文，5)已知a ＝log 23.6，b ＝log 43.2，c ＝log 43.6，则( ) A ．a >b >c B ．a >c >b C ．b >a >c D ．c >a >b[答案] B[解析] ∵a ＝log 23.6>1，c ＝log 43.6<1.∴a >c . 又∵c ＝log 43.6>log 43.2＝b .∴a >c >b .(理)(2011·重庆文，6)设a ＝log 13 12，b ＝log 13 23，c ＝log 334，则a 、b 、c 的大小关系是( )A ．a b 且a >0，b >0，又c <0.故c 0得x >3或x <2，由s ＝x 2－5x ＋6＝(x －52)2－14知s ＝x 2－5x ＋6在区间(3，＋∞)上是增函数，在区间(－∞，2)上是减函数，因此函数y ＝log 12 (x 2－5x ＋6)的单调增区间是(－∞，2)，选D.7．(2011·湖北重点中学联考)已知实数a 、b 满足等式log 12 a ＝log 13 b ，有下列四个关系式：①0<a a >1；③a ＝b ；④0<a <1013x ，x ≤0，那么不等式f (x )≥1的解集为________．[答案] {x |x ≤0或x ≥3}[解析] f (x )≥1化为⎩⎨⎧x >0log 3x ≥1或⎩⎪⎨⎪⎧x ≤013x≥1∴x ≥3或x ≤0.(理)(2011·浙江省宁波市“十校联考”)设a >0，a ≠1，函数f (x )＝ax 2＋x ＋1有最大值，则不等式log a (x －1)>0的解集为________．[答案] {x |1<x <2}[解析] ∵t ＝x 2＋x ＋1＝(x ＋12)2＋34≥34，f (x )＝ax 2＋x ＋1有最大值，∴0<a <1，∴不等式log a (x －1)>0化为0<x －1<1， ∴1<x <2.9．(2011·北京东城一模)设f (x )＝⎩⎪⎨⎪⎧2a x ，x ≤1，log a x 2－，x >1，且f (22)＝1，则f [f (2)]＝________. [答案] 6[解析] ∵f (22)＝log a [(22)2－1]＝log a 7＝1， ∴a ＝7.又f (2)＝log 73<1，∴f (f (2))＝2×7log 73＝2×3＝6.10．(文)(2010·南通模拟)已知函数f (x )＝log a (1－x )＋log a (x ＋3)(a >0，且a ≠1)． (1)求函数f (x )的定义域和值域；(2)若函数f (x )有最小值为－2，求a 的值．[解析] (1)由⎩⎪⎨⎪⎧1－x >0x ＋3>0得－3<x <1，所以函数的定义域为{x |－3<x <1}． f (x )＝log a (1－x )(x ＋3)，设t ＝(1－x )(x ＋3)＝4－(x ＋1)2，所以t ≤4，又t >0，则0<t ≤4.当a >1时，y ≤log a 4，值域为{y |y ≤log a 4}，当0<a <1时，y ≥log a 4，值域为{y |y ≥log a 4}． (2)由题意及(1)知：当0<a <1时，函数有最小值，所以log a 4＝－2，解得a ＝12.(理)已知函数f (x )＝log a (a x －1)(a >0且a ≠1)． (1)证明函数f (x )的图象在y 轴的一侧；(2)设A (x 1，y 1)，B (x 2，y 2)(x 1<x 2)是f (x )图象上两点，证明直线AB 的斜率大于0. [解析] (1)由a x －1>0，得a x >1.当a >1时，解得x >0，此时f (x )的图象在y 轴右侧；当0<a <1时，解得x <0，此时f (x )的图象在y 轴左侧． ∴对a >0且a ≠1的任意实数a ，f (x )的图象总在y 轴一侧． (2)①当a >1时，x >0，由0<x 1<x 2得，1<ax 1<ax 2，∴f (x 2)－f (x 1)＝log a (a x 2－1)－log a (a x 1－1)＝log a >0.直线AB 的斜率k AB ＝fx 2－fx 1x 2－x 1>0. ②当0<a <1时，由x 1<x 2<0得， a x 1>a x 2>1，f (x 2)－f (x 1)>0. 同上可得k AB >0.11.(2011·安徽省淮南市模拟)若x ∈(e －1,1)，a ＝ln x ，b ＝(12)ln x ，c ＝e ln x ，则( )A ．c >b >aB ．b >a >cC ．a >b >cD ．b >c >a[答案] D [解析] ∵x ∈(e－1,1)，∴a ＝ln x ∈(－1,0)；c ＝e ln x ＝x ∈(1e ，1)；b ＝(12)ln x ∈(1,2)．∴a <c 0时，log 2a ＝12，所以a ＝2，当a ≤0时，2a ＝12，所以a ＝－1.13．(2011·丹阳一模)已知函数f (x )＝⎩⎪⎨⎪⎧3x ＋1，x ≤0log 2x ，x >0，则使函数f (x )的图象位于直线y ＝1上方的x 的取值范围是________．[答案] {x |－1<x ≤0或x >2}[解析] 由y >1得，⎩⎪⎨⎪⎧ x ≤03x ＋1>1或⎩⎪⎨⎪⎧x >0log 2x >1，，∴－1<x ≤0或x >2.14．(2011·绍兴一模)已知偶函数f (x )在[0，＋∞)上单调递减，且f (lg x )＝f (1)，则x 的值等于________．[答案] 10或110[解析] ∵f (x )在[0，＋∞)上是单调函数，且为偶函数，又f (lg x )＝f (1)，∴lg x ＝±1，∴x ＝10或110.15．(文)已知函数f (x )＝log 4(4x ＋1)＋2kx (k ∈R)是偶函数． (1)求k 的值；(2)若方程f (x )＝m 有解，求m 的取值范围． [解析] (1)由函数f (x )是偶函数可知，f (－x )＝f (x )， ∴log 4(4x ＋1)＋2kx ＝log 4(4－x ＋1)－2kx ，即log 44x ＋14－x ＋1＝－4kx ，∴log 44x ＝－4kx ，∴x ＝－4kx ，即(1＋4k )x ＝0，对一切x ∈R 恒成立，∴k ＝－14.(2)由m ＝f (x )＝log 4(4x ＋1)－12x＝log 44x ＋12x ＝log 4(2x ＋12x )，∵2x >0，∴2x ＋12x ≥2，∴m ≥log 42＝12.故要使方程f (x )＝m 有解，m 的取值范围为[12，＋∞)．(理)(2011·金华模拟)设集合A ＝{x |2(log 12 x )2－7log 2x ＋3≤0}，若当x ∈A 时，函数f (x )＝log 2x 2a ·log 2x 4的最大值为2，求实数a 的值．[解析] ∵A ＝{x |2(log 2x )2－7log 2x ＋3≤0} ＝{x |12≤log 2x ≤3}＝{x |2≤x ≤8}，而f (x )＝(log 2x －a )(log 2x －2)＝(log 2x )2－(a ＋2)log 2x ＋2a ，令log 2x ＝t ，∵2≤x ≤8，∴12≤t ≤3.∴f (x )可转化为g (t )＝t 2－(a ＋2)t ＋2a ，其对称轴为直线t ＝a ＋22，①当t ＝a ＋22≤74，即a ≤32时，[g (t )]max ＝g (3)＝2⇒a ＝1，符合题意；②当t ＝a ＋22>74，即a >32时，[g (t )]max ＝g (12)＝2⇒a ＝116，符合题意．综上，a ＝1，或a ＝116.16．(2011·马鞍山市二检)设函数f (x )＝(1＋x )2－2ln(1＋x )．(1)若对任意的x ∈[0,1]，不等式f (x )－m ≤0都成立，求实数m 的最小值； (2)求函数g (x )＝f (x )－x 2－x 在区间[0,2]上的极值． [解析] (1)设f (x )在[0,1]的最大值为f (x )max ，依题意有f (x )max ≤m ，∵f ′(x )＝2(1＋x )－21＋x ＝2x 2＋4x 1＋x，当x ∈[0,1]时，f ′(x )≥0，故f (x )在[0,1]为增函数， f (x )max ＝f (1)＝4－2ln2，于是m ≥4－2ln2，即实数m 的最小值为4－2ln2.(2)g (x )＝f (x )－x 2－x ＝1＋x －2ln(1＋x )， g ′(x )＝1－21＋x ＝x －1x ＋1. 当x >1时，g ′(x )>0，当－1<x <1时，g ′(x )<0，故g (x )在[0,1]上是减函数，在(1,2]上是增函数，从而g (x )在[0,2]上的极小值为g (1)＝2－2ln2＝ln e 24.1．设a ＝lg e ，b ＝(lg e )2，c ＝lg e ，则( ) A ．a >b >c B ．a >c >b C ．c >a >b D ．c >b >a[答案] B[解析] ∵1<e <3，∴1<e <e <e 2<10， ∴0<lg e <1.则lg e ＝12lg e <lg e ，即c <a .∵c －b ＝12lg e －(lg e )2＝12lg e (1－2lg e )＝12lg e ·lg 10e2>0.∴c >b ，故选B. 2．已知0<a <1，log a m <log a n <0，则( )A ．1<n <mB ．1<m <nC ．m <n <1D ．n <m <1[答案] A[解析] 由0<a <1得函数y ＝log a x 为减函数．又由log a m <log a n <0＝log a 1，得m >n >1，故应选A.3．(2011·四川文，4)函数y ＝(12)x ＋1的图象关于直线y ＝x 对称的图象大致是( )[答案] A [解析]解法一：作y ＝(12)x 的图象，然后向上平移1个单位，得y ＝(12)x ＋1的图象，再把图象关于y ＝x 对称即可．解法二：令x ＝0得y ＝2，∴对称图象过点(2,0)，排除C 、D ；又令x ＝－1得y ＝3，∴对称图象过点(3，－1)，排除B ，故选A.4．函数f (x )＝|log 12x |的图象是( )[答案] A[解析] f (x )＝|log 12x |＝|log 2x |＝⎩⎪⎨⎪⎧log 2x x －log 2xx，故选A.[点评] 可用筛选取求解，f (x )的定义域为{x |x >0}，排除B 、D ，f (x )≥0，排除C ，故选A.5．已知函数f (x )＝log m (x ＋1)，且m >1，a >b >c >0，则fa a ，fb b ，fcc 的大小关系是( )A.fa a >fb b >fc cB.fc c >fb b >fa aC.fb b >fc c >fa aD.fa a >fc c >fb b[答案] B[解析] 本题考查数形结合思想，fxx可以转化成f (x )上的点与原点连线的斜率，据函数y ＝log 2(x ＋1)的图象，设A (a ，f (a ))，B (b ，f (b ))，C (c ，f (c ))，显然k OA <k OB <k OC ， ∴fa a ＜fb b ＜fcc，故选B. 6．定义在R 上的奇函数f (x )满足：当x >0时，f (x )＝2012x ＋log 2012x ，则方程f (x )＝0的实根的个数为( )A ．1B ．2C ．3D ．5 [答案] C[解析] 当x >0时，f (x )＝0即2012x ＝－log 2012x ，在同一坐标系下分别画出函数f 1(x )＝2012x ，f 2(x )＝－log 2012x 的图象(图略)，可知两个图象只有一个交点，即方程f (x )＝0只有一个实根，又因为f (x )是定义在R 上的奇函数，所以当x <0时，方程f (x )＝0也有一个实根，又因为f (0)＝0，所以方程f (x )＝0的实根的个数为3.7．方程log 3(x 2－10)＝1＋log 3x 的解是________． [答案] x ＝5[解析] 原方程化为log 3(x 2－10)＝log 3(3x )，由于log 3x 在(0，＋∞)上严格单增，则x 2－10＝3x ，解之得x 1＝5，x 2＝－2.∵要使log 3x 有意义，应有x >0，∴x ＝5.8．(2011·上海交大附中月考)函数f (x )＝lg(x ＋ax －6)(a ∈R)的值域为R ，则实数a 的取值范围是________．[答案] (－∞，9][解析] ①a ≤0时，x ＋ax －6能取遍一切正数，∴f (x )的值域为R ；②a >0时，要使f (x )的值域为R ，应使x ＋a x －6可以取到所有正数，故x >0时，x ＋ax －6的最小值2a －6≤0，∴0<a ≤9，综上a ≤9.。

人教B版高一数学上册第三单元知识点：对数与对数函数_知识点总结

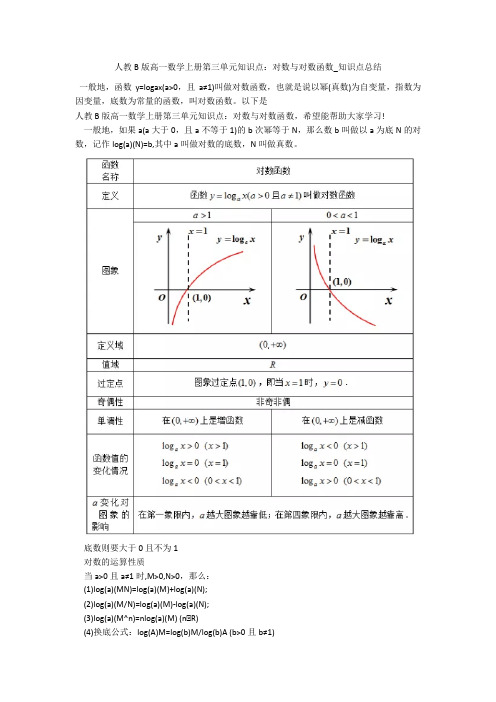
人教B版高一数学上册第三单元知识点：对数与对数函数_知识点总结一般地，函数y=logax(a>0，且a≠1)叫做对数函数，也就是说以幂(真数)为自变量，指数为因变量，底数为常量的函数，叫对数函数。

以下是人教B版高一数学上册第三单元知识点：对数与对数函数，希望能帮助大家学习!一般地，如果a(a大于0，且a不等于1)的b次幂等于N，那么数b叫做以a为底N的对数，记作log(a)(N)=b,其中a叫做对数的底数，N叫做真数。

底数则要大于0且不为1对数的运算性质当a>0且a≠1时,M>0,N>0，那么：(1)log(a)(MN)=log(a)(M)+log(a)(N);(2)log(a)(M/N)=log(a)(M)-log(a)(N);(3)log(a)(M^n)=nlog(a)(M) (n∈R)(4)换底公式：log(A)M=log(b)M/log(b)A (b>0且b≠1)对数与指数之间的关系当a>0且a≠1时,a^x=N x=㏒(a)N常用简略表达方式(1)常用对数:lg(b)=log(10)(b)(2)自然对数:ln(b)=log(e)(b)(3) log(a)+(b)=log(a)(b)e=2.718281828...通常情况下只取e=2.71828对数函数的定义对数函数的一般形式为y=㏒(a)x，它实际上就是指数函数的反函数(图象关于直线y=x对称的两函数互为反函数)，可表示为x=a^y。

因此指数函数里对于a的规定(a>0且a≠1)，同样适用于对数函数。

右图给出对于不同大小a所表示的函数图形：可以看到对数函数的图形只不过的指数函数的图形的关于直线y=x的对称图形，因为它们互为反函数。

定义域：(0，+∞)值域：实数集R定点：函数图像恒过定点(1，0)。

单调性：a>1时，在定义域上为单调增函数，并且上凸;0奇偶性：非奇非偶函数周期性：不是周期函数零点：x=1知识拓展：16世纪末至17世纪初的时候，当时在自然科学领域(特别是天文学)的发展上经常遇到大量精密而又庞大的数值计算，于是数学家们为了寻求化简的计算方法而发明了对数。

对数与对数函数-2025高考数学复习

高考一轮总复习 • 数学
[解析] 因为 a＝log36＝1＋log32，b＝1＋2log52，
②logaMN ＝_l_o_g_a_M_－__l_o_g_a_N__； ③logaMn＝_n__lo_g_a_M__(n∈R)．
第二章函数概念与基本初等函数Ⅰ
高考一轮总复习 • 数学
返回导航
知识点二对数函数的图象与性质 1．对数函数的定义、图象和性质
定义
函数___y_＝__lo_g_a_x_(_a_＞__0_，__且__a_≠_1_)___叫做对数函数
a＞1
0＜a＜1
图象
第二章函数概念与基本初等函数Ⅰ
高考一轮总复习 • 数学
返回导航
性质
定义域：___(_0_，__＋__∞__) ________ 值域：____(－__∞__，__＋__∞_)______
当x＝1时，y＝0，即过定点____(_1_,_0_) ______
当0＜x＜1时，y<0；当x＞1时，____y_＞__0______
5 log4 3
5
＝log2 8＝3log2 3，所以 a－3b＝log2 5－log2 3＝log2 3＝ log4 2 ＝2log4 3＝
25 log4 9 ，所以 4a－3b＝
25 ＝ 9 ，故选 C.
第二章函数概念与基本初等函数Ⅰ
高考一轮总复习 • 数学
返回导航
8 ． (2017·全国卷 Ⅱ ) 函数 f(x) ＝ ln(x2 － 2x － 8) 的单调递增区间是
1 ＝2，∴a<c<b.故选 C.
第二章函数概念与基本初等函数Ⅰ
返回导航
考点突破 · 互动探究

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

1.(2011·广东高州市大井中学模拟)函数y ＝lnx ＋1－x 2－3x ＋4的定义域为( ) A ．(－4，－1) B ．(－4,1) C ．(－1,1) D ．(－1,1][答案] C[解析] 要使函数有意义，须⎩⎪⎨⎪⎧x ＋1>0－x 2－3x ＋4>0，∴⎩⎪⎨⎪⎧x >－1－4<x <1，∴－1<x <1.2．函数y ＝log 2|x |的图象大致为( )[答案] C[解析] 由|x |＝1时，y ＝0排除A 、B ；由x >0时，y ＝log 2x 为增函数，排除D ，选C. 3．(2011·浙江省“百校联盟”交流联考)已知0<a <1，log a (1－x )<log a x ，则( ) A ．0<x <1 B ．x <12C ．0<x <12D.12<x <1 [答案] C [解析] 由⎩⎪⎨⎪⎧1－x >0x >01－x >x解得0<x <12.4．(文)(2011·山东实验中学模拟)已知函数f (x )＝⎩⎪⎨⎪⎧13x ，x ≥3f x ＋1，x <3，则f (2＋log 32)的值为( )A ．－227B.154C.227D ．－54[答案] B[解析] ∵0＜log 32<1，∴2<2＋log 32<3，∴f (2＋log 32)＝f (3＋log 32)＝f (log 354)＝(13)log 354＝154.(理)(2011·北京朝阳一模)已知函数y ＝f (x )是奇函数，当x >0时，f (x )＝lg x ，则f (f (1100))的值等于( ) A.1lg2B ．－1lg2C ．lg2D ．－lg2[答案] D[解析] 当x <0时，－x >0，则f (－x )＝lg(－x )．又函数为奇函数，f (－x )＝－f (x )，∴f (x )＝－lg(－x )． ∴f (1100)＝lg 1100＝－2，f (f (1100))＝f (－2)＝－lg2.5．(文)(2011·天津文，5)已知a ＝log 23.6，b ＝log 43.2，c ＝log 43.6，则( ) A ．a >b >c B ．a >c >b C ．b >a >c D ．c >a >b[答案] B[解析] ∵a ＝log 23.6>1，c ＝log 43.6<1.∴a >c . 又∵c ＝log 43.6>log 43.2＝b .∴a >c >b .(理)(2011·重庆文，6)设a ＝log 13 12，b ＝log 13 23，c ＝log 334，则a 、b 、c 的大小关系是( )A ．a b 且a >0，b >0，又c <0.故c 0得x >3或x <2，由s ＝x 2－5x ＋6＝(x －52)2－14知s ＝x 2－5x ＋6在区间(3，＋∞)上是增函数，在区间(－∞，2)上是减函数，因此函数y ＝log 12 (x 2－5x ＋6)的单调增区间是(－∞，2)，选D.7．(2011·湖北重点中学联考)已知实数a 、b 满足等式log 12 a ＝log 13 b ，有下列四个关系式：①0<a a >1；③a ＝b ；④0<a <1013x，x ≤0，那么不等式f (x )≥1的解集为________．[答案] {x |x ≤0或x ≥3}[解析] f (x )≥1化为⎩⎪⎨⎪⎧x >0log 3x ≥1或⎩⎪⎨⎪⎧x ≤013x≥1∴x ≥3或x ≤0.(理)(2011·浙江省宁波市“十校联考”)设a >0，a ≠1，函数f (x )＝ax 2＋x ＋1有最大值，则不等式log a (x －1)>0的解集为________．[答案] {x |1<x <2}[解析] ∵t ＝x 2＋x ＋1＝(x ＋12)2＋34≥34，f (x )＝ax 2＋x ＋1有最大值，∴0<a <1，∴不等式log a (x －1)>0化为0<x －1<1， ∴1<x <2.9．(2011·北京东城一模)设f (x )＝⎩⎪⎨⎪⎧2a x，x ≤1，log a x 2－1，x >1，且f (22)＝1，则f [f (2)]＝________.[答案] 6[解析] ∵f (22)＝log a [(22)2－1]＝log a 7＝1， ∴a ＝7.又f (2)＝log 73<1，∴f (f (2))＝2×7log 73＝2×3＝6.10．(文)(2010·南通模拟)已知函数f (x )＝log a (1－x )＋log a (x ＋3)(a >0，且a ≠1)． (1)求函数f (x )的定义域和值域；(2)若函数f (x )有最小值为－2，求a 的值．[解析] (1)由⎩⎪⎨⎪⎧1－x >0x ＋3>0得－3<x <1，所以函数的定义域为{x |－3<x <1}．f (x )＝log a (1－x )(x ＋3)，设t ＝(1－x )(x ＋3)＝4－(x ＋1)2，所以t ≤4，又t >0，则0<t ≤4.当a >1时，y ≤log a 4，值域为{y |y ≤log a 4}，当0<a <1时，y ≥log a 4，值域为{y |y ≥log a 4}． (2)由题意及(1)知：当0<a <1时，函数有最小值，所以log a 4＝－2，解得a ＝12.(理)已知函数f (x )＝log a (a x－1)(a >0且a ≠1)． (1)证明函数f (x )的图象在y 轴的一侧；(2)设A (x 1，y 1)，B (x 2，y 2)(x 1<x 2)是f (x )图象上两点，证明直线AB 的斜率大于0. [解析] (1)由a x－1>0，得a x >1.当a >1时，解得x >0，此时f (x )的图象在y 轴右侧；当0<a <1时，解得x <0，此时f (x )的图象在y 轴左侧． ∴对a >0且a ≠1的任意实数a ，f (x )的图象总在y 轴一侧． (2)①当a >1时，x >0，由0<x 1<x 2得，1<ax 1<ax 2，∴f (x 2)－f (x 1)＝log a (a x 2－1)－log a (a x 1－1)＝log a >0.直线AB 的斜率k AB ＝f x 2－f x 1x 2－x 1>0.②当0<a <1时，由x 1<x 2<0得，a x 1>a x 2>1，f (x 2)－f (x 1)>0.同上可得k AB >0.11.(2011·安徽省淮南市模拟)若x ∈(e －1,1)，a ＝ln x ，b ＝(12)ln x ，c ＝e ln x，则( )A ．c >b >aB ．b >a >cC ．a >b >cD ．b >c >a[答案] D [解析] ∵x ∈(e－1,1)，∴a ＝ln x ∈(－1,0)；c ＝e ln x ＝x ∈(1e ，1)；b ＝(12)ln x ∈(1,2)．∴a <c 02xx ≤0，若f (a )＝12，则实数a 等于( )A ．－1 B. 2 C ．－1或 2 D ．1或－ 2[答案] C[解析] 当a >0时，log 2a ＝12，所以a ＝2，当a ≤0时，2a＝12，所以a ＝－1.13．(2011·丹阳一模)已知函数f (x )＝⎩⎪⎨⎪⎧3x ＋1，x ≤0log 2x ，x >0，则使函数f (x )的图象位于直线y ＝1上方的x 的取值范围是________．[答案] {x |－1<x ≤0或x >2}[解析] 由y >1得，⎩⎪⎨⎪⎧x ≤03x ＋1>1或⎩⎪⎨⎪⎧x >0log 2x >1，，∴－1<x ≤0或x >2.14．(2011·绍兴一模)已知偶函数f (x )在[0，＋∞)上单调递减，且f (lg x )＝f (1)，则x 的值等于________．[答案] 10或110[解析] ∵f (x )在[0，＋∞)上是单调函数，且为偶函数，又f (lg x )＝f (1)，∴lg x ＝±1，∴x ＝10或110.15．(文)已知函数f (x )＝log 4(4x＋1)＋2kx (k ∈R)是偶函数． (1)求k 的值；(2)若方程f (x )＝m 有解，求m 的取值范围．[解析] (1)由函数f (x )是偶函数可知，f (－x )＝f (x )， ∴log 4(4x ＋1)＋2kx ＝log 4(4－x＋1)－2kx ，即log 44x＋14－x ＋1＝－4kx ，∴log 44x＝－4kx ，∴x ＝－4kx ，即(1＋4k )x ＝0，对一切x ∈R 恒成立，∴k ＝－14.(2)由m ＝f (x )＝log 4(4x＋1)－12x＝log 44x＋12x ＝log 4(2x＋12x )，∵2x >0，∴2x＋12x ≥2，∴m ≥log 42＝12.故要使方程f (x )＝m 有解，m 的取值范围为[12，＋∞)．(理)(2011·金华模拟)设集合A ＝{x |2(log 12x )2－7log 2x ＋3≤0}，若当x ∈A 时，函数f (x )＝log 2x 2a ·log 2x4的最大值为2，求实数a 的值．[解析] ∵A ＝{x |2(log 2x )2－7log 2x ＋3≤0} ＝{x |12≤log 2x ≤3}＝{x |2≤x ≤8}，而f (x )＝(log 2x －a )(log 2x －2)＝(log 2x )2－(a ＋2)log 2x ＋2a ，令log 2x ＝t ，∵2≤x ≤8，∴12≤t ≤3.∴f (x )可转化为g (t )＝t 2－(a ＋2)t ＋2a ，其对称轴为直线t ＝a ＋22，①当t ＝a ＋22≤74，即a ≤32时， [g (t )]max ＝g (3)＝2⇒a ＝1，符合题意； ②当t ＝a ＋22>74，即a >32时， [g (t )]max ＝g (12)＝2⇒a ＝116，符合题意．综上，a ＝1，或a ＝116.16．(2011·马鞍山市二检)设函数f (x )＝(1＋x )2－2ln(1＋x )．(1)若对任意的x ∈[0,1]，不等式f (x )－m ≤0都成立，求实数m 的最小值； (2)求函数g (x )＝f (x )－x 2－x 在区间[0,2]上的极值． [解析] (1)设f (x )在[0,1]的最大值为f (x )max ，依题意有f (x )max ≤m ，∵f ′(x )＝2(1＋x )－21＋x ＝2x 2＋4x1＋x，当x ∈[0,1]时，f ′(x )≥0，故f (x )在[0,1]为增函数，f (x )max ＝f (1)＝4－2ln2，于是m ≥4－2ln2，即实数m 的最小值为4－2ln2.(2)g (x )＝f (x )－x 2－x ＝1＋x －2ln(1＋x )，g ′(x )＝1－21＋x ＝x －1x ＋1. 当x >1时，g ′(x )>0，当－1<x <1时，g ′(x )<0，故g (x )在[0,1]上是减函数，在(1,2]上是增函数，从而g (x )在[0,2]上的极小值为g (1)＝2－2ln2＝ln e 24.1．设a ＝lg e ，b ＝(lg e )2，c ＝lg e ，则( ) A ．a >b >c B ．a >c >b C ．c >a >b D ．c >b >a[答案] B[解析] ∵1<e <3，∴1<e <e <e 2<10， ∴0<lg e <1.则lg e ＝12lg e <lg e ，即c <a .∵c －b ＝12lg e －(lg e )2＝12lg e (1－2lg e )＝12lg e ·lg 10e 2>0.∴c >b ，故选B. 2．已知0<a <1，log a m <log a n <0，则( ) A ．1<n <m B ．1<m <n C ．m <n <1 D ．n <m <1[答案] A[解析] 由0<a <1得函数y ＝log a x 为减函数．又由log a m <log a n <0＝log a 1，得m >n >1，故应选A.3．(2011·四川文，4)函数y ＝(12)x＋1的图象关于直线y ＝x 对称的图象大致是( )[答案] A [解析]解法一：作y ＝(12)x 的图象，然后向上平移1个单位，得y ＝(12)x＋1的图象，再把图象关于y ＝x 对称即可．解法二：令x ＝0得y ＝2，∴对称图象过点(2,0)，排除C 、D ；又令x ＝－1得y ＝3，∴对称图象过点(3，－1)，排除B ，故选A.4．函数f (x )＝|log 12x |的图象是( )[答案] A[解析] f (x )＝|log 12x |＝|log 2x |＝⎩⎪⎨⎪⎧log 2x x ≥1－log 2x0<x <1，故选A.[点评] 可用筛选取求解，f (x )的定义域为{x |x >0}，排除B 、D ，f (x )≥0，排除C ，故选A.5．已知函数f (x )＝log m (x ＋1)，且m >1，a >b >c >0，则f a a ，f b b ，f cc的大小关系是( )A.f a a >f b b >f cc B.f c c >f b b >f aa C.f b b >f c c >f aaD.f a a >f c c >f bb[答案] B[解析] 本题考查数形结合思想，f xx可以转化成f (x )上的点与原点连线的斜率，据函数y ＝log 2(x ＋1)的图象，设A (a ，f (a ))，B (b ，f (b ))，C (c ，f (c ))，显然k OA <k OB <k OC ， ∴f a a ＜f b b ＜f cc，故选B. 6．定义在R 上的奇函数f (x )满足：当x >0时，f (x )＝2012x＋log 2012x ，则方程f (x )＝0的实根的个数为( )A ．1B ．2C ．3D ．5 [答案] C[解析] 当x >0时，f (x )＝0即2012x＝－log 2012x ，在同一坐标系下分别画出函数f 1(x )＝2012x，f 2(x )＝－log 2012x 的图象(图略)，可知两个图象只有一个交点，即方程f (x )＝0只有一个实根，又因为f (x )是定义在R 上的奇函数，所以当x <0时，方程f (x )＝0也有一个实根，又因为f (0)＝0，所以方程f (x )＝0的实根的个数为3.7．方程log 3(x 2－10)＝1＋log 3x 的解是________． [答案] x ＝5[解析] 原方程化为log 3(x 2－10)＝log 3(3x )，由于log 3x 在(0，＋∞)上严格单增，则x 2－10＝3x ，解之得x 1＝5，x 2＝－2.∵要使log 3x 有意义，应有x >0，∴x ＝5.8．(2011·上海交大附中月考)函数f (x )＝lg(x ＋ax－6)(a ∈R)的值域为R ，则实数a 的取值范围是________．[答案] (－∞，9][解析] ①a ≤0时，x ＋a x－6能取遍一切正数， ∴f (x )的值域为R ；②a >0时，要使f (x )的值域为R ，应使x ＋a x －6可以取到所有正数，故x >0时，x ＋a x－6的最小值2a －6≤0，∴0<a ≤9，综上a ≤9.。